Numerical modeling of susceptibility-related MR signal dephasing with vessel size measurement: Phantom validation at 3T

Abstract

Purpose

MRI is used to obtain quantitative oxygenation and blood volume information from the susceptibility-related MR signal dephasing induced by blood vessels. However, analytical models that fit the MR signal are usually not accurate over the range of small blood vessels. Moreover, recent studies have demonstrated limitations in the simultaneous assessment of oxygenation and blood volume. In this study, a multi-parametric MRI framework that aims to measure vessel radii in addition to magnetic susceptibility and volume fraction was introduced.

Methods

The protocol consisted of gradient-echo sampling of the spin-echo, diffusion, T2 and B0 acquisitions. After correction steps, the data were post-processed with a versatile numerical model of the MR signal. An important analytical model was implemented for comparison. The approach was validated in phantoms with coiling strings as proxy for blood vessels.

Results

The feasibility of the vessel radius measurement is demonstrated. The numerical model shows an improved accuracy compared to the analytical approach. However, both methods overestimate the radius. The simultaneous measurement of the magnetic susceptibility and the volume fraction remains challenging.

Conclusion

The results suggest that this approach could be interesting in vivo to better characterize the microvasculature without contrast agent.

Introduction

MRI has become a powerful tool to investigate the cerebral microvasculature. Various MRI methods with and without contrast agent injection, including Dynamic Contrast Susceptibility (1), vessel size imaging (2–4), vessel density (5,6), and steady-state blood volume (3,7), have found widespread use in research and clinical applications to study important properties of blood vessels in normal brain and under disease conditions (8–12). In addition, measurements of the microvasculature play an important role for the quantification of the blood oxygen level dependent (BOLD) signal in functional MRI (13–15).

However, the microvascular characteristics are generally not directly measurable by MRI. They usually result from elaborate modeling of the MRI signal that can lead to significant limitations. For example, most MRI methods derive the microvascular parameters of blood oxygenation from modeling signal modulations associated with magnetic susceptibility variations within the blood pool, either induced by oxygenation changes or contrast agent (CA) injection. Water diffusion across the magnetic field perturbations and around magnetic inclusions is a major aspect which hugely complicates modeling, since water diffusion in brain tissue is a complex process that is also poorly understood. Over the years, various theoretical models have been developed with specific simplifying assumptions about water diffusion to approximate the MRI signal (6,16–19). These models compare the diffusion length of the tissue proton, L_D, to the extent of the magnetic field gradient which can be approximated by the radius of the vessel R. When the diffusion can be neglected (static dephasing regime (16)) or when the diffusion length is much shorter than R (near static dephasing regime (17)) the MRI signal decay can be approximated as a mono exponential decay. However, this assumption does not hold across the entire range of physiological vessel sizes. Accordingly, a discrepancy has been observed between the analytical predictions of the MR signal and the corresponding Monte Carlo (MC) simulations (17,20). In particular, the largest discrepancy has been found for small radius vessels (e.g. in the range of few microns), corresponding to capillaries, that can occupy around 50% of the vessel volume fraction of a voxel (21). Thus, improved methods are needed to accurately parameterize the MR signal modulations especially toward the lower scale of small vessels and capillaries.

An accurate parameterization of the MRI signal is also highly important for quantitative BOLD (qBOLD). qBOLD aims at estimating the tissue oxygenation level (OEF) and the deoxygenated blood volume fraction (dBV) simultaneously from the MR signal profile under the condition of a spin echo. Since qBOLD does not require a CA injection, the approach has a strong advantage for measurements of OEF and dBV compared to other techniques. Although promising results have been obtained with qBOLD (15), other studies demonstrated that the technique can lead to large uncertainty in the estimation of OEF and dBV (20,22). Indeed, it appears that these two parameters have a similar and interdependent impact on the BOLD signal either in the static dephasing regime (22,23) or in the near static dephasing regime (23). Although separate estimations of the two parameters have been proposed as improvement, the impact of proton diffusion was either disregarded entirely or confined to the near static dephasing regime (24). Recently, an attempt has been made to fully account for the diffusion in qBOLD by using Monte Carlo simulations (25). However, the vessel radii were set constant and the dependency of the MR signal was disregarded.

The aim of this study was to introduce a new multi-parametric MRI framework to estimate the vessel size in addition to the blood volume and magnetic susceptibility difference. To overcome the restrictions used in the analytical models, the MR signal was analyzed with a numerical approach. An important analytical model was also implemented for comparison. Based on simulations, we first demonstrate the ability of the proposed approach to estimate the vessel radius. The framework is then evaluated in two different phantoms where vessels were modeled by polyamide strings of known radius and volume. Results demonstrate a beneficial use of the numerical model for the estimation of the string radius. Remaining issues that impede accurate parameter estimation are discussed.

Theory

This section presents the different approaches used to model the MR signal. In the following, it is assumed that the blood vessels consist of infinite magnetic cylinders of radius R (as proxy of vessels) embedded in a medium (tissue). The cylinders occupy a volume fraction V_f. The magnetic susceptibility difference between the inner and outer part of the cylinders is given by Δχ. The proton diffusion coefficient around the cylinders is denoted D. In the following, only the transverse relaxation due to the diffusion effects across the perturbed magnetic field surrounding the microvasculature is considered.

Analytical model

Several analytical models have been proposed to describe the phase shift of spins that diffuse in a perturbed static magnetic field (6,16–19,26). The one considered here was proposed by Kiselev & Posse (K&P) and has been used in different qBOLD studies (23,25) and vessel size imaging application using contrast agent (3). This model considers vascular geometry where magnetic inclusions are random cylinders isotropic in space and orientation. Details about the model and MR signal expressions are listed in Appendix.

Numerical model

As an alternative to the analytical models, we developed a numerical approach for predicting the MRI signal modulations as a function of local susceptibility variations and proton diffusion. In the following, bold capital letters refers to 2D-lattices, × to the point wise multiplication, ⊗ to the convolution and $\mathbb{i}$ stands for a uniform lattice of 1. The time step of the simulation was dt=0.5ms. We refer to this numerical model as NumVox.

Geometry

To mimic vessels, magnetic circular inclusions with radius R were randomly distributed into a 2D continuous plane. These inclusions occupied V_f. The number of inclusions, N, was fixed to 96 and the space dimension of the plane was adapted accordingly to preserved V_f. If an inclusion intersected the border of the lattice, it was symmetrically repeated on the other side so that the geometry can be seen as a unit cell of a larger network. The geometry was subsequently sampled on a 2D lattice with L²=256×256 points. G was defined as the lattice with 1 inside the inclusions and 0 outside. The susceptibility lattice, Δχ, was defined as Δχ=Δχ.G.

Magnetic Field

The magnetic field induced by the inclusions, ΔB, was computed following the Fourier based approach proposed in (27,28) and applied here in 2D:

$$\Delta \mathit{B}=B_0.F{T}^{-1}\left\{\left(\frac{1}{3}-\frac{k_x^2{\sin }^2\theta }{k_x^2+k_y^2}\right)FT\left\{\Delta \chi \right\}\right\}$$ (1)

where k_x and k_y are the wave vectors in the Fourier space, θ the angle between the normal of the plane and the main magnetic field B₀ and the operators FT and FT⁻¹ denote the Fourier transform and inverse Fourier transform, respectively. To imitate an isotropic distribution of the vessel regarding B₀, the perturbations of the magnetic field was averaged over 3 orthogonal orientations as proposed in (29).

Magnetization

Magnetization changes were modeled using the deterministic approach originally described by Bandettini et al. (30,31). The evolution of the transverse magnetization lattice, M(t), was iteratively computed according to:

$$\mathit{M}(t+dt)=(\mathit{M}\left(t\right)\times \mathit{R})\otimes \mathit{D}$$ (2)

where R is the dephasing factor across the lattice and D is a kernel, simulating the diffusion process. R is given by:

$$\mathit{R}=e^{-i\gamma \Delta \mathit{B}dt}$$ (3)

where the symbol e denotes the point wise exponentiation. The discrete kernel D used in our study corresponds to the solution of the discretized diffusion equation in the scope of the scale-space theory (32):

$$\mathit{D}=e^{-{\sigma }^2}{\mathit{I}}_{\mathit{n}}\left({\sigma }^2\right)$$ (4)

where I_n(σ²) denotes the modified Bessel function of integer order and indicates the average displacement of the proton spins due to diffusion. The relation between sigma and D is given by σ² = 2 Ddt. The kernel was scaled to a pixel unit to match the integer order of the Bessel function. Using a discretized Gaussian distribution was of particular importance for narrow kernels (e.g. those representing slow diffusion, small dt and large N). In that case, a strong bias was observed when using a discrete sampling of the continuous Gaussian kernel (as pointed out in (32)). The convolution operation was applied in the Fourier space to speed up the computation and to benefit from the folding effect.

In the analytical models, only the outer space of the vessels was considered. Accordingly, we modeled the magnetic inclusions in our phantom experience as impermeable to water. The proton diffusion model was modified to model hindered diffusion (29). This results in the following equation:

$$\mathit{M}(t+dt)=(\mathbb{i}-\mathit{G})\times ((\mathit{M}\left(t\right)\times \mathit{R})\otimes \mathit{D}+\mathit{W}\times (\mathit{M}\left(t\right)\times \mathit{R}))$$ (5)

with

$$\mathit{W}=(\mathit{i}-\mathit{G})\times \mathit{G}\otimes \mathit{D}$$ (6)

where W takes the bounce mechanism at the wall of the inclusions into consideration.

The net MR signal was finally obtained at each time step by summing the complex values of the lattice M(t).

The 3D version of this numerical model was also implemented for comparison purpose. Vessels were mimicked by straight cylinders. Isotropic orientation of the cylinders was achieved by considering a sin(u)/2 random distribution of the polar angle and a uniform random distribution for the azimuthal one. Spatial positioning of the cylinders followed a uniform distribution within the voxel. The magnetic field was computed by convoluting the 3D form of the kernel defined by Eq. 1 with the 3D susceptibility lattice as described in (27,28).

Methods

MRI

The MRI phantom data used in this study are described in detail in (23). We outline here the main features. The phantoms were constructed to mimic a vascular network. Vessels were modeled using randomly coiled monofilament polyamide strings immersed in a NiSO₄ solution. Two phantoms, Phantom 1 (P₁) and Phantom 2 (P₂), with string radius R₁=13.5 μm and R₂=31.5 μm and NiSO4 concentrations 4.11 g/L and 3.76 g/L respectively were analyzed. The expected volume fractions occupied by the string were V_f1=2% and V_f2=2-3%.

The magnetic susceptibility differences, Δχ₁=1.25ppm and Δχ₂=1.15ppm, were evaluated based on a dedicated calibration experiment adapted from the single string method introduced in (22). We designed two different phantoms with an individual string with R=245 μm and R=194 μm immersed in NiSO₄ solutions. Four different NiSO₄ concentrations were considered. Phantoms were positioned inside the bore with the string perpendicular to the B₀ axis. A multi gradient-echo (GE) imaging was performed to obtain the FID profiles. Phase shift was applied in k-space to center the string within a single imaging voxel. The FID of that specific voxel was then fitted and Δχ was estimated based on the model described in (22). Linear relationships between NiSO4 concentration and Δχ were found for the two radii with 0.1ppm variation between the two single string phantoms. The mean value was eventually considered to estimate Δχ₁ and Δχ₂ in P1 and P2 at the corresponding NiSO4 concentrations.

The imaging protocol was performed at 3T (Magnetom Avanto/Trio, Siemens Medical Solutions, Erlangen, Germany) and consisted of:

• A Gradient-Echo Sampling of Spin-Echo sequence (GESSE) (33) with TR=2000 ms, FOV=192 mm, 64×64 matrix size, BW=1560Hz/Px, 1 slice, slice thickness 6mm, spin echo time TE=68 ms and 32 gradient-echoes acquired at 44, 45.6, [...], 93.6ms.

• A Carr-Purcell-Meibom-Gill (CPMG) sequence with TR=2000 ms, FOV=192 mm, 128x128 matrix size, BW=130Hz/Px, 1 slice, slice thickness 6mm and 12 spin echoes acquired at 12.6, 25.2, [...], 151.2ms.

• A high resolution 3D Multi Gradient-Echo (MGE) sequence with TR=100 ms, FOV=192 mm, 256×256×8 matrix size, BW=130Hz/Px, 8 slices, thickness 1.5mm and 5 gradient-echoes acquired at 4.92, 12.30, [...], 34.44ms.

• A diffusion weighted EPI sequence with TR=1200 ms, FOV=192 mm, 128×128 matrix size, BW=1954Hz/Px, 1 slice, slice thickness 6mm, TE=69ms, 3 orthogonal direction and b=1000s/mm².

Data Processing

The computation was performed in the Matlab environment (Mathworks Inc. Natick, MA, USA) using the Matlab Distributed Computing Server deployed with 24 workers on a 24 nodes cluster.

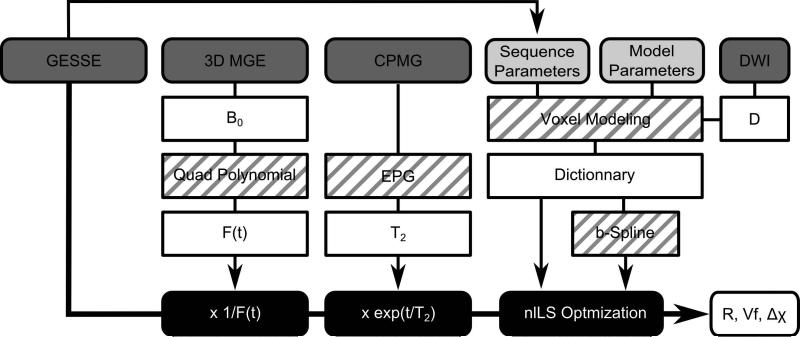
Figure 1 presents the flow chart of the data processing. Before the optimization process, the GESSE data were corrected for:

• The B₀ field inhomogeneity: The contribution of the macroscopic magnetic field to the MR signal decay was computed based on a quadratic polynomial fit of the field map derived from the high resolution 3D GE phase data (15). This contribution was subsequently evaluated around the spin echo and the GESSE signal corrected accordingly.

• The spin-spin T₂ relaxation: A single T₂ component was considered and the extended phase graph algorithm (EPG) was used to fit the CPMG data and derive the corresponding spin-spin T₂ decay (34). The T₂ relaxation was then evaluated at the time points of the GESSE sequence and the signal was corrected accordingly. The EPG was required due to the presence of stimulated echoes in the CPMG data.

• The apparent diffusion coefficient (ADC) of water was estimated from the diffusion weighted sequence and D=ADC was assumed.

For the specific MR parameters of the GESSE sequence, dictionaries of the MR signal modulations with a wide range of input values: R=1, 3, [...], 99 μm, V_f=0.2, 0.4, [...], 10 % and Δχ=0.05, 0.07, [...], 1.99 ppm were evaluated for the numerical and analytical models. Each dictionary consisted of 245,000 individual simulations. The parallel building of the dictionaries took about 4h and 30h for the analytical models and the numerical model respectively. To estimate the MR signal continuously in the range of the simulated input parameters, a b-spline was fitted to the dictionaries. A constrained non linear least square algorithm (nlLS) was then used to optimize the different model to the corrected GESSE signal measured on the phantoms and the parameters R, V_f, and Δχ were extracted. To avoid fitting an additional scaling parameter, the measured and modeled signals were normalized by their mean value. The Levenberg-Marquardt algorithm was employed for the least squares curve fitting. Init point was initialized by the input parameter of the closest dictionary curve, in term of the L2 norm, from the data. The analysis was done on ROI and voxel-wise.

Figure 1.

Flow chart of data processing. The GESSE data is first corrected for T₂ relaxation and B₀ inhomogeneity before fitting is applied. Black blocks indicate data processing; dark grey indicate derived MRI data; light grey highlight the parameters of the model; white indicate the various outputs from processing. Blocks with stripes indicate the methods and algorithms used. In white, the different outputs of the processing scheme.

Noise model

To evaluate the robustness of our approach to noise, a subset of MR signals was extracted from the simulated dictionary and Gaussian noise added. Each element of this noisy subset was then compared to the whole dictionary using the L2 norm and the R, V_f and Δχ values were retrieved. These estimated values were compared to the R, Vf and Δχ of the initial subset. The level of noise was defined in terms of SNR (mean value/standard deviation of noise). To reduce computational cost, only a subset of 1100 MR signals was analyzed corresponding to all possible combination of R=5, 15, [...], 95 μm, Vf = 1, 2, [...], 10 % and Δχ=0.75, 0.85, [...], 1.75 ppm.

Statistics

To assess the reliability of each model in terms of means and variances, the parameter distributions were obtained by jackknifing (35). This involved generating n random subsets from the data and applying the post processing to these n subsets to obtain a distribution of the estimates. We generated n=100 subsets each of them including 86% of the data set (5 points left apart). They were individually processed and the corresponding output parameters were expressed as mean ± standard deviation.

Results

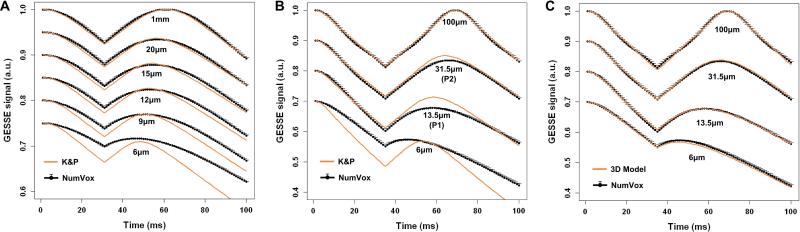
GESSE signal predictions for various vessel diameters using our numerical model (mean ± std computed over 50 different geometry arrangements) and the K&P theoretical model are compared in Figure 2 for a physiologically value of Δχ=0.45ppm corresponding to an OEF=40% (Fig.2A, given Δχ= 4π × Δχ_do × Hct × OEF with Δχ_do= 0.264ppm the susceptibility difference between fully oxygenated and deoxygenated blood (36) and Hct=0.34 the microvascular hematocrit rate) and for the two phantoms with Δχ=1.25ppm each (Fig.2B). Figure 2A is a replication of results published in (20) (and see therein Figure 3) using Monte Carlo based simulation. The agreement between K&P and our NumVox method is excellent, especially for large R values. However, as we get further of the near static dephasing regime (smaller R), discrepancies appear between the two models. Figure 2C compares the 2D and 3D versions of our NumVox method. The agreement is strong suggesting that our computation of the magnetic field distribution in 2D is coherent with an isotropic 3D model.

Figure 2.

A) Comparison between the numerical model (black) and the Kiselev & Posse model (orange) for B₀=3T, spin-echo at 60ms and physiological values matching those of (20): V_f=3%, R=[1000, 20, 15, 12, 9,6] μm, D=1000μm²/s, and Δχ corresponding to OEF=40% (Δχ=0.45ppm). The different MR signal curves corresponding to different R have been shifted along y-axis for better display. This plot is in good agreement with Monte Carlo simulations reproduced in (20). B) Simulation for the phantom setup: TE=68ms, V_f=2%, R=[6, 13.5, 31.5, 100]μm, D=2157μm²/s, B₀=3T and Δχ=1.25ppm. Comparison between the numerical model (black) and the Kiselev & Posse model (orange). When R=100μm, the effect of the diffusion can be neglected and the model matches the static dephasing regime case described by Yablonskiy and Haackee (16). For R<100 μm, a discrepancy between the two models is observed. C) Parameters are the same as in B. Comparison between the numerical model (black) and the 3D numerical model (orange) with isotropic cylinders distribution. The numerical model is displayed as mean±std with error bars computed over 50 different arrangements of the vessel geometry.

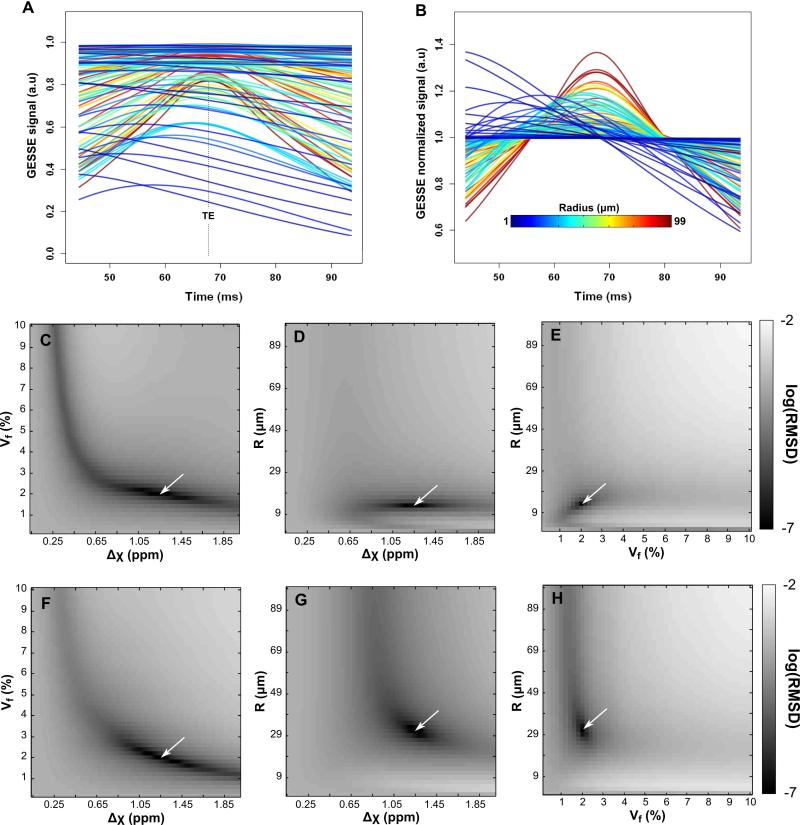
Figure 3.

A subset of the dictionary curves (outer left column) generated by the numerical approach before (A) and after (B) normalization by the mean. Colors code for the radius value. (C-H): Plots of the Root Mean Square Deviation (RMSD) in log scale between one MR reference signal (depicted by the white arrow, RMSD=0) to every others simulated curves of the dictionary produced by the numerical approach. RMSD maps were computed from a reference signal with R=13μm (closest value to string radius of Phantom 1, R₁=13.5 μm), V_f=2% and Δχ=1.25ppm (C-E) and with R=31μm (closest value to string radius of Phantom 2, R₂=31.5 μm), V_f=2% and Δχ=1.25ppm (F-H). Note the narrower valleys in the (R,V_f) and (R,Δχ) plots compared to (V_f, Δχ) suggesting that R can be estimated accurately in the case of Phantom 1.

A subset of simulated raw and normalized MR signals based on the NumVox approach for the GESSE sequence is presented in Fig. 3A and 3B, respectively. The refocusing of the spins at the echo time TE only occurs for large R values, i.e. when the static dephasing regime is the best achieved. On the contrary, for small R, the refocusing process can barely be distinguished and the MR signal largely exhibits a monotonic decay. In Fig. 3C-E, we illustrate the root mean square deviations (RMSD) between one curve of the normalized dictionary (chosen to correspond to the expected parameter value of the phantom 1, R=13.5μm, V_f=2% and Δχ=1.25ppm) and all the other ones. Fig. 3C is in agreement with Sohlin et al. (23). As already pointed out in (22,23), the broad valley observed in this plot makes the simultaneous estimation of V_f and Δχ a challenge with the qBOLD approach. On the contrary, the RMSD plots for R vs V_f and R vs Δχ exhibit a much narrower valley (Fig. 3D-E) indicating that an estimation of the vessel radius could be achieved based on the GESSE signal. Fig. 3F-H show similar plots in the case of Phantom 2 (R=31.5 μm). The valleys in plots involving R appear flatter along large R suggesting a higher sensitivity to noise and a less accurate measurement.

Noise model

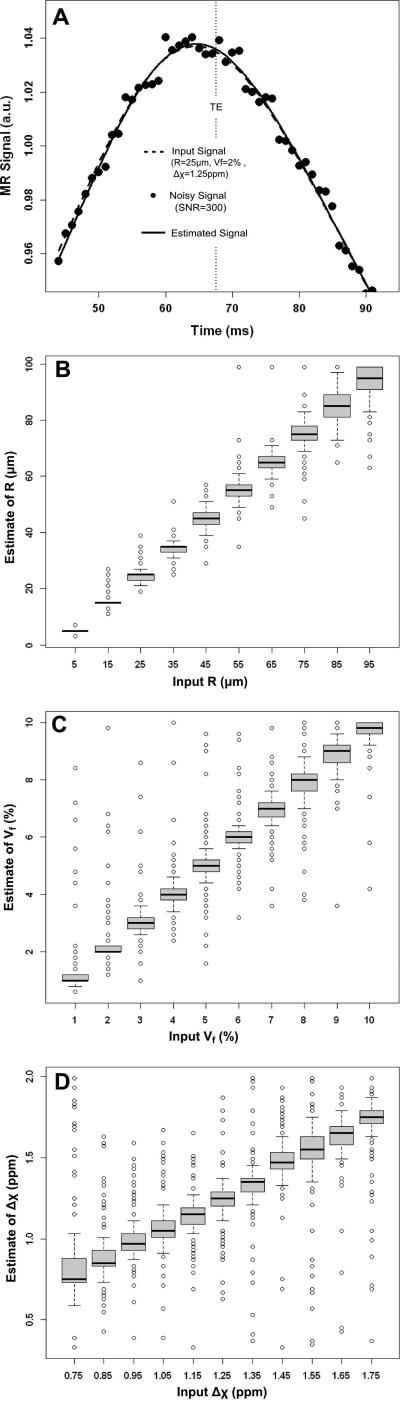
Figure 4 illustrates the influence of noise on the parameter estimations (SNR=300, matching the SNR of the weakest intensity voxel in the GESSE phantom dataset and evaluated at the spin echo time). Fig. 4A shows an example of the dictionary-based optimization process. Fig. 4B-D present the variations in estimates of R, V_f and Δχ summarized as box-and-whisker plots. For each box-and-whisker, the variation is derived by keeping one of the input parameters fixed while varying the 2 others.

Figure 4.

Noise dependence on parameter estimations. A) Illustration of the initial input signal from the dictionary (dashed line), the signal after adding noise (dotted line) and the estimated signal retrieve from the dictionary (solid line). B-C) Box-and-whisker plots of the input parameters vs estimated parameters for R (B), V_f (C) and Δχ (D). The graph illustrates variations in estimating one particular parameter, e.g. R, while changing others, e.g. V_f and Δχ. Note the larger dispersion in V_f and Δχ compared to R.

Linear trends are observed for each of the estimates. The average relative error on the range of the estimated R (5%) was twice lower than the ones found for V_f (14%) and Δχ (10%). The box-and-whisker plots for V_f and Δχ indicate a large number of outliers consistent with reduced accuracy (percentage of outliers: 7% for R, 15% for V_f and 18% for Δχ). This trend is accentuated in the evaluation of Δχ, in agreement with the shape of the valley in Fig.3C.

Phantom data

The mean ADC was 2157μm²/s in P1 and 2181μm²/s in P2.

Jackkniffing – ROI analysis

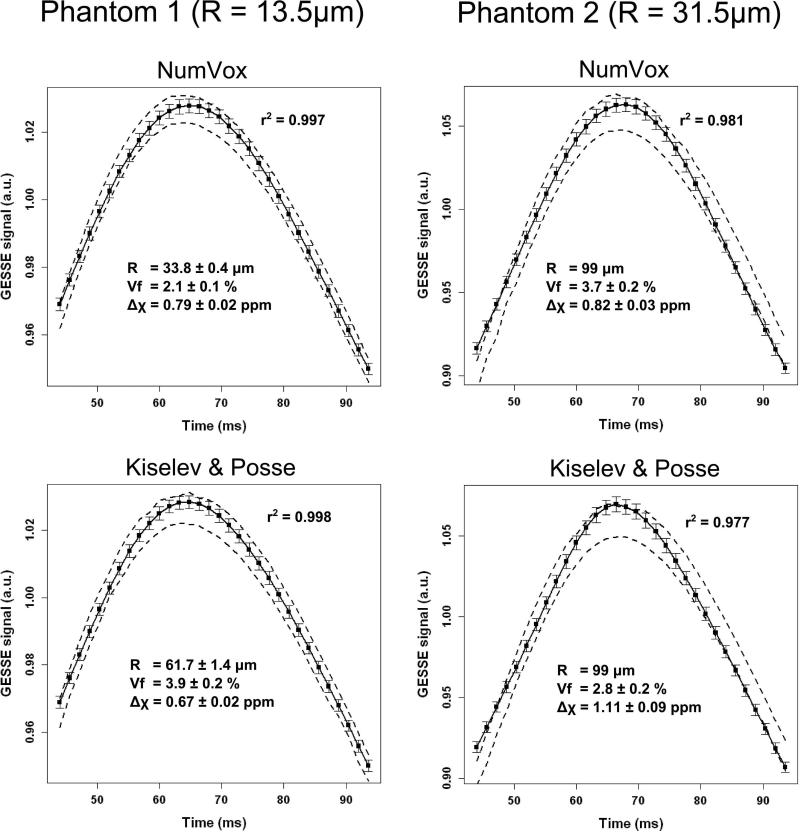
In Figure 5, we summarize the results obtained with the phantom datasets using the two different models and the Jackknife approach. For P₁, the NumVox and K&P models fit the experimental data comparatively well (r²=0.997 and r²=0.998). The estimations of R, V_f and Δχ from the fits differ between the models. The string radius is overestimated by both models: R was estimated to be 33.8±0.4μm and 61.7±1.4 μm for the proposed method and the K&P method respectively when the expected R value is 13.5 μm suggesting possible biases in the method and in the phantom design that are detailed in the discussion section. Overall, the NumVox model achieves a higher accuracy for R and V_f than the analytical model. The analytical model underestimates Δχ and overestimates V_f by more than 50% suggesting a cross-talk between these estimates in agreement with previously reported observations (22,23).

Figure 5.

Results from the Jackknife fitting of the phantom data. Dashed lines indicate the max/min range of corrected GESSE signals generated by the jackknife approach after normalization. Solid lines indicate mean values of the fits. The error bars indicate one standard deviation. The expected value of the phantom are respectively P1: R₁=13.5μm, V_f1=2%, Δχ₁=1.25ppm and P2: R₂=31.5μm, V_f2=2-3%, Δχ₂=1.15ppm. The mean r² value of the 100 Jackknife resamples is listed.

For P₂, which has about a 3 fold increase in R, all the models perform poorly in estimating R and return the maximum value allowed in the optimization process (i.e R=99μm). The overall correlation between the dataset and the models is slightly lower than with P₁.

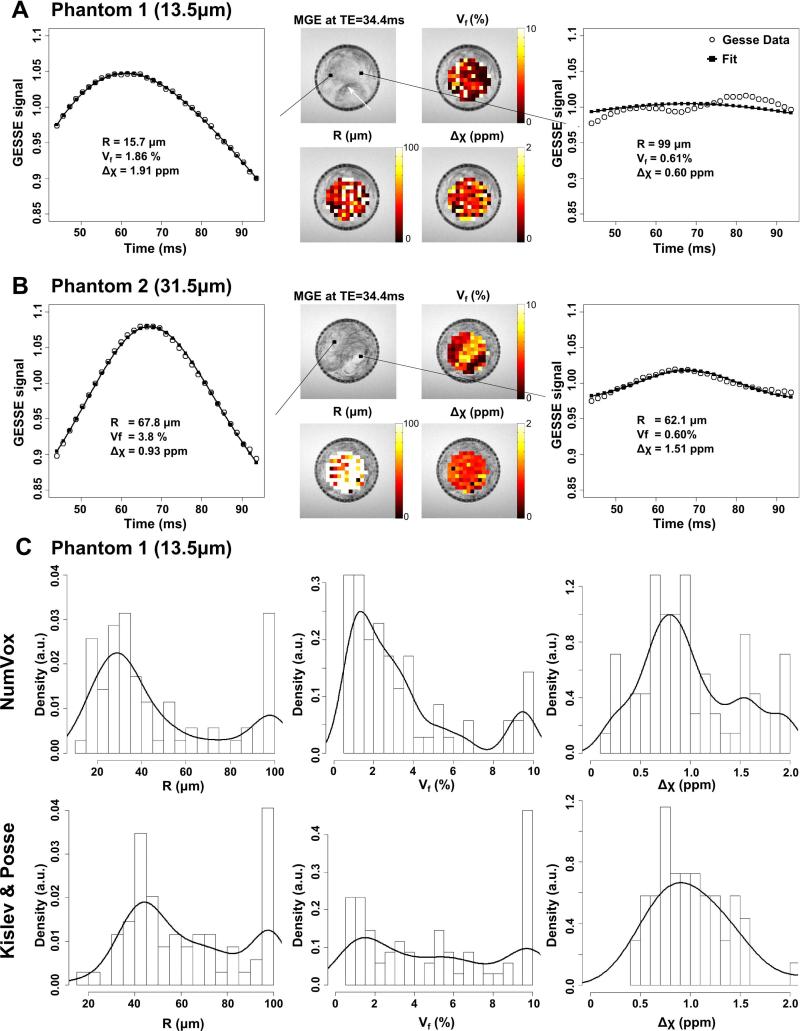
Voxelwise analysis

Figure 6 presents the results obtained from a voxelwise analysis fit with both phantoms. Fig.6A displays the maps of R, V_f and Δχ obtained from P₁. The inhomogeneity of the phantom appears clearly in the MGE images. Dark voxels that correspond to densely packed strings can be observed (white arrow). These densely packed regions exhibit high V_f estimates in the corresponding map. In these voxel, the estimation of the radius is close to the expected value R₁(graph on the far left). On the contrary, for thinly packed regions the volume fraction is small and the estimation of the radius is biased toward larger R (e.g. graph on the far right). Note the wiggling of the GESSE signal in such cases that may be caused by the sparsity of the strings in these areas (37).

Figure 6.

Parameter maps and parameter distributions from voxelwise analysis for data from Phantom 1 (A) and Phantom 2 (B). Maps of the parameters R, V_f, and Δχ overlay over the MGE acquisition. The far left and right graphs correspond to voxels with different MR profiles. Note the wiggling of the GESSE signal for the right panels that corresponds to voxel with small V_f values. C) Histograms and density plots of parameters distributions across the maps for the three different models in the Phantom 1 dataset. Note the difference in the maximum amplitude of the histogram of R between the models.

The results obtained from P2 are shown on Figure 6B. The V_f maps are consistent with the contrast observed on the MGE images. The radius however is overestimated.

Fig. 6C presents histograms of R, V_f and Δχ estimations across the P1 phantom regions, separately for each model fit. Results from poor fits (e.g. r² < 0.9) were excluded. The density function of the histogram is also shown as overlay. The corresponding numerical values are listed in Table 1. The high density at R=99μm in the histogram of R is an artifact and can be ascribed to voxels with very small volume fraction of the strings (graph on the far right in Fig.6A). The dispersion of the histograms for R is comparable across the models. Each model yields a maximum density value of R that is higher than the true value. Nonetheless, our NumVox model yields the smallest discrepancy (R=29μm) compared to the true value (R₁=13.5μm), whereas the K&P model leads to substantial overestimations of R (R=45μm). The histograms of V_f appear more dispersed than those of R, in agreement with the observed contrast inhomogeneity in the MGE images. Each model yields a maximum density value of V_f that is slightly lower than the expected value of V_f1=2%. In contrast to R and V_f1, all methods underestimate the true value of Δχ (Δχ₀=1.25ppm) by at least 25% or more. Similar trends of estimations are observed in phantom 2 for V_f and Δχ.

Table 1.

Parameters estimations obtained from the voxelwise analysis for each model.

Phantom 1		R (μm)		Vf (%)		Δχ (ppm)
Expected values		13.5		2		1.25
Model	%voxel fitted	Mean ± sd	Max density	Mean ± sd	Max density	Mean ± sd	Max density
NumVox	75%	46 ± 28	29	3.3 ± 2.8	1.5	1.00± 0.48	0.80
Kiselev and Posse	74 %	62 ± 24	45	5.0 ± 3.5	1.7	0.98 ± 0.58	0.62

Phantom 2		R (μm)		Vf (%)		Δχ (ppm)
Expected values		31.5		2-3		1.25
Model	%voxel fitted	Mean ± sd	Max density	Mean ± sd	Max density	Mean ± sd	Max density
NumVox	71%	83 ± 23	99	5.1 ± 2.2	6.3	0.86 ± 0.21	0.85
Kiselev and Posse	70%	91 ± 15	99	5.4 ± 2.9	3.1	1.33 ± 0.47	1.00

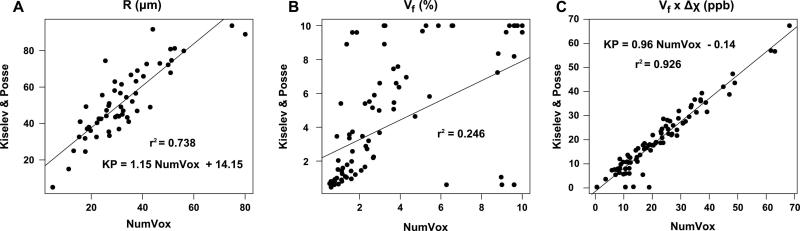
In Figure 7, we show the voxelwise correlation plots between the K&P model and the numerical model. Radii with value R=99μm were discarded. A good agreement is found between the two models in the estimates of R (r²=0.738) and larger R values are obtained when using the K&P model (Fig7A). On the contrary, poor correlations between the models are found for V_f and Δχ (data not shown): r²=0.246 and r²=0.372, respectively (Fig 7B). However, an excellent correlation is obtained by comparing the product V_f × Δχ: r² = 0.926 (Fig 7C).

Figure 7.

Voxelwise correlation plots between the numerical model and the K&P analytical model for: A) the string radius R, B) the volume fractions V_f and C) the products V_f × Δχ. R values at 99μm were considered as outliers. For R, a good correlation is observed with a deviation toward larger values with the Kiselev and Posse model. Poor correlations are found for V_f values and Δχ values (not shown) whereas excellent agreement is found for the product V_f × Δχ.

Discussion

We presented a computationally efficient 2D numerical approach that simulates the MR signal from local magnetic susceptibility variations with consideration of water diffusion. We proposed to use this model for extending qBOLD in two ways. First, by merging the data from a multi-parametric MR protocol into a single post-processing scheme, we demonstrated that the radius of the strings can be estimated in addition to the volume fraction and local magnetic susceptibility under static conditions, i.e. without contrast agent injection. Second, we also showed that the numerical method that integrates different underlying physical phenomena with fewer assumptions than theoretical models improves the estimations. In the following, we discuss the results and the limitations of the proposed method.

The discrepancy in predicting MR signal modulations between our numerical model and one important analytical model which is currently used for a wide range of applications (3,14,15,17) is consistent with results from previous studies using Monte Carlo simulations (20). Furthermore, the 2D and the 3D versions of our numerical approach yielded similar results. This suggests that our numerical model remains accurate at a small computational cost under conditions where the analytical models typically break down. This is of high importance for in vivo studies where the capillary size (≈3-4μm) falls in a range that no analytical model has properly described before (20). Our numerical approach furthermore facilitates exploring a wide range of physiological input parameters and allows building large dictionaries of the MR signal in a reasonable computational time.

The numerical model also benefits from a high versatility compared to analytical solutions. For instance, variations in vessel distribution can easily be incorporated. Further, the spatial distribution of magnetic inclusions, that has been shown to a have a significant effect on the MR signal (26,38), can be accounted for. More refined diffusion effects, such as hindered diffusion around cells and vessel walls, can readily be taken into account.

The MR signal modulations may also vary with the number of magnetic inclusions N. It has been shown that the standard deviation of the estimation is proportional to $1∕\sqrt{N}$ (16,31). A large N will accomplish a proper self-averaging mechanism but a “pixelated” description of the geometry. In contrast, a low N will induce modulation of the MR signal depending on the positions of the inclusions. In this latter case, the signal from different arrangements is usually averaged to integrate this variability (39,40). In this study, N was fixed to 96 and no averaging was considered. However, with different vessel arrangements, the standard deviation of the MR signals modulation remained low (Fig. 2) suggesting that N=96 was a reasonable choice.

To our knowledge, the only prior attempt to use simulations to fit the MR signal in the scope of qBOLD imaging was proposed by Dickson et al. (25). In this work, simulations were based on Monte Carlo methods and the 3D vascular network was designed with the same radius distribution for every voxel. Blood volume, magnetic susceptibility difference and water diffusion were varied to build up the dictionary but the impact of the vessel radius was not investigated. The computational cost for Monte Carlo limited the number of simulated signals to 3000 and larger incremental steps in the input parameters were used. The numerical model proposed here mainly benefits for an improved computational efficiency and versatility that allows exploring a wider range of parameters values. However, the dictionary generation still takes about 30 hours on a parallel computing cluster. The computational demand will further increase when considering additional MRI effects for the dictionary such as T1 and T2 relaxation as well as off-resonance variations.

The numerical model and the analytical model provide similar fit quality in the ROI analysis. The simultaneous estimation of Δχ and V_f remains a challenge for both models. However, the product Δχ × Vf is to some extent correctly estimated (Phantom 1: 1.25×2=2.5 expected, 2.61 measured in K&P, 1.66 measured with NumVox. Phantom 2: ≈1.15×2.5=2.88 expected, 3.10 measured in K&P, 3.03 measured with NumVox). A strong agreement was also observed in the voxelwise analysis for the estimation of Δχ × Vf. This strengthens the idea that the key parameters modulating the GESSE MR signal are the radius of the magnetic inclusions and the product Δχ × Vf.

With the Kiselev and Posse model, the estimation of Δχ and V_f are closer to the true values in Phantom 2 than in Phantom 1. This can be ascribed to the assumptions of this model. Kiselev et al. derived the criterion $R\gg \sqrt{DTE}$ which has been later modified to $R>3\sqrt{DTE}$ in (20), based on Monte Carlo simulations. In our case, the criterion leads to R>36μm suggesting that the K&P model is not suitable for Phantom 1 and not entirely fulfilled for Phantom 2. However, Figure 2B demonstrates that a good agreement is obtained for Phantom 2 between NumVox and K&P suggesting that K&P model is valid for this specific phantom. This discrepancy might be ascribed to the high values of Δχ and diffusion used in our setup.

In Phantom 1, the numerical model yielded a more accurate estimation of R than the analytical model, suggesting that a numerical approach offers an advantage. Whether the benefit extends to in-vivo MRI data needs to be determined. However, the radius was overestimated by every model, especially for thicker strings of Phantom 2. This is in agreement with the observed pattern in the RMSE plots of Fig. 3H. This indicates that the approach is accurate only within a certain range of vessels radii that requires further characterization.

One potential reason for the overestimation of the radius could be related to the heterogeneity of the coiling of the strings. First, self-tension of the strings may lead to geometric configurations where strings are most likely bound to each other, resulting in a larger effective radius. Second, this heterogeneity may result in wide areas occupied with no or few strings that lead to a poor self-averaging process not described by any model.

A more accurate estimation of the parameters based on the numerical model as compared to the analytical one was also found in the voxel analysis. In general, large variability was observed in the parameter estimations that may originate from the underlying variability in string configurations, especially within the inner sections of the phantoms. Indeed, the raw MGE images show voxels with densely packed string configurations whereas other revealed very sparse packing. This leads to a strong variation in the MR signal profiles (Fig6A-B, far left/right graphs) and consequently to a large variability in the estimates. Oscillations in the signal were observed for low packed voxels that led to inaccurate estimate of the parameters. These oscillations seem to originate from the GESSE signal and no evidences for ascribing this effect to the B₀ or T₂ correction steps were found. Such oscillations states have been recently described in simulation with few anisotropic cylinders (37). However, the characterization of these phenomena is still insufficient for an effective incorporation to numerical models.

Both, B₀ and T₂ corrections of the GESSE signal are critical steps for the accuracy of estimations. The B₀ correction is strongly dependent on the shim quality. Hardware improvement (high order shimming, localized shim) can readily be advantageous to diminish magnetic inhomogeneity and reduce the need for correction. Different post processing techniques have been suggested based on the field map acquisition (25,41). The method used here, based on a polynomial fit of the magnetic field map, corrected the GESSE signal in the scope of qBOLD imaging (15). The approach preserves the main feature of the magnetic field fluctuations and reduces the noise contribution through data fitting. A first order approximation of this approach has also been introduced and demonstrated satisfying results (25,41). A new approach, termed voxel spread function, has been reported recently in (42). It does not require a high resolution field map but uses the phase and the amplitude of the voxel and its neighboring information. Finally, modified acquisition schemes can also be used to reduce B₀-field variations. For instance, combining high 3D resolution images according to the GE slice excitation profile (43) was proven effective in qBOLD mapping (44).

The correction for the spin-spin T₂ is even more critical in our approach than B₀-field corrections, since T₂ has a strong impact on the maximum amplitude of the GESSE signal which in turn is critical for estimating the radius of vessels. The phantom dataset idealized a single T₂ component that was relatively straightforward to correct using the extended phase graph algorithm (34). This estimation can be further improved by incorporating the RF slice profile excitation (45). In vivo cases, however, exhibit multi components T₂ decays that correspond to different voxel compartments. One possibility to address the greater complexity of in-vivo data, is the use of generalized versions of the EPG algorithm for correcting multi-component relaxation as recently reported in (46). Other MR sequences than CPMG could also be used to measure T₂. However, the measured T₂ must ideally describe the T₂ spin-spin relaxation that occurs during the GESSE acquisition and any mismatch will propagate into errors in the estimates.

Using a dictionary of MR signals for fitting offers several computational advantages. Assuming smooth variations of the cost function along the parameter space and a dense representation of the continuum of MRI signal variations by the dictionaries, the approach facilitates an optimal initialization of the nlLS algorithm near the global minimum of solutions. Some refinements could be considered. For instance, since the information regarding the radius seems to be mainly held in the time shift of the maximum amplitude of the GESSE signal, cost function with higher weights around this maximum could be examined. Dimensionality reduction of the dictionary and related methods will also be of interest to reduce the computational cost of the spline function.

Lastly, the FID decay of the MR signal could be readily incorporated into our approach and would provide additional data points at almost no cost. To speed up the protocol, EPI-based sequences can also be used such as combined spin- and gradient-echo sequences (47). Furthermore, the CPMG and DWI sequence could also be incorporated into the numerical model and the optimization scheme. This would be of interest to take into account the susceptibility-related effect in the ADC measurement or the role of water diffusion in the CPMG sequence.

Conclusion

We demonstrated that a multi-parametric MRI acquisition scheme together with a versatile numerical model of the MR signal accomplish simultaneous estimations of the radii of microscopic cylinders (as proxy of small blood vessels), volume fraction and local susceptibility without contrast agent injection. Results on phantom are encouraging but further validation steps are required to fully demonstrate the potentiality of the proposed approach for in vivo data.

Appendix

The over-arching idea for modeling the MR signal analytically has been to integrate over all phase variations that proton spins accumulate as they diffuse through local magnetic field perturbations within a voxel. Accordingly, the signal is expressed as:

$$s\left(t\right)=<\exp \left(i\varphi \left(t\right)\right)>$$ (A1)

φ(t) defines the distribution of the phase within the voxel induced by a single vessel and < > indicates the average over all possible vessel configurations and proton positions. We here focus only on the signal from the outer part of the magnetic inclusions. The phase distribution of the protons depends on the assumptions of the model and on the geometry of the magnetic inclusions that perturbs the magnetic field. In the case of a spin echo sequence, one of the model that handles diffusion has been proposed by Kiselev and Posse (17).

The Kiselev and Posse model uses the Bloch-Torrey equation in the approximation of linear local field variations. Two different cases were evaluated: the near static dephasing regime (SDR) and the diffusion narrowing regime (17). Due to the dimension setup of the experiment used in our study, only the near SDR case was investigated. The envelope of the magnitude MR signal around the spin echo at TE can be written:

$$\begin{gathered} s\left(t\right)= \\ \{\begin{array}{c}\exp \left(-V_f{\int }_0^{\pi }\frac{\sin \theta }{2}{\int }_0^1\frac{1}{u^2} \\ \left[1-\exp \left(-\frac{4D}{3R^2}\delta {\omega }^2{t}^3{u}^3{\sin }^4\left(\theta \right)\right)J_0\left(\delta \omega tu{\sin }^2\theta \right)\right]dud\theta \right)\hfill \\ \text{if}\mathrm{t}\le \mathrm{TE}∕2\hfill \\ \exp \left(-V_f{\int }_0^{\pi }\frac{\sin \theta }{2}{\int }_0^1\frac{1}{u^2} \\ \left[1-\exp \left(-\frac{4D}{3R^2}\delta {\omega }^2{t}^3{u}^3\left(1-\frac{3}{2}{\left(\frac{\mathrm{TE}}{\mathrm{t}}\right)}^2+\frac{3}{4}{\left(\frac{\mathrm{TE}}{\mathrm{t}}\right)}^3\right){\sin }^4\left(\theta \right)\right)J_0\left(\delta \omega \mid TE-t\mid u{\sin }^2\theta \right)\right]dud\theta \right)\hfill \\ \text{if}\mathrm{t}>TE∕2\hfill \end{array} \end{gathered}$$ (A2)

with δω = 2πγΔχB₀, D the diffusion coefficient of the proton and J₀ the zero order Bessel function. This expression is adapted from (17) where the misprinted sign has been corrected as pointed out in (20).