Propagation mechanism of polymer optical fiber fuse

Abstract

A fiber fuse phenomenon in polymer optical fibers (POFs) has recently been observed, and its unique properties such as slow propagation, low threshold power density, and the formation of a black oscillatory damage curve, have been reported. However, its characterization is still insufficient to well understand the mechanism and to avoid the destruction of POFs. Here, we present detailed experimental and theoretical analyses of the POF fuse propagation. First, we clarify that the bright spot is not a plasma but an optical discharge, the temperature of which is ~3600 K. We then elucidate the reasons for the oscillation of the damage curve along with the formation of newly-observed gas bubbles as well as for the low threshold power density. We also present the idea that the POF fuse can potentially be exploited to offer a long photoelectric interaction length.

Compared with other glass fibers, polymer optical fibers (POFs)¹,² offer easy and cost-efficient connection, high safety, and extremely high flexibility. Consequently, despite their higher loss than that of silica single-mode fibers (SMFs), POFs have been used in medium-range applications such as home networks and automobiles³ and in large-strain monitoring applications⁴. Several years ago, Brillouin scattering⁵—one of the most important nonlinear effects—in POFs was observed for the first time⁶, and since then its properties have been investigated, especially for distributed strain and temperature sensing applications⁷,⁸,⁹,¹⁰,¹¹, suggesting its potential applicability to high-precision temperature sensing⁷ and to large-strain sensing⁸. The Brillouin-scattered power in POFs is, however, quite low on account of their relatively large core diameters and multimode nature⁶, which needs to be enhanced to improve the signal-to-noise ratio of Brillouin distributed sensing systems¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷. One solution is simply to raise the incident power, the validity of which has been experimentally confirmed⁹. Up to now, it has been reported that such high-power light injection into POFs causes not only burning or damage at the POF-to-SMF interfaces¹⁰ but also a so-called fiber fuse phenomenon.

Fiber fuse¹⁸,¹⁹,²⁰,²¹,²² is generally known as the continuous self-destruction of a fiber by propagating high-power light, which leads to local heating and the initiation of an optical discharge. It is then captured in the fiber core and travels back toward the light source, consuming the light energy and leaving damage. Since the fiber can no longer be used after the passage of the fuse, this effect is now regarded as one of the critical factors limiting the maximal optical power that can be delivered²³. Therefore, the fuse properties need to be well investigated so that all possible measures are taken to avoid this phenomenon. According to previous studies¹⁸,¹⁹,²⁰,²¹,²²,²⁴,²⁵,²⁶,²⁷, the fiber fuse in silica glass fibers is typically induced at an input optical power of one to several watts (one to several megawatts per square centimeter) and to have a propagation velocity of one to several meters per second.

Very recently, we have observed for the first time the fiber fuse in POFs with a graded-index profile using continuous light at telecom wavelength²⁸. Its macroscopic appearance is in perfect analogy to the fuse in silica SMFs, but its propagation velocity is as slow as ~0.02 m/s. The threshold power density is 6.6 kW/cm², which is 180 times lower than that of silica SMFs. The microscopic behavior of the POF fuse is also striking: the damage left after the passage of the bright spot looks like a black oscillatory curve, the period of which is moderately consistent with the theoretical oscillation period of the ray. In addition, fuse propagation can be terminated, by exploiting the high elasticity of the polymer, at a point pressed with an outer metal attachment. Thus, the fuse propagation mechanism in POFs appears distinctly different from that in silica glass fibers, and there are still many points to be further studied and better understood, such as (i) whether the POF fuse is a plasma or not, (2) the temperature of the bright spot, (3) the reason for the oscillation of the damage curve, and (4) the reason for the low threshold power density.

In this paper, we report detailed experimental and theoretical analyses of the POF fuse propagation, offering answers to the aforementioned questions. The spectral measurement suggests that the POF fuse is not a plasma but an optical discharge at a temperature of approximately 3600 K. The oscillatory damage curve is explained by taking the multimode nature into consideration, while the low threshold power density is explained by the unique temperature dependence of the optical absorption of the POF. We also show that gas bubbles are partially periodically formed after the passage of the bright spot, and that, by using the electrical conductivity of the damage curve, the POF fuse can be a candidate for providing a long photoelectric interaction length.

Results

Polymer carbonization

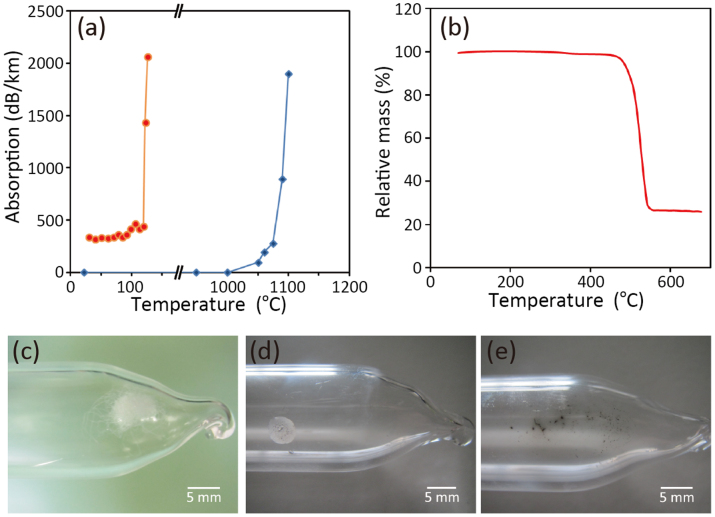
The measured temperature dependence of the optical absorption of a perfluorinated graded-index POF² (its detailed properties are provided in Methods) is shown in Fig. 1(a). The absorption increased drastically at around 120°C, which is much lower than the corresponding increase of a silica SMF that occurs at 1050°C (also shown in Fig. 1(a)). Then, using a thermal analyzer (STA 449 Jupiter; Netzsch), a thermogravimetry measurement was performed in an argon atmosphere with a sample prepared by selectively etching the overcladding layer of the POF using chloroform²⁹; the 10-mg sample consisted of only the core and cladding materials. As indicated in Fig. 1(b), the sample carbonized at ~500°C, which is probably a result of heat degradation and gas generation. Carbonization was confirmed by comparing two polymer samples, each held in an argon-filled quartz tube with an 18.5 mm outer diameter (Fig. 1(c)) and kept at ~350 or ~600°C for 10 min. Transparent polymer, solidified from the molten state, was observed when the sample was heated to ~350°C (Fig. 1(d)), while carbide was formed at ~600°C (Fig. 1(e)).

Figure 1.

(a) Optical absorption of a POF (orange) and silica SMF (blue) measured as a function of the temperature. Light of 20 dBm at 1546 nm was injected into an 8-m POF, and the data for a 1-m-long germanium-doped silica SMF is taken from Ref. 19 (wavelength of 1064 nm). (b) Thermogravimetry curve, i.e. relative mass as a function of the temperature, of the polymer. (c–e) Photographs of the polymer samples in argon-filled quartz tubes before the temperature increase, after heating at ~350°C for 10 min, and after heating at ~600°C for 10 min, respectively.

Spectral analysis

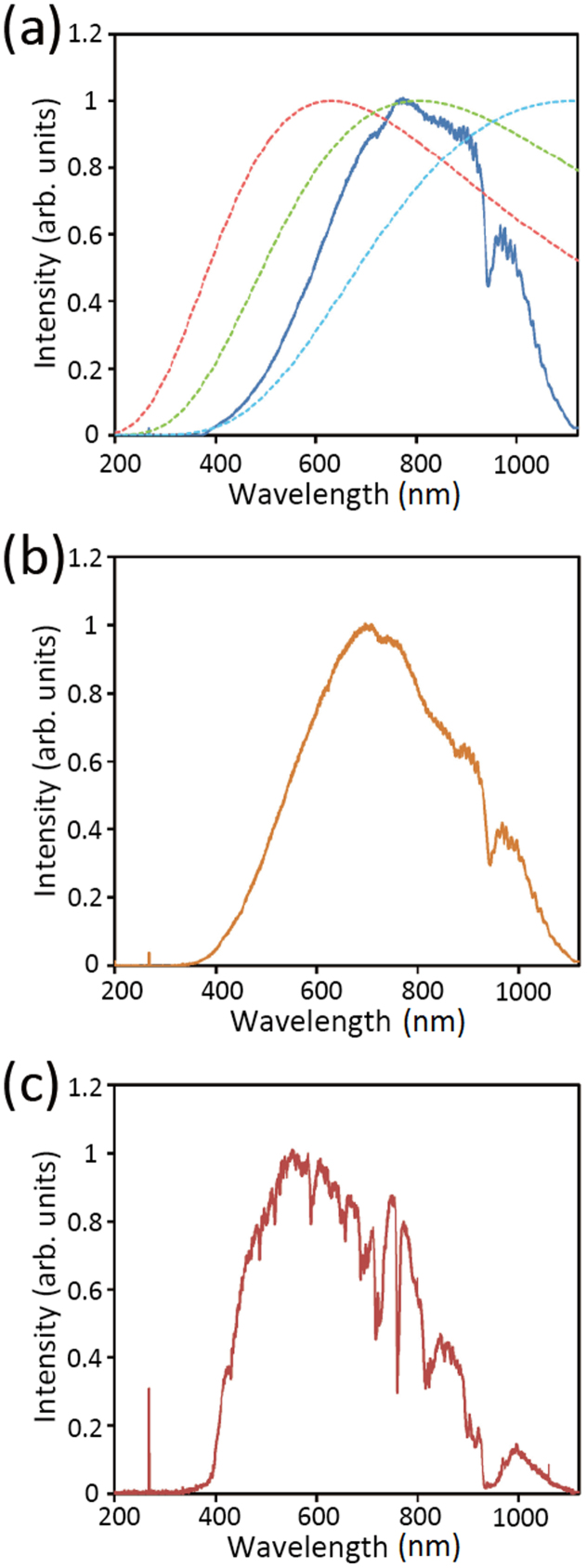
The emission spectrum of the bright spot propagating along the POF (~300 mW incident power) was measured using a spectrophotometer (Maya2000 Pro; Ocean Optics; 200–1100-nm wavelength), as shown in Fig. 2(a). The slow fuse propagation had hardly any influence on the measured spectral shape. Its comparison with the blackbody-like spectra of an incandescent light bulb (Fig. 2(b)) and sunlight (Fig. 2(c)) shows that, although the POF fuse spectrum has some characteristic peaks, all three spectra are similar (the sharp lines at ~280 nm are the instrumental noise). This would indicate that the bright spot of the POF fuse originates not so much from plasma emission as from thermal radiation, because if the bright spot mainly consists of plasma, the emission spectrum will generally contain some line-shaped components³⁰,³¹ (blackbody-like plasma emission can be induced by laser-driven implosion at a temperature of the order of keV (~10⁷ K)³²,³³, which is not the case here). Spectra theoretically calculated using Planck's law (Fig. 2(a)) indicate that the temperature of the bright spot is ~3600 K (also verified using Wien's displacement law); the difference in the spectral shape is due to the limited wavelength range of the spectrophotometer. Note that the temperature of the light bulb seems higher than that of the POF fuse by several hundreds of Kelvins, and that the surface temperature of the sun is >5000 K.

Figure 2. Emission spectra of (a) the bright spot of the POF fuse, (b) an incandescent light bulb, and (c) sunlight.

In (a), the aqua, green, and red dashed curves represent the normalized blackbody radiation spectra calculated theoretically at 2600, 3600, and 4600 K.

Propagation mechanism

The fiber fuse has also been observed in glass multimode fibers (MMFs), in which the shape of the molten area corresponds to a summation of the optical paths of all the propagating modes³⁴,³⁵. In contrast, the entire cross section of the core and cladding of a POF seems to melt (See Fig. 3(b) in Ref. 28), partly because their glass-transition temperature is as low as <108°C, and partly because the fuse propagation velocity is relatively slow; and the boundary between the molten and solid areas of the fiber cannot be observed. In the molten area of the POF, the bright spot travels only along the optical path of a particular propagating mode (that with the highest energy) that provides the bright spot with energy directly. The graded-index profile may be destroyed by high temperature, but the observed oscillating damage curve indicates that its time scale is long compared with the fuse propagation velocity. Here, the bright spot is probably attributed to the carbide; once generated at high temperature (>500°C), it absorbs the light and heats the adjacent polymer above the decomposition temperature, leading to its growth along the optical path. This behavior is analogous to metal particle manipulation by laser irradiation in glass³⁶,³⁷, i.e., carbide plays the same role as the metal particle that moves, emitting bright visible light and melting the surrounding glass by photothermal conversion, which supports the fact that the POF fuse is not a plasma but an optical discharge. The result is the oscillatory carbonized curve indicating the passage of the POF fuse. Interestingly, unlike the case for a silica MMF, light and electric current can simultaneously propagate through the POF after the passage of the fuse, because the generated continuous carbonized curve is electrically conductive while the optical propagation loss is approximately 1.4 dB/cm²⁸, which is too high for telecom use but sufficiently low for centimeter-order light propagation. This characteristic provides a possible scheme for a long photoelectric interaction length, and the optical absorption (or electric current/resistance) might be controlled by adjusting the electric current (or optical power) propagating along the POF, which will be useful in developing various optical/electrical devices.

Figure 3. (a,b) Two example micrographs of the POF fuse path containing voids.

Void formation

Figures 3(a) and (b) show the microscopic images of example POF fuse paths, obtained using a digital microscope (VHX-600; Keyence), along which gas bubbles are observed. The bubbles form randomly at places where the curvature of the fuse passage is maximal, but the formation is so irregular that sometimes bubbles are not observed, as in Fig. 3(b) in Ref. 28. As the surrounding polymer cools slowly, the gas generated by the passage of the fuse can move to energetically stable positions, as far away as possible from the hot solidified carbonized areas of the fiber. Despite their lateral shift from the optical path, the resulting bubbles are partially periodic, and somewhat similar to the void train observed in glass fibers. This experimental observation provides reasonable explanations for the slow propagation and the low threshold power density of the POF fuse, as discussed below.

Discussion

Irrespective of the fiber material, the fiber fuse phenomenon is an example of a dissipative soliton³⁸,³⁹, which is a useful concept to analyze the fuse properties including the fuse propagating velocity. According to the literature³⁹, by compressing the material contributions into one parameter, i.e. without using the physical properties particular to a silica SMF, the velocity of the fuse propagation can be mathematically expressed using a somewhat complicated equation (Eq. (9) in Ref. [39]), which can be simplified as Eq. (10) in Ref. [39]. Simple mathematical analysis of this equation qualitatively shows that, with decreasing thermal conductivity, the maximal velocity achievable is reduced. Here, the molten polymer after the fuse passage is cooled slowly enough for the generated gas to move, which indicates that the thermal conductivity in the POF is much lower than that in a silica SMF. Consequently, the velocity of the fuse propagation in the POF is slower than that in a silica SMF.

To explore the reason for the low threshold power density of the POF fuse, let us consider the threshold power P_th given as⁴⁰

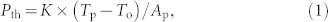where K is a proportionality constant, T_p is the temperature at which the optical absorption is maximal, T_o is room temperature (~300 K), and A_p is the absorption at T_p. This equation is valid under the assumption that the absorbed power is equal to the effective heat sink⁴⁰, i.e. that the velocity of the fuse propagation is sufficiently high compared to the thermal conduction so that it can be assumed that, from the viewpoint of the bright spot, a cold medium is constantly flowing by. This assumption is valid for the POF judging from the experimental results presented here. In the POF, P_th is 0.065 W, which corresponds to a power density of 6.6 kW/cm² and is much lower than the ~1.3-W threshold in a silica SMF⁴⁰. Consequently, the T_p and A_p values of the POF are much lower and higher, respectively, than those of the silica SMF. The lower threshold power density is thus a result of the lower temperature—at which the absorption is maximal—and the higher absorption at that temperature (as seen in Fig. 1(a)).

In summary, detailed analyses of the POF fuse propagation were presented. By spectral measurement, the bright spot was clarified to originate not from plasma emission but from thermal radiation, the temperature of which reaches approximately 3600 K. Furthermore, the reasons for the oscillation of the damage curve and for the low threshold power density were theoretically elucidated. The formation of gas bubbles was also newly reported. Moreover, potential use of the POF fuse as a scheme for a long photoelectric interaction length was presented. We hope that these findings will be useful in the design and implementation of future devices and systems exploiting high-power polymer fiber optics, including Brillouin-based distributed strain and temperature sensors.

Methods

POF samples

The POF used in the experiment is the same as in Ref. 28, i.e., a perfluorinated graded-index POF² (ID050; Sekisui Chemical) with a core (50 μm diameter), cladding (100 μm diameter), and overcladding (750 μm diameter) encased in polyvinyl chloride. The core and cladding layers are composed of doped and undoped polyperfluorobutenylvinyl ether, respectively. The refractive index at the center of the core is 1.356, whereas that of the cladding layer is 1.342. The propagation loss is relatively low (~250 dB/km) even at telecommunication wavelengths. The fiber fuse was initiated using a light source at 1546 nm in the same way as in Ref. 28.

Author Contributions

Y.M. and N.H. designed and performed the experiments. Y.M., H.T. and K.N. performed the experimental data analysis. Y.M. and S.T. performed the theoretical analysis. Y.M. wrote the manuscript with input from all co-authors.