Abstract
In this work we have developed a novel model of the deflection of primary cilia experiencing fluid flow accounting for phenomena not previously considered. Specifically, we developed a large rotation formulation that accounts for rotation at the base of the cilium, the initial shape of the cilium and fluid drag at high deflection angles. We utilized this model to analyze full three dimensional datasets of primary cilia deflecting under fluid flow acquired with high-speed confocal microscopy. We found a wide variety of previously unreported bending shapes and behaviors. We also analyzed post-flow relaxation patterns. Results from our combined experimental and theoretical approach suggest that the average flexural rigidity of primary cilia might be higher than previously reported (Schwartz et al. 1997). In addition our findings indicate the mechanics of primary cilia are richly varied and mechanisms may exist to alter their mechanical behavior.
Keywords: Primary Cilium, Modeling, Mechanical Loading, Mechanosensing, Fluid Dynamics
1. Introduction
The primary cilium was first described as an immotile cylindrical extension from the cell surface almost a century ago (Davenport and Yoder 2005). The cilium originates from the basal body that is anchored to the cell cytoskeleton through basal feet, microtubules, and striated rootlets. Recently the primary cilium has been implicated as a mechanosensor essential for regulating cell physiology in bone (Anderson et al. 2008; Temiyasathit and Jacobs 2010, Xiao et al. 2006 ), kidney (Gunay-Aygun 2009), liver (Gunay-Aygun 2009), and development in the embryonic node (Goetz and Anderson 2010). The structure of the primary cilium is critical for its function as defects are associated with diseases such as cancer (Michaud and Yoder 2006), polycystic kidney and liver disease (Gunay-Aygun 2009), obesity (Sen Gupta et al. 2009), and osteoarthritis (McGlashan et al. 2006). However relatively little is known about the mechanical properties of the primary cilium, the molecular mechanics that regulate ciliary deflection, and how this system is affected by physical stimulation.
Understanding the mechanical properties of the primary cilium is crucial to uncovering the specific molecular systems involved in mechanotransduction. Praetorius and Spring demonstrated that bending of kidney epithelial primary cilia results in a dramatic extracellular-calcium-dependent increase in intracellular calcium concentration, which was subsequently lost with removal of the primary cilium (Praetorius and Spring 2001; 2003). This mechanosensory response occurs via polycystin 2, a stretch-activated cationic channel located at the base of the primary cilium (Nauli et al. 2003; Masyuk et al. 2006). Cells subjected to orbital shaking also showed a reduction in primary cilium length that correlated with decreased cellular mechanosensing (Resnick and Hopfer 2007; Besschetnova et al. 2010). These data, and others, demonstrate that the primary cilium is a sensor for extracellular physical signals and may dynamically alter its mechanosensitive response by modulating its structure (Gardner et al. 2010).
There are only a few models present in the literature to describe the mechanical behaviors of the primary cilium. Schwartz et al. was the first to model the primary cilium as a thin elastic beam undergoing large rotations with constant fluid drag acting on the entire length (Schwartz et al. 1997). They quantified the product EI, or flexural rigidity as a measure of the effective beam stiffness accounting for both material and geometric factors. However, their model was limited by the assumption of constant fluid velocity as a function of length and did not account for the known linear velocity profile with distance from a no-slip boundary. Liu et al. developed a similar model utilizing a more realistic fluid flow profile. They examined the torque acting at the base of the primary cilium, but only allowed for only small angle rotations (Liu et al. 2005). A finite element model of the primary cilium incorporating the apical membrane was developed by Rydholm et al. to determine the relationship between shear stress due to flow and the release of intracellular calcium (Rydholm et al. 2010). These models have provided vital insight to our current understanding of the mechanics of the primary cilium, but a more sophisticated model incorporating base rotation, initial shape, and a realistic treatment of fluid drag are necessary to fully delineate the role of mechanics in mechanosensing by primary cilia.
In this study we investigated the mechanical properties of primary cilia by developing a coupled fluid-structure interaction model which, for the first time, combines 3D fluid dynamics with a large-rotation beam formulation and allowed for a curved initial shape and rotation of the cilium anchorage. Drag acting on the cilium was determined both analytically for 2D stokes flow around a cylinder and with a 3D fluid dynamics finite element simulation. For the first time high-speed confocal microscopy was used to acquire 3D images of primary cilia under flow, uncovering a wide range of deflection shapes and post flow relaxation patterns. With these novel modeling and imaging approaches we observed significantly different flexural rigidity (EI) values than had previously been reported and further, suggest that the mechanics of the primary cilium are more varied, and perhaps adaptable, than previously reported.
2. Methods
2.1 Cell Culture
Inner medullary collecting duct (IMCD) cells, transfected with a somatostatin receptor-3 GFP fusion protein that targets the primary cilium, were a gift from Prof. Brad Yoder (University of Alabama at Birmingham)(Berbari et al. 2008). The cells were cultured in DMEM/F12 (1:1) medium (Invitrogen) with 10% fetal bovine serum, 1% penicillin/streptomycin (Invitrogen) and 200μg/mL geneticin G4-18 antibiotic (Invitrogen) at 37°C with 5% CO2. For fluid flow imaging, cells were cultured on type I collagen (BD) coated 22 × 40 mm coverglass (Warner Instruments) and grown to 80-90% confluence followed by serum starvation (medium with no FBS) 48 hours prior to imaging (Ruhfus et al. 1998).
2.2 Fluid Flow
Steady fluid flow was applied to the cells in a RC-30 laminar flow chamber (Warner Instruments) by a syringe pump (Genie Plus, Kent Scientific) with a 30mL syringe (BD). The flow rate used was 500 μl/min with PBS as the perfusion liquid. Assuming laminar flow for a parallel plate geometry, the flow velocity is assumed to be 0 at the surface and increases linearly with distance from the surface. The flow velocity used corresponded to a 0.25 Pa wall shear stress. In a separate experiment on cilium recovery 1, 2 and 3 ml/min flow rates corresponding to 0.5, 1 and 1.5 Pa wall shear stress were used. Thermal gradients were minimized by allowing the flow chamber to adjust to room temperature for one hour prior to imaging.
2.3 Imaging
A Leica TCS SP5 laser scanning confocal microscope was used to capture full 3D images of primary cilia with a 100x, 1.46 NA oil immersion objective. The cells were imaged with an argon laser at 488nm excitation and the emitted light was collected at 509nm. The microscope was equipped with a 16kHz resonant bidirectional scanner and a SuperZ Galvo z-stage that was able to collect a z-stack of 30, 512×512 images of a single cilium in ≈ 2.5s. Cells were imaged in the center of the chamber to reduce wall effects (Bacabac et al. 2005).
2.4 Visualization of the plasma membrane
Wheat germ agglutinin (WGA) fluorescently labeled with Alexa 594 (Invitrogen) was used to stain the cell membrane of living cells. Cells were washed with PBS and then incubated with 5μg/mL WGA dissolved in Hank’s buffered salt solution (Invitrogen) for 10 min at 37°C and imaged immediately post incubation.
2.5 Imaging Processing
The image stacks were extracted as TIFF images and processed with Matlab to find the primary cilium coordinates. Images were read and converted into 8bit greyscale images and a Gaussian filter, with a smoothing parameter of σ =200nm and dimensions of 4σ × 4σ, was applied to decrease noise before applying a threshold. The x and y components of the sampled pixels were averaged and taken as the center of the cilium. Images of the plasma membrane were deconvoluted with Huygens Deconvolution Software (Scientific Volume Imaging, SVI) and were reconstructed in 3D with freeSFP (SVI).
3 Model Development
3.1 Theory
The primary cilium was modeled as a thin, elastic, homogenous beam with a uniform cross-section along its length. Assuming an elastic material with a uniform cross section, Euler-Bernoulli beam theory yields
| (1) |
where θ is the angle between the tangent and the vertical, M is the bending moment, s is the position along the beam ranging from the tip at 0, to the base at L, E is the Young’s modulus of elasticity and I is the second moment of inertia (Holden, 1972). Note that this formulation assumes infinitesimal strain, but it does not make a small angle approximation, so large rotations are acceptable. Figure 1 illustrates the parameterization our model utilizes.
Figure 1.
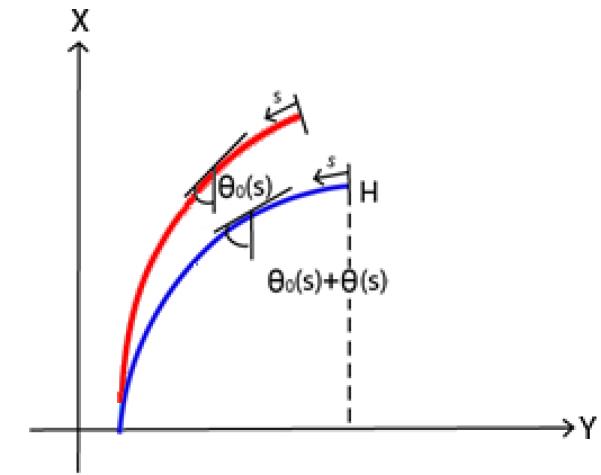
Parameter system used with the model. Here H is the vertical distance between the tip and the base, θ is the angle the cilium forms with respect to the vertical, and s is zero at the free end and L at the fixed end. The red line is the non-stressed position while the blue line is the deflected position. Here, θo(s) is the angle of the non-stressed cilium and θ(s) is angle of the cilium under fluid flow.
The equilibrium conditions for the beam in the x and y directions imply
| (2) |
where
| (3) |
| (4) |
where qx and qy are the force per unit length acting along the beam in the x and y directions, and σ is the location along the beam (Frisch-Fay 1962). As flow is unidirectional in the y direction, we assumeqx = 0 so Qx = 0 and thus Equation (2) becomes
| (5) |
To account for the initial shape of the non-stressed beam we introduceθ0(S), the beam configuration in the absence of load, thus Equation (5) becomes
| (6) |
We assumed cantilevered beam boundary conditions with a specified rotation θbase at the fixed end (s = L) and a zero bending moment at the free end (s = 0),
| (7) |
| (8) |
We also considered the relationship between the fluid velocity field and the hydrodynamic drag on the cilium, Qy. As mentioned previously, laminar flow velocity adjacent to the bottom surface of a parallel plate flow chamber increases linearly with distance from the surface. To determine the drag force acting on the cilium at a given height, h, a 2D approximation for drag per unit length based on the local fluid velocity V(h) can be used. We first find h for the cilium configuration,
| (9) |
where H is the height from the tip of the cilium to the cell surface and σ is the position along the beam. Using h we define the velocity V(h) as
| (10) |
where τ is the wall shear stress and μ is the dynamic viscosity. The 2D planar drag force acting on a cylinder in low Reynolds number Stokes flow is
| (11) |
Where d is the diameter and L is the length of the primary cilium (Venier et al. 1994).
Although using Equation (11) to derive the drag force per length acting on a cylinder is simple, it becomes invalid at large rotations, since the cross section of the cilium is no longer circular and there is an induced z-component of flow which the 2D approximation cannot account for. Thus a second method was developed using the commercial finite element code COMSOL. A section of a cilium was modeled as a cylinder in low Reynolds number Stokes flow (Figure 2) with roughly 25,000 elements. The angle between the cylinder and vertical was varied from 0 to 80° and total drag determined at each angle and fit with a polynomial regression. Convergence was verified by creating a refined mesh of 85,000 elements and observing less than a 15% change in predicted drag.
Figure 2.
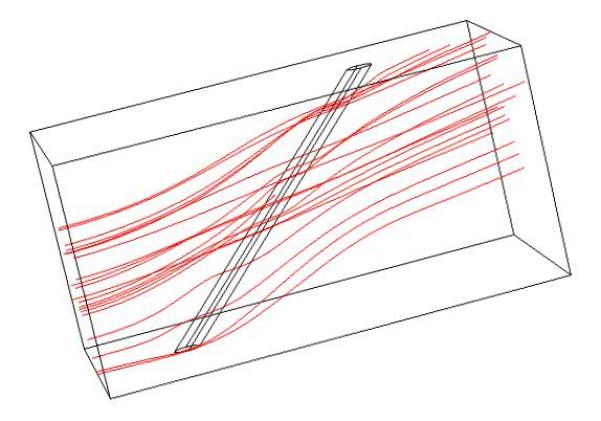
Typical fluid streamlines predicted from the Comsol finite element model. The model was re-solved for various cylinder angles and total drag force calculated.
3.2 Numerical Implementation
A numerical approach for solving (6) was implemented since there is no solution for this two-point boundary value problem. In addition, since the problem is non-local, that is the force at a given s depends on the entire θ(s) curve, traditional boundary value problem solvers cannot be utilized. Instead, a shooting method was employed which integrates a series of initial value problems to solve the boundary value problem (Osborne 1969). Specifically we used a fourth order Runge Kutta scheme to integrate (6) for trial values of θ(0) and H. We then used the residual at the distal boundary (s=L) and (9) to iteratively improve the trial values with the secant method alternating between θ(0) and H until the boundary condition (Equation 7) at s = L, the base of the cilium, was satisfied with a tolerance of 10−12m.
3.3 Parameter Estimation
A parameter optimization procedure was implemented to varying EI in (6) to minimize the difference between experimentally determined shapes and the predicted solution. The algorithm consisted of four steps: (1) The initial non-stressed configuration, θ0(s), was calculated, (2) the value of θbase was calculated, (3) EI was calculated for 2D analytic drag approximation, and (4) EI was calculated using the drag predicted from the 3D finite-element simulation.
To solve Equation (6) θ0(s) must be known. A fourth order polynomial was fit through the x, y, z coordinates in no-flow conditions and was used to interpolate to find θ0(s). Next, for the cilium in its deflected configuration the four θ(s) values nearest s=L were averaged to find θbase. The parameter estimation process then begins with an initial guess for EI and (6) is solved as described above. This solution is then compared with the coordinates of the primary cilium from experimental data and the residual error calculated as the average distance between the known coordinates and the generated solution
| (12) |
where R is the residual, D is the distance between each set of points, n is the maximum number of coordinates, xA,yA are the coordinates from the data, xB,yB are the coordinates from the solution in the same plane and i denotes the specific coordinate along the length of the cilium. We then iteratively minimized the residual with an update formula for EI such that
| (13) |
where α is the step size and β is the direction of the step (Figure 3:A). If the residual increases after a subsequent guess, the sign for β is changed to reverse the step direction, and α is halved. This was repeated until the change in the residual fell below a specified tolerance of 2.4 × 10−7 m (Figure 3:B).
Figure 3.

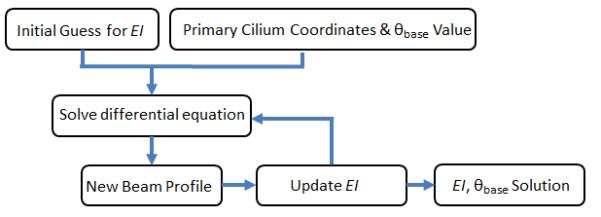
Estimating EI and θbase from the observed deflection. (A) Shows how the different values of EI affect the solution of the model. (B) A flowchart depicting the fitting algorithm.
4 Results
4.1 Cilia Deflection and Experimental Observations
We observed a variety of primary cilia deflection and post flow relaxation shapes. The vast majority exhibited a smooth bending curve similar to those previously reported (Figure 4:A-B)(Malone et al. 2007). Occasionally we observed rigid linear deflections as in Figure 5(A-B). These deflections are characterized by large rotations at the cilium base and relatively little bending of the axoneme, perhaps indicative of a decreased degree of cilium anchorage. Another behavior observed during higher flow rates was a kinked cilium (Figure 6) characterized by two linear segments of low bending joined by a localized region of high curvature. Interestingly some primary cilia subjected to the 3ml/min flow rate did not return to the same non-stressed, pre-flow position after flow had ceased as shown in Figure 7. Other cilia displayed a slight recovery towards the original non-stressed position after flow had ceased, but did not fully recover. This would indicate that primary cilia are capable of undergoing both elastic and plastic deformation.
Figure 4.
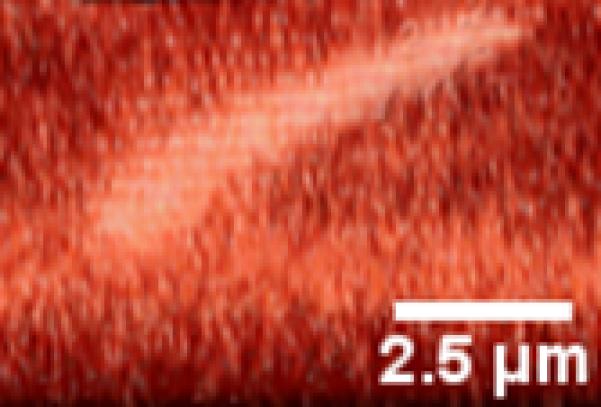
A primary cilium deflecting under increasing fluid flow. Direction of flow is from left to right. (A) Non-stressed conditions. (B) 500ul/min flow
Figure 5.

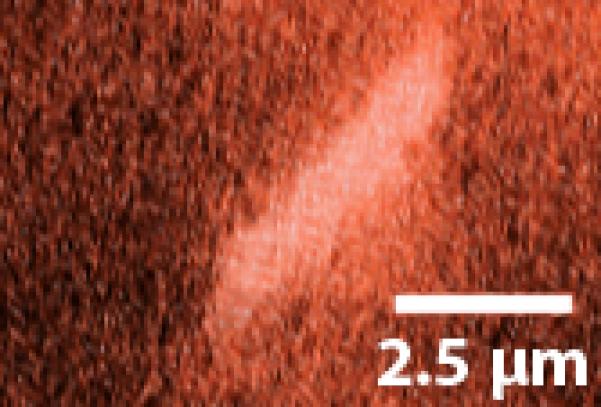
An example of a cilium exhibiting very little bending of the axoneme. Rather, deflection is caused by rotation of the base. (A) No-flow conditions (B) Flow.
Figure 6.

A “kinked” deflection profile. The primary cilium exhibits a unique non-linear bending profile with fluid flow.
Figure 7.
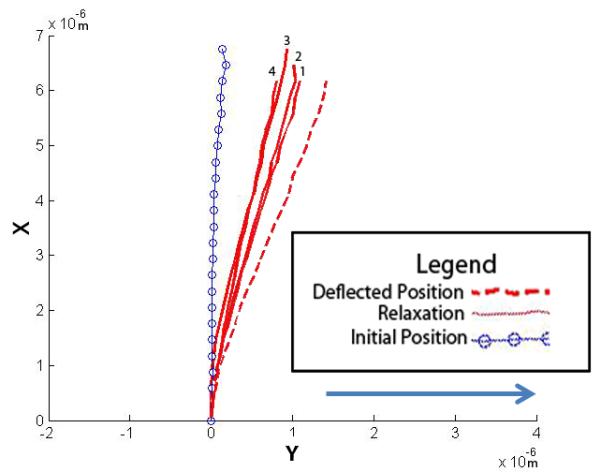
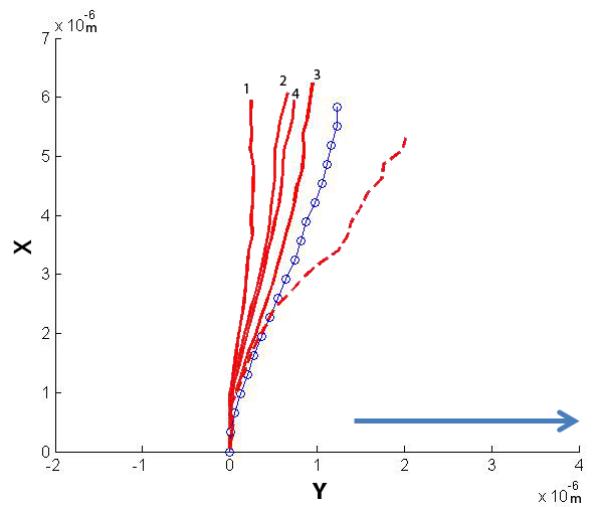
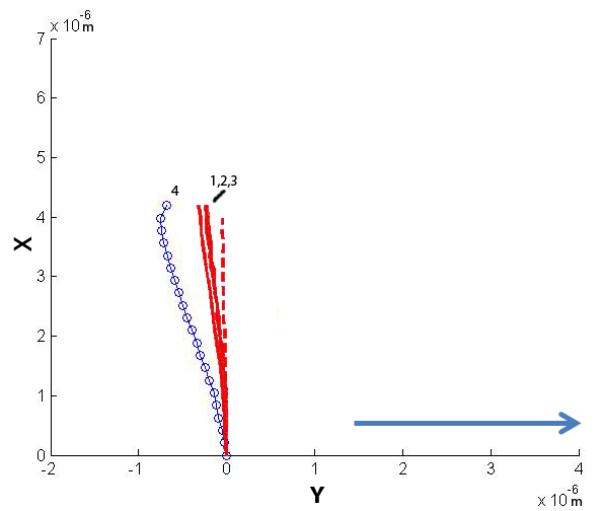
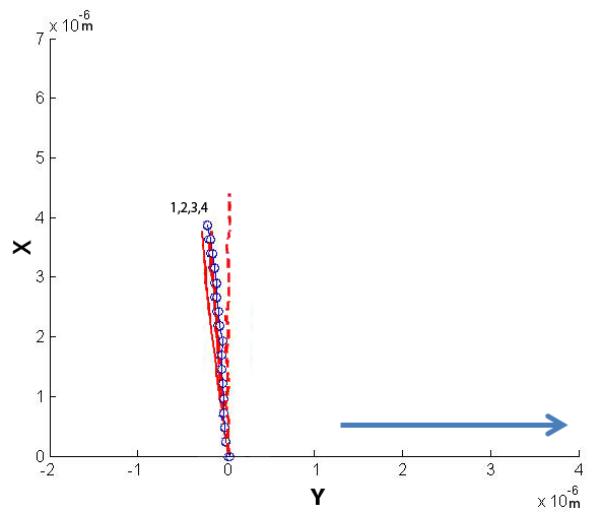
Four cilia were exposed to higher flow rates and their post-flow relaxation imaged. The plots show the initial non-stressed position, the maximum deflected position and the relaxation positions. The four relaxation positions are noted 1-4, with 1 being the first time point taken at time = 0 min, and 4 being the last at time = 2 min (30 second interval between each point). The arrow indicates the direction of fluid flow.
4.2 Parameter estimation
We solved the parameter estimation problem described above with both the analytical and fluid dynamics drag assumptions to find the flexural rigidity of the primary cilium for the physiological flow rate of 500μl/min (Figure 8). For the 6 individual cilia we examined under physiological flow conditions, the average basal rotation was found to be 10.1 ± 2.8° (mean ± SEM). The best-fit EI value for the analytical drag model were slightly larger (3.1 ± 0.7 × 10−22 Nm2) than for the finite element approach (2.1 ± 0.45 × 10−22 Nm2), but the difference was not statically significant. The parameter estimation allowed for a precise fit between the solution and the coordinates for an average cilium with a length of 5.2 ± 1.3 × 10−6m and a mean solution residual of 3.8 × 10−22m.
Figure 8.
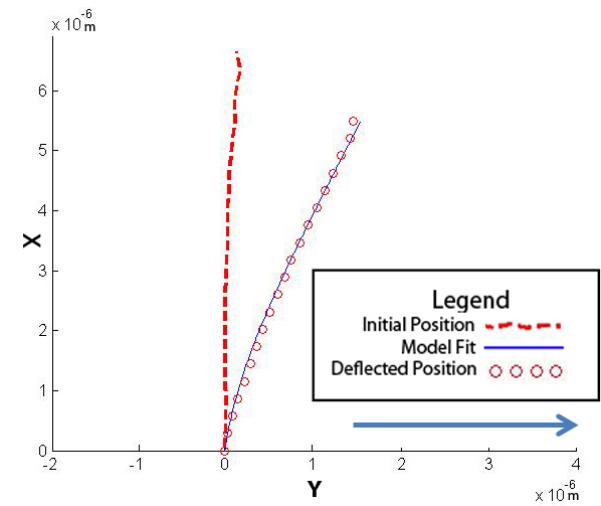
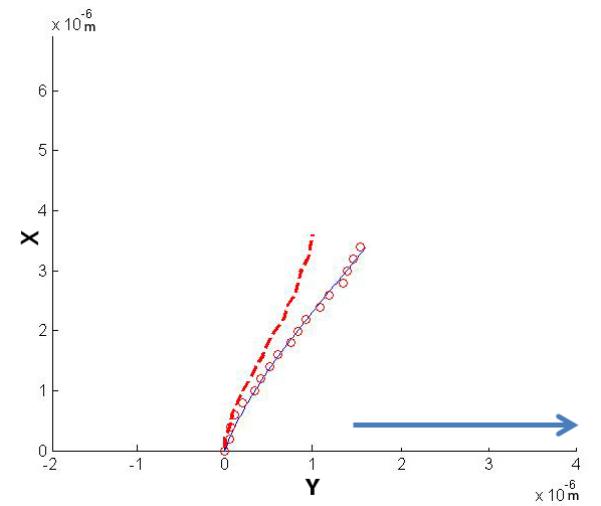
Representative numerical solutions for y and x from the parameter estimation of single primary cilium subjected to fluid flow at 500ul/min with (A) a vertical initial configuration and (B) a non-vertical initial configuration. The solution to the model fit the confocal images of a primary cilium deflection. The direction of fluid flow is indicated by the arrow.
4.3 Membrane Staining
Our membrane staining experiment allowed us to examine the spatial relationship between the primary cilia axoneme and the cell membrane. Many cilia were observed following the conventional archetype (Figure 9) of a vertical protrusion. Some of these cilia were non-vertical, yet still protrusive. Others were partially invaginated within the cell membrane and were observed to have significant portions of the axoneme embedded within the cell.
Figure 9.
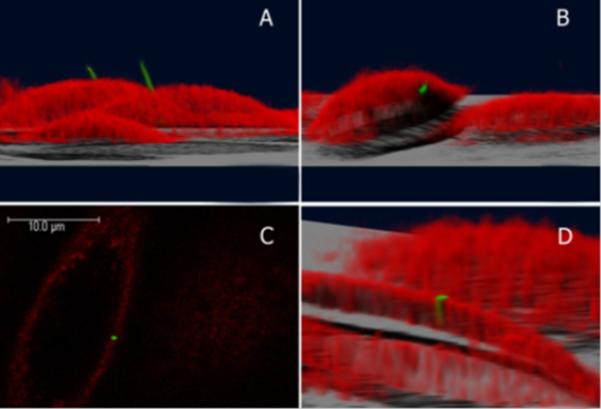
The position of the primary cilium on a cell. The cilium is green and the cell membrane is red. (A), (B), and (D) are 3D reconstructions of the cell. (A) The primary cilium projecting from the top of the cell into the extracellular space. (B) Sometimes the primary cilium is embedded within the cell membrane. (C) Confocal image slice from (B) of the cilium surrounded by the cell membrane. (D) A 3D reconstruction of (B) where the cell was cut at a selected height to visualize the embedded cilium.
5. Discussion
Here we advanced the current primary cilium modeling techniques by implementing, for the first time, a model that allowed for base rotation, accounted for the initial non-stressed shape of the cilium and utilized a 3D fluid dynamics model to determine the drag acting on the cilium. Our results indicate a greater variability in cilium mechanics than previously appreciated.
The work we have presented here resulted in a flexural rigidity for primary cilia of roughly 2 × 10−22 Nm2. This is a 17 fold higher value than that previously reported by Schwartz et al. This difference may be due to differences in the modeling approaches (Schwartz et al. 1997). It may also be due to experimental differences including a different cell line and that we used a shear stress (0.25 Pa) two order of magnitude higher (Donahue et al, 2003). For comparison purposes, the flexural rigidity of nine microtubules acting independently would be expected to be roughly 7 × 10−23 Nm2 (Kikumoto et al. 2006). Another point of comparison is the flexural rigidity of the microtubule-doublet-based Clamydomonas flagellum, reported to be 1-15 × 10−21 Nm2 (Okamoto et al. 2011), an order of magnitude higher than our observations. This is perhaps not surprising considering the flagellar structure. Flagella possess similar axoneme architecture to primary cilia (nine outer microtubule doublets), but these outer doublets are interconnected with nexin linking proteins. Flagella also have an additional central doublet, which is connected to the other doublets through radial spokes. Thus, the flagellum appears to be highly crosslinked which in the doublets act as part of an integrated whole. In contrast, primary cilia lack many of these crosslinking structures and our data are consistent with this. This suggests primary cilia possess less crosslinking than flagella, but a higher flexural rigidity than would be expected if the doublets acted entirely independent of each other.
Variations in the support structures and anchorage of the basal body would also have an effect on cilium mechanics. We observed on average a 10° rotation at the base of the cilium. The primary cilium projects from the basal body, which is anchored to the cell cytoskeleton through a variable number of basal feet (1-5 conical support structures oriented laterally in all directions), microtubules (10-100) and striated rootlets (varying number of filamentous structures branching out into the cytoplasm)(Alieva et al.1992). The number of these support structures is dynamic and varies during the cell cycle and appears to be under hormonal regulation (Hagiwara et al. 2000). This suggests that in addition to axonemal bending, the competence of the basal body anchorage may be under biological control regulating the mechanics of the overall structure.
Another fascinating observation was the kinked deflection profile suggesting that perhaps only a portion of the cilium was exposed to flow (Figure 6). This may occur because the lower portion is within a membrane invagination (Figure 9:D), or may be shielded from flow by the cellular glycocalyx (Reilly et al. 2003). It is possible that this effect completely protects short primary cilia from deflecting or may regulate mechanosensitivity by changing the length of the cilium exposed to flow. Wheatley et al. suggests that the coiled structure of the striated rootlets could act in a similar way to muscle for contraction (Wheatley, 2008). The striated rootlets could then act as an anchor able to pull the cilium into the cell in response to physical stimuli. Rydholm et al. reported the base portion of cilia they imaged did not deflect under fluid flow and they attributed this to a greater EI value near the base (Rydholm et al. 2010). We also observed this phenomenon for some cilia (Figure 9:D) and this may be due to a varying EI. It also may be the result of regions of the cilium being either embedded within the glycocalyx or invaginated within the membrane. If this were to occur, cilium deflection may be variable long the length with a constant flexural rigidity, although we do not have direct evidence either way.
A unique aspect of this study is that it is the first examination of the mechanics of primary cilia as they return to equilibrium after the removal of mechanical loading. Interestingly, of the four primary cilia observed only one exhibited an elastic response, i.e. returned to its initial non-stressed position after fluid flow. Two cilia exhibited a new non-stressed configuration ~2 minutes after fluid flow had stopped that was intermediate between the configurations during and prior to flow. Furthermore, in both cases they retained this configuration for at least 20 minutes after flow. This suggests that in some cilia there may be permanent or plastic deformation occurring due to fluid flow. Finally, one cilium moved past its pre-flow configuration when flow was removed. This is suggestive that active remodeling of the cilium structure is occurring because neither elastic nor plastic mechanisms can “overcorrect” in this manner.
Although our model is an advancement from previous models, there were some issues which have not been addressed. We assumed the force in the x direction (along the length of the cilium), qx, in Equation (2) was zero. This was justified in the development because the predominant component of drag is in the plane of flow. Even in the 3D calculation which accounted for drag in both directions, it was assumed that only the perpendicular component of force was affecting cilium bending. Thus, only bending was considered and tensional force within the cilium was neglected.
In this work we observed a wide spectrum of mechanical properties, initial cilium shapes, and unique post-flow relaxation responses. The molecular mechanism(s) responsible for this richness of mechanical behavior are unknown, but several potential candidates can be proposed. For example, the microtubule doublets in the primary cilium can undergo different levels of posttranslational modification including polyglutamylation, phosphorylation, and acetylation (Westermann and Weber, 2003). Interestingly, physiologic levels of mechanical stimulation has been shown to greatly increase acetylation levels by decreasing the activity of deacetylase enzyme HDAC6 (Geiger et al. 2009). This increase in acetylation coincides with the increase of microtubule associated proteins (MAPs) which bind to microtubules and have been shown to increase microtubule flexural rigidity as much as 8-fold (Takemura et al.1992; Felgner et al. 1997). Poole et al. have shown that MAPs can link neighboring microtubule doublets to each other as well as to collagen fibers (Poole et al. 2001). To fully understand how these molecular-level events affect primary cilium mechanics, mechanosensing, and ultimately cellular mechanobiology, a multi-scale modeling approach is necessary. Such an approach would need to incorporate complex fluid dynamics with coarse-grained molecular dynamics at one or more structural levels.
6. Conclusions
Our novel model of the primary cilium provides an approach to simulate its mechanical behavior and provide a more precise fit to in vitro data than previous models. Accounting for both the base rotation and the initial shape of the cilium allows for a more accurate estimate of flexural rigidity. Analysis of the data acquired from confocal microscopy suggests the mechanical properties of primary cilia are more heterogeneous than initially anticipated. Further investigation should probe the question of how the mechanics of the primary cilium relate to with the mechanics of the basal body and the cytoskeleton. The model presented here coupled with the advanced imaging techniques provides a valuable tool for investigating the mechanical properties of the primary cilium.
Acknowledgements
This publication was made possible by grants AR45989, AR54156 and AR62177 from NIAMS/NIH ; New York State Stem Cell Research Grant N08G-210; NSF Graduate Research Fellowship; and a IRCSET-Marie Curie International Mobility Fellowship in Science.
References
- Alieva IB, Nadezhdina ES, Vaisberg EA, Vorobjev IA. Microtubule and intermediate filament patterns around the centrosome in interphase cells. The Centrosome. 1992;15:103–129. [Google Scholar]
- Anderson CT, Castillo AB, Brugmann SA, Helms JA, Jacobs CR, Stearns T. Primary cilia: cellular sensors for the skeleton. Anat Rec (Hoboken) 2008;291(9):1074–1078. doi: 10.1002/ar.20754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbac RG, Smit TH, Cowin SC, Van Loon JJWA, Nieuwstadt FTM, Heethar R, Klien-Nulend J. Dynamic Shear Stress in Paralell-Plate Flow Chambers. J Biomech. 2005;38(1):159–167. doi: 10.1016/j.jbiomech.2004.03.020. [DOI] [PubMed] [Google Scholar]
- Besschetnova TY, Kolpakova-Hart E, Guan Y, Zhou J, Olsen BR, Shah JV. Identification of signaling pathways regulating primary cilium length and flow-mediated adaptation. Curr Biol. 2010;20(2):182–187. doi: 10.1016/j.cub.2009.11.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davenport JR, Yoder BK. An incredible decade for the primary cilium: a look at a once-forgotten organell. Am J Physiol Renal Physiol. 2005;289(6):F1159–69. doi: 10.1152/ajprenal.00118.2005. [DOI] [PubMed] [Google Scholar]
- Donahue TLH, Haut TR, Yellowley CE, Donahue HJ, Jacobs CR. Mechanosensitivity of bone cells to oscillating fluid flow induced shear stress may be modulated by chemotransport. J Biomech. 2003;36:1363–1371. doi: 10.1016/s0021-9290(03)00118-0. [DOI] [PubMed] [Google Scholar]
- Felgner H, Frank R, Biernat J, Mandelkow EM, Mandelkow E, Ludin B, Matus A, Schliwa M. Domains of neuronal microtubule-associated proteins and flexural rigidity of microtubules. J Cell Bio. 1997;138(5):1067–75. doi: 10.1083/jcb.138.5.1067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisch-Fay R. Flexible bars. Butterworths; Washington, D.C.: 1962. [Google Scholar]
- Gardner K, Lavagnino M, Caballero O, Leven J, Arnocky SP. The Effect of Stress Deprivation and Cyclic Loading on the Length of Tendon Cell Cilia. J Orthopaedic Res. 2011;29(4):582–587. doi: 10.1002/jor.21271. [DOI] [PubMed] [Google Scholar]
- Geiger RC, Kaufman CD, Lam AP, Budinger GR, Dean DA. Tubulin acetylation and histone deacetylase 6 activity in the lung under cyclic load. Am J Respir Cell Mol Biol. 2009;40(1):76–82. doi: 10.1165/rcmb.2007-0307OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goetz SC, Anderson KV. The primary cilium: a signalling centre during vertebrate development. Nature Reviews Genetics. 2010;11(5):331–344. doi: 10.1038/nrg2774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunay-Aygun M. Liver and kidney disease in ciliopathies. Am J Med Genet C Semin Med Genet. 2009;151C(4):296–306. doi: 10.1002/ajmg.c.30225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holden JT. On the finite deflections of thin beams. Int. J. Solids Structures. 1972;8:1051–1055. [Google Scholar]
- Hagiwara H, Kano A, Aoki T, Ohwada N. Immunocytochemistry of the striated rootlets associated with solitary cilia in human oviductal secretory cells. Histochem Cell Biol. 2000;114:205–212. doi: 10.1007/s004180000184. [DOI] [PubMed] [Google Scholar]
- Kikumoto M, Kurachi M, Tosa V, Tashiro H. Flexural rigidity of individual microtubules measured by a buckling force with optical traps. Biophys J. 2006;90:1687–1696. doi: 10.1529/biophysj.104.055483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb H. On the uniform motion of a sphere through a viscous fluid. Philosophical Magazine and Journal of Science. 1911;21(121):112–121. [Google Scholar]
- Liu W, Murcia NS, Duan Y, Weinbaum S, Yoder BK, Schwibert E, Satlin LM. Mechanoregulation of intracellular Ca2+ concentration is attenuated in collecting duct of monocilium-impaired orpk mice. Am J Physiol Renal Physiol. 2005;289(5):F978–988. doi: 10.1152/ajprenal.00260.2004. [DOI] [PubMed] [Google Scholar]
- Malone AMD, Anderson CT, Tummala P, Kwon RY, Johnston TR, Stearns T, Jacobs CR. Primary cilia mediate mechanosensing in bone cells by a calcium-independent mechanism. PNAS. 2007;104(33):13325–13330. doi: 10.1073/pnas.0700636104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masyuk AI, Masyuk TV, Splinter PL, Huang BQ, Stroope AJ, LaRusso NF. Cholangiocyte cilia detect changes in luminal fluid flow and transmit them into intracellular Ca2+ and cAMP signaling. Gastroenterology. 2006;131(3):911–920. doi: 10.1053/j.gastro.2006.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGlashan SR, Jensen CG, Poole CA. Localization of extracellular matrix receptors on the chondrocyte primary cilium. J Histochem Cytochem. 2006;54(9):1005–1014. doi: 10.1369/jhc.5A6866.2006. [DOI] [PubMed] [Google Scholar]
- Michaud EJ, Yoder BK. The primary cilium in cell signaling and cancer. Cancer Res. 2006;66(13):6463–6467. doi: 10.1158/0008-5472.CAN-06-0462. [DOI] [PubMed] [Google Scholar]
- Nauli SM, Alenghat FJ, Luo Y, Williams E, Vassilev P, Li X, Elia AE, Lu W, Brown EM, Quinn SJ, Ingber DE, Zhou J. Polycystins 1 and 2 mediate mechanosensation in the primary cilium of kidney cells. Nat Genet. 2003;33(2):129–137. doi: 10.1038/ng1076. [DOI] [PubMed] [Google Scholar]
- Okamoto RJ, Ying J, Lewis BL, Ranz EC, Sho J-Y, Dutcher SK, Bayly PV. Flexural rigidity of intact Chlamydomonas flagella measured with an optical trap. ASME: Summer bioengineering Conference; Farmington, Pennsylvania. 2011. [Google Scholar]
- Osborne MR. On shooting methods for boundary value problems (Shooting method difficulties in boundary value problem numerical solutions using computer programs to integrate differential equations) J Math An App. 1969;27:417–433. [Google Scholar]
- Poole CA, Zhang ZJ, Ross JM. The differential distribution of acetylated and detyrosinated alpha-tubulin in the microtubular cytoskeleton and primary cilia of hyaline cartilage chondrocytes. J Anat. 2001;199(Pt 4):393–405. doi: 10.1046/j.1469-7580.2001.19940393.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Praetorius HA, Spring KR. Bending the MDCK cell primary cilium increases intracellular calcium. J Membr Biol. 2001;184(1):71–79. doi: 10.1007/s00232-001-0075-4. [DOI] [PubMed] [Google Scholar]
- Praetorius HA, Spring KR. Removal of the MDCK cell primary cilium abolishes flow sensing. J Membr Biol. 2003;191(1):69–76. doi: 10.1007/s00232-002-1042-4. [DOI] [PubMed] [Google Scholar]
- Reilly GC, Haut TR, Yellowley CE, Donahue HJ, Jacobs CR. Fluid flow induced PGE2 release by bone cells is reduced by glycocalyx degradation whereas calcium signals are not. Biorheology. 40(6):591–603. [PubMed] [Google Scholar]
- Resnick A, Hopfer U. Force-Response Considerations in Ciliary Mechanosensation. Biophys. J. 2007;93(4):1380–1390. doi: 10.1529/biophysj.107.105007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruhfus HB, Bauernschmitt G, Kinne RKH. Properties of a polarized primary culture from rat renal inner medullary collecuting duct (IMCD) cells. In vitro Cell Dev Biol – Animal. 1998;34:227–231. doi: 10.1007/s11626-998-0128-4. [DOI] [PubMed] [Google Scholar]
- Rydholm S, Zwartz G, Kowalewski JM, Kamali-Zare P, Frisk T, Brismar H. Mechanical Properties of Primary Cilia Regulate the Response to Fluid Flow. Am J Physiol Renal Physiol. 2010;298(5):F1096–F1102. doi: 10.1152/ajprenal.00657.2009. [DOI] [PubMed] [Google Scholar]
- Schwartz EA, Leonard ML, Bizios R, Bowser SS. Analysis and modeling of the primary cilium bending response to fluid shear. Am J Physiol. 1997;272(1 Pt 2):F132–138. doi: 10.1152/ajprenal.1997.272.1.F132. [DOI] [PubMed] [Google Scholar]
- Sen Gupta P, Prodromou NV, Chapple JP. Can faulty antennae increase adiposity? The link between cilia proteins and obesity. J Endocrinol. 2009;203(3):327–336. doi: 10.1677/JOE-09-0116. [DOI] [PubMed] [Google Scholar]
- Takemura R, Okabe S, Umeyama T, Kanai Y, Cowan NJ, Hirokawa N. Increased microtubule stability and alpha tubulin acetylation in cells transfected with microtubule-associated proteins MAP1B, MAP2 or tau. J Cell Sci. 1992;103(Pt 4):953–64. doi: 10.1242/jcs.103.4.953. [DOI] [PubMed] [Google Scholar]
- Temiyasathit S, Jacobs CR. Osteocyte primary cilium and its role in bone mechanotransduction. Ann N Y Acad Sci. 2010;1192(1):422–428. doi: 10.1111/j.1749-6632.2009.05243.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venier P, Maggs AC, Carlier MF, Pantaloni D. Analysis of microtubule rigidity using hydrodynamic flow and thermal fluctuations. J Biol Chem. 1994;269(18):13353–13360. [PubMed] [Google Scholar]
- Westermann S, Weber K. Post-translational modifications regulate microtubule function. Nature Reviews Mol Cell Biol. 2003;4(12):938–947. doi: 10.1038/nrm1260. [DOI] [PubMed] [Google Scholar]
- Wheatley DN. Nanobiology of the primary cilium--paradigm of a multifunctional nanomachine complex. Methods Cell Biol. 2008;90:139–56. doi: 10.1016/S0091-679X(08)00807-8. [DOI] [PubMed] [Google Scholar]
- Xiao Z, Zhang S, Mahlios J, Zhou G, Magenheimer BS, Guo D, Dallas S, Maser R, Calvet JP, Bonewald L, Quarles LD. Cilia-like Structures and Polycystin-1 in Osteoblasts/Osteocytes and Associated Abnormalities in Skeletongenesis and Runx2 Expression. J Biol Chem. 2006;281(41):30884–20895. doi: 10.1074/jbc.M604772200. [DOI] [PMC free article] [PubMed] [Google Scholar]


