Membrane Remodeling by Surface-Bound Protein Aggregates: Insights from Coarse-Grained Molecular Dynamics Simulation

Abstract

The mechanism of curvature generation in membranes has been studied for decades due to its important role in many cellular functions. However, it is not clear if, or how, aggregates of lipid-anchored proteins might affect the geometry and elastic property of membranes. As an initial step toward addressing this issue, we performed structural, geometrical, and stress field analyses of coarse-grained molecular dynamics trajectories of a domain-forming bilayer in which an aggregate of lipidated proteins was asymmetrically bound. The results suggest a general mechanism whereby asymmetric incorporation of lipid-modified protein aggregates curve multidomain membranes primarily by expanding the surface area of the monolayer in which the lipid anchor is inserted.

Cell membranes can adopt different shapes by changing the composition and lateral organization of their constituent lipids and proteins,¹ a phenomenon behind numerous cellular functions including trafficking, motility, and fusion.^2,3 Defective membrane remodeling is implicated in various human diseases, including neuromuscular defects.⁴ Many experimental and computational studies have examined membrane remodeling due to changes in lipid acyl chain length and spontaneous curvature,⁵⁻⁷ shape and hydrophobic length of trans-membrane (TM) proteins,^8,9 and scaffolding or surface area modulation by peripheral proteins.^10,11 Among a variety of computational approaches, coarse-grained molecular dynamics (CGMD) simulations are playing an important role in providing detailed insights into how surface proteins, such as the BAR (Bin–Amphiphysin–Rvs) domain, modulate membrane structure, topology, and elasticity.¹²⁻¹⁵ However, few such studies have focused on oligomeric surface proteins.¹⁶ In particular, lack of a suitable molecular system and analysis tools have hampered investigation of curvature generation and/or stabilization by aggregates of lipid-modified proteins, such as nanoclusters of membrane-associated Ras proteins.¹⁷⁻¹⁹

Recently, we described the aggregation of full-length Ras on the surface of a domain-forming lipid bilayer using CGMD.²⁰ Although the stability and size of the aggregate we obtained was less than ideal due to various factors, such as force field limitations^20,21 and high protein concentration, it can serve as a useful model for probing membrane remolding upon aggregation of lipid-modified proteins on monolayer surfaces. On the technical front, recent work by Ollila et al.²² and Cui and colleagues^23,24 allow for a detailed characterization of curved membranes through (3D) stress field analysis. Of particular note in the context of the present work is the study of Yoo and Cui on curvature generation and pressure profile modulation of a dioleoylphosphatidylcholine (DOPC) bilayer upon asymmetric incorporation of a lysophosphatidylcholine (LPC) patch.²³

We have analyzed two previously described²⁰ simulations of a DPPC/DLiPC/cholesterol (DPPC = dipalmitoylphosphatidylcholine; DLiPC = dilinoleylphosphatidylcholine) bilayer in which 32 lipid-anchored H-Ras proteins were inserted into the lower leaflet. Each simulation was started from a symmetric bilayer with the proteins separated by at least 5 nm from one another (Figure 1a). During the course of each simulation, lipids segregated into DPPC- and cholesterol-enriched liquid ordered (L_o) and DLiPC-enriched liquid disordered (L_d) domains, and the protein self-assembled into a single large aggregate (Figure 1b). The aggregates from the two simulations differ in geometry and bilayer interaction,²⁰ but their effect on the structural (e.g., position dependent lipid density), geometrical (e.g., curvature) and mechanical (lateral pressure profile and surface tension) properties of the membrane turned out to be very similar. We will therefore focus on one of the simulations from hereon (data from the other simulation is included in the Supporting Information (SI)).

Figure 1.

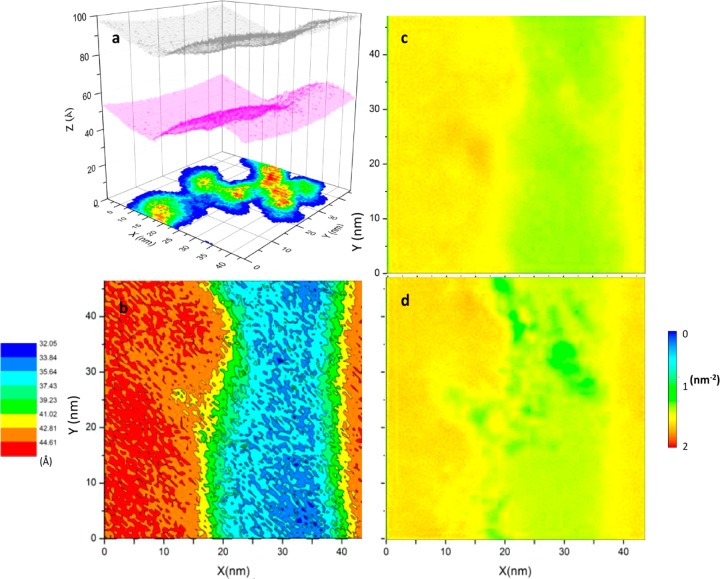
Top view of snapshots from a CGMD simulation of a domain-forming bilayer with asymmetrically bound lipid-modified proteins: (a) the initial setup at 0 μs; (b) the final configurations at 25 μs. DPPC is shown in red, DLiPC in green, cholesterol in white, and protein in yellow. Shown in blue is the actual simulation box, with the region outside being part of the periodic images in each direction. See Figure S1 (SI) for another aggregate from a different simulation.

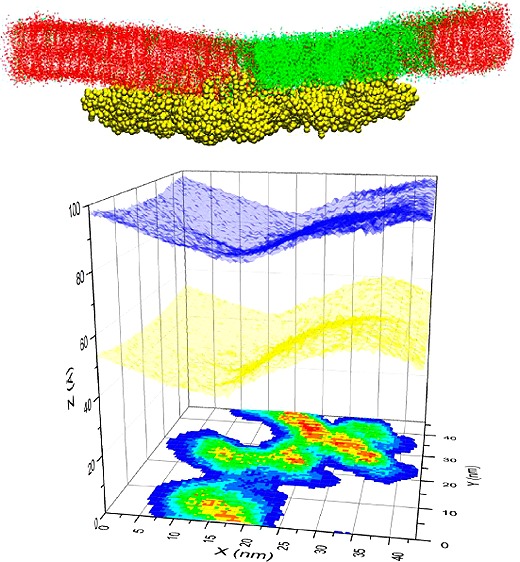
Membrane Remodeling. The average distribution of lipids (Figure 2a) and the bilayer thickness (Figure 2b) clearly show coexisting L_o/L_d phases, consistent with numerous previous reports.²⁵⁻²⁹ The profile of the bilayer shape in Figure 2c indicates that each leaflet is significantly bent when compared with the flat shape of a protein-free bilayer of the same lipid composition (see Figure 3a in ref (26)). This can be more clearly seen in Figure 3a, where we have plotted the average 3D shape of each monolayer along with the location of the aggregate: the surfaces are rugged, and the aggregate is localized in the most curved regions. In other words, despite the overall positive curvature of the protein-bound lower leaflet (and negative curvature of the upper), the highly irregular local curvature roughly mirrors the complicated architecture of the aggregate (Figure 3a).

Figure 2.

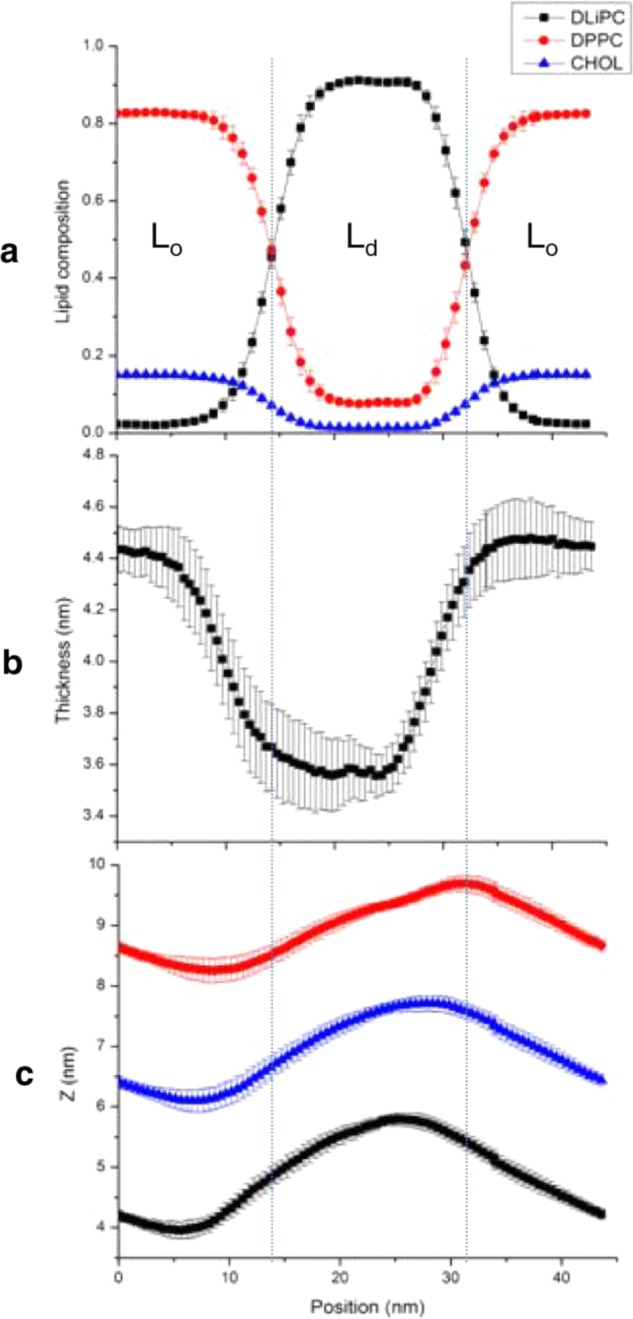
Lipid composition and structural properties of the simulated bilayer. (a) The equilibrium lipid composition in the liquid ordered (L_o) and disordered (L_d) domains. Dotted lines demarcate the approximate domain boundary defined by the intersection point for the DLiPC and DPPC distributions. (b) Bilayer thickness calculated as the average distance between the PO4 beads at the two leaflets. (c) Average shape of the upper (red) and lower (black) monolayers and the midplane (blue) described by the average z-coordinate of the PO4 and the terminal acyl chain beads, respectively. In each panel, data represents average over the 16–25 μs portion of the trajectory; error bars were obtained by time block averaging.

Figure 3.

Variations in structure and composition across the bilayer surface (in the xy-plane). (a) The 3D shape of each monolayer and the location of the aggregate. The upper and lower leaflet, described by the average z-position of the PO4 beads, are in gray and magenta, respectively, whereas the normalized probability distribution of the protein is shown in a heat map from high (red) to low (blue) density. (b) Change in thickness measured by the average distance between the phosphate bead positions within each bin, colored in red/orange for the L_o domain, blue/cyan for the L_d domain and green/yellow for the boundary between the two domains. (c,d) Lipid number density distribution at the upper (c) and lower (d) leaflets in blue (lowest density) through red (highest density).

Examination of the specific location of the aggregate with respect to the L_o and L_d domains could shed light on whether the curvature is a consequence of scaffolding by the aggregate or perturbation of lipid packing (or both). To this end, we compared the average location of the aggregate in the xy-plane (Figure 3a) with the variation of bilayer thickness in the same plane (Figure 3b). We found that the aggregate generally tracks the outline of the domain boundary, with just a small portion lying in both domains. This suggests that the aggregate prefers the boundary where lipid packing is less optimal. Moreover, the aggregate displaces a significance number of lipids underneath it (compare panel a with panels c and d in Figure 3), with regions of the lower leaflet corresponding to the average position of the aggregate having significantly fewer lipids.

No flip-flop of DPPC or DLiPC lipids was observed. However, approximately 27 cholesterols have transferred from the lower leaflet to the upper early in the simulation (data not shown). Thus, ∼0.75 cholesterols were displaced by each protein, which is similar to our previous observation that the isolated lipid anchor of H-Ras displaces one cholesterol molecule per peptide.²⁶ However, this interleaflet cholesterol transfer was found to only marginally contribute to monolayer area asymmetry and was not sufficient to explain the observed bilayer curvature.²⁶ Similarly, the large deformation of the bilayer in the current work (Figures 2c and 3a) could not be explained by the small difference in the number of cholesterol at the two layers. Moreover, the reduction in lipid density near the aggregate was not accompanied by a corresponding increase elsewhere in the lower leaflet (Figure 3d), suggesting that the headgroups displaced by the protein had to be accommodated by area expansion through positive curvature. Since the lipid density in the upper leaflet was not reduced to the same degree, the imbalance led to the overall convex and concave shape of the lower and upper leaflets, respectively (Figure 3a).

Stress Field Analyses. To further examine this issue, we analyzed the lateral stress profile along the membrane normal, π(z), calculated as a function of the radial distance r from the surface of the aggregate. The overall profile of π(z) follows the usual trend: large values of opposite sign at the core and the headgroup regions, respectively (hotter and colder colors in Figure 4a). However, the magnitude of π(z) varies with r, with the stress near the aggregate (r < ∼5 Å) and at intermediate distances (∼5 < r < ∼30 Å) being significantly different from that in the bulk membrane (r > 30 Å). For all values of r, the stress at the two monolayers is different in sign. Considering the link between pressure profile and lipid packing,^23,29,30 we conclude that a major source of the curvature is perturbation of lipid packing.

Figure 4.

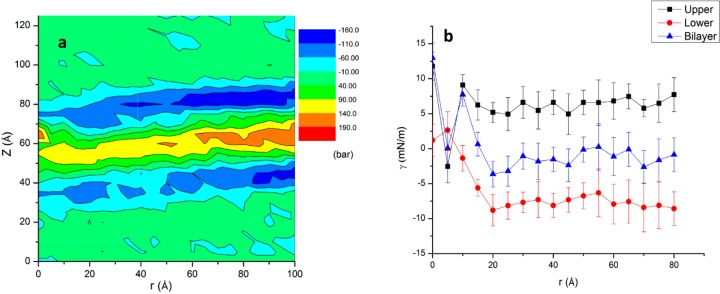
Lateral pressure profile and surface tension. (a) Lateral pressure profile π(z, r) as a function of the bilayer normal (z) and radial distance from the aggregate surface (r). (b) Time-averaged surface tension (γ) for each monolayer and the whole bilayer (error bars from time block averaging).

We have examined the mechanical properties of the bilayer based on the surface tension on a layer between z₁ and z₂ calculated as γ = −∫_z1^z2dzπ(z). We obtained average γ of −6.1 ± 3.5 mN/m and 6.2 ± 2.8 mN/m for the lower and upper leaflets, respectively. (The sum is close to 0 reflecting the tensionless system setup.) The upper and lower leaflets remain under positive and negative tension over the entire range of r, indicating membrane compression (decreased surface area) and dilation (increased surface area), respectively. This is consistent with the number density distribution (Figure 3c,d) and stress profile (Figure 4a). γ(r) (Figure 4b) exhibits significant fluctuation for r ≤ 30 Å and especially near the protein surface. This highlights the complicated effect of the irregularly shaped aggregate on membrane elastic properties. It is therefore difficult to find a material property that uniquely describes the whole bilayer. Nonetheless, we attempted to estimate the average spontaneous curvature, c₀, based on the following considerations: As described in ref (22) the product of c₀ and κ (i.e., bending modulus) can be calculated from c₀κ = ∫_z1 dzπ(z)(z – z₀), where z₀ is the pivotal surface roughly defined here by the mean z-position of the phosphate beads. We obtained c₀κ ≈ 121.2 ± 43.5 × 10^–13 J/m for the whole bilayer (including the protein region). Further, using (i) the available experimental estimate for κ of a DPPC bilayer (0.50 × 10^–19 J³¹), (ii) the observation that κ of a stearoyl-oleoyl phosphatidylcholine (SOPC) bilayer increases by 20% per mole fraction of cholesterol³² (our bilayer has 20% cholesterol), and (iii) neglecting contribution from DLiPC, we obtained κ ≈ 0.60 × 10^–19 J. This leads to c₀ ≈ 0.20 nm^–1, which qualitatively agrees with the overall positive curvature of the bilayer and suggests a significant effect of the aggregate on the membrane elasticity.

The various bilayer structural and mechanical properties derived from our CGMD trajectory are consistent in suggesting that asymmetric incorporation and aggregation of lipidated Ras proteins causes significant morphologic changes in the bilayer. As mentioned earlier and in the following paragraph, these results are reproducible in another simulation with different protein conformation (see SI), and even in the absence of the catalytic domain (see ref (25)). However, while the observed overall curvature is likely robust and can be faithfully captured by CG models, its magnitude may depend on detailed interactions between the bilayer lipids and the Ras lipid anchor, which is only approximately represented at the level of CGMD. Therefore, it would be interesting to see how detailed interactions and dynamics might affect the magnitude of membrane curvature using atomically detailed models, which is the subject of our future investigation.

In summary, we have shown that asymmetric binding of a lipid-anchored oligomer with irregular geometry causes significant membrane deformation (Figures 2c and 3a) by altering the lateral pressure and tension in a distance dependent manner (Figure 4). Variations in lipid density between leaflets and across the surface of each monolayer (Figure 3 c,d) corroborate the results from pressure field analysis. Our observations are similar to those of Cui and colleagues for a DOPC bilayer containing a patch of LPC on one leaflet.²³ Moreover, as mentioned earlier, we obtained very similar results for another oligomer that differs in geometry and protein–protein and protein–lipid interactions (see SI). Finally, the current results are very similar to our previous findings using the isolated lipid anchor of H-Ras.²⁵ Combined, these observations suggest that it is the cumulative effect on monolayer surface area asymmetry by the lipid anchors that directly insert into a monolayer, rather than the shape of the aggregate per se, that plays a major role in causing membrane deformation. In this context, it is worth noting that even oligomers of the scaffolding BAR domain generate membrane curvature not only due to shape effect, but also by inserting an amphipatic helix that creates monolayer area asymmetry.^1,10,14,33 We thus propose that aggregation of asymmetrically incorporated lipid-modified proteins on the surface of multidomain membranes generates curvature primarily through monolayer area expansion due to the insertion lipid anchors.

Computational Methods

As mentioned earlier, we have analyzed two CGMD trajectories that have been described before.²⁰ The simulation box was 44 nm × 46 nm in each case, but the z-dimension was 10 and 14 nm long, respectively, because the two simulations differed in the conformation of the H-ras proteins. This difference primarily involves the orientation of the catalytic domain with respect to the membrane plane. Although the final protein aggregates were generally similar, they differed in shape (compare Figures 1b and S1b) and internal organization.²⁰ In the current work, we have analyzed the shape, thickness, number density, pressure profile, and other equilibrium properties of the simulated bilayers using the well-equilibrated 16–25 μs portion of each trajectory. Most of the analysis involved binning the system into slabs of width 0.5 nm along the direction perpendicular to the domain boundary (Figure 2). The shape of the bilayer was defined by the averaged z-position of the phosphate beads and the midplane by that of the terminal acyl chain beads. In order to describe the deformation of the bilayer in the xy-plane, we divided each monolayer into 0.5 nm × 0.5 nm grids and obtained the average z-coordinate of the phosphate beads within each grid (Figure 3a). 3D pressure field analysis was carried out using the algorithm developed by Ollila et al. and implemented in GROMACS.²² Since the shape of the surface-bound aggregate in the present work is highly irregular, we modified Ollila’s scripts to calculate the pressure as a function of the radial distance r from the surface of the aggregate, as opposed to the distance from the center of mass of the trans-membrane MscL protein used in the example scripts. In addition, we assumed a cylindrical shape that spans the bilayer even though our aggregate is bound to only the lower leaflet.

Supporting Information Available

Results from a second simulation. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States