Exploring Variability in CT Characterization of Tumors: A Preliminary Phantom Study

Abstract

PURPOSE: To explore the effects of computed tomography (CT) slice thickness and reconstruction algorithm on quantification of image features to characterize tumors using a chest phantom. MATERIALS AND METHODS: Twenty-two phantom lesions of known sizes (10 and 20 mm), shapes (spherical, elliptical, lobulated, and spiculated), and densities [-630, -10, and +100 Hounsfield Unit (HU)] were inserted into an anthropomorphic thorax phantom and scanned three times with relocations. The raw data were reconstructed using six imaging settings, i.e., a combination of three slice thicknesses of 1.25, 2.5, and 5 mm and two reconstruction kernels of lung and standard. Lesions were segmented and 14 image features representing lesion size, shape, and texture were calculated. Differences in the measured image features due to slice thickness and reconstruction algorithm were compared using linear regression method by adjusting three confounding variables (size, density, and shape). RESULTS: All 14 features were significantly different between 1.25 and 5 mm slice images. The 1.25 and 2.5 mm slice thicknesses were better than 5 mm for volume, density mean, density SD gray-level co-occurrence matrix (GLCM) energy and homogeneity. As for the reconstruction algorithm, there was no significant difference in uni-dimension, volume, shape index 9, and compactness. Lung reconstruction was better for density mean, whereas standard reconstruction was better for density SD. CONCLUSIONS: CT slice thickness and reconstruction algorithm can significantly affect the quantification of image features. Thinner (1.25 and 2.5 mm) and thicker (5 mm) slice images should not be used interchangeably. Sharper and smoother reconstructions significantly affect the density-based features.

Introduction

With ever evolving technologies of medical imaging, details of tumor composition and morphology can be better depicted on conventional radiographical images such as high-resolution computed tomography (CT). Greater tumor details potentially reveal, to certain degrees, underlying cancer gene expression. However, to date, little is known about such correlations. Imaging radiogenomics studies the association of phenotypic radiologic characteristics with cancer genotype [1–3]. If successful, the radiogenomic characterization, particularly of solid tumors, will guide drug development through early imaging evaluation of therapeutic potential, stratify cancer therapy in a noninvasive fashion, and putatively identify treatments unlikely to be successful.

Tumor imaging phenotypes can be characterized not only qualitatively by radiologist's eyeballing but also quantitatively by computer through image feature analysis. Since the early 1970s, texture feature analysis has been applied to studying radiographical images [4]. In recent years, there is a renewed enthusiasm in the investigation of quantitative image features extracted from CT, positron emission tomography, and magnetic resonance imaging, for a variety of oncology applications, in particular for predicting disease prognosis and assessing response to targeted therapies [5–10].

Quantitative image features, especially those statistical texture features derived from two-dimensional (2-D) pixel or three-dimensional (3-D) voxel values [e.g., Hounsfield Unit (HU) on CT], can be considerably affected by scanning techniques and image reconstruction parameters. However, the majority of studies analyze existing image data sets retrospectively taken from either clinical practice or clinical trials. These studies often consist of heterogeneous image data acquired from various scanners using different scanning techniques and reconstruction parameters. To date, no study has been published to give an idea of how such imaging heterogeneities might influence the quantification of image features. The purpose of this work was to explore the effects of CT slice thickness and reconstruction algorithm on the quantification of image features using an anthropomorphic thorax phantom.

Materials and Methods

Phantom Image Data

An anthropomorphic thorax phantom was used in this study to explore the effects of CT scanning parameters on image features defined to characterize tumors [11]. There were 22 phantom lesions of different sizes (10 and 20 mm in effective diameter), shapes (spherical, elliptical, lobulated, and spiculated), and densities (-630, -10, and +100 HU) (Figure 1). Two lesion layouts were built: one had 12 lesions inserted into the two lungs (6 lesions per lung), and the other had 10 lesions (4 and 6 lesions per lung). Each layout thorax phantom was scanned three times on a 16-detector row scanner (LightSpeed, GE Healthcare, Milwaukee, WI). After one scan, the thorax phantom was moved out of the scanner bed, slightly tilted, and returned for another scan. The CT scanning parameters were 120 kVp, 100 mAs, 16 x 0.625 collimator configuration, and pitch of 1.375. The raw data of each CT scan were then reconstructed at six image series that were a combination of three slice thicknesses and two reconstruction algorithms, i.e., 1.25L, 1.25S, 2.5L, 2.5S, 5L, and 5S. For example, 1.25L represented the image series reconstructed using 1.25 mm slice thickness and lung reconstruction algorithm.

Figure 1.

The anthropomorphic thorax phantom. (A) The phantom, (B) phantom lesions of different shapes and sizes, (C) an example of a phantom CT image, and (D) an example of phantom lesions attached to vasculature.

Lesion Segmentation

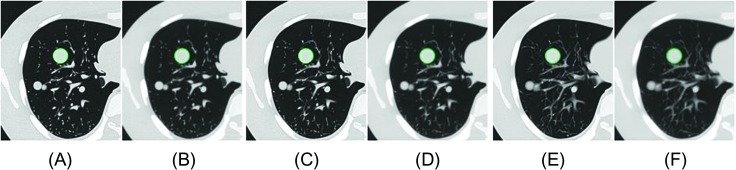
To characterize tumors, they needed to first be separated from surrounding anatomic structures. We used an in-house lung lesion algorithm to segment each phantom lesion [12]. Briefly, an operator needs to initialize the algorithm by specifying an elliptical region of interest enclosing the lesion. An isotropic volume of interest is derived from the region of interest, and its gradient image is calculated. A marker-controlled watershed transform is applied with markers derived from the volume of interest. The watershed segmentation result is then morphologically opened to serve as an initial contour for a geometric active contour. The geometric active contour with a strengthened potential well and a volume-preserving mean curvature flow term then evolve the contour to a high-gradient region near the initial contour while keeping the contour smooth. Figure 2 shows a 20 mm, -10 HU spherical lesion reconstructed at six different imaging parameter settings and segmented using this algorithm.

Figure 2.

One example image containing a 20 mm, -10 HU spherical phantom lesion on (A) 1.25 mm and lung, (B) 1.25 mm and standard, (C) 2.5 mm and lung, (D) 2.5 mm and standard, (E) 5 mm and lung, and (F) 5 mm slice thickness and standard reconstruction image series. The segmented lesion contours were overlapped on CT images.

Image Features

Fourteen image features were chosen for this exploratory study. They represented tumor size, shape, density, and both histogram-based and spatial density distribution [13–16]. Table 1 briefly explains the definitions of these image features.

Table 1.

Definitions of the 14 Image Features.

Feature	Description
Uni-dimension	The longest in-plane diameter of tumor in millimeter.
Volume	The volume of tumor in cubic millimeter.
Density mean	The arithmetic average of pixel densities in HU.
Density SD	The sample SD of the densities in HU.
Density skewness	The skewness of the density distribution.
Density kurtosis	The kurtosis of the density distribution.
Compactness	A measure of roundness. It is defined as
	$$Compactness=\frac{\sqrt[3]{Volume}}{\sqrt{SurfaceArea}}$$
Shape index 9	The proportion of the “spherical cap” of the nine types of shapes. Let κ1 and κ2 be the principle curvatures; the shape index is defined as
	$$s=\frac{2}{\text{π}}\text{arctan}\left(\frac{{\text{κ}}_{\text{2}}+{\text{κ}}_{\text{1}}}{{\text{κ}}_{\text{2}}-{\text{κ}}_{\text{1}}}\right)({\text{κ}}_{\text{1}}\ge {\text{κ}}_{\text{2}})$$
	The feature is the proportion of surface voxels having a shape index in the range [7/8, 1].
Fractal dimension	A measure of how fractal pattern changes with the scale with which it is measured. A differential box-counting method is used to estimate the fractal dimension at each voxel. The fractal dimension feature is taken as the mean fractal dimension of all voxels. For an image void of texture, the fractal dimension is 2.
Fractal lacunarity (box size = 3)	A measure of how patterns fill space (“gappiness”). The “gappiness” is measured at a scale of 3 x 3 x 3 (3 x 3 voxels in space and 3 HU in density). Let P(m) be the probability of having m points in a box of size 3. The lacunarity is defined as
	$$\text{λ}=\frac{M_2-M^2}{M^2}$$
	where $M={\displaystyle \sum }mP(m)\text{ and }{M}_2={\displaystyle \sum m^{2}P(m)}$. For an image void of texture, the lacunarity is 0.
GLCM energy (d = 2)	A measure of homogeneity. A co-occurrence matrix p is populated by the gray-level pairs I[x, y, z] and I[(x,y,z) + offset(2)] inside the tumor at a distance of 2 voxels in all directions (assuming that tumor texture has no preferred direction). The energy is the sum of squares of all entries in the matrix, i.e.,
	$$Energy={\displaystyle \sum _{i,j}p{(i,j)}^2}$$
GLCM contrast (d = 2)	A measure of the intensity contrast between a pixel and its neighbor over the tumor. The contrast is defined as
	$$Contrast={\displaystyle \sum _{i,j}{(i-j)}^{2}p(i,j)}$$
GLCM correlation (d = 2)	A measure of how correlated a voxel is to its neighbor over the tumor. The correlation is defined as
	$$Correlation={\displaystyle \sum _{i,j}{}_{{\sigma }_i{\sigma }_j}^{(j-u_j)p(i,j)}}$$
	where σi and σj are the marginal SDs.
GLCM homogeneity (d = 2)	A measure of the closeness of the distribution of elements in the GLCM to the GLCM diagonal. The homogeneity is defined as
	$${\displaystyle \sum _{i,j}\frac{p(i,j)}{1+\left|i-j\right|}}$$

Statistical Analysis

We employed regression method to analyze the effect of slice thickness and reconstruction algorithm on 14 image features adjusting three confounding factors (size, density, and shape of phantom lesions). There were 14 dependent variables, which were as follows: 1) uni-dimension, 2) absolute difference of measured volume and true volume, 3) absolute difference of measured density mean and true density, 4) density SD, 5) absolute value of density skewness, 6) absolute value of density kurtosis, 7) compactness, 8) shape index 9 [14], 9) fractal dimension [15], 10) fractal lacunarity [16], 11) gray level co-occurrence matrix (GLCM) [13] energy, 12) GLCM contrast, 13) GLCM correlation, and 14) GLCM homogeneity. The independent variables were slice thickness (two variables), reconstruction algorithms (one variable), size (one variable), density (two variables), and shape (three variables).

Results

Results from the multiple regression analysis are presented in Table 2. Because the true values of the phantom volume, density, and shape were provided, we knew that the smaller the Abs of volume difference and Abs of density mean difference, the more accurate the measurements. Furthermore, the phantom lesions were designed to be homogenous in density. Therefore, the smaller the density SD and contrast-related features and the larger the homogeneity-based image features, the better the measurements.

Table 2.

Effects of CT Slice Thickness and Reconstruction Algorithm on Image Features.

Image Features	Slice Thickness			Reconstruction Algorithms
	1.25 vs 5.00	2.50 vs 5.00	1.25 vs 2.50	Standard vs Lung
F1. Uni-dimension	§
F2. Abs of volume difference	†	†
F3. Abs of density mean difference	†	†	†	§
F4. Density SD	†	†	†	†
F5. Abs of density skewness	§	§	§	§
F6. Abs of density kurtosis	§	§	§	†
F7. Compactness	†	†
F8. Shape index 9	§	§	§
F9. Fractal dimension	§	‡	§	†
F10. Fractal lacunarity (box size = 3)	†	†		†
F11. GLCM energy (d = 2)	§	§		§
F12. GLCM contrast (d = 2)	§	§		†
F13. GLCM correlation (d = 2)	†	†	†	§
F14. GLCM homogeneity (d = 2)	§	§	‡	§

^*P ≤ .05 and A is smaller than B (A vs B).

^†P ≤ .01 and A is smaller than B (A vs B).

^‡P ≤ .05 and A is larger than B (A vs B).

^§P ≤ .01 and A is larger than B (A vs B).

Otherwise, A and B are not significant (A vs B).

As shown in Table 2 (the corresponding coefficient table is provided as an appendix in Table 2A), all 14 features were significantly different when computed on 1.25 and 5 mm slice images. The 1.25 and 2.5 mm slice thicknesses were significantly better than 5 mm for volume, density mean, density SD, GLCM energy, and GLCM homogeneity. As for the reconstruction algorithm, there was no significant difference in uni-dimension, volume, shape index 9, and compactness, but significant differences were found for all density and density texture features.

Table 2A.

Effects of CT Slice Thickness and Reconstruction Algorithm on Image Features.

Image Features	Constant	Slice Thickness			Reconstruction Algorithms
		5.00 (Reference)	1.25	2.50	Lung (Reference)	Standard
F1. Uni-dimension	8.8	0	.79†	.49	0	0.1
F2. Abs of volume difference	24.4	0	-133.8†	-134.2†	0	-10.5
F3. Abs of density mean difference	248.7	0	-120.9†	-95.5†	0	46.3†
F4. Density SD	209.0	0	-27.2†	-12.7†	0	-10.2†
F5. Abs of density skewness	.37	0	.66†	.48†	0	.12†
F6. Abs of density kurtosis	.41	0	2.09†	1.20†	0	-.88†
F7. Compactness	.42	0	-.01†	-.01†	0	-.001
F8. Shape index 9	.34	0	.13†	.08†	0	.004
F9. Fractal dimension	1.59	0	.06†	.02*	0	-.25†
F10. Fractal lacunarity (box size = 3)	.22	0	-.02†	-.01†	0	-.05†
F11. GLCM energy (d = 2)	-.01	0	.01†	.01†	0	.02†
F12. GLCM contrast (d = 2)	149.0	0	38.2†	33.8†	0	-24.0†
F13. GLCM correlation (d = 2)	.45	0	-.34†	-.22†	0	.12†
F14. GLCM homogeneity (d = 2)	.17	0	.04†	.03†	0	.09†

^*P ≤ .05.

^†P ≤ .01.

Otherwise, the slope b is not significantly different from zero.

Significant difference in uni-dimension was found only between 1.25 and 5 mm slice thicknesses, with a larger measurement value on 1.25 mm images. This is likely because uni-dimension (i.e., the maximal diameter) is measured in an axial plane, and an image series with thinner slices has a better chance of capturing the longest extent of a lesion than an image series with thicker slices. No significant uni-dimension difference was found, however, between 2.5 and 5 mm or between 1.25 and 2.5 mm. For the volume measurement, statistical difference was found between 1.25 and 5 mm and between 2.5 and 5 mm but not between 1.25 and 2.5 mm. This could be due to the greater partial volume effects on 5-mm than on 1.25 and 2.5 mm slice thickness images.

The density histogram-based features were significantly affected by both slice thickness and reconstruction algorithm. More accurate measurements of density mean and density SD on thinner slice images than on thicker slice images were likely due to the lesser effects of partial volume. Lung reconstruction was better for density mean, whereas standard reconstruction was better for density SD.

Compactness was significantly affected by the thicker slice thicknesses (5 vs 1.25 mm and 5 vs 2.5 mm) but unaffected by the thinner ones (1.25 vs 2.5 mm) or by the reconstruction algorithms (standard vs lung). This is understandable, as the thicker slice could considerably distort lesion shape due to the partial volume artifacts. The smaller values of compactness on the thinner slice images could be due to the depiction of more details in lesion morphology (e.g., spikes). The shape index 9 (the proportion of “spherical cap” voxels on surface) was affected significantly by slice thickness but not by reconstruction algorithm, which was a direct result of shape being distorted by the slice thicknesses but being preserved by the reconstruction algorithms conditioned on slice thickness.

Both slice thickness and reconstruction algorithm significantly affected fractal dimension and lacunarity. The fractal dimension reflected the fact that density changed more rapidly in space with decreased slice thickness and/or increased noise on sharper images. Fractal lacunarity described the “gappiness” of density patterns filling space. The smaller lacunarity on 1.25 and 2.5 mm compared to 5 mm slice thickness could be due to the narrower dynamic range of lesion density in thinner slice thickness; standard reconstruction had a smaller lacunarity value, possibly due to the narrower dynamic range too.

The four features of energy, contrast, correlation, and homogeneity, taken from the statistical texture method of GLCM, were significantly affected by both slice thickness and reconstruction algorithm to various degrees. For example, the standard reconstruction resulted in smoother images, therefore larger values of GLCM energy, correlation, and homogeneity. In contrast, the lung reconstruction resulted in sharper and noisier images and thus a larger value of GLCM contrast. Although it might initially seem counterintuitive that larger GLCM energy and homogeneity were observed on 1.25 and 2.5 mm than on 5 mm, the narrower dynamic range of lesion densities (i.e., more homogeneity) on thinner images could contribute to larger GLCM energy.

Discussion

Previous studies have considered the effects of CT imaging acquisition parameters on tumor size measurements (e.g., diameter and volume) in cancer screening programs as well as therapy response assessment [17–22]. To the best of our knowledge, this study is the first to report the effects of CT slice thickness and reconstruction algorithm on quantitative image features that are extracted to characterize not only tumor diameter and volume but also tumor shape, density, and density distributions (including spatial distribution) using an anthropomorphic thorax phantom.

In this pilot study, 14 representative image features were chosen to characterize tumor size, shape, density, and density distributions. Knowing the true volume, shape, density, and density homogeneity of the phantom lesions, we were able to compare certain morphology and texture features that were computed from CT images obtained using different reconstruction techniques and parameters and thereby provide valuable insights into the degrees these imaging settings affect the quantification of various image features.

The key findings of this study are summarized below. All 14 selected image features were significantly different when computed on 1.25 and 5 mm slice images. Certain image features, especially those quantifying tumor size (diameter and volume) and shape (compactness), were not statistically different when measured on 1.25 and 2.5 mm slice thickness images. The image features of volume, density mean, density SD, GLCM energy, and GLCM homogeneity were more accurately measured on 1.25 mm than on 2.5 mm and least accurately measured on 5-mm slice thickness images. Our findings of the effects of CT slice thickness on phantom size measurements confirmed the previously reported results of clinical studies [21,22]. As for the reconstruction algorithm, significant differences were found for all density-related image features but not for tumor size- or shape-related features. Our findings suggest that thinner (1.25 and 2.5 mm) and thicker (5 mm) slice images, as well as smoother and sharper images, should not be used interchangeably when studying radiogenomics.

Generally speaking, a thicker slice technique introduces larger partial volume artifacts compared to a thinner slice technique. As a result, density texture/contrast detail of images will be suppressed more on thicker slice images due to the oversmoothing effect, which affects not only the computation of image texture features but also the identification of (tumor) boundaries. Similarly, a smoother reconstruction algorithm (e.g., standard algorithm) generates smoother and less noisy images, whereas a sharper reconstruction algorithm (e.g., lung algorithm) creates sharper and noisier images. These should explain why differences can occur when calculating the same image feature on images reconstructed using different imaging reconstruction techniques and parameters.

There are several limitations to this study. Although we used an anthropomorphic thorax phantom, compared to real patient's chest images, the phantom images had less artifacts induced during the CT image acquisition procedure. Phantom lesions were designed homogenous in density and thus lacked image textures. Furthermore, image features were analyzed on the basis of the results of one segmentation algorithm. Different strategies employed by different algorithms can affect segmentation results and thus the quantifications of image features.

Future studies include, but are not limited to, extension of the 14 image features to additional 200+ well-defined quantitative image features, collaboration with other research teams to compare differences discovered using different segmentation algorithms and feature extraction programs, and correlation of quantitative image features with clinical outcome data (genetic expression).

Appendix

Table 2A lists the coefficients of slice thickness and reconstruction algorithms of the multiple regression adjusted for phantom size, density, and shapes.