The marginal valuation of fertility

Abstract

Substantial theoretical and empirical evidence demonstrates that fertility entails economic, physiological, and demographic trade-offs. The existence of trade-offs suggests that fitness should be maximized by an intermediate level of fertility, but this hypothesis has not had much support in the human life-history literature. We suggest that the difficulty of finding intermediate optima may be a function of the way fitness is calculated. Evolutionary analyses of human behavior typically use lifetime reproductive success as their fitness criterion. This fitness measure implicitly assumes that women are indifferent to the timing of reproduction and that they are risk-neutral in their reproductive decision-making. In this paper, we offer an alternative, easily-calculated fitness measure that accounts for differences in reproductive timing and yields clear preferences in the face of risky reproductive decision-making. Using historical demographic data from a genealogically-detailed dataset from 19th century Utah, we show that this measure is highly concave with respect to reproductive effort. This result has three major implications: (1) if births are properly timed, a lower-fertility reproductive strategy can have the same fitness as a high-fertility strategy, (2) intermediate optima are far more likely using fitness measures that are strongly concave with respect to effort, (3) we expect mothers to have strong investment preferences with respect to the risk inherent in reproduction.

1. Introduction

The highest average completed fertilities for human populations are still well below the physiological maximum (Wood, 1994). Most behavioral ecologists explain this disparity between biological potential and behavioral attainment by invoking trade-offs between quality and quantity of offspring under conditions of limited resources that create stabilizing selection for a fitness-maximizing intermediate value of offspring born (Lack, 1947; Smith & Fretwell, 1974). Models of intermediate optimal fertility, like the Lack Clutch, are appealing to behavioral ecologists because of the clear evidence for measurable demographic, energetic, and economic trade-offs associated with human reproduction in a wide range of societies.

One of the most important trade-offs is between fertility and resource production (Van Noordwijk & Dejong, 1986): some kinds of work provide more resources to support future reproduction or investment in existing offspring, but entail costs for current reproduction. Such trade-offs solved in favor of investments in work tend to increase interbirth intervals (IBIs) and thus lower fertility. For example, among Indian and Philippine women, autonomy and employment result in longer IBIs (Nath, Land, & Goswami, 1999; Upadhyay & Hindin, 2005). In Ghana, women who engage in “modern” types of work have significantly longer IBIs than those engaged in agriculture or “traditional” work and both types of employment produce longer IBIs than no employment (DeRose, 2002). In 19th century Belgium, stable work that generated higher earnings for women resulted in a slower pace of reproduction, while work that could be done at home for lower pay (lace-making) had little effect on IBIs (Van Bavel & Kok, 2004). !Kung forager women faced backload and travel constraints during the dry season when they traveled more than 12 kilometers to collect mongongo nuts and these trade-offs may have played a large role in their lengthy average IBIs of 48 months (Blurton Jones & Sibly, 1978; Blurton Jones, 1986; Anderies, 1996). Such trade-offs in work efficiency diminished when !Kung become more sedentary, and IBIs subsequently decreased to an average of 24 months (Howell, 1979). Recent work on fertility and economic constraints shows substantial economic cost of higher fertility in the contemporary United Kingdom (Lawson & Mace, 2010) as well as reduced ability of parents to directly invest in the enrichment of the children in large families (Lawson & Mace, 2009). Similarly, a study from Sweden shows that high fertility is associated with diminished socioeconomic status outcomes (Goodman, Koupil, & Lawson, 2012).

Another significant trade-off is that between fertility and offspring survival. While very short IBIs might provide for the highest levels of fertility, they also carry costs for both maternal and child health. IBIs of less than 18 months are associated with small size at birth, stunting and underweight, and are one of the major causes of infant mortality (Hobcraft, MacDonald, & Rutstein, 1983; Conde-Agudelo, Rosas-Bermudez, & Kafury-Goeta, 2006, 2007), increasing the risks of death significantly regardless of a mother's age or socioeconomic status (George, Everson, Stevenson, & Tedrow, 2000; Whitworth & Stephenson, 2002; Rutstein, 2005). Short birth intervals also jeopardize the sunk investment of already-born children because of early cessation of nursing and the demands of pregnancy and lactation on mothers' energy and time budgets (Hobcraft et al., 1983; Hagen, Barrett, & Price, 2006). Short IBIs increase mortality by increasing nutritional stress to the infant, primarily through reductions in nursing (Manda, 1999; Whitworth & Stephenson, 2002; Gibson & Mace, 2006), but nutritional deficiencies and maternal depletion may also play a role (Bhalotra & van Soest, 2008; van Eijsden, Smits, van der Wal, & Bonsel, 2008). Fertility has recently been shown to have a negative effect on child survival in a comprehensive analysis of studies from Sub-Saharan Africa (Lawson, Alvergne, & Gibson, 2012). Here, the mechanism producing the tradeoff appears to be sibling competition.

Substantial evidence suggests that resource limitation can intensify these somatic investment trade-offs. Conditions of social and economic stress, both chronic and acute, lengthen IBIs (Anderton & Bean, 1983; Boserup, 1985; Gurmu & Mace, 2008) and those who lack risk-buffering mechanisms often suffer more (Van Bavel & Kok, 2004; Bengtsson & Dribe, 2006). For example, savannah Pumé women in Venezuela who experience seasonal nutritional stress have longer IBIs than river Pumé women who are buffered from such variability. River Pumé have lower infant mortality and shorter IBIs leading to a greater number of surviving offspring (Kramer & Greaves, 2007). Nineteenth century Belgian families reliant on a husband's unstable, badly paid job of day laborer also experienced longer IBIs relative to those supported by more stable, highly paid employment (Van Bavel, 2003). Such patterning may either be a simple function of physiological constraints on fertility such as lactational amenorrhea or nutritionally-mediated subfecundity (Ellison, Panter-Brick, Lipson, & O'Rourke, 1993), or the product of intentional spacing attempts by mothers facing fertility trade-offs (Anderton & Bean, 1985; Van Bavel, 2004). Using the Utah Population Database, Bean, Mineau, and Anderton (1990) showed that IBIs for mid-parity women increased during the economic crises of the Panic of 1893 and the banking crisis that inaugurated the Great Depression. These increases were particularly strong for the Great Depression, with intervals increasing from 3 to 34%.

There is thus extensive evidence for the existence of trade-offs between maternal production and maternal reproduction, maternal fertility, and offspring mortality. Both the extent and magnitude of these trade-offs suggest that there should exist some optimal level of fertility (i.e., below the physiological maximum) relative to these trade-offs that maximizes long-term fitness. However, such intermediate optima have been difficult to find in human populations (Borgerhoff Mulder, 1998).

Understanding lower-than-maximum fertility is a life-history problem of reproductive effort. Intermediate fertility corresponds to a reduced reproductive-effort tactic. In their pioneering paper, Gadgil and Bossert (1970) note that intermediate levels of reproductive effort can only be optimal when there are diminishing marginal returns to effort. The typical measure of fitness in human populations, lifetime reproductive success (LRS), does not show diminishing marginal returns to increasing fertility as it is a linear measure of fitness with respect to fertility. Fitness increases identically by unity with each additional birth so that the second derivative with respect to effort (i.e., the curvature of the fitness function) is zero. Other similar measures such as mortality-discounted LRS or the number of grandchildren may show a degree of concavity with fertility, but this is typically modest and fitness is typically quite linear across a wide range of observed fertilities (Kaplan, Lancaster, Bock, & Johnson, 1995; Strassmann & Gillespie, 2002; Lawson et al., 2012). Other fitness measures frequently used in population biology can show a substantial degree of concavity with respect to fertility and are thus of great interest for life-history studies of trade-offs.

2. On fitness measures

Historically, the most common measure of fitness in the behavioral ecology of human life histories is individual LRS (Barkow, 1977; Turke & Betzig, 1985; Boone, 1986; Chagnon, 1988; Voland, 1988; Cronk, 1989; Borgerhoff Mulder, 2000). The use of LRS as a fitness measure implies that there are no inter-temporal preferences for births. In other words, births are perfectly substitutable for one another, conditional on maternal survival. Every child counts as much as every other child, regardless of when it was born or the mother's age when she gave birth. Furthermore, using LRS as a fitness measure entails the assumption of population stationarity - births are exactly offset by deaths and population size remains constant. When a population is not assumed, a priori, to be stationary, LRS is not an appropriate fitness measure (Caswell, 2001). The population-level expected fitness that corresponds to LRS is the net reproduction ratio, R₀, a generational measure of mean fitness. R₀ is also the ratio of the population size from one generation to the next as shown by the identity from stable population theory

$$R_0={\mathrm{\lambda }}^T,$$ (1)

where λ is the intrinsic rate of increase (i.e., the exponentiated instantaneous rate of increase, r) and T is the generation time (i.e., the mean age of childbearing).

Sophisticated studies will discount the count that determines LRS by the probability of child survival under different fertility regimes (e.g., Lawson et al., 2012), but this does not change its dynamic properties. The use of LRS as a fitness measure implies that the timing of reproduction does not matter for fitness. In a population that is growing by some period rate λ, the size of the population will increase by a factor of λ per period meaning that a delay of reproduction by t periods needs is discounted by a factor of λ^t. Thus, all things being equal, it pays to reproduce early. This population discounting induces time preferences in reproduction on the part of parents. A parent prefers a living child to one not yet born because the living child has higher reproductive value. Note that the Fisherian notion of reproductive value is really a way of accounting for time preference in reproductive decision-making (Fisher, 1958).

For an age-structured population, mean fitness is given by the unique real root, λ, of the Euler-Lotka equation, written here in discrete-time form,

$$1=\sum _{X=\mathrm{\alpha }}^{\mathrm{\beta }}{\mathrm{\lambda }}^{-x}{l}_x{m}_x,$$ (2)

where α is age at first reproduction, β is age at last reproduction, l_x is age-specific survivorship and m_x is the fertility rate in age-class x.

The simplest way to calculate λ is via the Leslie matrix, a compact means for representing the age-specific mortality and fertility schedules that are applied in each time step to a vector of the population age structure. A Leslie matrix contains the age-specific fertility rates along the first row, and the probabilities of surviving from one age class to the next along the subdiagonal. Everywhere else, there are zeros. In addition to being a convenient and compact means of representing the demography of an age-structured population, the Leslie matrix provides a wealth of dynamical and evolutionary information (Jones, 2009). The mean fitness of a population characterized by a Leslie matrix A is given by the dominant eigenvalue λ₀ of the matrix. This is the same as the real root of Eq. 2. λ₀ is the asymptotic growth rate of the population (i.e., once it has converged on its stable age distribution). Fitness is thus a growth rate. To maintain relative representation in a population, one must pace reproduction so one's lineage grows at a rate at least equal to the population at large.

The Leslie matrix provides us with a dynamic measure of mean fitness of the population, but to calculate individual fitnesses within a population we adopt an approach following McGraw and Caswell (1996) that is very similar to the Leslie matrix for the aggregate population. We define an individual-based Leslie matrix in which all subdiagonal elements are equal to 1 for ages that the individual was observed to survive. Similarly for fertility, we simply tally the observed births within an age class and use this tally as the row entry for each age. The dominant eigenvalue of this individual matrix measures the individual's fitness. The use of McGraw and Caswell's λ as a fitness measure will be particularly important when trade-offs specifically involve substantial differences in timing of life-history events (Kaar & Jokela, 1998; Brommer, Merila, & Kokko, 2002; Metcalf & Pavard, 2007). Substantial demographic evidence suggests that the massive demographic changes of the 20th century (that continue into the 21st) are largely about timing (Bongaarts, 1999; Billari & Kohler, 2004; Schoen, 2004), making λ an appealing fitness measure for understanding such questions. Furthermore, a fundamental difference between Lack's classic clutch-size manipulations (Lack, 1947) and human reproduction is that human “clutches” are spread out in time (Jones, 2011), bringing timing into the solution of the quality-quantity trade-off. The age-discounting that is built into λ as a fitness measure means that total fitness should show diminishing marginal returns to increased fertility. In what follows, we test the hypothesis that there are diminishing marginal individual fitness gains to fertility in a genealogically-detailed historical population.

3. Methods

3.1. Data

Our sample consists of the marriage cohorts of 1849–1929 derived from the Utah Population Database (UPDB). UPDB is housed at the Huntsman Cancer Institute, University of Utah, and is available for researcher use by application to the Institute. In this dataset we have information on 86,389 marriages and 628,730 individuals. Most women in the UPDB have full reproductive histories recorded and the structure of the database allows the construction of quite detailed genealogical information. We selected a sample of women born between 1850 and 1859, prior to substantial fertility decline in frontier Utah, totaling 15,074 women. We restricted our analysis to non-plural marriages. We then queried the database for all female births to this 1850-cohort, a total of 36,771. An important question relating to classical life-history trade-offs is the extent to which fertility trades-off with recruitment so we performed a third query to find only those daughters of the 1850-cohort who were successfully recruited into the breeding population (i.e., became mothers themselves). This subset of all births to the 1850-cohort totaled 13,528 women, yielding a 36.7% recruitment rate for female live births. All database work was done in MySQL.

3.2. Demography

We limited our sample to the one-sex population for demographic simplicity, consistent with much work in life history theory which relies on the principle of female demographic dominance (Charnov, 1991; Jones, 2009). Use of both sexes in demographic models requires the specification of a “marriage function” (Caswell, 2001) which relates fertility to the abundance of females and males of different ages. The resulting nonlinear renewal equation injects an unnecessary degree of complexity for the questions we are asking.

We constructed individual projection matrices with one-year projection intervals, by finding all parous women in the 1850 cohort and calculating their ages at all births. We analyzed two different fitness outcomes. One set of matrices (the “total fertility” sample) were constructed for all daughters born. The second set (the “recruitment” sample) included only those births in which the daughters born became mothers (of female offspring) themselves. Individual Leslie matrices contain a 1 on the subdiagonal for all ages the woman survived. In addition, they contain a 1 along the first row for every age in which the woman had a live birth (total fertility) or had a live birth that eventually was recruited into the breeding population (recruitment). A woman who had her last birth at age 38, will thus have a 38 × 38 individual matrix.

Using the R package demogR (Jones, 2007), we constructed the matrices and calculated eigensystems (Caswell, 2001). Individual fitness is given by the dominant eigenvalue of the individual matrix. Having calculated this for the full matrix, we then pruned each matrix back by one birth and re-calculated the eigensystem, continuing this process until we reached the first birth. By this process, we were able to construct curves showing how fitness increases, and marginal fitness changes, with each subsequent birth.

3.3. Statistical methods

To provide a quantitative measure of the nonlinear response of fertility to total fertility, we fit a series of nonlinear saturating functions to the individual fitnesses as a function of total fertility using the nls function of R (R Development Core Team, 2012). Functional forms employed included: (1) quadratic, (2) Michaelis-Menten, also known as a Holling Type II functional response, and (3) Holling Type III functional response. In addition to the pure functions, we also fit models including offsets. Details of the functional forms can be found in Bolker (2008). We chose the model with the lowest residual standard error.

4. Results

Of the 15,074 women born in the 1850–1859 interval, 9,358, or 63%, successfully reproduced. The 1850-cohort produced a total of 36,771 daughters, of whom 36.7% were successfully recruited into the breeding populationby becoming mothers (of daughters) themselves. For parous women, the mean number of live-born daughters is 4.07 with a standard deviation of 2.03 and the mean number of recruits is 2.01 with a standard deviation of 1.17.

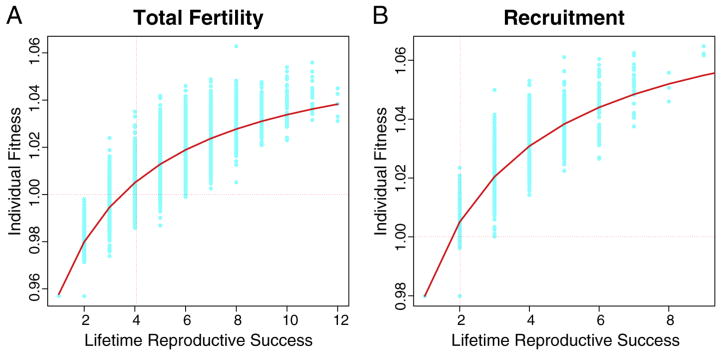
Fig. 1 plots values of individual fitness against total fertility (A) and recruitment fertility (B) respectively. These plots clearly show that fitness is a concave function of total fertility. Of the series of saturating models of the relationship between fitness and fertility, the best-fitting was a Michaelis-Menten model with an offset. This result remains when we restrict fertility to only those births that eventually recruit into the breeding population. Table 1 presents the results of the best-fit model for both the total-fertility and recruitment analyses.

Fig. 1.

(A) Individual fitness of 8,869 mothers of the 1850–1859 birth cohort as a function of total fertility (in daughters). The function shows strongly diminishing marginal fitness returns to parity. The red curve represents an offset Michaelis-Menten curve fit by nonlinear least-squares. (B) Individual fitness of 8,869 mothers of the 1850–1859 birth cohort as a function of recruitment fertility (in daughters). The function shows strongly diminishing marginal fitness returns to parity. The red curve represents an offset Michaelis-Menten curve fit by nonlinear least-squares.

Table 1.

Results of the best-fitting model relating individual fitness to total fertility.

	Parameter	Estimate	Std. Error	t value	P
TFR	a	0.147	0.0005	295.44	<0.001
	b	2.943	0.0659	44.62	<0.001
	c	0.921	0.0008	1168.99	<0.001
Recruit	a	0.153	0.0004	343.98	<0.001
	b	2.162	0.0501	43.17	<0.001
	c	0.932	0.0008	1241.43	<0.001

The best-fitting model was a Michaelis-Menton function with an offset taking the form: λ(TFR) = c + aTFR/(b +TFR). TFR model: 0.006421 on 8866 degrees of freedom. Recruitment model: residual standard error: 0.004149 on 6722 degrees of freedom.

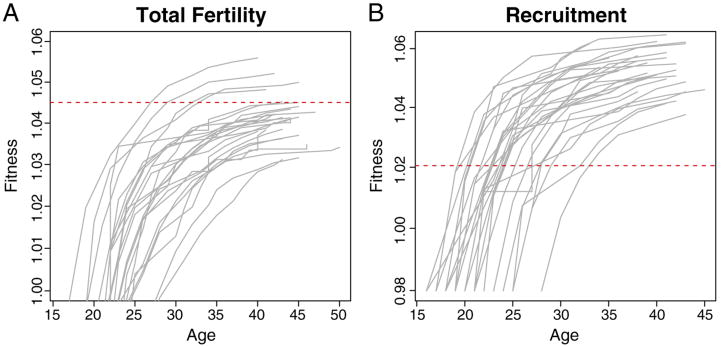
The diminishing marginal fitness gains with parity are particularly clear when we plot individual reproductive trajectories. Fig. 2 shows that the cumulative fitness function is highly concave. For these figures, we chose a sample of women with parity ≥10 live-births (A) or ≥6 recruits (B). Plotting the cumulative fitness function for these high-parity women emphasizes the concavity of the fitness function for parous women. It also separates the individual fitness trajectories for women with different ages at first birth and subsequent birth intervals quite distinctly on the log-scale. The method of McGraw and Caswell (1996) calculates the fitness corresponding to the first bout of reproduction, regardless of age, as λ = 1, while mean fitness is 1.045 for the total fertility sample and 1.021 for the recruit sample. Importantly, we must consider the conditionality of this mean. In this plot, mean fitness, by which the curves are normalized, is calculated across the sample of parous life histories. In reality, a substantial fraction of children ever born do not successfully reproduce. In historical populations such as frontier Utah, this typically happens because of pre-reproductive mortality. For the daughters of the 1850 Utah birth cohort, only 37% are known to become mothers of daughters in the F2 generation. While some mothers who migrated away from Utah were probably lost from the sample, attention to genealogical record keeping for religious reasons means this value is at least approximately correct. If we use the 37% recruitment value together with expected number of live female births of 4.07, then we can approximate R₀ to be 1.48 (= 0.37 * 4.07) and, assuming a average age of mothers of 27 (Keyfitz & Caswell, 2005), λ = exp(1.48)/27 = 1.01, meaning that a single bout of reproduction puts a woman approximately at the mean fitness of the population. This will typically be even more exaggerated for men because of the higher mortality rates of men throughout the life cycle. Thus, for low-status men with poor reproductive prospects, the gains to a single successful reproductive bout could be enormous.

Fig. 2.

(A) Sample of 26 individual cumulative fitness curves by parity for women with total parity of 10 or greater. The plot shows strongly diminishing marginal fitness with parity. Mean fitness is λ̅) = 1.045. (B) Sample of 28 individual cumulative fitness curves by parity for women with recruitment parity of six or greater. The plot shows strongly diminishing marginal fitness with parity. Mean fitness is λ̅ = 1.021.

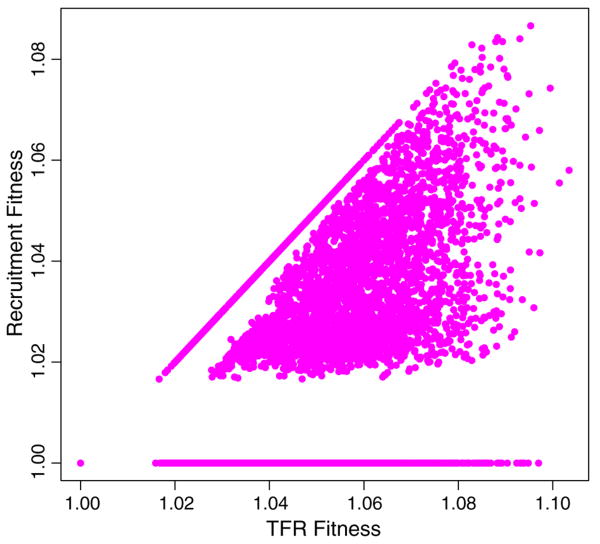
The relationship between individual fitness calculated with all live births and individual fitness calculated with only recruitment-fertility is presented in Fig. 3. The values are certainly correlated (r = 0.517) though there is a substantial amount of scatter at higher parities. Given that Fig. 3 really represents a part-whole correlation (Nee, Colegrave, West, & Grafen, 2005), and is constrained to fall on or below the line of equality, we must conclude that the relationship between individual fitness calculated from total fertility vs. recruitment fertility is quite weak. Two features of Fig. 3 merit discussion. The horizontal line at Recruitment Fitness = 1 represents women who had only one surviving daughter, regardless of the number of live female births. The dominant eigenvalue of a matrix with a single one along the top row will be unity regardless of the age at which it occurs. The line of points at a 45° angle represents women for whom all daughters born survived to recruit successfully.

Fig. 3.

Scatterplot comparing the values of individual fitness based on recruitment fertility against fitness values based on total fertility. The horizontal line at Recruitment Fitness = 1 represents women who had only one surviving daughter, regardless of the number of live female births. The line of points at a 45° angle represents women for whom all daughters born survived to recruit successfully.

5. Discussion

Timing matters for fitness and this is particularly true in rapidly increasing frontier populations, a common characteristic of a species that emerged from Africa to colonize all other continents in the span of approximately 100,000 years. The standard measure of fitness that most evolutionary anthropologists use, lifetime reproductive success, is a per generation measure, but the ESS life history in an age-structured population is one that has the higher instantaneous fitness (Charlesworth, 1994). The fundamental implication of this is that LRS is an appropriate fitness measure if and only if population growth is zero – and has been for a long time. As soon as population moves aroundan average of R₀ = 1, then the instantaneous measure applies. As Hill and Hurtado (1996) have noted, population growth appears to be the rule, rather than the exception, in human history. Globally, growth was modest (though not absent) for most of human history (Cohen, 1995), however, there is demographic and genetic evidence for sometimes quite rapid growth in local human populations (Hill & Hurtado, 1996; Excoffier & Schneider, 1999). While growth in local populations would have frequently entailed crashes as well (Boone, 2002), the key point pertaining to the current work is that stationarity cannot be safely assumed in human history and that fitness measures should reflect this nonstationarity.

Our results have three major implications for evolutionary analyses of human reproductive decision-making and patterns of fertility. First, a surprisingly small number of successful reproductive events suffice to move a woman above mean fitness when the frequency of non-reproducers is accounted for. Indeed, a single successful reproductive bout, if properly timed, is sufficient to place a woman in the vicinity of mean fitness for the population. There is an enormous range of achieved fitness, as measured by recruitment, apparent in Figs. 1–3. The variation in λ for a fixed parity is due to variation in timing. Women who reproduce successfully earlier in life, on average, achieve a greater marginal benefit for each reproductive bout, an idea encapsulated in Fisher's notion of reproductive value (Fisher, 1958). This greater marginal value of early-born offspring may also suggest why parental investment appears to be greater in first-born than later-born offspring (Jeon, 2008; Gibson & Sear, 2010). That one can achieve higher than average fitness with a small family size removes a bit of the mystery behind the remarkable fertility decline witnessed throughout the world starting in the 19th century (Borgerhoff Mulder, 1998) and lends support to explanations based on investments in human capital (e.g., Kaplan, 1994, 1996; Kaplan & Robson, 2002). This result is consistent with those of Korpelainen (2003) from historical Finland. She found that despite substantial declines in fertility from the 1875–1945 birth cohorts, fitness as measured by λ remained remarkably constant. The clear implication of marginal valuation of fertility – which is a quite robust result – is that the benefits of reducing fertility need not be huge for it to be favored by selection. This line of reasoning makes us focus on the ecological conditions surrounding the transition itself as mean fitness before and after a transition (i.e., high fertility/high mortality → low fertility/low mortality) can easily be equal. It is important to note that one fundamental feature of the Demographic Transition of the twentieth century is an often massive increase in the population growth rate, which is mean fitness (Notestein, 1953; Caldwell, 1982; Coale & Watkins, 1986). However, our analysis raises a new puzzle, at least for the literature on evolutionary demography. Much of fertility change in the most developed countries is related to changes in timing of first birth rather than the subsequent pace of reproduction and, consequently, the number of total births once a woman begins reproducing (Billari & Kohler, 2004; Kohler, Billari, & Ortega, 2006). A sufficient, evolutionarily-informed theory of human fertility needs to tackle this problem of delay more than the problem of reduced total fertility, given the clear premium we demonstrate on relatively early reproduction. The recently-documented trade-offs with socioeconomic status (Lawson & Mace, 2010, 2011; Goodman et al., 2012) and findings that childcare availability affects transition to first birth (Rindfuss, Guilkey, Morgan, Kravdal, & Guzzo, 2007) suggest a likely avenue for solving this mystery.

Second, the existence of a fitness function which is strongly concave with respect to total fertility means that intermediate optima are far more likely. As Borgerhoff Mulder (1998) noted, trade-off theories which predict optimal clutches substantially less than the maximum biologically attainable have proved exceptionally difficult to support using human demographic data. When fitness is simply a linear function of fertility, there is little capacity for intermediate optima. However, the existence of strongly diminishing fitness returns to fertility is highly suggestive of the existence of intermediate optima. Behavioral ecology is replete with models which require diminishing marginal returns to yield intermediate optima. The first of these is the Lack clutch (Lack, 1947), but other important, and highly successful, models include the patch model in foraging theory, and the optimal copula duration model, both of which rely on the marginal value theorem (Charnov, 1976; Parker & Stuart, 1976), and the optimal territory size model (Davies, 1978). Concavity of returns to reproductive effort has also played a central role in the development of life history theory. As with the MVT, as noted by Gadgil and Bossert (1970), the only way for intermediate effort to be favored is when the age-specific profit function of effort is concave.

Third, the highly concave fitness function depicted in Figs. 1 and 2 implies that there should be strong preferences regarding risk and reproduction. Concave utility curves are taken to be synonymous with risk-averse preferences in economics (Arrow, 1965). Such risk-aversion arises because of the asymmetry between the upside-benefit and downside-risk associated with a lottery played on a concave utility curve. When fitness is isomorphic with fertility, all births are exchangeable. However, with the time-discounting built into the renewal equation (Eq. 2) and associated fitness measures, earlier births are preferred to later births, ceteris paribus. A decision to recommence childbearing following a short interval is risky, jeopardizing both the infant and the older child defining the birth interval. Depending on the location on the curve, we predict mothers to be highly risk-averse, extending birth-intervals either behaviorally or through physiological means, during particularly risky periods such as economic crises, droughts, or periods of social strife. Understanding the interactions between risk-sensitive fertility and risk-sensitive parental investment (Quinlan, 2007) may be a particularly fruitful future avenue for understanding human life-history decisions.

When we compare the individual fitnesses calculated from all live female births to those calculated only from recruited daughters, we find that there is a remarkable degree of divergence at the higher parities (Fig. 3). This suggests that estimating fitness simply from the number of live-births can be quite misleading and means that factors contributing to both the timing of births and the likelihood of recruitment – which we expect to trade-off (Smith & Fretwell, 1974; Lawson et al., 2012) – need to be considered in assessing the success of specific life-history tactics. Failure to recruit a substantial number of the ever-born daughters, especially those born early in a woman's reproductive career, can lead to much lower fitness than expected based simply on total fertility.

The calculation of λ is quite straightforward and its use can be substituted for LRS-based measures, as has been done in a number of studies already (Korpelainen, 2003; Helle, Lummaa, & Jokela, 2004). Korpelainen (2003) notes that while LRS declined in historical Finland, λ actually remained remarkably constant, suggesting that families were successfully negotiating a fertility-survival trade-off and achieving the same mean fitness with lower fertility. She also notes that a previously-reported trade-off between fertility and longevity is substantially weakened by using λ as the fitness criterion (Korpelainen, 2000).

A series of important studies have recently deployed sophisticated statistical analyses and detailed demographic and social-survey data from contemporary populations to demonstrate the stark economic trade-offs associated with high fertility (Goodman et al., 2012; Lawson et al., 2012). From their statistical model, which was fit to DHS data from 27 African countries, Lawson et al. (2012) were able to predict an optimal fitness-maximizing level of fertility using a measure of expected mortality-discounted LRS (Lawson et al., 2012). They found that the observed fertility was substantially lower than their fitness-maximizing optimal level. Using a remarkable multi-generational dataset from Sweden, Goodman et al. (2012) show that children from high-fertility families pay a substantial cost in terms of various measures of socioeconomic status. However, they also find that high fertility maximizes fitness based on a LRS-like criterion (i.e., number of living descendants). In populations characterized by substantial demographic change, as all of these examples are, LRS is unlikely to be an appropriate fitness measure, suggesting that the mismatch between predicted and observed fertility on the one hand and between economic and fitness optimization, on the other, could be less than these studies suggest. It is important to note that the use of λ in studies of the trade-offs between fertility and socioeconomic status should not affect conclusions about the tradeoff, unlike the case of the diminished trade-off between longevity and fertility in historical Finland where fitness was intrinsic to the calculation of the trade-off (Korpelainen, 2000).

Overall, our results indicate that calculating fitness using a measure appropriate for non-stationary populations provides qualitatively different predictions for human life history tactics. Through the distinct concavity of the function that relates cumulative fitness to fertility, we expect to find intermediate fertility optima and strong preferences with regard to risky reproduction. We also find that relatively low fertility can place a woman above mean fitness if her births are well timed and her daughters survive to enter the breeding population themselves. We hope that these results will stimulate renewed interest in evolutionary explanations for fertility transitions and that new effort will be directed toward understanding the clear paradox of delayed reproduction in post-transition societies.