Latent class model with familial dependence to address heterogeneity in complex diseases: adapting the approach to family-based association studies

Abstract

Clinical diagnoses of complex diseases may often encompass multiple genetically heterogeneous disorders. One way of dissecting this heterogeneity is to apply latent class (LC) analysis to measurements related to the diagnosis, such as detailed symptoms, to define more homogeneous disease sub-types, influenced by a smaller number of genes that will thus be more easily detectable. We have previously developed a LC model allowing dependence between the latent disease class status of relatives within families. We have also proposed a strategy to incorporate the posterior probability of class membership of each subject in parametric linkage analysis, which is not directly transferable to genetic association methods. Under the framework of family-based association tests (FBAT), we now propose to make the contribution of an affected subject to the FBAT statistic proportional to his or her posterior class membership probability. Simulations showed a modest but robust power advantage compared to simply assigning each subject to his or her most probable class, and important power gains over the analysis of the disease diagnosis without LC modeling under certain scenarios. The use of LC analysis with FBAT is illustrated using autism spectrum disorder (ASD) symptoms on families from the Autism Genetics Research Exchange, where we examined eight regions previously associated to autism in this sample. The analysis using the posterior probability of membership to a LC detected an association in the JARID2 gene as significant as that for ASD (p = 3×10⁻⁵) but with a larger effect size (odds ratio = 2.17 vs. 1.55).

Introduction

Genetic heterogeneity within clinically-defined disease phenotypes remains an important obstacle to the identification of genes responsible for complex diseases, particularly for psychiatric disorders [Owen et al. 2007, Bearden et al. 2004]. This has led researchers to collect various measurements related to the diagnosis, such as detailed symptoms or endophenotypes. Latent class (LC) analysis [Clogg 1995] has previously been applied to such measurements to define more homogeneous disease sub-types, influenced by a smaller number of genes that will thus be more easily detectable (see for instance Fanous et al. [2008] and Todd et al. [2001]). However, traditional latent class models assume independence between subjects and, in family studies, this assumption is likely to be violated since the chosen symptoms are expected to be heritable. Hence, assuming independence does not use all available information to define disease classes. This led us to develop a latent class model allowing dependence between the latent disease class status of relatives within extended families [Labbe et al. 2009, Tayeb et al. 2011]. We modeled dependence between related individuals at the class level and assumed that the class of an individual only depends on the class of his or her two parents, like the genotype of an individual only depends on the genotype of his or her parents.

We previously investigated the use of LC-derived phenotypes in genetic linkage analysis [Bureau et al. 2008]. Our simulation study showed that the latent class approach can provide a substantial gain in power to detect disease genes over the standard heterogeneity approach of Smith and identity-by-descent sharing methods applied to the disease diagnosis. Taking into account familial dependence in the latent class model generally provided greater power than assuming independence. In addition to simply assigning subjects to their most probable class to define LC phenotypes, we have also proposed to incorporate the posterior probability of class membership of each subject in parametric linkage analysis by treating that probability as a covariate of the disease penetrance [Bureau et al. 2008]. That approach improved the power to detect genes over assigning subjects to their most probable class.

In addition to linkage analyses, family-based association studies have previously been performed on LCs, by assigning subjects to their most probable class [Todd et al. 2003]. The approach using posterior class probabilities that improved the power in parametric linkage analysis is not directly transferable to genetic association methods, where hypothesis tests are formulated in terms of expected numbers of transmitted alleles or genotypes instead of recombination fractions. Hence, our first objective was to present an approach to use the posterior probability of disease class membership in family-based association tests (FBATs), and to compare its power to that of the simple approach of assigning subjects to their most probable class.

Our second objective was to apply FBAT to the LCs derived from autism symptoms in families from the Autism Genetic Resource Exchange (AGRE), using both the proposed approach with the posterior probability of class membership and the simple approach of assigning subjects to their most probable class. We tested association in eight regions previously associated to autism spectrum disorder (ASD) in that sample.

Methods

Latent class model

We refer the reader to Labbe et al. [2009] and Tayeb et al. [2011] for a detailed description of the latent class model with familial dependence. Briefly, for family i, Y_i = (Y_i1, …, Y_ini) is the matrix of phenotypic measurement vectors and C_i = (C_i1, …, C_ini) is the vector of unobserved latent classes of the n_i family members. Phenotypic measurements Y_i may be traits that are observable on every subject, or they may be symptoms observable only on subjects affected by a disease, as in the analyses presented here. The model was designed to deal with systematically missing symptoms in unaffected subjects. Given the latent class C_ij, the symptom vector Y_ij of a subject is assumed independent of the symptoms of all other family members. Familial dependence is modeled at the latent class level, by letting the class of a non-founder depend on the class of his or her parents, that is P(C_ij|C_i1, …, C_ij−1, C_ij+1, …, C_ini) = P(C_ij|C_i,m(j), C_i,p(j)) where m(j) and p(j) denote the mother and father of subject j, respectively. Various parameterizations of the model and maximum likelihood estimation using an EM algorithm are described in Labbe et al. [2009] and Tayeb et al. [2011]. The estimated model is used to compute the posterior probability of membership to disease class k, Z_ijk = P(C_ij = k|Y_i = y_i) for subject j in family i.

FBAT reminder

The general FBAT statistic is a score statistic taking the form

$$S=\sum _{ij}{X}_{ij}(T_{ij}-{\mu }_{ij})$$ (1)

in which X_ij denotes some function of the genotype of the j^th offspring in nuclear family i at the marker being tested, T_ij is the same subject’s trait value, and μ_ij is the expectation of T_ij under the chosen null hypothesis. The expectation μ_ij may be a function of covariates [Lunetta et al. 2000]. In studies of dichotomous traits, T_ij = 1 for affected subjects and 0 otherwise. The contribution of an affected subject to the test statistic is therefore equal to 1 − μ_ij. In the classical transmission disequilibrium test (TDT) [Spielman et al. 1993], each affected subject contributes 1, i.e. μ_ij = 0. A Z statistic with a standard normal distribution under the null hypothesis is obtained by standardizing the statistic S:

$$Z=\frac{S-E[S]}{\sqrt{\mathit{Var}[S]}}$$ (2)

where each family contribution to E[S] and Var[S] is computed from the conditional distribution of S_i given the sufficient statistic for the parental genotypes, under the chosen null hypothesis.

Using the latent class posterior probabilities in association analysis

A first straightforward approach is to assign each subject to his or her most probable class, and then perform separate analyses for each class. Here we distinguish the affection status assigned for association analysis from the disease diagnosis. For example, we perform an association analysis on class 1 by assigning the affection status “affected” to all subjects diagnosed with the disease for which class 1 has the highest posterior probability and any other affection status (i.e. “unaffected” or unknown) to all other evaluated subjects. In this approach, we set μ_ij = 0 as in the TDT, so that only subjects assigned the “affected” status contribute to the analysis.

Although straightforward, this approach has the inconvenience of not taking into account the uncertainty of the class assignment. The form of the FBAT statistic suggests to use μ_ij to make the contribution of an affected subject proportional to his or her posterior probability Z_ijk to belong to the disease class k under study. We achieve this by setting

$${\mu }_{\mathit{ijk}}=\{\begin{array}{ll}1-Z_{\mathit{ijk}}\hfill & \text{if}{T}_{ij}=1\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (3)

The contribution of a subject to the FBAT statistic for class k then becomes:

$$S_{\mathit{ijk}}=\{\begin{array}{ll}{X}_{ij}{Z}_{\mathit{ijk}}\hfill & \text{if}{T}_{ij}=1\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (4)

and the FBAT statistic can be rewritten

$$S_k=\sum _{ij}{X}_{ij}{T}_{ij}{Z}_{\mathit{ijk}}$$ (5)

i.e., the posterior class probability is treated as a quantitative trait in affected subjects. When Z_ijk = 1, the subject belongs to class k with certainty, which is equivalent to assigning the subject to class k, while a value Z_ijk = 0 has the same effect as setting the affection status to unknown.

Simulation Study

Simulation study setup

Genetic disease class model

We considered disease models with two and four disease susceptibility (DS) variants all in different genes unlinked to each other. Each DS variant caused its own disease class. In addition to the genetic disease classes, an additional class contained the non-genetic disease cases, i.e. cases with low risk genotypes at all loci. The two latent class models are labelled 2G3C and 4G5C indicating the number of DS variants and the number of disease classes involved. The 2G3C model had a dominant and a recessive DS variant. The 4G5C model had two DS variants with additive allelic effects on the log-risk (i.e. multiplicative effects on the risk scale) in addition to a dominant and a recessive DS variant. The genetic models of disease for each variant under the two models are shown in Table 1. DS allele frequencies were obtained under the following constraints: fixed population prevalence of the disease, Hardy-Weinberg equilibrium at each disease locus and equal probabilities of carrying a high-risk genotype at either gene in the population.

Table 1.

Values of the parameters of the genetic heterogeneity models used in the simulation study.

DS variant	mode of inheritance	risk allele frequency	relative Dd	risk DD
Model 2G3Ca (φb = 0.009, Kc = 0.015)
1	Dominant	0.029	7.4	7.4
2	Recessive	0.239	1	7.4
Model 4G5C (φ = 0.008, K = 0.01)
1	Dominant	0.011	4	4
2	Recessive	0.147	1	4
3	Additive	0.032	2	4
4	Additive	0.032	2	4

^aSee text for definition of the model labels.

^bRisk of disease in subjects with low risk genotypes at all loci.

^cPopulation prevalence of the disease.

Symptom distribution

For the 2G3C model, we used the same within-class multivariate normal distributions for a set of five symptoms as in previous simulation studies [Bureau et al. 2008, Labbe et al. 2009]. For the 4G5C model, we specified mean symptom vectors and a within-class covariance structure such that the Mahalanobis distance between classes ranged from 2.7 to 4.2 within-class standard deviations (SDs) for a SD equal to σ = 10 and from 1.7 to 2.8 SDs for σ = 15. The mean and 95 percent probability interval of each symptom in each class is shown in Supplementary figure 1.

Family structure, ascertainment, and marker genotypes

We simulated samples of nuclear families with two children, both affected. Parents had no phenotypic information. We simulated biallelic markers with the same frequency as the DS variants. Marker genotypes were observed for all family members. For each of the two genes, we simulated one marker in perfect linkage disequilibrium with the DS variant, a second with a squared correlation r² = 0.8 and a third in linkage equilibrium with the other two. The phenotypes and marker genotypes of the family members were simulated using the computer package Simla [Schmidt et al. 2005] for the 2G3C model and our own program in the R statistical environment (www.r-project.org) for the 4G5C model, applying the ascertainment criterion that the nuclear family contains exactly two affected children.

Latent class models fitted to the simulated data

Latent class models with familial dependance were fitted to simulated symptom data on the nuclear family offsprings exactly as in Bureau et al. [2008] and Labbe et al. [2009], with selection of the best model among models with one to five classes by likelihood cross-validation. Traditional latent class models assuming independence between subjects were not fitted, since we have shown previously that they are inferior to latent class models with familial dependance to classify subjects.

Association analysis

We tested association of the markers to disease classes with the two approaches described above (i.e. using the latent class posterior probabilities as a quantitative trait and assigning subjects to their most likely class), and association to the affected/unaffected disease phenotype. All analyses were performed using the FBAT package (www.biostat.harvard.edu/~fbat). The null hypothesis of no association in the presence of linkage was specified [Lake et al. 2000] given the linkage to the disease present in the simulated families. We used a nominal significance level of 5 × 10⁻⁸. Analyses were performed under the additive (on the log scale), dominant and recessive models (with respect to the minor allele). We applied a Bonferroni correction to adjust for the number of latent classes analyzed.

Simulation results

The distribution of the number of classes selected in the various analyses is shown in Supplementary figure 2. The model selection procedure selected most often the correct number of classes, except for the 4G5C model with σ = 15 where four classes were selected more often than five. Under the 4G5C model, the two siblings were in the same class in 74 percent of sibling pairs. The sibling pair class concordance observed when assigning subjects to their most likely class was very close to this true concordance proportion, both with σ = 10 (73 percent concordance) and σ = 15 (75 percent concordance). The mean of the highest posterior probability across subjects and replicates was 0.951 (0.894) for the 2G3C model and 0.897 (0.802) for the 4G5C model with σ = 10 (σ = 15), respectively.

The Type I error rate of the association tests estimated by pooling together the results for the four markers in linkage equilibrium with each of the DS variants of the 4G5C model respected nominal levels (Table 2). The power to detect association to the DS variants of the 4G5C model is presented for markers correlated at r² = 0.8 (Figure 1) and r² = 1.0 (Supplementary figure 3) with the DS variant. The same results for the 2G3C model are shown in Supplementary figures 4 and 5. For each DS variant, the power is presented for analyses under the correct model (dominant on panel A, recessive on panel C and additive on panel E) and, for the dominant and recessive DS variants, under the additive model (panels B and D). Using phenotypes derived from latent classes (first four bars from the left on each panel) provided greater power than treating all symptomatic subjects as affected (bar marked “orig.”), except for the dominant DS variant of the 4G5C model with σ = 15. As expected, the power gain was greater with a smaller within class SD (σ = 10) than with a larger one (σ = 15). Using the posterior class probability provided a modest power advantage compared to simply assigning each subject to his most probable class, an advantage which was consistently observed for the dominant, recessive and additive DS variants, with σ = 10 and σ = 15, and under all three analysis models. When using phenotypes derived from latent classes, the power to detect the recessive DS variant was greater under the additive than the recessive model for the marker at r² = 0.8 (Figure 1C and D and Supplementary figure 4). We investigated this unexpected advantage of the additive model to detect the simulated recessive DS variant, and determined that it was due to a combination of a larger number of informative transmissions and a smaller impact of genotype misclassification (Supplementary figure 6). For a marker perfectly correlated with the DS variant, the recessive model remains sligthly more powerful than the additive model (Supplementary figures 3C and D and 5C and D). By contrast, in the analysis of the original affection status, the recessive model performed a lot better to detect the recessive DS variant.

Table 2.

Type I error rate of the family-based association tests

model	origa	σb = 10		σ = 15
		probc	classd	prob	class
p = 0.05
additive	0.049	0.045	0.041	0.044	0.050
dom	0.049	0.042	0.051	0.042	0.048
rec	0.039	0.039	0.040	0.038	0.042
p = 0.01
additive	0.009	0.007	0.007	0.004	0.005
dom	0.010	0.004	0.004	0.008	0.009
rec	0.008	0.004	0.004	0.004	0.005

^aoriginal phenotype where all symptomatic subjects are affected.

^bwithin-class standard deviation

^cposterior probability of class membership used as a quantitative trait in affected subjects

^dmost probable class used as phenotype

Fig. 1.

Power to detect association to a disease-susceptibility (DS) variant with a marker correlated at r² = 0.8 in simulations of an heterogeneity model with four DS variants (4G5C model). Datasets contain 400 families with two affected siblings and parents with no phenotypic information. Genotypes of all family members are observed. For latent class (LC)-derived phenotypes, p-values were multiplied by the number of classes. The significance level was set to 5 × 10⁻⁸. Results are based on 400 replicates. Panel A shows the results of an analysis under the dominant model, panel B, D and E results under the additive model and panel C results under the recessive model. Error bars represent exact 95% confidence intervals. The first four bars from the left on each panel represent power using LC-derived phenotypes: P: posterior probability of class membership used as a quantitative trait in affected subjects, C: most probable class used as phenotype, σ: within-class standard deviation. The rightmost bar (orig) represents power using the original phenotype where all symptomatic subjects are affected.

Application to autism

Previous association studies in the AGRE dataset

Two research teams recently reported family-based genomewide association studies of ASD in samples comprising families from AGRE. Weiss et al. [2009] combined a sample of 801 AGRE families with a sample of 341 families from the US National Institutes of Mental Health (NIMH) repository, and performed genomewide single nucleotide polymorphism (SNP) genotyping using the Affymetrix 5.0 array. Wang et al. [2009] instead genotyped only the AGRE sample using the Illumina HumanHap 550 array, and restricted their analysis to a subset of 780 families that they inferred to be of European ancestry based on the genotype data. None of these studies obtained genomewide significant results in their primary study sample. Weiss et al. [2009] reported seven genome regions where they obtained p-values < 10⁻⁵, which they followed-up in additional samples. Wang et al. [2009] only report the 5p14.1 region where they obtained a genomewide significant signal after combining their AGRE sample with an autism case-control cohort. We decided to examine the association in these eight regions reported by these two studies using the solution from the application of our LC model with familial dependence to measurements from the Autism Diagnostic Interview-Revised (ADI-R) [Lord et al. 1994] in the AGRE family sample.

Latent class analysis of the AGRE dataset

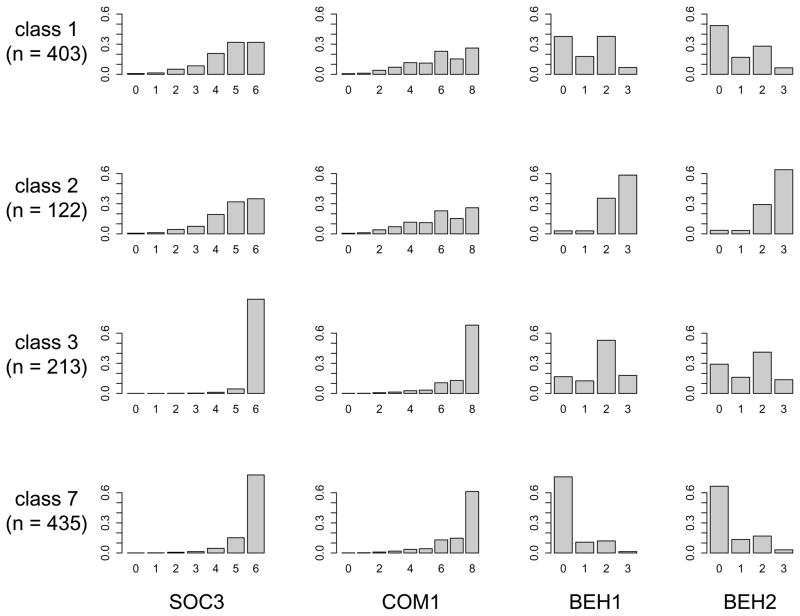
LC modeling of ADI-R measurements, including the selection of symptoms to include in the analysis, is described in detail in Labbe et al. [2009] and Bureau et al. [2008], where we reported an LC analysis restricted to nuclear families. With the extension of our model to multigenerational pedigrees [Tayeb et al. 2011], we were able to include extended pedigrees from AGRE in our analysis [Bureau et al. 2007], all other modeling choices remaining the same as in the nuclear family analysis. We use here the latent class solution from the latter analysis including extended pedigrees. In order to insure that children included in the analysis meet a minimum level of autistic symptoms, we performed our primary analysis on the children who satisfy the ADI-R autism spectrum disorder (ASD) definition 2 in Risi et al. [2006]. The sample is comprised of 757 nuclear families with 1 to 5 siblings with autism spectrum disorder (ASD), 13 first cousin pairs, 3 uncle-niece pairs, 8 sib pairs plus first cousin, 3 sib trios plus first cousin and 3 more complex families illustrated in Supplementary Figure 7, for a total of 787 families. The model selection procedure selected a seven-class model. The mean of the highest posterior probability was 0.557. In 70 percent of the sibling pairs the two siblings were assigned to the same class. Figure 2 shows the distribution of symptoms in the 4 classes containing at least 100 genotyped ASD subjects when assigning these subjects to their most likely class.

Fig. 2.

Distribution of symptoms in latent classes formed using four ADI-R items. SOC3: Item 3 of the subdomain “qualities of reciprocal social interaction”; COM1: Item 1 of the subdomain “communication and language”; BEH1 and BEH2: Items 1 and 2 of the subdomain “restricted and repetitive, stereotyped interests and behaviors”. The distribution of BEH1 is shown for 6 year old males, and the distribution of BEH2 for 6 year old children (no adjustment for sex). SOC3 and COM1 were not adjusted for any covariate. The distributions are shown for the 4 classes containing at least 100 genotyped ASD subjects when assigning these subjects to their most likely class.

FBAT analysis of latent classes in AGRE dataset

We elected to use the Illumina HumanHap 550 array genotype data from the Wang et al. [2009] study because genotypes were available for more families (777 out of 787) used in our latent class analysis than the Weiss et al. [2009] data. We included in our analysis SNPs within 300 kilobases from the SNP with the strongest association signal in the seven regions reported in Table 1 of Weiss et al. [2009] and the 5p14.1 region reported by Wang et al. [2009]. We required SNPs to have less than ten Mendelian errors and greater than 95% complete genotypes to be included in the analysis. The threshold of ten Mendelian errors was established by Weiss et al. [2009] for the AGRE dataset as eliminating biases detectable on a quantile-quantile (QQ) plot of the −log₁₀ of the observed and expected p-values. After removing these SNPs, we identified unlikely double recombinants using Merlin [Abecasis et al. 2002] and deleted genotypes identified as unlikely by applying the default criterion of the pedwipe option of Merlin. The 95% completeness criterion was then applied again to the cleaned genotypes. We applied the same analysis described in the section on the Simulation Study Setup using the FBAT package, except that we tested the composite null hypothesis of no association or no linkage, as in the original analyses. In addition, we fitted logistic models to estimate odds ratios, since the FBAT framework allows only to perform association tests and not to estimate association parameters. To estimate odds ratios for latent classes, we had to define the affected subjects based on the assignment of subjects to their most likely class. We opted for the likelihood function of Dudbridge [2008] for a dichotomous phenotype implemented in the Unphased computer package (www.mrc-bsu.cam.ac.uk/personal/frank/software/unphased). Partial genotype data were included, but the odds ratios were estimated using only the likelihood for the genotypes of the children conditional on the genotypes of the parents to achieve robustness to population substructure. Extended pedigrees were broken down into nuclear families by the FBAT and Unphased packages. We tested association of the 1113 SNPs satisfying quality criteria in the eight regions to the four largest classes and to the ASD phenotype. We used the additive model for our primary analysis as in the original analyses. Since the criteria for an affected individual used in the studies of Weiss et al. [2009] and Wang et al. [2009] are not precisely defined in their reports, we used the Risi et al. [2006] definition of ASD mentioned above as phenotype for comparison with the LC-derived phenotypes.

Among the eight tested regions, a p-value < 10⁻⁵ was achieved only for class 7, which is characterized by high levels of symptoms on qualities of reciprocal social interaction and communication and language, but low levels of restricted and repetitive, stereotyped interests and behaviors. This result was obtained under the additive model and using the posterior class probability with rs13193457 at 6p24-p23 (Figure 3). Less significant p-values were obtained with the dominant and recessive models (not shown). When applying a conservative Bonferroni correction for testing four classes, the p-value remains at the same level as that for the ASD phenotype (p = 3 × 10⁻⁵)(Table 3). That SNP is only weakly correlated to the SNPs rs13208655 and rs7766973 detected by Weiss et al. [2009] in the region (r² = 0.09 and 0.12 respectively), based on data from the HapMap CEU sample (www.hapmap.org) (Supplementary Figure 8). Although the two SNPs detected by Weiss et al. [2009] are not on the Illumina HumanHap550 array, they are captured by the SNPs rs6459404 and rs6921502, and these do show an association to the ASD phenotype in our analysis (Figure 3 and Table 3). Table 3 also shows that odds ratio are larger for class 7 than for the ASD phenotype, not only for rs13193457 but also for three other neighboring SNPs. In the case of rs6921502 and rs6459404, the odds ratio is larger despite a less significant signal for class 7 than for the ASD phenotype, because fewer subjects contribute importantly to class 7 signals. Testing association to haplotypes formed by rs6921502, rs6459404 and rs13193457 revealed that the rs6921502 G and rs6459404 C alleles form an associated haplotype (p = 9.8 × 10⁻⁴) distinct from a haplotype defined by the rs13193457 A allele (which has a protective effect, p = 1.0 × 10⁻⁵). The observation that p-values from a multi-marker test [Rakovski et al. 2007] of the five SNPs in Table 3 are more significant than the lowest p-values obtained from tests of individual SNPs is additional evidence of the presence of multiple distinct association signals. All of these SNPs are located within the same JARID2 gene (Supplementary Figure 8).

Fig. 3.

Association of SNPs to latent class 7 and to the ASD phenotype at 6p24-p23 in the AGRE sample. FBAT results under the additive model. For latent class 7 phenotypes, p-values were multiplied by 4, the number of tested classes.

Table 3.

SNPs associated to class 7 and to ASD in the JARID2 gene with p < 10⁻³.

marker	pos. (Mb)	risk allele	freq.a	class 7		ASD
				OR (95% CI)b	corrected pc	OR (95% CI)	nominal p
rs11962776	15.368	C	0.90	1.31 (0.98, 1.81)	0.17	1.43 (1.19, 1,71)	6.3 × 10−5
rs6921502	15.383	G	0.49	1.36 (1.11, 1,65)	0.0026	1.22 (1.10, 1.36)	0.00041
rs6459404	15.389	C	0.50	1.34 (1.10, 1.62)	0.0019	1.23 (1.11, 1.37)	0.00018
rs3759	15.406	G	0.85	1.50 (1.14, 1.98)	0.0015	1.21 (1.05, 1.40)	0.0090
rs13193457	15.454	C	0.93	2.17 (1.46,3.23)	2.9 × 10−5	1.55 (1.25, 1.92)	2.8 × 10−5
5 markersd					1.0 × 10−6		2.9 × 10−7

^aRisk allele frequency estimated from the genotype of parents in nuclear families only.

^bOR: odds ratio; 95% CI: nominal 95% confidence interval.

^cp-value after Bonferroni correction for analyzing four classes.

^dMulti-marker test with 5 degrees of freedom.

Outside of the 6p24-p23 region, p-values were subtantially less significant, both for LC-derived phenotypes and the ASD phenotype. The next smallest p-value was obtained also for class 7 with the SNP rs1909655 at 10q21 under the allelic model (p = 4 × 10⁻⁴).

Discussion

We have proposed an approach to use the posterior probability of class membership derived from LC analysis in family-based association studies by making the contribution to the FBAT statistic of an affected subject proportional to his or her posterior probability of belonging to the class being analyzed. Simulations under models of genetic heterogeneity revealed small but robust power gains with this approach compared to assigning subjects to their most probable class. The power gains over the analysis of the affected/unaffected phenotype without LC modeling were important under certain simulation scenarios. This power improvement only applies to disease subtypes caused by a smaller number of genes than the original definition of the disease. Power losses are expected when subtyping the disease does not reduce the genetic complexity, due to the reduced sample size within each class. In the AGRE dataset, using LCs derived from autism symptoms produced association with a LC as significant as with the ASD phenotype in the JARID2 gene, and using the posterior probability of membership to the class gave a more significant signal than assigning subjects to their most likely class. The increase in signal coming from the incorporation of the uncertainty in the class assignment when testing association to latent classes in this particular dataset is consistent with the power improvement obtained in simulations.

Lunetta et al. [2000] use standard score test theory for exponential family models to take covariate effects into account. The expectation μ_ij is then determined by the regression of the trait on the covariates under the null model excluding the marker genotype effect. With a dichotomous trait, this assigns a small contribution 1 − μ_ij to an affected subject whose affection is well predicted by the covariates, and a large contribution to an affected subject poorly explained by the covariates. Our proposal to substitute the posterior probability of class membership Z_ijk for 1 − μ_ijk is not derived from score test theory, but pursues the same intuitive goal as the covariate adjustment. Here however, Z_ijk is not an explanatory variable for the trait unrelated to the genetic marker being tested, it is instead an indication of membership to a disease class, influenced by a gene that one wants to detect by testing the marker. This is the justification for making the contribution of affected subjects to the FBAT statistic proportional to Z_ijk. Differences between using the posterior probability as phenotype and assigning subjects to their most likely class are expected to become more important as the posterior probabilities get further away from 1 and 0. It was indeed the case that the Z score mean difference was slightly larger with σ = 15 than with σ = 10 (data not shown). This did not always translate into larger power differences because of ceiling and floor effects when power is near 1 or 0.

While the FBAT framework provides this intuitive way to take into account uncertainty in LC assignment for hypothesis testing, it has the inconvenience of not providing estimates of association parameters. Assigning subjects to their most likely class remains an option allowing the use of any statistical method for association analysis in families.

In the AGRE analysis, the larger odds ratios obtained with class 7 for SNPs in the JARID2 gene indicate that LC analysis partially succeeded in creating more genetically homogeneous disease classes. Members of the same family tend to be assigned to the same class in both the simulated data and the AGRE dataset, as expected if they share the same DS genotypes. However, within-family heterogeneity is also expected in traits as complex as ASD due to segregation of multiple genes and to sporadic, non-genetic cases, and it is an advantage of our LC model that it offers the flexibility to assign different subjects from a same family to different classes when their symptom patterns differ [Labbe et al. 2009].

The association signals that we obtained in the JARID2 gene and in the other regions examined were weaker than those reported by Weiss et al. [2009]. The most likely explanation is that the Weiss et al. [2009] sample was larger, including an NIMH sample in addition to the AGRE sample that we analyzed. Slight differences between the definitions of ASD in the two analyzes, the contribution to the FBAT statistic of families with missing parental genotypes which were excluded from the TDT performed by Weiss et al. [2009], and the different SNPs used may also explain differences in results. At this level of significance, findings from a genomewide association study are likely to be false positives. However, what is noticeable here is that a signal as strong as the signal with the ASD phenotype could be obtained with a latent class in regions selected based on the strength of association with the ASD phenotype. If JARID2 is truly involved in ASD, our LC analysis suggests that it could affect reciprocal social interaction and communication and language, providing a refinement of the phenotype. The LC analysis also highlighted association to a different JARID2 haplotype than the Weiss et al. [2009] study.

In the present study, we focused on symptoms observable only on diseased subjects. In many contexts, the use of traits related to the disease phenotype and which are also observable on unaffected subjects, often called endophenotypes [Gottesman and Gould 2003], may be more appropriate than the use of symptoms to define genetically homogeneous sub-types of disease [Szatmari et al. 2007]. Our LC modeling approach is equally applicable with endophenotypes, as explained in Labbe et al. [2009].

With the present extension, the LC model with familial dependence that we have previously proposed to deal with genetic heterogeneity is now applicable to the two major types of genetic analysis in families: linkage and association. We have demonstrated in both cases an advantage from using the posterior probability of class membership to account for uncertainty of class assignment in the analysis.