Skip to main content
PMC home page
Applied Physics Letters logoLink to Applied Physics Letters
. 2014 Apr 17;104(15):153701. doi: 10.1063/1.4871861

Mimicking the mechanical properties of the cell cortex by the self-assembly of an actin cortex in vesicles

Tianzhi Luo 1,a), Vasudha Srivastava 1,3, Yixin Ren 1, Douglas N Robinson 1,2,3,a)
PMCID: PMC4000382  PMID: 24803681

Abstract

The composite of the actin cytoskeleton and plasma membrane plays important roles in many biological events. Here, we employed the emulsion method to synthesize artificial cells with biomimetic actin cortex in vesicles and characterized their mechanical properties. We demonstrated that the emulsion method provides the flexibility to adjust the lipid composition and protein concentrations in artificial cells to achieve the desired size distribution, internal microstructure, and mechanical properties. Moreover, comparison of the cortical elasticity measured for reconstituted artificial cells to that of real cells, including those manipulated using genetic depletion and pharmacological inhibition, strongly supports that actin cytoskeletal proteins are dominant over lipid molecules in cortical mechanics. Our study indicates that the assembly of biological systems in artificial cells with purified cellular components provides a powerful way to answer biological questions.

A common structural model of cells considers the cells as inner liquid cores wrapped by spherical outer shells composed of the actin cortex and plasma membrane.1, 2 The actin cortex is a thin sheet of actin meshwork formed by actin cytoskeletal proteins, including actin, actin crosslinkers (ACs), motor proteins, and other actin binding proteins (Fig. S1).3, 4, 5 The plasma membrane is largely a lipid bilayer embedded with transmembrane proteins. The actin cortex and plasma membrane are connected by anchoring proteins. The composite of actin cytoskeleton and plasma membrane plays important roles in sensing mechanical stimuli and subsequently remodeling its own microstructure, which governs many essential cellular events such as migration and morphogenesis.6, 7, 8, 9 The cell shape changes in these events can be largely considered mechanical processes. Therefore, understanding the mechanical properties of the composite can provide deep insight into the nature of important biological phenomena.

Currently, there are two complementary strategies for studying the mechanical properties of cells: the top-down and the bottom-up approaches. The former involves simplifying the cellular systems by the combination of genetic deletion or knockdown of nonessential genes and pharmacological inhibition of the function of certain proteins.4, 10, 11, 12 The latter relies on the reconstitution of the actin cytoskeleton with purified or synthesized components in in vitro systems.13, 14, 15, 16, 17, 18, 19, 20, 21 Previous measurements conducted with in vivo and in vitro systems suggest that the mechanical properties of the actin cortex depend on the force-dependent affinities of all of these proteins to F-actin as well as their concentrations. Despite the numerous experiments conducted in live cells, only a limited number of genes and proteins can be deleted or inhibited simultaneously, and when expressing genes of interest in cells, it can be difficult to control expression precisely. On the other hand, numerous proteins can be added in precisely controlled concentrations to in vitro reconstitution systems, though this can be labor intensive. One type of in vitro assay is to assemble the actin meshwork into a 2D flat sheet and measure its viscoelastic properties by particle tracking methods and shear micro-rheology.14, 15, 16, 18, 22, 23, 24 These assays provided many deep insights into the mechanical properties of cytoskeletal proteins. But the curvature effect of cytoskeleton-membrane composite in cells is missing in these measurements. An emerging technology involves building artificial cells by reconstituting the actin cortex in lipid vesicles using the emulsion-based technique.25, 26, 27 Besides possessing curvature, the vesicles synthesized by the emulsion method have the following advantages: adjustable lipid composition of inner and outer layers of the membrane, precisely controllable concentration of each essential component, efficient usage of the components, high yield of unilamellar vesicles, relative short processing duration, and simple experimental setup.

Over the past decade, a few attempts have been made to synthesize the actin cortex in vesicles to produce artificial cells.26, 28, 29, 30, 31 However, no mechanical measurements were conducted on these artificial cells, and some of the components were unnatural proteins. Here, we used natural proteins to assemble the actin cortex and anchor it to the lipid membrane of the unilamellar vesicles. Further, we showed that the stability and associated yield of artificial cells can be tuned by adjusting the actin concentration. Last, we measured the stiffness of the artificial cells with different concentrations of actin and its crosslinkers, and compared it to that of wild-type (WT) and mutant Dictyostelium cells. The comparison indicated that the top-down and bottom-up approaches indeed provide complementary strategies for understanding the collective behaviors of actin cytoskeletal proteins.

In brief, the synthesis of artificial cells consisted of two steps (Fig. S2).5 The first step involved the formation of micron-sized aqueous droplets wrapped by a monolayer of lipid in a mixture of mineral oil and lipids by mechanical vortexing. In the droplets, the protein concentrations were set to the desired levels. The lipid monolayer corresponded to the inner leaflet of the artificial cells and was composed of phosphatidylcholine (PC), phosphatidylethanolamine (PE), and phosphatidylinositol 4,5-bisphosphate (PIP2) as in real cells.32 In the second step, the aqueous droplets passed through a monolayer of lipid (mainly PC at the interface between mineral oil and buffer) with the aid of centrifugation force to form vesicles. This monolayer of lipids formed the outer leaflet of the bilayer membrane. The vesicles with desired protein concentrations inside and proper lipid composition were the artificial cells of interest.

We conducted control experiments to ensure that one can take the advantage of emulsion method to engineer the vesicles. To verify that the emulsion method is able to preserve the proteins of interest inside the aqueous droplets and vesicles, we used tetramethylrhodamine isothiocyanate (TRITC)-dextran as a volume marker. As shown in Figs. 1a, 1b, the intensity of TRITC-dextran is roughly proportional to the size of the aqueous droplets and vesicles, indicating the emulsion method is able maintain the protein concentrations as designed. Moreover, the number of vesicles in Fig. 1b suggests that emulsion method has a fair yield. To demonstrate that the lipid compositions of inner and outer leaflets can be controlled separately, we used fluorescein isothiocyanate (FITC)-PE and Pyrene-PE in the first and second steps, respectively, during synthesis. PE labeled with different fluorescent probes indeed was incorporated into the targeted lipid layers (Fig. 1c).

Figure 1.

Figure 1

Open in a new tab

Aqueous droplets and vesicles assembled using the emulsion method. Panels (a) and (b) show representative images of TRITC-dextran-labeled droplets and vesicles, respectively. (c) Images show FITC-PE and pyrene-PE in inner and outer leaflets of the bilayer membrane, respectively.

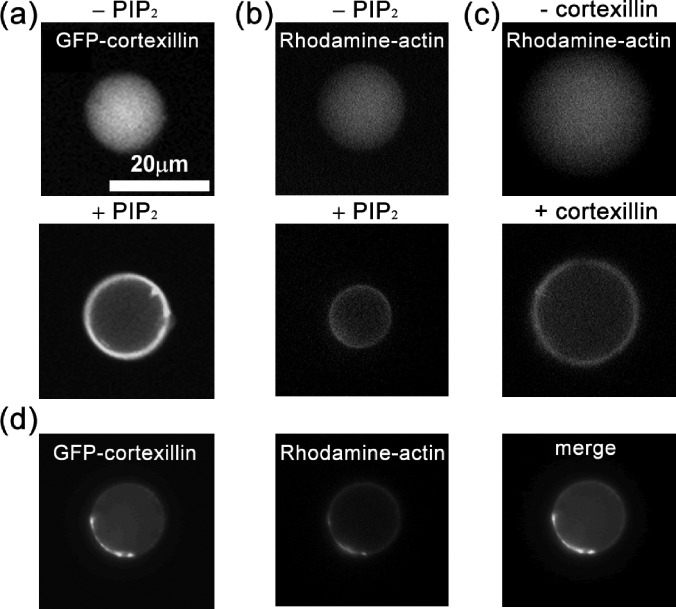
It is known that anchoring proteins are important for the structural integrity of cytoskeleton-membrane composite in cells since in vivo measurements demonstrated that cells with impaired expression of anchoring proteins displayed significant reduction of cortical tension.4, 33 Here, in the artificial cells, an anchoring protein, cortexillin-I having both actin-binding domains and PIP2-binding motifs,34 was purified and used to build the physical linkages between the actin cortex and the bilayer membrane.5 The concentration of cortexillin-I was 4 μM and the fraction of PIP2 was about 3%, close to that in Dictyostelium cells. As shown in Fig. 2a, the enrichment of cortexillin in the proximity to membrane was highly dependent on the presence of PIP2. Furthermore, in the absence of either PIP2 (Fig. 2b) or green fluorescence protein (GFP) tagged cortexillin-I (Fig. 2c), the actin labeled with rhodamine dye uniformly spread in the vesicles and failed to form a cortex next to the membrane. On the other hand, the presence of PIP2 and cortexillin-I was able to promote the formation of actin cortex, which was anchored to the membrane, suggesting that these two natural molecules are sufficient for the formation of an actin cortex (Fig. 2d).

Figure 2.

Figure 2

Open in a new tab

The formation of actin cortex depends on cortexillin and PIP2. (a) Cortexillin localization depends on PIP2. Actin cortex formation depends on PIP2 (b) and on cortexillin (c), respectively. (d) Cortexillin and actin colocalize in artificial cells. Cortexillin and actin were labeled with green and red fluorophores, respectively.

During the synthesis, the effective surface-tension together with the centrifugation speed determined the size distribution of the aqueous droplets and the artificial cells. First, the stabilities of aqueous droplets are largely governed by the composition of lipids encapsulating them. Second, the total force they experience can be simplified as F→total=F→C+F→B+F→T with the assumption that the droplet shape is close to a sphere.35 Here, F→C is the centrifugal force; F→B is the buoyancy force; and F→T is the composite tension accounting for various tensions at the interface. Further scaling analysis yields FC ∼ r3, FB ∼ r3, and FT ∼ r, where r denotes the radius of aqueous droplet.5 Projecting all the forces to the direction perpendicular to the interface gives Ftotal=(C−B)r3−Tr, where C, B, and T are the coefficients for centrifugal force, buoyancy force, and composite tension, respectively. Thus, aqueous droplets are able to pass through the interface and form vesicles only when Ftotal > 0, i.e., (C−B)r2−T>0. This criteria determines a critical radius, r*=T/(C−B). Aqueous droplets with sizes larger than r* are able to cross the interface and form vesicles with the aid of centrifugation. Meanwhile, the lipid composition affects the interfacial tension between the oil and water interface. Therefore, varying centrifugal speed and lipid composition allows the tuning of the size distribution of vesicles and artificial cells.

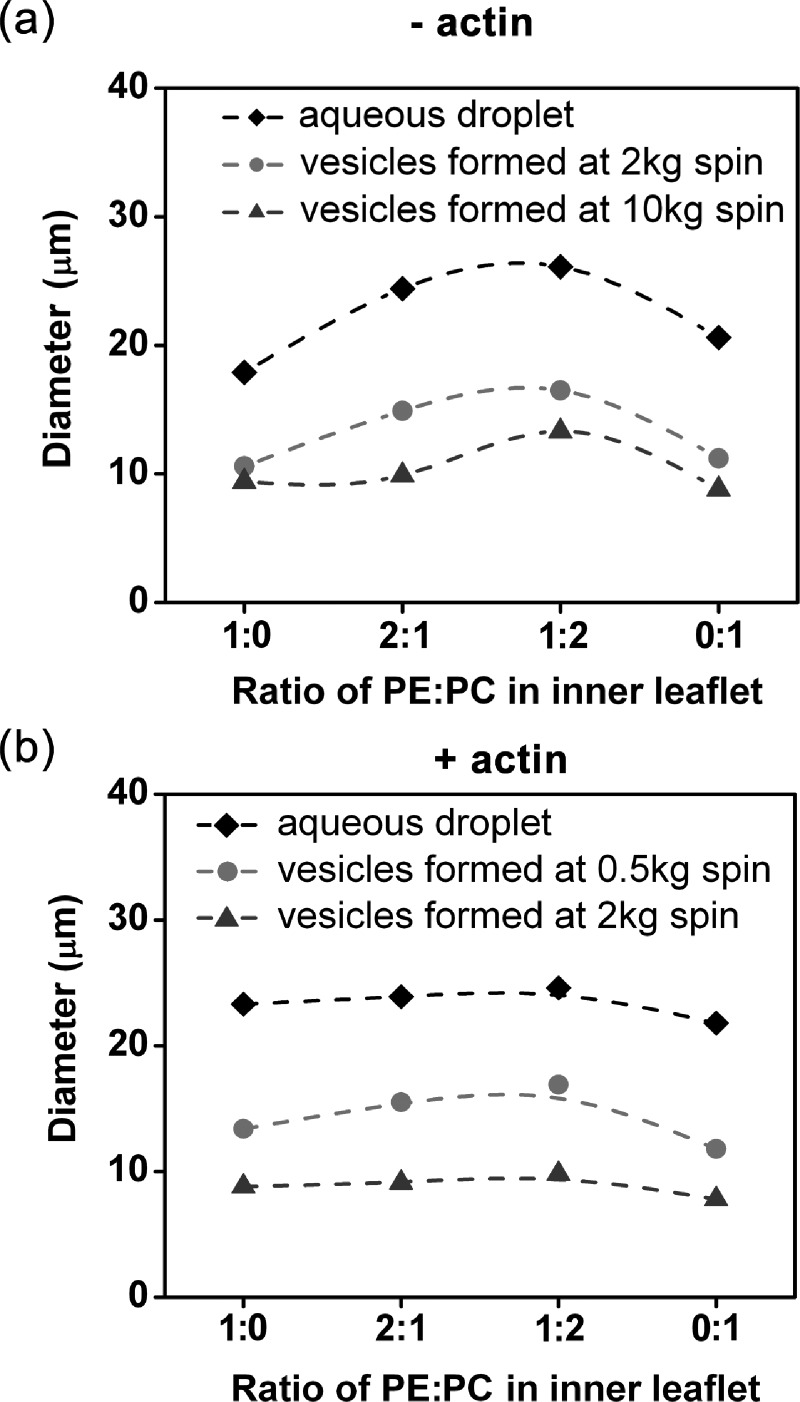
Different lipids have distinct geometries and favor specific local curvatures.36 PC is cylindrical in shape and favors the formation of a flat lipid layer without curvature; whereas, PE lipid is considered to have a cone shape and usually results in a curved lipid layer. Additionally, the head group of PC is larger than that of PE.37 These properties together make the PC dominant in the outer leaflet, while PC and PE coexist in the inner leaflet of the cellular plasma membrane.38, 39 To mimic the cellular properties, we used PC for the outer leaflet in the synthesized vesicles (artificial cells) and a mixture of PC and PE for the inner leaflet. Indeed, different lipid compositions (PE to PC ratio) in the membrane displayed significant effects on the size of aqueous droplets and vesicles where actin was absent (Fig. 3a). The images of aqueous droplets were taken immediately after the vortexing to avoid the coalescence.40 At the same centrifugation speed, the maximum size of droplets and vesicles located at PE:PC ∼ 1:1. This phenomenon could be explained by the increased tension due to the enhanced head-head interaction between lipids as the lipid composition changes from either pure PC or pure PE to PE:PC = 1:1.5 For aqueous droplets, the average size of the droplets R¯ is related to the surface tension γ, and the mechanical work (referred to vortexing here) performed during emulsification w, by R¯∝γ/w.41 Since the mechanical work was the same for the cases with different lipid compositions, the increased tension resulted in droplets with larger size R¯. Examples of the corresponding size distribution are shown in Fig. S4.5 For the formation of vesicles, the increased tension yielded a larger r* because of r*∼T as discussed earlier. Because r* is the smallest size of droplets that can pass though the oil-water interface, equimolar amounts of PE and PC favors the formation of larger vesicles. By comparison, the size distribution of artificial cells with actin cortex inside was almost independent of the lipid composition (Fig. 3b). The effect of actin cortex could be due to the composite of plasma and actin cortex. Cellular observations already suggested that the actin cytoskeleton provided major resistance to stretch deformation, while the plasma membrane mainly provides the resistance to bending deformation. Actin dominance in cortical tension possibly led to the insensitivity of the size to the lipid composition. This is further supported by the observation that higher actin concentrations resulted in larger artificial cells at the same spin speed (Fig. S5).5 Therefore, the size of synthesized artificial cells can be tuned by actin concentration as well as lipid composition.

Figure 3.

Figure 3

Open in a new tab

The average size of aqueous droplets and vesicles with different PE:PC ratios at the inner leaflet formed at different with relative centrifugal forces (RCFs). Aqueous droplets and vesicles were prepared in the absence (a) and presence (b) of actin. The outer leaflet is pure PC for all cases. Examples of size distributions can be found in supplementary Figs. S4 and S5.5 n > 200 from at least 3 different experiments for all cases. P-values obtained by Mann-Whitney test are less than 0.05 for most cases in (a), but larger than 0.05 for most cases in (b) when comparing at given spin speed.

Besides the effective surface-tension, the centrifugation speed also played an important role in tuning the size distribution of vesicles. The equation, r*=T/(C−B), suggests that r* decreases with increased C, or equivalently the centrifugation speed because the centrifugation force is linearly proportional to the square of the centrifugation speed. The average size of vesicles indeed decreased with increased centrifugation speeds (Fig. 3). However, the equation derived here assumed that the aqueous droplets were rigid spheres and did not include the local deformation of the droplets due to the shear force associated with centrifugation. Therefore, the equation can only interpret certain features of the experimental observations. For instance, it is noted that very large aqueous droplets did not successfully form vesicles, which could not be explained by the equation. We suggest that this might due to the breakdown of the rigid sphere assumption. We observed that large droplets were much more easily deformed by the shear force than small droplets were. Further, the large droplets adopted a dome shape at the interface during centrifugation.42 The dome shaped droplets had a much larger contact area with the water phase below, than a sphere with the same volume and thus presumably had a larger overall tension force, FT. Namely, FT ∼ r is not valid for large aqueous droplets. This deformation associated nonlinear relation between FT and r might explain why large aqueous droplets failed to form vesicles.

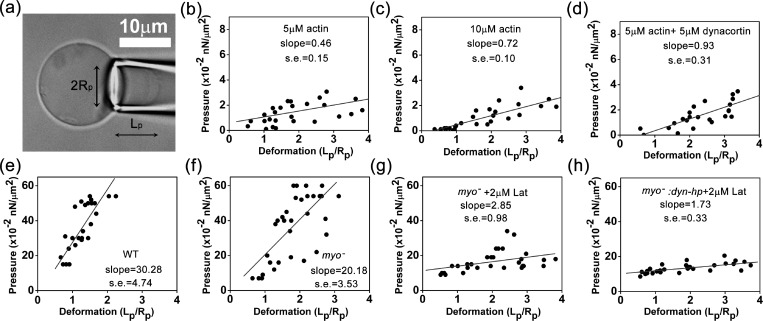
To characterize the mechanical properties of the artificial cells, we used micropipette aspiration to measure the cellular elongation at different pressures.43, 44 We varied the actin concentrations in the range of 0–15 μM and the concentration of actin crosslinker dynacortin in the range of 0–5 μM while keeping the concentrations of the other components the same. The concentration of cortexillin-I was 4 μM. The outer leaflet was 100% PC, whereas the inner leaflet had a PE:PC ratio of 1:1 and 3% PIP2.32 Similar to the behaviors of vesicles and live cells,43, 44 the elongation of the artificial cells in the micropipette increased almost linearly with respect to the applied pressure in low pressure range (Fig. 4a). We used linear least-squares regression to fit the measured data points to a straight line and calculated the slopes of artificial cells with different protein concentration inside (Figs. 4b, 4c, 4d). The slope derived from the deformation-pressure relation is thought to be proportional to the effective Young's modulus (Table TABLE I.).43 Since the large slope corresponds to high Young's modulus of the cell cortex, the measurements indicate that the Young's modulus of the artificial cells increased with the concentrations of actin and crosslinking protein dynacortin.

Figure 4.

Figure 4

Open in a new tab

The micropipette aspiration measurements of artificial and real cells. (a) The micrograph shows micropipette aspiration of an artificial cell. Panels (b), (c), and (d) show the measurements of artificial cells with 5 μM actin, 10 μM actin, and 5 μM actin + 5 μM dynacortin, respectively. Panels (e), (f), (g), and (h) show micropipette aspiration measurements for WT, myosin II null, myosin II null + 2 μM latrunculin-treated, and myosin II::dyn-hp + 2 μM latrunculin-treated Dictyostelium cells. n > 8 for all cases. The converted Young's moduli are provided in Table TABLE I..

TABLE I.

The Young's modulus of artificial cells and Dictyostelium cells obtained by micropipette aspiration measurements (converted from the slopes shown in Fig. 4).

Artificial cells (pN/μm2 or Pa) Dictyostelium cells (pN/μm2 or Pa)
5 μM actin 1.1 ± 0.4 WT 69 ± 11
10 μM actin 1.6 ± 0.2 myoII null 46 ± 8
5 μM actin + 5 μM dynacortin 2.1 ± 0.7 myoII + 2 μM latrunculin 6.5 ± 2.5
    myoII:dyn-hp + 2 μM latrunculin 3.9 ± 0.8
Open in a new tab

In addition to the bottom-up approaches described above, we adjusted the cellular properties using top-down strategies and made comparisons between real cells and the artificial ones. We lowered the concentration of actin filaments in Dictyostelium cells by adding actin depolymerization chemical, latrunculin A (in 0.1% dimethyl sulfoxide (DMSO)), and genetically depleted the expression level of one major actin crosslinker, dynacortin using a dynacortin hairpin (dyn-hp) plasmid. The cellular concentration of filamentous actin was reduced from 70 to ∼30 μM by 2 μM latrunculin A.45 The knockdown efficiency of dynacortin by dyn-hp is >98%.10 Consistent with previous results, myosin II null cells (deleted for the myosin II heavy chain (mhcA) gene, Fig. 4f) displayed a smaller slope (lower Young's modulus in Table TABLE I.) compared to WT cells (Fig. 4e). Additionally, latrunculin A treatment of myosin II null cells dramatically reduced the Young's modulus (Fig. 4g, Table TABLE I.). Meanwhile, DMSO was shown to have a negligible effect on our measurements (Fig. S6).5 Moreover, the depletion of dynacortin by dyn-hp together with latrunculin A treatment (Fig. 4h) further diminished the Young's modulus to a level similar to that of the artificial cells (Figs. 4b, 4c, Table TABLE I.). Last, these measurements suggest that the membrane contribution to the effective Young's modulus of the cell is very small (<2%–5%), compared to the contribution from cytoskeletal proteins.

In summary, we employed the emulsion method to synthesize artificial cells with a biomimetic actin-based cortex and measured the corresponding mechanical properties. We demonstrated that this method allows one to freely tune the lipid composition and protein concentrations in artificial cells to achieve the desired size distribution, internal microstructures, and mechanical properties of artificial cells. Additionally, our results provided further evidence that the actin cytoskeletal proteins play dominant roles in cortical tension, whereas plasma membrane's contribution is rather small. This study also suggests that a better understanding of the cellular properties may be achieved by the combination of the assembly of biological systems in artificial cells and the reduction of the counterparts in living cells. Currently, the major challenging issue of building artificial cells is the limited amount of purified proteins to begin with, which could be potentially solved by using high-yield protein purification methods.46

Acknowledgments

This work was supported by the National Institutes of Health Grants GM66817 and GM86704 (to D.N.R.).

References

  1. Discher D. E., Boal D. H., and Boey S. K., Biophys. J. 75, 1584–1597 (1998). 10.1016/S0006-3495(98)74076-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Robinson D. N., Kee Y. S., Luo T., and Surcel A., in Comprehensive Biophysics, edited by Edward H. E. (Elsevier, Amsterdam, 2012), pp. 48–72. [Google Scholar]
  3. Stossel T. P., Fenteany G., and Hartwig J. H., J. Cell Sci. 119, 3261–3264 (2006). 10.1242/jcs.02994 [DOI] [PubMed] [Google Scholar]
  4. Luo T., Mohan K., Iglesias P. A., and Robinson D. N., Nature Mater. 12, 1064–1071 (2013). 10.1038/nmat3772 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. See supplementary material at http://dx.doi.org/10.1063/1.4871861 for text detailing of experimental setup, methods of the synthesis of artificial cells, and additional supporting data.
  6. Vicente-Manzanares M., Ma X., Adelstein R. S., and Horwitz A. R., Nat. Rev. Mol. Cell Biol. 10, 778–790 (2009). 10.1038/nrm2786 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. He L., Wang X., Tang H. L., and Montell D. J., Nat. Cell. Biol. 12, 1133–1142 (2010). 10.1038/ncb2124 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hutson M. S., Tokutake Y., Chang M.-S., Bloor J. W., Yenakides S., Kiehart D. P., and Edwards G. S., Science 300, 145–149 (2003). 10.1126/science.1079552 [DOI] [PubMed] [Google Scholar]
  9. Friedl P. and Gilmour D., Nat. Rev. Mol. Cell Biol. 10, 445–457 (2009). 10.1038/nrm2720 [DOI] [PubMed] [Google Scholar]
  10. Girard K. D., Chaney C., Delannoy M., Kuo S. C., and Robinson D. N., EMBO J. 23, 1536–1546 (2004). 10.1038/sj.emboj.7600167 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Reichl E. M., Ren Y., Morphew M. K., Delannoy M., Effler J. C., Girard K. D., Divi S., Iglesias P. A., Kuo S. C., and Robinson D. N., Curr. Biol. 18, 471–480 (2008). 10.1016/j.cub.2008.02.056 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Simson R., Wallraff E., Faix J., Niewöhner J., Gerisch G., and Sackmann E., Biophys. J. 74, 514–522 (1998). 10.1016/S0006-3495(98)77808-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Zhang Y., Ruder W. C., and LeDuc P. R., Trends Biotechnol. 26, 14–20 (2008). 10.1016/j.tibtech.2007.09.006 [DOI] [PubMed] [Google Scholar]
  14. Gardel M. L., Nakamura F., Hartwig J. H., Crocker J. C., Stossel T. P., and Weitz D., Proc. Natl. Acad. Sci. U. S. A. 103, 1762–1767 (2006). 10.1073/pnas.0504777103 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Shin J. H., Gardel M. L., Mahadevan L., Matsudaira P., and Weitz D. A., Proc. Natl. Acad. Sci. U. S. A. 101, 9636–9641 (2004). 10.1073/pnas.0308733101 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Koenderink G. H., Dogic Z., Nakamura F., Bendix P. M., MacKintosh F. C., Hartwig J. H., Stossel T. P., and Weitz D. A., Proc. Natl. Acad. Sci. U. S. A. 106, 15192–15197 (2009). 10.1073/pnas.0903974106 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Ehrlicher A. J., Nakamura F., Hartwig J. H., Weitz D. A., and Stossel T. P., Nature 478, 260–263 (2011). 10.1038/nature10430 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Yao N. Y., Broedersz C. P., Depken M., Becker D. J., Pollak M. R., MacKintosh F. C., and Weitz D. A., Phys. Rev. Lett. 110, 018103 (2013). 10.1103/PhysRevLett.110.018103 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Wagner B., Tharmann R., Haase I., Fischer M., and Bausch A. R., Proc. Natl. Acad. Sci. U. S. A. 103, 13974–13978 (2006). 10.1073/pnas.0510190103 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Claessens M. M. A. E., Bathe M., Frey E., and Bausch A. R., Nature Mater. 5, 748–753 (2006). 10.1038/nmat1718 [DOI] [PubMed] [Google Scholar]
  21. Köhler S., Schaller V., and Bausch A. R., Nature Mater. 10, 462–468 (2011). 10.1038/nmat3009 [DOI] [PubMed] [Google Scholar]
  22. Gardel M. L., Shin J. H., MacKintosh F. C., Mahadevan L., Matsudaira P., and Weitz D. A., Science 304, 1301–1305 (2004). 10.1126/science.1095087 [DOI] [PubMed] [Google Scholar]
  23. Tseng Y., Kole T. P., Lee J. S. H., Fedorov E., Almo S. C., Schafer B. W., and Wirtz D., Biochem. Biophys. Res. Commun. 334, 183–192 (2005). 10.1016/j.bbrc.2005.05.205 [DOI] [PubMed] [Google Scholar]
  24. Hoffman B. D., Massiera G., Van Citters K. M., and Crocker J. C., Proc. Natl. Acad. Sci. U. S. A. 103, 10259–10264 (2006). 10.1073/pnas.0510348103 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Zhang L., Hu J., and Lu Z., J. Colloid Interface Sci. 190, 76–80 (1997). 10.1006/jcis.1997.4820 [DOI] [PubMed] [Google Scholar]
  26. Pautot S., Frisken B. J., and Weitz D. A., Proc. Natl. Acad. Sci. U. S. A. 100, 10718–10721 (2003). 10.1073/pnas.1931005100 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Noireaux V. and Libchaber A., Proc. Natl. Acad. Sci. U. S. A. 101, 17669–17674 (2004). 10.1073/pnas.0408236101 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Murrell M., Pontani L.-L., Guevorkian K., Cuvelier D., Nassoy P., and Sykes C., Biophys. J. 100, 1400–1409 (2011). 10.1016/j.bpj.2011.01.038 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Pontani L.-L., van der Gucht J., Salbreux G., Heuvingh J., Joanny J.-F., and Sykes C., Biophys. J. 96, 192–198 (2009). 10.1016/j.bpj.2008.09.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Limozin L. and Sackmann E., Phys. Rev. Lett. 89, 168103 (2002). 10.1103/PhysRevLett.89.168103 [DOI] [PubMed] [Google Scholar]
  31. Carvalho K., Tsai F. C., Lees E., Voituriez R. l., Koenderink G. H., and Sykes C., Proc. Natl. Acad. Sci. U. S. A. 110, 16456–16461 (2013). 10.1073/pnas.1221524110 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Weeks G. and Herring F. G., J. Lipid Res. 21, 681–686 (1980). [PubMed] [Google Scholar]
  33. Octtaviani E., Effler J. C., and Robinson D. N., Mol. Biol. Cell 17, 5275–5286 (2006). 10.1091/mbc.E06-08-0767 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Faix J., Steinmetz M., Boves H., Kammerer R. A., Lottspeich F., Mintert U., Murphy J., Stock A., Aebi U., and Gerisch G., Cell 86, 631–642 (1996). 10.1016/S0092-8674(00)80136-1 [DOI] [PubMed] [Google Scholar]
  35. Xu T., Jin M., Xie Z., Jiang Z., Kuang Q., Wu H., Huang R., and Zheng L., Langmuir 24, 2281–2283 (2008). 10.1021/la7038569 [DOI] [PubMed] [Google Scholar]
  36. Sprong H., van der Sluijs P., and van Meer G., Nat. Rev. Mol. Cell Biol. 2, 504–513 (2001). 10.1038/35080071 [DOI] [PubMed] [Google Scholar]
  37. Raja M., J. Membr. Biol. 242, 137–143 (2011). 10.1007/s00232-011-9384-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Janmey P. A. and Kinnunen P. K. J., Trends Cell Biol. 16, 538–546 (2006). 10.1016/j.tcb.2006.08.009 [DOI] [PubMed] [Google Scholar]
  39. Zachowski A., Biochem. J. 294, 1–14 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Bremond N., Doméjean H., and Bibette J., Phys. Rev. Lett. 106, 214502 (2011). 10.1103/PhysRevLett.106.214502 [DOI] [PubMed] [Google Scholar]
  41. Strokes R. J. and Evans D. F., Fundamentals of Interfacial Engineering (Wiley—VCH, New York, 1997). [Google Scholar]
  42. Huang Z.-H., Abkarian M., and Viallat A., New J. Phys. 13, 035026 (2011). 10.1088/1367-2630/13/3/035026 [DOI] [Google Scholar]
  43. Hochmuth R. M., J. Biomech. 33, 15–22 (2000). 10.1016/S0021-9290(99)00175-X [DOI] [PubMed] [Google Scholar]
  44. Evans E. and Rawicz W., Phys. Rev. Lett. 64, 2094–2097 (1990). 10.1103/PhysRevLett.64.2094 [DOI] [PubMed] [Google Scholar]
  45. Luo T., Mohan K., Srivastava V., Ren Y., Iglesias P. A., and Robinson D. N., Biophys. J. 102, 238–247 (2012). 10.1016/j.bpj.2011.12.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Girard P. P., Cavalcanti-Adam E. A., Kemkemer R., and Spatz J. P., Soft Matter 3, 307–326 (2007). 10.1039/b614008d [DOI] [PubMed] [Google Scholar]

Articles from Applied Physics Letters are provided here courtesy of American Institute of Physics

RESOURCES