Skip to main content
PMC home page
Medical Physics logoLink to Medical Physics
. 2014 Apr 18;41(5):052302. doi: 10.1118/1.4870966

Longitudinal, intermodality registration of quantitative breast PET and MRI data acquired before and during neoadjuvant chemotherapy: Preliminary results

Nkiruka C Atuegwu 1, Xia Li 2, Lori R Arlinghaus 2, Richard G Abramson 3, Jason M Williams 4, A Bapsi Chakravarthy 5, Vandana G Abramson 6, Thomas E Yankeelov 7,a)
PMCID: PMC4000383  PMID: 24784395

Abstract

Purpose: The authors propose a method whereby serially acquired DCE-MRI, DW-MRI, and FDG-PET breast data sets can be spatially and temporally coregistered to enable the comparison of changes in parameter maps at the voxel level.

Methods: First, the authors aligned the PET and MR images at each time point rigidly and nonrigidly. To register the MR images longitudinally, the authors extended a nonrigid registration algorithm by including a tumor volume-preserving constraint in the cost function. After the PET images were aligned to the MR images at each time point, the authors then used the transformation obtained from the longitudinal registration of the MRI volumes to register the PET images longitudinally. The authors tested this approach on ten breast cancer patients by calculating a modified Dice similarity of tumor size between the PET and MR images as well as the bending energy and changes in the tumor volume after the application of the registration algorithm.

Results: The median of the modified Dice in the registered PET and DCE-MRI data was 0.92. For the longitudinal registration, the median tumor volume change was −0.03% for the constrained algorithm, compared to −32.16% for the unconstrained registration algorithms (p = 8 × 10−6). The medians of the bending energy were 0.0092 and 0.0001 for the unconstrained and constrained algorithms, respectively (p = 2.84 × 10−7).

Conclusions: The results indicate that the proposed method can accurately spatially align DCE-MRI, DW-MRI, and FDG-PET breast images acquired at different time points during therapy while preventing the tumor from being substantially distorted or compressed.

Keywords: registration, DCE-MRI, FDG-PET, breast cancer, prone PET, PET/MRI, longitudinal registration, treatment response

INTRODUCTION

In recent years there have been dramatic increases in both the quality and quantity of noninvasive imaging methods for assessing (and even predicting) the response of breast tumors to neoadjuvant therapy (NAT). In particular, dynamic contrast enhanced magnetic resonance imaging (DCE-MRI),1 diffusion weighted MRI (DW-MRI),2, 3 and 18F-fluorodeoxyglucose positron emission tomography (FDG-PET) (Refs. 4 and 5) have matured to the point where each modality offers unique and, importantly, complementary information on several clinically relevant tumor characteristics. Typically, changes in these quantitative imaging parameters are summarized on a region of interest (ROI) basis4, 5, 6, 7, 8, 9, 10 which discards spatial information on tumor heterogeneity. However, there has been an increasing interest in the study of the tumor at the voxel level rather than the ROI level.11, 12 Such analysis typically requires temporal and spatial registration of image datasets in order to measure voxelwise parameter changes in a meaningful way. In this effort, we present the first report which presents a method for rigorous registration of quantitative PET and MRI breast data acquired during NAT, which is a necessary step to allow for a more comprehensive analysis of tumor treatment response.

MATERIALS AND METHODS

Patient population and data acquisition

Data were acquired from ten patients with Stage II/III breast cancer enrolled in a IRB-approved clinical study prior to any treatment (t1), after one cycle of NAT (t2), and at the completion of NAT (t3). The data were not available at t3 for five of the patients. Table 1 provides the clinical characteristics of the patients included in this study.

Table 1.

Summary of patient data.

      Receptor status
      
Patients Age (yr) Treatment regimens ER PR HER2 Tumor grade Pathologic response Excised tumor size (cm)
1 36 AC → taxol + + + 2 Residual disease 1
2 48 Taxotere + carboplatin + herceptin − − + 3 pCR 0
3 58 Cisplatin + taxol ± everolimus − + − 2 Residual disease 1.7
4 33 AC → taxol + + − 3 Residual disease 1.2
5 39 AC → taxol − − − 3 pCR 0
6 43 Cisplatin + taxol ± everolimus − − + 3 Residual disease 0.7
7 57 AC → taxol − − − 3 Residual disease N/A
8 55 AC → taxol + + − 2 Residual disease 3.5
9 46 Taxotere + carboplatin + herceptin + + + 3 Residual disease 0.3
10 39 AC → taxol + + − 1 Residual disease 2.5
Open in a new tab

PET/CT data were acquired with a GE Discovery STE (GE Healthcare, Waukesha, WI) using methods previously described.13 DW- and DCE-MRI were performed using a Philips 3T Achieva MR scanner (Philips Healthcare, Best, The Netherlands) using previously described methods.14, 29 Following the DCE-MRI acquisition, a 3D T1-weighted high-resolution isotropic volume examination (THRIVE) scan was acquired. To improve the registration between the PET and MR data sets, a specially designed device that is an exact geometric replica of the breast support in the double-breast radiofrequency coil (In vivo Inc., Gainesville, FL) was constructed for PET/CT imaging.13

Data analysis

While details of the DCE-MRI, DW-MRI, and FDG-PET analysis are presented in Refs. 15, 16, the salient features are as follows. DCE-MRI data were analyzed using the extended Tofts-Kety relationship17 and a population arterial input function18 to yield estimates of the volume transfer constant (Ktrans), the extravascular extracellular volume fraction (ve), and the blood plasma fraction (vp), maps. The DW-MRI data were used to calculate the apparent diffusion coefficient (ADC) maps,19 and the FDG-PET data were used to calculate parametric maps of the FDG standard uptake value (SUV).20

Image registration at each time point

Due to its relatively high spatial resolution and tissue contrast, we used the THRIVE images to align the PET and MR data sets acquired at each individual time point. This was achieved by using a rigid body registration (RBR) algorithm which searches for the optimal rotation and translational parameters by maximizing the normalized mutual information (NMI).21 The obtained transformations between the DCE-MRI and the THRIVE data, TRBR_DCE, at each time point (t1, t2, and t3), were directly applied to the Ktrans, ve, vp, and ADC maps at each time point to put all MRI parametric maps into a common image space. As the PET/CT and THRIVE images were acquired on different scanners, the placement of the breast within each scanner resulted in different deformations. Thus, the CT data were first rigidly registered to the THRIVE images at each time point with the RBR, then a nonrigid body registration (NRBR) algorithm22 was applied. The RBR and the NRBR algorithms yielded the transformations TRBR_CT and TNRBR_CT, respectively, which were applied to the SUV maps from the FDG-PET data.

Image registration across time

For a given patient, the two sets (or three sets for five of the patients) of THRIVE images were serially registered using the RBR and a modified version of the NRBR algorithm described above. In the modified algorithm, a constraint term was computed as a Jacobian determinant over the tumor ROI and was incorporated into the NMI based cost function:

fcost=−NMI+α∑x|log(JT(x))|M, (1)

where JT(x) is the Jacobian determinant on the current voxel x, M is the total number of voxels in the area, and α is the weight of the constraint term. For the patient data sets in this study we empirically chose α = 0.4. This algorithm was designed to preserve the tumor volume while maximally registering surrounding tissues23, 24

For all the patients, the THRIVE image at t1 was registered to the THRIVE image at t2 using both the RBR and the constrained NRBR algorithm to yield the transformations TRBR_T1_T2 and TNRBR_T1_T2, respectively. Similarly, the THRIVE image at t2 was registered to the THRIVE image at t3 to yield the transformation TRBR_T2_T3 and TNRBR_T2_T3, respectively, for the five patients whose data at t3 were also available. To register the THRIVE images at t1 to t3, TRBR_T1_T2, TNRBR_T1_T2, TRBR_T2_T3, and TNRBR_T2_T3 were then applied to the THRIVE images at t1. Since the ADC, Ktrans, ve, vp, CT, and SUV maps at each time point were registered to their corresponding THRIVE image, these parametric maps could then be directly placed into a common image space by applying the transformation obtained from registering the THRIVE images longitudinally.

Registration validation

The tumor voxels in the SUV maps were determined by using a threshold of 40% of the maximum SUV uptake in the tumor ROIs (chosen based on previous reports25, 26), while the tumor in the DCE-MRI data was defined as the voxels within the outlined ROI that showed a postcontrast signal intensity that was ≥80% (Refs. 27, 28) of the precontrast signal intensity.

We qualitatively and quantitatively tested the validity of our approach. Qualitative assessment was performed by visual inspection of the alignment of the breast contours and tumors after registration. Quantitative assessment was done by calculating: (1) a modified Dice similarity index, (2) the bending energy,24 and (3) the change in the tumor volume after registration across time. Since the SUVs estimated from the FDG-PET data and the DCE-MRI data report on different aspects of tumor biology and moreover, different strategies were used to segment the tumor due to the large differences in the spatial resolutions in the PET and MR images, the original Dice similarity is not appropriate to compare two items of the same size. When two tumor regions are not in the same size, the largest possible Dice occurs when one segmented tumor region contains the other completed. Hence, we modified the Dice similarity measure to compare the degree of overlap between two objects (i.e., the tumor volumes as determined by PET and MRI) of difference sizes. That is, the modified Dice similarity is calculated as the original Dice similarity29 of the tumors between the SUV and the DCE-MR images divided by the largest possible Dice:

Dicenew=2×n(A∩B)n(A)+n(B)/2×min(n(A),n(B))n(A)+n(B)=n(A∩B)min(n(A),n(B)), (2)

where A and B are two regions and n( ) is the number of voxels in a region.

The bending energy describes the smoothness of the deformation field. The smoother the deformation field, the lower the bending energy. The bending energy and change in the tumor volume were calculated after applying the unconstrained and the constrained NRBR algorithms and compared using a Wilcoxon rank sum test to determine: (1) if the results returned by the two algorithms were significantly different and (2) if the algorithms significantly affected the tumor volume. This second point is of particular interest, as it is imperative that longitudinal registration minimally impact tumor size so that any changes in tumor size are due to biological changes and not those artificially induced by the registration algorithm.

RESULTS

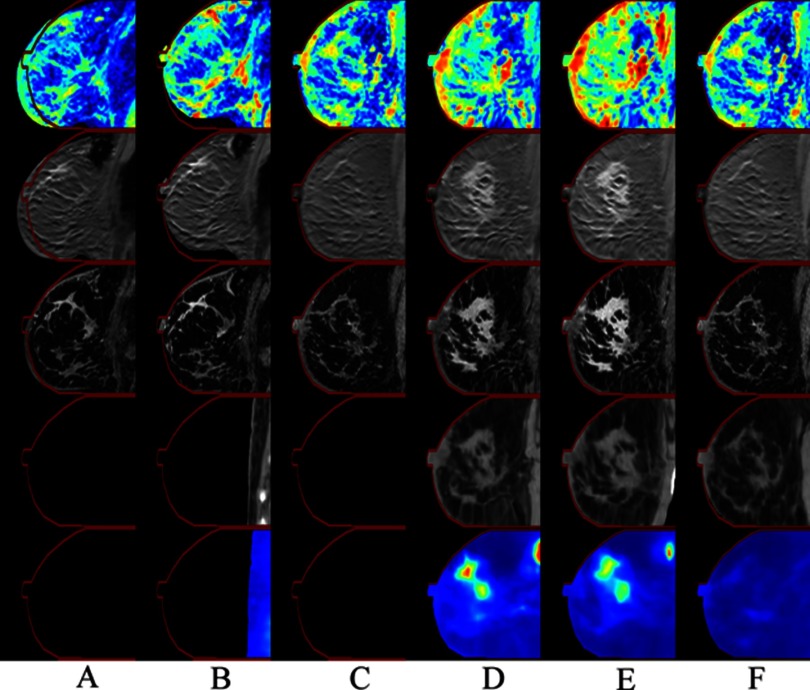
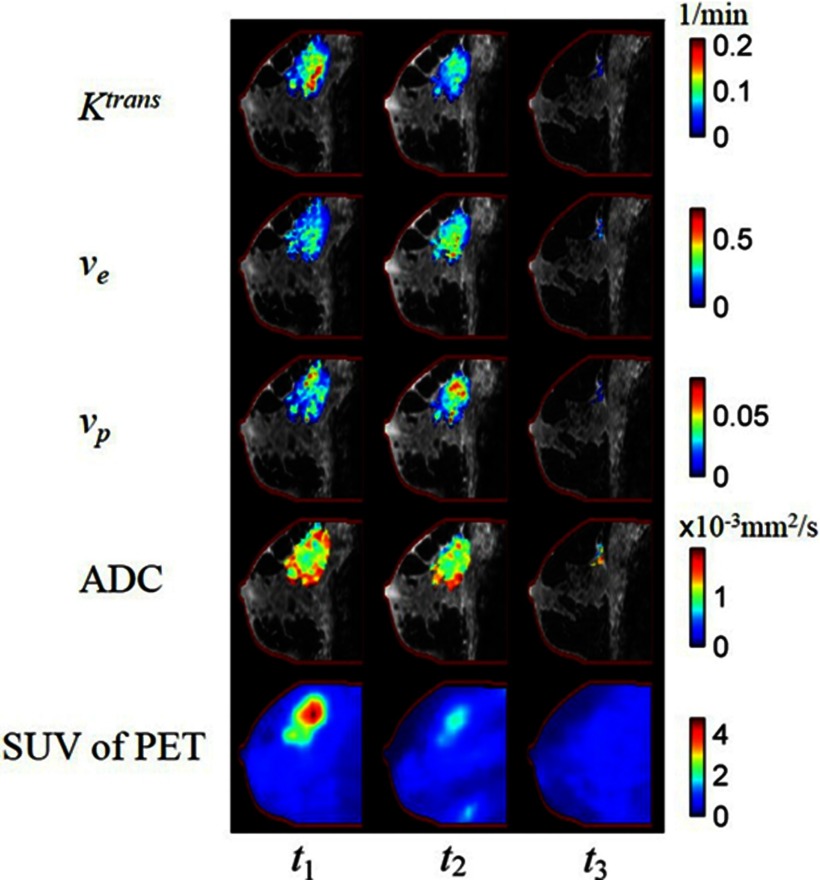
The rows of Fig. 1 display the ADC, postcontrast DCE-MRI, THRIVE-MRI, CT, and the SUV of the FDG-PET images before (Columns A, B, and C) and after (D, E, and F) registration for a nonresponder at three time points. As demonstrated in the figure, there was poor alignment of the breast contours and the tumors before registration, but after registration there was excellent alignment of the breast contours and the tumors between the modalities at all imaging time points. Figure 2 shows the results of the registration of the parameter maps Ktrans, ve, vp, ADC, and SUV of the FDG-PET maps (rows 1–5, respectively) superimposed on the anatomical THRIVE image at three time points for a representative patient. Note the (visually) excellent alignment which allows for examination of the variations in intratumoral spatial distributions of the various parameters.

Figure 1.

Figure 1

Open in a new tab

Columns A, B, and C correspond to the images before registration acquired at baseline before initiation of NAT (t1), after one cycle of NAT (t2), and at the conclusion of NAT (t3). Columns D, E, and F correspond to the images after both intra- and interscanning session registrations. The rows correspond to the ADC, postcontrast DCE-MRI, THRIVE-MRI, CT, and the SUV of the FDG-PET, respectively. The contour of the THRIVE image at t3 was copied to the other images in order to facilitate visual comparison of the registration results. The patient was a nonresponder (i.e., a non-pCR).

Figure 2.

Figure 2

Open in a new tab

Parametric maps overlain on THRIVE anatomical scans. The columns correspond to the images obtained at t1, t2, and t3, respectively. Five rows correspond to Ktrans, ve, vp, ADC, and SUV. The contour of the THRIVE at t3 is copied to the other images in order to facilitate comparison of the registration result. Note the variations in intratumoral spatial distributions of the various parameters. By performing longitudinal, intermodality registrations, such comparisons at the voxel level are now possible.

The median of the modified Dice was 0.92. The medians of the percentage change in the tumor volumes from t1 to t2 were −9.25% and −1.13% for the unconstrained and constrained algorithms (p = 0.038), respectively. Similarly, the medians of the percentage change in the tumor volumes from t2 to t3 were −65.12% and 0.07%, respectively (p = 0.008). Finally, the medians from t1 to t3 were −56.64% and 0.84%, respectively (p = 0.008).

The medians of the bending energy from t1 to t2 were 0.0022 and 0.0001 for the unconstrained and constrained algorithms (p = 0.0003), respectively. Similarly, the medians from t2 to t3 were 0.0422 and 0.0000, respectively (p = 0.0079). Finally, the medians from t1 to t3 were 0.0973 and 0.0003, respectively (p = 0.0079). The median bending energy for all the time points was 0.0092 and 0.0001 for the unconstrained and constrained algorithms, respectively (p = 2.84 × 10−7).

DISCUSSION AND CONCLUSIONS

A survey of the literature reveals that the overwhelming majority of studies on breast registration focus on the registration of dynamic scans to correct for bulk motion that occurs during a single imaging session. There are only a few of studies11, 12, 30, 31 that have made use of longitudinal registration of breast MRI data. However, these studies either did not focus on the registration method itself or did not account for tumor changes observed between scans. Our study is the first report of a method that enables the longitudinal registration of multimodal breast images and the corresponding parametric maps (i.e., Ktrans, ve, vp, ADC, SUV) to a common space, thereby allowing for a more comprehensive analysis of tumor behavior at the voxel level. The results of this study are potentially of general interest as more efforts are made to synthesize multiparametric studies for predicting the response to breast cancer in the neoadjuvant setting. We showed good alignment between the images both by visual assessment and by the calculation of the intersection of the tumor volumes, the bending energy, and the change of tumor volumes. The error in the intersection was mainly due to the differences in positioning of the breast between the PET and the MRI acquisitions at each individual time point (i.e., t1, t2, or t3). Another source of error is that the contrast between the tumor and normal tissues of low-dose CT images is much lower than the MR images collected in this study; this brings difficulties during the alignment between CT and MR. Ideally, we would want to achieve a registration error that is within the spatial resolution of the PET image.

One of the limitations of this study is that the parameter α is selected empirically and cannot (currently) be determined automatically. Moreover, the registration algorithm may not correct the change in the whole breast volume over time due to, for example, hormonal fluctuations over the menstrual cycle. Future technical efforts will focus on automating the optimal selection of this parameter, as well as employing external fiducial markers to improve the registration performance. Future clinical efforts will include identifying the spatial-temporal relationships between the parametric maps at the voxel level and integrating the relationships between parameter maps to optimize the prediction of the response of breast tumors to NAT. The aligned parameter maps can also be used to initialize and constrain mathematical models of tumor growth and treatment response.32

ACKNOWLEDGMENTS

The authors thank the NCI for funding through Grant Nos. 1R01CA129961, U01 CA142565, 1U01CA174706, P50 CA098131, and P30 CA68485.

References

  1. Yankeelov T. E. and Gore J. C., “Dynamic contrast enhanced magnetic resonance imaging in oncology: Theory, data acquisition, analysis, and examples,” Curr. Med. Imaging Rev. 3, 91–107 (2009). 10.2174/157340507780619179 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Sugahara T., Korogi Y., Kochi M., Ikushima I., Shigematu Y., Hirai T., Okuda T., Liang L., Ge Y., Komohara Y., Ushio Y., and Takahashi M., “Usefulness of diffusion-weighted MRI with echo-planar technique in the evaluation of cellularity in gliomas,” J. Magn. Reson. Imaging 9, 53–60 (1999). [DOI] [PubMed] [Google Scholar]
  3. Hayashida Y., Hirai T., Morishita S., Kitajima M., Murakami R., Korogi Y., Makino K., Nakamura H., Ikushima I., Yamura M., Kochi M., Kuratsu J.-i., and Yamashita Y., “Diffusion-weighted Imaging of metastatic brain tumors: Comparison with histologic type and tumor cellularity,” Am. J. Neuroradiol. 27, 1419–1425 (2006). [PMC free article] [PubMed] [Google Scholar]
  4. Doot R. K., Dunnwald L. K., Schubert E. K., Muzi M., Peterson L. M., Kinahan P. E., Kurland B. F., and Mankoff D. A., “Dynamic and static approaches to quantifying 18F-FDG uptake for measuring cancer response to therapy, including the effect of granulocyte CSF,” J. Nucl. Med. 48, 920–925 (2007). 10.2967/jnumed.106.037382 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ah-See M.-L. W., Makris A., Taylor N. J., Harrison M., Richman P. I., Burcombe R. J., Stirling J. J., d’Arcy J. A., Collins D. J., Pittam M. R., Ravichandran D., and Padhani A. R., “Early changes in functional dynamic magnetic resonance imaging predict for pathologic response to neoadjuvant chemotherapy in primary breast cancer,” Clin. Cancer Res. 14, 6580–6589 (2008). 10.1158/1078-0432.CCR-07-4310 [DOI] [PubMed] [Google Scholar]
  6. Pickles M. D., Gibbs P., Lowry M., and Turnbull L. W., “Diffusion changes precede size reduction in neoadjuvant treatment of breast cancer,” Magn. Reson. Imaging 24, 843–847 (2006). 10.1016/j.mri.2005.11.005 [DOI] [PubMed] [Google Scholar]
  7. Sharma U., Danishad K. K. A., Seenu V., and Jagannathan N. R., “Longitudinal study of the assessment by MRI and diffusion-weighted imaging of tumor response in patients with locally advanced breast cancer undergoing neoadjuvant chemotherapy,” NMR Biomed. 22, 104–113 (2009). 10.1002/nbm.1245 [DOI] [PubMed] [Google Scholar]
  8. Yankeelov T. E., Lepage M., Chakravarthy A., Broome E. E., Niermann K. J., Kelley M. C., Meszoely I., Mayer I. A., Herman C. R., McManus K., Price R. R., and Gore J. C., “Integration of quantitative DCE-MRI and ADC mapping to monitor treatment response in human breast cancer: Initial results,” Magn. Reson. Imaging 25, 1–13 (2007). 10.1016/j.mri.2006.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Jensen L. R., Garzon B., Heldahl M. G., Bathen T. F., Lundgren S., and Gribbestad I. S., “Diffusion-weighted and dynamic contrast-enhanced MRI in evaluation of early treatment effects during neoadjuvant chemotherapy in breast cancer patients,” J. Magn. Reson. Imaging 34, 1099–1109 (2011). 10.1002/jmri.22726 [DOI] [PubMed] [Google Scholar]
  10. Berriolo-Riedinger A., Touzery C., Riedinger J.-M., Toubeau M., Coudert B., Arnould L., Boichot C., Cochet A., Fumoleau P., and Brunotte F., “[18F]FDG-PET predicts complete pathological response of breast cancer to neoadjuvant chemotherapy,” Eur. J. Nucl. Med. Mol. Imaging 34, 1915–1924 (2007). 10.1007/s00259-007-0459-5 [DOI] [PubMed] [Google Scholar]
  11. Maday P., Khurd P., Ladic L., Schnall M., Rosen M., Davatzikos C., and Kamen A., “Imaging as a surrogate for the early prediction and assessment of treatment response through the analysis of 4-D texture ensembles (ISEPARATE),” in Medical Computer Vision. Recognition Techniques and Applications in Medical Imaging, Vol. 6533, edited by Menze B., Langs G., Tu Z., and Criminisi A. (Springer, Berlin, 2011), pp. 164–173. [Google Scholar]
  12. Ma B., Meyer C. R., Pickles M. D., Chenevert T. L., Bland P. H., Galban C. J., Rehemtulla A., Turnbull L. W., and Ross B. D., “Voxel-by-voxel functional diffusion mapping for early evaluation of breast cancer treatment,” Inf. Process Med. Imaging 21, 276–287 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Li X., Abramson R. G., Arlinghaus L. R., Chakravarthy A. B., Abramson V., Mayer I., Farley J., Delbeke D., and Yankeelov T. E., “An algorithm for longitudinal registration of PET/CT images acquired during neoadjuvant chemotherapy in breast cancer: Preliminary results,” EJNMMI Res. 2, 62–72 (2012). 10.1186/2191-219X-2-62 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Arlinghaus L. R., Welch E. B., Chakravarthy A. B., Xu L., Farley J. S., Abramson V. G., Grau A. M., Kelley M. C., Mayer I. A., Means-Powell J. A., Meszoely I. M., Gore J. C., and Yankeelov T. E., “Motion correction in diffusion-weighted MRI of the breast at 3T,” J. Magn. Reson. Imaging 33, 1063–1070 (2011). 10.1002/jmri.22562 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Li X., Welch E. B., Chakravarthy A. B., Xu L., Arlinghaus L. R., Farley J., Mayer I. A., Kelley M. C., Meszoely I. M., Means-Powell J., Abramson V. G., Grau A. M., Gore J. C., and Yankeelov T. E., “Statistical comparison of dynamic contrast-enhanced MRI pharmacokinetic models in human breast cancer,” Magn. Reson. Med. 68, 261–271 (2012). 10.1002/mrm.23205 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Arlinghaus L. R., Li X., Rahman A. R., Welch E. B., Xu L., Gore J. C., and Yankeelov T. E., “On the relationship between the apparent diffusion coefficient and extravascular extracellular volume fraction in human breast cancer,” Magn. Reson. Imaging 29, 630–638 (2011). 10.1016/j.mri.2011.02.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Tofts P. S., “Modeling tracer kinetics in dynamic Gd-DTPA MR imaging,” J. Magn. Reson. Imaging 7, 91–101 (1997). 10.1002/jmri.1880070113 [DOI] [PubMed] [Google Scholar]
  18. Li X., Welch E. B., Arlinghaus L. R., Chakravarthy A. B., Xu L., Farley J., Loveless M. E., Mayer I. A., Kelley M. C., Meszoely I. M., Means-Powell J. A., Abramson V. G., Grau A. M., Gore J. C., and Yankeelov T. E., “A novel AIF tracking method and comparison of DCE-MRI parameters using individual and population-based AIFs in human breast cancer,” Phys. Med. Biol. 56, 5753–5769 (2011). 10.1088/0031-9155/56/17/018 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Stejskal E. O. and Tanner J. E., “Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient,” J. Chem. Phys. 42, 288–292 (1965). 10.1063/1.1695690 [DOI] [Google Scholar]
  20. Stahl A., Ott K., Schwaiger M., and Weber W. A., “Comparison of different SUV-based methods for monitoring cytotoxic therapy with FDG PET,” Eur. J. Nucl. Med. Mol. Imaging 31, 1471–1478 (2004). 10.1007/s00259-004-1626-6 [DOI] [PubMed] [Google Scholar]
  21. Maes F., Collignon A., Vandermeulen D., Marchal G., and Suetens P., “Multimodality image registration by maximization of mutual information,” IEEE Trans. Med. Imaging 16, 187–198 (1997). 10.1109/42.563664 [DOI] [PubMed] [Google Scholar]
  22. Rohde G. K., Aldroubi A., and Dawant B. M., “The adaptive bases algorithm for intensity-based nonrigid image registration,” IEEE Trans. Med. Imaging 22, 1470–1479 (2003). 10.1109/TMI.2003.819299 [DOI] [PubMed] [Google Scholar]
  23. Li X., Dawant B. M., Welch E. B., Chakravarthy A. B., Freehardt D., Mayer I., Kelley M., Meszoely I., Gore J. C., and Yankeelov T. E., “A nonrigid registration algorithm for longitudinal breast MR images and the analysis of breast tumor response,” Magn. Reson. Imaging 27, 1258–1270 (2009). 10.1016/j.mri.2009.05.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Li X., Dawant B. M., Welch E. B., Chakravarthy A. B., Xu L., Mayer I., Kelley M., Meszoely I., Means-Powell J., Gore J. C., and Yankeelov T. E., “Validation of an algorithm for the nonrigid registration of longitudinal breast MR images using realistic phantoms,” Med. Phys. 37, 2541–2552 (2010). 10.1118/1.3414035 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Miller T. R. and Grigsby P. W., “Measurement of tumor volume by PET to evaluate prognosis in patients with advanced cervical cancer treated by radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 53, 353–359 (2002). 10.1016/S0360-3016(02)02705-0 [DOI] [PubMed] [Google Scholar]
  26. Bradley J., Thorstad W. L., Mutic S., Miller T. R., Dehdashti F., Siegel B. A., Bosch W., and Bertrand R. J., “Impact of FDG-PET on radiation therapy volume delineation in non-small-cell lung cancer,” Int. J. Radiat. Oncol., Biol., Phys. 59, 78–86 (2004). 10.1016/j.ijrobp.2003.10.044 [DOI] [PubMed] [Google Scholar]
  27. Atuegwu N. C., Arlinghaus L. R., Li X., Chakravarthy A. B., Abramson V. G., Sanders M. E., and Yankeelov T. E., “Parameterizing the logistic model of tumor growth by DW-MRI and DCE-MRI data to predict treatment response and changes in breast cancer cellularity during neoadjuvant chemotherapy,” Transl. Oncol. 6, 256–264 (2013). 10.1593/tlo.13130 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Li X., Arlinghaus L. R., Ayers G. D., Chakravarthy A. B., Abramson R. G., Abramson V. G., Atuegwu N., Farley J., Mayer I. A., Kelley M. C., Meszoely I. M., Means-Powell J., Grau A. M., Sanders M., Bhave S. R., and Yankeelov T. E., “DCE-MRI analysis methods for predicting the response of breast cancer to neoadjuvant chemotherapy: Pilot study findings,” Magn. Reson. Med. 71, 1592–1602 (2014). 10.1002/mrm.24782 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Zijdenbos A. P., Dawant B. M., Margolin R. A., and Palmer A. C., “Morphometric analysis of white matter lesions in MR images: Method and validation,” IEEE Trans. Med. Imaging 13, 716–724 (1994). 10.1109/42.363096 [DOI] [PubMed] [Google Scholar]
  30. Catherwood T., Patterson A., Zaki K., Iddawela M., Earl H., Caldas C., Sayal K., Graves M., and Gilbert F., “Non-rigid registration of sequential DCE-MRI in the assessment of response to neoadjuvant chemotherapy in breast cancer,” Proc. Intl. Soc. Mag. Reson. Med. (ISMRM) 21, 3730 (2013). [Google Scholar]
  31. Boehler T., Schilling K., Bick U., and Hahn H., Deformable Image Registration of Follow-Up Breast Magnetic Resonance Images (Springer-Verlag, Berlin, 2010). [Google Scholar]
  32. Yankeelov T. E., Atuegwu N., Hormuth D., Weis J. A., Barnes S. L., Miga M. I., Rericha E. C., and Quaranta V., “Clinically relevant modeling of tumor growth and treatment response,” Sci. Transl. Med. 5, 187ps9 (2013). 10.1126/scitranslmed.3005686 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Medical Physics are provided here courtesy of American Association of Physicists in Medicine

RESOURCES