Abstract
Purpose: To evaluate a three-equation three-unknown dual-energy quantitative CT (DEQCT) technique for determining region specific variations in bone spongiosa composition for improved red marrow dose estimation in radionuclide therapy.
Methods: The DEQCT method was applied to 80/140 kVp images of patient-simulating lumbar sectional body phantoms of three sizes (small, medium, and large). External calibration rods of bone, red marrow, and fat-simulating materials were placed beneath the body phantoms. Similar internal calibration inserts were placed at vertebral locations within the body phantoms. Six test inserts of known volume fractions of bone, fat, and red marrow were also scanned. External-to-internal calibration correction factors were derived. The effects of body phantom size, radiation dose, spongiosa region segmentation granularity [single (∼17 × 17 mm) region of interest (ROI), 2 × 2, and 3 × 3 segmentation of that single ROI], and calibration method on the accuracy of the calculated volume fractions of red marrow (cellularity) and trabecular bone were evaluated.
Results: For standard low dose DEQCT x-ray technique factors and the internal calibration method, the RMS errors of the estimated volume fractions of red marrow of the test inserts were 1.2–1.3 times greater in the medium body than in the small body phantom and 1.3–1.5 times greater in the large body than in the small body phantom. RMS errors of the calculated volume fractions of red marrow within 2 × 2 segmented subregions of the ROIs were 1.6–1.9 times greater than for no segmentation, and RMS errors for 3 × 3 segmented subregions were 2.3–2.7 times greater than those for no segmentation. Increasing the dose by a factor of 2 reduced the RMS errors of all constituent volume fractions by an average factor of 1.40 ± 0.29 for all segmentation schemes and body phantom sizes; increasing the dose by a factor of 4 reduced those RMS errors by an average factor of 1.71 ± 0.25. Results for external calibrations exhibited much larger RMS errors than size matched internal calibration. Use of an average body size external-to-internal calibration correction factor reduced the errors to closer to those for internal calibration. RMS errors of less than 30% or about 0.01 for the bone and 0.1 for the red marrow volume fractions would likely be satisfactory for human studies. Such accuracies were achieved for 3 × 3 segmentation of 5 mm slice images for: (a) internal calibration with 4 times dose for all size body phantoms, (b) internal calibration with 2 times dose for the small and medium size body phantoms, and (c) corrected external calibration with 4 times dose and all size body phantoms.
Conclusions: Phantom studies are promising and demonstrate the potential to use dual energy quantitative CT to estimate the spatial distributions of red marrow and bone within the vertebral spongiosa.
Keywords: quantitative computed tomography, bone marrow, phantom study, subregion analysis
INTRODUCTION
Recent studies have demonstrated a clear correlation between tumor radiation absorbed dose and progression free survival in I-131 tositumomab radio-immunotherapy (RIT) treatment of non-Hodgkin's lymphoma.1 The need to mitigate toxic response in marrow, however, limits the absorbed dose that can be delivered to tumors in such therapies. Individualized treatment planning thus requires accurate estimation of absorbed red marrow dose for the prediction of toxic response.
The trabecular marrow space (or spongiosa) is a complex lattice of microscopic dimension filled with active (red) and inactive (yellow) marrow. Ideally, dose assessment to active marrow should include direct coupling of radiation transport codes to 3D imaging with explicit delineation of the trabecular microstructure, as has been done for selected cadaveric bone samples using NMR microscopy.2 Such microscopic resolution is not practical for in vivo patient imaging at present. An accurate alternative to direct simulation was demonstrated in a recent work3 which coupled macroscopic-level Monte Carlo dosimetry simulations with marrow and bone electron energy absorption fractions derived from cadaver and simulated spongiosa studies. It was shown in that study that computed dose to active marrow can vary by as much as 10% over the range of representative patient bone volume fractions and up to 20% over the range of red marrow cellularities. It is clear, therefore, that the goal of patient-specific RIT treatment planning depends upon the development of an accurate method for determination of bone volume fraction and active marrow cellularity.
While various MRI methods have shown promise in accurately measuring either bone mineral density4 or active bone marrow cellularity,5, 6, 7, 8 such methods are expensive. Patients undergoing RIT treatment are typically scanned with diagnostic CT or PET/CT during staging and evaluation of treatment response and sometimes scanned with SPECT/CT for dosimetry.9 Therefore, a quantitative CT method that could be used in conjunction with such scans and that could in addition provide estimates of bone volume and marrow volume fractions would be highly useful. Toward that end, we propose to use a previously developed dual energy quantitative CT (DEQCT) method for estimating the bone, fat, and fat-free red marrow composition of vertebrae. That method10, 11 can be implemented using special calibration standards on a CT system, to determine regional bone spongiosa composition on a patient-by-patient basis. The elemental composition of the trabeculae in the spongiosa is the same as that of cortical bone,10 and hereafter we use the term “bone” to refer to a material having the composition and density of cortical bone.
In this paper, we present results from a phantom study investigating the accuracy of the DEQCT method in estimating the spatial distributions of bone and fat-free red marrow spongiosa constituents. The present study is a significant extension of phantom tests in a previous study.11 That previous phantom study only involved use of DEQCT to estimate the compositions of a set of test spongiosa inserts that were placed within a simulated vertebra in a medium size lumbar section body phantom using one set of x-ray technique factors. For that analysis the mean CT numbers of calibration and test inserts were measured in large regions of interest (ROIs) that were placed within the insert areas in the CT images. Because it is desirable to investigate the sensitivity of active marrow dose computations on the spatial distribution of active marrow, in the present study, we partitioned the large ROIs into various subregions to evaluate the accuracy of the method for estimating the spatial distributions of the marrow contents within smaller size subregions. In addition, we determined the effects of “patient body size,” radiation dose (mAs), and external vs internal calibration on the accuracies of the measurements. Also, in the present study, we employed a three-equation three-unknown DEQCT method instead of the four-equation four-unknown DEQCT method used in Ref. 11.
MATERIALS AND METHODS
Three-equation three-unknown DEQCT method
A three-equation three-unknown method for determining the composition of marrow regions using dual energy CT was employed. That method and a variant of that method, the four-equation four-unknown method have been described previously.10 Both methods assume three distinct components in the marrow region: fat, fat-free red marrow, and bone. Calibration standards that mimic pure fat, pure fat-free red marrow, and various concentrations of bone in a fat-free red marrow background are used to estimate the composition of a given region.11 The three-equation three–unknown method was selected because it is more amenable to correcting for negative (nonphysical) solutions to the equations for the fat, fat-free red marrow, and/or bone contents. For simplicity of nomenclature, with a few exceptions, we will hereafter refer to “fat-free red marrow” as “red marrow” in this paper. It should be noted that according to the Report of the Task Group on Reference Man, the mass fraction of lipid in red marrow is 0.397.12 The elemental composition and mass density of “fat-free red marrow” for the calibration standards was determined by removing the 0.397 mass fraction lipid elements from normal red marrow.11
The three equations of the three-equation three-unknown DEQCT method are as follows:
| (1) |
| (2) |
| (3) |
where B, R, and F are, respectively, the computed volume fractions of bone, red marrow, and fat in the marrow mixture of interest. is the measured mean CT number within a ROI in the spongiosa area of a vertebra or other bone of interest in the CT images. , , and are the measured mean CT numbers of the pure bone, pure red marrow, and pure fat calibration standards, respectively. These are also determined from regions of interest placed within CT images of calibration materials of each type. E1 and E2 are ideally two monochromatic energies. For conventional CT scanners with polyenergetic x-ray spectra, E1 and E2 correspond with the peak kilovoltages (kVp's) of the polyenergetic beams (e.g., 80 and 140 kVp).
The method is implemented with either external calibration standards that are scanned simultaneously with the patient or with internal calibration standards that are scanned separately within a tissue mimicking body phantom of a size similar to that of the patient. Two of the three calibration standards are made of materials that mimic the x-ray attenuation properties of pure fat-free red marrow and fat. These are used to determine and at E1 and E2 in the equations. Because pure cortical bone is highly attenuating, it would cause beam hardening artifacts and errors in the measured CT numbers. Instead, to estimate , several standards of known bone concentrations (e.g., 100, 200, and 300 mg/cc) are employed to derive CT# (HU) vs bone density (mg/cc) calibration lines. The calibration lines are then extrapolated to the mass density of bone (1920 mg/cc) (Ref. 13) to compute the CT# of pure bone using the following equation:
| (4) |
where, as above, E is the kVp (either 80 or 140 kVp) and 1920 mg/cc is the mass density of pure bone.13 Although this extrapolation does not account for nonlinearities in the CT numbers for high bone densities due to beam hardening, it should be acceptable for spongiosa regions in which the volume averaged bone densities of trabecular bone are much less than the density of pure cortical bone.
As mentioned above, infrequently due to noise, the measured CT numbers of the mixed marrow are such that one of the solutions to the three equations is a negative volume fraction. Such a result is physically impossible. In order to account for this, we reformulated the problem to be two equations, three unknowns [e.g., Eqs. 1, 2] with constraints that the solutions are non-negative and the solutions sum to 1. We used a least squares method to compute the solutions. This methodology is appropriate since the two equations contain noise components, but the constraints do not have any noise.
Phantoms
The phantoms and calibration standards and test inserts were manufactured by CIRS, Inc. (Norfolk, VA). They are made of epoxy resins with special particulate fillers to produce solid tissue substitutes having approximately the same linear x-ray attenuation coefficients as the desired tissues. The “internal” calibration standards and test samples are in the form of inserts, which are placed within cavities in the spongiosa regions of a lumbar vertebra within an abdomen section phantom that simulates a patient. That abdomen section includes regions that simulate subcutaneous fat, organs, muscle, and the cortical rim of a vertebra. The base abdomen section phantom simulates a small sized patient. Additional fat rings of two sizes can be added to the periphery of the phantom section to simulate medium and large sized patients. CT images of the three sized phantoms are shown in Fig. 1.
Figure 1.
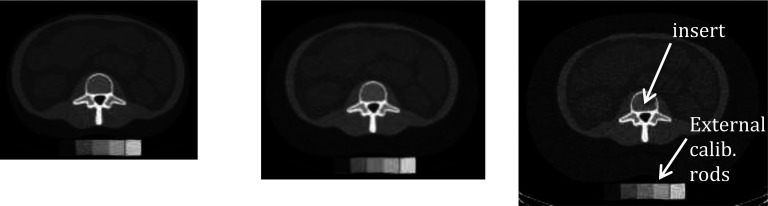
Images of the small (left), medium (center), and large (right) sized phantoms. Internal calibration (or test) inserts and external calibration rods are indicated.
The phantoms in Fig. 1 are shown on top of external calibration blocks simulating (from left to right) fat, red marrow, 100 mg/cc bone in red marrow, 200 mg/cc bone in red marrow, and 300 mg/cc bone in red marrow. The compositions of these external calibration blocks are identical to those of the corresponding internal calibration inserts, which are placed in a cavity within the spongiosa region of the vertebra as indicated in Fig. 1. Note that the use of external rods was evaluated because in patient studies it is more practical than using the calibration phantom with internal inserts. The rods can be placed under the patient's back during the regular imaging session; whereas, for the internal calibration the size-matched body phantom and internal calibration inserts have to be scanned either before or after the patient imaging session. Today's CT scanners produce more stable CT numbers than in the past, so the internal calibration scans of the three size body phantoms with the calibration inserts may only have to be performed every week or month.
The lateral and anterior–posterior (AP) dimensions of the three patient phantoms are: small (28.8 × 19.2 cm) medium (33.5 × 22.5 cm), large (37 × 25.7 cm), with effective diameters (= square roots of AP × lateral dimensions) of 23.5, 27.5, and 30.8 cm.
Compositions of calibration standards and test inserts
The elemental compositions and mass densities of the calibration materials11 used in the internal and external calibration standards and test inserts are listed in Table 1. Note that cortical bone is 58% mineral by mass,13 so the 100, 200, and 300 mg/cc bone concentration values in Table 2 correspond with mineral concentrations of 58, 106, and 174 mg/cc, respectively.
Table 1.
Elemental compositions (% by mass) and mass densities (g/cc) of materials used in internal and external calibration standards and test inserts.
| Material | H | C | N | O | Elements with Z > 8) | Mass density |
|---|---|---|---|---|---|---|
| Fat | 12.21 | 76.05 | … | 11.74 | 0.92 | |
| Fat-free red marrow | 9.3 | 18.6 | 5.6 | 65.1 | P(0.2) S(0.3) Cl(0.3) K(0.3) Fe(0.2) | 1.118 |
| Cortical bone | 3.4 | 15.5 | 4.2 | 43.5 | Na(0.1) Mg(0.2) P(10.3) S(0.3) Ca(22.5) | 1.92 |
Table 2.
Bone concentration (mg/cc), and volume fractions of bone, fat-free red marrow, and fat in the calibration and test inserts employed in this study.
| mg/cc | Volume | Volume | Volume fraction | |
|---|---|---|---|---|
| bone | fraction bone | fraction fat | fat-free red marrow | |
| Calibration standards | 0 | 0 | 0 | 1.0 |
| 0 | 0 | 1.0 | 0 | |
| 100 | 0.052 | 0 | 0.948 | |
| 200 | 0.104 | 0 | 0.896 | |
| 300 | 0.156 | 0 | 0.844 | |
| Test inserts | 100 | 0.052 | 0.8 | 0.148 |
| 200 | 0.104 | 0.2 | 0.696 | |
| 200 | 0.104 | 0.3 | 0.596 | |
| 300 | 0.156 | 0.1 | 0.744 | |
| 300 | 0.156 | 0.3 | 0.544 | |
| 300 | 0.156 | 0.5 | 0.344 |
The general compositions of the calibration standards and test inserts are listed in Table 2.
Each calibration and test insert is manufactured to be homogeneous and contains the same constituents throughout their volumes.
Scanner and base techniques
All images were generated on a General Electric Discovery CT750HD CT scanner (GE Healthcare, Milwaukee, WI). This scanner was selected because it is similar to the GE 9800 scanner used in our previous work, and it enabled use of similar x-ray technique factors. This does not preclude the use of other scanners some of which use different maximum kVp factors such as 130 kVp on a Siemens Biograph TruePoint PET/CT scanner (Siemens Healthcare, Forchheim, Germany). Initial scans on the GE Discovery CT750 CT scanner were performed using a “base” dual-energy axial scan technique of 80 kVp, 140 mA, 1 s, 5 mm slices, and 140 kVp, 80 mA, 1 s, 5 mm slices with the scanner couch height set so the centers of the test and internal calibration inserts were at isocenter for each size phantom. This “base” technique is identical to the “low-dose dual-energy” technique employed by Steiger et al. in their patient studies in the 1980s and 1990s,14 except Steiger et al. employed 10 mm slices with a GE 9800 CT scanner, and we used 5 mm slices with a more modern multirow detector GE CT scanner. (Note that the GE dual energy fast kVp switching Gemstone Spectral Imaging mode that is available on the CT750 HD CT scanner was not utilized for the acquisition of the dual energy images in this study because that mode does not produce individual CT images at 80 and 140 kVp.) Scans were repeated 3 times for each scanning condition. Large (∼17 × 17 mm) ROIs were positioned within the resulting images at the centers of each insert to determine the CT numbers used in Eqs. 1, 2, 3, 4. The averages of the individual mean CT numbers within the ROIs for the three scans of each calibration insert at each energy (80/140 kVp) were used as the CT numbers of the calibration standards in the equations. The individual mean CT numbers of each test insert for each of the three scans at each kVp rather than the averages were used in the equations to evaluate the scan-to-scan variability of the results for the test inserts. Software code written in MATLAB (MathWorks, Natick, MA) was used in all cases to position the ROIs at identical locations within the inserts in the images, calculate the mean CT numbers, determine the bone calibration lines, and solve the set of three equations for the three unknowns. The MATLAB function “fmincon” was used to solve the equations.
Specific studies
Subregion analysis
Most quantitative CT methods only analyze single relatively large regions of interest. For our goal of determining the spatial distribution of bone marrow, we investigated segmenting a relatively large region of interest into subregions and computed the marrow composition in each subregion. We compared results for the original regions of interest and those regions divided into 2 × 2 subregions and 3 × 3 subregions for each of the test inserts. This was performed for the three phantom sizes described in Sec. 2E2. The subregions are illustrated in Fig. 2 and the dimensions of the subregions are discussed in Sec. 2E2a. Since the test inserts are homogeneous, the true compositions in each subregion are the same as the compositions in the large region.
Figure 2.
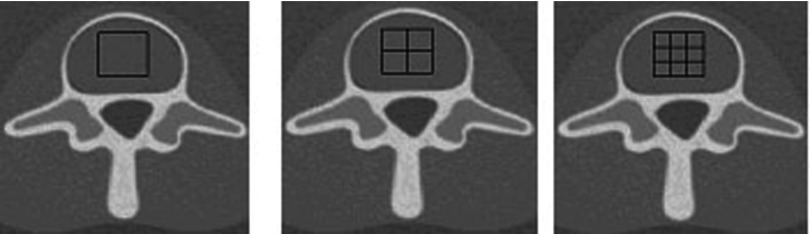
Examples of the single region and multiple subregion ROIs. A zoomed-in image of the single (1 × 1) ROI is shown on the left, and zoomed-in images of the 2 × 2 and 3 × 3 segmentations to produce the subregions are shown in the middle and right, respectively.
Effect of body phantom size
When larger patients are scanned, there will be greater x-ray beam hardening and x-ray scatter, which will affect the measured CT numbers in the vertebral spongiosa. However, these effects on the CT numbers should be countered with a dual-energy QCT method that uses internal calibration in which a phantom of about the same size as the patient is employed to scan the internal calibration inserts at the same position as the patient's vertebra. To investigate whether this is true, we performed scans with small, medium, and large abdomen section phantoms and compared the accuracies of the computed marrow compositions of the test inserts for the different size phantoms. For our studies, the patient phantom and the calibration phantom in which the internal calibration standards and test inserts were scanned were identical, which corresponds with the ideal situation.
Dimensions of regions of interest
The small and medium size abdomen section phantoms were scanned using a medium field of view and reconstructed with a 36 cm field of view (pixel size = 360 mm/512 = 0.703 mm). The large abdomen section phantom was scanned with the large field of view and reconstructed with a display field of view of 50 cm (pixel size = 500 mm/512 = 0.977 mm). The dimensions of the single ROIs were chosen to be numbers of pixels that are evenly divisible by 2 and 3. For the small and medium sized phantoms, the single ROIs were 24 pixel × 24 pixel or 16.88 × 16.88 mm. For the large sized phantom the single ROIs were 18 pixels × 18 pixels (17.58 × 17.58 mm). In the tables that follow, for all phantom sizes, we round the dimensions of the single ROI's to 17 × 17 mm, the dimensions of the 2 × 2 segmentations to 9 × 9 mm subregions, and the dimensions of the 3 × 3 segmentations to 6 × 6 mm subregions.
Effect of radiation dose (mAs)
Steiger et al.14 and others in the past employed the same x-ray technique factors for patients of different sizes, and we did the same in our study. Lower radiation doses will result in more quantum mottle and greater variability in the CT numbers. For large regions of interest, it has been found that the mean CT numbers do not vary much with radiation dose; which is why Steiger et al. and others were able to use “low dose” techniques. This however may not be true for smaller subregions of interest. To investigate this, we performed scans with two and four times the mAs or dose of the standard “base” technique at 80 and 140 kVp and compared the results for the three size phantoms. Although the single axial slice scanning procedure we used is not directly amenable to dose measurements with the CT dose index (CTDIvol), the CTDIvol values provide an indication of x-ray tube output and relative dose. The CTDIvol values displayed on the scanner for the standard techniques with the small and medium body phantoms were: 5.87 mGy for the 80 kVp scans and 14.2 mGy for the 140 kVp scans. The corresponding values for the large body phantom (large bowtie filter) were 5.68 and 13.72 mGy. The CTDIvols for the 2× dose and 4× dose techniques are simply twice and four times the above values.
Effect of external vs internal calibration
As shown in Fig. 1, all scans were performed with the external calibration blocks placed beneath the phantoms. We computed the compositions of the test inserts using the external calibration standards and compared the results to those obtained with the internal calibration standards for all three phantom sizes. External calibration is expected to be less accurate than internal calibration because the beam hardening and scatter at the external location (and hence the CT numbers) are different from those at the internal location. For ease of implementation of the DEQCT method, it would be desirable if only the external calibration standards were used and a set of phantom/patient size independent correction factors were derived for transforming the CT numbers of the external calibration standards to those of the internal standards. We investigated this possibility. The equations that were utilized for implementing the correction factors were
| (5) |
| (6) |
| (7) |
where for Eq. 5, CT#B(E)cor is the corrected CT# of bone at energy E (i.e., 80 or 140 kVp), S(E)C is the slope of the bone calibration line for the external calibration standard determined for condition C (i.e., for the specified dose and body phantom size), Scor(E) is the slope correction factor which is equal to the ratio of the average slopes of the insert calibration lines to the average slopes of the external rods for all phantom body sizes at energy E, 1920 mg/cc is the mass density of pure bone,13i(E) is the intercept of the external calibration line at energy E, icor(E) is the intercept correction factor which is equal to the difference between the average of the intercepts of the calibration lines for the internal inserts minus the average of the intercepts of the calibration lines for the external rods for all phantom body sizes at energy E. For Eq. 6, CT#R(E)cor is the corrected CT number of red marrow at energy E, CT#Rext(E)C is the measured CT number of the red marrow external calibration standard at energy E for condition C, and CT#Roff(E) is the offset correction at energy E which is the average CT number of the marrow insert minus the average CT number of the marrow external rod for all phantom body sizes at energy E. The values in Eq. 7 are similar to those in Eq. 6, but the values are for the internal and external fat calibration standards.
Statistical analysis
The effects of all of the above factors (body phantom size, dose, number of subregions, type of calibration (external vs internal) were evaluated for statistical significance using the Wilcoxon rank sum test (Mann–Whitney test) (Refs. 15, 16, 17, 18) with the null hypothesis that the two populations (denoted as X and Y) have the same distribution.17, 18 For each assessment, we compared the distributions of the squared differences between the calculated and the true values for the two groups (e.g., the ith element in group X would be xi = (ui,calc − ui,true)2, where u denotes the corresponding volume fraction). The Wilcoxon version of the test is used here, and the rank-sums are calculated and tested for significance. p < 0.05 was considered statistically significant.
RESULTS
Effects of phantom body size and dose on calibration values
The effects of phantom body size and x-ray dose on the bone calibration lines and mean CT numbers of the three calibration materials (bone, fat, and marrow) are illustrated in Table 3. The slopes and intercepts are determined from linear fits to the CT number vs bone concentration (mg/cc) calibration data. The CT# of pure bone was calculated with Eq. 4. The CT numbers of red marrow and fat are the mean values for the corresponding red marrow and fat inserts made of materials simulating the x-ray attenuation properties of the pure materials.
Table 3.
Computed calibration values for the body size and radiation dose conditions investigated in this study.
| Phantom size | Slope, | Intercept, | Slope, | Intercept, | CT# bone, | CT# bone, | CT# red marrow, | CT# red marrow, | CT# fat, | CT# fat, |
|---|---|---|---|---|---|---|---|---|---|---|
| and dose level | 80 kVp | 80 kVp | 140 kVp | 140 kVp | 80 kVp | 140 kVp | 80 kVp | 140 kVp | 80 kVp | 140 kVp |
| Internal calibration | ||||||||||
| Small | ||||||||||
| 1× | 0.95 | 125.32 | 0.63 | 109.35 | 1958.0 | 1310.5 | 124.7 | 109.5 | −112.2 | −88.3 |
| 2× | 0.95 | 124.24 | 0.63 | 109.35 | 1957.4 | 1311.8 | 123.6 | 109.8 | −112.6 | −87.6 |
| 4× | 0.96 | 124.84 | 0.63 | 109.52 | 1962.6 | 1312.5 | 124.5 | 109.9 | −112.0 | −87.2 |
| Medium | ||||||||||
| 1× | 0.93 | 127.02 | 0.61 | 109.46 | 1907.8 | 1283.2 | 127.0 | 109.9 | −107.6 | −85.8 |
| 2× | 0.93 | 124.94 | 0.61 | 109.53 | 1917.5 | 1278.1 | 124.9 | 109.5 | −109.3 | −86.1 |
| 4× | 0.94 | 125.62 | 0.61 | 109.22 | 1926.4 | 1284.5 | 125.5 | 109.2 | −109.9 | −86.1 |
| Large | ||||||||||
| 1× | 0.88 | 116.37 | 0.59 | 107.58 | 1805.7 | 1235.2 | 117.0 | 107.1 | −106.9 | −84.9 |
| 2× | 0.89 | 120.47 | 0.59 | 106.38 | 1831.4 | 1245.1 | 120.6 | 106.6 | −109.2 | −85.6 |
| 4× | 0.90 | 120.51 | 0.59 | 106.92 | 1857.1 | 1241.8 | 120.8 | 107.0 | −109.2 | −85.8 |
| External calibration | ||||||||||
| Small, 4× | 0.99 | 110.3 | 0.65 | 105.7 | 2013.9 | 1354.9 | 109.7 | 105.5 | −131.3 | −97.2 |
| Medium, 4× | 0.96 | 110.0 | 0.63 | 104.5 | 1954.7 | 1321.7 | 111.4 | 106.0 | −132.3 | −97.0 |
| Large, 4× | 0.94 | 108.7 | 0.62 | 101.4 | 1917.5 | 1293.5 | 108.0 | 102.1 | −128.8 | −97.0 |
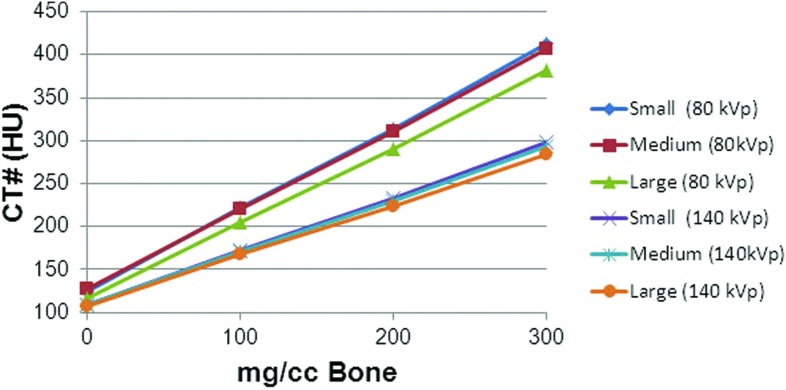
Plots of the insert (“internal”) calibration lines for the three phantom body sizes at standard dose (1× dose) are shown in Fig. 3.
Figure 3.
CT number vs bone concentration (mg/cc) calibration lines for the small, medium, and large body phantoms at standard dose determined at 80 and 140 kVp.
Effects of phantom size with single (1 × 1) regions of interest
The errors in the estimated compositions of the six individual test inserts for single (unsegmented) regions of interest with the internal calibration method using the base (1× dose) technique for the small, medium, and large size phantoms are listed in Table 4.
Table 4.
Single region of interest analysis: Mean errors of the estimated volume fractions (vf) of bone, fat, and red marrow for each of the six test inserts are listed as are the standard deviations of those errors (in parentheses) for the three repeat scans for each condition. Also listed are the overall RMS errors for all of the test inserts. Standard dose, internal calibration.
| Test insert nominal composition (vf) |
Mean bone error (vf) |
Mean fat error (vf) |
Mean red marrow error (vf) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bone | Fat | Red marrow | S | M | L | S | M | L | S | M | L |
| 0.052 | 0.800 | 0.148 | 0.0023 | 0.0026 | 0.0013 | 0.028 | 0.038 | 0.032 | −0.031 | −0.041 | −0.033 |
| (0.0031) | (0.0040) | (0.0072) | (0.018) | (0.025) | (0.046) | (0.021) | (0.029) | (0.053) | |||
| 0.104 | 0.200 | 0.696 | 0.0018 | 0.0012 | −0.0055 | 0.003 | 0.002 | −0.038 | −0.006 | −0.003 | 0.043 |
| (0.0044) | (0.0015) | (0.0058) | (0.031) | (0.043) | (0.036) | (0.035) | (0.050) | (0.041) | |||
| 0.104 | 0.300 | 0.596 | (0.0075 | 0.0015 | −0.0008 | 0.037 | −0.003 | −0.019 | −0.044 | 0.001 | 0.020 |
| (0.0070) | (0.0096) | (0.0074) | (0.043) | (0.061) | (0.047) | (0.050) | (0.070) | (0.054) | |||
| 0.156 | 0.100 | 0.744 | 0.0051 | 0.0088 | −0.0063 | 0.047 | 0.069 | −0.032 | −0.053 | −0.077 | 0.038 |
| (0.0012) | (0.0044) | (0.0079) | (0.008) | (0.025) | (0.049) | (0.009) | (0.029) | (0.057) | |||
| 0.156 | 0.300 | 0.544 | 0.0054 | −0.0013 | −0.0049 | 0.016 | −0.026 | −0.049 | −0.021 | 0.027 | 0.054 |
| (0.0045) | (0.0040) | (0.0064) | (0.031) | (0.029) | (0.042) | (0.036) | (0.033) | (0.048) | |||
| 0.156 | 0.500 | 0.344 | 0.0054 | 0.0064 | 0.0011 | 0.026 | 0.035 | −0.008 | −0.031 | −0.042 | 0.007 |
| (0.0025) | (0.0049) | (0.0078) | (0.017) | (0.031) | (0.043) | (0.020) | (0.035) | (0.051) | |||
| Overall RMS error | 0.0061 | 0.0067 | 0.0071 | 0.037 | 0.048 | 0.048 | 0.043 | 0.054 | 0.055 | ||
Note: S = small phantom; M = medium phantom; L = large phantom.
Effects of single region of interest vs multiple subregions of interest
Comparisons of the errors for the single region of interest vs multiple subregions of interest for internal calibration using the base techniques for all three phantom sizes are listed in Table 5. Root mean square (RMS) errors between the computed and nominal bone, fat, and red marrow compositions were determined for each region/subregion. Overall RMS errors were computed for multiple subregions.
Table 5.
Single region vs multiple subregion analysis: Overall RMS errors of the volume fractions of bone, fat, and red marrow of the six test inserts. Standard dose, internal calibration.
| Standard (1×) dose |
Bone RMS error (vf) |
Fat RMS error (vf) |
Red marrow RMS error (vf) |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Partition | Region/subregion size (mm) | S | M | L | S | M | L | S | M | L |
| 1 × 1 | 17 × 17 | 0.0061 | 0.0067 | 0.0071 | 0.037 | 0.048 | 0.048 | 0.043 | 0.054 | 0.055 |
| 2 × 2 | 9 × 9 | 0.0092 | 0.0116 | 0.0141 | 0.060 | 0.078 | 0.091 | 0.069 | 0.089 | 0.105 |
| 3 × 3 | 6 × 6 | 0.0140 | 0.0169 | 0.0202 | 0.092 | 0.110 | 0.127 | 0.106 | 0.126 | 0.147 |
S = small phantom; M = medium phantom; L = large phantom.
For the small and medium size body phantoms and all constituents (bone, red marrow, and fat), the RMS errors for the 3 × 3 segmentations are significantly greater than those for both the 2 × 2 and 1 × 1 segmentations (p values < 0.05). On the other hand, for those size phantoms, the 2 × 2 vs 1 × 1 RMS error comparisons are not significantly different. For the large body phantom and all constituents, the RMS errors for 3 × 3 segmentations are significantly greater than those for 2 × 2 which are significantly greater than those for 1 × 1, with the exception of fat 2 × 2 vs 1 × 1 which has a p value = 0.058.
With respect to phantom size effects, there were no significant differences between the RMS errors for the small, medium, and large size phantoms for full 1 × 1 regions. However, for 2 × 2 segmentation, the RMS errors for all constituents in the small body phantom are significantly less than those in the large phantom. Also, for 3 × 3 segmentation, the RMS errors in the small phantom are significantly less than those in the medium and the large phantoms.
Effect of radiation dose
Results for two and four times the total dose (two and four times the base technique mAs values at both 80 and 140 kVp) for all three phantom sizes are listed in Table 6. These results should be compared with those for the base technique in Table 5.
Table 6.
Single region vs multiple subregion analysis for 2× and 4× base technique dose: Overall RMS errors of the bone (vf), fat (vf), and red marrow (vf) of the six test inserts. Internal calibration.
| Bone RMS error (vf) |
Fat RMS error (vf) |
Red marrow RMS error (vf) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Partition | Region/subregion size (mm) | S | M | L | S | M | L | S | M | L |
| 2× dose | ||||||||||
| 1 × 1 | 17 × 17 | 0.0047 | 0.0034 | 0.0074 | 0.031 | 0.023 | 0.050 | 0.036 | 0.026 | 0.057 |
| 2 × 2 | 9 × 9 | 0.0063 | 0.0078 | 0.0112 | 0.041 | 0.050 | 0.071 | 0.047 | 0.057 | 0.081 |
| 3 × 3 | 6 × 6 | 0.0102 | 0.0110 | 0.0169 | 0.069 | 0.071 | 0.107 | 0.079 | 0.082 | 0.124 |
| 4× dose | ||||||||||
| 1 × 1 | 17 × 17 | 0.0049 | 0.0041 | 0.0041 | 0.032 | 0.030 | 0.032 | 0.037 | 0.033 | 0.036 |
| 2 × 2 | 9 × 9 | 0.0060 | 0.0066 | 0.0069 | 0.039 | 0.043 | 0.047 | 0.045 | 0.049 | 0.053 |
| 3 × 3 | 6 × 6 | 0.0076 | 0.0084 | 0.0106 | 0.050 | 0.056 | 0.070 | 0.058 | 0.064 | 0.080 |
S = small phantom; M = medium phantom; L = large phantom.
For all size body phantoms, and both 2× and 4× dose, the RMS errors of the bone, fat, and red marrow volume fractions for 3 × 3 segmentations are significantly greater than the RMS errors for 2 × 2 segmentations, and the RMS errors for 3 × 3 segmentations are significantly greater than those for full 1 × 1 regions, with the exceptions of bone, medium body, 4× dose (p = 0.137) and bone, small body, 4× dose 3 × 3 vs 2 × 2 (p = 0.171) and 3 × 3 vs 1 × 1 (p = 0.084). The RMS errors for all segmentations, all constituents and all size body phantoms are significantly less for 4× dose than for 1× dose. Furthermore, except for the full 1 × 1 regions for all components, the RMS errors for all other segmentations with 4× dose are significantly less than those with 2× dose. With respect to the RMS errors of the bone, fat, and red marrow in the small body vs medium vs large bodies, at 2× dose, the RMS errors in the medium body are significantly less than those in the large body, and the RMS errors in the small body are significantly less than those in the large body for both 2 × 2 and 3 × 3 segmentations. Also at 2× dose, for full 1 × 1 regions, the RMS errors in the medium body phantom are significantly less than those in the large body phantom, but not for small body vs large body. At 4× dose, the RMS errors were not significantly different for the different phantom sizes for all segmentations, except for 3 × 3, small vs large, fat, and red marrow.
Results for external calibration standards
Results computed using the external calibration standards with the 4× dose techniques with 5 mm slice thickness for the six test inserts and the three phantom sizes are listed in Table 7.
Table 7.
RMS errors of estimated compositions of the six test inserts computed using external rather than internal calibration standards and 1 × 1, 2 × 2, and 3 × 3 segmentation.
| Bone RMS error (vf) |
Fat RMS error (vf) |
Red marrow RMS error (vf) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Partition | Region/subregion size (mm) | S | M | L | S | M | L | S | M | L |
| 1 × 1 | 17 × 17 | 0.0215 | 0.0286 | 0.0164 | 0.128 | 0.163 | 0.095 | 0.150 | 0.192 | 0.111 |
| 2 × 2 | 9 × 9 | 0.0217 | 0.0291 | 0.0169 | 0.129 | 0.166 | 0.098 | 0.151 | 0.195 | 0.155 |
| 3 × 3 | 6 × 6 | 0.0220 | 0.0295 | 0.0183 | 0.132 | 0.169 | 0.109 | 0.154 | 0.199 | 0.127 |
External to internal calibration correction factors
The average (for all body phantom sizes) external to internal calibration correction factors are listed in Table 8.
Table 8.
External to Internal calibration correction factors.
| Correction factor | 80 kVp | 140 kVp |
| Slope (multiplicative) | 0.967 | 0.960 |
| Intercept (offset) | 14.0 HU | 4.7 HU |
| Red marrow (offset) | 13.9 HU | 4.2 HU |
| Fat (offset) | 20.4 HU | 10.6 HU |
Errors using external calibration with external to internal calibration correction factors
The results that were obtained after applying the above average (for all body phantom sizes) external to internal calibration correction factors to the external calibration values determined for the small, medium, and large sized phantoms at 4× dose with 5 mm slice thickness are listed in Table 9.
Table 9.
RMS errors of estimated compositions of the six test inserts computed using external rather than internal calibration standards with average (for all body phantom sizes) external to internal calibration correction factors. 4× dose.
| Bone RMS error (vf) |
Fat RMS error (vf) |
Red marrow RMS error (vf) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Partition | Region/subregion size (mm) | S | M | L | S | M | L | S | M | L |
| 1 × 1 | 17 × 17 | 0.0038 | 0.0095 | 0.0065 | 0.028 | 0.055 | 0.043 | 0.031 | 0.064 | 0.050 |
| 2 × 2 | 9 × 9 | 0.0051 | 0.0107 | 0.0086 | 0.035 | 0.062 | 0.056 | 0.040 | 0.073 | 0.064 |
| 3 × 3 | 6 × 6 | 0.0068 | 0.0120 | 0.0118 | 0.047 | 0.072 | 0.077 | 0.053 | 0.084 | 0.088 |
The RMS errors for external corrected calibration are significantly greater than those for internal calibration (Table 6, 4× dose) for the medium and large body phantoms. However, the corresponding RMS errors are not significantly different for the small body phantom. The RMS errors are significantly different (greater in some cases, less in others) for external corrected vs internal calibration for all segmentations except fat, 1 × 1, for which p = 0.0522.
DISCUSSION
Effects of phantom size and dose on the calibration values
The calibration values in Table 3 reflect the effects of the increased x-ray beam hardening and scatter with larger body size on the measured mean CT numbers of the calibration standards and on the calibration lines. Increased x-ray scatter for larger phantom sizes causes more x-rays to be detected, which is interpreted by the scanner as a decrease in linear x-ray attenuation coefficient and a corresponding decrease in CT number. Beam hardening causes a shift in the energy of the x-ray beam to a higher effective energy. This causes a reduction in the CT numbers of most tissues because the linear x-ray attenuation coefficients of those tissues decrease with x-ray energy relative to the linear attenuation coefficient of water. However, the CT numbers of tissues with high hydrogen content and low atomic number (like fat) respond in an opposite manner. Although as with other tissues, the linear x-ray attenuation coefficients of low atomic number tissues decrease with increasing energy (beam hardening), the rate of decrease is less than that of water, so their CT numbers increase with increasing energy (beam hardening). That is, they become less negative. These effects are in general observed in our measurements. The CT numbers of bone, the slopes of the bone calibration lines, and the CT numbers of red marrow decrease with increasing phantom size, and the CT numbers of fat increase with increasing phantom size both at 80 and 140 kVp. One minor exception is that the CT numbers of red marrow in the medium size body phantom at 80 kVp for all doses and at 140 kVp for 1× dose are slightly greater than those in the small body phantom, but the differences are small. The effect of dose (1× vs 2× vs 4×) on the measured mean CT numbers of the calibration standards and on the calibration lines is minimal (about 3% at most, with a majority less than or equal to 1%).
Effect of body size and subregion segmentation on the RMS errors
From the data in Table 4, it is observed that the RMS errors of the computed compositions are least for the small body phantom and greatest for the large body phantom. In particular for the estimates of the volume fractions of red marrow for which we are developing this application, the RMS errors for the medium body phantom are 1.2–1.3 times greater than those for the small body phantom and the RMS errors for the large body phantom are 1.3–1.5 times greater than those for the small body phantom. Also, the RMS errors for full 1 × 1 regions are the least, and those for the 3 × 3 segmentation are the largest. Specifically, from Table 5, for the red marrow the RMS errors for 2 × 2 segmentation are 1.6–1.9 times greater than those for 1 × 1 and the RMS errors for 3 × 3 segmentation are 2.3–2.7 times greater than those for full 1 × 1 regions.
These results indicate that the matching of the body phantom size for the internal calibration and test inserts does not completely compensate for the body size effect on the accuracy of the computed compositions of the test inserts. There is greater variability in CT numbers for larger body phantoms due to greater x-ray attenuation and therefore detection of fewer x-ray photons for each projection. Also, the effects of possible small changes in the x-ray tube potential (kVp) for each scan of each insert would be greater for larger phantoms due to increased attenuation and therefore greater shifts in the x-ray spectrum at the insert position. The results are also consistent with greater variability in the CT numbers when sampling smaller numbers of pixels for the subregions. The number of photons intercepting the subregions will be less for the larger phantoms, which will increase the variability in the mean CT numbers.
Sensitivity of three-equation three-unknown method to small changes in the CT number of the test vertebral inserts
The data in Table 4 indicate there are large standard deviations in the computed volume fractions of bone, red marrow, and fat for the three repeated scans for each insert. The mean CT numbers of these inserts for the three scans typically varied by about 1 HU, but sometimes varied by up to 3 or more HU, with greater variability occurring at 80 kVp than at 140 kVp. Furthermore, the mean CT numbers in the various subregions even in a single scan of the homogeneous test objects could sometimes differ by as much as 36 HU at 80 kVp (greatest difference observed for 1× dose, large body phantom, and 3 × 3 subregion segmentation). It is interesting to note that the same two subregions that differed by 36 HU differed by only 7 HU in a second identical scan.
To better examine the effect of small changes in CT numbers on our DEQCT results, we further evaluated results for a test insert that contains 0.104 vf bone, 0.30 vf fat, and 0.596 vf red marrow in a medium size body, with measured (reference) mean CT numbers at 80 and 140 kVp of 244 and 175 HU, respectively. Note, these measured CT numbers result in computed volume fractions that are very accurate for bone (0.104), but slightly off for fat (0.29) and red marrow (0.61). We varied these measured CT numbers by ±1 HU and ±2 HU and computed the bone, fat, and red marrow compositions using the three-equation three-unknown method with the determined bone calibration lines and measured mean CT numbers of fat and red marrow at 80 and 140 kVp. The results, which indicate significant sensitivity of the equations to small changes in the measured CT numbers of the test inserts, are shown in Table 10.
Table 10.
Example of the effect of small changes in the CT numbers of the test insets on the computed bone (vf), and red marrow (vf). Actual (reference) CT numbers are 244 HU at 80 kVp and 175 HU at 140 kVp for a 0.104 vf bone, 0.30 vf fat, and 0.596 vf red marrow test insert. The effects of deviations from the nominal CT numbers of the test inserts by up to ±1 HU (inner dark border) and up to ±2 HU (all values in table) are indicated. (a) Computed bone volume fraction (vf) (reference CT numbers and computed volume fractions of bone for those reference CT#'s are in bold). (b) Computed red marrow volume fraction (vf) (actual = 0.596 vf) (reference CT numbers and computed volume fractions of red marrow for those reference CT#'s are in bold).
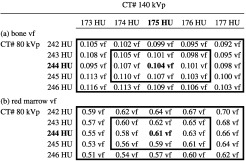 |
Note there is minimal effect on the results for changes in the CT# of the insert at 80 and 140 kVp by the same amount. For example, for an increase in the CT# at 80 kVp from 244 to 245 HU and an increase in the CT# at 140 kVp from 175 to 176 HU, the bone volume fraction changes from 0.104 to 0.103 and the red marrow volume fraction remains at 0.61. (See the values along the diagonal from top left to bottom right, which correspond to these changes.) The largest error occurs for an increase in the reference CT# at 80 kVp by 2 HU and a decrease in the reference CT# at 140 kVp by 2 HU, and vice versa (bone errors of ∼11% and marrow errors of ∼16%). Maximum errors for changes in CT#'s by 1 HU from the reference values are ±−6% for bone and ±7% for red marrow. Results for the volume fraction of fat exhibit even greater errors (maximum error for ±2 HU change = 28%, and for ±1 HU change = 14%).
Effect of dose and slice thickness
Comparing the RMS errors in 5 with those in 6, we see that increasing the dose by a factor of 2 reduces the RMS errors by an average factor of 1.40 ± 0.29 for all marrow constituents and all partitions. Increasing the dose by another factor of 2 (total increase = factor of 4) reduces the RMS errors by an average factor of 1.71 ± 0.25 for all marrow constituent and all partitions. These results are consistent with increased dose reducing the spatial variability in the relative number of photons [standard deviation/mean number (i.e., mottle)] and hence the variability in the CT numbers.
Another dose effect that is observed is that at 4× dose, the RMS errors are less influenced by phantom size. For example, at 4× dose, and all partitions, the ratios of the RMS errors of the red marrow volume fractions for the large-to-small phantom, medium-to-small phantoms, and large-to-medium phantoms are 1.18, 1.03, and 1.14, respectively. Corresponding values at 1× dose are 1.40, 1.24, and 1.12. This is expected due to the improved quantum statistics at 4× dose. It is confirmed by the fact that at 4× dose, the RMS errors are not significantly different for nearly all comparisons relative to phantom size (small vs medium, medium vs large, and large vs small). The only ones that were significant were 3 × 3 large vs small for fat (p = 0.017) and red marrow (p = 0.023).
Finally, we did perform an investigation of the effect of slice thickness on the RMS errors of the computed volume fractions of the test inserts, in which we acquired images with half the slice thickness (2.5 mm). In general, the results of that study corresponded with those obtained with half the dose (mAs). For example, the results for half-slice, double dose were similar to those for full-slice, 1× dose. In the interest of brevity the slice thickness study is not included in this paper.
Results for external calibration standards
When external calibration standards are used without correction (Table 7), the RMS errors are very large (compare Table 7 to Table 6, 4× dose). This is to be expected because the external calibration standards are displaced from the vertebra by a sizable distance (about 9.6, 11.2, and 13.8 cm for the small, medium, and large phantoms, respectively) and the beam hardening conditions and hence CT numbers are different at the internal and external locations.
Results for external calibration using external to internal calibration correction factors
Implementation of average (for all phantom body sizes) external to internal calibration correction factors reduces the RMS errors for external calibration (Table 9). Except for the results for the small body phantom, the RMS errors with this correction (Table 9) are still worse than those for internal calibration (Table 6, 4× dose). Smaller RMS errors are expected for internal calibration because the phantom body sizes (and hence scatter and beam hardening conditions) are perfectly matched for internal calibration. In contrast, the external to internal correction factors are averaged for all body sizes and therefore are not expected to be perfect matches for any particular size phantom. In this case, the match with the correction was very good for the small phantom resulting in errors that were slightly less than those for internal calibration.
Acceptable RMS errors for volume fractions of marrow and bone
The RMS error in the volume fraction of red marrow or the cellularity that would be acceptable for the marrow dosimetry application depends upon the expected range of cellularity in the vertebrae of the patients. For example, an RMS error of 0.1 might be acceptable for expected cellularity of 0.5 (0.1/0.5 = 20% error) but would not be acceptable for an expected cellularity of 0.1 (0.1/0.1 = 100% error). Trabecular marrow space contains not only active marrow and fat, but also components such as marrow stromal cells, blood sinuses and vessels, and other marrow support cells.19 Bolch et al.19 note that as these structures inhabit relatively small volumes, they can be ignored and that marrow cellularity can then be approximated as roughly as 1 − the fat fraction. Fat fractions in vertebrae that have been measured with MRI techniques include:
-
(1)
Schellinger et al.'s study of 71 lumbar vertebrae of 32 subjects (32–70 years old), for which the fat fraction range for normals was 36%–70% (mean 48.5%), and that for bone weakening was 38%–75% (mean = 56.3%).20
-
(2)
Liney et al.'s study of 16 normal subjects (8–57 years old, mean = 33 years) with a percent fat fraction of 14.3% to 71.1%.21
-
(3)
Kugel et al.'s study of 154 healthy volunteers, 11–95 years old for which the mean fat contents ranged from 23.9% ± 8.3% to 54.2% ± 5.4%.22
Using Bolch et al.'s equation, the corresponding cellularities are 0.3–0.64 with a mean of 0.52 for the normal appearing vertebrae in Schellinger et al., 0.29–0.86 for Liney et al., and 0.46–0.76 for Kugel et al.
Let us assume a minimum cellularity (volume fraction red marrow) of about 0.3. Then, to estimate the cellularity within subregions that are about 5 × 5 × 5 mm [similar to our 6 × 6 × 5 mm (slice thickness) for 3 × 3 segmentation], this 0.3 cellularity must be compared with maximum RMS errors (see Table 6) of 0.147 (3 × 3, 1× dose, 5 mm slice, large phantom), 0.124 (3 × 3, 2× dose, large phantom), 0.082 (3 × 3 2× dose, medium phantom), and 0.080 (3 × 3, 4× dose, large phantom) for internal calibration and 0.088 (3 × 3, 4× dose, large phantom) for corrected external calibration. For implementation practicality, the latter (corrected external calibration) would probably be the best choice and would result in a maximum RMS error that is about 29% (0.088/0.3), with a typical RMS error in the estimate of the volume fraction of red marrow of about 18% (0.088/0.5). Internal calibration with a 2× dose technique would achieve similar RMS errors for small and medium size phantoms but a larger and perhaps unacceptable RMS error of 0.124 for the large phantom.
For the 4× dose, 3 × 3 segmentation conditions that would result in acceptable RMS errors in the volume fractions of red marrow, the corresponding maximum RMS errors in the volume fractions of bone are 0.0106 for internal and 0.0118 for external calibration. The range of bone volume fractions in vertebrae can be estimated from a human cadaver vertebra study performed by Reinbold et al.23 They found that for 45 lumbar vertebral bodies obtained from 39 subjects aged 28–89 years (mean 58.6 years), without any known bone-related diseases, the minimum bone mineral density was about 35 mg/cc and the maximum was about 160 mg/cc with a fairly uniform distribution in between. Taking the facts that bone is 58% mineral, and that the mass density of bone is 1920 mg/cc, this range of bone mineral density corresponds with a volume fraction range of 0.031–0.144. Thus, the 0.0106 and 0.0118 RMS errors in bone volume fraction for 3 × 3 segmentation with 4× dose represents relative errors of 7%–34% for internal calibration and 8%–38%, for external calibration, both of which should also be acceptable.
Limitations of present study
The present study has several limitations/simplifications including:
-
(1)
We used homogenous phantom materials; whereas, true vertebral spongiosa would be heterogeneous mixtures of trabecular bone and red and yellow marrow.
-
(2)
The calibration objects and test objects were made of the same base materials; whereas, there would be variability in the compositions of the bone, red marrow, and yellow marrow constituents within patients (see Ref. 13).
-
(3)
There was a perfect match between the phantom body used for the calibration and test procedures; whereas, there could be differences in the shapes and compositions of patient bodies relative to the calibration phantom bodies which would affect the beam hardening and scatter and hence the measured CT numbers.
-
(4)
The bone, fat and fat-free red marrow compositions of the calibration, and test inserts were based on the compositions in the Report of the Task Group on Reference Man12 and may not be exact, especially for red marrow, which may contain much less fat than assumed in the Report of the Task Group on Reference Man. This could result in inaccuracies in the computed compositions.24
-
(5)
The calibration and test inserts were scanned at the isocenter of the scanner; whereas, such meticulous horizontal and vertical positioning may not be achievable in actual patient studies, and this could affect the measured CT numbers.
-
(6)
The locations of the vertebra within the phantoms were identical for the calibration and test inserts; whereas, the location of the vertebra in a patient (e.g., position relative to the patient's back) might be different (higher or lower), resulting in different tissue attenuation and therefore different measured CT numbers.
CONCLUSION
The results of this experimental study using patient simulating phantoms demonstrate the potential to use the three-equation three-unknown dual energy quantitative CT technique to estimate the spatial volume fractions of red marrow and bone within vertebral spongiosa to reasonable accuracy (0.08 vf for red marrow and 0.01 for vf for bone). Such accuracies may be achieved within 6 × 6 × 5 mm (thick) subregions for small and medium size phantoms/patients with internal calibration using x-ray technique factors that are 2 times those of the “low-dose dual-energy” technique employed by Steiger et al.14 in their patient studies in the 1980s and 1990s. Such accuracies can also be achieved with 4× those technique factors for all size phantoms/patients, including large, using internal calibration or corrected external calibration. Since we used a 5 mm slice thickness and Steiger et al. used one that was twice as large (10 mm) the number of x-rays utilized for our 2× technique would be about the same as that of Steiger et al., and the number utilized for our 4× technique would be twice as great as in Steiger et al.
Future studies using human cadaver vertebrae are needed to further investigate the marrow volume fraction accuracies achievable with this DEQCT method. “Truth” for the bone, fat and marrow volume fractions would be ascertained by histology. Such studies may include use of model based iterative reconstruction,25 which results in good CT image quality at much lower radiation doses and could mitigate the higher x-ray technique factor (dose) requirements found in the present study. Finally, for improved accuracy, we plan to investigate a combination of the image-based three-equation three-unknown DEQCT method with the projection-based basis material decomposition DEQCT method used by Reinbold et al.23 That basis material decomposition method has been shown to have an accuracy of 1.4% in estimating bone mineral density in human cadaver experiments.23 Volume fractions of bone estimated with this method would be input into the three equations and the two other parameters, the volume fractions of fat and red marrow would be computed from the remaining two equations with two unknowns, with constraints that the solutions are non-negative and the solutions sum to 1. Use of additional tin filtration with the 140 kVp x-ray beam will also be investigated as the resulting increased separation of the energies of the dual energy (80/140 kVp) polyenergetic spectra has been shown to improve differentiation of materials with dual energy CT.26, 27
ACKNOWLEDGMENTS
This work was supported in part by Grant No. R01 EB001994 from the National Institutes of Health. The content of this paper does not necessarily reflect the position of the funding agencies and no official endorsement of any equipment and product of any companies mentioned should be inferred.
References
- Dewaraja Y. K., Avram A. M., Roberson P. L., Smith L. B., Wilderman S. J., Shen J., Savas H., Youssef E., Kaminski M. S., and Schipper M. J., “Tumor absorbed dose predicts progression free survival (PFS) following I-131 radioimmunotherapy (RIT),” J. Nucl. Med. 54, 16P (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah A. P., Bolch W. E., Rajon D. A., Patton P. W., and Jokisch D. W., “A paired-image radiation transport model for skeletal dosimetry,” J. Nucl. Med. 46, 344–353 (2005). [PubMed] [Google Scholar]
- Wilderman S. J., Roberson J. P. L., Bolch W. E., and Dewaraja Y. K., “Investigation of effect of variations in bone fraction and red marrow cellularity on bone marrow dosimetry in radio-immunotherapy,” Phys. Med. Biol. 58(14), 4717–4731 (2013). 10.1088/0031-9155/58/14/4717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho K.-Y., Hu H. H., Keyak J. C., Colletti P. M., and Powers C. M., “Measuring bone mineral density with fat–water MRI: Comparison with computed tomography,” J. Mag. Res. Imaging 37(1), 237–242 (2013). 10.1002/jmri.23749 [DOI] [PubMed] [Google Scholar]
- Ballon D., Jakubowski A., Gabrilovem J., Graham C., Zakowski M., Sheridan C., and Koutcher J. A., “In vivo measurements of bone marrow cellularity using volume-localized proton NMR spectroscopy,” Mag. Res. Med. 19, 85–95 (1991). 10.1002/mrm.1910190108 [DOI] [PubMed] [Google Scholar]
- Ballon D., Jakubowski A. A., Graham M. C., Schneider E., and Koutcher J. A., “Spatial mapping of the percentage cellularity in human bone marrow using magnetic resonance imaging,” Med. Phys. 23(2), 243–250 (1996). 10.1118/1.597796 [DOI] [PubMed] [Google Scholar]
- Ishizaka H., Horikoshi H., lnoue T., Fukusato T., and Matsumoto M., “Bone marrow cellularity: Quantification by chemical-shift misregistration in magnetic resonance imaging and comparison with histomorphometrical techniques,” Australas Radiol. 39, 411–414 (1995). 10.1111/j.1440-1673.1995.tb00325.x [DOI] [PubMed] [Google Scholar]
- Pichardo J. C., Milner R. J., and Bolch W. E., “MRI measurement of bone marrow cellularity for radiation dosimetry,” J. Nucl. Med. 52, 1482–1489 (2011). 10.2967/jnumed.111.087957 [DOI] [PubMed] [Google Scholar]
- Dewaraja Y. K. et al. , “131I-tositumomab radioimmunotherapy: Initial tumor dose-response results using 3-dimensional dosimetry including radiobiologic modeling,” J. Nucl. Med. 51, 1155–1162 (2010). 10.2967/jnumed.110.075176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodsitt M. M., Rosenthal D. I., Reinus W. R., and Coumas J., “Two postprocessing CT techniques for determining the composition of trabecular bone,” Invest. Radial. 22, 209–215 (1987). 10.1097/00004424-198703000-00005 [DOI] [PubMed] [Google Scholar]
- Goodsitt M. M., Johnson R. H., and Chesnut C. H., “A new set of calibration standards for estimating the fat and mineral content of vertebrae via dual energy QCT,” Bone Miner. 13, 217–233 (1991). 10.1016/0169-6009(91)90070-G [DOI] [PubMed] [Google Scholar]
- International Commission on Radiological Protection, “Report of the Task Group on Reference Man,” ICRP Publication 23 (Pergamon, Oxford, England, 1975). [Google Scholar]
- Woodard H. Q. and White D. R., “The composition of body tissues,” Br. J. Radiol. 59,1209–1219 (1986). 10.1259/0007-1285-59-708-1209 [DOI] [PubMed] [Google Scholar]
- Steiger P., Block J., Steiger J. S., Heuck A. F., Friedlander A., Ettinger B., Haris S. T., Gluer C. C., and Genant H. K., “Spinal bone-mineral density measured with quantitative CT—Effect of region of interest, vertebral level, and technique,” Radiology 175, 537–543 (1990). [DOI] [PubMed] [Google Scholar]
- Wilcoxon F., “Individual comparisons by ranking methods,” Biom. Bull. 1(6), 80–83 (1945). 10.2307/3001968 [DOI] [Google Scholar]
- Mann H. B. and Whitney D. R., “On a test of whether one of two random variables is stochastically larger than the other,” Ann. Math. Stat. 18(1), 50–60 (1947). 10.1214/aoms/1177730491 [DOI] [Google Scholar]
- Bauer D. F., “Constructing confidence sets using rank statistics,” J. Am. Stat. Assoc. 67, 687–690 (1972). 10.1080/01621459.1972.10481279 [DOI] [Google Scholar]
- Hollander M. and Wolfe D. A., Nonparametric Statistical Methods (Wiley, New York, 1973). [Google Scholar]
- Bolch W. E., Paton P. W., Rajon D. A., Shah A. P., Jokish D. W., and Inglis B. A., “Considerations of marrow cellularity in 3-dimensional dosimetric models of the trabecular skeleton,” J. Nucl. Med. 43, 97–108 (2002). [PubMed] [Google Scholar]
- Schellinger D., Lin C. S., Lim J., Hatipoglu H. G., Pezzullo J. C., and Singer A. J., “Bone marrow fat and bone mineral density on proton MR spectroscopy and dual-energy X-ray absorptiometry: Their ratio as a new indicator of bone weakening,” Am. J. Roentgenol. 183(6), 1761–1765 (2004). 10.2214/ajr.183.6.01831761 [DOI] [PubMed] [Google Scholar]
- Liney G. P., Bernard C. P., Manton D. J., Turnbull L. S., and Langton C. M., “Age, gender, and skeletal variation in bone marrow composition: A preliminary study at 3.0 Tesla,” J. Magn. Reson. Imaging 26(3), 787–793 (2007). 10.1002/jmri.21072 [DOI] [PubMed] [Google Scholar]
- Kugel H., Jung C., Schulte O., and Heindel W. “Age- and sex-specific differences in the 1H-spectrum of vertebral bone marrow,” J. Magn. Reson. Imaging 13(2), 263–268 (2001). [DOI] [PubMed] [Google Scholar]
- Reinbold W. D., Adler C. P., Kalender W. A., and Lente R., “Accuracy of vertebral mineral determination by dual-energy quantitative computed tomography,” Skeletal Radiol. 20(1), 25–9 (1991). 10.1007/BF00243717 [DOI] [PubMed] [Google Scholar]
- Goodsitt M. M., Hoover P., Veldee M. S., and Hsueh S. L., “The composition of bone marrow for a dual-energy quantitative tomography technique: A cadaver and computer simulation study,” Invest. Radiol. 29, 695–704 (1994). 10.1097/00004424-199407000-00006 [DOI] [PubMed] [Google Scholar]
- Nuyts J., De Man B., and Fessler J. A., “Modeling the physics in the iterative reconstruction for transmission computed tomography,” Phys. Med. Biol. 58(12), R63–R96 (2013). 10.1088/0031-9155/58/12/R63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Primak A. N., Ramirez Giraldo J. C., Liu X., Yu L., and McCollough C. H., “Improved dual-energy material discrimination for dual-source CT by means of additional spectral filtration,” Med. Phys. 36(4), 1359–1369 (2009). 10.1118/1.3083567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung G. S., Kawamoto S., Matlaga B. R., Taguchi K., Zhou X., Fishman E. K., and Tsui B. M., “Differentiation of kidney stones using dual-energy CT with and without a tin filter,” Am. J. Roentgenol. 198(6), 1380–1386 (2012). 10.2214/AJR.11.7217 [DOI] [PubMed] [Google Scholar]