Finite element analysis of helical flows in human aortic arch: A novel index

Abstract

This study investigates the helical secondary flows in the aortic arch using finite element analysis. The relationship between helical flow and the configuration of the aorta in patients of whose three-dimensional images constructed from computed tomography scans was examined. A finite element model of the pressurized root, arch, and supra-aortic vessels was developed to simulate the pattern of helical secondary flows. Calculations indicate that most of the helical secondary flow was formed in the ascending aorta. Angle α between the zero reference point and the aortic ostium (correlation coefficient (r) = −0.851, P = 0.001), the dispersion index of the cross section of the ascending (r = 0.683, P = 0.021) and descending aorta (r = 0.732, P = 0.010), all correlated closely with the presence of helical flow (P < 0.05). Stepwise multiple linear regression analysis confirmed angel α to be independently associated with the helical flow pattern in therein (standardized coefficients = −0.721, P = 0.023). The presence of helical fluid motion based on the atherosclerotic risks of patients, including those associated with diabetes, hypertension, hyperlipidemia, or renal insufficiency, was also evaluated. Numerical simulation of the flow patterns in aortas incorporating the atherosclerotic risks may better explain the mechanism of formation of helical flows and provide insight into causative factors that underlie them.

INTRODUCTION

The human aorta is the major blood vessel with complex geometry and such characteristics as non-planar curvature, branches at the apex, the tapering of distensible vessel walls, and ventricular twisting.^{1, 2, 3} All of these features are responsible for the onset of helical or secondary flow patterns in aortic blood flow, which are assumed to facilitate ventricular ejection,⁴ promote oxygen transfer,⁵ and reduce the concentration of low-density lipoproteins on luminal surface.⁶ This helical flow pattern arises because the centrifugally-induced pressure gradient, approximately uniform over the cross section, drives the slower-moving fluid near the wall inward, while the faster-moving fluid in the core is swept outward.^{7, 8} Blood flow in the human aorta system is of particular interest because the aorta is the largest and most highly curved vessel in the human vascular system. Since secondary flow motions are expected to improve heat exchange and mixing between the fluid and its surroundings, a better understanding of the mechanism of flows in the aortic arch is important. Various researchers have reported the presence of helical secondary flows in the aortic arch,^{1, 9, 10} but the origins and mechanism of formation of such flows, as well as their relationships with the aorta and the characteristics of patients, have not been well clarified.

Stiffening and atherosclerosis can modify the unique characteristics of the aorta, weakening helical flow.⁶ Aorta stiffening is related to the macrovascular complications of various atherosclerotic factors, which causes damage to the target organs.^{11, 12} Diabetes, along with hypertension, hyperlipidemia, and smoking, are risk factors for coronary artery disease, which accelerates the formation of advanced atherosclerotic lesions.^{13, 14} These lesions reduce arterial compliance, which is one of the earliest manifestations of detrimental structural and functional changes within the vessel wall.¹⁵ Additionally, since the arteriosclerosis and atherosclerosis involve similar pathobiologic processes, the vessel wall becomes progressively injured. The vessel wall matrix and adjacent cells undergo reparative inflammatory responses to prevent further damage. Consequently, arterial wall calcification and increased stiffness occur, promoted by the above risk factors, altering the characteristics of the aorta.^{16, 17}

We believe that the configuration of the aorta strongly affects the helical secondary flow therein, and we hypothesize that this flow is directly related to the characteristics of heart of the patient, such as the curved, three-dimensional (3D) structure of the ascending and descending aortas. To confirm this hypothesis, a comparative numerical study of helical flow performance in the aorta was performed using in vivo computed tomography (CT) images of human aortas and a perfectly curved tube.

Helical secondary flows in the aortas of all 11 subjects were analyzed by finite element analysis (FEA). Geometrical information on subject-specific aortas was obtained from contrast-enhanced CT scan data. The CT images were imported into medical image processing software to construct 3D models of the aortas. The flow patterns inside the arterial vessels were calculated. The mechanism of formation of the helical flows and its relationship with the aorta geometry was investigated. The relationships between subject characteristics and the presence of the helical flows were also examined. The results of the flow analysis explain the mechanism of formation of the helical flows and provide insight into causative factors that may be responsible for them.

MATERIALS AND METHODS

The Institutional Review Board approved this investigation.

Constructing 3D images using CT

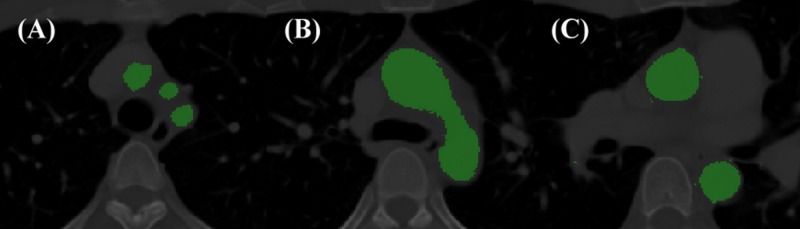
This study involved 11 subjects whose information was in the medical database of Chang Gung Memorial Hospital. Their ages were from 41 to 84 (mean, 56.2 ± 10.1 yr). Table TABLE I. presents the characteristics of the subjects. Information about the geometry of the aortic vessels of the subjects was extracted from the contrast-enhanced CT scan data. Each subject provided informed written consent before enrollment. The study was carried out in line with the Helsinki Declaration. CT scans were performed using 64-slice scanners (Siemens Medical Solutions, Pennsylvania, USA), with an intravenous injection of 80–120 ml of nonionic iodinated contrast dye (Omnipaque 350, GE Amersham, Milwaukee, USA). The thickness of the slice was 1 mm, and the voxel resolution was approximately 0.6 mm. All of the CT scans were interpreted by cardiovascularly trained radiologists. The CT images were imported into, and analyzed using, Mimics 13.0 (Materialise, Leuven, Belgium) medical image processing software: a semiautomatic segmentation algorithm was used to detect the arterial wall to construct 3D models of the aortic arch. The algorithm used user-defined seed points and lower and upper grey-level thresholds. Figure 1 presents the results obtained using the segmentation algorithm.

TABLE I.

Characteristics of analyzed patients. ACEI, angiotensin converting enzyme inhibitor; ARB, angiotensin II receptor blocker; HDL, high-density lipoprotein.

	All patients (n = 11)	Helical flow (n = 6)	Non-helical flow (n = 5)	P valve
Age (yr)	58 ± 15	57 ± 8	60 ± 23	0.741 a
Male gender (%)	8(73)	5(83)	3(60)	0.387 b
Diabetes mellitus (%)	3(27)	0(0)	3(60)	0.026b
Hypertension (%)	6(55)	3(50)	3(60)	0.740 b
Chronic renal insufficiency	3(27)	2(33)	1(20)	0.621 b
Total cholesterol (mg/dl)	181.6 ± 32.1	179.7 ± 37.0	183.8 ± 29.1	0.844 a
HDL cholesterol (mg/dl)	42.5 ± 4.9	42.8 ± 3.8	42.0 ± 6.5	0.796 a
Glycohemoglobin (%)	6.7 ± 2.7	5.1 ± 0.7	8.7 ± 2.8	0.006a
Current smoker (%)	4 (36)	1(17)	3(60)	0.137 b
Body mass index (kg/m2)	25.2 ± 4.8	26.5 ± 6.0	23.5 ± 2.7	0.334 a
Medications
ACEI or ARB (%)	2(18)	2(33)	0(0)	0.154 b
Beta Blockers (%)	3(27)	2(33)	1(20)	0.621 b
Loop diuretics (%)	2(18)	0(0)	2(40)	0.087 b
Calcium channel blockers (%)	5(46)	3(50)	2(40)	0.740 b

^aMann-Whitney U-test (bold type indicates P < 0.05).

^bChi-square test (bold type indicates P < 0.05).

Figure 1.

Segmentation of aortic arch. (a) Brachiocephalic artery, left common carotid artery, and left subclavian artery; (b) level of aortic arch; and (c) aortic root.

Each slice was visually examined to ensure that each slice had an accurately controlled and smooth surface. A Gaussian filter with a 3 × 3 kernel was applied to smooth the lumen borders. The patient-specific 3D arterial wall surfaces were constructed from the two-dimensional contour stack and tessellated to eliminate skewed elements, which would otherwise have produced artificial stress concentrations. Figure 2 displays one of the solid models of the reconstructed aortic arch. To elucidate the mechanism of formation of the helical secondary flow in the aorta, a “perfectly prismatic curved” aorta was constructed using SolidWorks 2013 (Dassault System SolidWorks Corp., USA) as a blank reference.

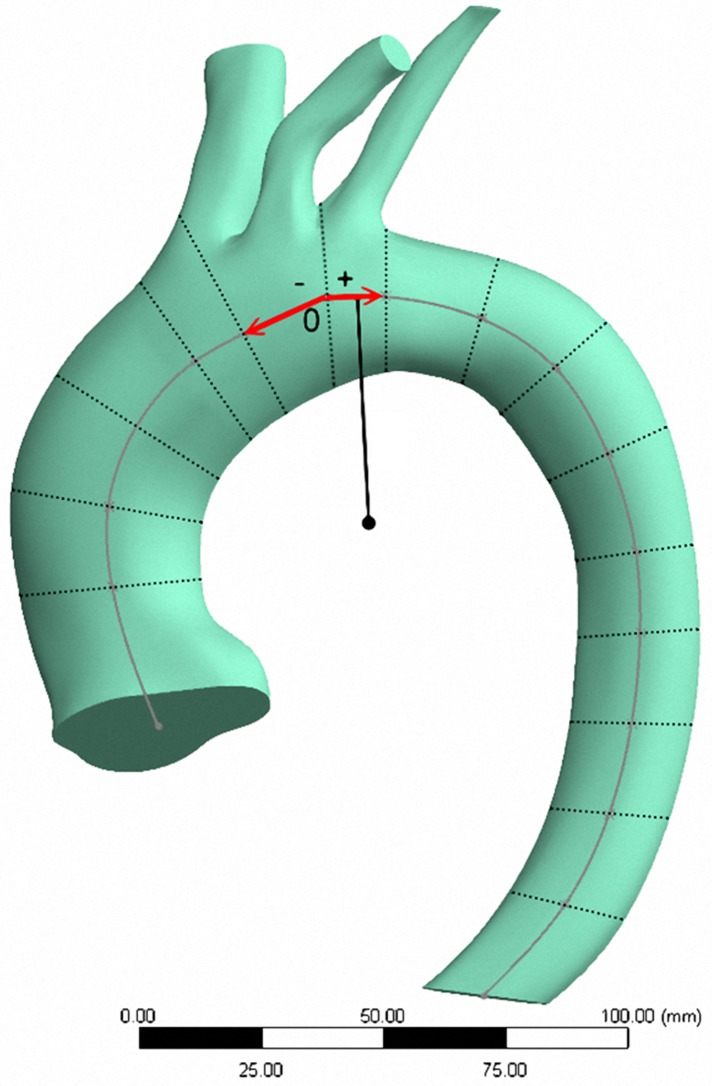
Figure 2.

Solid model of aortic arch. (O: reference zero point.)

Following the construction of the solid models, the following three parameters were calculated for each subject.

• (1)Mean values of cross section of the different levels of ascending and descending aorta.
• (2)Dispersion indices of the cross-sectional area, which are defined as the standard deviation as a percentage of the average cross-sectional area at various levels in the ascending (Da) and descending aorta (Dd).¹⁸
• (3)Angle α between aortic ostium and reference zero point, and angle β between suprarenal aorta and reference zero point (Fig. 3).

Figure 3.

Angle α (between aortic ostium (A) and reference zero point (O)), and angle β (between suprarenal aorta (B) and reference zero point (O)).

Quantification of helical flow

To quantify the helical flow, based on the work of Lorenz et al., helicity was used.¹⁹ Helicity is a conserved quantity and remains for incompressible fluids with zero viscosity and uniform density. Briefly, for each analysis plane and for each timeframe, the aortic lumen was manually segmented. The helicity of the fluid flow is defined as the integrated scalar product of the local velocity vector u(r,t) and the vorticity vector x(r,t) in 3D Euclidean space (R³)

$$H={\displaystyle \int u(r,t)\cdot \omega (r,t)dV}.$$

The vorticity vector field is defined as the curl of the velocity vector field

$$\omega (r,t)=\nabla x\hspace{0.17em}u(r,t).$$

The dot product of the velocity and vorticity vectors yields the helicity density Hd

$$Hd=u(r,t)\cdot \omega (r,t).$$

Both the helicity and the helicity density are pseudo-scalar quantities. For forward flow (from the heart to the aorta), the sign provides information on the direction of rotation of the fluid (either clockwise or counterclockwise). The angle γ between the velocity and the vorticity vectors is the relative helicity or relative helicity density, Hr

$$Hr=\frac{u(r,t)\cdot \omega (r,t)}{|u(r,t)||\omega (r,t)|}=\cos (\gamma ).$$

This angle has a value in the range [0°, 180°], yielding relative helicities of values between −1 (maximum counterclockwise rotation when viewed in the direction of flow) and +1 (maximum clockwise rotation). High values of relative helicity correspond to regions where the velocity and vorticity are parallel or anti-parallel meaning that the angle between the velocity and the vorticity is 0° or 180°. Notably, the definition of helicity direction is valid only for forward flow. In summary, obvious helical flow (with angle γ of more than 90°) was identified, while another group exhibited minor helical flow (with angle γ of about 90°).

Boundary conditions and flow models

The numerical simulation was carried out in a commercial finite element package, Ansys 13.0 (Ansys Inc., USA). The blood that flows through the aorta was assumed to be a homogeneous, incompressible Newtonian fluid,^{20, 21} with the dynamic viscosity of blood taken to be 0.0036 Pa.s²² and its mass density taken to be 1060 kg/m³. The aortic wall was assumed to be rigid so the no-slip condition was applied at the aortic wall. Blood flow is normally assumed to be laminar in large vessels because the mean flow velocity is predicted to be sufficiently low to result in a relatively low Reynolds number. For pulsatile unsteady flow, turbulence occurs at a Reynolds number that is much larger than is expected for steady flow because accelerating flow is more stable than decelerating flow.²³ Following the work of Shahcheraghi et al.²⁴ to simulate the oscillating cycle, a steady state solution at the maximum flow rate or Reynolds number is first obtained. Next, this steady-state solution is used as the initial solution to the unsteady equations, which are solved using the inlet pulse for a particular number of cycles before a time-periodic solution is reached. Four unsteady cycles were required to reach a periodic solution. The fifth cycle yielded the final periodic solution. The flow pressure and velocity at the aorta inlet were 120 mmHg (systolic blood pressure)²⁵ and 0.123 m/s,²⁶ respectively, while the pressure on the brachiocephalic, left-common carotid, and left-subclavian arteries was 80 mmHg (diastolic blood pressure).

Meshing and elements

A semi-automatic adaptive meshing approach was utilized in Hyper Mesh 10.0 (Altair Hyper Works, Troy, MI, USA) to set the number of elements to optimize computational efficiency and element quality. When the adequate boundary conditions were applied to each model, a mesh was obtained on each aortic arch with a high spatial resolution (<0.4 mm in all axes). Mesh independence was verified by increasing the number of elements in the mesh until the peak stress differed by less than 2% from that obtained using the previous mesh. The optimal mesh thus obtained was 1.0 to 1.5 × 10⁶ cellular meshes.

Tetrahedral elements were adopted in modeling the aortas. Figure 4 presents a mesh typical of those used in the analysis.

Figure 4.

Finite element meshes used to model aortic arch.

Perfectly prismatic curved aorta

A perfectly prismatic curved aorta with a cross-sectional area similar to that of the average of the aortas of the subjects of this study was produced. The novel indices of Da, Dd, angles α and β were all zero. This investigation mainly focuses on the flow dynamics in the aortic arch and its three major branches, so the branches of the thoracic aorta were neglected.^{24, 25} The boundary conditions used, including the blood pressure and flow velocity at the aorta inlet and the branches, were the same as those of the other analyzed aortas.

Statistical analysis

Continuous variables are expressed as mean ± standard deviation, while categorical variables are expressed as a number and a percentage. The difference between the clinical characteristics of the two groups (helical flow and non-helical flow) was determined by performing a Mann-Whitney U-test (continuous variables) and a chi-squire test (categorical variables). Univariate association between the presence of helical flow and parameters extracted from the CT images was evaluated using Pearson's correlation coefficient (r) with two interval or ratio variables or the point biserial correlation coefficient (when the first variable is the interval/ratio and the second is dichotomous). Multivariate association between helical flow pattern and the CT parameters was determined by stepwise multiple linear regressions with variables that reached significance (P < 0.1) in the previous, unadjusted analysis as covariates for the 11 patients. P ≤ 0.05 was regarded as indicating statistical significance). All CT parameters were adjusted for age, gender, diabetes, hypertension, chronic renal insufficiency, and body mass index.^{16, 17} SPSS software (version 17.0 for Windows; SPSS Inc, Chicago, Illinois, USA) was used for analyzing the data.

RESULTS

Characteristics of subjects

Table TABLE I. presents the clinical characteristics of the 11 study subjects. The flow patterns in these 11 subjects were simulated using the finite element method. The numerical results thus obtained suggested that of the 11 patients, six exhibited obvious helical flow (angle γ = 131.3° ± 5.9°), while five had minor helical flow (angle γ = 94.8° ± 3.8°) (P < 0.001). Figure 5a and integral multimedia display typical simulated aortas with obvious helical secondary flow (angle γ = 135°). Figure 5b with integral multimedia show aortas with minor helical flow (angle γ = 90°). The two corresponding groups of patients resembled each other in age, male gender, hypertension, chronic renal insufficiency, total and high-density lipoprotein cholesterol, being a current smoker, and body mass index. Additionally, the two groups are similar in terms of medications, including angiotensin-converting enzyme inhibitors or angiotensin II receptor blockers, beta blockers, loop diuretics, and calcium channel blockers. Patients without diabetes exhibited a greater percentage of helical flow (60% vs. 0%, P = 0.026) and lower glycohemoglobin (5.7 ± 0.7 vs. 8.7 ± 2.8, P = 0.006) levels than patients with diabetes.

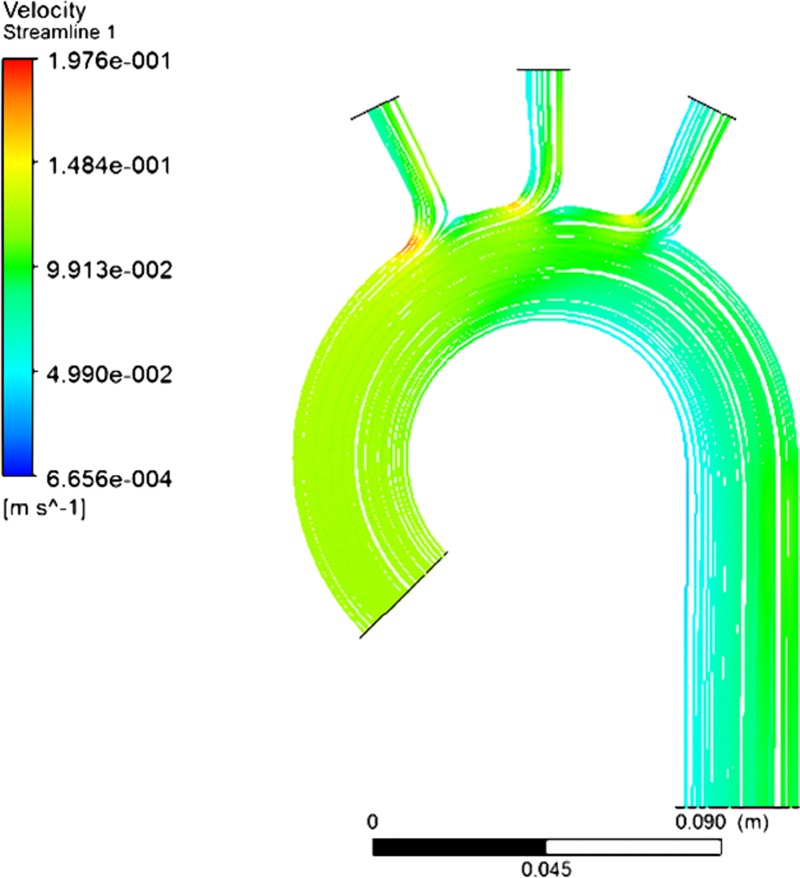
Figure 5.

Download video file ^{(4.9MB, avi)}

Download video file ^{(5MB, avi)}

Simulated results concerning aortic arch that show helical secondary flow (a). Simulated results, showing minorhelical secondary flow (b). (Multimedia view)

3D reconstructions of ascending and descending aortas

Patients with and without helical flow had ascending and descending aortas with equal average cross-sectional areas and equal angle β. Patients with helical flow had significantly higher Da (16.4 ± 3.0% vs. 11.6 ± 2.8%, P = 0.021) and Dd (23.3 ± 6.0% vs. 13.5 ± 3.4%, P = 0.010) than those without (Table TABLE II.). Figure 6a displays the variations in the cross-sectional areas of the ascending (Da = 16.5%) and descending (Dd = 22.5%) aortas of one of the subjects with obvious helical secondary flow, while Fig. 6b shows the variation in the cross-sectional areas, Da (13.5%) and Dd (8.80%), respectively, in a subject with minor helical flow.

TABLE II.

Findings from three-dimensional reconstructions of ascending and descending aortas.

	All patients	Helical flow	Non-helical flow	P valve
Ascending aorta
Cross section area (mm2)	839.9 ± 273.6	818.4 ± 304.7	865.6 ± 263.7	0.855 a
Dispersion index (%)	14.2 ± 3.8	16.4 ± 3.0	11.6 ± 2.8	0.018a
Descending aorta
Cross section area (mm2)	541.5 ± 228.8	613.9 ± 250.2	454.6 ± 187.8	0.273 a
Dispersion index (%)	18.9 ± 7.0	23.3 ± 6.0	13.5 ± 3.4	0.028a
Angle α (deg)	44.3 ± 21.6	28.3 ± 11.4	63.5 ± 12.6	0.006a
Angle β (deg)	75.1 ± 7.6	78.1 ± 7.2	71.5 ± 6.9	0.120 a

^aMann-Whitney U-test (bold type indicates P < 0.05). Angle α is angle between aortic ostium and reference zero point; angle β is angle between suprarenal aorta and reference zero point.

Figure 6.

(a) Influence of variations in cross-sectional area on helical secondary flow in ascending and descending aortas. Variation of cross-sectional area of ascending aorta is Da = 16.5% and that of descending aorta is Dd = 22.5%. (b) Effect of variations of cross-sectional area on helical secondary flow in ascending and descending aortas in subjects with minor helical flow. Cross-sectional area variations Da = 13.5% and Dd = 8.80% were determined in subjects with minor helical flow.

A low angle α was found among the helical flow group. Figure 7 presents the typical values of angles α and β in subjects with (α = 9.1°; β = 65.7°) and without (α = 43.9°; β = 72.4°). The angle α in the patients with helical flow was lower than that in those without helical flow, whereas angle β did not differ significantly between these two groups (Table TABLE II.).

Figure 7.

Angle α (between aortic ostium and reference zero point) and angle β (between suprarenal aorta and reference zero point). (a) Patient with helical flow (α = 9.1°; β = 65.7°). (b) Patient without helical flow (α = 43.9°; β = 72.4°).

Relationship between helical flow and CT parameters

Helical flow was significantly associated with Da (r = 0.683, P = 0.021), Dd (r = 0.732, P = 0.010), and angle α (r = −0.851, P = 0.001). When patients with helical flow were defined as the outcome variable, and Da, Dd, as well as angle α were covariates, only angle α (standardized coefficients = −0.721, P = 0.023) was independently related to the other covariates on the presence of helical flow following adjustments for age, gender, diabetes, hypertension, chronic renal insufficiency, and body mass index.

Perfectly prismatic curved aorta

To understand better the mechanism of formation of helical flow, a perfectly prismatic curved aorta was constructed as a control for numerical analysis. The simulated results in Fig. 8 show the absence of helical flow in such an aorta. The flow progressively slows down in the region of the arch. Non-helical flow produces greater outwardly directed forces just beyond the branch and less inward pressures at more distal sites than outward flow does.

Figure 8.

A perfectly prismatic curved tube does not exhibit any helical secondary flow. Da, Dd, angle α and angle β are all zero.

DISCUSSION

This study examined the relationship between helical flow and the configuration of the aorta in patients of whose 3D images were constructed from CT scans. The angle α between the zero reference point and the aortic ostium is the independent correlated with the helical flow pattern in the aorta. Moreover, Da, Dd, and angle α correlated closely with the presence of helical flow after adjustment with clinical risk factors.

Angles α and β

Decreased angle α promotes the presence of helical flow, the helical motion of blood flow in the human aorta is a typical example of “form follows function” in the long distance of vascular system; it can eliminate stagnation flow regions and ensure the smoothness of the inner surface of the ascending aortic wall and even its flushing by blood. Of particular interest in relation to the flow in the aorta is the entry length of the aorta, which is the distance required for the flow to become fully developed.²⁷ The flow field requires an inviscid core immediately downstream of the entrance, in which the centrifugal force in a thin boundary layer provides a balance between viscous and inertia forces. Accordingly, the change in the distance to the top of arch and curvature of the ascending aorta may influence the helical secondary flow due to the decelerated initial blood velocity of aorta. Moreover, the descending abdominal aorta begins at the diaphragm as a continuation of the thoracic aorta and runs down to where the aorta ends. The abdominal aorta travels and constrains in the posterior mediastinum to supply oxygenated blood to all of the abdominal and pelvic organs and the legs. The anatomy and position of descending aorta help explain the compatible angle β in both groups.

Dispersion index of cross-sectional area

In biological sciences, the index of dispersion is useful for the testing homogeneity of certain types of data, such as data on ventricular repolarization, QT dispersion, and tissue Doppler imaging with a particular view to determining cardiac outcomes.^{28, 29, 30} A genetically programmed asymmetric development of the aorta leads to the special hemodynamic feature in the aorta arch.³¹ The geometry of the system, its roughness, and the difference in it may dominate the control of helical secondary flow.³² Liu et al. suggested that aortic torsion induces helical flow, which eliminates stagnation flow regions.⁶ K. B. Chandran demonstrated that the cross-sectional area of the aorta varies among segments and tapers significantly.² The taper of the aorta can further stabilize the flow of blood, making the helical flow in the ascending aorta proceed far beyond the arch and into the top part of the descending aorta. Without the taper, the helical flow might have been attenuated more rapidly.⁶

The above findings help to explain the increased heterogeneity of the value of the dispersion index in patients who have been diagnosed with helical flow. In a perfectly curved tube, no helical flow pattern appears in the prismatic tube where the dispersion index of the cross-sectional area is zero. Patients without helical flow have a low dispersion index of the cross-sectional area owing to elimination of any variation of the cross-sectional area.²⁷

Characteristics of patients

Diabetes, hypertension, hyperlipidemia, and renal insufficiency markedly increase the risk of developing coronary, cerebrovascular, or peripheral arterial disease. Vascular diseases, particularly atherosclerosis, are major causes of disability and death in patients with the above risk factors.^{33, 34} The helical flow in the aorta has an important physiological impact on circulation because flow may positively affect the transport of low-density lipoprotein (LDL) in the lumen of the aorta, reducing the polarization of LDLs in the aortic arch, protecting them against atherogenesis.⁶

Perfectly prismatic curved aorta

A zero dispersion index of the cross-sectional area corresponds to the absence of a taper, and a small index would support a low initial velocity, resulting from easy energy attenuation.⁶ Furthermore, the perfectly curved aorta had a shorter distance to top of the arch and a lower curvature than did those in the other way around, and the non-helical group exhibited considerably lower flow velocities over the top of the aortic arch, resulting in significant turbulent flow in the branches, including the brachiocephalic, the left common carotid, and the left subclavian artery (Fig. 6).

In summary, a smaller angle between the reference point and the aorta and a higher dispersion of the cross section promoted helical flow. Moreover, patients with angle α exhibited significant, negative associated with the presence of helical flow. Therefore, different characteristic of aortas may help to determine the mechanism of formation of helical flows and give insight into their causes.

LIMITATIONS

Despite the importance of its contributions, this study provides only a first approximation to the simulation of a real aorta blood flow since it neglects many issues, which should be considered. The elastic aortic wall dynamics may cause local effects on hemodynamics, which was not simulated in this study. Nevertheless, the effect of aortic wall dynamics is of secondary order to the distinct aortic anatomy and the variation in the mean aortic size in the entire cardiac cycles is considered as minimal significant.³⁵ Another drawback would be the non-subject specific boundary conditions and viscosity taken from the previous published work^{20, 21} since subject-specific flow conditions would be a more accurate prediction of cardiovascular pathology. However, it would be inadequate to apply different subject-specific flow conditions in the comparison study. Additionally, blood is not a Newtonian fluid as cell deformation results in complex phenomena such as shear thinning and thixotropy, especially at the high Reynolds numbers that are used herein. The flow of blood or any other complex fluid in cavities with various cross-sections and contraction expansion geometries leads to a combination of shear and extensional flows. The pulsatile flow of complex fluid results in such phenomena as flow enhancement.³⁶ A high level of cholesterol in the blood would increase blood viscosity and even cause such phenomena as yield stress. Moreover, whereas some of the results have statistical power, the involvement of only 11 patients is somewhat limiting with respect to the overall objective to establish a correlation between helical flows and potential clinical risk factors. All these will be the future topics of our studies.

CONCLUSION

In this investigation, helical secondary flow in an aortic arch was simulated using a finite element method. The simulated results were compared with clinical data concerning the subjects under analysis. Calculations indicate that most of the helical secondary flow was formed in the ascending aorta. Angle α between the zero reference point and the aortic ostium, the dispersion index of the cross section of the ascending and descending aorta, all correlated closely with the presence of helical flow (P < 0.05). Stepwise multiple linear regression analysis confirmed angel α to be independently associated with the helical flow pattern in therein. The numerical results confirm that helical flow may be an important atherosclerotic factor in vessels, and its strength can be used as a fluid dynamic index for stratifying risk. Numerical simulation of flow patterns in aortas can also effectively elucidate the mechanism of formation of helical flows and give insight into causative factors that underlie them.

NOMENCLATURE

CT

Computed tomography

Da

Average cross-sectional area at various levels in the ascending aorta

Dd

Average cross-sectional area at various levels in the descending aorta

FEA

Finite element analysis

LDL

Low-density lipoprotein

r

Correlation coefficient