Fast Acquisition and Reconstruction of Optical Coherence Tomography Images via Sparse Representation

Abstract

In this paper, we present a novel technique, based on compressive sensing principles, for reconstruction and enhancement of multi-dimensional image data. Our method is a major improvement and generalization of the multi-scale sparsity based tomographic denoising (MSBTD) algorithm we recently introduced for reducing speckle noise. Our new technique exhibits several advantages over MSBTD, including its capability to simultaneously reduce noise and interpolate missing data. Unlike MSBTD, our new method does not require an a priori high-quality image from the target imaging subject and thus offers the potential to shorten clinical imaging sessions. This novel image restoration method, which we termed sparsity based simultaneous denoising and interpolation (SBSDI), utilizes sparse representation dictionaries constructed from previously collected datasets. We tested the SBSDI algorithm on retinal spectral domain optical coherence tomography images captured in the clinic. Experiments showed that the SBSDI algorithm qualitatively and quantitatively outperforms other state-of-the-art methods.

I. Introduction

We introduce a simultaneous image denoising and interpolation method that recovers information that was corrupted due to acquisition limitations of clinical tomographic imaging systems. In particular, we focus on spectral domain optical coherence tomography (SDOCT). SDOCT is a noninvasive, cross-sectional imaging modality that has been widely used for diagnostic medicine, especially in ophthalmology [1], [2]. For clinical analysis, ophthalmologists require high resolution and high signal-to-noise ratio (SNR) SDOCT images. SDOCT acquires a depth profile at a single point of a target, and through a flying-spot scanning technique, laterally samples the target to generate a three dimensional tomographic image of the target. Higher resolution images require more samples of the target, while higher contrast images require a longer dwell time at each lateral spot. Both increase total image acquisition time. A trade-off for an increase in acquisition time is an increase in motion artifacts due to involuntary patient motion [3], [4]. Utilizing a lower spatial sampling rate will reduce total image acquisition time but may result in a sub-Nyquist spatial sampling. In addition, regardless of sampling rate, noise will be inevitably created in the SDOCT image acquisition process [5]–[8]. To accurately reconstruct a high resolution, high SNR image from an original subsampled image requires utilization of efficient interpolation and denoising techniques.

Interpolation and denoising are two of the most widely addressed problems in the field of image processing [9]. The classic techniques are applicable to a variety of images from different sources [10]–[12], and in many cases, providing a specific data model can improve results [13]. One may perform image interpolation and denoising simultaneously [14]–[17]. An alternative computationally efficient yet generally suboptimal approach is to separate the denoising and interpolation processes. This can be achieved by first interpolating, which may be accompanied by deblurring and registration, and then denoising one [18] or multiple frames [19]. An alternative approach reverses the order by denoising the data first followed by interpolation [20]. Many of these algorithms have been previously implemented for SDOCT denoising applications [5]–[8].

To improve denoising and interpolation performance for SDOCT imaging, utilization of modern sparse representation and the closely related compressive sensing techniques have been addressed to some extent in the literature. We divide these techniques into two categories: those algorithms that directly modify the unprocessed, interferometric Fourier domain SDOCT data and those algorithms that utilize processed spatial domain SDOCT data. The methods in the former group [21]–[23], while very promising, cannot currently be adapted by end-users for improving the quality of images from existing commercial clinical systems.

In this paper, we address sparse representation algorithms for spatial domain SDOCT data, as they may be easily adapted by current users of commercial SDOCT imaging systems. Several papers in this category have utilized sparse representation techniques by random sampling of processed SDOCT data [24]–[27]. This is a promising approach for recovery of globally repeated or slow-changing features, such as retinal nerve fiber layer thickness, even if spatially sampled at a rate below the Nyquist limit [28]. We note that unlike random-projection [29] based compressive sensing algorithms [30], random point-wise (nonprojective) sampling in the image space does not provide any additional information about the signal in a global sense. That is, while projective data is guaranteed to have at least a signature of the signal of interest, point-wise sampling data may completely miss a sparse event in the imaging space. As an example, if an SDOCT system implementing random point-wise sampling did not acquire any A-scans at the location of a small retinal drusen [31], it would be impossible to recover any information about that drusen, regardless of the postprocessing approach used. Assuming a random sampling pattern, there is no fundamental lower limit on the size of “nonrepeating” detectable signals to be recovered by these techniques. Thus in some cases, pure random sampling may miss objects larger than the Nyquist limit of a regular pattern scan utilizing an equal number of samples. To reduce this effect, it is suggested to enforce limited maximum spacing between acquired samples [26].

In contrast to the above techniques, we employ sparse representation as a special case of statistical learning methods [32]–[36] and utilize a conventional method of sampling the image space in a regularly spaced pattern. In brief, this method first develops a reference dictionary consisting of the inferred relationships between a set of reference image pairs. Each image pair is comprised of one high-quality and one low-quality image from the same scene. Next, our method utilizes these inferred relationships to predict the missing information within newly acquired low-quality images. Utilizing this idea, we can simultaneously denoise and interpolate one or a set of low-SNR-low-resolution (LL) images (e.g., sparsely sampled SDOCT data) to create one or a set of high-SNR-high-resolution (HH) images (e.g., densely sampled and averaged SDOCT data), if their underlying relationship is obtained from the reference set of image pairs.

To attain an HH image in the reference (learning) dataset, we employed a customized scanning pattern in which a sequence of densely sampled, repeated low-SNR-high-resolution (LH) B-scans from spatially very close positions are captured, registered, and averaged to create an HH image [37], [38]. Accordingly, we subsampled an individual LH B-scan from the above process to construct one LL reference image. Since the noise in these frames can be approximated as random and uncorrelated, we can average these frames to reduce the noise according to basic denoising principle. This is similar to the approach chosen by the clinical practitioners of OCT [39] and is also used in most commercial SDOCT imaging systems, such as Spectralis (Heidelberg Engineering, Heidelberg, Germany) and Bioptigen SDOCT system (Bioptigen Inc., Research Triangle Park, NC, USA).

We utilize the sparse representation principle [32], [33], [38], [40]–[43] to establish the mathematical relationship between the above constructed reference pairs. To achieve this, we propose the sparsity based simultaneous denoising and interpolation (SBSDI) framework. In this framework, we first train a synchronized mathematical basis for a known LL image and a corresponding unknown HH image. We then introduce a computationally efficient mapping scheme to infer the HH image based on the sparse representation of the LL image. Furthermore, to enhance the robustness of the SBSDI framework, we propose a joint 3-D operation to exploit the high correlation and complementary information among the nearby slices of a 3-D SDOCT volume.

The rest of the paper is organized as follows. In Section II, we briefly review the sparse representation model and how to apply it to interpolation. Section III introduces the proposed SBSDI framework for simultaneous denoising and interpolation of SDOCT image. The experimental results for both simulated and real clinical data are presented in Section IV. Section V concludes this paper and suggests future works.

II. Background: Sparse Representation Based Image Interpolation

A. Sparse Representation

The objective of the sparse representation is to approximate an image as a weighted linear combination of a limited number of basic elements called atoms, often chosen from a large dictionary of basis functions [44]. We represent a small rectangular patch of this image as X ∈ ℝ^n×m and its vector form as X ∈ ℝ^q×1; q = n×m, which is attained by lexicographic ordering [45]. We utilize dictionary D ∈ ℝ^q×k that consists of k atoms (columns) ${\{{\mathbf{d}}_j\}}_{j=1}^k$ to represent the patch as x ≈ Dα, satisfying ||x − Dα||₂ ≤ ε, where ε is the error tolerance and ||·||_p stands for the p-norm. If D is a suitable dictionary for compressive representation of this patch, then the coefficient vector α ∈ ℝ^k is sparse:||α||₀ ≪ q, which means only a few scalar coefficients in vector α are nonzero. To attain dictionary D for representing the input patch, popular learning approaches suggest inferring the dictionary from a set of example reference patches ${\{{\mathbf{x}}^i\}}_{i=1}^Z$ [46], [47], where Z is the number of patches. Concretely, the objective function of learning a dictionary can be stated as the following minimization problem:

$$\underset{\mathbf{D},{\{{\mathit{\alpha }}^i\}}_{i=1}^Z}{min}\sum _{i=1}^Z{\Vert {\mathbf{x}}^i-\mathbf{D}{\mathit{\alpha }}^i\Vert }_2^2\text{subject}\text{to}{\Vert {\mathit{\alpha }}^i\Vert }_0\le T$$ (1)

where T is the sparsity level representing the maximum number of nonzero coefficients in αⁱ. A practical optimization strategy is to split the aforementioned problem into sparse coding and dictionary updating parts, which are solved within an iterative loop [46], [47]. The sparse coding first keeps the D fixed and pursues the sparse coefficients ${\{{\mathit{\alpha }}^i\}}_{i=1}^Z$ while the dictionary updating finds the new D with the current updated coefficients ${\{{\mathit{\alpha }}^i\}}_{i=1}^Z$. As described in [46], we update each dictionary atom by utilizing some selected training patches and the positions of the nonzero coefficients in ${\{{\mathit{\alpha }}^i\}}_{i=1}^Z$ correspond to indices of these selected training patches. One popular sparse coding algorithm is the orthogonal matching pursuit (OMP) [48], which pursues the sparse coefficient αⁱ of one patch xⁱ at a time. At each iteration, the OMP algorithm selects the best atom d_g, that exhibits the highest correlation with the residual vector ${\mathbf{R}}_{\mathbf{x}}^i={\mathbf{x}}^i-\mathbf{D}{\mathit{\alpha }}^i$, by searching over the whole dictionary

$${\mathbf{d}}_g=arg\underset{{\mathbf{d}}_j}{max}\mid \langle {\mathbf{R}}_{\mathbf{x}}^i,{\mathbf{d}}_j\rangle \mid ,j=1,\dots ,k$$ (2)

where 〈 ·, · 〉 denotes the inner product. Then, a sub-dictionary D_G is constructed by stacking the selected atoms as columns, thus allowing the sparse coefficient αⁱ to be iteratively updated by projecting the patch xⁱ on D_G

$${\mathit{\alpha }}^i={({\mathbf{D}}_{\mathrm{G}}^T{\mathbf{D}}_{\mathrm{G}})}^{-1}{\mathbf{D}}_{\mathrm{G}}^T\mathbf{x}.$$ (3)

Once the sparse coefficients ${\{{\mathit{\alpha }}^i\}}_{i=1}^Z$ are obtained, we can update the dictionary atoms by the singular value decomposition (SVD) [46] or quadratically constrained quadratic program (QCQP) [49], [50].

B. Sparse Representation Based Image Interpolation

The image interpolation problem can be formulated as follows: denote the original noiseless high resolution (HH) image as Y_H ∈ ℝ^N×M, the decimation operator as S, and the sub-sampled low resolution version of the original image as Y_L = SY_H ∈ ℝ^(N/s)×(M/s). Given an observation image Y_L, the problem is to find Ŷ_H such that Ŷ_H ≈ Y_H. In [32], Yang et al. extended the above sparse model to image interpolation by jointly learning two dictionaries D_L and D_H and for the low resolution feature space χ_L and high resolution feature space χ_H, respectively. This technique assumes that the sparse coefficient of the low resolution image patch x_L ∈ χ_L in terms of D_L should be the same as that of the high resolution image patch x_H ∈ χ_H with respect to D_H. Accordingly, if x_L is observed, the image reconstruction phase can seek its sparse coefficient and recover the latent image patch x_H as well as the corresponding high resolution image Ŷ_H utilizing D_H. To enforce the similarity between the sparse coefficients of these two feature spaces, the Yang et al. dictionary learning stage concatenates the example image patches of the two spaces [32] x̄ = [x_L/x_H] for training the joint dictionary D̄ = [D_L/D_H]. However, such a joint learning scheme can only be allowed to be optimal in the concatenated feature space, instead of each feature space individually. Therefore, as described in detail in [50], the dictionaries D_L and D_H trained in such a joint scheme may not optimally represent x_L and x_H, respectively. In addition, the reconstruction phase places little weight on enforcing the equivalent constraint on the sparse coefficients of x_L and x_H, as had been done in the dictionary training stage [50]. In the very recent work of Yang et al. [50], they introduce a bilevel coupled dictionary learning scheme to ensure that the sparse coefficients of x_L and x_H in terms of the trained coupled dictionaries are closer in both training and reconstruction phase.

III. Proposed Sparsity Based Simultaneous Denoising and Interpolation Framework for Ocular SDOCT Images

In real SDOCT applications, the low resolution unaveraged image is contaminated with significantly high levels of noise as compared to the mentioned methods in the previous section. In this section, we introduce the SBSDI framework, which utilizes the sparse model to simultaneously denoise and interpolate LL SDOCT images.

A. Relating the Captured LL Image to Desired HH Image

Motivated by several previous learning based methods [32]–[36], the objective of the SBSDI framework is to infer the relationship between two feature spaces: LL space χ_L,L and ideal HH space χ_H,H from a large number of reference datasets. Once the relationship is found, we can directly reconstruct the ideal HH image Y_H,H ∈ χ_H,H from the observed LL image Y_L,L ∈ χ_L,L.

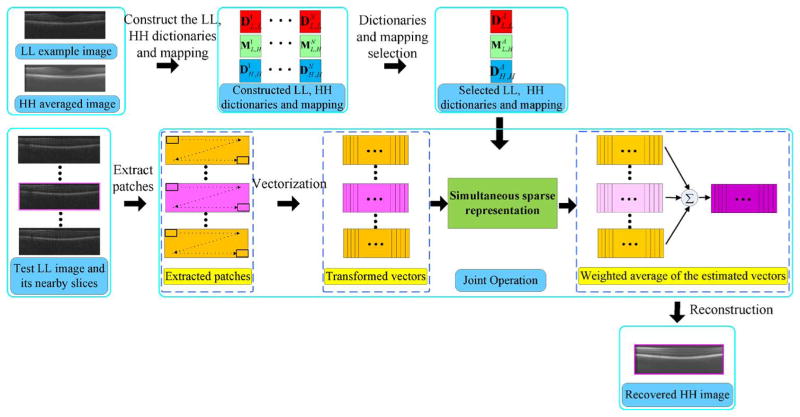
1) Dictionary and Mapping Learning (Training) Phase

To attain ideal HH images required to construct example datasets of χ_H,H space, we employ a customized scanning pattern in which a number of repeated densely sampled B-scans are captured from spatially very close positions. In a postimage capturing step, we register and average all these images, creating an ideal HH image [37], [38]. We consider a single frame from this sequence as the noisy yet equally high-resolution version of the averaged image. We downsample this noisy image to generate the corresponding LL image. The process for creating the HH example image and its LL counterpart is shown in Fig. 1.

Fig. 1.

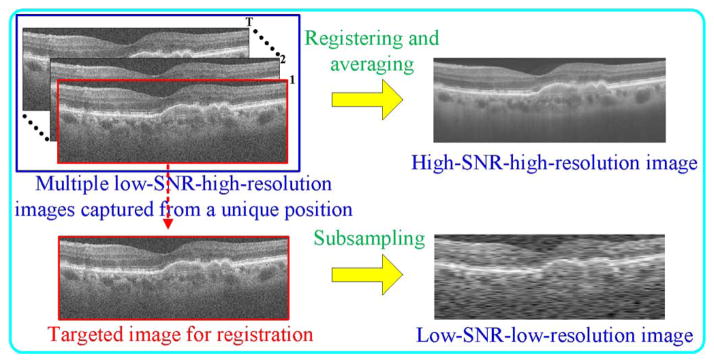
Process schematic for creating an HH SDOCT image and its LL counterpart.

We relate these two feature spaces by establishing a relationship between their corresponding dictionary atoms and sparse coefficients. Rather than enforcing the equality condition on the sparse coefficients [32], [50], we require that the dictionaries (denoted as D_L,L and D_H,H) for the two feature spaces be strictly matched. That is, we only require that the selected dictionary atoms representing the observed LL image correspond to the counterpart atoms for recovering the HH image. To meet this requirement, one simple way is to directly extract a large number of spatially matched LL and HH patches from reference image pairs (Fig. 2). Since the sparse representation is more efficient to process the patch in the vector format [46], we perform lexicographic ordering on both LL and HH patches to transform them as columns for dictionary atoms. However, sparse coding over a large sampled patch database will result in expensive computation. To achieve a more compact representation, we can learn the dictionary pair on a large number of extracted patches [46], [50]. Next, we make the learned dictionary pair matched. As mentioned in the above section, the positions of the nonzero sparse coefficients determine the selected training patches to update the atom [46]. Therefore, if the positions of nonzero coefficients in ${\{{\mathit{\alpha }}_{L,L}^i\}}_{i=1}^Z$ are the same as that in ${\{{\mathit{\alpha }}_{H,H}^i\}}_{i=1}^Z$, the dictionary atoms in D_L,L and D_H,H will be updated with the spatially matched patch pairs and thus D_L,L will still match with D_H,H in the learning process. Based on this idea, we modify the original OMP algorithm [48], and propose the coupled OMP (COMP) algorithm to seek the position matched coefficients ${\{{\mathit{\alpha }}_{H,H}^i\}}_{i=1}^Z$ and ${\{{\mathit{\alpha }}_{L,L}^i\}}_{i=1}^Z$. Since D_H,H is unknown in the image reconstruction phase, during the atom selection process, we require that positions of the selected atoms in D_H,H follow that of the chosen atoms in D_L,L. To achieve this, we first use the original OMP algorithm to pursue the sparse coefficient ${\mathit{\alpha }}_{L,L}^i$ of ${\mathbf{x}}_{L,L}^i$ and preserve the index set of the selected atoms G. Then, we compute ${\mathit{\alpha }}_{H,H}^i$ with the atoms set

Fig. 2.

Selection of patches from the LL and HH images to construct their corresponding dictionaries of basis functions. Since the patch positions in these two images are known, the constructed dictionaries can be strictly matched. In mathematical representation, both LL and HH patches are lexicographically ordered as columns (atoms) of the corresponding dictionary.

$${\mathit{\alpha }}_{H,H}^i={({\mathbf{D}}_{\mathrm{G}}^T{\mathbf{D}}_{\mathrm{G}})}^{-1}{\mathbf{D}}_{\mathrm{G}}^T{\mathbf{x}}_{H,H}^i.$$ (4)

Once ${\{{\mathit{\alpha }}_{L,L}^i\}}_{i=1}^Z$ and ${\{{\mathit{\alpha }}_{H,H}^i\}}_{i=1}^Z$ are obtained, we update the dictionary pair D_L,L and D_H,H utilizing the QCQP [50] algorithm, due to its efficiency. Note that we initialize dictionaries D_L,L and D_H,H from spatially matched training patches.

After the above dictionary training step, the positions of the nonzero coefficients in both ${\mathit{\alpha }}_{L,L}^i$ and the latent ${\mathit{\alpha }}_{H,H}^i$ are identical. However, the nonzero values in ${\mathit{\alpha }}_{L,L}^i$ and ${\mathit{\alpha }}_{H,H}^i$ might be different, as illustrated in Fig. 3. Therefore, we find a mapping function (M) which relates sparse coefficients in the LL space to the sparse coefficients in the HH space

Fig. 3.

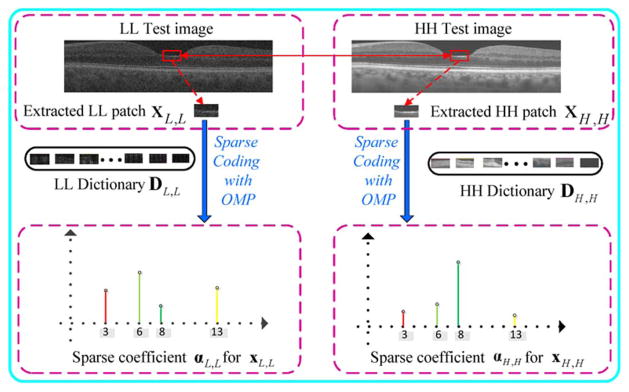
Illustration of the sparse coefficients α_L,L and α_H,H obtained by the decomposition of LL patch x_L,L and HH patch x_H,H over dictionaries D_L,L and D_H,H with OMP algorithm. The positions of the nonzeros coefficients in α_L,L and α_H,H are identical while their values might be different.

$${\mathit{\alpha }}_{H,H}^i=\mathbf{M}{\mathit{\alpha }}_{L,L}^i.$$ (5)

Following [52] and [53], we learn this mapping matrix by using the sparse coefficients ${\{{\mathit{\alpha }}_{H,H}^i\}}_{i=1}^Z$ and ${\{{\mathit{\alpha }}_{L,L}^i\}}_{i=1}^Z$ created in the dictionary learning stage

$$\widehat{\mathbf{M}}=arg\underset{\mathbf{M}}{min}{\Vert {\{{\mathit{\alpha }}_{H\mathrm{\alpha }H}^i\}}_{i=1}^Z-\mathbf{M}{\{{\mathit{\alpha }}_{L,L}^i\}}_{i=1}^Z\Vert }_F^2+\beta {\Vert \mathbf{M}\Vert }_F^2$$ (6)

where β is a regularization parameter to balance the terms in the objective. As (6) is a ridge regression problem [54], it can be derived as

$$\mathbf{M}=\left({\{{\mathit{\alpha }}_{H,H}^i\}}_{i=1}^Z\right){\left({\{{\mathit{\alpha }}_{L,L}^i\}}_{i=1}^Z\right)}^T\times {\left(\left({\{{\mathit{\alpha }}_{L,L}^i\}}_{i=1}^Z\right){\left({\{{\mathit{\alpha }}_{L,L}^i\}}_{i=1}^Z\right)}^T+\beta ·\mathbf{I}\right)}^{-1}$$ (7)

where I is an identity matrix. The dictionary and mapping learning algorithm is summarized in Fig. 4.

Fig. 4.

Dictionary and mapping learning algorithm.

For the specific case of retinal SDOCT images, we advocate giving priority to images captured from the fovea to train the dictionary and mapping function. Compared to the periphery area, the foveal region contains more complex and diverse structures (as shown in Fig. 5). Such diversity in the structure of the foveal image results in a more generalizable dictionary and mapping. However, if computation time is not of concern, images obtained from all macular regions should be included in the learning stage.

Fig. 5.

SDOCT B-scan acquired from the fovea (d) often have more complex structures than those in periphery regions (b), (c), (e), (f). (a) Summed-voxel projection [51] (SVP) en face SDOCT image of a nonneovascular age-related macular degeneration (AMD) patient. (b), (c), (e), (f) B-scans acquired from the green, yellow, blue, and purple lines (periphery regions). (d) B-scan acquired from the red line (fovea region).

2) Image Reconstruction Phase

For image reconstruction, we use the learned dictionary D_L,L to seek the sparse coefficients α_L,L of the observed LL patches (x_L,L) from

$${\widehat{\mathit{\alpha }}}_{L,L}=arg\underset{{\mathit{\alpha }}_{L,L}}{min}{\Vert {\mathbf{x}}_{L,L}-{\mathbf{D}}_{L,L}{\mathit{\alpha }}_{L,L}\Vert }_2+\lambda {\Vert {\mathit{\alpha }}_{L,L}\Vert }_0.$$ (8)

Then, we reconstruct the latent HH patch as D_H,HMα̂_L,L.

B. Structural Clustering

The conventional approach for effective representation of complex structures within the input image involves constructing one comprehensive dictionary with a large number of atoms during the learning phase. However, utilizing a large dictionary comes with a high computation cost during image reconstruction, as sparse solution algorithms (e.g., OMP and the proposed COMP) require to search all dictionary atoms every iteration. In addition, the mapping created by (7) is a linear function, and a single mapping is often not enough to cover variations among different structures within the SDOCT image. Therefore, following the work in [55], we adapt the structural clustering strategy which divides the training patches ${\{{\mathbf{x}}_{L,L}^i\}}_{i=1}^R$ and ${\{{\mathbf{x}}_{H,H}^i\}}_{i=1}^R$ into many structural clusters and learns one compact dictionary and mapping function for each cluster. To cluster the patch ${\mathbf{x}}_{L,L}^i$, we utilize its high-frequency component (denoted as ${\mathbf{x}}_{L,L}^{HF,i}$) as the representative feature. The high-frequency patch ${\mathbf{x}}_{L,L}^{HF,i}$ is extracted from the high-pass filtered image ${\mathbf{Y}}_{L,L}^{HF}$ created by ${\mathbf{Y}}_{L,L}^{HF}={\mathbf{Y}}_{L,L}-{\mathbf{Y}}_{L,L}^{LF}$, where ${\mathbf{Y}}_{L,L}^{LF}$ is the low-pass Gaussian filtered image. By using the standard deviation for the high frequency patch ${\mathbf{x}}_{L,L}^{HF,i}$ [56], we first cluster the extracted patches ${\{{\mathbf{x}}_{L,L}^{HF,i}\}}_{i=1}^R$ into the smooth group G_s and the detailed group G_d via

$$\{\begin{array}{cc}i\in {\mathbf{G}}_s,& \mathit{std}\left({\mathbf{x}}_{L,L}^{HF,i}\right)<\sqrt{{\sigma }^2+b}\\ i\in {\mathbf{G}}_d,& \mathit{std}\left({\mathbf{x}}_{L,L}^{HF,i}\right)\ge \sqrt{{\sigma }^2+b}\end{array}$$ (9)

where σ is the standard deviation of the noise in the LL image, b is a constant, and std(●) represents the standard deviation. Then, we use the k-means approach to divide the detailed patch group into f structural clusters and the smooth patch group into v structural clusters. We should note that since the dataset created by drawing patches from multiple images is very large, the first step of partitioning the patches into smooth and detailed groups increases the accuracy of the following k-means clustering step while reducing the computational cost and memory requirement. Indeed, the k-means approach is very simple and might fall into local minimum. Some other more powerful clustering approaches (such as spectral clustering [57]) might further enhance our performance, but we adopt the k-means approach because it is computationally very efficient and can be applied to large scale datasets utilized in our application. For each cluster, we find the indices of the clustered LL high-frequency patches and use their corresponding LL patches to learn the structural LL sub-dictionary ${\mathbf{D}}_{L,L}^s$, s = 1, …, (f + v). Meanwhile, one centroid atom, c_s, will be obtained to represent this cluster. Accordingly, to match LL and HH dictionaries, the structural HH dictionary ${\mathbf{D}}_{H,H}^s$, s = 1, …, (f + v) is trained from HH patches by selecting appropriate indices in the LL space. Finally, we train one mapping function (M^s) for each cluster using (7). Fig. 6 shows a schematic representation of the construction processes for structural dictionaries and mapping functions. Note that in each structural cluster, the mapping M^s corresponds the related LL and HH dictionaries ${\mathbf{D}}_{L,L}^s$, and ${\mathbf{D}}_{H,H}^s$.

Fig. 6.

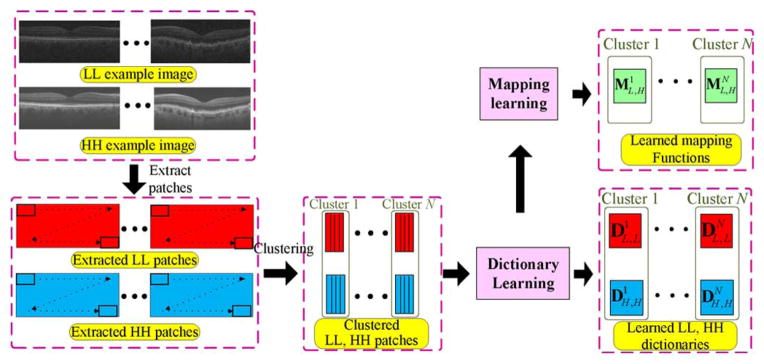
Algorithmic flowchart illustrating learning processes for structural dictionaries and mapping functions.

In the image reconstruction stage, for each test LL patch ${\mathbf{x}}_{L,L}^i$ we find the best sub-dictionaries ( ${\mathbf{D}}_{L,L}^A$ and ${\mathbf{D}}_{H,H}^A$) and mapping transform (M^A) based on the Euclidian distance between ${\mathbf{x}}_{L,L}^i$ and c_s

$$A=s_i=arg\underset{s}{min}{\Vert {\mathbf{c}}_s-{\mathbf{x}}_{L,L}^i\Vert }_2^2.$$ (10)

After the best sub-dictionary is found, the sparse solution algorithm only needs to search through atoms in the selected sub-dictionary instead of the complete dictionary, accelerating the sparse solution process [55]. Then, following (8), we can estimate its sparse coefficient ${\mathit{\alpha }}_{L,L}^i$. The corresponding HH patch is then directly estimated as ${\mathbf{D}}_{H,H}^A{\mathbf{M}}^A{\mathit{\alpha }}_{L,L}^i$.

C. Exploiting the Information in 3-D SDOCT Volume for Image Reconstruction

The methodology explained above can be directly used for reconstructing single 2-D images. In the case of 3-D image data, information from nearby slices may be used to enhance the performance of image denoising [55], [58], [59]. This is particularly important for ophthalmic SDOCT data for which common clinical imaging protocols result in high degrees of correlation among neighboring B-scans. Thus, for the case of tomographic data, we propose to utilize the information of nearby slices in the reconstruction process with a joint operation. To assure a high-level of similarity between neighboring SDOCT slices, we register all B-scans to correct for possible eye motion. Next, we estimate the mean square difference between neighboring patches and remove those patches which do not show high level of correlation.

The cardinal assumption of our joint operation is that similar patches from nearby slices can be efficiently represented by the same atoms of the selected dictionary, but with different coefficient values. We name the current processed patch ${\mathbf{x}}_{L,L}^i$ and the patches from its nearby slices ${\{{\mathbf{x}}_{L,L}^{i+w}\}}_{w=-W}^W$. Simultaneous decomposition of these patches with the above assumption amounts to the problem

$${\left\{{\widehat{\mathit{\alpha }}}_{L,L}^{i+w}\right\}}_{w=-W}^W=\underset{{\left\{{\mathit{\alpha }}_{L,L}^{i+w}\right\}}_{w=-W}^W}{min}\sum _{w=-W}^W{\Vert {\mathbf{x}}_{L,L}^{i+w}-{\mathbf{D}}_{L,L}^A{\mathit{\alpha }}_{L,L}^{i+w}\Vert }_2\text{subject}\text{to}{\Vert {\mathit{\alpha }}_{L,L}^{i+w}\Vert }_0\le T,w=-W,\dots ,W$$ (11)

where T is the maximum number of nonzero coefficients in ${\mathit{\alpha }}_{L,L}^{i+w}$, and the position of the nonzero coefficients in ${\{{\widehat{\mathit{\alpha }}}_{L,L}^{i+w}\}}_{w=-W}^W$ remain the same while coefficient values are varied. A variant of the OMP algorithm called the simultaneous orthogonal matching pursuit (SOMP) [60], [61] can be used to efficiently obtain an approximate solution. Then, the joint operation can predict the current processed HH patch as: ${\widehat{\mathbf{x}}}_{H,H}^i={\sum }_{w=-W}^W{b}_i^w{\widehat{\mathbf{x}}}_{H,H}^{i+w}$, where ${\widehat{\mathbf{x}}}_{H,H}^{i+w}={\mathbf{D}}_{H,H}^A{\mathbf{M}}_i^A{\widehat{\mathit{\alpha }}}_{L,L}^{i+w}$ is the estimated patch and $b_i^w$ is the weight [17] which is computed by

$$b_i^w=\frac{exp\left(-{\Vert {\mathbf{x}}_{L,L}^{i+w}-{\mathbf{x}}_{L,L}^i\Vert }_2^2/h\right)}{\text{Norm}}.$$ (12)

In (12), h is a predetermined scalar and Norm is a normalization factor.

Finally, we reformat the estimated patches to their original rectangular shape and return them to their original geometric position. Since these patches are highly overlapped, we average their overlapping sections to reconstruct the HH image. The outline of the SBSDI framework is illustrated in Fig. 7. Note that, dictionary construction and map learning are offline (one-time calibration) processes without adding to the computation time of the image reconstruction.

Fig. 7.

Outline of the SBSDI framework.

IV. Experimental Methods and Results

We evaluated the proposed SBSDI method on two types of retinal SDOCT images: 1) synthetic images generated from high resolution images that were then subsampled and 2) real experimental images consisting of images acquired at a natively low sample rate. For synthetic datasets we utilized previously acquired high-resolution images, and subsampled them in both random and regular patterns, thus reducing the total number of A-scans in each B-scan. For real experimental datasets we directly acquired low-resolution images using a regularly sampled pattern.

For the synthetic study, we used the dataset from the Age-Related Eye Disease Study 2 (AREDS2) Ancillary SDOCT (A2A SDOCT), which was registered at ClinicalTrials.gov (Identifier: NCT00734487) and approved by the institutional review boards (IRBs) of the four A2A SDOCT clinics (the Devers Eye Institute, Duke Eye Center, Emory Eye Center, and National Eye Institute). We acquired part of the real experimental datasets from volunteers at the Duke Eye Center (Durham, NC, USA). All human subject research was approved by the Duke University Medical Center Institutional Review Board. Prior to imaging, informed consent was received for all subjects after explanation of the possible consequences and nature of the study. All portions of this research followed the tenants of the Declaration of Helsinki. In addition, we captured a dataset in laboratory from a mouse retina.

We first implemented a compressive sampling method [62] utilizing both randomly and regularly subsampled synthetic datasets to examine the random sampling scheme advocated by others [24]–[27]. While a valid approach in general, we found that random sampling had insignificant benefits over a more conventional sampling scheme for our specific application.

Next, using both the regularly sampled synthetic and real experimental datasets, we compared our proposed SBSDI method with several competing approaches: Tikhonov [63], Bicubic, BM3D [64]+Bicubic, and ScSR [32]. The BM3D+Bicubic method is a combination of the state-of-the-art denoising algorithm BM3D with interpolation utilizing a bicubic approach. The ScSR method utilizes the joint dictionary learning operation to train the LL and HH dictionaries from the related LL and HH training patches, but does not consider the 3-D information from nearby slices.

A. Algorithm Parameters

For the specific case of reconstructing retinal SDOCT images, we empirically selected algorithmic parameters which were kept unchanged for all images in both synthetic and real experimental datasets. Since most of the similar structures within SDOCT images lay along the horizontal direction, we chose the patch size to be 4 × 8 and 4 × 16 pixel wide rectangles for 50% and 75% data missing, respectively. As the patch size increases, our algorithm is expected to suppress noise more efficiently but may result in more aggressive smoothing and the loss of image detail. The number of nearby slices for the joint operation was set to 4 (two slices above and two slices below the current processed image, respectively). We did not include slices that are far distant from the target B-scan being processed because often they have different image content. Thus, utilizing them not only might create unexpected artifacts but also will increase the computational cost of the COMP algorithm. In the clustering stage, we chose the cluster number f in the detailed group and v in the smooth group to 70 and 20, respectively. Since the detailed group contains more types of detailed structures than the smooth group, the f number of the detailed group is larger than that of the smooth group. From each cluster, we randomly selected 500 vectors to construct the initial structural sub-dictionary. Utilizing a larger cluster number and a larger sub-dictionary with more vectors might slightly improve performance, but would also increase computational cost. The stopping conditions for both COMP and SOMP algorithms were chosen based on the sparsity level, which was set to T = 3. Increasing the sparsity level for the COMP and SOMP algorithm might preserve more details but would also increase noise in the final image. The iteration number J of the dictionary learning process is set to 10, which almost reaches convergence in our learning problem. That is, further increasing the iteration number hardly provides better results, while still creating additional computational burden. The parameters β in (7), b in (9), and h in (12) were set to 0.001, 12, and 80, respectively. Utilizing a larger h will deliver a smoother appearance, whereas a smaller value of h will create more noise and artifacts. In addition, we found that the performance of our algorithm shows negligible change for nonzero β values ranging from 0.001 to 0.000001 and b values between 12 and 50.

B. Data Sets

For the synthetic datasets, we used low-SNR-high-resolution datasets previously utilized for our work involving sparsity based denoising of SDOCT images [38]. These datasets were acquired from 28 eyes of 28 subjects with and without nonneovascular age-related macular degeneration (AMD) by 840-nm wavelength SDOCT imaging systems from Bioptigen, Inc. (Durham, NC, USA) with an axial resolution of ~ μm per pixel in tissue. For each patient, we acquired two sets of SDOCT scans. The first scan was a square (~ 6.6 × 6.6mm) volume containing the retinal fovea with 1000 A-scans per B-scan and 100 B-scans per volume. The second scan was centered at the fovea with 1000 A-scans per B-scan and 40 azimuthally repeated B-Scans. We selected the central foveal B-scan within the first volume and further subsampled this scan with both random and regular patterns, to create simulated LL test images [e.g., Fig. 8(a) and (c)]. We registered the set of azimuthally repeated B-scans using the StackReg image registration plug-in [65] for ImageJ (software; National Institutes of Health, Bethesda, MD, USA) to construct the HH averaged image [e.g., Fig. 8(l)]. From the 28 datasets, we randomly selected 18 LL and HH pairs from 18 different datasets to test the performance of the proposed method; 10 LL and HH pairs from the remaining datasets were used to train the dictionaries and the mapping functions. From our experiments, we found that further increasing the number of training datasets only slightly enhances the performance of SBSDI, while increasing computation cost in the dictionary and mapping learning stage. The subjects and corresponding dataset pairs used for creation of the dictionaries and mapping functions in the training phase were strictly separate from subjects used in the testing phase and for the comparison of reconstruction techniques. We used the same constructed dictionaries and mapping functions for the real experimental datasets described in the following.

Fig. 8.

Two types of sampling patterns and their reconstruction results by CS-recovery [62], Bicubic, Tikhonov [63], BM3D [64]+Bicubic, ScSR [32], 2-D-SBSDI-nomap, 2-D-SBSDI, and our SBSDI method. (a) Randomly sampled image with 50% data missing. (b) Image (a) reconstructed by CS-recovery [62] (PSNR = 19.46). (c) Regularly sampled image with 50% data missing. (d) Image (c) reconstructed by CS-recovery [62] (PSNR = 19.01). (e) Image (c) reconstructed by Bicubic (PSNR = 17.77). (f) Image (c) reconstructed by Tikhonov [63] (PSNR = 22.23). (g) Image (c) reconstructed by BM3D [64] +Bicubic (PSNR = 23.26). (h) Image (c) reconstructed by ScSR (PSNR = 22.11). (i) Image (c) reconstructed by 2-D-SBSDI-nomap (PSNR = 23.05). (j) Image (c) reconstructed by 2-D-SBSDI (PSNR = 23.96). (k) Image (c) reconstructed by SBSDI (PSNR = 24.56). (l) Registered and averaged image which was acquired 80 times slower than the image in (i)–(k).

For the real experimental datasets, we utilized one of the Bioptigen SDOCT imagers used in the synthetic experiment with ~ 4.5μm axial resolution in tissue and directly acquired full and subsampled volumes from 13 human subjects with a regularly sampled pattern in clinic. That is, for each subject we scanned a square (~ 6.6 × 6.6mm) volume centered at the retinal fovea with 500 A-scans per B-scan and 100 B-scans per volume.

We also performed a mouse imaging experiment in laboratory, utilizing a different ultra high-resolution SDOCT system, (Bioptigen Envisu R2200), which was equipped with a 180 nm Superlum Broadlighter source providing ~2 μm axial resolution in tissue. On the same animal, we covered a square (~ 1.0 × 1.0 mm) volume centered at the optic nerve with 100 B-scans per volume and 1000, 500, and 250 A-scans per B-scan, respectively.

To provide quantitative and qualitative comparisons, for each human and animal subject within the experimental dataset population, we acquired azimuthally repeated B-scans (1000 A-scans/B-scan as described above) from selected positions to create corresponding averaged images [e.g., Fig. 10(h)]. For each human and mouse subject, at regularly spaced positions we captured, registered, and averaged 40 and 16 azimuthally repeated B-scans from spatially very close positions, respectively. We used these averaged images only for validation of the various reconstruction techniques and they were not used in the creation of the SBSDI dictionaries or for the mapping function training.

Fig. 10.

An example real experimental dataset with results reconstructed by Tikhonov [63], Bicubic, BM3D [64]+Bicubic, 2-D-SBSDI-nomap, 2-D-SBSDI, and SBSDI method. The left and right columns show images from the fovea and 1.5 mm below the fovea area, respectively. (a) Original images (b) bicubic reconstruction (Left: PSNR = 18.51, Right: PSNR = 17.84). (c) Tikhonov [63] reconstruction (Left: PSNR = 23.07, Right: PSNR = 21.99). (d) BM3D [64]+Bicubic reconstruction (Left: PSNR = 26.33, Right: PSNR = 23.24). (e) 2-D-SBSDI-nomap reconstruction (Left: PSNR = 25.06, Right: PSNR = 22.46). (f) 2-D-SBSDI reconstruction (Left: PSNR = 26.20, Right: PSNR = 23.10). (g) SBSDI reconstruction (Left: PSNR = 26.77, Right: PSNR = 23.52). (h) Registered and averaged images which were acquired 80 times slower than the image in (g).

C. Quantitative Metrics

We adapted the mean-to-standard-deviation ratio (MSR) [66], contrast-to-noise ratio (CNR) [67], and peak signal-to-noise-ratio (PSNR) as the objective metrics to evaluate the quality of reconstructed results. The MSR and CNR are defined as follows:

$$\text{MSR}=\frac{{\mu }_f}{{\sigma }_f},$$ (13)

$$\text{CNR}=\frac{\mid {\mu }_f-{\mu }_b\mid }{\sqrt{0.5\left({\sigma }_f^2+{\sigma }_b^2\right)}}$$ (14)

where μ_b and σ_b are the mean and the standard deviation of the background region (e.g., red box #1 in Fig. 8), while μ_f and σ_f are the mean and the standard deviation of the foreground regions (e.g., red box #2–6 in Fig. 8).

The PSNR is a global quality criteria, which is computed as

$$\text{PSNR}=20·{log}_{10}{\left(\frac{{\text{Max}}_{\mathbf{R}}}{\sqrt{\frac{1}{H}{\displaystyle \sum _{h=1}^H}{({\mathbf{R}}_h-{\widehat{\mathbf{R}}}_h)}^2}}\right)}^{}$$ (15)

where R_h is the intensity of the hth pixel in the reference HH image R, R̂_h represents the same hth pixel of the recovered image R̂, H is the total number of pixels, and Max_R is the maximum intensity value of R. For the experimental datasets, we used the registered and averaged images generated from the azimuthally repeated scans as HH approximations to the corresponding B-scans from the LL volumetric scan. We identi-fied the LL B-scan corresponding to an averaged scan by visual comparison. For optimal comparisons, the averaged and reconstructed images were registered to one another using the StackReg plug-in for ImageJ [65]. This registration step is necessary for reducing the motion between the reconstructed and average images since the LL test image and LH images (used to create the HH averaged image) are acquired at different points in time.

We applied the Wilcoxon signed-rank test between our SBSDI method’s CNR, MSR, and PSNR distribution and all other compared methods [68]. Methods for which the difference was statistically significant (p < 0.05) are marked with an * in each table.

D. Synthetic Experiments on Human Retinal SDOCT Images

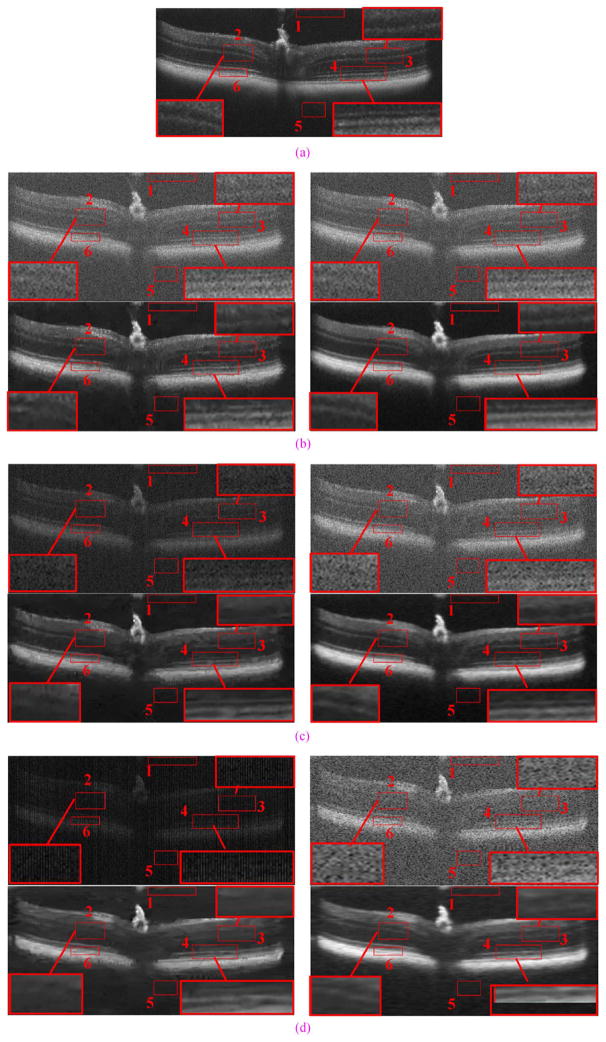
Fig. 8(a)–(d) and Fig. 9(a)–(d) show qualitative comparisons of regularly and randomly sampled foveal images (with 50% and 75% of the original data discarded) and their reconstructed versions obtained from the CS-recovery method [62] utilizing the shift invariant wavelets [69]¹ (a refined variation of this technique was later used in [24]). We observe that the CS-recovery results from the random sampling scheme [Fig. 8(b) and Fig. 9(b)] have more areas exhibiting striped blurring (e.g., blue ellipse areas) than their regularly sampled counterparts [Fig. 8(d) and Fig. 9(d)]. Considering this, we tested the Tikhonov [63], Bicubic, BM3D [64]+Bicubic and the proposed SBSDI method on regularly sampled images [Fig. 8(c)]. In addition, we incorporated two simplified versions of our method (called 2-D-SBSDI-nomap and 2-D-SBSDI) that do not exploit the information of neighboring frames. The 2-D-SBSDI uses the mapping function for the reconstruction whereas the mapping function is not employed in the 2-D-SBSDI-nomap. 2-D-SBSDI-nomap keeps the sparse coefficients of the LL space the same as the coefficients of the HH space. For better visual comparison, three boundary areas (boxes #2, 3, 4) in these images were marked with red rectangles and magnified. Results from the Tikhonov, Bicubic, ScSR, and 2-D-SBSDI-nomap methods appeared noisy with indistinct boundaries for many meaningful anatomical structures. Although the BM3D [64]+Bicubic technique provides improved noise suppression, it introduces splotchy/blocky (cartoonish) artifacts, which obscure some important structural details. The 2-D-SBSDI provides comparatively better structural details but does not efficiently remove noise. In contrast, application of our SBSDI method that considers the 3-D information resulted in noticeably improved noise suppression while preserving details in comparison to other methods. Especially in the regions marked by red boxes #3, 4, the SBSDI result even shows clearer layers compared with the densely sampled averaged image [Fig. 8(l) and Fig. 9(l)].

Fig. 9.

Two types of sampling patterns and their reconstruction results by CS-recovery [62], Bicubic, Tikhonov [63], BM3D [64]+Bicubic, ScSR [32], 2-D-SBSDI-nomap, 2-D-SBSDI, and our SBSDI method. (a) Randomly sampled image with 75% data missing. (b) Image (a) reconstructed by CS-recovery [62] (PSNR = 20.83). (c) Regularly sampled image with 75% data missing. (d) Image (c) reconstructed by CS-recovery [62] (PSNR = 20.67). (e) Image (c) reconstructed by Bicubic (PSNR = 17.75). (f) Image (c) reconstructed by Tikhonov [63] (PSNR = 22.68). (g) Image (c) reconstructed by BM3D [64] +Bicubic (PSNR = 23.28). (h) Image (c) reconstructed by ScSR (PSNR = 23.09). (i) Image (c) reconstructed by 2-D-SBSDI-nomap (PSNR = 23.68). (j) Image (c) reconstructed by 2-D-SBSDI (PSNR = 23.99). (k) Image (c) reconstructed by SBSDI (PSNR = 24.58). (l) Registered and averaged image which was acquired 160 times slower than the image in (i)–(k).

To quantitatively compare reconstruction methods, we measured six regions of interest (similar to the red boxes #1–6 in Figs. 8 and 9) from 18 test images of different subjects. For each image, we averaged the MSR and CNR values for five foreground regions (e.g., #2–6 in Figs. 8 and 9). Note that, for the boxes #2–4, we selected the boundary areas, since boundaries between retinal layers contain meaningful anatomic and pathologic information [70]. Regions #5–6 are selected to evaluate denoising capabilities of these algorithms in homogeneous areas. The mean and standard deviation of these averaged MSR and CNR results across all the test images are tabulated in Tables I and III (corresponding to the conditions when 50% and 75% data are missing, respectively). In addition, we compared the PSNR of these methods for the whole image. We report the mean and standard deviation of the PSNR results in Tables II and IV (corresponding to the conditions when 50% and 75% data are missing, respectively).

TABLE I.

Mean and Standard Deviation of the MSR and CNR for 18 SDOCT Foveal Images (With 50% Data Missing) Reconstructed by CS-Recovery [62] With Random Sampling Pattern, CS-Recovery [62] With Regular Sampling Pattern, Bicubic, Tikhonov [63], BM3D [64]+Bicubic, ScSR [32], 2-D-SBSDI-Nomap, 2-D-SBSDI, and SBSDI Methods With Regular Sampling Pattern.

	CS-recovery [62]- Random*	CS-recovery [62] - Regular *	Bicubic -Regular*	Tikhonov [63]-Regular*	BM3D [64] +Bicubic - Regular*	ScSR [32]-Regular*	2-D-SBSDI-nomap Regular*	2-D-SBSDI-Regular*	SBSDI - Regular
Mean (CNR)	1.96	1.91	1.66	3.14	4.19	3.03	3.67	5.15	5.80
Standard deviation (CNR)	0.62	0.63	0.56	1.13	1.12	1.05	1.15	1.37	1.54
P value (CNR)	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
Mean (MSR)	4.46	4.19	3.57	6.02	9.41	7.00	8.30	12.74	13.74
Standard deviation (MSR)	0.51	0.51	0.45	0.91	2.35	0.89	0.85	3.19	3.52
P value (MSR)	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.001

^*CNR and MSR: p < 0.05.

Best Results in the Mean Values are Labeled in Bold

TABLE III.

Mean and Standard Deviation of the MSR and CNR for 18 SDOCT Foveal Images (With 75% Data Missing) Reconstructed by CS-Recovery [62] With Random Sampling Pattern, CS-Recovery [62] With Regular Sampling Pattern, Bicubic, Tikhonov [63], BM3D [64]+Bicubic, ScSR [32], 2-D-SBSDI-Nomap, 2-D-SBSDI, and SBSDI Methods With Regular Sampling Pattern.

	CS-recovery [62] -Random*	CS-recovery [62] - Regular*	Bicubic -Regular*	Tikhonov [63]-Regular*	BM3D [64] +Bicubic - Regular*	ScSR [32]-Regular*	2-D-SBSDI-nomap Regular*	2-D-SBSDI-Regular*	SBSDI -Regular
Mean (CNR)	2.31	2.30	1.68	2.53	4.62	3.82	4.39	5.19	5.89
Standard deviation (CNR)	0.79	0.81	0.57	0.81	1.27	1.27	1.33	1.32	1.43
P value (CNR)	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002
Mean (MSR)	5.26	5.25	3.63	5.35	10.72	9.00	10.33	13.20	14.53
Standard deviation (MSR)	0.61	0.62	0.46	0.53	2.61	1.03	1.25	3.15	4.56
P value (MSR)	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0013

^*CNR and MSR: p < 0.05.

Best Results in the Mean Values are Labeled in Bold

TABLE II.

Mean and Standard Deviation of the PSNR (dB) for 18 SDOCT Foveal Images (With 50% Data Missing) Reconstructed by CS-Recovery [62] With Random Sampling Pattern, CS-Recovery [62] With Regular Sampling Pattern, Bicubic, Tikhonov [63], BM3D [64]+Bicubic, ScSR [32], 2-D-SBSDI-Nomap, 2-D-SBSDI, and SBSDI Methods With Regular Sampling Pattern.

	CS-recovery [62] - Random*	CS-recovery [62] - Regular*	Bicubic -Regular*	Tikhonov [63] -Regular*	BM3D [64] +Bicubic -Regular*	ScSR [32]-Regular*	2-D-SBSDI-nomap Regular*	2-D-SBSDI-Regular*	SBSDI -Regular
Mean	20.36	19.86	18.68	23.30	27.12	24.26	25.94	27.63	28.32
Standard deviation	0.65	0.58	0.98	1.76	2.49	1.32	1.80	2.34	2.57
P value (PSNR)	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0003

^*PSNR: p < 0.05.

Best Results in the Mean Values are Labeled in Bold

TABLE IV.

Mean and Standard Deviation of the PSNR (dB) for 18 SDOCT Foveal Images (With 75% Data Missing) Reconstructed by CS-Recovery [62] With Random Sampling Pattern, CS-Recovery [62] With Regular Sampling Pattern, Bicubic, Tikhonov [63], BM3D [64]+Bicubic, SCSR [32], 2-D-SBSDI-Nomap, 2-D-SBSDI, and SBSDI Methods With Regular Sampling Pattern.

	CS-recovery [62] - Random*	CS-recovery [62] - Regular*	Bicubic -Regular*	Tikhonov [63] - Regular*	BM3D [64] +Bicubic - Regular*	ScSR [32]-Regular*	2-D-SBSDI-nomap Regular*	2-D-SBSDI-Regular*	SBSDI -Regular
Mean	21.78	21.65	18.52	22.52	27.26	25.76	26.95	27.64	28.30
Standard deviation	0.77	0.75	0.49	0.95	2.50	1.63	2.04	2.31	2.54
P value (PSNR)	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0002	0.0003

^*PSNR: p < 0.05.

Best Results in the Mean Values are Labeled in Bold

Also, we report the average running time of the proposed SBSDI algorithm and the compared approaches to reconstruct one image with 50% and 75% data missing on Tables V and VI. All the programs are executed on a laptop computer with an Intel Core i7-3720 CPU 2.60 GHz and 8 GB of RAM. Note that our SBSDI algorithm is coded in MATLAB (except OMP and SOMP codes²), which is not optimized for speed.

TABLE V.

Average Run Time (Seconds) for Reconstructing the Foveal Image With 50% Data Missing by CS-Recovery [62] With Random Sampling Pattern, CS-Recovery [62] With Regular Sampling Pattern, Bicubic, Tikhonov [63], BM3D [64]+Bicubic, SCSR [32], 2-D-SBSDI-Nomap, 2-D-SBSDI, and SBSDI Methods With Regular Sampling Pattern

	CS-recovery [62]-Random*	CS-recovery [62] - Regular*	Bicubic -Regular*	Tikhonov [63]- Regular*	BM3D [64] +Bicubic -Regular*	ScSR [32]- Regular*	2-D-SBSDI-nomap Regular*	2-D-SBSDI- Regular*	SBSDI -Regular
Runtime (seconds)	39.489	40.021	0.005	3.074	2.580	5.302	5.315	5.610	12.462

TABLE VI.

Average Run Time (Seconds) for Reconstructing the Foveal Image With 75% Data Missing by CS-Recovery [62] With Random Sampling Pattern, CS-Recovery [62] With Regular Sampling Pattern, Bicubic, Tikhonov [63], BM3D [64]+Bicubic, SCSR [32], 2-D-SBSDI-Nomap, 2-D-SBSDI, and SBSDI Methods With Regular Sampling Pattern

	CS-recovery [62]-Random*	CS-recovery [62] - Regular*	Bicubic -Regular*	Tikhonov [63]-Regular*	BM3D [64] +Bicubic - Regular*	ScSR [32]- Regular*	2-D-SBSDI-nomap Regular*	2-D-SBSDI-Regular*	SBSDI -Regular
Runtime (seconds)	59.363	60.582	0.025	1.423	0.882	2.757	2.755	2.867	5.931

E. Real Experiments on Human Retinal SDOCT Images

For reconstruction comparisons involving real experimental datasets of human subjects, from each dataset we used the central foveal B-scan as well as two additional B-scans located approximately 1.5 mm above and below the fovea. Therefore, we used 3 × 13 = 39 images for this experiment. We included this additional comparison to test the robustness of SBSDI in nonfoveal retinal regions, given dictionaries and mapping function training based on foveal images of the 10 subjects in the training set. We report the quantitative results (MSR, CNR, and PSNR) for the Tikhonov [63], Bicubic, BM3D [64]+Bicubic, 2-D-SBSDI-nomap, 2-D-SBSDI, and SBSDI methods in Tables VII and VIII. We selected six regions within each image (similar to red boxes #1–6 in Fig. 10) to compute the MSR and CNR. Fig. 10 provides a qualitative comparison of the proposed SBSDI method with Tikhonov [63], Bicubic, BM3D [64]+Bicubic, 2-D-SBSDI-nomap, and 2-D-SBSDI approaches on these real experimental datasets. Subjectively, the visual quality of the SBSDI method appeared superiorly to reconstructions from the Tikhonov [63], Bicubic, BM3D [64]+Bicubic, 2-D-SBSDI-nomap, and 2-D-SBSDI approaches. Note that some meaningful information (e.g., low contrast layers highlighted in regions 2, 3, and 4) are distorted or missing in the Tikhonov [63], Bicubic, BM3D [64]+Bicubic, 2-D-SBSDI-nomap, and 2-D-SBSDI results while appearing well preserved in reconstructions utilizing the SBSDI method. In a 3-D volume, the proposed SBSDI method exploits information from nearby slices to reconstruct a target image slice. This additional information may aid in the reconstruction of low contrast details within an image.

TABLE VII.

Mean and Standard Deviation of the MSR and CNR for 39 Experimental SDOCT Images From 13 Subjects (Including Foveal Images and Nonfoveal Images) Reconstructed by Bicubic, Tikhonov [63], BM3D [64]+Bicubic, 2-D-SBSDI-Nomap, 2-D-SBSDI, and SBSDI Methods.

	Bicubic*	Tikhonov [63]*	BM3D [64] +Bicubic*	2-D-SBSDI-nomap Regular*	2-D-SBSDI-Regular*	SBSDI
Mean (CNR)	1.62	3.07	4.07	3.59	4.93	5.32
Standard deviation (CNR)	0.40	0.79	1.04	1.13	1.39	1.50
P value (CNR)	0.00000005	0.00000005	0.00000005	0.00000005	0.0000001
Mean (MSR)	3.52	5.82	9.34	8.02	12.15	12.72
Standard deviation (MSR)	0.33	0.58	1.62	1.08	2.50	3.00
P value (MSR)	0.00000005	0.00000005	0.00000005	0.00000005	0.0004

^*CNR and MSR: p < 0.05.

Best Results in the Mean Values are Labeled in Bold

TABLE VIII.

Mean and Standard Deviation of the PSNR (dB) for 39 Experimental SDOCT Images From 13 Subjects (Including Foveal Images and Nonfoveal Images) Reconstructed by Bicubic, Tikhonov [63], BM3D [64]+Bicubic, 2-D-SBSDI-Nomap, 2-D-SBSDI, and SBSDI Methods.

	Bicubic*	Tikhonov [63]*	BM3D [64] +Bicubic*	2-D-SBSDI-nomap Regular*	2-D-SBSDI- Regular*	SBSDI
Mean	18.04	22.10	24.50	23.68	24.61	25.37
Standard deviation	0.56	1.35	1.95	1.64	1.94	2.23
P value (PSNR)	0.00000005	0.00000005	0.00000005	0.00000005	0.0000001

^*PSNR: p < 0.05.

Best Results in the Mean Values are Labeled in Bold

F. Real Experiments on Mice Retinal SDOCT Images Utilizing a Suboptimal Training Set

In this experiment, to enhance images captured from the optic nerve of a mouse, we used the same training set we previously used for human experiments. Furthermore, we utilized an SDOCT system with a different axial resolution than the training set. Thus, the training dataset is suboptimal for this experiment. While we strongly advocate utilizing training sets which are structurally close to the test set, this example tests the robustness of proposed algorithms for enhancing datasets which are not optimally represented in the training set. Fig. 11 shows qualitative and quantitative comparisons of densely sampled averaged image and results reconstructed by Bicubic, BM3D [64] +Bicubic, and SBSDI on real mouse images with three sampling conditions (without subsampling, with 50% data missing and with 75% data missing). As can be observed, though the training samples used in the dictionary and mapping learning stage are from human foveal, separate from the mouse images, SBSDI results are very competitive as compared to the Bicubic and BM3D+Bicubic methods. We note that despite our best efforts, due to the animal’s slight movements, the images captured for each of these sampling rates are slightly displaced as compared to the averaged image. However, such slight differences can be ignored and are expected in any such realistic imaging situation.

Fig. 11.

A real experimental dataset from a mouse optic nerve with results reconstructed by Bicubic, BM3D [64]+Bicubic, and SBSDI methods. We intentionally selected a suboptimal training set for the SBSDI method based on human images captured on a different SDOCT system to evaluate robustness of the SBSDI algorithm with respect to training sets. (a) Average image. (b) Top Left: Test image (with no subsampling). Top Right: Bicubic reconstruction, PSNR = 28.63, CNR = 0.85, MSR = 3.12. Bottom Left: BM3D+Bicubic reconstruction, PSNR = 31.89, CNR = 2.26, MSR = 11.15. Bottom Right: SBSDI reconstruction, PSNR = 32.69, CNR = 2.64, MSR = 13.69. (c) Top Left: Test image (with 50% data missing). Top Right: Bicubic reconstruction, PSNR = 28.43, CNR = 0.77, MSR = 3.31. Bottom Left: BM3D+Bicubic reconstruction, PSNR = 31.27, CNR = 2.03, MSR = 11.36. Bottom Right: SBSDI reconstruction, PSNR = 32.48, CNR = 2.33, MSR = 13.72. (d) Top Left: Test image (with 75% data missing). Top Right: Bicubic reconstruction, PSNR = 29.18, CNR = 0.69, MSR = 3.30. Bottom Left: BM3D+Bicubic reconstruction, PSNR = 33.26, CNR = 2.06, MSR = 19.50. Bottom Right: SBSDI reconstruction, PSNR = 32.93, CNR = 2.47, MSR = 20.96.

V. Conclusion and Future Works

In this paper, we proposed an efficient sparsity based image reconstruction framework called SBSDI that is directly applicable to clinical SDOCT images. Unlike our previous technique [38], SBSDI performs simultaneous interpolation and denoising and does not require capturing images of differing quality from the target subject. We demonstrated that the SBSDI method outperforms other current state-of-the-art denoising-interpolation methods.

Since our SBSDI algorithm reduces the time needed to obtain high quality reconstructed results, it could have a wide range of applications, such as reducing patient discomfort during retinal imaging, applying it to lower cost OCT machines that have slower acquisition speeds, postprocessing already acquired OCT images with low SNR and low resolution, and as a preprocessing step for automatic image analysis (e.g., segmentation). In addition, a promising area of potential future research is to greatly accelerate the SBSDI algorithm by more efficient coding coupled with utilizing a general purpose Graphics Processing Unit (GPU) [26], so that it can be incorporated into daily clinical practice.

To our knowledge, this is the first sparsity based interpolation algorithm that demonstrates superior performance on clinical ophthalmic SDOCT data over other state-of-the-art nonsparse representation techniques. We showed that for our specific experiment, this algorithm may improve the imaging speed of the SDOCT system by a factor of 80 over standard registration and averaging without a significant reduction in image quality.

Since the code for the CS-recovery method of [24] is not publicly available, our implementation for Figs. 8 and 9 may differ in details with the algorithm in [24]. Also, to better illustrate the differences between the regular and sparse sampling strategies, we focused on the 2-D implementation of the method in [24]. Indeed, regardless of the sampling strategy, we expect that a 3-D implementation of [24] will result in better reconstructions.

Following our previous work in this field, we have made the data set and the software developed for this project publically available at http://www.duke.edu/~sf59/Fang_TMI_2013.htm. We are the first group in the SDOCT sparse imaging and image processing field that has made their paper’s code and dataset freely available online. We hope that this paper will encourage other colleagues to share their code and data online as well.

In this paper, we demonstrated the applicability of our algorithm for simultaneously denoising and interpolating images from normal and nonneovascular AMD subjects. In our future publications, we will demonstrate the applicability of our method for analyzing SDOCT images of other ocular diseases such as cystoid macular edema retinas. In addition, we selected the parameters empirically in the experimental section, and kept them fixed for all images. Note that, the optimal choices for such parameters might be different for varied applications. Therefore, another future work will establish a more systematic way of selecting these parameters for different conditions. Moreover, while our interpolation method was more successful than the popular methodologies that it has been compared with, careful evaluation of experimental results shows that all these techniques are more successful as a denoising mechanism rather than as an interpolator. For example, in an optimal imaging scenario, we would expect to be more successful in creating high-quality images from 10 images with 1000 A-scans as compared to an imaging scenario in which 40 images, each with 250 A-scans, are captured. Of course, in real-world clinical applications, we do not always have the luxury of designing our image acquisition protocol.