Subtype diversity and reassortment potential for co-circulating avian influenza viruses at a diversity hot spot

SUMMARY

1. Biological diversity has long been used to measure ecological health. While evidence exists from many ecosystems that declines in host biodiversity may lead to greater risk of disease emergence, the role of pathogen diversity in the emergence process remains poorly understood. Particularly, since a more diverse pool of pathogen types provides more ways in which evolutionary innovations may arise, we suggest that host-pathogen systems with high pathogen diversity are more prone to disease emergence than systems with relatively homogeneous pathogen communities. We call this prediction the diversity-emergence hypothesis.

2. To show how this hypothesis could be tested, we studied a system comprised of North American shorebirds and their associated low-pathogenicity avian influenza (LPAI) viruses. These viruses are important as a potential source of genetic innovations in influenza. A theoretical contribution of this paper is an expression predicting the rate of viral subtype reassortment to be proportional to both prevalence and Simpson’s Index, a formula that has been used traditionally to quantify biodiversity. We then estimated prevalence and subtype diversity in host species at Delaware Bay, a North American AIV hotspot, and used our model to extrapolate from these data.

3. We estimated that 4 to 39 virus subtypes circulated at Delaware Bay each year between 2000 and 2008, and that surveillance coverage (percent of co-circulating subtypes collected) at Delaware Bay is only about 63.0%. Simpson’s index in the same period varied more than fourfold from 0.22 to 0.93. These measurements together with the model provide an indirect, model-based estimate of the reassortment rate. A proper test of the diversity-emergence hypothesis would require these results to be joined to independent and reliable estimates of reassortment, perhaps obtained through molecular surveillance.

4. These results suggest both that subtype diversity (and therefore reassortment) varies from year to year and that several subtypes contributing to reassortment are going undetected. The similarity between these results and more detailed studies of one host, Ruddy Turnstone (Arenaria interpres), further suggest that this species may be the primary host for influenza reassortment at Delaware Bay.

5. Biological diversity has long been quantified using Simpson’s Index. Our model links this formula to a mechanistic account of reassortment in multi-pathogen systems in the form of subtype diversity at Delaware Bay, USA. As a theory of how pathogen diversity may influence the evolution of novel pathogens, this work is a contribution to the larger project of understanding the connections between biodiversity and disease.

INTRODUCTION

The role of biological diversity in the emergence and transmission of infectious diseases is poorly understood (Keesing et al. 2010). Some effects of biological diversity at the level of host species include demographic interference (Rohani et al. 1998; Rohani et al. 2003), reciprocal manipulation of the host immune system (Corbett et al. 2002), and the dilution effect whereby incompetent hosts diminish the collective transmission of a pathogen within a mixed community of host species (Schmidt & Ostfeld 2001; Keesing, Holt, & Ostfeld 2006). Within host species, genetic diversity plays a role both in the effectiveness of host (Hornef et al. 2002) and vector (Rottshaefer et al. 2011) immune defenses and in the evolution of pathogens with respect to pathogenicity (Baba et al. 2008), transmissibility (Badrane & Tordo 2001), or immune escape (Alcami & Koszinowski 2000). In contrast, while parasite diversity has recently been shown to play a role in emergence and transmission of infectious diseases through coinfection and cross-reactive immunity (Johnson & Hoverman 2012), the role of pathogen diversity in infectious disease emergence and transmission at the level of genetic variability remains poorly understood in natural systems.

Avian influenza virus (AIV) is a model for understanding the role of genetic variability in pathogen evolution. The influenza A virus is composed of 8 gene segments: hemagglutinin (HA), neuraminidase (NA), nucleoprotein (NP), matrix proteins (M), non-structural proteins (NS), and RNA polymerases (PA, PB1, and PB2; Hutchinson et al. 2010), but it is HA and NA, which are found in the surface envelope of the influenza virion, that are particularly important as viral antigens responsible for host cell infiltration and escape (Wagner, Matrosovich, & Klenk 2002). Because these proteins routinely interact with host cell receptors, the HA and NA genes play key roles in influenza evolution (Kilbourne, Johanssen, & Grajower 1990). A total of 17 HA subtypes and ten NA subtypes have been identified based on binding affinity for a total of 170 possible combinations (Dugan et al. 2008; Tong et al. 2012). This gene pool forms the basis for any future pandemic or domestic animal strains (Taubenberger & Kash 2010).

While one HA type and one NA type are currently confined to bats (HA17 and N10; Tong et al. 2012), the main reservoir of the remaining gene pool is a large complex of low pathogenicity avian influenza (LPAI) viruses that are naturally widespread and continuously circulating in wild waterfowl, gulls, and shorebirds. Because HA/NA subtypes differentially infect various vertebrate host species (e.g., birds, swine, horses, humans) with some overlapping host ranges, various scenarios for the emergence of a pandemic strain can be constructed from the possible sequences of infection and coinfection that might allow a stable HA subtype to reassort with viruses containing genes that confer a propensity to infect and replicate within humans. Understanding the ecological conditions under which reassortment occurs is therefore crucial to understanding the circumstances under which emergence of a pandemic strain is most likely. Reassortment within low pathogenicity avian influenza viruses provides an ideal model for such a study. To date, 103 of the 144 possible subtype combinations have been detected in North America (Table S1), and are maintained in waterfowl, gulls, and shorebirds with little or no morbidity or mortality. While extensive research exists on LPAI, much of it is in direct relation to the ecology or immunology of individual subtypes (e.g. Capua et al. 2004; Swayne & Slemons 2008; Woolcock, Suarez, & Kuney 2003). The purpose of our study was to investigate the role that subtype diversity plays in reassortment. We first developed a model to relate subtype diversity and prevalence to the rate at which coinfections accumulate in a population of hosts. We then estimated subtype diversity and prevalence at Delaware Bay, a North American “hotspot” for avian influenza transmission (Krauss et al. 2010). These results provide the first theoretical basis for understanding how the community ecology of virus antigenic subtypes relates to pathogen evolution and an application of this theory to understanding evolutionary potential at a key site.

MODEL

In this section we derive a model for the rate at which reassorted subtypes accumulate in a population, which is specified up to a coefficient of proportionality concerning the probability that the two different subtypes in a mixed infection result in one or more reassorted combinations. This is a “strategic” model in the sense that it aims to develop a set of concepts under the most idealized circumstances, neglecting such details as seasonal breeding, migration, social aggregation, and the age or immunological structure of the host population. As such, it is appropriate only as an approximation over a relatively short period of time (i.e. less than one breeding season). We believe that its value is its generality, and that the key conclusions (role of prevalence and diversity in reassortment) are robust in the sense that similar conclusions must apply to a very wide range of more detailed models.

We begin by considering coinfection in a system of co-circulating pathogens, where coinfection is the simultaneous infection of a single host by two different pathogens. We assume that coinfection of a single host cell by two different pathogens is proportional to the probability of host coinfection. We break the problem into two pieces: the rate at which coinfection occurs and the probability that a coinfection will be of two different subtypes (i.e. a second infection can consist of a completely different HA+NA combination, a virus different only with respect to HA type, or a virus different only with respect to NA type). That is, the rate at which reassorted subtypes occur is assumed to be proportional to the product of: (i) infection rate, (ii) the probability that an infection becomes a coinfection, and (iii) the probability that the coinfecting virus is of a different antigenic type (all assumed to be independent via mixing in the environment).

Coinfection rate

In what follows, we make minimally restrictive assumptions. For instance, we make no assumption about whether infectious are immunizing (SI vs. SIR dynamics) and neglect age-dependent susceptibility to infection. In general, then, the rate of coinfection is the rate at which infected individuals at time t, I(t), become doubly infected. First, we assume that each encounter of an infectious dose of virus by a single host is an independent event. The infection rate is therefore a Poisson process with rate λ(t) where λ(t) is the conventionally defined force-of-infection (Anderson & May 1991). Also, for a given infection, we assume that the infectious period (empirically, the shedding period) is distributed according to the probability density function g(x). Then, the probability that a second infection is acquired before the first is cleared is given by

$$P(\mathit{coinfection})={\displaystyle \underset{0}{\overset{\infty }{\int }}F\left(x\right)g\left(x\right)dx,}$$

where F(x) is the cumulative distribution function of the inter-event times of the infection process. If we make the quasi-equilibrium assumption that λ(t)=λ may be taken as fixed for the duration of an infection, then the time to infection is exponentially distributed with distribution function

$$F\left(x\right)=1-e^{-\mathrm{\lambda }x}.$$

If we make the routine assumption that the infectious period, g(x), is exponentially distributed with mean γ⁻¹, we have

$$P(\mathit{coinfection})={\displaystyle \underset{0}{\overset{\infty }{\int }}(1-e^{-\mathrm{\lambda }x})\mathrm{\gamma }{e}^{-\mathrm{\gamma }x}dx}=\frac{\mathrm{\lambda }}{\mathrm{\lambda }+\mathrm{\gamma }}.$$

We note that according to this model P(coinfection)=0.5 when the average time-to-infection and the infectious period are equal (i.e., λ⁻¹=γ⁻¹) and that when λ ranges over orders of magnitude, during outbreaks, the behavior is switch-like: at times where λ<γ, where γ is recovery rate, the probability of coinfection is negligible, but where λ>γ the probability of coinfection is approximately one.

Probability that the second infection is of different type

The probability that the second infection is of a different type than the first depends on the diversity of the pool of potentially infecting strains. For concreteness, let z_i(t) be the prevalence of infections of subtype i at time t, and

$$p_i\left(t\right)=\frac{z_i\left(t\right)}{{\displaystyle \sum _{i=1}^n{z}_i\left(t\right)}}$$

be the relative abundance of subtype i. Assuming that there is an infinite source pool that changes only slowly with respect to the course of an infection (i.e., that the number of free virus particles is large so that sampling with replacement is valid) and (as above) that infection events are independent, the probability that two subsequent infections will be of type i is $p_i^2$. Summing over n subtypes, we have the total probability of infection with identical subtype

$$D={\displaystyle \sum _{i=1}^n{p}_i^2}$$

This quantity was proposed by Simpson (1949) as a measurement of diversity. From its complement we obtain the total probability of infection with a different subtype

$$\mathrm{\pi }\left(z\right)=1-D=1-{\displaystyle \sum _{i=1}^n{p}_i^2,}$$

which is widely used in ecology as an index of diversity.

Reassortment rate

Combining these expressions, we have the rate of increase of coinfected individuals, W, which depends on the number of susceptible hosts at time t, S(t),

$$\frac{\mathit{dW}}{\mathit{dt}}=\mathrm{\lambda }\left(t\right)S\left(t\right)\frac{\mathrm{\lambda }\left(t\right)}{\mathrm{\lambda }\left(t\right)+\mathrm{\gamma }}\mathrm{\pi }\left(z\right),$$

where we assume that the composition of infectious strains z(t)=(z₁(t), z₂(t), z₃(t),…) does not greatly affect the force of infection λ(t). Assuming that the rate at which reassorted combinations occur is proportional to the rate at which double infections arise, we draw the following conclusions:

1. Regardless of prevalence, reassortment rate is proportional to subtype diversity π(z).

2. If λ(t) ≫ γ, reassortment rate is proportional to: (i) the force-of-infection λ(t), and (ii) I*R₀ = λ(t)/γ, where R₀ is the basic reproductive rate of an infection.

3. If λ(t) ≪ γ, reassortment rate is proportional to λ(t)².

Assuming an ongoing epidemic (which further implies that λ(t) > γ), we ignore the effects of environmental transmission, such as are considered for avian influenza viruses in Rohani et al. (2009), and substitute $\mathrm{\lambda }(t)=\beta \mathit{SI},$ where β is the contact rate between individual hosts and I represents disease prevalence, so that we have

$$\frac{\mathit{dW}}{\mathit{dt}}\approx \beta \mathit{SI}\mathrm{\pi }\left(z\right).$$

Thus, in the special case that transmission is dominated by density dependent direct transmission, we see that reassortment rate is proportional to both diversity and prevalence.

MATERIALS AND METHODS

Study System

Because subtype diversity is a precondition for reassortment, and because our model shows that subtype diversity is proportional to subtype reassortment, we sought next to estimate the diversity of LPAI viruses in migratory shorebirds at Delaware Bay, USA from 2000–2008, a known hot spot for avian influenza. Delaware Bay, located between the states of New Jersey and Delaware on the east coast of North America (Figure 1), is an important stopover on the Atlantic Flyway during spring migration to breeding grounds in the Arctic. During migrations, over 200,000 birds use Delaware Bay in a given day (Clark, Niles, & Burger 1993). The six most abundant species are all shorebirds and gulls, including Ruddy Turnstone (Arenaria interpres), Red Knot (Calidris canutus), Semipalmated Sandpiper (Calidris pusilla), Sanderling (Calidris alba), Herring Gull (Larus smithsonianus), and Laughing Gull (Leucophaeus atricilla; Delany & Scott 2006). Due to simultaneous use of this stopover site by a vast number of birds, Delaware Bay is considered a hotspot for pathogen transmission both within and among bird species (Brown et al. 2013; Krauss et al. 2010; Maxted et al. 2012). Our dataset consisted of 9,746 individual birds sampled from 24 locations within a 27 km radius during peak spring migration over the nine years of study (Maxted et al. 2012). Data were collected each year from 2000 through 2008 between April 26 and June 4 as part of a long-term population study and are representative of avian influenza subtypes present in shorebirds at Delaware Bay (see Influenza Research Database [www.fludb.org] for a list of all avian influenza subtypes detected according to location and host species). Birds were captured with cannon nets and samples collected using cloacal swabbing (Maxted et al. 2012). Of the 9,746 samples, 439 (4.5%) were determined to be positive for AIV through virus isolation in embryonating chicken eggs, followed by confirmation with RT-PCR using primers targeting the matrix gene of AIV (Fouchier et al. 2000; Stallknecht et al. 2012). Subtypes were determined using traditional serological subtyping (hemagglutinin and neuraminidase inhibition tests; National Veterinary Services Laboratories, Ames, IA). The final dataset included the collection date and location (e.g. beach name), host species, infection status (positive or negative), and if positive, the subtype.

Figure 1.

Map of Delaware Bay indicating AIV sampling locations.

Subtype Diversity

The total number of co-circulating subtypes was estimated using the abundance-based coverage estimator (ACE) of Chao and Lee (1992) and Chao, Ma, & Yang (1993) implemented in program SPADE (available from: http://chao.stat.nthu.edu.tw/softwareCE.html). ACE is a nonparametric richness estimator that estimates the total number of types from the observed frequencies of “rare” types. It takes a single tuning parameter (k), the cutoff such that type i is considered rare if and only if the frequency of observations of type i in the sample is less than or equal to k. We followed Chao and Lee in setting k=10. Because ACE is a nonparametric estimator, it makes minimal assumptions concerning the relative frequency of different types and generalizes on the principle found in both Good-Turing theory and the earlier Chao1 estimator that the rare types contain virtually all the information about the relative frequency of unobserved types. By dividing the number of subtypes identified in each year by our ACE estimate, we also obtained an estimate of surveillance coverage (fraction of circulating subtypes identified). We also estimated subtype diversity (Simpson’s Index; Simpson 1949) using the maximum likelihood estimator (MLE) of Magurran (1988). Our final estimates were reported as 1-D, where D = MLE value. Confidence intervals were calculated using nonparametric jackknife (Chao & Shen 2003). Subtype diversity was estimated both for all host species combined and separately by host species. Prevalence was calculated as the fraction of samples within a pool from which influenza was isolated. Confidence intervals on estimated prevalence were obtained from the likelihood function for the binomial distribution.

RESULTS

Subtype diversity and prevalence within an avian host community

Overall, we recorded about half of all subtypes (52 of 103) ever detected in North America at Delaware Bay between 2000 and 2008, with a minimum (n=3) in 2004 and a maximum (n=19) in 2008 (Table 1, Figure 2). The number of subtypes estimated to co-circulate ranged from 4 (in 2005) to 39 (in 2008; Figure 2). For the years 2001 and 2005, the Chao1 estimator was used in place of ACE. Chao1 is a lower-bound non-parametric estimator that does well in data containing numerous singletons (Chao 1984). Combining these results, we estimate that coverage (percent of circulating subtypes collected) ranged from 31.8% in 2001 to 81.6% in 2005 with an average of 63.0% (Table 1). Unsurprisingly, the number of isolates collected was correlated with the number of individuals sampled (Spearman rank order correlation: ρ=0.67, p=0.039). There was also evidence for an effect of sample size on the number of species estimated using ACE (Spearman rank order correlation: ρ=0.72, p=0.02), but we did not find evidence for an effect of sample size on the percent coverage (Spearman rank order correlation: ρ=−0.48, p=0.17). Simpson’s Index ranged from 0.22 in 2006 to 0.89 in 2003 with an average of 0.62 (Table 1). The variation among these estimates across years suggests that subtype diversity is based on subtype turnover in Delaware Bay, and means that some years represent higher potential for reassortment among LPAI subtypes.

Table 1.

Subtype diversity statistics for all avian host species at Delaware Bay. Total sample size is denoted by n, and the number of positive samples is equal to the number of subtypes collected.

	2000	2001	2002	2003	2004	2005	2006	2007	2008	Combined
	(n=1492)	(n=1087)	(n=1701)	(n=669)	(n=534)	(n=858)	(n=768)	(n=994)	(n=1651)	(n=9754)
Number of isolates collected	39	34	80	52	20	32	50	21	103	431
Subtype coverage* (estimated % subtypes collected)	76.9%	31.8%	65.2%	77.3%	73.1%	81.6%	39.7%	53.8%	49.2%	19.8%
Simpson (95% confidence interval)	0.79 (0.70, 0.89)	0.32 (−1.3, 1.93)	0.85 (0.77, 0.92)	0.89 (0.85, 0.93)	0.49 (0.06, 0.91)	0.62 (0.45, 0.79)	0.22 (−0.89, 1.33)	0.59 (0.33, 0.85)	0.82 (0.73, 0.92)	0.93 (0.9, 0.95)

^*Calculated as subtype count divided by ACE (multiplied by 100 to obtain percentage)

Figure 2.

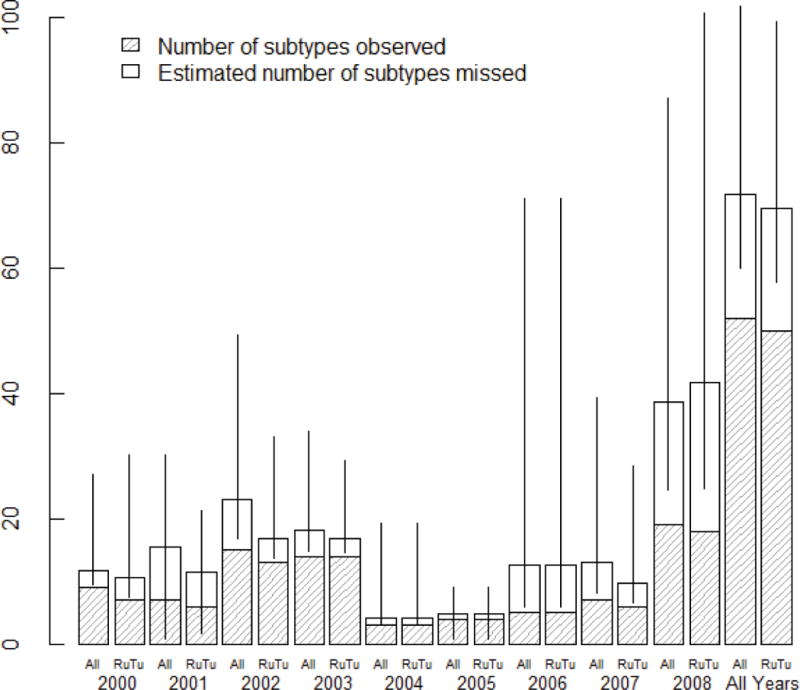
Barplot indicating the number of observed subtypes (i.e. subtypes collected) and number of subtypes missed at Delaware Bay for each year and for all years combined for all species at Delaware Bay and for Ruddy Turnstones only. Estimated number of subtypes (ACE) incorporates both observed subtypes and missed subtypes. Error bars indicate the 95% confidence intervals for ACE estimates. Note that for 2001 and 2005, the Chao 1 estimate is used in place of the ACE estimate. Also note that for 2005, the number of missed subtypes is 0 and the confidence intervals are (4.0, 4.07). These data suggest high variability in LPAI subtypes among years regardless of whether the entire host community is sampled or just Ruddy Turnstones are sampled.

Prevalence overall ranged from 0.5% to 10.6% among host species with an average of 2.6% (Table 2); there was no evidence for a trend in prevalence over time (Spearman rank order correlation: ρ=0.23, p=0.55). When prevalence was broken up by host species, Ruddy Turnstones exhibited the highest prevalence of LPAI over all years (10.6%; CI: 9.7%–11.6%), but again there was no evidence for a trend in prevalence over time when Ruddy Turnstones were compared to the remainder of the host community (Spearman rank order correlation: rho=0.4, p=0.29 and ρ= −0.43, p=0.25 respectively, Figure S1). By contrast, prevalence in the next most infected species, Herring Gull, was lower by a factor of ~10, corresponding to an infection odds ratio of ~8. Prevalence in the remaining species was similar (Table 2). These results suggest that Ruddy Turnstone may play an important role in the transmission of avian influenza viruses in shorebirds as a major amplifying host.

Table 2.

Subtype prevalence of the six most abundant avian host species at Delaware Bay. Numbers in parentheses indicate confidence intervals for estimates.

Species	Prevalence
Ruddy Turnstone (Arenaria interpres)	10.6% (9.7%–11.6%)
Sanderling (Calidris alba)	0.9% (0.5%–1.7%)
Red Knot (Calidris canutus)	0.8% (0.5%–1.2%)
Semipalmated Sandpiper (Calidris pusilla)	0.5% (0.2%–1.4%)
Herring Gull (Larus smithsonianus)	1.4% (0.4%–5.1%)
Laughing Gull (Leucophaeus atricilla)	1.2% (0.5%–2.7%)

Subtype diversity and prevalence within a Ruddy Turnstone population

Plots of subtype diversity by host over all years also show that Ruddy Turnstone was the most permissive host species (in the sense that Ruddy Turnstone harbored the greatest range of subtypes), representing 50 of the 52 (96.1%) subtypes collected during this period (Figure S2). By contrast, the second ranked species, Red Knot represented only nine of 52 (17.3%) subtypes. These results, interpreted through the assumptions of our model, suggest that Ruddy Turnstones are most likely to be coinfected by multiple subtypes and most likely to play a role in reassortment.

Taken together, these results suggest that Ruddy Turnstone is the most probable host for avian influenza virus reassortment at Delaware Bay. We therefore next considered the diversity of subtypes circulating just within this species. Restricting analysis to isolates collected only from this species, abundance-based coverage estimates still indicated that the number of subtypes actually circulating in each year was greater than the number collected, despite isolation of the greatest number of subtypes from this species (Figure 2). However, on average we collected 92.3% of estimated co-circulating subtypes at Delaware Bay from Ruddy Turnstones. As for all host species combined, the estimated number of co-circulating subtypes was greatest in 2008, although the numbers of isolates collected in 2002 and 2003 were similar (Figure 2). As with the analysis of all species, year by year levels of subtype number and diversity were considerably lower than for the pooled sample, confirming the earlier impression of high turnover. While the correlation between yearly prevalence in the Ruddy Turnstone population and yearly prevalence in the remainder of the host community was not significant (Figure 3), the correlation between Simpson’s Index in the Ruddy Turnstone population and Simpson’s Index in the remainder of the host community was significant (Figure 4) suggesting that the Ruddy Turnstone is a good indicator of influenza dynamics in the community overall. Hall et al. (2012) found that the duration of shedding for Ruddy Turnstones to be between two and eight days, which is comparable to other bird species (Lu & Castro 2004; Brown et al. 2006; Brown, Stallknecht, & Swayne 2008; VanDalen et al. 2010; Maxted et al. 2012). They also found that while Ruddy Turnstones arrive at Delaware Bay with low levels of infection, prevalence in Ruddy Turnstones increases during the stopover season and decreases near the end (Maxted et al. 2012). All four major migratory shorebird species (Ruddy Turnstone, Red Knot, Semipalmated Sandpiper, and Sanderling) arrive at and depart from Delaware Bay at approximately the same time, and no other migratory species exhibits the increase in prevalence seen in Ruddy Turnstones (Maxted et al. 2012). Together with the fact that Ruddy Turnstones are more than eight times more likely to be infected than any other species, this suggests that Ruddy Turnstones are a driver, not just a barometer, of reassortment in this system.

Figure 3.

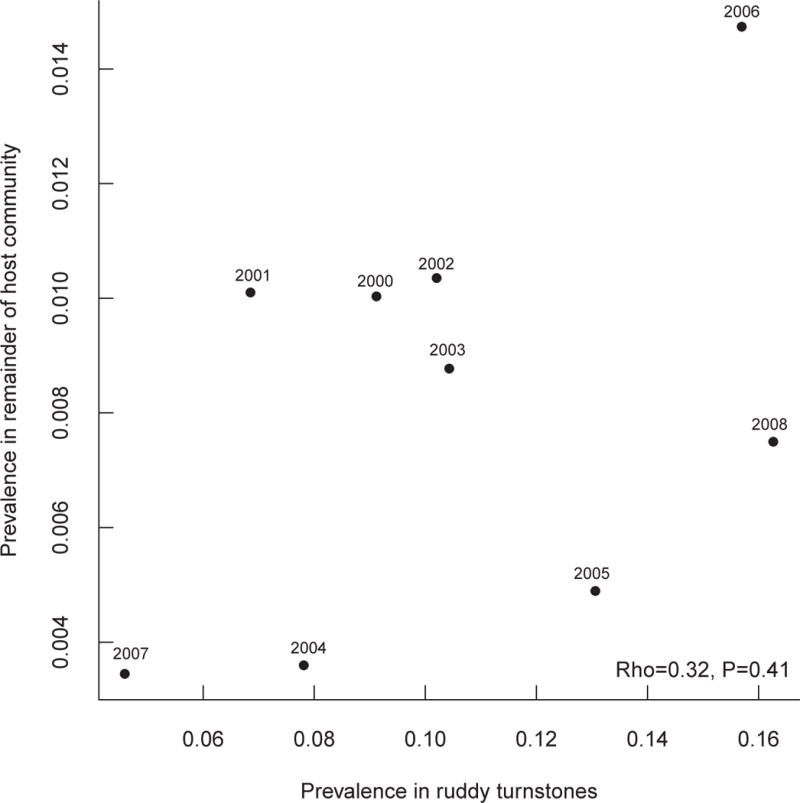
Scatterplot of AIV prevalence in the host community at Delaware Bay with Ruddy Turnstones excluded vs. AIV prevalence in only Ruddy Turnstones at Delaware Bay reveals a correlation (though not significant) between community prevalence and prevalence in Ruddy Turnstones.

Figure 4.

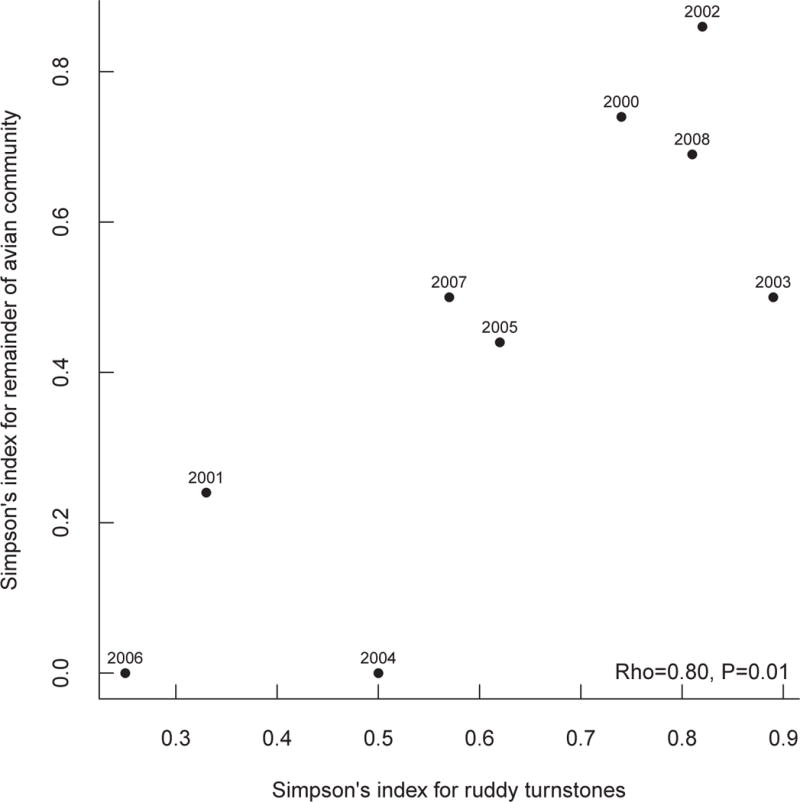
Scatterplot of Simpson’s Index for the host community at Delaware Bay with Ruddy Turnstones excluded vs. Simpson’s Index for only Ruddy Turnstones at Delaware Bay reveals a significant correlation between the two indices.

DISCUSSION

In this paper we present a new model for the rate of coinfection in a multi-pathogen disease system. Applied to avian influenza, this model predicts that subtype reassortment rate will be proportional to subtype diversity, as quantified by Simpson’s Index. During periods of intense transmission, when the force-of-infection is greater than the recovery rate (often much greater than recovery rate), the model predicts that reassortment rate will also be proportional to the force-of-infection, R₀, and prevalence. Alternatively, when the force-of-infection is less than the recovery rate (i.e. low-level transmission), the model predicts that reassortment rate will increase quadratically with the force-of-infection.

The simplicity of our model, which is the source of its generality and what enables the link between pathogen diversity reassortment to be transparent, is also a limitation. More detailed models might include seasonal breeding, host migration, a mixture of direct and environmental transmission and overlap in habitat use by the multiple host species (Breban et al. 2009, Rohani et al. 2009, Brown et al. 2013). Additionally, environmental changes, such as declines in the number of spawning horseshoe crabs (Krauss et al. 2010) or phenological asynchrony due to climate change (Brown & Rohani 2012) could radically alter the potential of this ecosystem to serve as a site for reassortment. One final possible extension of this theory would consider multiple hosts and viral subtype combinations with host-dependent fitness so that circulating viruses are subject to evolutionary trade-offs. Such a model might provide more detailed guidance about the potential paths by which novel human strains might arise, but are currently almost certainly not parameterizable given the well-known complexities of influenza evolution. Such a synthesis of the ecological and evolutionary dynamics of influenza remains an open problem.

The central finding of this paper is more modest: our main theoretical result implies that, in addition to estimating prevalence, estimation of Simpson’s Index should be a standard component of surveillance activities. As a demonstration of application, we retrospectively analyzed prevalence and subtype diversity of avian influenza in shorebirds at Delaware Bay, a key hotspot for avian influenza transmission in North America. Although previous studies have investigated total prevalence of AIVs at Delaware Bay (Maxted et al. 2012), none has studied the relative prevalence of subtypes, used statistical estimators to extrapolate to unsampled individuals, or quantified the potential for reassortment. Results of our analysis showed that not only prevalence but also diversity of avian influenza viruses varies widely among years. Thus, the potential for reassortment of new subtype combinations in avian hosts also varies greatly from year to year. This is significant because reassortment is an important pathway by which avian influenza genes enter human and domestic animal influenza virus gene pools and because waterfowl and shorebirds are the dominant wildlife hosts currently harboring the greatest genetic diversity of influenza strains.

Predicting the identity of future reassortments requires knowing the conditions of prevalence and diversity under which reassortment is likely to occur, parameters which we estimate here. However, it also requires knowing which influenza subtypes are circulating within the avian community and are therefore available for reassortment, which involves surveillance and laboratory diagnosis. It is widely understood that the number of species in a collection is necessarily less than or equal to the number of species in the community from which the sample is drawn and that, unless the sample is truly exhaustive, the raw count of types is biased. In communities containing large numbers of individuals and highly skewed distributions of relative frequency, even a fairly large sample may contain only a minority of the species present. Therefore, in addition to estimating prevalence and diversity, we also estimated the number of co-circulating subtypes using the abundance-based coverage estimator of Chao and Lee (1992). This method uses statistical extrapolation to provide much less biased estimates of species diversity. Indeed, our analysis finds that on average only 63% of circulating subtypes are actually detected during surveillance. While it is unlikely that one could detect all subtypes circulating in a given year, undetected or rare subtypes can increase in abundance and contribute to subtype reassortment and transmission in subsequent years. We would therefore conclude that additional surveillance effort is warranted. Using ecological techniques for estimating the number of subtypes in a collection such as those we have deployed here, it is possible to estimate in advance the sample size that is expected to yield a collection of circulating isolates with arbitrary desired coverage. We advocate that such statistical procedures be used in the design of future surveillance studies.

The model we have developed makes clear testable predictions about the functional relationships among coinfection rate, prevalence, and subtype diversity. It is not presently possible to perform a direct test of this model, however, due to the fact that detection of coinfections must be by PCR or other molecular detection methods from the raw sample to reliably detect and identify coinfecting subtypes (Dugan et al. 2008; El Zowalaty et al. 2011), a procedure which is used only occasionally in influenza surveillance. A direct test might be performed in other systems that have served as models for understanding the ecology of multi-pathogen systems (e.g. rabies in bats; Streicker et al. 2010). We know of no other system that exhibits the same degree of diversity and reassortment potential as LPAI, however. The extent to which subtype diversity (such as exists in the LPAI system at Delaware Bay) is relevant to pathogen evolution and emergence in other systems remains unknown. Development of appropriate models for understanding the role that biological diversity at multiple levels plays in the emergence and transmission of infectious diseases therefore remains a high priority for research.

Supplementary Material

Supp Fig S1

Figure S1. Plots of prevalence through time for the host community at Delaware Bay with Ruddy Turnstones excluded (solid black line) and for Ruddy Turnstones only (dashed red line) at Delaware Bay. There was no significant trend in prevalence in either case, nor were there any significant trends in within-year prevalence in either case.

Supp Fig S2

Figure S2. Subtype diversity from 2000 through 2008 at Delaware Bay separated by host species.

Supp Table S1

Table S1. Documented avian influenza subtypes in North America and globally.

Table 3.

Subtype diversity statistics in Ruddy Turnstones at Delaware Bay. Total sample size is denoted by n, and the number of positive samples is equal to the number of subtypes collected.

	2000	2001	2002	2003	2004	2005	2006	2007	2008	Combined
	(n=296)	(n=394)	(n=735)	(n=441)	(n=256)	(n=245)	(n=293)	(n=414)	(n=584)	(n=3658)
Isolates collected	27	27	70	50	19	29	44	19	95	380
Subtype coverage* (estimated % subtypes collected)	66.0%	52.6%	76.9%	82.8%	73.2%	81.6%	39.7%	61.2%	43.1%	71.9%
Simpson (95% confidence interval)	0.74 (0.60, 0.89)	0.33 (−1.25, 1.90)	0.82 (0.74, 0.91)	0.89 (0.86, 0.93)	0.50 (0.09, 0.91)	0.62 (0.47, 0.77)	0.25 (−0.78, 1.27)	0.57 (0.3, 0.85)	0.81 (0.71, 0.92)	0.93 (0.90, 0.96)
Richness	7	6	13	14	3	4	5	6	18	50

^*Calculated as subtype count divided by ACE (multiplied by 100 to obtain percentage)