Predicting an SF-6D Preference-Based Score Using MCS and PCS Scores from the SF-12 or SF-36

Abstract

Background

The SF-6D preference-based scoring system was developed several years after the SF-12 and SF-36 instruments. A method to predict SF-6D scores from information in previous reports would facilitate backwards comparisons and the use of these reports in cost-effectiveness analyses.

Methods

This report uses data from the 2001–2003 Medical Expenditures Panel Survey (MEPS), the Beaver Dam Health Outcomes Survey, and the National Health Measurement Study. SF-6D scores were modeled using age, sex, mental component summary (MCS) score, and physical component summary (PCS) score from the 2002 MEPS. The resulting SF-6D prediction equation was tested with the other datasets for groups of different sizes and groups stratified by age, MCS score, PCS score, sum of MCS and PCS scores, and SF-6D score.

Results

The equation can be used to predict an average SF-6D score using average age, proportion female, average MCS score, and average PCS score. Mean differences between actual and predicted average SF-6D scores in out-of-sample tests was −0.001 (SF-12 version 1), −0.013 (SF-12 version 2), −0.007 (SF-36 version 1), and −0.010 (SF-36 version 2). Ninety-five percent credible intervals around these point estimates range from ±0.045 for groups with 10 subjects to ±0.008 for groups with more than 300 subjects. These results were consistent for a wide range of ages, MCS scores, PCS scores, sum of MCS and PCS scores, and SF-6D scores. SF-6D scores from the SF-36 and SF-12 from the same data set were found to be substantially different.

Conclusions

Simple equation predicts an average SF-6D preference-based score from widely published information.

Introduction

The SF-36 and SF-12 are two of the most widely used health measurement instruments [1,2]. Results from the SF-36 can be reported as eight health dimension scores. Results from the SF-36 and SF-12 can be reported as two summary scores: the mental component summary (MCS) score and physical component summary (PCS) score. These component scores are constructed using normative values so the average score is 50 and the standard deviation of scores is 10. The most commonly used normative values were collected in the United States in 1990 (for version 1) and 1998 (for version 2). The health dimension and component scores, however, are not appropriate for use in cost-effectiveness analyses (CEA). The US Panel on Cost-Effectiveness in Health and Medicine recommended a single preference-based score be used in CEA. A preference-based score, referred to as “health utility,” is constructed so that full health is anchored at 1.0 and death is anchored at 0 [3].

To facilitate the use of SF-12 and SF-36 in CEA, several groups have constructed equations which use results from the SF-12 and SF-36 to predict a preference-based summary score from a different health utility instrument. There are equations which predict Quality of Well-being and Health Utility Index Mark 2 scores from the eight health dimension scores of the SF-36 [4,5]. There are also equations which predict EQ-5D and Health Utilities Index Mark 3 scores from the MCS and PCS scores of the SF-12 [6-10]. Because these equations predict scores across different health measurement systems, the error associated with them is large.

Recently, researchers developed a single, preference-based score which can be directly calculated for SF-family called the SF-6D. In 2004, Brazier et al published consistent models for both the SF-36 and SF-12 [11]. The SF-6D health description system uses a common subset of item responses from both version 1 and version 2 of these instruments. This model was published 14 years after the development of the SF-36 and 9 years after the development of the SF-12. Given the time difference between the SF-36/SF-12 development and the SF-6D development, there are a substantial number of reports which include the eight health dimension scores or MCS and PCS scores, but not SF-6D scores. Ara and Brazier have developed an equation to predict SF-6D preference-based score from the eight health dimension scores from the SF-36 [12]. There is, however, no published prediction equation based on MCS and PCS scores.

This report includes the develop an equation to predict an average SF-6D score from group level demographics and variables commonly reported in the literature: average age, proportion female, average MCS score, and average PCS score. The equation was estimated using Bayesian methods, and credible intervals are presented for these point estimates which include both parameter estimate uncertainty and individual uncertainty. This equation allows comparisons to previously published studies when it is impractical to access individual level data to directly calculate the SF-6D.

Data and Methods

Data for Equation Estimation

The equation was estimated using data from the Medical Expenditures Panel Survey (MEPS) which includes the SF-12 [13]. MEPS is a nationally representative survey of health care utilization and expenditures for the US noninstitutionalized civilian population. MEPS is a 2-year panel survey, with an overlapping cohort design, taken from the National Health Interview Survey cohort. MEPS over-samples Hispanics, blacks, functionally impaired adults, children with activity limitations, working-age adults predicted to have high medical expenditures, and individuals with incomes predicted to be less than 200% of the poverty level. Each year, a new cohort is initiated and followed longitudinally through a series of five in-person interviews at 6-month intervals. Cross-sectional analyses combine information from two MEPS cohorts. MEPS conducts interviews with one or more persons per household who report on health care utilization, expenditures, insurance coverage, and medical conditions for each household member.

Beginning in 2000, MEPS included a self-administered questionnaire (SAQ) to obtain information that potentially would be unreliable if reported by a proxy. The SAQ was distributed to all adults aged 18 years old or older in eligible households participating in MEPS. The SAQ included the SF-12. For the equation estimation, data was used from 2002 MEPS, which includes the SF-12 version 1 (SF-12v1).

Data for Equation Testing

The resulting equation was evaluated using data from several sources. The equation was evaluated for use with the SF-12v1 with data from 2001 MEPS. The equation was evaluated for use with the SF-12 version 2 (SF-12v2) with data from 2003 MEPS.

Data from the Beaver Dam Health Outcomes Study (BDHOS) includes the SF-36 version 1 (SF-36v1) [14]. The BDHOS was a random subset of older adults sampled from the Beaver Dam Eye Study [15], a community-based study of eye-disease prevalence and risk factors in Beaver Dam, WI. BDHOS included 1430 participants between January 1991 and July 1992. These data were collected in face-to-face interviews.

Data from the National Health Measurement Study (NHMS) includes the SF-36 version 2 (SF-36v2). NHMS was a random digit dial, telephone survey of US adults aged 35–89 collected between June 2005 and August 2006 with 3844 participants. This survey over-sampled individuals of African-American descent and individuals over age 65 to decrease sampling error in these subgroups. This survey also included administration of the EQ-5D, Health Utilities Index, and Quality of Well-Being Scale [16].

From all surveys, respondents were included in this analysis if they were aged 18 and older with known age and sex who completed the entire SF instrument. Individuals over the age of 85 in MEPS have a recorded age of 85 for increased confidentiality.

Variables

The SF-36 was developed for the Medical Outcomes Study and the standard form for version 1 was published in 1990. The SF-12, developed in 1995, is a standardized subset of questions which most closely estimates the MCS and PCS scores of the SF-36 [2]. Both instruments have two versions. When necessary, the version of these instruments is indicated by postscripts (e.g., SF-12v1 and SF-12v2).

MCS and PCS scores are used in these analyses. MCS and PCS scores can be calculated using all items from either version of the SF-36 or SF-12. The SF-12 was constructed so that MCS and PCS scores from this instrument would be equivalent to those from the SF-36 [2]. These scores are constructed to have a mean of 50 and a standard deviation of 10 using population norms [1,2]. There are two widely used sets of US norms; the 1990 normative values are most often used with version 1 although the 1998 normative values are most often used with version 2. The normative values used to calculate the MCS and PCS scores are indicated by subscripts (e.g., MCS₁₉₉₀ and MCS₁₉₉₈). A simple correction can be used to compare MCS and PCS scores using different US population norms. These corrections are Eqs. 1 and 2 [1].

$${\mathit{PCS}}_{1990}={\mathit{PCS}}_{1998}-1.07897$$ (1)

$${\mathit{MCS}}_{1990}={\mathit{MCS}}_{1998}+0.16934$$ (2)

The SF-6D is computed using 11 items from the SF-36 or 7 items from the SF-12.[11] When necessary, the version of the SF-6D is indicated by subscripts (i.e., SF-6D₁₂ and SF-6D₃₆). The items are used to describe six health domains: physical functioning, role limitations, social functioning, pain, mental health, and vitality. These domains have four to six levels which allows for 18,000 unique health states—a health state is a specific combination of levels across the six domains. A household sample of adults from the United Kingdom (n = 611) provided standard gamble valuations for 249 SF-6D health states. These valuations were fit in an ordinary least squares regression to create an equation which can be used to convert any combination of domain levels to an SF-6D score. The maximum SF-6D₁₂ score is 1.0 and the minimum score is 0.345 [11].

Age and sex variables are also used in these analyses. Age is the respondent’s age in years and sex is indicated with a binary variable called “female” which is 1 when the respondent is female and 0 when the respondent is male.

Analyses

Part 1: Descriptive information

Average MCS, PCS, and SF-6D scores were computed by age group for all datasets. For the BDHOS and NHMS, scores were calculated using the full SF-36 and an extracted SF-12. These averages were calculated using STATA (version 10.0, StataCorp, College Station, TX) to allow application of the sampling and poststratification weights in the MEPS and poststratification weights in NHMS. Use of these weights yields nationally representative estimates for non-institutionalized civilian adults.

Part 2: SF-6D prediction equation development

SF-6D scores were regressed on age, sex, MCS score, and PCS score from the 2002 MEPS (SF-12v1) using WinBUGS 1.4.3 [17]. For observations i, i = 1 … n: SF − 6D_i = constant + β_age(age_i) + β_female(female_i) + β_MCS(MCS_i) + β_PCS(PCS_i) + ε_i, where each constant, β_age, β_female, β_MCS, and β_PCS was assigned a noninformative prior N(0, 1000). ε is a normally distributed error term with mean equal to zero and variance 1/τ, where τ was assigned a noninformative prior, gamma (0.001, 0.001).

All models were considered which used subsets of these four predictor variables and Deviance Information Criterion was used as the model selection criterion [18]. The use of interaction or power terms was excluded so that the equations can be used with summary level statistics from previously published reports (see results for more details). All models had three chains with a 10,000 iteration burnin and a 1000 iteration statistical sample for the creation of a prediction equation and credible intervals. These values are available from the author upon request. Model convergence was assessed using the Gelman–Rubin statistic. The SF-6D prediction equation was created using the means from the posterior distribution of each parameter estimate from the best model.

Part 3: Creating credible intervals around estimates by sample size (SF-12v1)

Using data from the 2001 MEPS (SF-12v1), subjects were randomly selected to form groups of 10, 20, 30, 400 observations. Each observation was combined with a random set of estimates for each parameter and individual error drawn from the posterior distribution of the best model from Part 2. These parameter estimates were used to generate a predicted SF-6D score for the observation. The difference between the actual and average SF-6D score was calculated for each group. Using 500 repetitions for a particular group size, a 95% credible interval was calculated.

Part 4: Testing the prediction equation for the SF-12v2, SF-36v1, and SF-36v2

The analysis for Part 3 was repeated using data from BDHOS (SF36-v1, SF-12v1), 2003 MEPS (SF-12v2), and NHMS (SF-36v2, SF-12v2).

Part 5: Testing the prediction equation with restrictions on age, MCS score, PCS score, the sum of MCS and PCS scores, and SF-6D score

The analysis for Part 3 was repeated using data from 2001 MEPS where group size was 50 observations and group membership was restricted by age, MCS score, PCS score, the sum of MCS and PCS scores, and SF-6D score. Age groups included [20–25), [25–30), … [80–85), and 85 and over. MCS score and PCS score groups included [15–20), [20–25), … [70–75) for groups with more than 100 observations. The groups for the sum of MCS and PCS scores included [40–55), [55–70), … [100–115), and [115–117]. The differences between actual and predicted average SF-6D scores for 500 groups were compared. SF-6D group strata included [0.30–0.45), [0.325–0.475), [0.35–0.5), [0.375–0.525), [0.40–0.45), [0.425–0.575), [0.45–0.6), [0.475–0.625), [0.50–0.45), [0.525–0.675), [0.55–0.7), [0.575–0.725), [0.60–0.45), [0.625–0.775), [0.65–0.8), [0.675–0.825), [0.70–0.45), [0.725–0.875), [0.75–0.9), [0.775–0.925), [0.80–0.45), [0.825–0.975), [0.85–1.0), [0.875–1.0), [0.90–1.0), [0.925–1.0), and [0.95–1.0). Ten groups of 50 observations were randomly selected from each of the strata.

Part 6: Comparison to previously published equations

There are several previously published equations which predict a health utility score from SF-family scores to other health measurement systems such as the EQ-5D, Health Utilities Index, and Quality of Well-Being Scale [4-10]. For the first time in a nationally representative survey, all of these health measurement systems were simultaneously administered in the NHMS. Predicted and observed health utility scores were compared for these different equations using the 3386 respondents who completed all health measurement systems in NHMS. Normalized root mean squared error (NRMSE) was used for this comparison because the range of health utility scores from each system is different.

Results

Part 1: Descriptive Information

All respondents in these surveys who were aged 18 and over with known age, sex, MCS score, PCS score, and SF-6D score were included in these analyses. This included 19,708 subjects from 2001 MEPS, 22,936 subjects from 2002 MEPS, 19,907 subjects from 2003 MEPS, 1417 subjects from BDHOS, and 3739 subjects from NHMS. Figure 1 illustrates the distribution of SF-6D scores from each of these data sources. It illustrates that SF-6D scores calculated from the SF-36 are more evenly distributed over the range of SF-6D scores than those calculated from the extracted SF-12 in the same data set. It also illustrates that SF-6D scores became more evenly distributed over their range in MEPS from the use of version 1 in 2002 to the use of version 2 in 2003. The SF-6D does not show a floor effect in any of these general population surveys with less than 1% of all respondents reporting the lowest scores. There are more respondents reporting the highest SF-6D scores in these surveys with nearly 9% reporting scores of 1.0 in NHMS.

Figure 1.

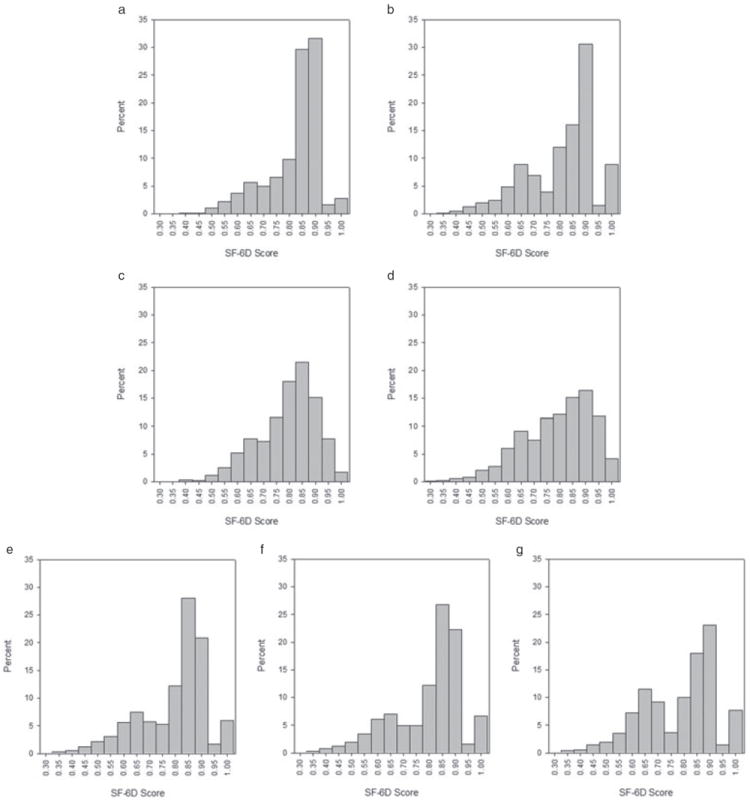
Distribution of SF-6D scores from all data sources. Data from 2002 MEPS were used for equation estimation and all other data were used for equation testing. (a) BDHOS SF-12v1. (b) NHMS SF-12v2. (c) BDHOS SF-36v1. (d) NHMS SF-36v2. (e) 2001 MEPS SF-12v1. (f) 2002 MEPS SF-12v1. (g) 2003 MEPS SF-12v2. BDHOS, Beaver Dam Health Outcomes Survey; MEPS, Medical Expenditure Panel Survey; NHMS, National Health Measurement Survey.

Descriptive values from each sample are presented in Table 1 which allows for comparisons of the scores across age within each survey, SF-12 scores across surveys, across versions of the SF-12 within MEPS, and across SF-12 and SF-36 scores extracted from the same dataset. Consistent with previous reports, PCS and SF-6D scores decline with age (P < 0.001 for all surveys), although MCS scores increase with age (P < 0.030 for all surveys) [1,2,16].

Table 1.

Number of observations and average mental component summary (MCS), physical component summary (PCS), and SF-6D scores by age group for the SF-36 and extracted SF-12 from the Beaver Dam Health Outcomes Survey (BDHOS) and National Health Measurement Survey (NHMS). Average MCS, PCS, and SF-6D scores by age group for the SF-12 version 1 and version 2 from the 2002 and 2003 Medical Expenditure Panel Survey (MEPS). MCS and PCS values were calculated using 1990 US population norms for BDHOS and 2002 MEPS. These values were calculated using 1998 US population norms for NHMS and 2003 MEPS. Values from NHMS and MEPS were calculated using poststratification weights making these estimates nationally representative

Unweighted number of respondents used in this report
	BDHOS		NHMS		MEPS
	1991–1992	1991–1992	2005–2006	2005–2006	2002	2003
Age group	SF-36v1	SF-12v1	SF-36v2	SF-12v2	SF-12v1	SF-12v2
20–29	N/A	N/A	N/A	N/A	4035	3662
30–39	N/A	N/A	311	311	4621	3945
40–49	139	139	723	727	4765	4104
50–59	393	396	774	778	3707	3080
60–69	431	431	846	852	2352	2010
70–79	316	316	744	755	1684	1533
80+	138	138	341	348	808	748
MCS mean(SE)
	BDHOS		NHMS		MEPS
	1991–1992	1991–1992	2005–2006	2005–2006	2002	2003
Age group	SF-36v1	SF-12v1	SF-36v2	SF-12v2	SF-12v1	SF-12v2
20–29	N/A	N/A	N/A	N/A	51.1 (0.2)	50.9 (0.2)
30–39	N/A	N/A	52.9 (0.6)	53.4 (0.6)	51.1 (0.2)	50.6 (0.2)
40–49	53.3 (7.5)	52.5 (7.3)	52.9 (0.5)	53.0 (0.5)	50.6 (0.2)	50.5 (0.2)
50–59	54.6 (6.8)	53.7 (6.6)	53.7 (0.4)	53.7 (0.5)	50.7 (0.2)	50.6 (0.2)
60–69	56.1 (6.4)	54.8 (6.2)	55.2 (0.4)	55.1 (0.4)	52.3 (0.2)	52.4 (0.3)
70–79	55.5 (7.4)	54.3 (7.1)	54.9 (0.4)	54.9 (0.4)	52.3 (0.3)	52.0 (0.3)
80+	56.2 (6.3)	54.0 (6.6)	54.9 (0.7)	55.3 (0.7)	51.1 (0.4)	50.1 (0.5)
PCS mean(SE)
	BDHOS		NHMS		MEPS
	1991–1992	1991–1992	2005–2006	2005–2006	2002	2003
Age group	SF-36v1	SF-12v1	SF-36v2	SF-12v2	SF-12v1	SF-12v2
20–29	N/A	N/A	N/A	N/A	53.4 (0.1)	54.5 (0.1)
30–39	N/A	N/A	52.3 (0.6)	52.0 (0.6)	52.2 (0.1)	53.2 (0.1)
40–49	49.6 (9.1)	49.9 (8.6)	51.6 (0.4)	51.3 (0.4)	50.2 (0.2)	51.0 (0.2)
50–59	50.7 (7.8)	50.9 (7.7)	49.6 (0.5)	49.3 (0.5)	48.0 (0.2)	48.4 (0.2)
60–69	48.1 (9.5)	48.7 (9.2)	46.5 (0.6)	46.4 (0.6)	45.2 (0.3)	46.1 (0.3)
70–79	45.4 (9.8)	45.9 (9.6)	45.4 (0.6)	45.0 (0.7)	41.3 (0.3)	42.0 (0.4)
80+	41.6 (12.0)	42.0 (11.9)	43.9 (0.9)	42.6 (0.9)	36.8 (0.5)	37.8 (0.6)
SF-6D mean(SE)
	BDHOS		NHMS		MEPS
	1991–1992	1991–1992	2005–2006	2005–2006	2002	2003
Age group	SF-36v1	SF-12v1	SF-36v2	SF-12v2	SF-12v1	SF-12v2
20–29	N/A	N/A	N/A	N/A	0.834 (0.002)	0.823 (0.003)
30–39	N/A	N/A	0.802 (0.010)	0.833 (0.010)	0.826 (0.002)	0.810 (0.003)
40–49	0.787 (0.111)	0.825 (0.115)	0.798 (0.007)	0.823 (0.007)	0.807 (0.003)	0.793 (0.002)
50–59	0.808 (0.102)	0.846 (0.101)	0.790 (0.007)	0.817 (0.007)	0.793 (0.003)	0.772 (0.003)
60–69	0.803 (0.105)	0.845 (0.104)	0.778 (0.007)	0.812 (0.008)	0.790 (0.004)	0.776 (0.004)
70–79	0.782 (0.108)	0.820 (0.116)	0.766 (0.007)	0.795 (0.008)	0.763 (0.004)	0.745 (0.004)
80+	0.743 (0.118)	0.775 (0.131)	0.758 (0.011)	0.787 (0.012)	0.709 (0.007)	0.691 (0.007)

N/A, not applicable.

Also consistent with previous reports, MCS, PCS, and SF-6D scores are higher in NHMS than MEPS. These mean estimates were created using sampling and poststratification weights, so both data sets purport to be representative of the US civilian, noninstitutionalized population. As discussed by Hanmer et al., the difference in scores is most likely due to differences in mode of administration; NHMS was a telephone interview and MEPS was self-completed on paper and pencil. Likewise, SF-12v1 scores are higher in BDHOS than in 2002 MEPS, either because the community sample used in BDHOS is healthier than MEPS or because BDHOS was collected by an in-person interviewer and MEPS was self-completed [19].

Comparing the SF-12v1 from 2002 MEPS and the SF-12v2 from 2003 MEPS shows that both MCS and PCS scores across years and versions are within 1.1 of each other. After the corrections from Eqs. 1 and 2, MCS scores are within 0.8 of each other and PCS scores are within 0.7 of each other (data not shown). SF-6D scores are within 0.021 of each other. Comparing SF-12 to SF-36 scores from the same dataset shows that MCS scores from the SF-36 are within 2.2 of MCS scores from the SF-12. Likewise, PCS scores from the SF-36 are within 0.7 of the PCS scores from the SF-12. SF-6D₁₂ scores are larger than SF-6D₃₆ scores from the same dataset by as much as 0.042.

Part 2: SF-6D Prediction Equation Development

Given the substantial differences between SF-6D₃₆ scores and the SF-6D₁₂ scores extracted from the same dataset, the relationship between MCS and PCS scores to SF-6D scores will be dependent on which version of the SF-6D is used. These analyses were limited to models predicting the SF-6D₁₂. The best fitting model, using Deviance Information Criterion, included all four predictor variables: age, female, MCS score, and PCS score (data not shown).

Using the mean of the posterior distribution for each parameter estimate, the best fitting prediction equations are:

$$\begin{array}{lll}\mathit{SF}-6D_{12}& =& -0.06449-0.00328(\mathrm{female})+0.00012(\mathrm{age})\\ & & +0.00946({\mathit{MCS}}_{1990})+0.00781({\mathit{PCS}}_{1990})\end{array}$$ (3)

$$\begin{array}{lll}\mathit{SF}-6D_{12}& =& -0.06449-0.00328(\mathrm{female})+0.00012(\mathrm{age})\\ & & +0.00946({\mathit{MCS}}_{1998}+0.16934)\\ & & +0.00781({\mathit{PCS}}_{1998}-1.07897)\end{array}$$ (4)

The mean of the posterior distribution for each parameter estimate was the same as its median to five decimal places. The 95% credible intervals from the posterior distribution for the parameter estimates were −0.06988–−0.5908 for the constant, 0.00008–0.00016 for age, −0.00460–−0.00195 for female, 0.00939–0.00953 for MCS, and 0.00774–0.00788 for PCS.

Note that Eqs. 3 and 4 predict the SF-6D₁₂, regardless of the use of SF-12 or SF-36 to calculate MCS and PCS. Equation 3 is most appropriate for studies which used version 1 of either the SF-12 or SF-36, although Eq. 4 is most appropriate for studies which used version 2 of either instrument.

Because the equations do not include interaction or power terms, they can be used to predict an average SF-6D score using average group information. Often, calculating an average score for a group would require access to individual level data. For example, using SF-6D₁₂ with MCS and PCS scores normed to 1990 values could be calculated using Eq. 5.

$$\begin{array}{lll}\frac{1}{n}\sum _{i=1}^n\mathit{SF}-6D_{12,i}& =& \frac{1}{n}\sum _{i=1}^n[-0.06449-0.00328(\mathrm{female})\\ & & +0.00012(\mathrm{age})+0.00946({\mathit{MCS}}_{1990,i})\\ & & +0.00781({\mathit{PCS}}_{1990,i})]\end{array}$$ (5)

If individual level data are available, however, Eq. 5 would not be useful because the SF-6D scores could be directly computed. This equation is useful when only summary information is available, such as the information published in a journal article. A simple algebraic rearrangement, Eq. 6, creates an average SF-6D score using the proportion female, average age, average MCS score, and average PCS score from the sample:

$$\begin{array}{lll}\frac{1}{n}\sum _{i=1}^n\mathit{SF}-6D_{12,i}& =& -0.06449-0.00328\left(\frac{1}{n}\sum _{i=1}^n{\mathrm{female}}_i\right)\\ & & +0.00012\left(\frac{1}{n}\sum _{i=1}^n{\mathit{age}}_i\right)\\ & & +0.00946\left(\frac{1}{n}\sum _{i=1}^n{\mathit{MCS}}_{1990,i}\right)\\ & & +0.00781\left(\frac{1}{n}\sum _{i=1}^n{\mathit{PCS}}_{1990,i}\right)\end{array}$$ (6)

Part 3: Creating credible intervals around estimates by sample size (SF-12v1)

These equations provide a point estimate for the average SF-6D score using group level statistics. The error of this point estimate should depend on the original sample size. Five hundred groups were created for each size. Sizes were 10, 20, 30, …, 400. The difference was calculated between the true and predicted average SF-6D score from 2001 MEPS. Table 2 lists the standard deviation of these differences and the suggested 95% credible interval to use with groups of various sizes. The estimate of an average SF-6D score from other summary information becomes more accurate with larger sample sizes, and this accuracy reaches an asymptote when there are 300 or more subjects.

Table 2.

The standard deviation of differences between the true average SF-6D score and the predicted SF-6D score for various group sizes using SF-12 version 1 from 2001 Medical Expenditure Panel Survey. The suggested credible interval around point estimates for a group size is the standard deviation* 1.96

Group size	Standard deviation of differences	Suggested 95% credible interval
10	0.0230	±0.045
20	0.0158	±0.031
30	0.0129	±0.025
40	0.0115	±0.023
50	0.0106	±0.021
60	0.0091	±0.018
80	0.0081	±0.016
100	0.0076	±0.015
120	0.0064	±0.013
140	0.0062	±0012
160	0.0055	±0.011
180	0.0052	±0.010
200	0.0049	±0.010
220	0.0049	±0.010
240	0.0045	±0.009
260	0.0044	±0.009
280	0.0044	±0009
>300	0.0041	±0.008

Part 4: testing the prediction equation for the SF-12v2, SF-36v1, and SF-36v2

When out-of-sample tests were performed for other versions of the SF instrument, several similarities and differences emerged. The shape of the credible intervals across group sizes was similar for all versions; the standard deviations of differences between observed and predicted means decreased as sample sizes increased and reached an asymptote around a sample size of 300 observations. The standard deviation of these differences was very similar for the SF-36v1 from BDHOS (an average change of −0.2%) and slightly larger for both the SF-12v2 from MEPS (an average change of 12.8%) and the SF-36v2 from NHMS (an average change of 11.4%). The mean difference in actual and predicted averages was very close to 0 for the SF-36v1 from BDHOS (mean = −0.007) and larger for both the SF-12v2 from MEPS (mean = −0.013) and SF-36v2 from NHMS (mean = −0.010).

Part 5: testing the prediction equation with restrictions on age, MCS Score, PCS Score, sum of MCS and PCS score, and SF-6D score

Figure 2 illustrates the mean difference and root mean squared error between actual average SF-6D scores and predicted average SF-6D scores by various strata. Within each stratum, there are 500 groups of 50 observations. Inclusion to the group was restricted by age, MCS score, PCS score, or sum of MCS and PCS score. For groups created from 2001 MEPS, age does not appear to have an effect on predictive error or root mean squared error. Just as in the overall comparisons from Part 4, predictive error was close to zero. There is a slight increase in error for those over the age of 85, though the recorded age for all these respondents is 85 to increase confidentiality in the public data set. Using groups stratified by MCS score or PCS score created more predictive error. It should be noted that these groups are very artificial as the range of observed scores in any population, even a population with a specific diagnosis, has substantial variation [4]. Predictive error was close to zero and well below the SF-6D’s minimally important difference [20,21] for MCS and PCS scores from 20 to 60. Scores at the extreme values of MCS and PCS, those below 20 and above 60, are associated with increased mean predictive error and root mean squared error. However, the increase in error associated with groups that have extreme values of summed MCS and PCS scores is not as dramatic.

Figure 2.

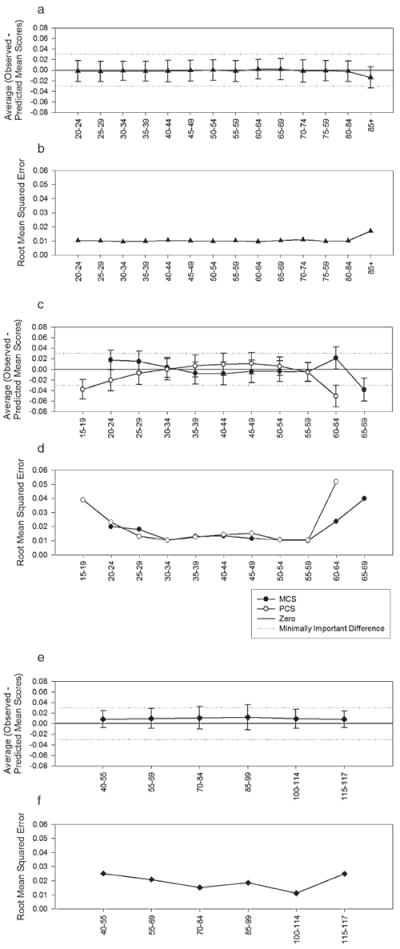
Average difference in observed and predicted SF-6D score and root mean squared error by age, mental component summary (MCS) score, physical component summary (PCS) score, and summed MCS and PCS score. Each point represents 500 groups of 50 observations that were randomly selected from the 2001 MEPS. Inclusion in the groups was constrained by either age, MCS score, or PCS score. The difference between the observed average SF-6D score of the group and the predicted average SF-6D score was calculated. This figure illustrates the mean of these differences with 95% confidence intervals by age strata (a), MCS score strata or PCS score strata (c), and sum of MCS and PCS score strata (e). This figure also illustrates the mean squared error of by age strata (b), MCS score strata or PCS score strata (d), and sum of MCS and PCS score strata (f).

Figure 3 illustrates observed and predicted SF-6D scores for groups of 50 observations. There is an over-prediction of mean SF-6D scores for groups with observed mean SF-6D scores between 0.5 and 0.8 and an under-prediction for groups with observed mean SF-6D scores above 0.9.

Figure 3.

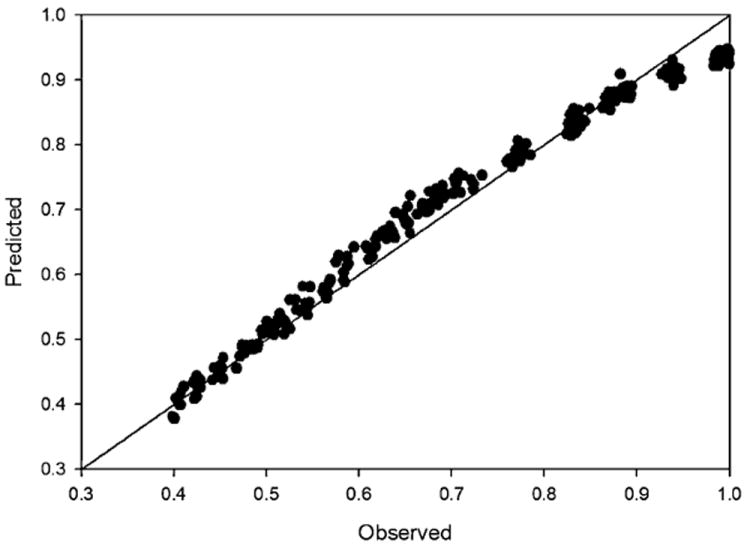
Observed and predicted mean SF-6D scores for groups with 50 observations. This figure illustrates the mean observed and mean predicted SF-6D scores for groups of 50 observations were randomly selected from the 2001 Medical Expenditure Panel Survey. SF-6D group strata included 0.30–0.45, 0.325–0.475, 0.35–0.5, 0.375–0.525, 0.40–0.45, 0.425–0.575, 0.45–0.6, 0.475–0.625, 0.50–0.45, 0.525–0.675, 0.55–0.7, -0.575–0.725, 0.60–0.45, 0.625–0.775, 0.65–0.8, 0.675–0.825, 0.70–0.45, 0.725–0.875, 0.75–0.9, 0.775–0.925, 0.80–0.45, 0.825–0.975, 0.85–1.0, 0.875–1.0, 0.90–1.0, 0.925–1.0, and 0.95–1.0. Ten groups were randomly selected from each of the strata.

Part 6: Comparison to previously published equations

Using data from NHMS, the NRMSE of the equations developed in this report perform better than all previously reported equations. NRMSE was 0.070 when predicting the SF-6D₁₂ from MCS₁₂ and PCS₁₂. Predictions of EQ-5D health utility scores also performed well with NRMSE values of 0.077 [8], 0.078 [7], 0.082 [10], and 0.083 [6]. The NRMSE values for predictions of Health Utilities Index scores were 0.092 [6], 0.093 [5], and 0.173 [9]. The NRMSE value for predictions of SF-6D scores using the eight health dimension scores was 0.123 [12]. The NRMSE value for predictions of Quality of Well-Being Scores was 0.137 [4].

Discussion

This report presents the development of an equation which can be used to predict an average SF-6D₁₂ score based on commonly reported statistics in publications using the SF-12 or SF-36, namely, average age, proportion female, average MCS score, and average PCS score of any given sample. A credible interval for this point estimate is dependent on the original sample’s size. This equation is useful for predicting an SF-6D₁₂ score when it is impossible or impractical to obtain individual level data from previously published studies. Use of these predicted SF-6D scores is subject to the same limitations as directly calculated SF-6D scores: limitations such as a known floor effect relative to other health utility measurement systems [11].

This report includes several out-of-sample tests of this equation for both versions of the SF-36 and SF-12. In these tests, mean predictive error was very close to zero for version 1 and near −0.01 for version 2. Researchers and analysts using this equation to predict an SF-6D score from reports of version 2 instruments may wish to adjust the prediction by −0.01 in sensitivity analyses. Mean predictive error and root mean squared error are similar across a large range of ages, MCS scores, PCS scores, and the sums of MCS and PCS scores. Figure 2 illustrates that root mean squared error increases for groups with a PCS score below 20, PCS score above 60, and MCS score above 60. There does not appear to be an increasing error when both MCS and PCS scores are high or both are low as there are not large changes in mean predictive error or root mean squared error at the extreme ends of the range of summed MCS and PCS scores.

Development and testing of this equation was limited to population-based data sets. Further validation in patient samples would be appropriate as CEA is often concerned with very ill populations. Such a validation could closely mimic the compilation and analysis of health condition-based data sets presented by Ara and Brazier [10,12]. For example, Boonen et al. [22] report MCS, PCS, and SF-6D scores from a multicenter clinical trial of patients with ankylosing spondylitis. The observed and predicted mean SF-6D scores were 0.71 and 0.73 for the group receiving Etanercept treatment and were 0.65 and 0.66 for the group receiving placebo at the beginning of the extension study. These results are consistent with Fig. 3 which illustrates that there may be an over-prediction of mean SF-6D scores for groups with observed mean SF-6D scores between 0.5 and 0.8. Figure 3 also indicates there may be an under-prediction for groups with observed mean SF-6D scores above 0.9, but no systematic difference for groups with observed mean SF-6D scores below 0.5.

CEA requires an estimate of the change in health utility from one health state to another health state. CEA models can be constructed using absolute health utility scores for a set of health states. The change in health utility from one health state to another is estimated as the difference in the absolute health utility scores and only requires cross-sectional data. The prediction equation proposed in this report sought to predict these absolute health utility scores from cross-sectional data. CEA may also be performed using the observed change in health utility scores from longitudinal data. This report did not test the proposed equation’s ability to predict change scores. Recent reports by Ara and Brazier have found that their prediction equations are reasonably accurate at predicting out-of-sample incremental changes [10,12]. It is unclear if their findings are generalizable to similar prediction equations such as the one presented in this report.

The equation estimated in this report predicts an SF-6D score based on seven items from the SF-12. These seven items are present in both the SF-12 and SF-36. An SF-6D score can also be calculated using 11 items from the SF-36. SF-6D₃₆ score averages were as much as 0.042 lower than SF-6D₁₂ score averages in BDHOS and NHMS. This difference may have a substantial impact on analyses which combine absolute SF-6D scores from different sources where some sources report SF-6D₁₂ scores and other sources report SF-6D₃₆ scores. This observed difference in absolute scores does not necessarily indicate that the longitudinal changes in health utility measured by each of these scores would be different. Researchers who have access to SF-36 data are encouraged to extract and report absolute values and change values for both the SF-6D₁₂ and SF-6D₃₆

This equation can also be used with reports from the SF-36 which include mean scores for the eight health dimensions but not MCS or PCS scores. Because MCS and PCS scores are a linear combination of the eight health dimensions, mean MCS and PCS scores can be directly calculated from mean scores for the eight health dimensions using the same arithmetic logic as presented in Part 2 of the results section [1,2]. There is also an equation available which directly predicts SF-6D scores from the eight health dimension scores [12].

As with most equations based on linear regression, there are combinations of predictor variables which can generate nonsense predictions. Possible observed SF-6D₁₂ scores range from 0.345 to 1.0. The equation presented in this report would predict SF-6D₁₂ scores lower than 0.345 for a group with half females, an average age of 50, and average MCS and PCS scores below 23. SF-6D₁₂ scores higher than 1.0 would be predicted for a group with half females, average age of 50, and average MCS and PCS scores above 61. Although these scores are possible for individuals, they are highly unlikely for group level statistics because scores vary widely within any group of interest [4].

There are several other published equations to predict a preference-based summary score from the SF-12 and SF-36 [4-9]. These equations, however, predict across instruments (e.g., SF-12 to EQ-5D) [6-8]. The equation presented in this report predicts a summary score: the SF-6D, from a set of summary scores (MCS and PCS) that are constructed using the same instrument. As such, the equation presented in this report is associated with less predictive error than previously published equations. The equation presented in this report does have some predictive error because the SF-6D is scored from a subset of items, although MCS and PCS scores are constructed from all items in the instrument. For example, in NHMS, NRMSE for the prediction equation presented here was 0.070. Previously published equations had NRMSEs from 0.077 [8] to 0.173 [9].

The subset of questions used to score the SF-6D from the SF-36 or SF-12 may exhibit differential item functioning relative to the unused questions. The prediction equation constructed in this report uses information about the average age, proportion female, average MCS score, and average PCS score for a group. Age and sex were considered for model estimation because they may cause differential item functioning. These variables were found to improve model performance and were included in the final equation. The impact of age and sex on the relationship between MCS and PCS scores to SF-6D scores is small, suggesting a small amount of differential item functioning between the questions used to score the SF-6D and all questions in the SF-12 and SF-36 instruments.

This report presents a simple equation to predict an average SF-6D₁₂ score from the average age, proportion female, average MCS score, and average PCS score reported in other publications. This equation provides a point estimate for the average SF-6D₁₂ score and this report provides guidelines for assigning error to this estimate based on the size of the original sample. This equation is useful for estimating the SF-6D₁₂ score for CEA which is using estimates of health utility scores from previous reports when it is impossible or impractical to access individual level data.