Abstract
The Sequential Surface Integration Process (SSIP) hypothesis was proposed to elucidate how the visual system constructs the ground surface representation in the intermediate distance range. According to the hypothesis, the SSIP constructs an accurate representation of the near ground surface using reliable near depth cues. The near ground representation then serves as a template for integrating the adjacent surface patch using the texture gradient information as the predominant depth cue. By sequentially integrating the surface patches from near to far, the visual system obtains the global ground representation. A critical prediction of the SSIP hypothesis is that when an abrupt texture gradient change exists between the near and far ground surfaces, the SSIP can no longer accurately represent the far surface. Consequently, the representation of the far surface will be slanted upward toward the frontoparallel plane (owing to the visual system's intrinsic bias), and the egocentric distance of a target on the far surface will be underestimated. Our previous findings in the real 3D environment have shown that observers underestimated the target distance across a texture boundary. Here, we used the virtual reality (VR) system to first test distance judgments with a distance-matching task. We created the texture boundary by having virtual grass and cobblestone textured patterns abutting on a flat (horizontal) ground surface in Experiment 1, and by placing a brick wall to interrupt the continuous texture gradient of a flat grass surface in Experiment 2. In both instances, observers underestimated the target distance across the texture boundary, compared to the homogeneous-texture ground surface (control). Second, we tested the proposal that the far surface beyond the texture boundary is perceived as slanted upward. This was done by using a virtual checkerboard-textured ground surface that was interrupted by a texture boundary. We found that not only was the target distance beyond the texture boundary underestimated relative to the homogeneous-texture condition, but the far surface beyond the texture boundary was also perceived as relatively slanted upward (Experiment 3). Altogether, our results confirm the predictions of the SSIP hypothesis.
1 Introduction
The physical space that spans about 2-25 meters from the observer is an important operational range for space perception and visual guidance of actions. A number of studies have found that within this intermediate distance range, human observers can accurately judge the egocentric distance of a target located on a continuous ground surface with homogeneous texture (Creem-Regehr et al 2005; Elliott 1987; Loomis et al 1992, 1996; Ooi et al 2001; Philbeck 2000; Rieser et al 1990; Sinai et al 1998; Thomson 1983; Wu et al 2004). But how does the visual system obtain the accurate egocentric distance? Specifically, what depth information in the environment is used by the visual system? According to the Ground Theory advanced by J J Gibson (1950, 1979), the distance information on the ground surface that extends from one's feet to the horizon is critical for space perception (also see Sedgwick 1983, 1986).
Recent studies support the notion that the visual system constructs a ground surface representation for use as a reference frame to localize objects on the ground. When the ground representation was based on “non-optimal” ground surface information in the real 3D environment, for instance, when the ground surface between the observer and the target was interrupted by a gap, a partially occluding obstacle, or an abrupt change in texture (concrete vs. grass field), judged egocentric distance of the target was underestimated (He et al 2004; Sinai et al 1998). On the other hand, when the ground surface representation was accurately constructed, it could be used in conjunction with the angular declination (height in the field) of the target to derive the target's egocentric distance (Ooi et al 2001, 2006; Philbeck and Loomis 1997; Wallach and O'Leary 1982; Wu et al 2004; Wu et al 2005). Furthermore, when the ground surface is not visible in the dark (i.e., no external depth information to delineate the ground surface), the visual system relies on its intrinsic bias, which can be approximated as an implicit surface that slants upward from the ground toward the frontoparallel plane, to determine the location of a dimly lit target (Ooi et al, 2001, 2006). As such, a dimly lit target on the ground surface in a completely dark environment is perceived at the intersection between its projection line from the eye and the implicit slant surface. It is as if the intrinsic bias in the dark has a similar function (reference frame) as the ground surface in the full cue environment. The significance of the ground surface in space perception has also been demonstrated with displays presented on the computer screen that simulated the ground surface environment (Bian et al 2005; Feria et al 2003; Madison et al 2001; McCarley and He 2000; Meng and Sedgwick 2001, 2002; Wu 2004).
We have proposed a Sequential Surface Integration Process (SSIP) hypothesis to explain how the visual system constructs the ground surface representation (He et al 2004; Wu et al 2004). According to the hypothesis, the SSIP begins by representing the near ground surface (<2-3 m) with the aid of a variety of near depth cues on the ground surface about one's feet (vergence, binocular disparity, motion parallax, etc.). An accurate representation of the near ground surface is critical to the SSIP. This is because the near ground representation is used by the SSIP as a template for integrating the farther patches of the ground surface, whose main viable depth cue is the texture gradient information. Thus, if the texture gradient (retinal image) changes continuously from the near ground surface patch to an adjacent (and farther) surface patch, the SSIP will represent the adjacent (farther) surface patch with the same slant as the near ground representation. In a sequential manner, the SSIP proceeds forward until the farthest ground surface patch is integrated, culminating in a global ground surface representation. An important assumption required of the SSIP for obtaining an accurate global ground surface representation is that the ground surface has a homogeneous texture pattern. (This assumption is reasonable since an abrupt change in the texture gradient is highly correlated with a surface separation in the real 3D environment.) When this assumption is violated, such as when the near and far ground surface areas are covered by two different texture patterned-surfaces, which produces an abrupt change in the texture gradient at the boundary between the two patternedsurfaces, the SSIP will be impacted.
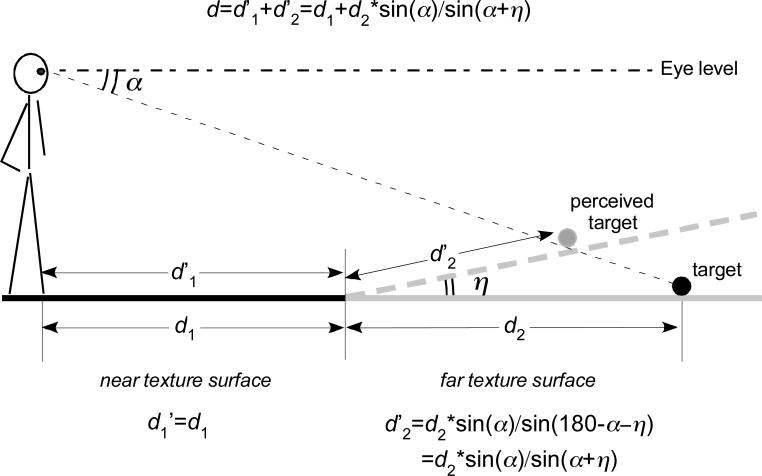
Figure 1 depicts a scenario (side view) where the SSIP is impacted at the texture boundary between a near texture surface (black line) and a far texture surface (gray line) by different texture patterns. To construct a representation of the far texture surface located beyond the texture boundary, the SSIP has to start anew with a second template surface, for use in integrating the more distant surface patches. The SSIP, however, cannot form an accurate second-template surface based on the far texture surface information. This is because the far texture surface is in the intermediate distance range (>2-3 m) where reliable near depth cues are no longer available to accurately construct/represent the second-template surface. Confronted with unreliable extrinsic depth information, the construction of the second-template surface becomes more reliant on the intrinsic bias of the visual system. Doing so causes the secondtemplate surface to be represented with a slant error, η (He et al 2004; Ooi et al 2001, 2006). Thus, the second-template surface representation will be slanted upward by η, with its far-end toward the frontoparallel plane. [The intrinsic bias takes the form of an implicit slant surface that curves up from near to far (Ooi et al, 2006). In theory, the far texture surface is represented as a curved surface. But for simplicity, we are approximating the far texture surface representation as having a constant slant error, i.e., as a slant plane surface.] When the SSIP uses this second-template surface to represent the farther surface patches, these patches will also have the slant error (η). Consequently, the egocentric distance of a target on the far texture ground surface can be described by the equation d=d1+d2*sin(α)/sin(α+η), where d=target distance and α=angular declination of the target below the eye level. The positive sign of η in the equation indicates a slant upward from the ground toward the frontoparallel plane; a negative value of η would indicate a slant downward (opposite direction). Since d is smaller than d1+d2, the target distance will be underestimated.
Figure 1.
The slant hypothesis. A texture boundary is created when two different texture surfaces (depicted in side view as black and gray lines) abut on a flat ground surface. According to the SSIP hypothesis, the far texture surface will not be represented as coplanar with the near texture surface. Instead, the far texture surface will be subjected to the influence of the visual system's intrinsic bias. This leads the far texture surface to be represented with a slant error, η; hence, its upward slant representation (gray dash line). Accordingly, d’1=d1 and d’2=d2*sin(α)/sin(α+η), in which the latter is derived from the trigonometric relationship, d’2/sin(α)=d2/sin(180-α-η). Thus, the perceived egocentric distance of a target on the far texture surface (d=d’1+d’2) is less than the actual physical distance (d1+d2).
There is empirical support for the analysis above (figure 1) (He et al 2004; Sinai et al 1998; Wu et al 2004). For example, Sinai et al (1998) found that when an observer in the real 3D environment stood on the concrete surface to judge a target located on the grass surface, he/she underestimated the egocentric target distance. A similar underestimation of distance occurred when the target was located on the concrete surface and the observer viewed from the grass surface.
To reiterate, the analysis depicted in figure 1 (the slant hypothesis) is based on the SSIP hypothesis that the ground surface representation is influenced by both the environmental depth cues and the visual system's intrinsic bias (Ooi et al 2001, 2006). The influence of the intrinsic bias increases when the extrinsic depth cues are insufficient, which causes a flat (horizontal) surface to be represented with a slant error, η. This affects the SSIP's construction of the second-template surface for representing the far texture surface beyond the texture boundary.
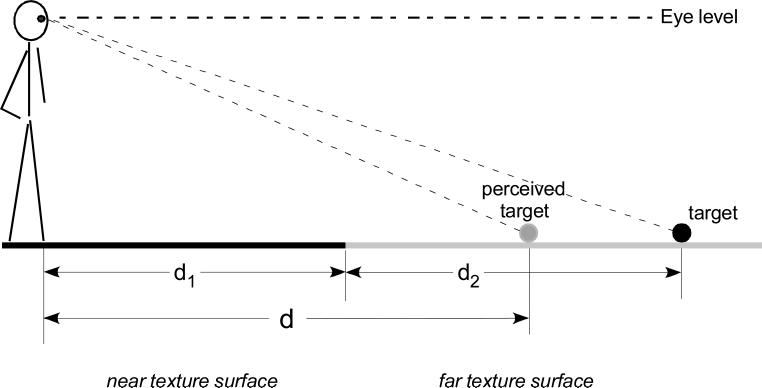
Indeed, the findings by Sinai et al (1998) suggest that the surface beyond the texture boundary is perceived as slanted. This is because the observation of distance underestimation of a target located beyond the texture boundary is consistent with the prediction depicted in figure 1. Yet, one could still argue that a possibility exists that the far texture surface is represented as horizontally compressed (figure 2: the horizontal compression hypothesis), and not as slanted upward (figure 1). Being represented as horizontally compressed could also lead to distance underestimation. In view of this, the goal of the current paper is to investigate the hypothesis that human observers perceive the far texture surface as slanted upward.
Figure 2.
The horizontal compression hypothesis. Instead of the slant hypothesis (figure 1), the egocentric distance underestimation observed when the flat ground surface has a texture boundary could be explained by an alternative horizontal compression hypothesis. It predicts that a horizontal compression of the far texture surface representation leads to the egocentric distance of a target on the far surface (d) being perceived as less than the actual distance (d1+d2).
A straightforward way of verifying the two hypotheses (slant hypothesis vs. horizontal compression hypothesis) is to measure the observer's perceived slant of the far texture surface in the real 3D environment. This, however, is not very practical since one cannot easily vary the slant of the far texture ground surface in the real 3D environment. Therefore, we conducted our experiments in the virtual reality (VR) environment and measured both the observer's perceived target distance and perceived slant of the far texture surface. Our first two experiments tested the observer's judged distance of a target on the far texture surface beyond the texture boundary. The texture boundary was created by having two different texture regions on the ground surface in Experiment 1, and by having a vertical wall partially occluding part of the ground surface in Experiment 2. Both experiments showed that the observer underestimated distance, which confirm previous findings in the real 3D environment (He et al 2004; Sinai et al 1998). Experiment 3 tested the two opposing hypotheses by measuring both the perceived target distance and the perceived slant of the far texture surface that supported the target. Our results indicate that the observer underestimated the target distance and had a bias for perceiving the far texture surface as slanted upward, thus, confirming the slant hypothesis.
2 Experiment 1. Judged egocentric distance beyond a texture boundary
As mentioned above, a previous study in our laboratory showed that observers underestimated the egocentric distance of a target located beyond a texture boundary in the real 3D environment (Sinai et al 1998). Such an underestimation was revealed both when the observers were tested using the blindfolded walking and perceptual distance-matching tasks. We now used the perceptual distance-matching task in a virtual visual environment to replicate Sinai et al's study. The virtual reality (VR) environment was provided to the observer using a head-mounted-display (HMD) that was fitted with a head-tracker. The goal of this study was to investigate if our previous finding in the real 3D environment could be reproduced in the virtual environment generated by the VR system.
2.1 Methods
2.1.1 Observers
Eight observers who were naïve to the purposes of the study participated in all the three experiments reported in this paper. These observers had normal or corrected-to-normal vision and stereo acuity of 40 sec of arc or better. They all provided informed consent before the experiments.
2.1.2 Instruments and stimuli
The VR system comprised of a Dell Precision 350 Workstation with an nVidia Quadro4 XGL900 graphics card, coupled with an IS-600 Mark2 tracking system (6-DOF tracking with a sampling rate of up to 150 Hz; Intersense, Inc.). A V8 head-mounted-display (HMD) with 60° diagonal field of view and a 640×480 pixel resolution (Virtual Research Systems, Inc) was used to display the visual stimuli. EAI's WorldUp software was used to create the virtual environment. A head tracker mounted on the HMD continuously monitored the observer's head position and orientation. In this way, the virtual environment could be displayed from the correct viewpoint and updated in real-time.
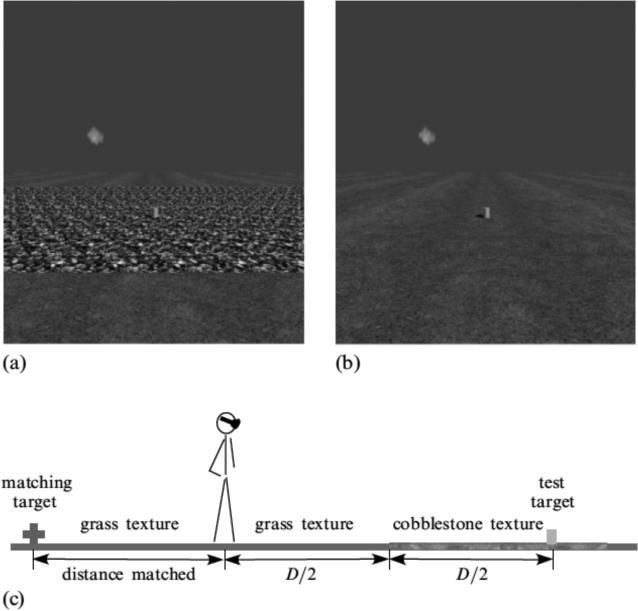
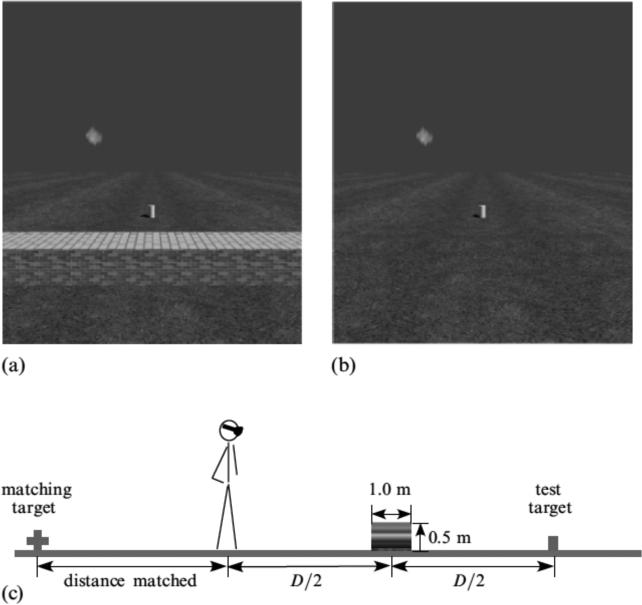
Two display modes were used to create the 3D virtual environment. The first, bi-ocular display mode where the two eyes see the same images (Andersen et al, 1998; Koenderink et al, 1994) included motion parallax (induced by self-motion) and texture gradient information on the ground surface. The second, stereoscopic display mode had binocular disparity information added to the bi-ocular display mode with the motion parallax and texture gradient information. For both display modes, two ground surface conditions were tested. Condition 1 was a discontinuous-texture condition in which a grass-textured field and a cobblestone-textured field covered the flat ground surface (figure 3a). The texture boundary created between the grasstextured field and the cobblestone-textured field was always set halfway in between the observer and the test-target (figure 3c). In addition, the grass field was always set to be the nearer of the two texture surfaces. Condition 2 was a homogeneous-texture condition in which a continuous grass-textured field covered the flat ground surface (figure 3b). It essentially served as the baseline control. For both conditions, the test-target was randomly selected from a set of 36 possible objects of different shapes and sizes with 6 different colors [rods: 0.3m(height) × 0.09m(radius) or 0.24m(height) × 0.18m(radius); cones: 0.24m(height) × 0.18m(base radius) or 0.3m(height) × 0.12m(base radius); spheres: 0.2m(vertical radius) × 0.08m(horizontal radius), 0.15m(vertical radius) × 0.15m(horizontal radius)]. The matching-target employed in the perceptual distance-matching task was a 3D-cross (0.3m × 0.3m), and it was always presented on the homogeneous grass field (figure 3c).
Figure 3.
The VR displays used in Experiment 1. (a) In the discontinuous-texture condition, a grass-textured field and a cobblestone-textured field covered the flat ground surface. (b) In the homogeneous-texture condition, a continuous grass-textured field covered the flat ground surface. (c) An illustration (side view) of the general layout for measuring the judged target distance in the discontinuous-texture condition. The observer stood on the grass-textured field to view the test-target on the cobblestone-textured field. The texture boundary between the two textured-fields was always set halfway in between the observer and the test-target. To respond to the perceived distance, the observer turned around by 180° to view the grass-textured field and performed a distance-matching task.
2.1.4 Procedures
We measured the observer's eye height (physical height from the eye to the feet on the ground) before the experiment, for use in rendering the 3D virtual environment around the observer. At the start of the experiment, the observer donned the HMD to fit snugly to ensure a proper view of the VR environment. The observer was then asked to explore the various structures in the virtual display to familiarize himself/herself to the VR environment. This was done by encouraging the observer to look in all directions and walk about until he/she felt immersed in the virtual environment. Thereafter, the observer performed 12 practice trials using the distance-matching task.
At the beginning of a trial, the observer viewed the test-target on the test ground surface and estimated its egocentric distance (a virtual, thick yellow line on the ground represented the location of the observer's feet). The observer was explicitly told to judge the egocentric distance from the yellow line to the target. When he/she was ready to respond, he/she turned his/her body around (the vertical axis) by 180 deg to view a matching-target on a homogeneous grass field (figure 3c). By using the arrow keys on the computer keyboard, the observer adjusted the egocentric distance of the matching-target until it appeared at the same distance to him/her as the test-target. The observer was permitted to turn around multiple times to compare the two distances on the test and matching surfaces, and to make the necessary distance adjustment in the matching-target until he/she was satisfied. When the observer was satisfied with the setting of the matching-target, he/she verbally informed the experimenter, who then pressed a key that led to a full-screen presentation of a random-dots mask for 1.3 sec to end the trial. The next trial began after the mask display was withdrawn. No feedback regarding the performance was given to the observer. A typical test trial during the experiment took less than 2 min, and the entire block of 16 trials took about 35 min.
For both conditions, and using both the stereoscopic and bi-ocular display modes, the test-target was placed at one of four predetermined distances (5m, 7m, 9m, and 11m) on the ground. Each distance was measured twice and their average was taken as the final result. There were 16 randomized trials [2(repeats) × 4(distances) × 2(display-modes)] for each condition tested. The testing order of the two conditions was counterbalanced across the observers.
2.2 Results and discussion
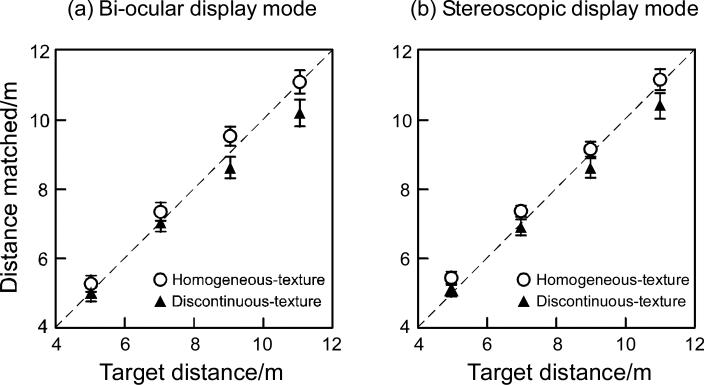
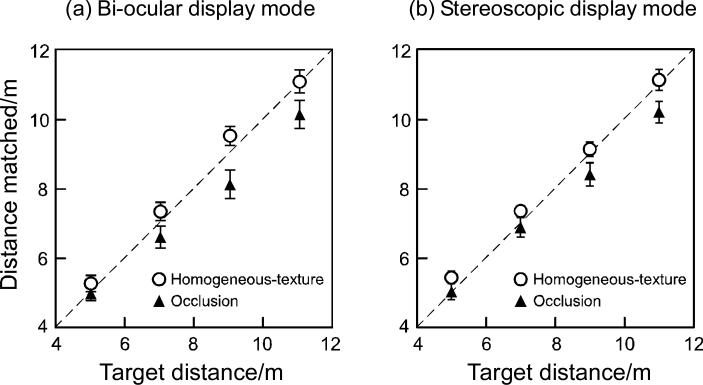
Figures 4a and 4b plot the average matched distances for the four test-target distances in the two conditions, with the bi-ocular and stereoscopic display modes, respectively. Both graphs show that the matched distances were underestimated in the discontinuous-texture (grass/cobblestones) condition compared to the homogeneous-texture condition (F(1,7)=36.113, p<0.001; three-way ANOVA with repeated-measures). The magnitude of the distance underestimation in the discontinuous-texture condition increased with the test-target distance (interaction effect of texture-continuity × distance: F(3,21)=4.170, p<0.02). There was no significant effect of the two different display modes on the results of the discontinuous-texture condition. Overall, these results are in agreement with the previous finding by Sinai et al (1998), where observers underestimated the egocentric distance of a target across the texture boundary in the real 3D environment. A three-way repeated-measures ANOVA (display × distance × surface-continuity) found no significant main effect of the display types (bi-ocular vs. stereoscopic displays), nor significant interaction effects involving this factor [Main effect: F(1,7)=0.184, p=0.681; interaction effect of display × distance: F(3,21)=2.349, p=0.102; interaction effect of display × surface-continuity: F(1,7)=2.123, p=0.188; interaction effect of display × distance × surfacecontinuity: F(3,21)=1.110, p=0.367].
Figure 4.
Results of Experiment 1 with displays presented in the bi-ocular (a) and stereoscopic (b) modes. The average matched distances were underestimated in the discontinuous-texture condition compared to the homogeneous-texture condition (n=8).
A number of studies that measured judged egocentric distance in the virtual environment created by a VR system similar to ours (using the head-tracker and HMD) have found, in general, that performances in the virtual environment were not as veridical as in the real 3D environment (Bingham et al 2001; Ellis and Menges 1997; Knapp and Loomis 2004; Loomis et al 1999 Loomis and Knapp 2003; Tcheang et al 2005; Thompson et al 2004; Wann et al 1995; Witmer and Sadowski 1998). These studies suggest that more research is needed to improve the immersive quality of the virtual environment, and at the same time, raises a concern regarding the results obtained using the VR system. Mindful of this concern, we nonetheless, believe that the interpretation of our results is less affected by the shortcoming of the VR system. This is because our results are based on the comparison between two texture conditions in the virtual environment. Therefore, the imperfection of the VR system would induce a systematic error that affects both texture conditions. To further demonstrate the utility of the VR system, Experiment 2 below showed distance underestimation when an obstacle partially occluded the ground surface.
3 Experiment 2. Judged egocentric distance beyond an obstacle (brick wall)
He et al (2004) found that when an observer was instructed to judge the egocentric distance of a target directly in front of himself/herself, he/she underestimated the target distance if an obstacle was added to an otherwise homogeneous ground surface. This is because the obstacle partially occluded the texture of the ground surface, which according to the SSIP hypothesis interrupts the continuous surface integration from the near texture to the far texture surface. The current experiment replicated this finding in the virtual environment.
3.1 Methods
3.1.1 Stimuli and procedures
The same VR setup as in Experiment 1 was used to create the virtual environment display. Figures 5a and 5b show the two virtual ground conditions tested, which are, respectively, the occlusion condition and the homogeneous-texture condition. The latter condition was the same one as the homogeneous-texture condition (baseline control) in Experiment 1. The occlusion condition comprised of a brick wall [0.5m(height) × 1m(depth) × 10m(width)] on an otherwise homogeneous grass field. The brick wall was always placed halfway in between the observer and the test-target (figure 5c). The test-target was placed at one of four pre-determined distances (5m, 7m, 9m, and 11m) on the ground. Both the bi-ocular and stereoscopic viewing modes were used to generate the virtual environments in the two conditions tested. The observers followed the same experimental procedures as in Experiment 1.
Figure 5.
The VR displays used in Experiment 2. (a) In the occlusion condition, a brick wall occluded part of the flat, grass-textured ground surface. (b) In the homogeneous-texture condition, a continuous grass-textured field covered the flat ground surface. (c) An illustration (side view) of the general layout when measuring the judged target distance in the occlusion condition. The observer stood on the grass-textured field to view the test-target on the grass surface beyond the brick wall. The brick wall (0.5m × 1m) was always set halfway in between the observer and the test-target. To respond to the perceived distance, the observer turned around by 180° to view the grass-textured field and performed a distance-matching task.
3.2 Results
Figures 6a and 6b show the average matched distances with the bi-ocular and stereoscopic display modes, respectively. Consistent with our previous finding in the real world environment (He et al, 2004), the observers significantly underestimated distances in the occlusion condition (F(1,7)= 21.113, p<0.01; three-way ANOVA with repeated-measures). The magnitude of the underestimation in the occlusion condition increased with target distance (interaction effect of occlusion x distance: F(3,21)=5.384, p<0.01). Although the magnitude of distance underestimation was slightly smaller with the stereoscopic display mode compared to the bi-ocular display mode, the difference was not statistically significant [Main effect: F(1,7)=1.904, p=0.207; interaction effect of display × distance: F(3,21)=0.876, p=0.469; interaction effect of display × occlusion: F(1,7)=1.439, p=0.269; interaction effect of display × distance × occlusion: F(3,21)=1.238, p=0.321)].
Figure 6.
Results of Experiment 2 with displays presented in the bi-ocular (a) and stereoscopic (b) modes. The average matched distances were underestimated in the occlusion condition compared to the homogeneous-texture condition (n=8).
3.3 Discussion and a control experiment for the SSIP hypothesis
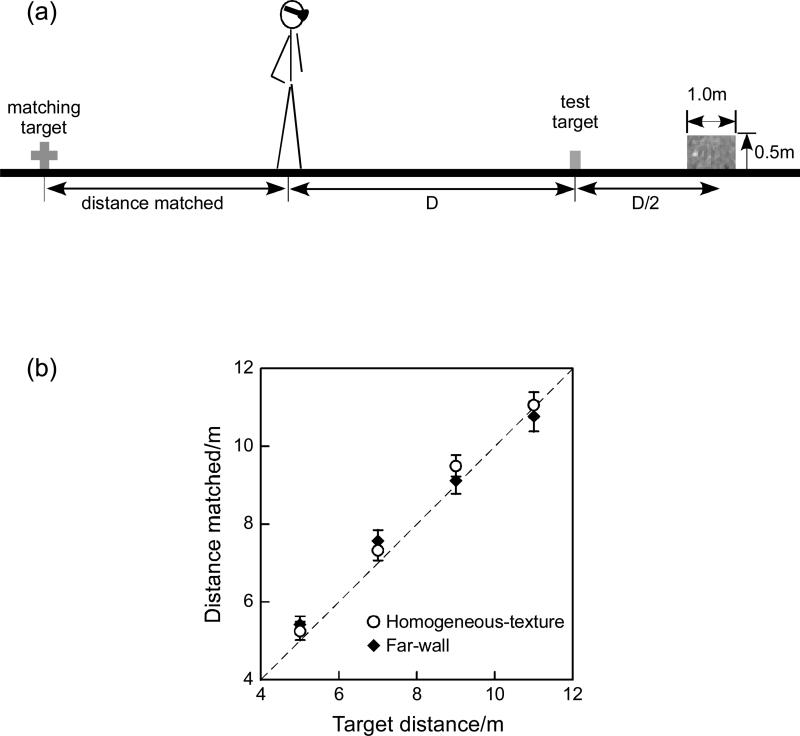
When one reexamines the visual scenes in figures 5a and 5b, one might ask if the target distance underestimation was due to the “attraction” of the target toward the brick wall in the occlusion condition. This explanation is based on the well known “equidistance tendency” phenomenon (Gogel 1965; 1990), where the depth separation between two neighboring objects in a reduced viewing environment and sometimes even in a well-structured visual environment tends to be underestimated. Thus the equidistance tendency phenomenon, if applied to the occlusion condition in figure 5a, predicts that the target would appear closer (attracted) to the brick wall. This explanation could also apply to the discontinuous-texture condition in Experiment 1 above. Arguably, the equidistance tendency phenomenon (mechanism) is more likely to operate in the virtual environment scene that carries fewer depth cues than in the real environment scene. To evaluate the equidistance tendency phenomenon explanation, we created a virtual environment where a brick wall was placed beyond the target on the ground (figure 7a, far-wall condition). The equidistance tendency phenomenon explanation predicts that the observer will overestimate the target distance since the target will be attracted to the far brick wall. On the other hand, the SSIP hypothesis predicts an accurate distance judgment since the grass surface between the observer and the target is homogeneous. In other words, the far brick wall should not directly impact the SSIP's ability to form an accurate ground surface representation.
Figure 7.
(a) A (side view) schematic of the layout used in the control experiment to test the equidistance tendency phenomenon explanation. In the far-wall condition shown, a brick wall (0.5m × 1m) was placed beyond the test-target. The distance of the far brick wall to the testtarget was always set at half the physical distance between the observer and the test-target. To respond to the perceived distance, the observer turned around by 180° to view the grass-textured field and performed a distance-matching task. (b) The average results indicate that no systematic distance overestimation was found in the far-wall condition compared to the homogeneoustexture condition (n=8).
3.3.1 Control experiment
The same observers as above performed the perceptual distance-matching task in both the homogeneous-texture (baseline control) and far-wall conditions. The visual scene in the homogeneous-texture condition was the same as in the main experiment (figure 5b; grass field). The visual scene in the far-wall condition (with grass-textured field) had the distance of the far brick wall to the test-target set at half the physical distance between the test-target and the observer (figure 7a). Only the bi-ocular display mode was used for testing in both conditions. The same testing procedures as in the main experiment were used.
The average judged distances are plotted in figure 7b. No systematic distance overestimation was found in the far-wall condition compared to the homogeneous-texture condition [F(1,7)=0.037, p>0.8, partial η2=0.005; F(3,21)=2.981, p>0.05, partial η2=0.005; twoway ANOVA with repeated measures]. Since no statistically significant effects were found, we performed a power analysis to assess if the sample size was sufficiently large. First, we assumed that the distance estimation in the control experiment would be of a similar magnitude to a distance underestimation caused by placing the same wall before the target. We found the power analysis revealed that our sample size was sufficient to detect a significant overestimation, had one existed (power > 0.97 at the 0.05 alpha level). Second, we found that the sample size was sufficient to detect a significant interaction of distance x occlusion with a power of > 0.71, at the 0.05 alpha level. Clearly, this finding does not support the equidistance tendency phenomenon explanation that predicts an overestimation in the far-wall condition. Instead, it is consistent with the distance underestimation prediction of the SSIP hypothesis.
4 Experiment 3. Judged egocentric distance and the slant of the far texture surface beyond the texture boundary
Experiments 1 and 2 above demonstrated that an observer underestimated the egocentric distance in the virtual environment when the target was seen beyond a texture boundary. These experiments replicate previous findings in the real 3D environment (He et al 2004; Sinai et al 1998), and support the prediction of distance underestimation by the SSIP hypothesis. Fundamental to the SSIP hypothesis is the proposal that the distance underestimation stems from a slant ground surface representation when the homogeneous texture information on the ground is disrupted (see figure 1 where the far surface is perceived as slanted upward toward the frontoparallel plane). The current experiment examined this slant surface representation prediction by testing two opposing hypotheses (slant hypothesis vs. horizontal compression hypothesis; see figures 1 and 2).
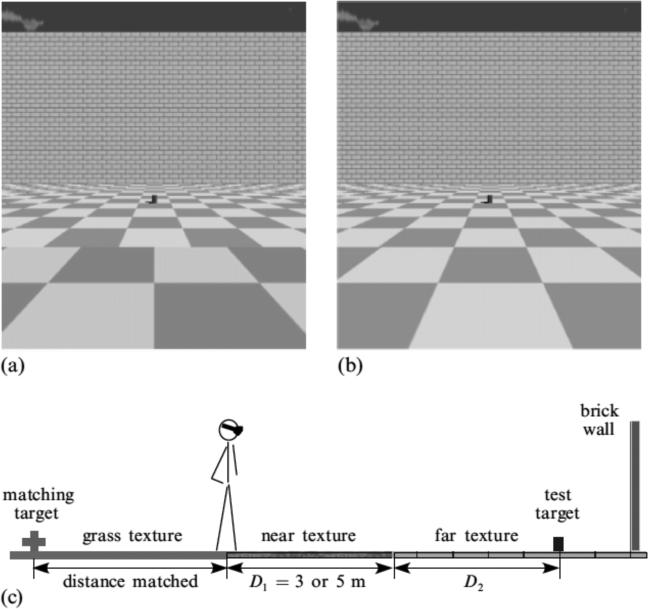
Figures 8a and 8b show the virtual visual conditions tested. The discontinuous-texture condition (figure 8a) had a phase shift between the near and far checkerboard-textured surfaces, which created an explicit texture boundary. The visibility of the texture boundary was enhanced by the color difference between paired tiled components of the near and far checkerboardtextured surfaces. The homogeneous-texture condition (figure 8b, baseline control) had the ground surface covered with regular checkerboard tiles. For each condition, we performed two types of measurements. The first was a distance judgment measurement (as in Experiments 1 and 2), in which we tested the perceived distance of a target beyond the texture boundary using the perceptual distance-matching task. The second was a surface-slant judgment measurement, in which we tested the perceived slant of the far texture surface by asking the observer to adjust its perceived slant (controlled with a computer keyboard) until it appeared coplanar with the near texture surface. According to the slant hypothesis, the observer will set the far checkerboard-textured surface as slanted downward to compensate for the bias due to the slant error (figure 9), in order to perceive the near and far checkerboard-textured surfaces as coplanar. The horizontal compression hypothesis, on the other hand, predicts that the observer will set the far checkerboard-textured surface as coplanar with the near checkerboard-textured surface.
Figure 8.
The VR displays used in Experiment 3. (a) In the discontinuous-texture condition, an explicit texture boundary was created by a 90° phase shift between the near and far checkerboard-textured surfaces. (b) In the homogeneous-texture condition, regular checkerboard tiles covered the ground surface. For both conditions, a vertical brick wall was placed at the farend of the checkerboard-textured surface to block the horizon. (c) An illustration (side view) of the general layout when measuring the judged target distance in the discontinuous-texture condition. The observer stood on the near checkerboard-textured surface to view the test-target on the far checkerboard-textured surface. The distance of the texture boundary from the observer was either 3m or 5m. To respond to the perceived distance, the observer turned around by 180o to view the grass-textured field and performed a distance-matching task.
Figure 9.
A (side view) schematic depicting the general layout in the surface-slant judgment measurement (discontinuous-texture condition) in Experiment 3. In the virtual environment, the observer stood on the flat, near checkerboard-textured surface to judge if the near and far checkerboard-textured surfaces were coplanar. The slant of the far checkerboard-textured surface was initially set at a random value between +12° (downward) and −12° (upward). The distance of the texture boundary from the observer was 3m, 4m or 5m.
4.1 Methods
4.1.1 Stimuli
Only the stereoscopic display mode was used in the current experiment. The regular checkerboard-textured floor in each condition (figures 8a and 8b) had alternating colored tiles (0.4×0.4m). Additionally, in the discontinuous-texture condition (figure 8a) a relative horizontal displacement (90° phase shift) was created between the near and far regions of the checkerboard pattern. These near and far checkerboard regions (texture surfaces) were painted with different colors (magenta/cyan vs. tan/light-wheat) to enhance their common texture boundary. In the experiment, the assignments of the paired tile colors to the near and far checkerboard-textured surfaces were fully counterbalanced. The distance between the texture boundary and a virtual yellow line reference (observer's feet) in the virtual environment was set at one of two distances (3m or 5m) for the distance judgment measurement (figure 8c), and one of three distances (3m, 4m, or 5m) for the surface-slant judgment measurement (figure 9).
A vertical brick wall was placed at the far-end of the far checkerboard-textured surface in both conditions, to block the view of the vanishing line of the far checkerboard-textured surface at infinity. This was to prevent the observer from using the height of the vanishing line as a cue for judging the surface orientation of the far checkerboard-textured surface in the discontinuoustexture condition. Arguably, without the wall, the observer could use the height of the vanishing line in the projection plane to judge the slant of the far checkerboard-textured surface (Sedgwick 1986). For example, a vanishing line that was above the horizon in the projection plane would indicate that the far checkerboard-textured surface was slanted upward. Before the experiment, the observers were informed that the absolute distance of the wall would change in a random manner from trial to trial (20m-40m), and therefore, they were discouraged from using the distance between the target and the wall to determine the target's egocentric distance. They were explicitly told to judge the egocentric distance from the virtual yellow line (reference for their feet) to the target. The observers were also told not to use the relative height of the boundary of the far checkerboard-textured surface with the wall to judge the surface slant in the surface-slant judgment measurement.
Both the near and far checkerboard-textured surfaces were flat and coplanar in the distance judgment measurement. Similar to Experiment 1 the test-target was chosen from the (same) set of 36 different objects. It was placed at one of three distances from the yellow line reference (observer's feet) in the virtual environment (7m, 9m, or 11 m). The matching-target, a 0.3m × 0.3m plus sign, was placed on the flat grass field without a vertical wall at the far-end (figure 8c); essentially, it was the same matching display as the ones used in Experiments 1 and 2. In the surface-slant judgment measurement, the near checkerboard-textured surface was always flat whereas the orientation (slant) of the far checkerboard-textured surface was variable and adjustable.
4.1.2 Procedures
Each observer participated in both the distance judgment and surface-slant judgment measurements. The perceptual distance-matching task (in the distance judgment measurement) was the same one as in Experiments 1 and 2. There were 36 trials that included 24 trials for the discontinuous-texture condition [2(repeats) × 2(texture boundary distances) × 3(target distances) × 2(paired-color counterbalanced)], and 12 trials for the homogeneous-texture condition [2(repeats) × 2(paired-color counterbalance) × 3(target distances)]. The trials and their parameters were fully randomized within a single test block.
In the surface-slant judgment measurement, the near checkerboard-textured surface was always flat whereas the slant of the far checkerboard-textured surface was initially set at a random value between −12° and +12° (note: a negative value indicates a downward slant relative to the flat ground surface and a positive value indicates an upward slant). During the trial, the observer was instructed to face the texture display directly and to judge if the near and far checkerboard-textured surfaces were coplanar, while avoiding making any unnecessary head or body movements. If the two surfaces did not appear coplanar, he/she should rotate the slant of the far checkerboard-textured surface upward or downward by pressing one of two keys on the computer keyboard until the two checkerboard-textured surfaces appeared coplanar. Once set, the observer should verbally informed the experimenter to end the trial. Twenty-four randomized trials [4(repeats) × 2(paired-color counterbalance) × 3(texture boundary distances)] were tested within a single block. All observers were tested in the distance judgment measurement before the surface-slant judgment measurement.
4.2 Results and discussion
We first examined whether the distance and surface-slant judgments were affected by the “texture order effect”, that is, by the colors of the texture patterns in the paired-colored tiles (magenta/cyan vs. tan/light-wheat colored tiles, figure 8a) that covered the near ground surface. For the distance judgment measurement, both the main effect of texture order [F(1,7)=4.125, p>0.08] and the interaction effects were not significant [texture order × distance: F(2,14)=1.304, p>0.3; texture order × boundary location: F(2,14)=0.373, p>0.5; texture order × distance × boundary location: F(2,14)=1.777, p>0.2]. Similarly, for the surface-slant judgment measurement, we found no significant effect of texture order [main effect: F(1,7)=0.002, p>0.9; interaction effects (texture order × boundary location): F(2,14)=0.603, p>0.5]. Overall, these analyses show that the texture order effect did not significantly affect the distance and surfaceslant judgment measurements. These analyses also permit us to justifiably combine the data obtained from testing with the two differently paired-colored tiles for further analyses (in figures 10 and 11).
Figure 10.
Results of Experiment 3 in the distance judgment measurement (n=8). Graphs (a) and (b), respectively, plot the average results when the texture boundary was 3m and 5m from the observer. Overall, the average judged distances were underestimated in the discontinuoustexture condition (filled symbols) compared to the homogeneous-texture condition (open symbols).
Figure 11.
Results of Experiment 3 in the surface-slant judgment measurement (n=8). Overall, the far checkerboard-textured surface had to be slanted downward for it to be perceived as coplanar with the near checkerboard-textured surface (filled diamonds). The derived, predicted slant errors, based on the judged distance (d) and the equation, d=d1+d2*sin(α)/sin(α+η), are plotted as the open circles. There is no significant difference in the magnitudes of the judged and predicted slant errors.
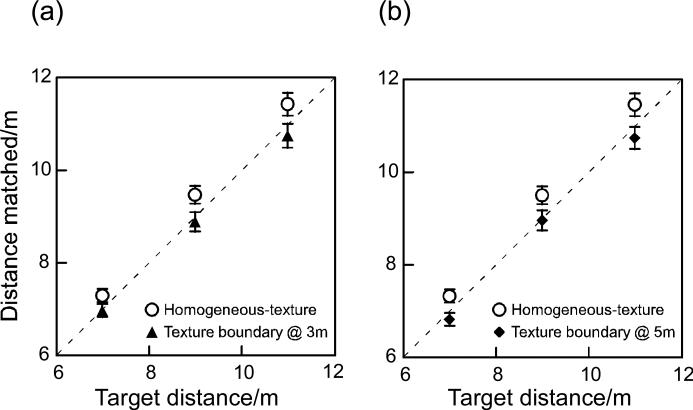
Figure 10a plots the average judged target distances in the homogeneous-texture condition (open circles) and the discontinuous-texture condition (triangles) when the texture boundary was 3m from the virtual yellow line reference (observer's feet). Figure 10b plots the data obtained when the texture boundary was 5m from the observer. The open circles are data from the homogeneous-texture condition and the diamond symbols are data from the discontinuous-texture condition. For both texture boundary distances, the data for the homogeneous-texture condition show distance overestimation (above the diagonal line) whereas the data for the discontinuous-texture condition show accurate judgment (almost on the diagonal line, figure 10). We believe this apparent paradox in which the distance data in the control (homogeneous-texture) condition were overestimated rather than accurate as in Experiments 1 and 2 can be attributed to the often observed phenomenon where distances are generally underestimated in the virtual reality environment that uses head mounted displays (e.g., Knapp & Loomis 2004; Thomson et al 2004; Witmer & Sadowski 1998). This fact was not evident in our Experiments 1 and 2 because we used the same grass surface as the test and matching scenes. But in the current Experiment 3, the test scene was a checkerboard-textured floor and the matching scene was a homogeneous grass surface. A checkerboard-texture floor at the far distance carries more effective depth information (e.g., linear perspective information) than a homogeneous grass surface. Therefore, when compared to the homogeneous grass surface, distances on the checkerboard-textured floor are, relatively speaking, “overestimated”.
However, the abovementioned “overestimation” error should not detract us from the goal of the current experiment, which is the comparison of distance judgments between the homogeneous-texture and discontinuous-texture conditions. This is because we used the same grass surface display as the matching scenes in both conditions. An examination of figures 10a and 10b clearly shows that the average judged distances were underestimated in the discontinuous-texture condition relative to the homogeneous-texture condition in both. This was confirmed by a two-way ANOVA with repeated measures (main effect). For texture boundary at 3m, F(1,7)=24.419, p<0.002; F(2,14)=3.287, p=0.068. For texture boundary at 5m, F(1,7)=35.655, p<0.001; F(2,14)=1.297, p=0.304.
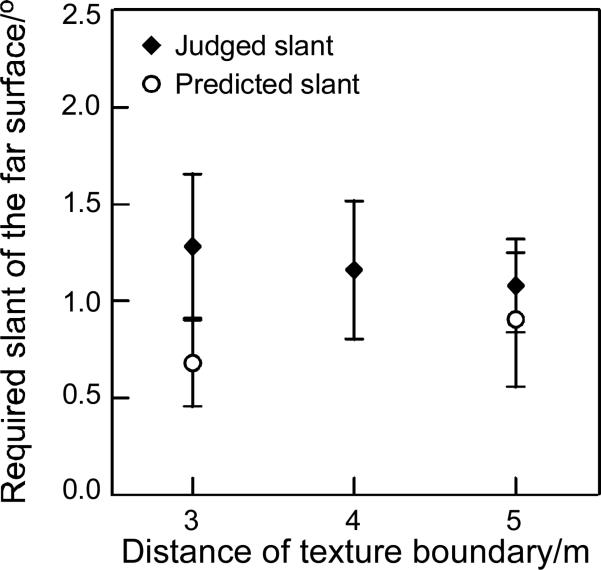
Figure 11 plots the average surface-slant judgment results (filled diamonds). Overall, the observers required the far checkerboard-textured surface to be slanted downward to perceive it as coplanar with the flat, near checkerboard-textured surface. The average slant judgment when the texture boundary was 3m from the observer's feet was 1.28°±0.37° (t(7)=3.457, p<0.025). The average slant judgment when the texture boundary was at 4m was 1.16°±0.36° (t(7)=3.255, p<0.025), and when the texture boundary was at 5m was 1.08°±0.24° (t(7)=4.492, p<0.025). The effect of texture boundary distance on the surface-slant judgment was not significant (F(1,7)=0.622, p=0.551, one-way ANOVA with repeated measures).
Assuming that the measured surface slant (downward) was used to compensate for, or to cancel, the visual system's tendency or bias to represent the flat, far checkerboard-textured surface as slanted upward, we can treat the average measured slant as the judged slant error, η, as depicted in figure 1. For each texture boundary distance, we can also derive the predicted slant error, η, with the judged distance (d) value obtained from the distance judgment measurement using the equation, d=d1+d2*sin(α)/sin(α+η). To do so, we first fitted each observer's judged distances with the equation using the least squares method, wherein we assume that the perceived egocentric distance to the texture boundary (d1) and angular declination of the target (α) are veridical. We then obtained the slant error (η) that provided the best fit (least squares method) for each of the two conditions tested (the discontinuous-texture and homogeneoustexture conditions). Subsequently, the difference in the slant errors between the two conditions is taken as the predicted slant error. This calculation was done for each observer's data, and the averages of all the observers’ predicted slant errors for the two texture boundary distances are plotted with the open circles in figure 11. Clearly, the predicted slant errors are quite close to the judged slant errors (filled diamonds); for the texture boundary at 3m, t(7)=1.699, p>0.1; for the texture boundary at 5m, t(7)=1.591, p>0.1. Altogether, the findings plotted in figures 10 and 11 support the prediction of the slant hypothesis that when the ground surface is disrupted by a texture boundary, the far ground surface beyond the boundary is perceived as slanted upward, rather than horizontally compressed. And, the egocentric distance of the target on the far ground surface beyond the texture boundary is underestimated.
Our findings also suggest that the effect of texture boundary on distance judgment cannot be attributed entirely to a perceptual mechanism that operates in 2-D space. Using computersimulated displays presented in the frontoparallel plane, Feria et al (2003) showed that their observers underestimated the distance between two objects separated by a texture boundary. This finding indicates that the perceived distance between two objects is affected by the context of the 2-D background. It also poses a potential challenge to our SSIP hypothesis that is based on an analysis of the 3-D space, as Feria et al's finding implies that the underestimation of distance does not depend on the texture gradient information. To investigate this issue, we conducted experiments similar to Feria et al (2003) by presenting the stimuli on a computer screen (Wu, 2004). We first showed, as they did, that when the texture surface was in the frontoparallel plane, a texture surface separated by a rectangular occluding surface resulted in distance underestimation. Then, we added perspective information to the same visual scene to scale the texture surface in 3-D depth, which rendered the texture surface to be seen as slanted into the distant. We found that this manipulation led to a significantly larger magnitude of underestimation error. Thus, our observation reveals that the effect of texture boundaries on distance perception is not caused solely by a distance mechanism that operates on the retinal image. In fact, our current study showing that the texture boundary can affect perceived surface slant in 3-D space further argues against the notion that a purely 2-D mechanism could underlie the texture boundary effect.
5 General discussion
Our study used a head-mounted-display (HMD) with a head-tracker to generate the virtual visual environment. We demonstrated that when the ground surface was spanned by different texture patterns, or was interrupted by an obstacle, observers underestimated the egocentric distances of targets beyond the texture boundary. This finding is consistent with previous observations in the real 3D environment. We further showed that, consistent with the finding of egocentric distance underestimation in a discontinuous-texture condition (figure 1), the far texture surface was perceived as slanted upward. In all, our findings support the predictions of the SSIP hypothesis, including the notion that the intrinsic bias is in the form of an implicit slant surface (He et al 2004; Ooi et al 2001; Wu et al 2004).
The visual system depends on both its intrinsic bias and the depth information on the ground surface to construct the ground surface representation (e.g., Ooi et al 2001; 2006; Wu et al, 2000; Wu J et al, 2004). Previous studies conducted in the intermediate distance range under various real environmental settings (darkness, reduced depth information and restricted visual field) have revealed three major lines of evidence for the influence of the intrinsic bias on the ground surface representation. First, we found that when the flat ground surface was not visible in the dark, the visual system could determine the egocentric location of a dimly lit target using the intrinsic bias (implicit slant surface) and the angular declination of the target. Admittedly, the target location determined in this way was inaccurate in most cases. For example, a target on the flat ground surface in the intermediate distance range was judged as higher and nearer since the implicit surface was slanted upward (around 13-15 deg) instead of being flat.
Second, we showed that the intrinsic bias affected space perception when the depth information on the ground surface was reduced (not optimal for the SSIP). Studies in our laboratory have found that the judged distance of a dimly lit target was more accurate when it was seen against an array of fluorescent dots or light emitting diodes (LEDs) (arranged in parallel) placed on the ground surface in an otherwise dark environment (background), than when there was no visible background (in complete darkness) (Wu et al 2002; Wu J et al 2004). Our data analysis revealed that the judged target locations could be fitted by an implicit surface that was slanted upward, though with a smaller slant magnitude than the slant of the implicit surface found in complete darkness (intrinsic bias) (Wu J et al 2004). Taken together, these suggest that the slant of the implicit surface that affects judged target location is influenced by the external depth information from the array of fluorescent dots or LEDs. In other words, the slant of the implicit surface is likely to be due to the weighted contribution of the external depth information and the visual system's intrinsic bias.
Third, the effect of the intrinsic bias on egocentric distance judgment was revealed when observers were deprived of the near depth information on the ground surface owing to a restricted visual field/environment (Creem-Regehr et al 2005; Dolezal 1982; Hagen et al 1978; Shah and Sedgwick 2004; Wu et al 2004). For example, we found that observers underestimated the target distance on the ground when they wore goggles that limited the visual field of view (to less than 21 deg in the vertical extent) (Wu et al 2004). We also found that the distance underestimation owing to the restricted field of view could be deduced from related data that assumed an upward slant ground surface representation. This suggests that the impact of the intrinsic bias on the ground surface representation increases when the near depth information is unavailable for the visual system to sample.
The current study provides a direct empirical support for the notion that the ground surface beyond a texture boundary is perceived as slanted upward. Our finding verifies the slant hypothesis, which predicts that the intrinsic bias contributes to the ground surface representation (figure 1). In addition, by negating the horizontal compression hypothesis (figure 2), our finding highlights an important conceptual difference between the two hypotheses. Namely, the slant hypothesis (figure 1) adopts a fundamental principle that in the formation of the perceptual space the egocentric direction of a point remains more or less veridical. In fact, the principle of veridical representation of egocentric direction has been observed in the dark environment (Ooi et al 2001, 2006, Wu et al 2000). Our previous studies found that whereas the judged location (distance and height) of a dimly lit target in the dark was inaccurate, its visual direction was more or less veridical. We believe that this principle of direction constancy also applies to space perception in the light environment. Following this assumption, it is clear that the horizontal compression hypothesis (figure 2) violates the principle of direction constancy. This serves as a further support against the argument that the far ground surface beyond the texture boundary is represented as horizontally compressed.
The discussion above also reveals a distinction between the concept of the intrinsic bias and Gogel's principle of equidistance tendency. The shape of the intrinsic bias is approximated as an implicit slant surface, which forms the basis of the slant hypothesis and not the horizontal compression hypothesis tested in the current study. On the other hand, the principle of equidistance tendency does not distinguish between the predictions of the slant hypothesis and the horizontal compression hypothesis. This difference can be taken as one justification for the concept of the intrinsic bias for understanding space perception in the intermediate distance range, at least for now.
Acknowledgment
This study was supported by a grant from the NIH (R01 EY014821) to both Z.J.H. and T.L.O.
Parts of the work reported in this paper have been presented in an abstract form elsewhere (Wu et al 2002).
References
- Andersen GJ, Braunstein ML, Saidpour A. The perception of depth and slant from texture in three-dimensional scenes. Perception. 1998;27:1087–1106. doi: 10.1068/p271087. [DOI] [PubMed] [Google Scholar]
- Bian Z, Braunstein ML, Andersen GJ. The ground dominance effect in the perception of 3-D layout. Perception & Psychophysics. 2005;67:815–828. doi: 10.3758/bf03193534. [DOI] [PubMed] [Google Scholar]
- Bingham GP, Bradley A, Bailey M, Vinner R. Accommodation, occlusion, and disparity matching are used to guide reaching: A comparison of actual versus virtual environments. Journal of Experimental Psychology: Human Perception & Performance. 2001;27:1314–1334. doi: 10.1037//0096-1523.27.6.1314. [DOI] [PubMed] [Google Scholar]
- Creem-Regehr SH, Willemsen P, Gooch A, Thompson W B. The influence of restricted viewing conditions on egocentric distance perception: Implications for real and virtual indoor environments. Perception. 2005;34:191–204. doi: 10.1068/p5144. [DOI] [PubMed] [Google Scholar]
- Dolezal H. 1982 Living in a world transformed: Perceptual and performatory adaptation to visual distortion. Academic Press; New York: [Google Scholar]
- Elliot D. Continuous visual information may be important after all: A failure to replicate Thomson (1983) Journal of Experimental Psychology: Human Perception and Performance. 1987;12:388–391. doi: 10.1037//0096-1523.12.3.388. [DOI] [PubMed] [Google Scholar]
- Ellis SR, Menges BM. Judgments of the distance to nearby virtual objects: Interaction of viewing conditions and accommodative demand. Presence: Teleoperators and Virtual Environments. 1997;6:452–459. doi: 10.1162/pres.1997.6.4.452. [DOI] [PubMed] [Google Scholar]
- Feria CS, Braunstein ML, Andersen GJ. Judging distance across texture discontinuities. Perception. 2003;32:1423–1440. doi: 10.1068/p5019. [DOI] [PubMed] [Google Scholar]
- Gibson JJ. The Perception of the Visual World. Houghton Mifflin; Boston, Mass: 1950. [Google Scholar]
- Gibson JJ. The Ecological Approach to Visual Perception. Erlbaum; Hillsdale, NJ: 1979. [Google Scholar]
- Gogel WC. Equidistance tendency and its consequence. Psychological Bulletin. 1965;64:153–163. doi: 10.1037/h0022197. [DOI] [PubMed] [Google Scholar]
- Gogel WC. A theory of phenomenal geometry and its applications. Perception and Psychophysics. 1990;48:105–123. doi: 10.3758/bf03207077. [DOI] [PubMed] [Google Scholar]
- Hagen MA, Jones RK, Reed ES. On a neglected variable in theories of pictorial perception: Truncation of the visual field. Perception & Psychophysics. 1978;23:326–330. doi: 10.3758/bf03199716. [DOI] [PubMed] [Google Scholar]
- He ZJ, Wu B, Ooi TL, Yarbrough G, Wu J. Judging egocentric distance on the ground: Occlusion and surface integration. Perception. 2004;33:789–806. doi: 10.1068/p5256a. [DOI] [PubMed] [Google Scholar]
- Knapp JM, Loomis JM. Limited field of view of head-mounted displays is not the cause of distance underestimation in virtual environments. Presence-Teleoperators and Virtual Environments. 2004;13:572–577. [Google Scholar]
- Koenderink JJ, Vandoorn AJ, Kappers A. On so-called paradoxical monocular stereoscopy. Perception. 1994;23:583–594. doi: 10.1068/p230583. [DOI] [PubMed] [Google Scholar]
- Loomis JM, Blascovich JJ, Beall AC. Immersive virtual environment technology as a basic research tool in psychology. Behavior Research Methods Instruments and Computers. 1999;31:557–564. doi: 10.3758/bf03200735. [DOI] [PubMed] [Google Scholar]
- Loomis JM, DaSilva J, Fujita N, Fukusima S. Visual space perception and visually directed action. Journal of Experimental Psychology: Human Perception & Performance. 1992;18:906–921. doi: 10.1037//0096-1523.18.4.906. [DOI] [PubMed] [Google Scholar]
- Loomis JM, DaSilva J, Philbeck JW, Fukusima S. Visual perception of location and distance. Current Directions in Psychological Science. 1996;5:72–77. [Google Scholar]
- Loomis JM, Knapp JM. Visual perception of egocentric distance in real and virtual environments. In: Hettinger LJ, Hass MW, editors. In Virtual and Adaptive Environments. Erlbaum; Hillsdale, NJ: 2003. pp. 21–46. [Google Scholar]
- Madison C, Thompson W, Kersten D, Shirley P, Smits B. Use of inter-reflection and shadow for surface contact. Perception & Psychophysics. 2001;63:187–194. doi: 10.3758/bf03194461. [DOI] [PubMed] [Google Scholar]
- McCarley JS, He ZJ. Asymmetry in 3-D perceptual organization: Ground-like surface superior to ceiling-like surface. Perception & Psychophysics. 2000;62:540–549. doi: 10.3758/bf03212105. [DOI] [PubMed] [Google Scholar]
- Meng JC, Sedgwick HA. Distance perception mediated through nested contact relations among surface. Perception and Psychophysics. 2001;63:1–15. doi: 10.3758/bf03200497. [DOI] [PubMed] [Google Scholar]
- Meng JC, Sedgwick HA. Distance perception across spatial discontinuities. Perception and Psychophysics. 2002;64:1–14. doi: 10.3758/bf03194553. [DOI] [PubMed] [Google Scholar]
- Ooi TL, Wu B, He ZJ. Distance determined by the angular declination below the horizon. Nature. 2001;414:197–200. doi: 10.1038/35102562. [DOI] [PubMed] [Google Scholar]
- Ooi TL, Wu B, He ZJ. Perceptual space in the dark affected by the intrinsic bias of the visual system. Perception. 2006;35:605–624. doi: 10.1068/p5492. [DOI] [PubMed] [Google Scholar]
- Philbeck JW. Visually directed walking to briefly glimpsed target is not biased toward fixation location. Perception. 2000;29:259–272. doi: 10.1068/p3036. [DOI] [PubMed] [Google Scholar]
- Philbeck JW, Loomis JM. Comparison of two indicators of perceived egocentric distance under full-cue and reduced-cue conditions. Journal of Experimental Psychology: Human Perception & Performance. 1997;23:72–85. doi: 10.1037//0096-1523.23.1.72. [DOI] [PubMed] [Google Scholar]
- Rieser JJ, Ashmead D, Talor C, Youngquist G. Visual perception and the guidance of locomotion without vision to previously seen targets. Perception. 1990;19:675–689. doi: 10.1068/p190675. [DOI] [PubMed] [Google Scholar]
- Sedgwick HA. Environment centered representation of spatial layout: available information from texture and perspective. In: Rosenthal A, Beck J, editors. In Human and machine vision. Academic Press; New York: 1983. pp. 425–458. [Google Scholar]
- Sedgwick HA. Space perception. In: Boff KR, Kaufman L, Thomas JP, editors. Handbook of Perception and Human Performance. Wiley; New York: 1986. pp. 21.1–21.57. [Google Scholar]
- Shah D, Sedgwick HA. Spatial compression and adaptation with the low vision telescope. Optometry and Vision Science. 2004;81:785–793. doi: 10.1097/00006324-200410000-00011. [DOI] [PubMed] [Google Scholar]
- Sinai MJ, Ooi TL, He ZJ. Terrain influences the accurate judgement of distance. Nature. 1998;395:497–500. doi: 10.1038/26747. [DOI] [PubMed] [Google Scholar]
- Tcheang L, Gilson SJ, Glennerster A. Systematic distortions of perceptual stability investigated using immersive virtual reality. Vision Research. 2005;45:2177–2189. doi: 10.1016/j.visres.2005.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson JA. Is continuous visual monitoring necessary in visually guided locomotion? Journal of Experimental Psychology: Human Perception & Performance. 1983;9:427–443. doi: 10.1037//0096-1523.9.3.427. [DOI] [PubMed] [Google Scholar]
- Thompson WB, Willemsen P, Gooch AA, Creem-Regehr SH, Loomis JM, Beall AC. Does the quality of the computer graphics matter when judging distances in visually immersive environments? Presence-Teleoperators and Virtual Environments. 2004;13:560–571. [Google Scholar]
- Wallach H, O'Leary A. Slope of regard as a distance cue. Perception & Psychophysics. 1982;31:145–148. doi: 10.3758/bf03206214. [DOI] [PubMed] [Google Scholar]
- Wann JP, Rushton S, Mon-Williams M. Natural problems for stereoscopic depthperception in virtual environments. Vision Research. 1995;35:2731–2736. doi: 10.1016/0042-6989(95)00018-u. [DOI] [PubMed] [Google Scholar]
- Witmer BG, Sadowski WJ. Nonvisually guided locomotion to a previously viewed target in real and virtual environments. Human Factors. 1998;40:478–488. [Google Scholar]
- Wu B, Ooi TL, He ZJ. Perceived object's location in the dark is not veridical, but not fortuitous. 2000;41:S228. [Abstract] ARVO. [Google Scholar]
- Wu B, He ZJ, Ooi TL. A ground surface based space perception in the virtual environment. Journal of Vision. 2002;2(7):513a. [Abstract] http://journalofvision.org/2/7/513/ [Google Scholar]
- Wu B. Doctoral dissertation. University of Louisville; Louisville, KY, USA: 2004. The Visual Perception of Distance in Action Space. [Google Scholar]
- Wu B, Ooi TL, He ZJ. Perceiving distance accurately by a directional process of integrating ground information. Nature. 2004;428:73–77. doi: 10.1038/nature02350. [DOI] [PubMed] [Google Scholar]
- Wu J, He ZJ, Ooi TL. Stimulus duration and binocular disparity factors in representing the ground surface and localizing object in the intermediate distance range. Journal of Vision. 2004;4(8):21a. [Abstract] http://journalofvision.org/4/8/21/ [Google Scholar]
- Wu J, Ooi TL, He ZJ. Visually perceived eye level and horizontal midline of the body trunk influenced by optic flow. Perception. 2005;34:1045–1060. doi: 10.1068/p5416. [DOI] [PubMed] [Google Scholar]