Limited knowledge of fraction representations differentiates middle school students with mathematics learning disability (dyscalculia) vs. low mathematics achievement

Abstract

Fractions pose significant challenges for many children, but for some children those challenges persist into high school. Here we administered a fractions magnitude comparison test to 122 children, from Grades 4 to 8, to test whether their knowledge of fractions typically learned early in the sequence of formal math instruction (e.g., fractions equivalent to “one-half,” and fraction pairs with common denominators) differentiates those with mathematical learning disability (MLD) versus low achievement (LA) or typical achievement (TA) in mathematics, and whether long term learning trajectories of this knowledge also differentiate these groups. We confirmed that although 4^th graders with LA (n = 18) or TA (n = 93) are more accurate evaluating one-half vs. non-half fractions (until they reach ceiling performance levels on both types of fractions), children with MLD (n=11) do not show a one-half advantage until Grade 7 and do not reach ceiling performance even by Grade 8. Both the MLD and LA groups have early difficulties with fractions, but by Grade 5 the LA group approaches performance levels of the TA group and deviates from the MLD group. All groups showed a visual model advantage over Arabic number representation of fractions, but this advantage was short lived for the TA group (because ceiling level was achieved across formats), slightly more persistent for the LA group, and persisted through Grade 8 for children with MLD. Thus, difficulties with fractions persist through Grade 8 for many students, but the nature and trajectories of those difficulties varies across children with math difficulties (MLD or LA).

Introduction

Fractions pose significant challenges for many children (Hecht, Vagi, & Torgesen, 2007; Mazzocco & Devlin, 2008) and adults (Stafylidou & Vosniadou, 2004). This is concerning because reliance on fractions is pervasive throughout daily life, during activities as varied as recipe conversion, calculating a tip, or determining appropriate medicinal doses based on, for instance, a person's body weight. That life-long difficulties with fractions persist is intriguing given that fractions are introduced by third grade and continue to be a focus of instruction throughout elementary and middle school (Common Core State Standards Initiative (CCSSI), 2010). Early difficulties in learning fractions is of significant concern, because elementary school students’ knowledge of fractions is a stronger predictor of their overall later high school mathematics achievement than is their elementary whole number arithmetic knowledge (Siegler, Duncan, Davis-Kean, Duckworth, Claessens, Engel, Susperreguy, & Chen, 2012). Thus, it is not surprising that the National Mathematics Advisory Panel (NMAP, 2008) described the teaching of fractions as critically important, and in need of improvement, if gains in student achievement in the U.S. are to be realized.

Efforts to improve children's knowledge of fractions include improving instruction, instructional materials, and mathematics curriculum (NMAP, 2008; Siegler et al., 2010). Here we propose that efforts should also focus on identifying individual differences in cognitive skills relevant to learning fractions – such as differences in the strength with which children's whole number knowledge interferes with learning fractions – and on identifying the children who are at greatest risk for life-long struggles. For instance, although the aforementioned “whole number bias” that interferes with learning fractions (Ni & Zhou, 2005) is a well-described source of early misconceptions (e.g., that ¼ is larger than ½ because 4 > 2; Behr, Harel, Post, & Lesh, 1992; Hartnett & Gelman, 1998), its persistence over time may vary across children. Typically developing children gradually abandon this whole number bias sometime between Grades 5 and 12, when they understand that quantities can be represented by a single numerical ratio (Stafylidou & Vosniadou, 2004) and that, therefore, fractions represent one quantity rather than two (the numerator and denominator). It is possible that some children do not experience this shift, or that children with a weak concept of whole numbers will lack this bias but face different obstacles to learning fractions.

Knowledge of the sources of errors in fractions knowledge informs instructional practices, as does information concerning the likelihood that obstacles to learning fractions will persist. In this study we evaluate whether subgroups of children can be characterized by distinct and measurable variation in their learning trajectories for rational number knowledge. Specifically, we test the notion that learning and performance trajectories from Grades 4 to 8, measured with magnitude comparisons involving fractions, vary as a function of whether children meet criteria for mathematical learning disability (MLD) versus low mathematics achievement not otherwise specified (LA), despite that fact that both of these groups of children have difficulty learning mathematics in general (Murphy, Mazzocco, Hanich, & Early, 2007; Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007) and fractions specifically (Mazzocco & Devlin, 2008). In the absence of a gold standard definition of MLD, we use cut off scores as a proxy classification, and in doing so we attempt to reduce false positives in our MLD sample by adopting a cut-off score closer to the MLD prevalence ratings reported of ~ 6 – 11% across many studies (Shalev, 2007).

We differentiate between these two low performing groups – MLD and LA – because of the growing evidence base that not all children with mathematics difficulties have MLD and that children with MLD vs. LA have distinct cognitive and performance profiles relative to each other (e.g., Geary et al., 2007; Mazzocco, Feigenson, & Halberda, 2011; Murphy et al., 2007). For instance, in an earlier study of fractions knowledge, we found that 6^th graders with MLD (but not those with LA) have significant misconceptions about what fractions represent, as indicated by their errors rank ordering sets of fractions, their inability to identify equivalent fraction pairs, and even their inability to accurately name common decimal representations. Specifically, children with MLD are more likely than children with LA to identify unequal fractions as equivalent (e.g., to state that 0.50 = 0.05) even through Grade 8 (Mazzocco & Devlin, 2008). Children with LA rarely made these types of errors. These data reveal that children with LA and MLD struggle with math for potentially different reasons. The persistence with which some middle school students fail to rank order fractions leads to questions that concern the nature of children's knowledge of fractions prior to Grade 6, and if fraction knowledge differs between children with MLD or LA early in the elementary school years. If students with MLD or LA differ in terms of initial misconceptions in their understanding of fractions, these differences should emerge early and lead to different learning trajectories.

A logical starting point for this work is to study children's knowledge of fractions depicting “one-half” (½), because research supports the notion that “one-half” is a relatively easy concept for children to master, and because instructional practices operate on this assumption. For instance, many students have an informal understanding of one-half prior to formal instruction in fractions, and this prior knowledge may facilitate their learning about fractions (Hunting & Sharpley, 1988). Second and third graders are more accurate and use more sophisticated fraction addition strategies when the fraction ½ is used as an anchor in instruction rather than non-half fraction values (Spinillo & Cruz, 2004). When comparing magnitudes of fractions, even six year olds perform better if the comparison involves the fraction ½ or if two values being compared cross the ½ boundary (Spinillo & Bryant, 1991, 1999). But if children have a conceptual gap at the level of understanding that a fraction represents a quantity, the fraction ½ may offer little if any advantage over knowledge of or performance on other fractions.

Are additional types or classes of categories likely to provide similar advantages? Children may experience less difficulty comparing fractions with the common (vs. different) denominators (Sophian, 2000; Behr, Wachsmuth, Post & Lesh, 1984), in part because same denominator problems are introduced early in fraction instruction, and because whole number knowledge facilitates performance in this context. That is, it is true that larger numbers are bigger than smaller numbers when denominators match (e.g., – > –). This advantage does not apply to fractions with common numerators (e.g., it is not true that – > –). Middle school students are faster and less prone to making errors when comparing fractions with common denominators than when comparing fractions with common numerators (Meert, Grégoire, & Noël, 2010). Over time, children move from understanding fractions as two independent numbers to recognizing that fractions represent only one number, but do not immediately recognize that a fraction may be larger than its represented unit (Stafyloida & Vosniadou, 2004). As concepts of fractions become more sophisticated, so do the strategies used to make judgments about the relative magnitude of two fractions. Indeed, both children and adults may employ different strategies (e.g., accessing numerical information for the numerator only, or for the entire fraction) depending on the type of fraction being compared, (e.g., common numerator or common denominator; Meert et al., 2010). But this depends on whether different strategies exist in a person's repertoire, and if the strategies are selected appropriately in a given context.

It is an untested assumption that these general patterns described above, such as the sequences dictating which fractions are easiest to evaluate early in development, apply to all children – including those with MLD or LA. Although our study does not directly concern the existence or use of specific strategies to evaluate a fraction quantity, as an initial investigation of these notions we focus on whether children with MLD or LA have sufficient knowledge of these “easy” fractions (“one-half” fractions, and “common denominator” fractions) to accurately judge which of two fractions represents a larger number. To explore differences in children's knowledge of these types of fractions, we examine children's accuracy on magnitude judgments of fractions from Grades 4 to 8. We selected Grade 4 as an entry point for the study in part because formal introduction of fractions begins in Grade 3 (National Research Council, 2001). Our focus through Grade 8 spans the years during which instruction continues to focus on operating on fractions and proportional reasoning relevant to algebra, a practice that persists through the 21^st century as reflected by the standards proposed nation wide (e.g., CCSSI, 2010). We compared performance on magnitude judgments using number pairs that include a fraction equal to ½ (one-half items) to magnitude judgments where neither item of the fraction pairs equals ½ (non-half items); we also compare performance on magnitude judgments of fraction pairs with matching denominators or matching numerators. For both sets of comparisons, we evaluate performance differences across two groups of children with poor mathematics achievement, including children with LA or MLD, both relative to children with typical achievement in math (TA). We predicted that children with TA would initially outperform both the LA and MLD groups overall and maintain their advantage over time. We also predicted that children with LA would have more difficulty than their peers with TA, but would surpass their peers with MLD on both performance accuracy and rates of growth in fraction knowledge over time, whereas children with MLD would continue to struggle with even the allegedly easy fraction comparisons throughout middle school.

We further evaluated the impact of representation format, and predicted that children with MLD would show more persistent difficulties with the most symbolic of the formats evaluated (Arabic numbers, such as ½) compared to visual fraction models (i.e., pictorial representations), relative to their LA and TA peers, because their limited knowledge of fractions would interfere with transfer of knowledge from the visual fraction models to the more symbolic (numeral-based) representations. These predictions are based on the notions that understanding “easy” fractions nonetheless requires at least some basic understanding of fractions, and that since children with MLD lack this basic knowledge, they will not be subject to the “easy fractions” advantage that will be evident in their peers with LA or TA.

Method

Participants

Participants were drawn from a completed longitudinal study of mathematics ability and disability described elsewhere in detail (Mazzocco & Myers, 2002; 2003). Briefly, participants were recruited for the larger study from 23 kindergarten classrooms in one large and socioeconomically diverse metropolitan public school district. The participating schools were targeted for having relatively low rates of mobility and free or reduced lunch participation (FRLP) thereby diminishing attrition and the likelihood that observed poor math performance was related to very low socioeconomic status. Still, the schools that did participate were representative of public schools in the overall school district, with a mean FRLP rate of 16.5% (range = 1.58% to 29.04) and a mean mobility rate at the onset of the study that was also 16.5% (range = 6.8% to 18.9%). All 445 kindergartners with proficient English were invited to participate in the study, and 249 (120 boys) enrolled. Most participants were White (86%).

The present study focused on an assessment administered during Years 5 to 9 of the longitudinal study, when most participants were in Grade 4 to 8 (Table 1). Therefore, our participants were limited to the 142 students who completed 9 years of the study, including 5 participants who had repeated a school grade once during the study.

Table 1.

Mean (SD) Age of Participants at Each Year of the Study

	Participant Group
Grade	TA (n = 93)	LA (n = 18)	MLD (n = 11)	Total (n = 122)
4	9.59 (0.31)	9.92 (0.32)	9.80 (0.22)	9.66 (0.32)
5	10.61 (0.28)	10.96 (0.28)	10.96 (0.27)	10.70 (0.32)
6	11.76 (0.28)	12.06 (0.30)	12.05 (0.26)	11.83 (0.31)
7	12.79 (0.29)	13.09 (0.31)	13.00 (0.33)	12.85 (0.32)
8	13.74 (0.31)	14.03 (0.33)	13.97 (0.31)	13.80 (0.33)

During the longitudinal study, standardized and investigator designed assessments of mathematics and related skills were individually administered to all participants. Scores from annual standardized mathematics achievement tests administered through Grade 6 were used to determine MLD status, based on published criteria (e.g., Mazzocco & Devlin, 2008). Briefly, of the 142 children seen at all five study time points, 11 met our criteria for mathematics learning disability (MLD) by scoring <10^th percentile (relative to the study sample) on a standardized math assessment at least twice between 3^rd and 6^th grades (MLD). A total of 18 children met criteria for low achievement in mathematics (LA) by scoring within the 11^th – 25^th percentile on the assessment during that same time period. The 93 children who consistently scored above the 25^th percentile were assigned to the typically achieving group (TA). The remaining 20 participants were excluded because their WJ-R-Calc scores were too inconsistent over time to confidently apply classification of MLD, LA, or TA status. Thus 122 participants were included in the final study sample.

Our reliance on sample-based vs. standard normative percentiles was based on the two following reasons. First, we used the same version of the standardized tests over time to maintain consistency throughout our longitudinal study. For instance, early in the study, the WJ-R was replaced by the WJ-III in the field, but we maintained use of the WJ-R. Over time this led to inflated test scores associated with practice effects and outdated norms. Second, although our cut-off points were somewhat arbitrary in the absence of a gold standard for MLD, we selected them to be aligned with the reported prevalence of MLD (~6-11%, e.g., as reviewed by Shalev, 2007). The investigator designed math tests were based on procedures and concepts introduced during grades prior to a given target grade level, and the relative easiness of these tests was confirmed by near ceiling performance observed among typically achieving (TA) participants.

Materials

Mathematics achievement

We used age-referenced standard scores from the Calculations (Calc) subtest of the Woodcock Johnson Psycho-Educational Battery-revised (WJR; Woodcock & Johnson, 1990) to determine MLD status. The WJ-R Calc involves untimed paper-and-pencil calculations, and includes a range of arithmetic problems presented in order of increasing difficulty. Internal consistency reliability for the WJ-R Calc subtest ranges from r = .89 to r = .93 across the ages 6-14 years (Woodcock & Mather, 1990). In view of findings that math performance is typically weaker on timed versus untimed assessments regardless of math difficulty (Kellogg, Hopko, & Ashcraft, 1999), using an untimed measure of math performance to establish MLD status is consistent with our emphasis on acquired knowledge of mathematics rather than performance efficiency (i.e., rapid response rates).

General cognitive ability

We obtained age-referenced full scale IQ scores (FSIQ) from the four subtests version of the Wechsler Abbreviated Scale of Intelligence (WASI, Wechsler, 1999) when participants were in Grade 3 (at approximately 8 years of age), with the exception of four students who were in 2^nd grade during the fourth year of the study and one student who missed the Grade 3 assessment and completed the WASI at Grade 5. In one set of analyses, we included FSIQ scores as covariates to address the impact of IQ on the primary outcomes of interest. The WASI has high internal consistency (r = .95) for 8-year-olds and also is highly correlated with the Wechsler Intelligence Scale for Children –third edition (WISC-III, r =.87).

Magnitude comparison of representations of fractions

. Our primary outcome variable of interest was children's knowledge of formal, symbolic representations of fractions. The Symbolic Magnitude Comparison of Fractions (SymMCoF) test was designed and administered for this purpose. Unlike items from many magnitude comparison tasks used in MLD or numerical processing research, all SymMCoF items are symbolic and administered without a time limit. This practice reflects our emphasis on knowledge of fractions, vs. intuitive or automatized responses. Each SymMCoF item involves comparing two quantities, and either circling the larger quantity (the one that represented the “larger part of a whole”) or placing an equal sign between the two quantities to represent equivalence (“if the two amounts are the same”).

During each year of the study, the SymMCoF included a set of core items, including eight whole number comparisons that served as a check that children understood the task expectations (in Grades 4 and 5 only), and fraction comparisons administered during all five grades. In view of ceiling effects for these eight items, they were dropped from the SymMCoF after Grade 5, at which time eight items involving variables were added, but which are not considered further in the present study. The 60 fraction items are the focus of this study, including 22 item pairs that included at least one representation of one-half and 38 pairs of non-half fractions.

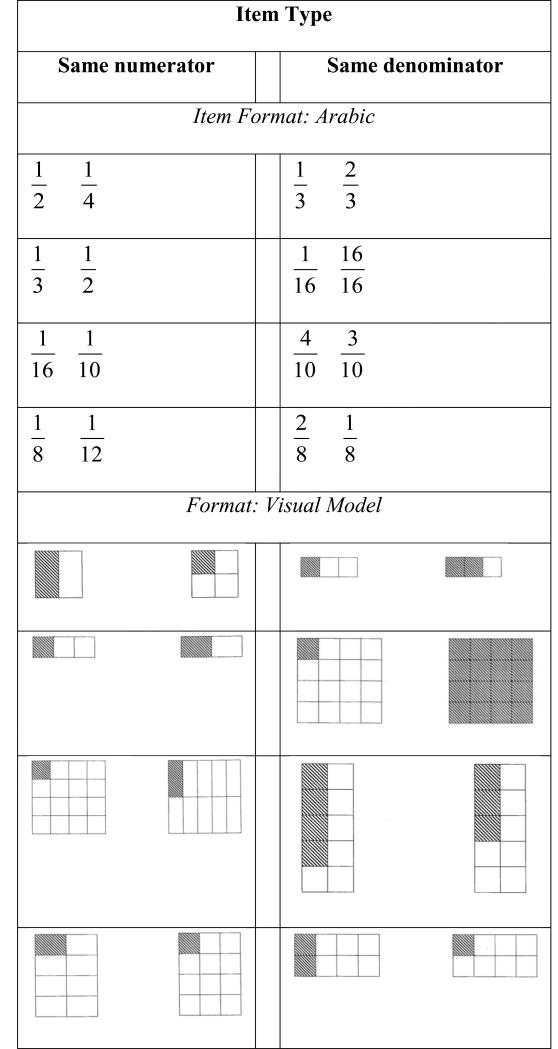
The format of the SymMCoF fraction item pairs was manipulated to allow us to test hypotheses regarding the relative success children have with different forms of symbolic representation of proportions. One of four formats included Arabic number-based fractions (e.g., – vs. –), for 12 fraction pairs. The three remaining mutually exclusive formats were comprised of visual fraction models depicting partially shaded-in boxes. Of these three, the “matching wholes” format involved 16 pairs of fractions, each represented by two visual models identical in overall size and shape. The “matching parts” format involved 8 pairs of visual models, each with identically sized individual units, regardless of how many of these units were shaded. The third format involved 16 incongruent pairs of visual models; these matched on neither of these two features and were manipulated to be deliberately misleading, such that the shaded unit(s) in the fraction representing the larger quantity (i.e., the correct response) appeared physically smaller than the shaded unit for the incorrect response, such as in the visual models for ½ and ¼ presented in a manner that depicts ¼ as a physically larger unit than the unit representing ½ (), despite the fact that the number ½ is larger than the number ¼. Note that 8 visual model pairs that had both matching parts and matching wholes were excluded from statistical analyses of specific visual model formats.

Finally, among this same set of 60 fractions item pairs, 12 SymMCoF fraction item pairs had identical denominators (including 4 Arabic number fraction pairs, and 8 visual model pairs). Twenty eight item pairs had identical numerators (in all cases, the identical numerator was “1”), and these 28 pairs included 4 Arabic number fraction pairs and two duplicate sets of 12 visual model pairs. All 20 remaining item pairs had different numerators and denominators.

The test trials were preceded by an extensive warm up session, during which children were explicitly shown and taught each of several principles that they were then prompted to demonstrate on a pre-test. The warm up trials were also used to convey the purpose of the task and the representational systems used throughout. For instance, the examiner explicitly conveyed that the aim of the task was to indicate which of two items represents the larger amount, not the physically larger item. These trials proved to be well understood even at Grade 4 (the first year of the study), because even prior to our review of the entire set of SymMCoF instructions, all but six of the 122 fourth graders readily accepted that “9” was larger than “6,” despite obvious differences in font size used in this particular warm up trial. Children who missed this trial were in the TA (n=5) or LA (n=1) groups), but all participants correctly solved later practice trials of this type. At Grade 5, all participants answered this item correctly. Children were also explicitly informed that the amounts being compared within any given pair may differ or match in quantity, and were instructed to mark equivalent pairs with an equal sign placed between two stimuli (e.g., – = –). To avoid confounding calculation fluency with judgments of fractional quantity, these comparisons tasks involved limited or no arithmetic calculations, and the entire test was untimed.

Following the warm up trials, the SymMCoF test items were administered in a fixed order. Children marked their response directly on a stimulus book. On each page, the examiner reminded children to circle the larger item, or, in the case of visual models, to circle the “colored in part (that) shows the bigger amount of a whole.” These instructions were identical to those used in the warm up session.

The reliability of the SymMCoF was good during all years of the study, ranging from .938 (Grade 6) to .968 (Grade 4).

Procedure

The SymMCoF was administered annually from Grades 4 to 8. Parent consent and child assent were obtained prior to testing, in accordance with our institutional human subjects board approved protocol. Most participants were tested in their school, in a private room with minimal interruption. Participants who elected to avoid missing classroom time for study participation were tested either after school, or at the PI's research lab, or at a location in their community (e.g., a rented meeting room at a local library).

Children were individually tested by a female examiner. Tests were presented in a fixed order. The 4 subtest WASI was administered once, in Grade 3. The WJ-R Calc was administered from Grades K to 6, except at Grade 1.

Results

Variables and Analyses

The dependent variables used in analyses of variance (ANOVA) represent performance accuracy across specific subsets of items, measured as uncorrected percent of correct responses. The ANOVA models include three levels of MLD Status (TA, LA, and MLD) and five levels of Grade (Grades 4 to 8). We anticipated unequal sample sizes across levels of our grouping variable (MLD status) based on our prospective study design and because our three levels of MLD status correspond to 10%, 15%, or 75% of the general population classified as MLD, LA, or TA, respectively. This representative distribution of samples should not bias grouping effects (Gamst, Meyers, & Guarino, 2008, p. 496). Still, as a conservative response to unequal samples sizes, we used Wilks’ Lambda values from multivariate analyses of our repeated measures and interactions, which do not assume sphericity. In addition, all post hoc multiple comparisons of within subject variables were calculated using a Bonferroni correction. For some but not all analyses, variance across MLD groups was not equal, so our planned comparisons between MLD, LA, and TA groups were Tamhane post hoc comparisons, which do not assume equal variance.

When interactions implicated group differences in SymMCoF performance trajectories over time, we confirmed or ruled out group differences using Growth Curve Models (GCM) based on raw test scores, to model the effects of MLD status. For all models, the intercept was set at Time 1 (Grade 4) to reflect children's performance at the start of the study. The slope refers to children's growth in monthly increments across five years (Grades 4 through 8). For each primary outcome variable of interest, a pair of models was conducted in which either the MLD or the TA group served as a reference group, to allow us to examine all possible comparisons between our growth rates between the three levels of MLD status.

All analyses were conducted using SPSS version 20.

Preliminary Analysis

We verified whether children in all three groups performed at ceiling on whole number items. There were no significant difference between the performance of the TA, LA, or MLD groups, with accuracy on whole number problems during Grade 4 at 99.6, 97.2, and 96.6%, respectively. This analysis confirmed that participants were aware of and complied with the task demands.

Primary analyses: Overall accuracy on SymMCoF fraction items

We first sought to confirm that children with MLD, relative to their LA and TA peers, were less accurate on symbolic magnitude comparison tasks involving pairs of fractions. We carried out a 5 (Grade) × 3 (MLD Status) ANOVA on percent of correct responses across all 60 SymMCoF fraction items. As expected, there was a main effect of Grade, Wilks’ Lambda F(4, 116) = 37.61, p < .0001, η²_p = .57, with the percent correct increasing from 70.5 to 93.6% from Grades 4 to 8. Post hoc comparisons (using Bonferroni adjustment for multiple comparisons) showed that accuracy increased significantly at each subsequent grade (ps < .001) except between Grades 7 and 8, when performance plateaued at a mean of ~ 92 % across all groups (p = .92). The expected main effect of MLD status also emerged, F(2, 119) = 46.30, p < .0001, partial η² = .438. Levene's test indicated inequality of variance across groups, so we used the Tamhane mulitiple comparison to evaluate that students in the TA group were more accurate (89.8%) than peers with either LA (77.9%, p < .01) or MLD (62.1%, p < .001), which also differed from each other, p < .04.

There was a small but significant Grade × MLD Status interaction, Wilks’ Lambda F(8, 232) = 2.429, p = .015, η²_p = .077. As illustrated in Figure 1, the previously described main effects were evident across grades (performance improved across grades for all participants) and across levels of MLD status (poorest performance emerged for the MLD group at all grades). Whereas children in the TA group were significantly more accurate than their peers with LA or MLD across all grades, ps < .006, the LA and MLD groups had comparable rates of accuracy at Grade 4 (p = .180) but not thereafter, ps < .007. The MLD group underperformed relative to the LA group from Grades 5 to 8 (Figure 1). Thus during Grade 4 only, the MLD and LA groups both showed remarkable difficulty on the SymMCoF relative to their TA peers but by Grade 5, children in the LA group made gains of a magnitude not observed in the MLD group.

Figure 1.

Mean accuracy rates (and standard error) across all SymMCoF fraction items among participants meeting criteria for typical math achievement (TA, n = 93), low math achievement (LA, n=18), or mathematical learning disability (MLD, n=11).

This pattern of findings suggests that the three groups may differ in their rates of growth on the SymMCoF. However, results of the GCMs revealed no significant differences in the growth rates between any of the three groups, ps > .35 (Table 2).

Table 2.

Growth Curve Results for Effects of Math Ability Status

Parameter	SymMCoF total score	One-half items	Non-half items	Arabic Numeral Fractions	Visual Models: Matching Wholes	Visual Models: Matching Parts	Spatially Misleading Incongruent Pairs
MLD as reference group
Intercept	43.40***	11.57***	20.61***	1.25***	4.16***	3.01***	3.39***
Slope	0.18***	0.11***	0.10**	0.02***	0.01*	0.01*	0.05***
Intercept on TA	19.92***	8.26***	8.97***	2.16***	1.32***	0.87***	3.76***
Slope on TA	0.03	−0.06**	0.08*	−0.01*	−0.00	−0.01	−0.03***
Intercept on LA	11.07***	5.74***	4.06*	1.49***	0.69*	0.61*	2.71***
Slope on LA	0.05	−0.03	0.06	−0.00	0.01	−0.01	−0.02*
TA as reference group
Intercept	63.33***	19.83***	29.58***	3.40***	5.48***	3.88***	7.16***
Slope	0.21***	0.05***	0.17***	0.01***	0.01***	0.00	0.02***
Intercept on LA	−8.85***	−2.53**	−4.92***	−0.67**	−0.63**	−0.26	−1.05**
Slope on LA	0.02	0.03	−0.02	0.01	0.01*	0.00	0.01

Note.

^*p < .05

^**p < .01

^***p < .001

This analysis confirms that MLD and LA groups differ from each other, and from the TA group, on symbolic magnitude comparisons on a test that involves fractions. These differences are apparent in performance at a given time, but not in rate of growth over time, in that all students improved from Grades 4 to 8. We subsequently evaluated whether this same pattern emerges for test items involving the fraction one-half.

One-half and non-half items

A central premise underlying our study design and analysis plan was that magnitude comparisons of representations of “one-half” are easier to correctly resolve than are fraction items that do not include a representation of one-half. To evaluate the validity of this premise, we carried out a 2 (Item Type: one-half vs. non-half) × 5 (Grade) × 3 (MLD Status) ANOVA for performance accuracy, with repeated measures on Item Type and Grade. In addition to the anticipated effect of Grade (also noted previously for all SymMCoF items, Wilks’ Lambda F(4, 116) = 38.73, η²_p = .572), the predicted main effect emerged for Item Type, Wilks’ Lambda F(1, 119) = 59.41, p < .0001, η²_p = .333, with more accurate performance on items that included representations of one-half vs. items that did not (correct responses = 89.2 vs. 83.4%, respectively).

There was no significant Item Type × Grade interaction, suggesting that the discrepancy in performance across half vs. non-half items was roughly equivalent across grades, p = .549, at least when collapsed across groups. Thus, Item Type and Grade each accounted for significant variance in performance accuracy, with one-half items appearing easier than non-half items from Grades 4 onward and performance accuracy improving for both item types over time.

Does this pattern emerge equally for children with vs. without MLD? The primary hypothesis motivating this study was that children with MLD have atypical conceptualization of fractions, and fail to recognize that fractions represent a specific quantity; thus we predicted that children with MLD would have a significant delay in mastering the concept of “one-half.” We further hypothesized that this delay would be manifested as a protracted period during which magnitude comparison accuracy does not differ across one-half and non-half items, for children with MLD. We expected that performance of children with LA would be comparable to that of their TA peers and would have higher accuracy rates on one-half vs. non-half items.

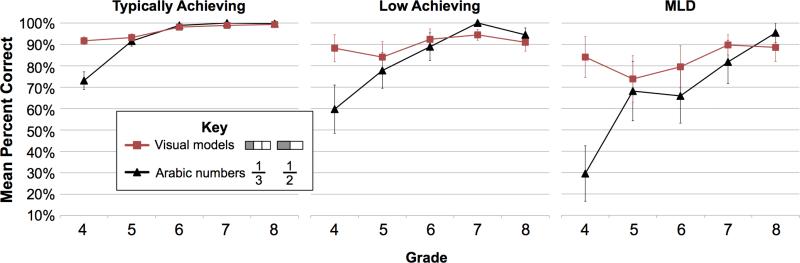
As predicted, there was a main effect of MLD Status, Wilks’ Lambda F(2, 119) = 46.81, p < .0001, η²_p = .440, on performance accuracy. As reported earlier, across both item types and all five grades, children with TA outperformed children with LA (Tamhane p < .02) or MLD (p < .001), who in turn differed from each other (p < .04). However, both two-way interactions involving MLD status and either Grade, Wilks’ Lambda = .837, F(8, 232) = 2.69, p = .008, η²_p = .085; or Item Type, Wilks’ Lambda F(2, 119) = 4.48, p<.02, η²_p = .070, were significant, as was the three-way interaction with all three variables discussed below, Wilks’ Lambda F(8, 232) = 3.45, p = .001, η²_p = .106. These interactions prompted us to further evaluate the alleged main effects of Item Type and Grade. First, Bonferroni-adjusted pairwise comparisons revealed that the TA group outperformed both the LA and MLD groups at all grades, although effects increased with Grade (as illustrated by Figure 1), all ps < .001 except for the TA and LA comparisons at Grades 4 and 5, ps < .02). Second, the effect of Item Type was evident for all three levels of MLD Status, in that one-half items led to higher (better) accuracy scores than did non-half items, for children with TA or LA (ps < .00001) and also for children with MLD, although the effects for the MLD group were smaller (Figure 2, p < .02).

Figure 2.

Mean accuracy rates (and standard error) on SymMCoF item as a function of item type (one-half vs. non-half items) and MLD status. TA = Typically achieving children, LA = low achieving children, and MLD = mathematical learning disability.

These pairwise comparisons for the two-way interactions qualify – but do not negate – the previously reported main effects. This was also the case for posthoc comparisons of the three way interaction, which were consistent with the previously described profiles. First, children with TA outperformed the children with MLD during all years of the study, on both one-half and non-half items (ps ranged from .002 to < .0001), and also outperformed the LA group during all years of the study (ps ranged from .008 to < .0001) with the single exception of no significant difference in performance on the more difficult items (non-half items, p = .082) during Grade 5, the year during which children with LA showed gains not evident in their MLD peers. Second, the one-half advantage (that is, the higher rates of accuracy on one-half items compared to non-half items) is evident across Grades 4 to 7 for the TA group (Bonferroni adjusted ps < .001), but not at Grade 8 when ceiling performance levels are reached for both item types (p = .065); for the LA group the one-half advantage is evident from Grades 5 onward (ps < .0001), but during Grade 4 performance is equivalent for both item types (p = .739); and for the MLD group the one-half advantage does not emerge until Grades 7 and 8 (ps < .005), and is quite absent prior to then (ps range from .134 to .689). These qualitative difference in performance profiles (Figure 2) suggested distinct rates of growth trajectories across groups. In summary, greater accuracy on one-half items is evident by Grade 4 for children with TA, and by Grade 5 for children with LA, ps < .001, but it only reaches statistical significance for children with MLD at Grade 7, p < .005. Moreover, children with LA eventually perform as accurately as their TA peers on one-half items, but children with MLD never exceed performance accuracy levels ~75% on one-half items, even at Grade 8. For children with MLD, the relative difference between one-half vs. non-half items never reaches the differences observed in Grades 5 to 8 for children with LA. Thus, whether and when one half items are easier than non-half items varies across MLD status.

We carried out two sets of GCM to evaluate rate of growth on the two types of items (one-half, non-half) as a function of MLD status. The results are consistent with the ANOVAs, and show that, at study entry (Grade 4), children in the TA group had higher rates of accuracy on the one-half items than their LA (p < .01) or MLD (p < .001) peers, that this pattern also emerged for the non-half items (ps < .001), and that children with LA had higher rates of accuracy than their MLD peers on the one-half (p < .001) and non-half items (p < .05). Regarding rates of growth, for one-half items, children with MLD have a faster rate of growth than their TA peers (p < .01), reflecting their lower intercept at study entry and the TA group's ceiling-level performance midway through the study. Children with LA or TA reach and maintain ceiling performance on one-half items over time, whereas children with MLD do not. For non-half items, the pattern is reversed, and the TA group is growing significantly faster than the MLD group (p < .05).

Effects of Item Format on one-half items

Having established that children with MLD (and, at Grade 4, also children with LA) have difficulty comparing fractions, and that even one-half items pose a challenge for children with MLD, we examined whether performance is facilitated (or hindered) by any of the representational formats discussed previously, across the TA, LA, and MLD groups. Accuracy (% correct) on these specific subsets of items was evaluated with a 4 (Format: Arabic numeral fractions, and visual models with “matching wholes” versus “matching parts” or spatially misleading incongruent pairs) × 5 (Grade) × 3 (MLD Status) ANOVA, with repeated measures on the first two variables.

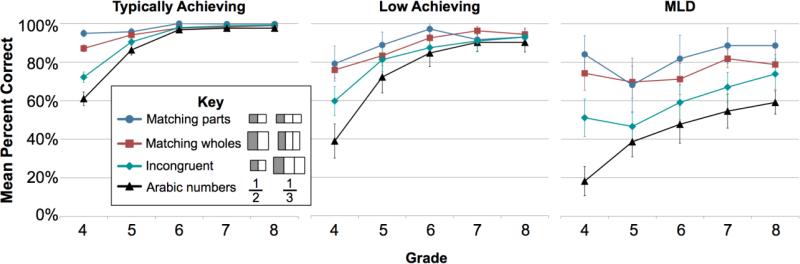
In addition to the anticipated main effects of Grade and MLD Status paralleling those reported earlier (Wilks’ Lambda F(4, 116) = 29.19, p<.001, η²_p = .502; and F(2, 119) = 42.25, p < .0001, partial η² = .415; respectively), Item Format accounted for significant variance in performance accuracy, Wilks’ Lambda F(3, 117) = 59.54, p < .001, η²_p = .604, and all pairwise comparisons of the four item formats reached statistical significance, Bonferroni adjusted ps ranged from <.020 when comparing matching “wholes” versus matching “parts” to <.0001 for the five remaining comparisons. Accuracy was greatest when visual models involved matching parts (units of comparable sizes), and lowest when fractions were represented by Arabic numbers (Figure 3).

Figure 3.

Mean accuracy rates (and standard error) across SymMCoF “one-half” items as a function of item format. TA = typically achieving; LA = low achieving; MLD = mathematical learning disability.

A significant interaction between Item Format and MLD Status, Wilks’ Lambda F(6, 234) = 8.73, p<.0001, η²_p = .183, prompted inspection of relative format effects within each of the three participant groups (to test for possible specific sources of within-group difficulties) and a confirmation of the anticipated effects of MLD status across item formats.

First, within groups, we found that the effect size of Item Format was comparable for the TA and LA groups, η²_p = .508 and .546, respectively; and larger still for the MLD group, η²_p = .889. Next, across groups, the TA group outperformed the LA and MLD groups on all four item formats, ps < .008 (Figure 3). For formats involving Arabic numbers, matching wholes, or spatially misleading visual models, the LA group outperformed children with MLD, ps < .001. For items with visual models depicting matching parts, accuracy among the LA and MLD groups did not differ p = .08. At Grade 4 there was no group difference across the LA and MLD groups on any item formats, but by Grade 5, the LA group outperformed the MLD group on all item formats, ps < .027.

GCMs showed that there were no significant differences across groups on rates of growth when visual models involved matching parts, presumably due to relatively accurate performance across all participant groups, ps > .08). When visual models included matching “wholes”, the LA group grew faster than the TA group, p < .05, consistent with the notion of a general “catching up” after Grade 4. Children with MLD showed a faster rate of growth than the TA group, for the Arabic number format, relative to the TA group, p = .042; and grew faster then the LA or TA group on the spatially misleading format, ps < .03, presumably because of their markedly low initial performance levels on these formats (Figure 3). Rates of growth did not differ between the MLD and LA group, on the Arabic number notations, p = .61, although accuracy rates did.

Common Denominator /Numerator Items

Having demonstrated that Arabic number notation is associated with the lowest levels of accurate magnitude comparison relative to the visual model formats, and that this effect of format was (at least initially) observed for all three participant groups and persists through Grade 8 for children with MLD, we evaluated whether this effect generalizes to other item types. We used 12 items with common denominators, in part because these items are among those with which children have the earliest instructional experiences, as discussed previously. This set of analyses was limited to item pairs consisting of either Arabic number or visual model formats representing the same values (Appendix A). As a contrast to common denominator items, we also included 12 items pairs with common numerator. Each of the two sets of 12 problems consisted of 4 Arabic number and 8 visual model pairs. We did not differentiate among visual model formats in this analysis, because these features were not mutually exclusive in this set of items (Appendix A). Thus, we conducted a 2 (Item Type: Common Numerator or Denominator) × 2 (Item format: Arabic number vs. Visual Models) × 5 (Grade) × 3 (MLD Status) ANOVA, with repeated measures on the first three variables.

In addition to the anticipated main effects of Grade and MLD Status paralleling those reported for all previous analyses (Wilks’ Lambda F(4, 115) = 13.30, p<.0001, η²_p = .316; and F(2, 118) = 54.18, p < .0001, η²_p = .479; respectively), the main effect of Format did generalize to the common numerator and common denominator items, and accounted for significant variance in performance accuracy, Wilks’ Lambda F(1, 118) = 76.39, p < .0001, η²_p = .393, with visual model items generally leading to more accurate performance (92.5% correct) than Arabic number representations of fractions (83.5%) overall, p < .0001. This was evident (and for both common numerator and common denominator item pairs specifically, as seen in Figures 4 and 5), consistent with our previous finding (as per Figure 3). Tamhane posthoc comparisons of MLD status showed that children with TA outperformed children with LA (p < .04) or MLD (p < .0001), who differed from each other (p < .01).

Figure 4.

Mean accuracy rates (and standard error) across SymMCoF “common denominator” items as a function of item format and MLD status. TA = typically achieving; LA = low achieving; MLD = mathematical learning disability.

Figure 5.

Mean accuracy rates (and standard error) across SymMCoF “common numerator” items as a function of item format and MLD status. TA = typically achieving; LA = low achieving; MLD = mathematical learning disability.

The main effect of Item Type (common numerator vs. common denominator) was significant, Wilks’ Lambda F(1, 118) = 8.22, p < .005, η²_p = .065, with same denominator items leading to more accurate performance (90.3%) than same numerator fractions (85.7%), p < .005, consistent with our hypothesis (Figure 6).

Figure 6.

Mean accuracy rates (and standard error) for SymMCoF items as a function of common numerator versus denominator and MLD status. TA = typically achieving; LA = low achieving; MLD = mathematical learning disability.

Next we evaluated if these main effects of Item Format and Type generalized to all levels of MLD status. There was no significant interaction between MLD status and Item type, Wilks’ Lambda F(2, 118) = 0.872, p = .421, η²_p = .015, but there was a significant interaction between MLD status and Item Format, Wilks’ Lambda F(2, 118) = 15.37, p < .0001, η²_p = .207. There was no significant interaction between Grade and MLD status, p = .559 .001, η²_p = .157. The three-way interaction between MLD status, Item Format, and Item Type was not significant, Wilks’ Lambda F(2,118) = 0.396, p = .674 , η²_p = .007, whereas the four way interaction between MLD status, Item Format, Item Type, and Grade was small but statistically significant, Wilks’ Lambda F(8, 230) = 2.646, p = .01, η²_p = .084.

This four way interaction is best summarized by Figure 6, which depicts the unique relationship between common numerator vs. denominator problems for the MLD group (relative to the LA and TA groups), with performance diminishing over time for the latter (relative to a high entry point) and not for the former (relative to a very low entry point). At Grade 4, there were no significant group differences (based on MLD status) on performance accuracy for problems of either format (Arabic or visual models), with the exception of a significant difference between the MLD and TA groups on same numerator problems (p < .001). By Grade 5, additional pairwise comparisons between MLD and TA groups were significant, on same numerator and same denominator items of Arabic or visual model formats and same denominator items of Arabic formats (ps < .01); no significant differences emerged between the MLD and LA groups, nor between the LA and MLD groups. In Grade 6, all comparisons between MLD and TA groups were significant, ps < .001, and these persisted throughout the subsequent years. Also, at Grade 6, all comparisons between MLD and LA became significant, ps < .01, and then persisted and strengthened over time. The comparisons between the LA and TA groups were not significant except for same numerator item pairs presented in Arabic number format (p < .03) in Grade 6, pairs presented in visual model format in Grade 7, and pairs in either format in Grade 8. Only the MLD group showed a negative correlation between accuracy on same numerator and same denominator problems, such that the significant group differences that emerged on the former in the early grades disappear by Grade 8.

Full Scale IQ as a covariate

We repeated each of the analyses reported above this time as ANCOVAs, to evaluate whether the effects reported above persist when FSIQ score is included as a covariate. First, all significant main effects reported above persisted when FSIQ was included in the models. Second, no additional significant main effects or interactions emerged from the ANCOVAs, relative to the ANOVAs conducted without FSIQ. Third, all significant two-way interactions reported previously also re-emerged from the ANCOVAs. Finally one interaction that previously met criteria for statistical significance was no longer significant when FSIQ was added as a covariate. The small 4 way interaction between Item Type (numerator vs. denominator), Item Format (Arabic number vs. Visual Models), Grade, and MLD status was no longer significant, p = .13, η²_p = .053. In summary, all but one previously reported result remained when FSIQ was added as a covariate.

Discussion

In this study, we confirmed some assumptions about patterns of relative difficulty of fraction concepts among all children, found differences in those patterns across specific subgroups of children, and demonstrated how persistently some children continue to struggle with fractions throughout middle school. Specifically, we confirmed that fractions equivalent to one-half (which are typically introduced at Grade 3) are easier to conceptualize than are non-half fractions, at Grade 4 and beyond, at least as measured by our fractions based magnitude judgment tasks. The effect size for this facilitative effect is moderate to large (η²_p = .33), and is roughly equivalent across Grades 4 to 8 when collapsed across groups. Yet there are important group differences in the strength, emergence, and persistence of this facilitative effect. One-half items are consistently easier than non-half items for children with typical or low math achievement (TA or LA) until ceiling performance levels are reached, but not consistently so for children with MLD. Also, although a delay pattern is evident for the LA group, it does not characterize the MLD group. That is, one-half items are easier than non-half items by Grade 4 for the TA group and by Grade 5 for the LA group, but only in Grade 7 do we begin to see a one-half item advantage in children with MLD. Even then (and even at Grade 8), children with MLD never exceed performance accuracy levels of 75% on one-half items, whereas their LA and TA peers’ accuracy rates exceed 92% by Grade 8. Difficulties with fractions persist for both the LA and MLD groups, but by Grade 5, gains made by the LA group approach performance levels of the TA group and begin to deviate from the pattern observed in children with MLD. Thus, difficulties with fractions persist through Grade 8 for many students, but the nature of those difficulties varies across children.

For children with LA, all fraction items appear equally difficult in Grade 4. Later, the very large gains made on one-half items (between Grades 4 and 5) precede comparable (and later) gains made by this group on non-half items. One possibility is that knowledge gained from one-half items gradually transfers to “harder” fractions. For children with MLD, the one-half items do not seem to support conceptual learning of non-half fractions in the manner implicated for the LA group (Figures 1 and 2). This variation in the timing of gains across item types suggests (but does prove) that enhanced knowledge of the principles surrounding one-half support children's learning of non-half fractions, at least for LA children. We did not see this pattern among children with TA because their overall accuracy and relative achievement gains appeared comparable (and near ceiling) for both types of fractions early on. Perhaps we would have observed this pattern in the TA group had our assessments began at Grades 3.Importantly, none of these findings was accounted for by FSIQ, as tested when analyses were repeated with FSIQ as a covariate.

Considered together, one interpretation of these findings is that because children with MLD fail to extract conceptually meaningful information from fraction representations, even “easier” (one-half) fractions are not meaningful, and thus do not support learning “more complex” (non-half) fractions, nor do they offer any performance advantage. Gains are made, but whatever strategies children with MLD used to solve SymMCoF items are strategies that failed to generalize to all fractions, keeping performance accuracy relatively low through Grade 8. This suggests that strategies being used by children with MLD may be effective despite inaccuracies, but for only a limited set of fractions. From an instructional perspective, querying children with regard to strategy used for approaching fraction comparisons may be more informative than their overall accuracy at solving problems.

Data from the one-half and non-half items do not reveal specific strategies, but findings from common denominator vs. common numerator items shed some light on possible strategy use, and at the very least they support the notion that children with MLD use strategies that do not generalize to all fractions. Comparison of one-half and non-half items, and those for common numerator vs. common denominator problems, both reveal qualitative differences across the TA, LA, and MLD groups, but the differences across analyses are quite striking. First, unlike the effect of one-half vs. non-half items, there is a cross over interaction revealed in Figure 5, showing that although children with MLD make gains on common numerator items (unit fractions) at comparable or greater rates relative to their peers from Grades 4 to 8, their performance on common denominator items drops annually despite initial accuracy levels comparable to the TA group at Grade 4. Perhaps children with MLD are initially slow to adhere to the notion that, in fractions, larger denominators indicate smaller values (when numerators are the same), and once they establish this rule-governed behavior it leads to success for common numerator items, but simultaneously leads to failure on common denominator items. The rule is not firmly ingrained in Grade 4 (presumably when it is first over-learned; hence, performance is accurate where the rule does not apply, but is less accurate where it does apply), but as the rule becomes more established (with over-learning, but without a conceptual basis), performance accuracy shifts in opposite directions for the two item types, which is precisely what Figure 6 shows. One instructional implication of this finding is that assessing accuracy and strategy use on one-half items at the conclusion of 4^th and 5^th grades may be a relatively efficient way to identify children in need of additional instructional support with fraction concepts and to assess readiness to learn more advanced fraction concepts.

Another striking finding from this study concerns the persistent challenge children face with the most symbolic notation of fractions we explored – Arabic numerals – and that this challenge was observed among children of all three math ability levels examined (albeit to different degrees), across both sets of analyses (one-half vs. non-half, and same numerator vs. same denominator items). Even typically achieving children showed a visual model advantage on magnitude comparison accuracy, which may simply reflect the fact that visual models are commonly used (and thus familiar) instructional aids related to fractions. However, this advantage was short lived for the TA group, disappearing by Grade 6, suggesting that the visual models helped to support learning about fractions and were no longer needed to support conceptual mastery in middle school. This represents an intended and expected effect of pedagogy and learning, but one that did not emerge for the MLD group. Among children with TA, there appears to be a corresponding developmental shift in formal Arabic notation becoming aligned with visual model representations of the same fraction quantity, seen also among children with LA (seen in Figures 3 to 5), albeit later relative to the TA group. For the MLD group, the visual model advantage persists through Grade 8 and does not become aligned with Arabic number representations, the latter of which remain significantly lower even in Grade 8. Finally, the spatially misleading representations also continues to be more challenging for the MLD group (relative to the LA and TA groups) through middle school, suggesting that – for this group – the visual models are not treated as abstract representations of fractions supportive of fraction principles, but are instead viewed concretely. In this study, the spatially misleading format was tested against only the “easiest” fractions (one-half) and yet still proved to misguide students with MLD.

From an instructional perspective, children in the MLD group may benefit from continued use of visual models as one of several a strategies to support learning about fractions and solving problems involving fractions. However, if children with MLD rely on models as concrete rather than abstract representations of fractions, use of visual models may not promote the intended thorough conceptual understanding of fractions, especially when visual models are spatially misleading or when transitioning from visual models to Arabic notation.

The emergence of children's knowledge of fractions described in the Introduction is consistent with performance patterns observed in the TA and LA groups, although our findings offer no direct evidence to this effect (as this was not the purpose of the present study). That is, concepts of fractions become more sophisticated, so do the strategies used to make judgments about the relative magnitude of two fractions (Stafyloida & Vosniadou, 2004). Individuals may select from a range of available strategies, based on their knowledge of the type of fraction being compared (Meert et al. 2010). Among children with MLD, this knowledge appears significantly limited and often inaccurate, perhaps resulting in a different and more limited repertoire of strategies than observed in TA peers, and one that is suggestive of rote performance as a back up strategy in the absence of fractions knowledge. Instructional priorities in these cases may need to be refocused not on effective strategies, but on the principles of fractions that offer a foundation for the strategies – foundations we may assume to be present when, in fact, they are not. Accordingly, research priorities need to include evaluation of the prerequisite skills leading to this early and persistent failure to recognize what a fraction represents.

Highlights.

• Children with dyscalculia show limited knowledge of “one half,” through 8^th grade.

• Visual models lead to better performance than Arabic number fractions at Grade 4

• This disadvantage decreases by Grade 5 except in children with dyscalculia

• Accuracy across different fraction types is positively correlated in most students

• Accuracy across select fraction types is negatively correlated in dyscalculics

Appendix

Appendix A.