Colloidal aggregation and dynamics in anisotropic fluids

Significance

The formulation of colloidal particle/liquid crystal (LC) composites is a well-identified route toward the design of smart responsive materials with tunable optical or mechanical properties. However, the particles aggregate because they distort the intrinsic order of LC phases, which costs elastic energy. For micrometer-sized inclusions, the resulting elastic forces dominate the coarsening of the system. In this paper, we find a previously unidentified regime where elastic interactions no longer prevail when the particles are downsized to the nanometer scale. Instead, the system evolution is governed by an anisotropic Brownian diffusion coupled to attractive depletion interactions. This finding opens up new possibilities to better control the clustering of colloids in such media. We provide both experimental evidence and numerical simulations.

Abstract

We present experiments and numerical simulations to investigate the collective behavior of submicrometer-sized particles immersed in a nematic micellar solution. We use latex spheres with diameters ranging from 190 to 780 nm and study their aggregation properties due to the interplay of the various colloidal forces at work in the system. We found that the morphology of aggregates strongly depends on the particle size, with evidence for two distinct regimes: the biggest inclusions clump together within minutes into either compact clusters or V-like structures that are completely consistent with attractive elastic interactions. On the contrary, the smallest particles form chains elongated along the nematic axis, within comparable timescales. In this regime, Monte Carlo simulations, based on a modified diffusion-limited cluster aggregation model, strongly suggest that the anisotropic rotational Brownian motion of the clusters combined with short-range depletion interactions dominate the system coarsening; elastic interactions no longer prevail. The simulations reproduce the sharp transition between the two regimes on increasing the particle size. We provide reasonable estimates to interpret our data and propose a likely scenario for colloidal aggregation. These results emphasize the growing importance of the diffusion of species at suboptical-wavelength scales and raise a number of fundamental issues.

Colloidal dispersions are metastable systems consisting of small solid particles (size < 1 μm) immersed in a liquid phase. Compared with homogeneous liquids, they are characterized by a huge amount of interfaces, and their physical properties are mainly controlled by the aggregation state of the constitutive particles, which depends on their mutual interactions. In general, van der Waals attractions compete with the osmotic pressure of liquid films surrounding the particles, due to the presence of ions or molecules (electrostatic and steric effects, respectively) (1). Depletion interactions may also be invoked when several populations of objects, differing in size, coexist and diffuse in the same medium (2, 3). Hence, depending on the global balance of forces, the suspended particles may either remain isolated from each other or cluster into various kinds of structures ranging from compact aggregates to interconnected networks. A whole variety of different states are achievable, i.e., from solid opaque pastes to transparent newtonian fluids, which makes colloidal dispersions very attractive from a practical viewpoint as we can easily switch from one state to the other through chemical and/or physical means (pH, salt, additives, shear flow, etc.). A good example is provided by electrorheological fluids (and their magnetic counterparts), whose viscosity can be tuned by the application of an external field (4, 5). Needless to say, colloidal dispersions are ubiquitous in a broad spectrum of applications including food, cosmetics, and coating industries. Given their paramount importance, a great deal of both experimental and theoretical work was devoted to the understanding of structural and kinetic aspects of colloidal aggregation (6).

A characteristic of such systems is their sensitivity to Brownian motion, which can couple to local attractive interactions between the objects and give rise to a variety of colloidal aggregates. These diffusion limited aggregation (DLA) phenomena were extensively studied over the last three decades to explain the large-scale (often fractal-like) structures of numerous natural objects, mostly in isotropic medium (7, 8). In the present work, we deal with an anisotropic matrix made up of a nematic liquid crystal (LC) phase. In such a partially ordered medium, with a long-range orientational order of anisotropic molecules but no positional order, the particles experience elastic interactions in addition to the aforementioned ones (9–15). These interactions are long ranged, anisotropic, and originate from the distortions of the LC intrinsic order in the vicinity of the particles. The amplitude and symmetry of these distortions, which cost elastic energy, are to a large extent controlled by the boundary conditions at the colloid-LC interface. Typical pair interaction energies are 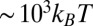for micrometer-sized particles (16) and result in the building of large-scale ordered clusters (linear and kinked chains and 2D and 3D crystals), which are insensitive to thermal fluctuations and remain stable over time (17–20). However, downsizing the particles to the nanometer scale makes elastic interaction energies fall down to a few 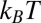as shown in refs. 21–23. In this regime, anisotropic Brownian diffusion can no longer be ignored, and its coupling to elastic forces is expected to play a significant role in both the aggregation kinetics and the structure of the formed clusters. The system thus becomes an anisotropic version of DLA where the anisotropy comes from the intrinsic ordering field of the LC environment. To our knowledge, the issue of the aggregation structure and dynamics of Brownian sticky colloidal particles immersed in an anisotropic fluid has not been addressed in the literature. However, it should be relevant for the broad and fast-growing field of nanocomposite systems whenever small inclusions are immersed in a complex fluid matrix (24).

In this work, we investigate the structural and kinetic aspects of colloidal aggregation in a micellar nematic liquid. Our primary goal is to achieve a basic understanding of the clustering of submicrometric particles due to the interplay of anisotropic Brownian diffusion and elastic interactions. Among the salient results of our study, we show that the morphology of aggregates depends significantly on the particle size: although big particles self-organize into aggregates whose morphology is consistent with attractive elastic interactions, the small particles quickly cluster into linear structures that cannot be accounted for by elastic phenomena. In this regime, we provide evidence that the coarsening of the system is dominated by an anisotropic rotational Brownian diffusion of the species combined with depletion interactions. We present experimental measurements obtained through optical microscopy techniques coupled to Monte Carlo simulations and complemented with some analytical estimates. The overall results agree with the proposed interpretation.

Results and Discussion

Experiments.

The system consists of submicrometer-sized polystyrene (PS) spheres dispersed in the nematic calamitic (N_C) phase of a lyotropic LC (SI Text). As shown previously, the prolate micelles tend to align parallel to the particles surface to maximize their entropy, resulting in planar anchoring conditions of the nematic director 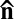(25, 26). Following Koenig et al. (21), we investigated the influence of particle size on interparticle interactions and morphology of aggregates. Much less deformation of the LC matrix is expected when downsizing the inclusions below the characteristic length 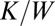whose value ranges from 100 nm to 1 μm depending on the precise values of the surface anchoring strength 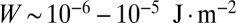and the lyotropic LC elastic constant 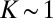pN (15, 27, 28). Nanometer-sized objects are therefore good starting candidates to achieve sparse nematic dispersions with the hope of increasing substantially the particle load (i.e., up to volume fractions 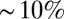). To check this idea, it is natural to first investigate the energetics of colloids immersed in the N_C phase. We then start with the measurement of the pair interaction potential before focusing on the collective behavior of nanoparticles of various sizes.

Pair Interaction Potential.

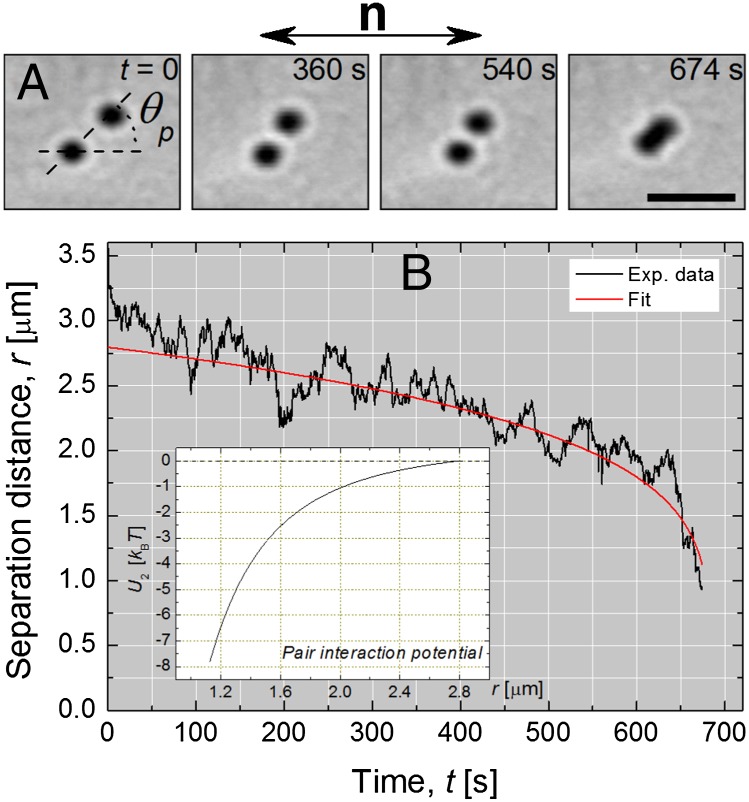
We probed the pair interaction potential between 780-nm-diameter particles using a standard video microscopy technique (SI Text). A series of snapshots of two interacting particles is shown in Fig. 1A. Here, the elastic forces have a quadrupolar symmetry (planar anchoring conditions); hence, the particles attract at an angle 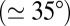with respect to the far-field director 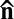. The time evolution of the center-to-center distance, 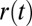, is plotted in Fig. 1B. The noise level is rather high because of the Brownian motion of the particles. This Brownian noise gives an idea of the weakness of the interactions existing in lyotropic LCs compared with their thermotropic counterparts (21, 23). In the latter case, the involved interaction energies are of the order 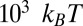, and a noise-free, ballistic-like attraction occurs (16, 19, 29, 30). From the recorded trajectory 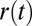, it is possible to extract the elastic pair interaction potential, 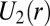, using a standard procedure detailed in SI Text. The result is shown in Fig. 1C, where it is seen that, close to contact, i.e., for 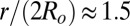, , 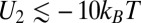an upper bound is found in all our data sets. This value is weaker by two orders of magnitude than typical interaction energies reported in thermotropic LCs. The estimated experimental value of 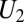agrees qualitatively well with that computed from the available theoretical model in the case of quadrupolar interactions (31)

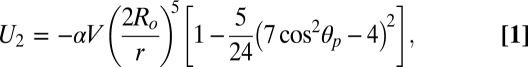where 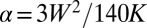is a characteristic pressure, V the particle volume, and 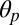the angle defined between the line joining the particle centers and the far-field director (Fig. 1A). Even though Eq. 1 is only formally valid at long range [i.e., when 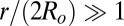], it was shown to hold down to 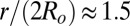(29). Taking 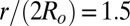, 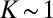pN, 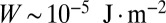, 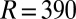nm, and angle 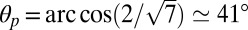(value that minimizes the angular part of 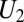), we get 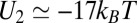, which is close to the experimental value (Fig. 1C). This rough estimate gives a plausible value of the anchoring strength W in our experiments (32). Furthermore, because the anchoring of micelles is mostly governed by entropy (25, 26) (SI Text), we expect W to remain constant in a broad range of particle sizes. Therefore, Eq. 1 predicts interaction energies below 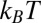for 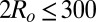nm, which forbids elastic interactions to trigger any sizeable aggregation of particles in this size range within our experimental conditions.

Fig. 1.

(A) Optical microscopy pictures of two interacting 780-nm-diameter spheres in the N_C phase tracked over time. (Scale bar, 5 μm.) (B) Time evolution of the separation distance r between the two spheres. The red curve is the best fit to the data with the empirical function 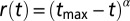with 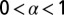(SI Text). (Inset) Elastic pair interaction potential 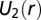derived from the red curve plotted in B (see Results and Discussion for details).

Collective Behavior of Nanoparticles in the Nematic Phase.

We prepared series of samples by introducing PS spheres with diameters 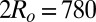, 520, or 190 nm into the N_C phase (SI Text). Typical snapshots of the resulting dispersions are shown in Fig. 2.

Fig. 2.

Optical microscopy pictures of latex spheres of different diameters 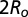in the N_C phase of the SDS/DeOH/water system at T = 20 °C (SI). (A) 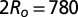nm. (Scale bar, 5 μm.) (B) Lower magnification: 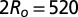nm. (Scale bar, 5 μm.) (C) 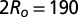nm. (D) 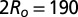nm. The local directions of the nematic axis is indicated by double arrows.

As anticipated, both the 780- and 520-nm-diameter spheres form dense, compact aggregates and “V-like” structures within a few minutes after sample preparation. Smaller chains tilted with respect to can also be distinguished (Fig. 2 A and B, Insets). The morphology of all these clusters reflect the quadrupolar symmetry of elastic interactions with planar anchoring conditions (13, 26, 29). More surprisingly, the 190-nm-diameter particles also aggregate massively within the same timescales as the bigger particles (Fig. 2 C and D). Moreover, the 190-nm-diameter particles self-organize into straight chains, or filaments, parallel to the local director: neither tilted chains nor compact clusters can be evidenced, even after several hours. Although the detailed arrangement of the nanospheres inside the chains cannot be optically resolved (SI Text), the linear structure of these aggregates does not seem to be consistent with quadrupolar elastic structuring forces. These observations were reproduced with fluorescent particles of the same size, which highlights the absence of any influence of the particle surface chemistry.

What can be the physical origin of the attraction between the smallest spheres? Because of the high ionic strength in our samples, electrostatic repulsions are negligible beyond a surface-to-surface separation distance 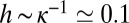nm (SI Text). Both the micelle-particle and particle-particle interactions are of the hard core type here. One may invoke van der Waals (vdW) interactions, but they are only effective at very small range (SI Text) and cannot explain the presence of chain-like aggregates. Furthermore, these interactions should occur as well in simple aqueous dispersions of PS spheres with the same ionic strength, which was not observed. Depletion interaction is another possibility due to the high volume fraction of rod-like micelles, 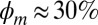, in the N_C phase (33). Like vdW interactions, they are short ranged and fade away for separation distances exceeding the micelle size (approximately nanometers). Depletion interactions are clearly evidenced in our samples when the system is formulated in the isotropic micellar phase L₁ of the phase diagram at 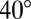. Both the 190- and 780-nm-diameter particles cluster into compact and fairly isotropic aggregates (Fig. S1), in stark contrast to the anisotropic structures observed in the N_C phase. These compact aggregates disappear when the micellar solution is diluted by a factor of 50, which again rules out vdW interactions that are insensitive to dilution. By contrast, the depletion potential, U_depl, is proportional to the osmotic pressure of the solution, and a reasonable estimate in the N_C phase leads to 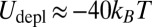(SI Text). This value is greater than the elastic pair interaction energy inferred above, and therefore, depletion forces ensure a strong sticky condition at short range, i.e., when the surface-to-surface distance between colloids becomes of the order of a micelle size.

At this point, the physical picture that emerges out of the observations is as follows: in our experiments, aggregation occurs over comparable timescales whatever the particle size. However, the physical mechanisms that drive the clumping of particles seem to differ depending on their size. Long-range anisotropic elastic interactions appear to dominate the aggregation of big particles (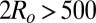 nm), whereas for small ones ( 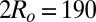nm), enhanced Brownian motion combined with strong depletion interactions at short range are more likely to be the leading process. Thus, downsizing the particles would result in a transition from an elasticity-dominated to a diffusion-dominated clustering regime. However, it is not clear whether depletion interactions are anisotropic in a nematic phase and are able to generate chain-like aggregates of small spheres. This problem was theoretically addressed by van der Schoot (34), who showed that depletion interactions can indeed be stronger along 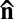; however, this result holds only in a size regime that does not apply to our experiments. Another aspect is the anisotropy of the diffusion of colloids in nematic phases (23, 35–41). In the present lyotropic N_C phase, we recently reported a high anisotropy ratio, 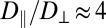, where D_∥ (respectively, D_⊥) is the diffusion coefficient parallel (respectively, perpendicular) to 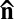(42). Small particles, diffusing faster than big ones, explore more configurations with separation distances within the range of attractive depletion forces, thereby increasing the probability of sticky contacts. Thus, it is tempting to relate the chain-like structures of Fig. 2 C and D to the enhanced Brownian diffusion along 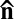. This conjecture prompted a series of tests using numerical simulations that we shall now present.

Numerical Simulations.

In this part, we present numerical simulations of the aggregation of colloidal particles embedded in a nematic LC. The main objective of our approach, based on effective potentials, is to elucidate the relevance of elastic quadrupolar interactions and particle diffusion anisotropy on the morphology of the observed aggregates. We start with a presentation of the main physical ingredients of the model before outlining the main steps of the Monte Carlo numerical scheme and the obtained results. Last, we propose an interpretation of the simulations based on heuristic arguments and provide a link with experiments.

Quadrupolar Interaction Energy.

Modeling an aggregating system of colloidal particles in a nematic liquid crystal must take into account the two-body anisotropic elastic interaction mediated by the fluid elasticity. We use the quadrupolar interaction U₂ defined in Eq. 1. For two touching spheres, U₂ is minimized for 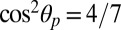and takes the value 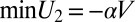. Aggregation occurs when the value of α is larger than the characteristic pressure 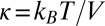, resulting from thermal energy. Then, the nondimensional ratio

characterizes the aggregation strength: strong (respectively, weak) aggregation corresponds to 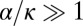(respectively, to 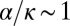). For the typical values, 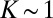pN and 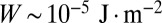, we get 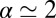Pa; then, strong aggregation is expected to hold for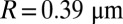 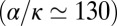and weak aggregation for .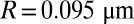

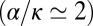Translational and Rotational Brownian Motion.

Brownian diffusion is anisotropic in a nematic LC (35–38, 40, 41). The ratio of the translational diffusion coefficients 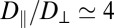(42) indicates an easier particle motion along 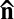than in the transverse direction. A rotational bias was predicted (43) and measured (44) for rods or ellipsoids dispersed in a nematic LC. The elastic energy cost of rod realignement to an angle θ from the equilibrium angle 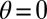may be estimated as (with strong planar anchoring conditions) 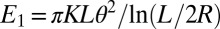, where L (respectively, R) is the length (respectively, radius) of the rod. [Using another formula for E₁ (Eq. 3), valid in the weak anchoring regime, does not change the results (Fig. S2).] We use the form, convenient for comparison with U₂:

where the nondimensional positive coefficient Γ reads

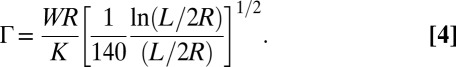Putting in the typical values 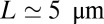and 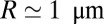together with those used above for K and W, one gets 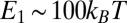for 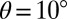. Then, nonspherical objects or aggregates experience rotational diffusion with a significant net drift of the tilt angle toward the nematic axis.

Monte Carlo Mumerical Model: Common Features.

Let us consider a system of moving particles in the presence of the interaction potential (Eq. 1) and random Brownian motion (possibly biased). Generally, evolution of such an aggregating system is represented by a sequence of diffusion limited cluster aggregation (DLCA) processes (8, 45). Because of the low volume fractions, only two-body collisions are significant, and we can use the cluster-cluster hierarchical model (46). The system is initially made of a dispersion of N spheres of radius 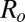(the monomers) with particle volume density n. Simulation of a sticking event between two aggregates of s monomers proceeds as follows. (i) Two clusters, A and B, are chosen randomly. B is put randomly on a sphere of radius 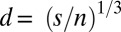, defined as the average distance between two neighboring clusters of size s, centered on A. (ii) Cluster B moves in the continuous 3D space by discontinuous step (random walk) of length λ, chosen randomly according to the translational anisotropy of the diffusion (SI Text). (iii) Clusters A and B undergo independent random rotations of angles 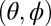such that the largest monomer displacement is equal to 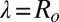(SI Text). (iv) The actual motion (translation and rotation) is performed if it results in an energy decrease of the system 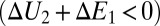, or occurs with the probability 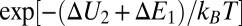in case of an energy increase. (v) If clusters A and B collide, aggregation is performed to make a rigid cluster of size 2s, and the simulation goes on to i; if A and B do not collide, simulation goes on to ii. Actually, the numerical simulations use three nondimensional parameters. Two parameters are related to the system energy, namely 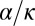(Eq. 2), which characterizes the aggregation strength, and Γ (Eq. 4), which compares the intensity of the two-body interaction potential U₂ (Eq. 1) to the one-body orientational elasticity E₁ (Eq. 3). The last parameter is related to the anisotropy of the diffusion: 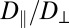. The other quantities (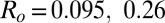, or 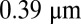, 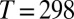K, and 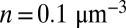) are the same as in the experiments.

Importance of the Biased Rotational Brownian Motion.

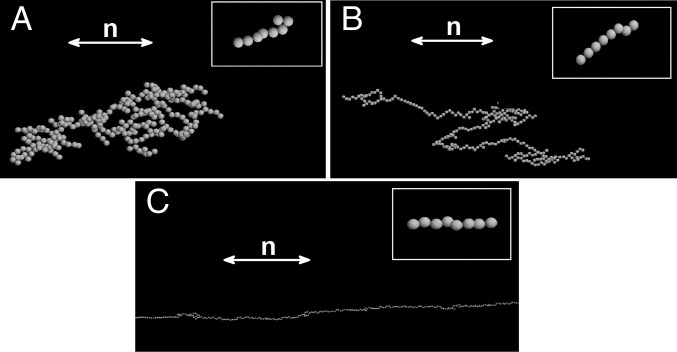
We first consider either isotropic or anisotropic Brownian translation, as well as different kinds of rotations, for a system of aggregating monomers with 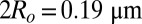. Typical clusters of 512 monomers are shown in Figs. 3 and 4 [In the simulations, we used the value 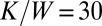nm because it better illustrates the experimental results and their interpretation. However, this ratio implies 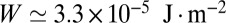if 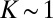pN, which differs from the usual value 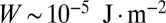( 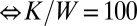nm) used in all our estimates. However, because one looks primarily for a qualitative agreement between the simulations and the experiments and because we only know the rough order of magnitude of W, its precise value does not matter at this point as long as it is reasonable.] Fig. 3A (respectively, Fig. 3B) was obtained without (respectively, with) translational anisotropy and in the absence of cluster rotations. In both cases, the cluster structures look very similar and, consequently, whethe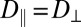r or 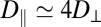does not matter. Only the particular symmetry of the two-body quadrupolar potential is clear, with many 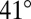-tilted bonds, characteristic of the angle minimization of U₂. Comparing the two figures, we notice a detail that may first appear as counterintuitive: easy translation along 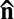favors cluster extension in the transverse directions because of the small cross section along 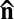, making head-to-head collisions unlikely. Conversely, the small transverse diffusion becomes efficient because of the large transverse cross sections of clusters. Similar features were also experimentally evidenced for sedimenting particles where the clusters have a larger extension in the direction perpendicular to the easy diffusion axis (47).

Fig. 3.

(A) Projection on a plane of a 3D aggregate of 512 interacting monomers of diameter 190 nm, grown with isotropic translational Brownian motion 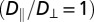and no cluster rotation. The values K/W = 0.03 μm and 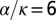were used. (B) Same as in A but with anisotropic translation 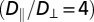. The cluster anisotropy is slightly less pronounced than in A.

Fig. 4.

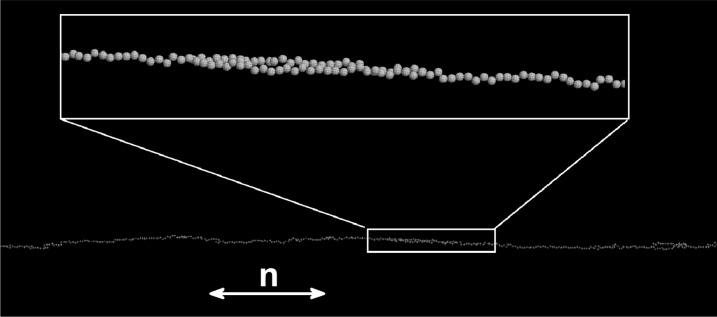
Plane projection of a 3D aggregate of 512 interacting monomers of diameter 190 nm, grown with anisotropic translational Brownian motion 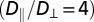and biased cluster rotation. Same parameters as in Fig. 3A. The almost perfect alignment along is indisputable. Zoomed-in view: part of the aggregate composed of two aligned chains stuck side by side.

It is clear from these figures that the translational anisotropy in the nematic LC cannot explain the linear morphology and alignment of the clusters made of 190-nm-diameter particles (Fig. 2 C and D). Then, another cause must be invoked to account for the chain-like structures seen in the experiments. The correct one seems to be a biased random rotation of the clusters, which includes an orientational relaxation mediated by the intrinsic uniaxial order of the nematic phase. Indeed, when looking at the aggregates generated with the bias resulting from Eq. 3, such as the one displayed in Fig. 4, one can see that it reproduces quite well the experimental pictures (Fig. 2 C and D).

Role of the Monomer Size.

We consider the complete set of particle sizes used in the experiments, namely 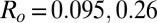, and 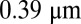. Simulation data are shown in Fig. 5 for each size, with anisotropic translation, biased cluster rotation, and elastic quadrupolar interactions. The obtained morphologies are strikingly similar to the experimental ones (see Fig. 2). In addition, the effect of the monomer size on the aggregate structure is neatly reproduced in the simulations (Fig. S3). Then, quadrupolar interactions coupled to a biased rotation of the clusters are the two key physical ingredients we should consider to explain the experimental facts. We will now provide simple arguments to strengthen this conclusion.

Fig. 5.

Aggregation of (A) 0.78-μm–diameter spheres, (B) 0.52-μm spheres, and (C) 0.19-μm spheres. Same parameters as in Fig. 3.

Interpretation of the Numerical Results.

Basically, two characteristic times govern the clustering of particles and the morphology of the resulting aggregates: the aggregation time, 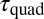, due to attractive elastic interactions, and the orientation time of the clusters, 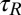, due to the biased Brownian rotational motion. We first provide estimates of these two times, which will be helpful when outlining a likely scenario for the orientation process of dimers.

Characteristic Times.

Aggregation time .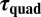

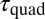is the time needed for a cluster, A, of size s to interact and collide with another cluster, B, of same size through elastic quadrupolar forces in a fluid with (effective) viscosity η. Using Eq. 1, neglecting inertia and Brownian motion and further assuming a straight trajectory, 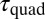can be readily estimated via a standard approach (31) because all system parameters are known (SI Text). For example, for the two interacting spheres of Fig. 1A, we find 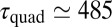s, which compares well with the 670 s found experimentally in this case (Fig. 1).

Orientation time .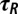

As we have seen, cluster orientation results essentially from particle rotation in the anisotropic medium. 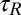may be estimated by integrating the equation 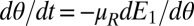, where E₁ is given by Eq. 3, and 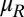is the rotational mobility of the cluster (SI Text). For a dimer with 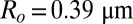, we find 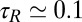s, although increasing fast with the cluster elongation (for 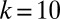, 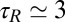s).

Thus, the condition 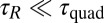is generally fulfilled, i.e., the two timescales are totally decoupled. From these rough estimates, we conclude that, during their motion, the wandering clusters should always remain well oriented along 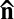due to the intrinsic elastic properties of the nematic phase.

Scenario of the Orientation Process for Dimers.

To see in more detail how the orientation process works, let us take the simple example of two interacting dimers (aggregates of two monomers of radius 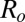) oriented in the field 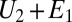during their trajectory, leading to aggregation. Brownian motion is neglected. By symmetry, both clusters share the same tilt angle θ with respect to the nematic axis. The orientation elastic energy E₁ is given by Eq. 3, with 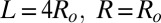. On the other hand, U₂ is built from the quadrupolar interactions between the two monomers of the first cluster 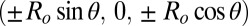and the two monomers of the second cluster 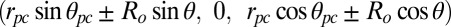. 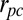is the distance between the centers of mass of both clusters, and 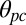is their orientation direction with respect to 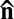. Because we know that 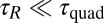, the final tilt angle is decided by the conditions just before the sticking event. 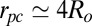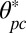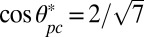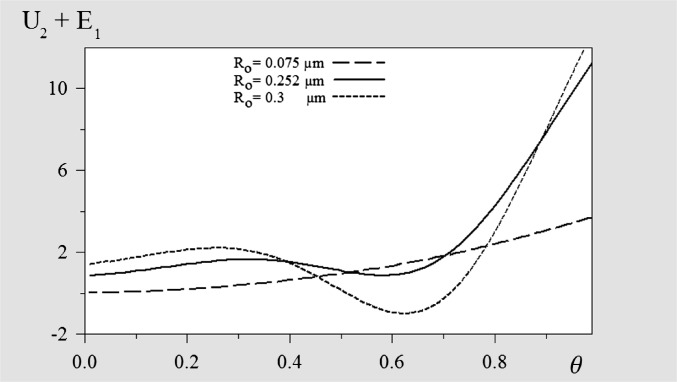At this moment, the approaching clusters are such that and the inclination angle between both dimers is close to , with , minimizing the quadrupolar energy. Considering these values, the total energy, 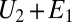, is then an analytic function (although not simple) of the tilt angle θ, with the only control parameter 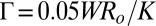. Typical energy curves are displayed in Fig. 6 for three different values of R_o. For the smallest value of 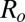(corresponding here to 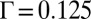), the energy has an absolute minimum for 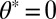, and then the clusters orientate along 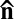. For the largest value of 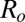(corresponding here to 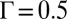), a clear minimum appears for a positive value of the tilt angle, 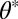, close to 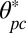. [On testing other W values in Eq. 4 (and leaving K unchanged), we noticed that the elastic to diffusive transition (Figs. 6 and 7) shifts to lower (or greater) 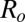values as W is increased (or decreased).] Fig. 7 shows the plot of θ as a function of 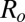, derived from Fig. 6. This behavior can be simply explained: according to Eqs. 1 and 3, when the monomer radius is varied, the reduced energy 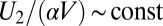for fixed tilted angle and aspect ratio, whereas the energy 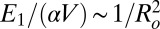in the same conditions. Then, for the small monomer radius, orientation of the clusters along n is effective, whereas for large monomer radius, the quadrupolar energy U₂ is dominant.

Fig. 6.

Value of the total potential energy 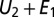for two interacting dimers, expressed in the unit 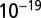J as a function of the tilt angle in radians for three values of the radius 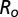in micrometers.

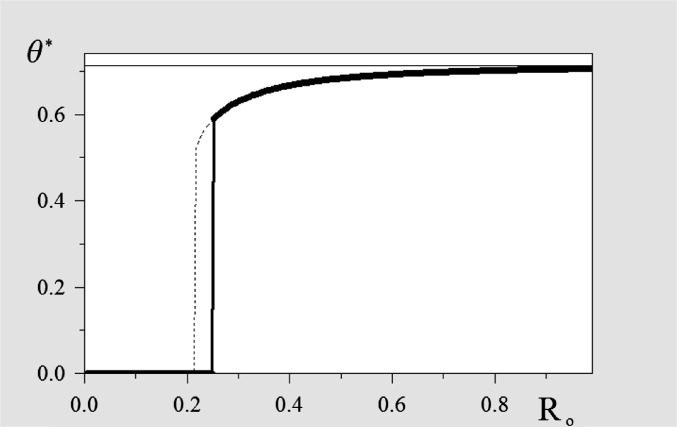
Fig. 7.

Value of the stable-equilibrium tilt angle (thick solid line) of two aggregating dimers as a function of the monomer radius 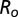in micrometers. The horizontal line corresponds to 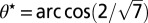(value that minimizes U₂ for two identical spheres; Eq. 1). The dotted line corresponds to metastable tilt angles.

A marked symmetry breaking occurs for a definite value of 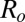(and hence of Γ). More precisely, if 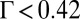(small sizes), orientation occurs along 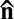(orientational energy dominant), whereas if 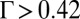(large sizes), orientation occurs with an angle 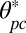, which minimizes the energy U₂ (quadrupolar energy dominant). The threshold value 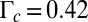is valid for dimers close to aggregation, but the argument can be extended more generally to large clusters as well (SI Text).

Conclusion.

To conclude, the main message of the present work is that self-assembly of colloidal particles in micellar nematic solvents markedly depends on their size: both experiments and Monte Carlo simulations show that elastic forces dominate the coarsening of the system for big particles (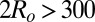 nm), whereas for small ones ( 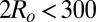nm), biased rotational diffusion combined to depletion interactions controls cluster morphology and aggregation kinetics. Interestingly, the anisotropic translational Brownian motion is irrelevant. In all cases, the clusters exhibit a varying degree of anisotropy that obviously arises from the intrinsic ordering field of the nematic matrix.

Although very insightful, our approximate DLCA simulations, based on effective potentials, could be improved to take into account the dynamics of the nematic phase. Such computations would require solving the equations of nematohydrodynamics in the presence of a biased Brownian motion of the particles. It would be quite a challenging task but seems to be within the reach of current computer dynamic simulations (48).

As possible follow-up work in the area, it would be worthwhile to try out experiments using either even smaller particles (size < 100 nm) to minimize the intensity of depletion interactions or thermotropic LCs. In the latter case, depletion phenomena are absent, and only a biased diffusion coupled to weak elastic interactions would have to be considered (21, 23). Collective behaviors involving numerous particles have not been reported thus far; however, as pointed out in refs. 21 and 23, such a system would allow, on paper, the making of homogeneous colloids-in-LC dispersions with tunable interparticle separations and high particle loads (volume fraction 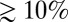). Reaching high particle contents is still a puzzling challenge today with the long-term goal of designing LC-based materials with peculiar properties, such as those expected for metamaterials (49).

Materials and Methods

Complementary information about the liquid crystal, particles and samples preparation are provided in Supporting Information. Details pertaining to the measurement of the elastic pair interaction potential are specified. Also included are additional comments on Monte Carlo simulations and theoretical estimates of colloidal forces.