Renormalization of myoglobin–ligand binding energetics by quantum many-body effects

Significance

Heme-based metalloproteins play a central role in respiration by transporting and storing oxygen, a function that is inhibited by carbon monoxide. Density-functional theory has been unable to provide a complete description of the binding of these ligands to heme's central iron atom, predicting an unrealistically high relative affinity for carbon monoxide. Here, we solve this problem using dynamical mean-field theory in combination with linear-scaling density-functional theory, thus allowing for a simultaneous description of crucial quantum entanglement and protein discrimination effects in the ground-state of the oxygen-heme complex. By simulating the binding process within a 1,000-atom quantum-mechanical model of the myoglobin metalloprotein, we obtain a significantly improved description of its spectroscopic and energetic observables.

Abstract

We carry out a first-principles atomistic study of the electronic mechanisms of ligand binding and discrimination in the myoglobin protein. Electronic correlation effects are taken into account using one of the most advanced methods currently available, namely a linear-scaling density functional theory (DFT) approach wherein the treatment of localized iron 3d electrons is further refined using dynamical mean-field theory. This combination of methods explicitly accounts for dynamical and multireference quantum physics, such as valence and spin fluctuations, of the 3d electrons, while treating a significant proportion of the protein (more than 1,000 atoms) with DFT. The computed electronic structure of the myoglobin complexes and the nature of the Fe–O₂ bonding are validated against experimental spectroscopic observables. We elucidate and solve a long-standing problem related to the quantum-mechanical description of the respiration process, namely that DFT calculations predict a strong imbalance between O₂ and CO binding, favoring the latter to an unphysically large extent. We show that the explicit inclusion of the many-body effects induced by the Hund’s coupling mechanism results in the correct prediction of similar binding energies for oxy- and carbonmonoxymyoglobin.

The ability of metalloporphyrins to bind small ligands is of great interest in the field of biochemistry. One such example is the heme molecule, which reversibly binds diatomic ligands, such as oxygen (O₂) and carbon monoxide (CO), and plays a crucial role in human respiration. Heme is used in myoglobin (Mb) and hemoglobin proteins to store and transport O₂ in vertebrates. The heme group of Mb is packed within a predominantly α-helical secondary structure and is coordinated by a histidine residue (known as the proximal histidine) as the fifth ligand of the heme’s central Fe ion.

Despite intensive studies (1–6), the nature of the bonding of O₂ to the iron-binding site of the heme molecule remains poorly understood, mainly due to the strong electronic correlation effects associated with its localized Fe 3d electrons. It is known that these electrons are energetically well-aligned with the 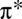acceptor orbitals of CO and O₂, and that the molecules’ bound conformations seek to maximize intermolecular orbital overlap (7–9). In the case of MbO₂, the short Fe–O bond (1.81 Å) (9) implies that σ-bonding is supplemented, to some extent, by π-bonding (8). Indeed, calculations using the ab initio complete active space self-consistent method, in combination with a molecular mechanics force field to describe the protein (CASSCF/MM) (4), have identified a weak π-bonding mechanism in the Fe–O₂ bond that gives rise to an antiferromagnetic (open-shell singlet) state.

However, recent Fe L-edge X-ray absorption spectroscopy measurements on small biomimetic heme models lack the signature low-energy peak that is characteristic of the 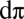hole, formed by metal-to-ligand charge transfer into the ligand 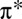orbitals (10). Although these spectroscopic results are more consistent with a strong Fe–O π interaction, some uncertainty remains about whether the same bonding picture holds in MbO₂ because the experiment was performed on a small model system [Fe(picket fence porphyrin)1-MeImO₂], which, in particular, neglects the distal histidine (His-64) that hydrogen bonds directly with O₂ in the protein.

Furthermore, although the diamagnetic nature of MbO₂ is well established, there is little experimental evidence that directly addresses the extent of the charge transfer from Fe to O₂. Both CASSCF/MM (4) and L-edge X-ray absorption spectroscopy (10) suggest strong σ-donation from O₂ into the 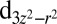orbital of iron (ligand-to-metal back charge transfer), which is hypothesized to limit the charge on the O₂ molecule to around 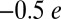(4). However, the stretching frequency of the O–O bond in MbO₂ has been shown to be close to that of the free 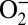ion (8, 11), which motivates further study.

The energetics of diatomic ligand binding to the Mb protein are expected to depend strongly on the electronic structure of the heme site, and in particular on its orbital polarization. Specifically, Mb reduces the heme group’s natural preference for CO binding: Based on experimental equilibrium association constants, the binding free energy of CO, relative to O₂, is reduced from around 5.9 kcal/mol in a nonpolar solvent to 1.9 kcal/mol in the protein environment (12). The combination of the strong electronic correlation centered at the Fe-binding site and long-ranged interactions between the protein and the charged O₂ molecule make computational modeling of the energetics of these complexes extremely challenging.

Typically, such studies calculate the protein effect (13–15), or relative spin state energies (16), or focus on small model systems (6). However, most approaches applied to large system sizes did not include a proper treatment of electronic correlations. The effect of electronic correlations in the iron 3d states was investigated by some of us (13), where it was included, to an extent, in ab initio simulations of ligand discrimination in Mb via a density functional theory (DFT) + U treatment. DFT + U has been shown to be an efficient method for correcting self-interaction errors in the approximate DFT description of transition-metal chemistry (17), and when combined with linear-scaling approaches (18, 19), it allows us to tackle such systems comprising thousands of atoms. It was found, in the case of Mb (13), that the protein discrimination effect is dominated by polar interactions between O₂ and the distal protein residue His-64. However, a problem in the DFT + U calculations is that a strong residual energetic imbalance that favors CO over O₂ binding was observed (13), suggesting that approaches beyond static DFT + U are called for to obtain a proper description of Mb.

Recent progress has been made in the study of strongly correlated electrons by means of dynamical mean-field theory (DMFT) (20), a sophisticated method which includes quantum dynamical effects, and takes into account both valence and spin fluctuations. DMFT is routinely used to describe materials, and recently has also been extended to nanoscopic systems (21, 22). DMFT also explicitly includes the Hund’s exchange coupling typically, although not always, neglected in DFT and DFT + U studies. DMFT was recently combined with linear-scaling DFT (23) to produce a linear-scaling DFT + DMFT approach (24). By means of the latter, we have pointed out that strong correlation effects in heme are controlled by the Hund’s coupling J, and not the Hubbard repulsion U alone (25), suggesting that subtle quantum many-body effects are missing in the DFT + U treatment of Mb (13). However, the computational model included just the heme group and diatomic ligands, neglecting entirely the protein environment and proximal histidine ligand, thereby strongly overestimating the binding energy of CO relative to O₂.

In the present work, we bridge state-of-the-art DMFT many-body calculations with large-scale DFT calculations. We perform simulations of realistic models of the MbO₂ and MbCO complexes, comprising 1,007 atoms, using linear-scaling DFT + DMFT. We thereby treat the electrostatic, steric, and hydrogen-bonding effects due to protein materials together with the multireference, finite-temperature, and explicit Hund’s exchange coupling effects associated with the iron 3d-binding site in single, self-consistent calculations for, to our knowledge, the first time. We systematically investigate how the Hund’s coupling alters the electronic structure at the heme site and, at the same time, corrects the long-simulated, unphysical imbalance between CO- and O₂-binding affinities.

Results

We first discuss our results for the porphyrin-plane component of the optical absorption spectra of ligated Mb, computed using DFT + DMFT (Fig. 1), where a realistic value of the Hund’s coupling 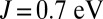is considered (results obtained for 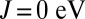are shown for comparison). The absorption spectrum of this protein has been reported experimentally to be qualitatively dependent on its ligation state, in that a peak is present in the infrared region in the MbO₂ case but not for MbCO (26). Our theoretical absorption spectrum is in good agreement with the experimental data obtained from sperm whale MbO₂ single crystals (27), and reproduces an MbO₂ infrared absorption band at 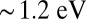, observed experimentally at 1.3 eV (28). Our calculations associate this feature with a charge-transfer band generated by the hybridization of the Fe atom and the O₂ molecule, in particular transitions of occupied porphyrin π and iron d orbital states into empty O₂ orbitals. In MbCO, due to the strong covalent bond, the porphyrin π and d hybridized orbitals are at a lower energy and, hence, there is no contribution to the infrared spectrum. The double-peak structure in the optical transition obtained at 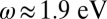and 2.2 eV is also very close to experiments, where they are obtained respectively at 2.1 and 2.3 eV (27, 28). We attribute this feature to the porphyrin Q band (π to absorptions) and to corresponding charge transfer excitations. We find a broad Soret band centered theoretically at 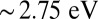, close to the experimental peak obtained at 2.95 eV (27, 28). For MbO₂, the spectrum at 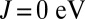is qualitatively similar. However, Fig. 1 also reveals that a nonzero J is required to recover the experimentally observed double-peak structure of the MbCO Q band (27). Analysis of the spectral weight below the Fermi level in MbCO reveals the source of this splitting. For , the orbital character of the HOMO is almost degenerate between the three 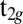orbitals. However, for J = 0.7 eV, we observe a splitting of the spectral weight of the d_xy and the d_xz,yz orbitals of 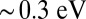, thus recovering the expected splitting of the charge transfer Q band in the optical absorption spectrum.

Fig. 1.

Optics. Porphyrin-plane component of the optical absorption spectrum calculated using DFT + DMFT at 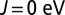(dashed curves) and 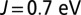(continuous curves) for MbCO (blue) and MbO₂ (red).

To further understand the nature of the bonding in the MbO₂ complex, we have found it instructive to transform the atomic basis functions, used to expand the DFT + DMFT density matrix (that is, the frequency-integrated Green’s function), into a set of natural bond orbitals (NBOs) (29–31). The transformation is constructed such that the resulting orbitals may be categorized into localized Lewis-type bonding and lone pair orbitals, as well as their antibonding and Rydberg counterparts, thus allowing a chemically intuitive population analysis to be applied to the DFT + DMFT many-body wave-function. Fig. 2 shows the σ- and π-bonding many-body NBOs of the MbO₂ complex. We find, in particular, that an O₂ 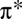NBO (Fig. 2A), which has an occupancy of 1.5 e, and an antibonding NBO formed between Fe and the proximal histidine, with occupancy 0.5 e and a strong 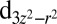character, interact strongly via the DFT Hamiltonian. We note that the 0.5 e occupancy of the antibonding orbital on Fe is consistent with the ligand–metal back charge transfer process between O₂ and the Fe 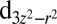orbital, which is observed both in CASSCF/MM (4) and L-edge X-ray absorption spectroscopy (10). Ligand–metal back charge transfer is also present at 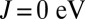, albeit with a smaller magnitude (0.34 e). Thus, electronic delocalization is expected to provide a greater energetic stabilization in the MbO₂ complex at .

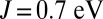Fig. 2.

NBO analysis of the DFT + DMFT Green’s function for MbO₂. (A) An O₂ type many-body NBO (cyan/magenta) of occupancy 1.5 e, which strongly interacts (via the DFT Hamiltonian) with an antibonding Fe-based many-body NBO (red/blue) of occupancy 0.5 e. (B and C) Many-body NBOs showing π-bonding between Fe and O₂; the NBO occupancies are 1.4 and 1.8 e, respectively.

The net charge on the O₂ molecule, from natural population analysis, is 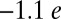, which is consistent with the Weiss picture of bonding in MbO₂ (2). It is worth noting that state-of-the-art CASSCF/MM calculations point toward a smaller O₂ charge of 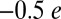(4). Metal-to-ligand charge transfer is expected to occur via π-bonding interactions between Fe d orbitals and O₂ 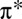(4, 10). Indeed, Fig. 2 B and C are characteristic of the multiconfigurational CASSCF orbitals that make up the proposed π-type bonding in a previous study (4). A notable difference between these calculations and the CASSCF/MM study is that the π-bonding is much stronger than previously reported. Here, 3.25 e are involved in π-bonding, as opposed to ∼2 e in CASSCF/MM. Our calculations yield a 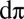hole character of 19%. This compares extremely favorably with recent Fe L-edge X-ray absorption spectroscopy measurements of a small biomimetic heme model, which estimates the 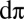hole character to be 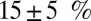(10). We therefore find that the π-bonding character in MbO₂ is similar to that in isolated porphyrins. We note that the stronger π-bonding interaction between the iron and O₂ also suggests that spin polarization of the π electrons is less likely (10), suggesting that a broken spin symmetry description of MbO₂ might not be entirely reliable.

Next we show in Table 1 a comparison of the computed Fe orbital density with and without the explicit inclusion of Hund’s coupling J in the Hamiltonian. We find that the effect of J in MbO₂ is to bring the 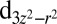, d_xy, and orbitals closer to single-electron occupation, so that the Hund’s coupling enhances the spin magnetic moment on the Fe atom. 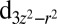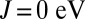Indeed, we find, in our calculations, a build up of a magnetic moment in the , , and d_xy orbitals, with a concomitant electron occupation of absent from our calculation and from the CASSCF/MM approach. The latter discrepancy may be due to the fact that CASSCF does not include dynamical correlation effects and may also be dependent on the chosen active space. In MbCO, unlike MbO₂, we observe that the doublet on the d_xy orbital is not emptied as the Hund’s coupling is increased. In Fig. 3A we show the dependence of the Fe charge, computed using Mulliken analysis in the nonorthogonal generalized Wannier function (NGWF) (32) basis, on the Hund’s coupling J for MbO₂ and MbCO, respectively. For MbO₂, we find that the charge of the Fe is transferred to the porphyrin ring and protein as the Hund’s coupling is increased. In contrast, for MbCO we find a very weak dependence of the Fe charge on the Hund’s coupling parameter (Table 1). In our view, the latter indicates a very strong Fe–CO covalent bond, which remains stable against the Hund’s coupling. We find that the charge transferred from the Fe to O₂ is 1.1 e at the physical value of the Hund’s coupling 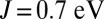(Fig. 3B), confirming the estimation obtained using natural population analysis.

Table 1.

3d orbital occupations of the Fe atom in ligated Mb

Protein		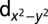	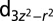dxy	dxz	dyz
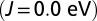
MbO2	0.82	0.38	1.99	1.90	1.92
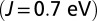
MbO2	0.96	0.96	1.10	1.87	1.96
MbCO	0.95	1.13	1.99	1.88	1.89
MbCO	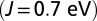1.00	1.15	1.99	1.84	1.84
MbO2 (CASSCF/MM)	0.44	0.59	1.93	1.86	1.13

The CASSCF/MM values are shown for comparison (4).

Fig. 3.

Polarization. (A) The dependence on J of the DFT + DMFT Mulliken charge of the Fe atom in MbO₂ and MbCO. (B) Mulliken charges in MbO₂ of the two O atoms of O₂ (O-1 is bonded to Fe and O-2 forms a hydrogen bond with His-64). Also shown are the corresponding charges of the in-plane N atoms of the heme group and His93 (the fifth ligand of Fe).

Fig. 4 depicts the computed spin fluctuations in MbO₂ and MbCO, specifically, a histogram of the spin quantum number distribution obtained by looking at the 16 dominant states in the reduced (3d subspace) density matrix, obtained by tracing the atomic DMFT problem over the bath degrees of freedom. This gives an effective representation of the quantum states of the Fe atom. The ground-state wave function is not a pure state with a single allowed value for the magnetic moment (singlet, doublet, triplet, etc.), yet we can describe the fluctuating magnetic moment of the Fe atom by analyzing the distribution of the magnetic moments obtained from the dominant configurations. In particular, we find that the reduced density matrix of MbCO has states with dominant 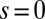configurations, and MbO₂ has dominant contributions from 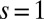, with higher spin contributions at 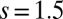. This is consistent with our general observation that MbO₂ has larger valence fluctuations (entanglement in the ground-state) than MbCO.

Fig. 4.

Spin fluctuations. Spin-state distribution obtained by analyzing the 16 dominant states in the DFT + DMFT reduced density matrix (see Results) at 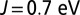. The reduced density matrix of MbCO has states with dominant 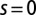configurations, and MbO₂ has dominant contributions from 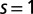, with higher spin contributions at .

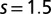Having shown how the Hund’s coupling affects the orbital occupancy of the Fe site in Mb, and the associated charge transfer to the O₂ molecule, we investigate in what follows how the energetics of ligand binding to Mb are determined by these effects, and how the protein uses quantum fluctuations to discriminate between O₂ and CO. Fig. 5 shows the binding energies of O₂ and CO to Mb (to within a constant shift), calculated using DFT + DMFT, as a function of the Hund’s exchange coupling J. At 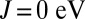, the binding energy of MbCO is ∼1 eV more favorable than the binding energy of MbO₂, yielding an unphysical energetic imbalance. For 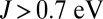, we find on the contrary that the binding energy of MbO₂ is dramatically reduced. We attribute this to the enhancement of the spin magnetic moment in the Fe atom. In the intermediate regime, close to 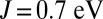, we find that the imbalance between MbO₂ and MbCO is thereby also dramatically reduced. In fact, the experimental binding free-energy difference between the two ligands of 1.9 kcal/mol is recovered from our calculations when J is near 0.7 eV, a typical value used for iron-based materials (33). In this case, the effect of J on the binding energy of O₂ may be regarded as a balance between two competing effects. The charge analysis (Fig. 3) reveals that metal-to-ligand charge transfer is higher for 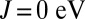, which is expected to enhance ligand–protein interactions for small values of J. However, NBO analysis reveals a larger ligand-to-metal back charge transfer for , which is consistent with the increased occupancy of the Fe 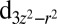orbital (Table 1), and is expected to cause variational energetic lowering at higher values of J due to electronic delocalization.

Fig. 5.

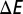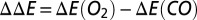Binding energetics. Hund’s exchange coupling J dependence of the DFT + DMFT total energy of MbCO (blue) and MbO₂ (red), where the DFT energy of the diatomic ligand CO or O₂ has been subtracted to give . A global arbitrary constant shift of the energy has been applied for clarity. The difference of binding energies is obtained by . The physical regime, where 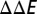is small, is shaded.

Compared with previously reported DFT studies, including our own DFT + U study of the same system (13), the present study predicts a significantly larger charge on the O₂ molecule (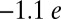 versus 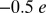). This charge is expected to stabilize the O₂ molecule in the Mb protein via hydrogen bond interactions with His-64. Hence, we propose that both dynamical and multireference quantum effects, and large system sizes, must be accounted in order to correctly determine the energetics of ligand binding in proteins with strongly correlated subspaces.

Conclusions

We have presented the application of a recently developed methodology, designed to treat strong electronic interaction and multireference effects in systems of relatively very large numbers of atoms, to a molecule of important biological function. In particular, we have found that the Hund’s coupling J is the crucial ingredient necessary to increase the multireference high-spin character of the ground state, and so to bring binding energetics into qualitative agreement with experiment. This provides a route to the solution of a long-standing problem in the density-functional theory-based simulation of heme proteins, which often underestimates the Hund’s coupling and incorrectly describes multireference effects, namely an unphysically large imbalance of CO- and O₂-binding energies. Our many-body description of the ligated Mb ground state is further supported by quantitative agreement with experimental findings on both the ligand dependence of the optical absorption spectra and the nature of the π-bonding in Fe–O₂. Our approach, optimized to describe molecules and nanoparticles involving transition metal ions, supports a large range of applications, e.g., to strongly correlated oxide nanoparticles (34) or to enzymes (35).

Methodology

In this work we have carried out a detailed theoretical study of the electronic structure of the Mb molecule by means of a combination (19, 24) of linear-scaling DFT and DMFT (20, 36), a model which treats subspace local dynamical, finite temperature and multideterminantal effects, for given Hamiltonian parameters. The Order-N Electronic Total Energy Package (ONETEP) linear-scaling DFT code (19, 23, 37) was used to obtain the DFT ground state. The ONETEP method is particularly advanced in terms of its accuracy, equivalent to that of a plane-wave method, which is arrived at by means of an in situ variational optimization of the expansion coefficients of a minimal set of spatially truncated NGWFs (32), and is based on direct minimization of the total energy with respect to the single-particle density matrix. The use of a minimal, optimized Wannier function representation of the density matrix allows for the DFT ground state to be solved with relative ease in large systems, particularly in molecules where their explicit truncation implies that the addition of vacuum does not increase the computational cost. Preparation of the structures for DFT + DMFT analysis have been described in detail elsewhere (13). Briefly, the computational models are based on the X-ray crystal structures of sperm whale Mb in oxygenated and carbonmonoxygenated ligation states (Protein Data Bank ID codes 1A6M and 1A6G) (9). The heme group, ligand, and 53 closest residues (1,007 atoms in total) were extracted from the MbO₂ crystal structure and optimized using spin-polarized DFT, with the Perdew–Burke–Ernzerhof (38) gradient-corrected exchange-correlation functional augmented by damped London potentials to describe van der Waals interactions (39). Following optimization, the heme group and three closest residues were replaced by their positions in the MbCO crystal structure and reoptimized. This scheme ensures that energy differences are directly attributable to local changes in the binding site, while accounting for long-ranged polarization and constraints of the protein scaffold. The DFT binding energy was converged to better than 0.02 eV with respect to changes in the plane-wave energy cutoff and NGWF cutoff radii, and no additional restrictions on the variational freedom, such as the density kernel truncation, were invoked.

We refined our DFT calculations using the DFT + DMFT method (20, 36) to obtain a more accurate treatment of strong electronic correlation effects. In particular, DMFT introduces both quantum and thermal fluctuations, which are multireference effects not captured at the level of the Kohn–Sham DFT. In this, the Mb molecule was mapped within DMFT to an Anderson impurity model Hamiltonian (40), and we used a recently developed extended Lanczos solver (41) to obtain the DMFT self-energy. Because only a single impurity site (3d orbital subspace) is present, the system becomes crystal momentum-independent in the molecular limit, and because the Kohn–Sham Green’s function is computed in full by inversion before projection onto the impurity subspace, the Anderson impurity mapping is effectively exact and the necessity of invoking the DMFT self-consistency is not required. However, in DFT + DMFT there is also a charge self-consistency cycle, albeit not routinely invoked at present due to computational cost, where the DFT + DMFT density kernel is used to generate a new Kohn–Sham Hamiltonian, which in turn provides a new input to the DMFT; the procedure being repeated until convergence is achieved. In this work our data are obtained in the absence of charge self-consistency, however we checked that the corrections are small. Indeed, for MbO₂ at 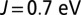, the changes obtained by converging the charge self-consistent DFT + DMFT induce a change in the energy of 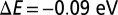, which corresponds to the energy of MbO₂ at 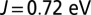when the charge self-consistency is absent. Other changes are also small, for example, the chemical potential changes by 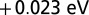, and we find a change in the Fe charge of 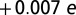. All these variations are consistent with a renormalized J (J increased by 3% at ).

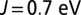To obtain the Kohn–Sham Green’s function, we performed the matrix inversion, as well as all matrix multiplications involved in the DMFT algorithm, on graphical computational units (GPUs) using a tailor-made parallel implementation of the Cholesky decomposition written in the CUDA programming language.

Electronic correlation effects are described within the localized subspace by the Slater–Kanamori form of the Anderson impurity Hamiltonian (42, 43), specifically

where 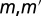are orbital indices,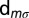 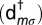annihilates (creates) an electron with spin σ in the orbital m, 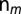is the orbital occupation operator. The first term describes the effect of intraorbital Coulomb repulsion, parametrized by U, and the second term describes the interorbital repulsion, proportional to 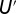, which is renormalized by the Hund’s exchange coupling parameter J to ensure a fully rotationally invariant Hamiltonian (for further information on this topic, we refer the reader to ref. 44). The third term is the Hund’s rule exchange coupling, described by a spin exchange coupling of amplitude J. 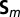denotes the spin corresponding to orbital m, so that 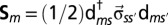, where 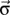is the vector of Pauli matrices indexed by s and . In this work, we used for the screened Coulomb interaction (16) and we explored the dependence of several observables on the Hund’s coupling (in the range 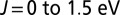). Our DMFT calculations were carried out at room temperature, 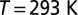. In this work, we used the canonical form of the double-counting potential 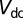, given by 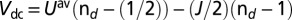, assuming paramagnetic occupancy of the d orbitals. Here, the parameter 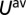is the intra- and interorbital averaged repulsion (45). In our calculations we found that the DMFT solution remains paramagnetic, although the possibility of spontaneous formation of a magnetic moment (spin symmetry broken state) was allowed for. However, the low energy states are in a quantum superposition of polarized states, giving a fluctuating magnetic moment at the iron site. The theoretical optical absorption was obtained in DFT + DMFT within the linear-response regime (Kubo formalism), in the no-vertex-corrections approximation (46), where it is given by

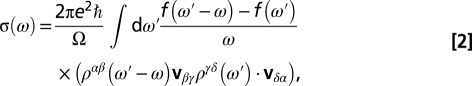and the factor of two accounts for spin degeneracy, Ω is the simulation-cell volume, e is the electron charge, ћ is the reduced Planck constant, 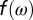is the Fermi–Dirac distribution, and 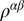is the density matrix given by the frequency integral of the interacting DFT + DMFT Green’s function. The matrix elements of the velocity operator, , noting that we do not invoke the Peierls substitution (46), are given by

This expression is general to the NGWF representation (47), used in this work, where the contribution to the noninteracting Hamiltonian due to the nonlocal part of the norm-conserving pseudopotentials (48, 49), represented by 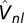, is included. Once the self-energy matrix is obtained, it can be used to correct the DFT total energy with the DMFT correction (50, 51):

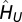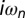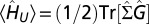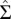
where indicates the many-body interaction vertex of the DMFT, and the primed sum is over the occupied states. Tr indicates the one-electron trace for a generic representation and the sum over the Matsubara frequencies of the finite-temperature many-body formalism. The interaction term is obtained with the Galitskii–Migdal equation (52): , 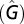is the self-energy (Green’s function) matrix in the NGWF representation. We note that both the self-energy and the Green’s function are slowly decaying functions, hence the trace over Matsubara frequencies has to be done with care (50, 51). Finally, the double-counting correction 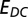must be introduced because the contribution of interactions between the correlated orbitals to the total energy is already partially included in the exchange-correlation potential derived from DFT. The most commonly used form of the double-counting term is 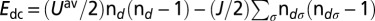(45).

An important approach used in this work is the generation of NBOs based on the many-body Green’s function provided by DFT + DMFT, to obtain greater chemical insight into the ligand binding process. NBOs (29) are postprocessed linear combinations of the basis functions in which the density matrix is expanded, such that the projection of the density matrix onto the subspace formed by atom-based and atom pair-based subsets of basis functions is maximally diagonal. In the current calculations the basis functions in question are NGWFs (32), transformed to NBOs using the NBO 5 program (30), recently interfaced to ONETEP, as described in ref. 31. This procedure is carried out in such a manner that the final NBOs are then categorized into largely occupied bonding and lone-pair orbitals, and largely vacant antibonding and Rydberg orbitals. Although normally applied to Kohn–Sham density-functional theory, to date, the NBO generation procedure is independent of the model (and so the Hamiltonian and self-energy) generating the density matrix, and so we may apply it to the density matrix integrated from the DFT + DMFT full Green’s function, to our knowledge, for the first time. The resulting many-body NBOs largely retain the familiar profile of DFT-based NBOs, in this study, but their occupancies may be expected to deviate further from integer values due to quantum-mechanical and finite-temperature multireference effects captured within DFT + DMFT. We computed the energy of MbCO and MbO₂ as a function of the Hund’s exchange coupling J. Defining 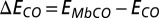and 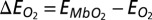, the binding energy difference 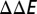is given by 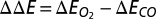. When 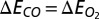, the MbO₂- and MbCO-binding energies are identical. In comparisons with the experimental relative free energy of binding, we have assumed that the relative change in entropy of the two ligands upon binding is zero, which is a reasonable approximation for two sterically similar diatomic ligands.