Influence of vapor wall loss in laboratory chambers on yields of secondary organic aerosol

Significance

Atmospheric secondary organic aerosol (SOA) has important impacts on climate and air quality, yet models continue to have difficulty in accurately simulating SOA concentrations. Nearly all SOA models are tied to observations of SOA formation in laboratory chamber experiments. Here, a comprehensive analysis of new experimental results demonstrates that the formation of SOA in laboratory chambers may be substantially suppressed due to losses of SOA-forming vapors to chamber walls, which leads to underestimates of SOA in air-quality and climate models, especially in urban areas where anthropogenic SOA precursors dominate. This analysis provides a time-dependent framework for the interpretation of laboratory chamber experiments that will allow for development of parameterized models of SOA formation that are appropriate for use in atmospheric models.

Abstract

Secondary organic aerosol (SOA) constitutes a major fraction of submicrometer atmospheric particulate matter. Quantitative simulation of SOA within air-quality and climate models—and its resulting impacts—depends on the translation of SOA formation observed in laboratory chambers into robust parameterizations. Worldwide data have been accumulating indicating that model predictions of SOA are substantially lower than ambient observations. Although possible explanations for this mismatch have been advanced, none has addressed the laboratory chamber data themselves. Losses of particles to the walls of chambers are routinely accounted for, but there has been little evaluation of the effects on SOA formation of losses of semivolatile vapors to chamber walls. Here, we experimentally demonstrate that such vapor losses can lead to substantially underestimated SOA formation, by factors as much as 4. Accounting for such losses has the clear potential to bring model predictions and observations of organic aerosol levels into much closer agreement.

Most of the understanding concerning the formation of secondary organic aerosol (SOA) from atmospheric oxidation of volatile organic compounds (VOCs) over the past 30 y has been developed from data obtained in laboratory chambers (1). SOA is a major component of particulate matter smaller than 1 μm (2) and consequently has important impacts on regional and global climate and human health and welfare. Accurate simulation of SOA formation and abundance within 3D models is critical to quantifying its atmospheric impacts. Measurements of SOA formation in laboratory chambers provide the basis for the parameterizations of SOA formation (3) in regional air-quality models and global climate models (4). A number of studies indicate that ambient SOA concentrations are underpredicted within models, often substantially so, when these traditional parameterizations are used (e.g., 5, 6). Some of this bias has been attributed to missing SOA precursors in emissions inventories, such as so-called intermediate volatility organic compounds, to ambient photochemical aging of semivolatile compounds occurring beyond that in chamber experiments (7) or to aerosol water/cloud processing (8). The addition of a more complete spectrum of SOA precursors into models has not, however, closed the measurement/prediction gap robustly. For example, recent analysis of organic aerosol (OA) concentrations in Los Angeles revealed that observed OA levels, which are dominated by SOA, exceed substantially those predicted by current atmospheric models (9), in accord with earlier findings in Mexico City (10).

Here, we demonstrate that losses of SOA-forming vapors to chamber walls during photooxidation experiments can lead to substantial and systematic underestimation of SOA. Recent experiments have demonstrated that losses of organic vapors to the typically Teflon walls of a laboratory chamber can be substantial (11), but the effects on SOA formation have not yet been quantitatively established. In essence, the walls serve as a large reservoir of equivalent OA mass that compete with the particulate SOA for SOA-forming compounds.

Toluene Photooxidation Experiments

The effect of vapor wall loss on SOA formation has been comprehensively assessed based on results from a series of 18-h toluene photooxidation experiments conducted in the California Institute of Technology (Caltech) environmental chamber under both high- and low-NO_x conditions (SI Appendix, Toluene Photooxidation Experiments and Table S1). Toluene is a component of motor vehicle emissions and an important SOA precursor (1). Initial [VOC]/[NO_x] ratios were 5.4 ± 0.3 ppbC/ppb, similar to current conditions in Los Angeles. In these experiments, the ratio of initial seed particle surface area (SA) to chamber wall SA was systematically varied by changing the concentration and diameter of (NH₄)₂SO₄ seed aerosol and keeping all other conditions the same [i.e., hydroxyl radical (OH) and toluene concentration]. In this manner, the influence of seed SA on SOA formation can be isolated.

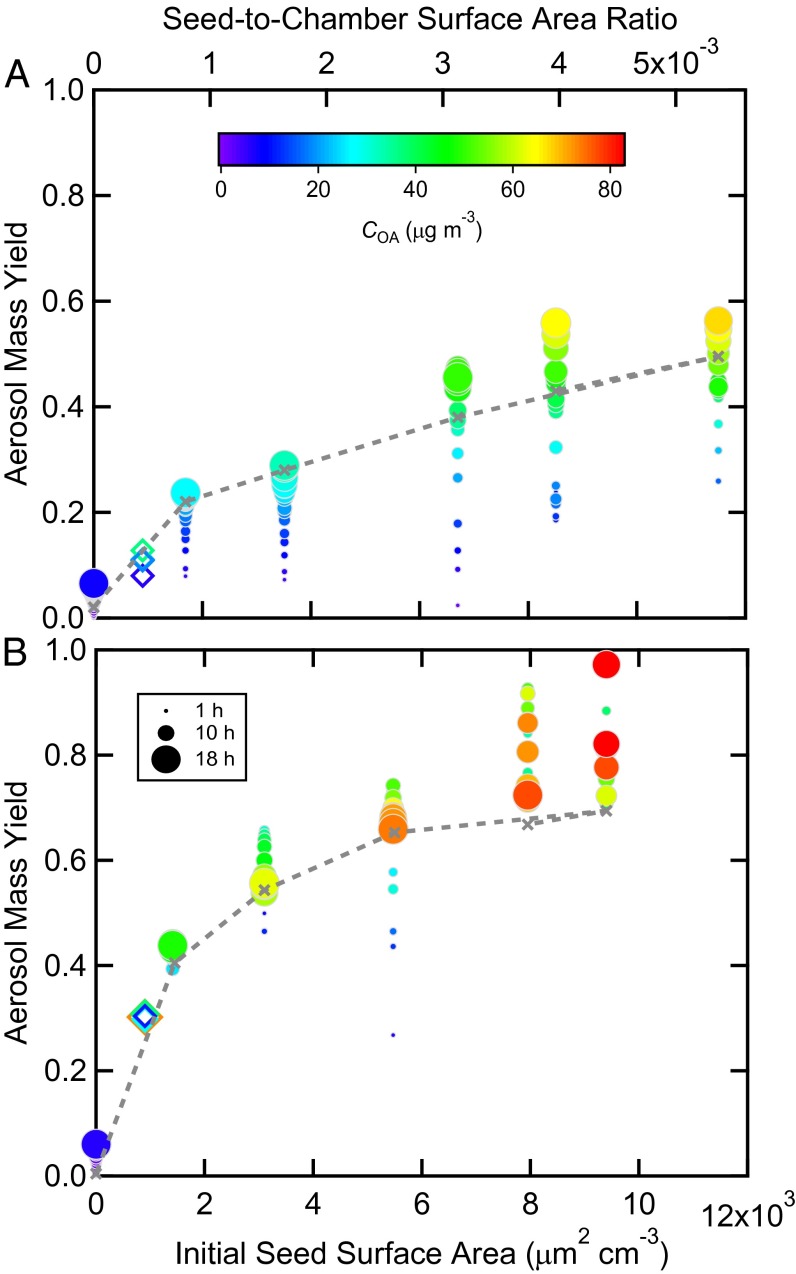
Fig. 1 shows the observed time-dependent SOA yields, defined as the mass of SOA formed per mass of VOC reacted, determined from the evolution of the particle size distributions (SI Appendix, Fig. S1) as a function of initial seed SA for the high- and low-NO_x experiments. The SOA concentrations have been corrected for physical deposition of particles to the walls (SI Appendix, Particle Wall Loss Correction), which is the appropriate correction to use here as our analysis explicitly accounts for loss of vapors to the walls, discussed further below. Except for the unseeded experiment, the SOA yield for each low-NO_x experiment is reasonably constant with time (from 4 to 18 h) and C_OA at any given SA. For each high-NO_x experiment there is a clear increase in the yield with C_OA and time. The toluene SOA yield at a given C_OA is generally lower for high-NO_x than for low-NO_x conditions at a comparable initial seed SA. These differences in the time-dependent yields indicate differences in the chemical pathways leading to SOA formation between low- and high-NO_x conditions. Most importantly, the absolute amount of SOA formed for the same initial conditions increases with seed SA, consistent with refs. 12 and 13, with an indication of a plateau being reached at the highest seed SA. The SOA formed in the unseeded experiments is particularly small. Typical laboratory chamber experiments use initial seed SA < 10³ μm² cm⁻³, which corresponds to seed-to-wall ratios of <1 × 10⁻³ in most chambers. These experiments definitively demonstrate that SOA yields vary with seed SA. This variability may partially explain some of the differences in SOA yields reported in the literature.

Fig. 1.

Hourly averaged lower bound SOA yields over the course of a toluene photooxidation experiment as a function of initial ammonium sulfate seed surface area for (A) high-NO_x and (B) low-NO_x conditions. Symbol color indicates the SOA mass concentration and symbol size the time after lights were turned on. The filled circles are from the current experiments and the open diamonds from ref. 21. The dashed gray line and × are the end-of-experiment yields from the optimized best-fit SOM simulations.

SOA Modeling and the Influence of Vapor Wall Loss

The increase in yield with seed SA is consistent with loss of vapors to the chamber walls, and likely results from an increase in the rate of mass transfer of vapor species to the particles relative to the walls. Quantitative understanding of the role of vapor wall loss is necessary to characterize the extent to which SOA yields in chamber experiments are underestimated relative to the atmosphere. The loss of “extremely low volatility” organic compounds to chamber walls has recently been implicated as important for understanding SOA formation for a different chemical system, α-pinene + O₃ (13, 14). The competition between vapor condensation to particles versus to chamber walls is quantitatively examined here using a time-dependent, parameterizable model of SOA formation, the statistical oxidation model (SOM; refs. 15, 16; SI Appendix, The Statistical Oxidation Model). The SOM accounts for vapor wall losses based on observations showing that wall losses of semivolatile species in Teflon chambers are reversible (11). Such wall loss is modeled dynamically and depends on the equivalent OA mass of the chamber walls (C_w, mg m⁻³), the first-order vapor wall loss rate coefficient (k_w, s⁻¹), and the vapor saturation concentration of compounds i (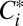, μg m⁻³). k_w reflects the combined effects of turbulent mixing in the chamber, molecular diffusion of vapor molecules through the near-wall boundary layer, and any penetration into chamber walls. k_w is likely to be chamber specific, as the extent of turbulent mixing depends on specific chamber operating conditions, but is reasonably independent of compound identity (11). Values of k_w for a range of gases were estimated in one study (17) to range from ∼2 × 10⁻⁵ to 10⁻³ s⁻¹, corresponding to timescales of many hours to 10 min. The largest k_w values are appropriate only for chambers with active mixing, which the Caltech chamber does not have (SI Appendix, Vapor Wall Loss). Observations (11) suggest that C_w varies somewhat with compound identity, ranging from ∼2 to 24 mg m⁻³, compared with chamber OA concentrations that are usually 1–3 orders of magnitude smaller; a value of 10 mg m⁻³ is used here as the base case. Gas-particle partitioning is modeled dynamically assuming absorptive partitioning, including correction for noncontinuum effects and imperfect accommodation, the latter of which is characterized by the mass-accommodation coefficient, α. The accommodation coefficient reflects the overall transfer of vapor molecules into the particle bulk, and is likely dependent on the chemical makeup of both the vapor and particle phases and processes that occur at the particle surface. This formulation is more general than most previous analyses of SOA formation in environmental chambers, which typically assume instantaneous gas-particle equilibrium.

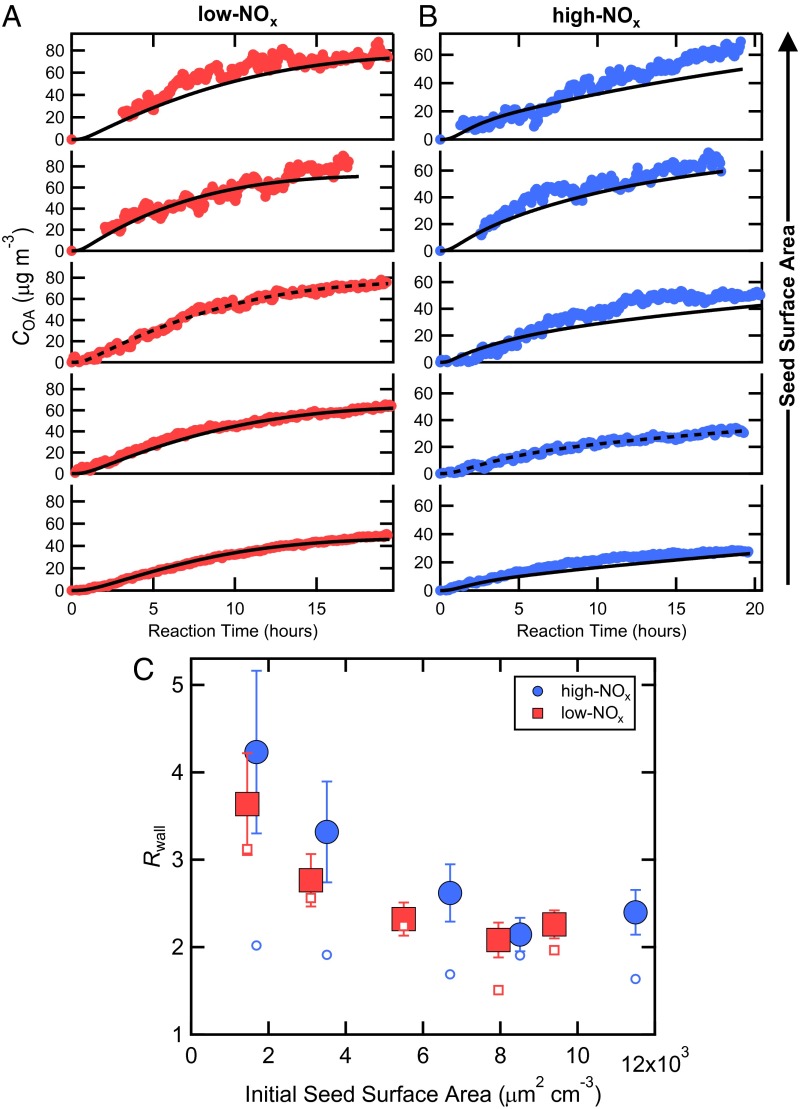
Optimal values for k_w and α have been determined for the sets of low- and high-NO_x experiments by comparing observed and simulated best-fit time-dependent C_OA profiles for a wide range of k_w and α. The k_w/α pair that provides for the best overall agreement with the time-dependent SOA formation observed across all experiments at a given NO_x condition, excluding the nucleation experiments, is considered the optimal solution (Fig. 2 A and B) (SI Appendix, Optimizing k_wand α and Fig. S3). For low-NO_x experiments, the optimal k_w = 2.5 × 10⁻⁴ s⁻¹ and α = 2 × 10⁻³. The independently determined values for high-NO_x experiments are similar: k_w = 2.5 × 10⁻⁴ s⁻¹ and α = 1 × 10⁻³. The simulations provide good overall agreement with the observed seed SA dependence only for a combination of a small α and a k_w on the order of 10⁻⁴ s⁻¹, indicating that both parameters are important to describing chamber SOA formation. (It should be noted that a reasonable fit for an individual experiment can be obtained for many k_w/α pairs, including when instantaneous gas-particle equilibrium is assumed, i.e., when α = 1. This is not meant to imply that the absolute values of these parameters are not important, but that only in analyzing the combined datasets at multiple seed SA can optimal k_w and α values be uniquely established.) The determined optimal k_w values are consistent with theoretical estimates (SI Appendix, Vapor Wall Loss and Fig. S4) and some observations (11), but larger than some previous observations in the Caltech chamber (18), most likely reflecting the limited time resolution of those observations, which might not have allowed for separation of filling and mixing of the chamber from wall loss, but potentially also reflecting differences between chemical systems.

Fig. 2.

Observed (points) and simulated (lines) SOA concentrations for each photochemical oxidation experiment performed for different initial inorganic seed surface area for (A) low-NO_x and (B) high-NO_x conditions. The dashed lines indicate the experiment to which the SOM was explicitly fit, and the solid lines indicate simulation results based on those fits. (C) The wall loss bias factor, R_wall, as a function of seed surface area. Filled symbols use the optimal k_w/α pair and the corresponding best-fit SOM parameters determined from A and B. Open symbols assume α = 1 and each experiment was individually fit using the optimal k_w. The error bars indicate the 1σ SD in R_wall for each experiment over the period when C_OA > 0.5 μg m⁻³.

The small optimal α values required to reproduce the observed seed SA dependence likely reflect mass-transfer limitations within the particle phase, which can occur for highly viscous SOA particles (19). When α ∼10⁻³, mass accommodation is relatively slow and the vapors and particles cannot be assumed to be in instantaneous equilibrium. The timescale associated with reaching gas-particle equilibrium (τ_g-p,eqm) varies with seed SA and size (SI Appendix, Gas-Particle Partitioning Timescales and Fig. S5). Given α = 10⁻³, τ_g-p,eqm ranges from ∼230 min for the smallest seed SA to only ∼30 min for the largest seed SA. Thus, at the smallest seed SA τ_g-p,eqm is similar to the timescale determined for gas wall loss (1/k_w = 67 min) and the influence of gas wall loss is more pronounced.

Importantly, loss of condensable vapors to the chamber walls leads to a low bias in the observed SOA formed even for the experiments with the highest seed SA. To quantitatively assess this bias, simulations have been performed using the best-fit SOM parameters determined for the optimal k_w/α pair above, but with k_w = 0 (no wall loss). The ratio R_wall = C_SOA(k_w = 0)/C_SOA(k_w,optimal) has been calculated for each experiment and quantifies the bias in the SOA yield due to traditionally unaccounted for vapor wall losses. The magnitude of R_wall depends on the experiment considered, decreasing with increasing seed SA and reaching a plateau at large seed SA (Fig. 2C). For the seeded experiments, R_wall averaged over the period when C_OA > 0.5 μg m⁻³ varied from 3.6 (±0.6) to 2.1 (±0.2) for low NO_x and from 4.2 (±0.9) to 2.1 (±0.2) for high NO_x in going from lowest to highest seed SA, and where the uncertainties are 1 SD over the averaging period. These ratios correspond to end-of-experiment corrected mass yields of 1.6 (low NO_x) and 0.93 (high NO_x), substantially exceeding the values currently used in chemical transport models for toluene (∼0.47 for low NO_x and ∼0.12 for high NO_x; ref. 4). Given an O:C ratio for toluene + OH SOA of ∼0.7 (20), the carbon yields would be 0.94 (low NO_x) and 0.55 (high NO_x). [The calculated end of experiment O:C are 0.67 (low NO_x) and 0.91 (high NO_x).] This implies that ∼6% and ∼55% of the product carbon mass remains in the gas phase for low- and high-NO_x conditions, respectively. The oxidation process is a balance between functionalization and fragmentation. In the absence of fragmentation, the carbon yield would asymptote to 100%. The low-NO_x carbon yield in the absence of vapor wall loss is close to 100% and the SOA yield is approximately independent of the total OA mass, which together indicate that fragmentation plays only a minor role. Fragmentation is comparably more important under high-NO_x conditions.

Interestingly, R_wall values similar to those determined for the optimal k_wall/α pair are obtained when vapor wall loss is accounted for (i.e., k_w ≠ 0) but when it is assumed that α = 1 (i.e., that gas-particle equilibration is effectively instantaneous) during fitting of each individual experiment (Fig. 2C). This indicates that the magnitude of α is not key to fitting of an individual experiment, but when the experiments are taken together as a combined dataset α is indeed key to matching the observed dependence on seed surface area. Related, α is not key to there being an influence of vapor wall loss on the overall SOA yield, which is controlled more so by the magnitude of k_w, although at lower seed SA for a given k_w, the derived R_wall increases as α decreases. The finding that large R_wall values are obtained even when α = 1 indicates that the general conclusions here regarding vapor wall loss are robust with respect to knowledge of α. This is important because other chemical systems might not exhibit as slow mass accommodation but could still be affected by vapor wall loss. Clearly, loss of condensable vapors to the chamber walls can suppress SOA yields relative to those that are relevant for the atmosphere.

Dependence on Experimental Conditions

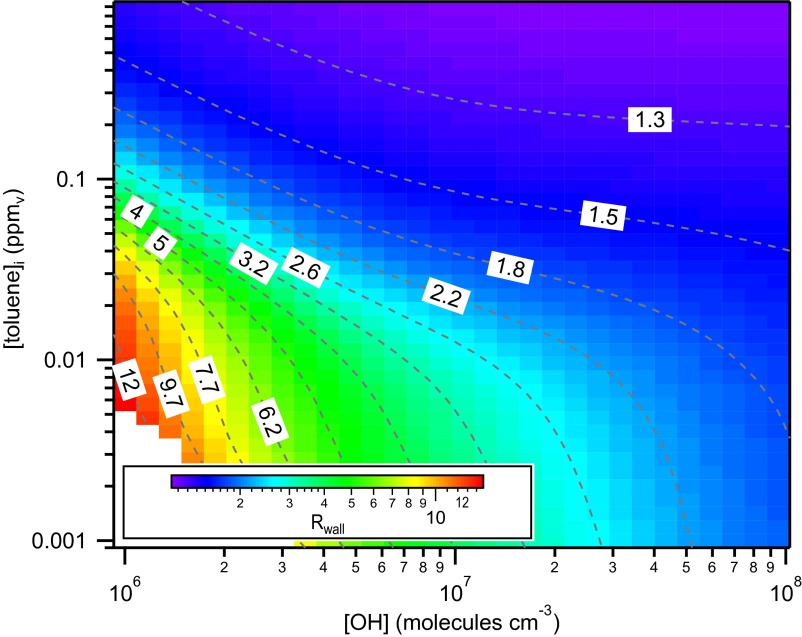
For a given chamber, the extent to which vapor wall loss affects SOA yield will depend on the combination of (i) the rate of oxidation and duration of a given experiment, (ii) the precursor VOC concentration, (iii) the particular chemical pathways associated with oxidation of a given species, i.e., the precursor identity, and (iv) the seed SA. This is illustrated for the toluene low-NO_x system by carrying out a series of 18-h simulations where [OH] is varied from 1 to 100 × 10⁶ molecules cm⁻³ and [toluene]_initial from 1 to 900 ppb for a seed SA = 1,000 μm² cm⁻³ using the SOM parameters and optimal k_w/α determined above. The calculated R_wall varies with oxidant and precursor concentration (actually, VOC loss rate), with smaller R_wall when oxidation is faster and at larger precursor VOC concentration (Fig. 3 and SI Appendix, Fig. S6). (Note that these calculations do not account for differences that might result from changes in the relative importance of RO₂ + HO₂ versus RO₂ + RO₂ reactions as [VOC]_initial and [OH] are varied.) Such “rate effects” have been observed for SOA produced in aromatic systems (21). The seed SA dependence is substantially reduced when the [VOC]_initial is large, especially at high [OH]. Overall, these dependencies, along with differences in the initial seed SA, may help explain some of the differences (and similarities) in historical aerosol yields measured in different chambers.

Fig. 3.

Calculated SOA yield bias as a function of initial toluene concentration and OH concentration when k_w = 2.5 × 10⁻⁴ s⁻¹ and C_w = 10 mg m⁻³. The R_wall values for a given [toluene] and [OH] are indicated by colors and contours, and are averaged over the period when C_SOA > 0.5 μg m⁻³ to the end of an experiment at 18 h. Results are based on the optimal fit of the SOM to the low-NO_x experiments.

Vapor Losses and Sensitivity to C_w

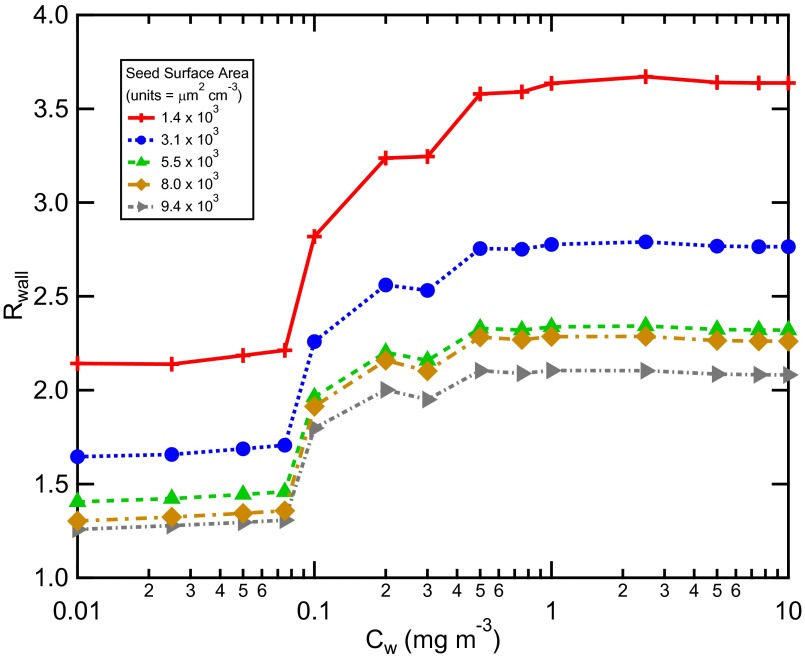
The observed time-dependent C_OA to which the SOM was fit were corrected to account for physical deposition of the particles to the walls. Loss of vapors, excluding growth of suspended particles, was separately accounted for assuming that the vapors continuously interact with the Teflon chamber walls, with C_w = 10 mg m⁻³ (11). Some previous studies (22, 23) have alternatively assumed that vapors interact only with particles that have deposited to the walls during that experiment, as opposed to with the walls directly, and further that the timescales associated with partitioning between vapors and suspended or wall-deposited particles are the same (SI Appendix, Particle Wall-Loss Correction). In this alternative scenario, the effective C_w is time dependent (and zero at the start of an experiment) and related to the suspended particle concentration and the particle wall loss rate. Most chamber experiments aim to limit the extent of particle deposition, and thus it is reasonable to assume that, in general, the concentration of wall-deposited particles is less than the suspended particle concentration. Further, most modern experiments limit the observed C_OA to < 0.1 mg m⁻³, and thus the effective C_w in this alternative case will be substantially smaller than when vapors are assumed to partition into the chamber walls.

It is therefore useful to examine the dependence of the calculated R_wall on the assumed C_w, where an assumed C_w < ∼0.1 mg m⁻³ corresponds approximately to the wall-deposited particle alternative scenario (22, 23). This has been done for the low-NO_x experiments where the SOM was fit to the observations for different assumed C_w, with good fits obtained for all C_w. Above C_w = 0.2 mg m⁻³ (= 200 μg m⁻³) the calculated R_wall is constant. Below 0.2 mg m⁻³ the calculated R_wall falls off, reaching a second plateau at small C_w that is still above unity (Fig. 4). The plateaus at high and low C_w result from the best-fit SOM parameters varying with C_w to compensate for the differing amounts of loss of vapors to the walls and still maintaining the same suspended C_OA time profile (SI Appendix, Fig. S7). Because measurements demonstrate that vapors are lost directly to Teflon walls (11), this indicates that when vapor wall loss is accounted for assuming that the vapors interact only with wall-deposited particles, the extent of the vapor loss is underestimated. That R_wall is constant above C_w = 0.2 mg m⁻³ demonstrates that our conclusions are robust with respect to the assumption regarding the exact value of C_w.

Fig. 4.

Calculated vapor wall loss bias, R_wall, as a function of the effective wall mass concentration, C_w, for the low-NO_x toluene photooxidation experiments at varying initial seed surface area. For each C_w, the SOM was fit to the experiment with seed surface area = 5.5 × 10³ μm² cm⁻³ using k_w = 2.5 × 10⁻⁴ s⁻¹ and α = 2 × 10⁻³. The determined best-fit SOM parameters were then used to simulate SOA formation for the experiments performed at other seed concentrations but assuming the same C_w.

Consideration of Historical Experiments

To estimate the potential influence of vapor wall losses for systems other than toluene, we calculated SOA yield biases for a variety of other VOCs (16, 20, 21, 23, 24) (SI Appendix, Fitting of Historical Chamber Data). It should be noted that the experimental conditions in the historical experiments are not identical to those for the toluene experiments, especially for high-NO_x conditions (SI Appendix, Historical Experiments). Although k_w for a given chamber is reasonably independent of the precursor compound, α may depend on the precursor identity. The results for the toluene experiments indicate that smaller α values generally correspond to larger R_wall. Therefore, a conservative, likely lower-bound estimate of R_wall has been obtained for each precursor assuming that α = 1 during fitting and using k_w = 1 × 10⁻⁴ s⁻¹ (instead of 2.5 × 10⁻⁴) to account for potential differences in the chamber used for these historical experiments (SI Appendix, Figs. S8–S10). The use of a smaller k_w will decrease R_wall, all other factors being equal. Calculated R_wall values range from as small as 1.1 to as large as 4.1 (Table 1 and SI Appendix, Fig. S11). The typically smaller values for the high-NO_x vs. low-NO_x experiments reflect the much shorter reaction timescales and higher oxidant and NO_x concentrations in the historical high-NO_x experiments, compared with the current experiments with toluene. Evidently, the extent to which vapor wall loss will have influenced historical experiments is variable, yet potentially substantial and deserving of further investigation through new experiments and consideration of other datasets. Importantly, the results here indicate that quantitative analysis of SOA formation in chambers requires use of an explicitly time-dependent model that accounts for the simultaneous and competing condensation of vapors onto particles versus onto the chamber walls, representing a major shift from most historical analyses, which did not take time explicitly into account.

Table 1.

Average biases in SOA yields due to vapor wall losses for various VOCs under low- and high-NO_x conditions

VOC*	Low-NOx	High-NOx
	†	†
Toluene‡ (this study)	2.1–3.6	2.1–4.2
n-dodecane (16)	4.1 ± 0.8¶	1.16 ± 0.08
2-methylundecane (16)	3.7 ± 0.5	1.4 ± 0.2
Cyclododecane (16)	3.0 ± 0.3	1.10 ± 0.05
Hexylcyclohexane (16)	2.4 ± 0.3	1.16 ± 0.07
Toluene (21)	1.9 ± 0.4	1.13 ± 0.06
Benzene (21)	1.8 ± 0.4	1.25 ± 0.1
M-xylene (21)	1.8 ± 0.4	1.2 ± 0.1
M-xylene (23)	1.6 ± 0.3
Naphthalene (24)	1.2 ± 0.1	1.2 ± 0.1
α-pinene + OH (20)	1.6 ± 0.3	1.3 ± 0.1
Isoprene + OH (20)	3.1 ± 1.3	2.2 ± 0.5

^*For all VOC’s except toluene (this study), k_w = 1 × 10⁻⁴ s⁻¹ and α = 1. For toluene (this study), k_w = 2.5 × 10⁻⁴ s⁻¹ and α = 0.002 (low NO_x) or 0.001 (high NO_x).

^†Calculated for the period when C_SOA > 0.5 μg m⁻³ through the end of a given experiment.

^‡For toluene, the reported R_wall indicate the range of values determined at different initial seed SA.

^¶Uncertainties are 1σ over the averaging period.

Implications

Our results show that the effect of vapor wall loss on SOA yields can be substantial. If reported SOA yields are low by factors of ∼1.1–4.2, as our results suggest they may be, then SOA concentrations simulated in 3D models will be correspondingly low. Although the analysis presented here for the toluene SOA system needs to be comprehensively expanded to other main classes of SOA precursors, beyond the assessment above, it is likely that a lack of proper accounting for vapor wall losses that suppress chamber-derived SOA yields contribute substantially to the underprediction of ambient SOA concentrations in atmospheric models.

Materials and Methods

Chamber Experiments.

Toluene photooxidation experiments were carried out in the new 24-m³ Teflon environmental reaction chambers at Caltech. Liquid toluene was evaporated into the chamber to achieve a concentration of ∼38 ppb gas-phase mixing ratio (= 143 μg m⁻³). Hydroxyl radicals were generated from photolysis of H₂O₂ either with (high NO_x) or without (low NO_x) addition of NO to the chamber. Dried ammonium sulfate seed particles were added via atomization of an aqueous solution of ammonium sulfate solution until the desired seed concentration was obtained. The toluene, seed particles, H₂O₂ and NO_x were allowed to mix in the chamber for 1 h, after which time the black lights were turned on to initiate H₂O₂ photolysis. Particle number size distributions were measured using a cylindrical differential mobility analyzer coupled to a condensation particle counter. More details are available in the SI Appendix.

SOA Modeling.

The statistical oxidation model (15) was used to analyze the experimental observations. The SOM simulates the multigenerational gas-phase oxidation of a precursor VOC that has N_C carbon atoms and N_O oxygen atoms as reactions cause the precursor and product species to functionalize, increasing N_O, and/or fragment, decreasing N_C. Addition of oxygen atoms leads to a decrease in vapor pressure, which drives condensation of the gas-phase species. Mass transfer between the gas and particle phases is treated dynamically. The parameters that describe functionalization, fragmentation, and the decrease in vapor pressure upon oxygen addition are adjusted by fitting to the experimental observations of time-dependent SOA formation. More details are provided in the SI Appendix.