Bending forces plastically deform growing bacterial cell walls

Significance

Regulation of cell wall growth is a process of fundamental importance in cell biology. In this paper, to our knowledge, we demonstrate for the first time that mechanical stress directly influences cell wall synthesis of bacteria. In a series of simple experiments, we elastically and plastically deform cell walls as they grow by applying anisotropic mechanical stresses to bacteria. Using a theory of dislocation-mediated growth, we explain how growth and form of the cell walls are quantitatively related to one another in bacteria.

Abstract

Cell walls define a cell’s shape in bacteria. The walls are rigid to resist large internal pressures, but remarkably plastic to adapt to a wide range of external forces and geometric constraints. Currently, it is unknown how bacteria maintain their shape. In this paper, we develop experimental and theoretical approaches and show that mechanical stresses regulate bacterial cell wall growth. By applying a precisely controllable hydrodynamic force to growing rod-shaped Escherichia coli and Bacillus subtilis cells, we demonstrate that the cells can exhibit two fundamentally different modes of deformation. The cells behave like elastic rods when subjected to transient forces, but deform plastically when significant cell wall synthesis occurs while the force is applied. The deformed cells always recover their shape. The experimental results are in quantitative agreement with the predictions of the theory of dislocation-mediated growth. In particular, we find that a single dimensionless parameter, which depends on a combination of independently measured physical properties of the cell, can describe the cell’s responses under various experimental conditions. These findings provide insight into how living cells robustly maintain their shape under varying physical environments.

Biological systems exhibit many properties rarely found in condensed matter physics which are often caused by growth. When coupled to mechanical forces, growth can drive a wide range of cellular phenomena such as regulation of the eukaryotic cell morphology by actin networks (1), collective behavior in tissues (2), cell differentiation (3), and the shape and division of yeast and plant cells (4, 5). Of fundamental interest as well as practical importance is understanding the relationship between growth, form, and structure of bacterial cell walls (6). Bacterial cell walls define a cell’s morphology and maintain large internal (turgor) pressure. Many antibiotics target them to efficiently hamper cell growth and reproduction. As such, cell walls and their synthesis have been the subject of extensive biochemical (7) and biophysical (6) studies in the context of cell growth (8), cell shape (9), and cell division (10).

Despite a long history (11), however, we are still far from being able to predict the shape or dimensions of any cells from first principles based on the information obtained from studies so far. Recent experimental work sheds new insights in this regard. For example, bacteria can significantly deform when grown with constraints (12, 13) and yet are able to recover their native shape (13). However, the mechanism underlying deformation and recovery, as well as the cues which regulate cell wall growth, have not been well-understood.

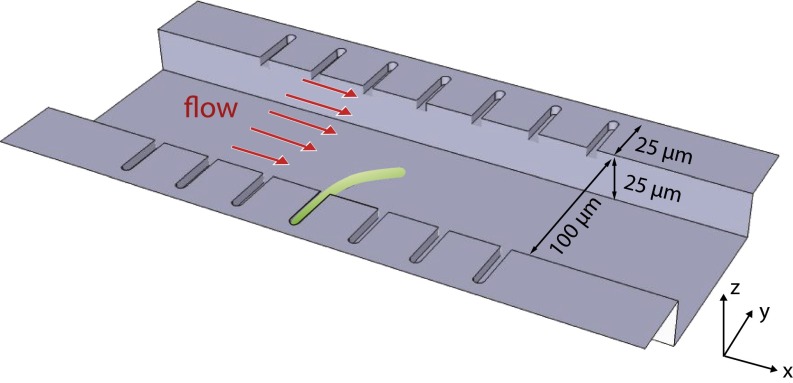
We have developed combined experimental and theoretical methods to directly address how mechanical stresses are involved in the regulation of cell wall growth. Our experimental approach is illustrated in Fig. 1. Rod-shaped Escherichia coli or Bacillus subtilis cells are inserted into snuggly fitting microchannels where they are grown in a controlled environment (see Fig. S1). Filamention is induced in these cells by suppressing division (see Materials and Methods for further details).

Fig. 1.

Illustration of the experimental approach. Single E. coli or B. subtilis cells are inserted into microchannels 25 μm in length. The cross-section of the microchannels is square (∼1.2 μm × 1.2 μm) and the cells fit snuggly. Cell division is blocked to induce filamentation. The cells were grown typically up to 50 μm during measurements. Controlled hydrodynamic forces are exerted on the cells by the viscous drag of the growth media (Supporting Information).

The filamentous cell is subjected to precisely calibrated hydrodynamic forces. This simple approach has two notable advantages to previous methods: (i) we can directly probe the mechanical properties and responses of the cell walls noninvasively for a wide temporal range (from <1 s to over 1 h), and (ii) we can achieve force scales several orders of magnitude larger than what is possible by optical traps (14) or atomic force microscopy (AFM) (15). Using this approach, we demonstrate that the cells can exhibit two fundamentally different modes of deformations and recover from them. The first mode is elastic in that the cell recovers its shape as soon as the external force is removed. The other mode is plastic and requires growth for morphological recovery. The plastic deformations are due to differential growth, as a result of varying mechanical stresses acting on the cell walls.

We also provide a theoretical framework that quantitatively explains our experimental findings. The basic idea is that external forces are transduced to the activity of the cell wall growth machinery. To explain shape deformations, we calculated the effect of force transduction by extending the theory of dislocation-mediated growth of bacterial cell walls (16). We found that for pulse-like forces that are transient the cell walls respond elastically in agreement with ref. 14. In contrast, if the duration of applied forces is comparable or longer than the timescale of cell wall growth, the force transduction causes differential growth of the cell walls and plastic deformations as seen in ref. 13.

Results and Discussion

Cells Deform Elastically by Pulse-Like Forces.

To show that our approach can accurately probe the mechanical properties of E. coli and B. subtilis cells, we applied short pulses of hydrodynamic force to cells and monitored their response (Fig. 2; also see Fig. S2 for the algorithm used for image processing). For this, the cells were grown in excess nutrients initially without flow. As the cells formed long, straight filaments, we applied a series of pulse-like flows. Each of these pulses lasted for less than 10 s so that the effect of growth was negligible. In our setup, for the maximum flow rate used, the force on a cell (per length) was ∼40 pN/μm. Thus, for filamentous cells, the force due to viscous drag is significantly higher than forces achievable with optical tweezers. Fig. 2 and Movie S1 show our typical experimental result. The cells bent transiently at each pulse, and fully recovered their shape immediately after the applied force was removed.

Fig. 2.

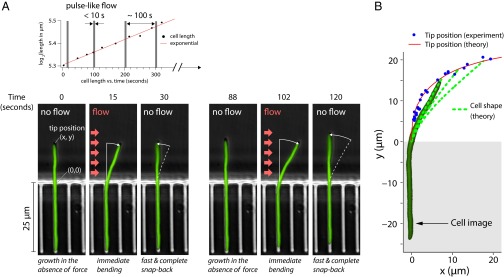
Cells are deformed elastically by pulse-like forces. (A) Microscopy images of the E. coli cell from Movie S1 taken at different stages of the experiment. The cell initially grows straight out of the microchannel. We applied pulse-like flow to the straight cell repeatedly every several minutes (Upper). This resulted in completely reversible deformations (two examples are shown, Lower Left and Lower Right). (B) The tip positions (x, y) of the cell from multiple experiments are compared with the theoretical predictions of the linear elasticity theory (Supporting Information). An actual cell shape is superimposed on one of the theoretical curves.

We can explain the experimental results using the theory of linear elasticity. In the theory, the long filamentous cell can be thought of as a cylindrical beam that is bent by a hydrodynamic force (Supporting Information; also see Fig. S3). Shown in Fig. 2B is the comparison between data and theory for the tip position (thus the degree of cell bending) of the cell during a representative experiment in Fig. 2A. From these experiments, we extracted a flexural rigidity of approximately 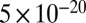N⋅m², comparable to the result of approximately 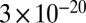N⋅m² obtained by mechanical manipulation of E. coli cells using optical traps (14). Assuming a cell wall thickness of 4 nm, this corresponds to a Young’s modulus of MPa. It should be noted that the small mismatch between the bacterium’s diameter and the width of the end of the channel has to be taken into account (see Supporting Information and Fig. S4 for further details). We also show in Supporting Information that the turgor pressure does not contribute to the restoring torque (Fig. S5). Similar experiments were performed for B. subtilis (Fig. S6) giving a Young’s modulus of MPa, consistent with past results (17). From these results, we conclude that both E. coli and B. subtilis cells respond to fast mechanical perturbations as a linear elastic rod.

Plastic Deformations Require Growth and Long-Term Forces.

The elastic deformation and recovery of the cells from pulse-like forces is consistent with the view that E. coli and B. subtilis cells can be thought of as elastic cylindrical beams (14, 15). The linear elasticity theory, however, cannot explain the observations that bacteria can also deform plastically (12, 13). For plastic deformations, we noticed that the cells in refs. 12 and 13 were grown with geometric constraints for a duration comparable to or longer than their mass-doubling time. Because these geometric constraints may exert forces on the cells, we hypothesized that external forces were transduced to the cell wall synthesis machinery during growth. Therefore, force transduction may cause differential growth of the cell wall, and, thus, shape deformation.

As a first step to testing our hypothesis, we grew the cells with a constant hydrodynamic flow of the growth medium. The filamentous cells grew into a curved shape because of continuous hydrodynamic forces (Fig. 3). The curved shape of the cell, however, was not easily distinguishable from the elastically deformed cells in Fig. 2. To confirm that the cells deformed plastically, we abruptly switched off flow when the cells significantly bent. The cells did not recover their straight shape immediately, i.e., they deformed plastically (Fig. 3A and Movie S2).

Fig. 3.

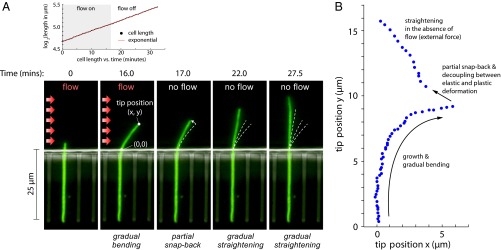
Decoupling the two fundamental modes of deformation. (A, Lower) At t = 0–16 min, an E. coli cell is growing in the presence of a constant flow for a period comparable to the cell division time. The deformation represents the sum of elastic and plastic modes (Movie S2). At t = 17 min, as the flow is abruptly turned off, the elastic mode vanishes and the cell partly recoils. The residual deformation reflects the cumulative effect of force transduction, which resulted in differential growth of the cell wall. At 17 min, in the absence of the flow, the cell straightens gradually as it grows. (A, Upper) The length of the cell increases exponentially despite the large deflections induced by the external mechanical forces—the mass-doubling time does not change appreciably during the experiment and is comparable to that of nonfilamentous cells. (B) Scatter plot of the experimental results for the tip position as time progresses through the snap-back experiment from A.

We repeated the experiments with nongrowing filamentous cells, and the cells did not show plastic deformation despite the long-term application of forces (Fig. S7). We conclude that plastic deformation requires both cell wall synthesis and the application of forces for a duration in which substantial cell wall synthesis can occur.

Elastic and Plastic Components of Deformation Can Be Decoupled.

The plastic deformation experiments in Fig. 3 unraveled an important feature of bacteria cell walls. As the external forces were removed, the cells always partially snapped back. This is clearly seen in the time trace of the cell’s tip position (Fig. 3B). The partial snap-back suggests that the cell bending in Fig. 3 has both elastic and plastic components. In other words, external forces not only cause elastic bending, but may also lead to differential growth which further bends the cell. The two components may be decoupled by removing the external forces, upon which the elastic component should vanish instantly.

To test our hypothesis, we developed a quantitative, phenomenological model that incorporated force transduction and growth. We describe our model next and its comparison with data. We found the data and theory in good quantitative agreement.

Theoretical Framework for Coupling Mechanical Stresses to Cell Wall Growth.

Our starting point for understanding the data is the theory of dislocation-mediated growth that we developed recently (16, 18). The model was inspired by recent experimental observations that, in both Gram-positive (19, 20) and -negative (21) bacteria, actin homolog MreB proteins, associated with cell wall growth, move processively along the cell’s circumference. Processive circumferential insertions resemble the climb of edge dislocations in a 2D crystal (22), and thus one can use the well-developed theory of dislocations from materials science.

In the previous version of the growth model, we studied the motion of dislocations on a perfect cylinder in the absence of external forces (16, 23). Therefore, the previous version cannot account for deformations. We extended our theory to allow for differential growth by transduction of external stress to dislocations (growth machinery).

In our theory, tensile (stretching) stress can have two different effects: (i) increase the speed of processive motion of dislocations (Fig. 4A) or (ii) reduce the activation energy for nucleation (Fig. 4B). Compressive stress will have the opposite effect. The forces on the elongation machinery are given by the Peach–Koehler force (24) acting on dislocations:

where 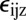is the Levi-Civita tensor, is the stress tensor, and 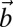the Burgers vector characterizing the dislocation.

Fig. 4.

Illustration of the differential growth driven by coupling between mechanical stress and cell wall synthesis. (A) Tensile (stretching) stress increases the processive motion speed of strand elongation machinery. Compressive stress has the opposite effect. Black arrows indicate the trajectories of activated dislocations. (B) Similarly, tensile stress will lower the activation energy for insertion of a new glycan strand, and compressive stress will increase it. (C) Asymmetric insertion of dislocations is enhanced by the large aspect ratio of the filamentous bacteria, leading to the large observed angular deflections.

For the cylindrical geometry of the cells in our experiment, the theory predicts that the component of the stress tensor is the one which couples to the circumferential growth, where y is the coordinate along the cell’s long axis (Fig. 1). As the cell grows in the presence of a constant flow, the cell wall of thickness h, length l (measured from the channel end to the cell tip), and radius r experience a position-dependent mechanical stress that depends on its position in the cell (Fig. 4 and Fig. S8):

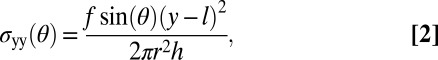where θ is the azimuthal angle of the cylinder along the circumference (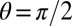 for the cell front facing the flow, and 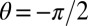for the back), f is the force per unit length induced by the flow, y is the position along the cylinder’s axis, and 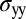is the mechanical stress induced by the flow. The surface directly facing the incoming flow feels a tensile stress (a surface-stretching force), whereas the other side feels a compressive stress (which acts to shorten the distance between adjacent glycan strands). Accordingly, the cell walls grow differentially, growing faster on the upstream side of the flow. In our experiments, the external hydrodynamic force would increase the Peach–Kohler force by 10 pN for the cell front (at the channel end, for μm), and decrease the force by the same amount on the opposite side. This force is comparable, for example, to the one generated by RNA polymerase (25). It is also comparable to the force due to the turgor pressure (approximately 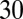pN for E. coli) (16), and thus we expect the mechanical stress to significantly change the activation energy for enzymatic reactions (see ref. 11, p. 165).

This differential growth leads to a dynamically deformed cell shape. Due to the large aspect ratio of the filamentous bacteria in our experiments, a relatively small asymmetry in growth leads to a large angular deflection. In Supporting Information we show that the angular deflection due to differential growth in a small segment of the cell is given by

where 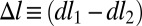is the net difference on opposite sides of the cell wall due to the asymmetric growth. Therefore, for a small segment of length l the relative asymmetry 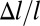is amplified by the aspect ratio 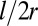. This amplification of differential growth often appears in nature, in a diverse range of systems, such as in the mechanics of plants and the human gut (26, 27).

Data Supports Anisotropic Mechanical Stress-Driven Differential Growth of Cell Walls.

A key result that emerged from our theory is a single dimensionless parameter χ that quantifies the relative contribution of the elastic and the plastic components of deformation (Fig. S9). The parameter χ depends only on the intrinsic physical parameters of the cell, independent of the experimental conditions. We show in Supporting Information that

where p is the turgor pressure, r is the cell’s radius, Y is the Young’s modulus, and h is the thickness of the cell wall. For 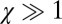, the elastic effects dominate, and there should be full snap-back. For 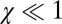, the nature of deformation is plastic, and there would be no snap-back. We find χ is of order 1 for the measured values for E. coli (Table S1), i.e., the snap-back should be partial. B. subtilis also has a similar χ value because B. subtilis has a proportionally thicker cell wall and higher turgor pressure (Table S1).

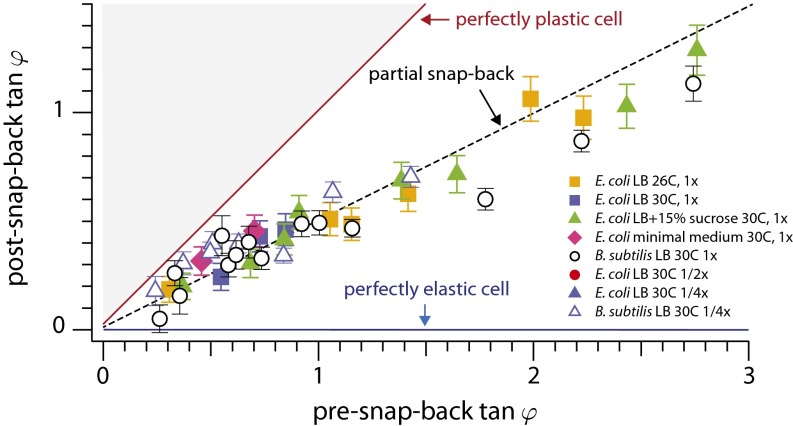
Our predictions can be tested quantitatively by measuring the magnitude of snap-back and relating it to χ. Note that the local curvature is proportional to the local growth asymmetry on the front and back sides of the cell. We find that the slope of the line connecting the tip and the hinge of the cell is a good measure for the integrated differential growth [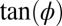] (Fig. 4). With this, our theory (Supporting Information) predicts that for small deflections the angles before and after snap-back should be proportional, with a slope depending on χ: Large values of χ imply a small slope (because the relative importance of plastic deformations is smaller for larger turgor pressure). Fig. 5 confirms this prediction and shows the snap-back events of 33 E. coli and 33 B. subtilis cells performed under eight different experimental conditions. As predicted, data for each species collapse onto a master line regardless of the growth medium, temperature, and Stokes force. The slope of the master line is approximately 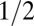, consistent with a value of χ of order unity.

Fig. 5.

Relative importance of elastic vs. plastic modes. The snap-back of the cell upon switching off the flow (Fig. 3), parameterized in terms of the slope of the tip position, as measured for 66 cells (33 E. coli and 33 B. subtilis) in differing growth conditions [see the key in the figure for growth media, temperature, and flow rate (1× being the maximal flow rate)]. For each snap-back, we quantified its magnitude by measuring the deflection angle ϕ of the tip before and after the snap-back. The snap-back angle is approximately proportional to the initial angle of deflection when the angles are small, confirming the prediction of the dislocation-mediated growth theory (Supporting Information). The ∼1/2 slope shows that the contributions by the two fundamental modes of deformation (elastic vs. plastic) are comparable with one another, regardless of the temperatures and growth conditions. Error bars are propagated from the uncertainty in calculating cell tip and channel end positions during image analysis.

Implications on Cell Shape Regulation.

That our prediction is verified by two species of bacteria as evolutionarily distinct as E. coli and B. subtilis indicates that force transduction may have more general biological consequences for growth. For example, recent studies indicate that mechanical force plays a major role in cell shape deformation leading to tissue morphogenesis in higher organisms (28).

If mechanical stress regulates the rate of cell wall synthesis, it should play a central role in shape regulation. On a cylinder the circumferential stress due to turgor pressure is twice as large as the stress along the cell’s long axis. This difference in stresses will provide a natural cue for orienting the growth machinery and coordinating glycan strand insertions. In Gram-positive bacteria, the stress regulation will further lead to a constant thickness of the cell wall by a negative feedback mechanism: The mechanical stress is inversely proportional to the thickness of the cell wall, and thinner parts of the cell wall will have larger stresses due to turgor pressure, leading to enhanced local growth.

Note that, throughout the experiments, there were cell-to-cell variations in the bending rates, which was about 30–50% of the mean. This suggests that the variability of elastic constants between different cells might be smaller than what was found in earlier studies (14).

Conclusion

We have developed a simple experimental approach to directly probe the mechanical properties of bacterial cell walls. Our results indicate that the cell wall growth rate depends on the mechanical stress, where faster growth is obtained for tensile (stretching) stress. This mechanism is likely involved in shape regulation and the maintenance of a stable rod-shaped cell over time. We found that bending forces cause the cell walls to grow differentially. The differential growth leads to persisting plastic deformations, whose recovery requires cell wall synthesis. This is in sharp contrast to the elastic deformations by pulse-like forces.

The elastic and plastic deformations represent two fundamental modes of cellular response to external mechanical forces, and can be decoupled experimentally as predicted by our theory. These effects can be revealed only by applying bending forces, and cannot be studied by means which can only change the uniform pressures that have to exist inside and outside the cell walls (e.g., osmotic shocks): Because cell wall growth is not the bottleneck for the cell growth rate (29), the growth rate is not dictated by the cell wall synthesis rate.

In the future, it would be illuminating to study deformation behavior in other types of bacteria such as tip-growers (30). Based on the mechanism described here, unlike E. coli or B. subtilis, we expect purely elastic deformations regardless of the duration of applied external forces. At the molecular level, direct observation of the asymmetric growth would provide critical information for the mechanism of cell wall synthesis. In particular, any changes in the speed of the cell wall synthesis rate or nucleation rate would be a direct test of our model. This would be a challenging but experimentally feasible based on the technology available to us (19–21). Finally, it would be fascinating to study similar mechanisms in higher organisms. What is the role of forces in guiding the vast diversity of organism shapes in nature? Previous works have shown the importance of mechanical forces in controlling the shapes of mammalian cells, where the properties of the extracellular matrix can have a large effect on the shape of the cells (31), their fate in differentiation (3), and tissue morphogenesis (28).

The bacterial model system studied here provides insights into the growth process itself, indicating that coupling of mechanical forces should be taken into account to understand robust morphological regulation of single-cell organisms.

Materials and Methods

To deform growing cells noninvasively by applying a well-defined force, we used a microfluidic device, a “mother machine,” previously developed by some of us (32). This device ensures balanced growth of individual cells for hundreds of generations. Furthermore, by controlling the flow speed in the device, the ambient buffer or the content of growth medium surrounding the cells can be switched within fractions of a second (33). Thus, we can tune the force applied to the growing cell because the force is directly proportional to the speed of the flow and the size of the cell (34). The force which we achieve in this setup far exceeds that attainable with AFM and optical tweezers. Also, our technique provides much more control of the applied forces in comparison, for example, with cells confined to microfluidic chambers of fixed or deformable shape. In contrast to the work of Ref. 35, we use a pressure-based pump rather than a syringe pump, which is necessary to perform the snap-back protocol that was instrumental to obtain our results.

For the purpose of our experiments, it was beneficial to work with filamentous cells with cell division suppressed. We grew the cells typically up to 50 μm long. This allowed us to precisely monitor the deformation of the cells in the presence of external mechanical forces. For the E. coli experiments, we used strain MG1655 with sulA under an inducible promoter [a gift from Debu Raychaudhuri (Tufts Medical School, Boston); see a description of the plasmid pDB192 in ref. 36] and cytoplasmic YFP. SulA inhibits polymerization of FtsZ, and upon induction with a 1-mM concentration of isopropyl β-d-1-thiogalactopyranoside the cells became filamentous. YFP is constitutively expressed to increase the signal-to-noise ratio of the images taken. For the B. subtilis experiments, we used a YlaO (homolog of FtsW) knockout with YlaO reinserted under a d-xylose inducible promoter (Pxyl) [a gift from Michael Elowitz (California Institute of Technology, Pasadena, CA)]. This strain is typically grown in the presence of 0.5% xylose; filamentation is induced by removing xylose from the growth media.

We used the hydrostatic pressure due to the controlled height difference between the inlet and outlet to control the flow through the device and achieve short (subsecond) response times of the flow velocity, as we verified using fluorescent beads. In Supporting Information we analyze the flow profile through the microfluidic device, both analytically and experimentally. We calculate the resulting forces and torques on the cell due to the viscous flow, and provide details of the microscopy and image processing algorithms used.