Systematic Structural Characterization of Metabolites in Arabidopsis via Candidate Substrate-Product Pair Networks^,

An algorithm is presented for visualizing reversed phase LC-MS metabolome data in biochemical reaction networks, which led to the structural elucidation of 145 of the 229 profiled compounds and included phenylpropanoids, flavonoids, (neo)lignans/oligolignols, benzenoids, indolics, glucosinolates, and apocarotenoids.

Abstract

Plant metabolomics is increasingly used for pathway discovery and to elucidate gene function. However, the main bottleneck is the identification of the detected compounds. This is more pronounced for secondary metabolites as many of their pathways are still underexplored. Here, an algorithm is presented in which liquid chromatography–mass spectrometry profiles are searched for pairs of peaks that have mass and retention time differences corresponding with those of substrates and products from well-known enzymatic reactions. Concatenating the latter peak pairs, called candidate substrate-product pairs (CSPP), into a network displays tentative (bio)synthetic routes. Starting from known peaks, propagating the network along these routes allows the characterization of adjacent peaks leading to their structure prediction. As a proof-of-principle, this high-throughput cheminformatics procedure was applied to the Arabidopsis thaliana leaf metabolome where it allowed the characterization of the structures of 60% of the profiled compounds. Moreover, based on searches in the Chemical Abstract Service database, the algorithm led to the characterization of 61 compounds that had never been described in plants before. The CSPP-based annotation was confirmed by independent MSⁿ experiments. In addition to being high throughput, this method allows the annotation of low-abundance compounds that are otherwise not amenable to isolation and purification. This method will greatly advance the value of metabolomics in systems biology.

INTRODUCTION

Metabolomics is increasingly used as a powerful systems biology tool. The identification of the many metabolites in biological samples, however, remains the main bottleneck in the field. Since 2000, methods have been developed to profile as many metabolites as possible from living tissues (Oliver et al., 1998; Nicholson et al., 1999; Tweeddale et al., 1999). The ongoing attempts to cover the whole metabolome have led to the optimization of separation methods based on gas chromatography–mass spectrometry (Fiehn et al., 2000), liquid chromatography–mass spectrometry (LC-MS) (Tolstikov and Fiehn, 2002; von Roepenack-Lahaye et al., 2004), capillary electrophoresis-MS (Soga et al., 2003; Sato et al., 2004), and NMR spectroscopy (Nicholson et al., 1999). Whichever separation technology is used, only a minority of the profiled metabolites can be identified (Fernie, 2007), limiting the information that is gained in systems biology experiments. Compounds that remain unknown can be purified for structural elucidation with NMR, but the purification step is tedious, not always successful, and not a reasonable option for low-abundance peaks. The limited identification approaches are especially cumbersome for secondary metabolites that are relatively unknown and outnumber the primary metabolites. This necessitates the development of new methods to characterize the structures of as many compounds as possible that, as a consequence, will yield extra information on the various biochemical pathways operating in the considered tissue. Currently, high-throughput structural annotation of compounds is based on the availability of databases containing chemical formulae and/or mass spectral fragmentation data. When an accurate mass can be obtained, the chemical formula can be computed and databases screened for candidate molecules (Aharoni et al., 2002; Kind and Fiehn, 2006). This approach can lead to tens or hundreds of candidate molecules, but does not guarantee that any of these corresponds with the actual structure. Complementary, mass spectral fragmentation data can be consulted. For this purpose, metabolomics-based mass spectral libraries, such as the Golm Metabolome Database (Kopka et al., 2005), MassBank (Horai et al., 2010), or METLIN (Smith et al., 2005), have been constructed. Nonetheless, the donation of MS fragmentation spectra occurs at a low pace; hence, these libraries currently represent only a few thousand compounds, whereas the number of metabolites in, for example, the plant kingdom is estimated to be 200,000 (Dixon and Strack, 2003; Fernie et al., 2004). Alternatively, software is being developed to improve the elucidation of MS fragmentation data (Neumann and Böcker, 2010). These libraries and software packages are promising for structure elucidation and indeed have led to the structural elucidation of 167 metabolites via reversed phase LC-MS analyses of nine Arabidopsis thaliana tissues harvested at multiple developmental stages (Matsuda et al., 2010), for example. Furthermore, based on the similarity of their MS fragmentation spectra, these authors also constructed a network containing 467 metabolites, including 95 structurally assigned compounds. The obtained clusters represent different classes of secondary metabolites, underscoring the assertion that mutually comparing MS fragmentation spectra of peaks offers a promising avenue for high-throughput structural elucidation.

Reversed phase LC-MS profiles of plant extracts are rich in diverse classes of secondary metabolites. Because most of the profiled compounds from each of these classes are expected to show mass and retention time differences corresponding with those between substrates and products of well-known enzymatic reactions, we hypothesized that it should be possible to annotate pairs of peaks (often referred to as m/z features in metabolomics literature) that represent candidate substrate-product pairs (CSPPs) for a particular enzymatic conversion. Based on this fundamental idea, we developed an algorithm to search all possible CSPPs, based on a given list of (bio)chemical conversions. Assembling these CSPPs into a network permitted the proposal of structures for unknown peaks whenever they were connected to peaks with known structures. As a proof of concept, we applied this algorithm to the data obtained from reversed phase LC–negative electrospray ionization–MS profiling of the rosette leaf extracts from biological replicates of Arabidopsis Columbia-0 plants. The CSPP approach lead to the structural annotation of 145 of the estimated 229 metabolites belonging to various classes, for example, glucosinolates, flavonoids, benzenoids, phenylpropanoids, (neo)lignans/oligolignols, indolics, and apocarotenoids. Remarkably, based on searches in the CAS database, 61 of these compounds, all of which were quite compellingly structurally elucidated, have not been described before in any plant species.

RESULTS

CSPP Network Method Overview

To elaborate the concept of CSPPs, methanol extracts from rosette leaves of 19 biological replicates of Arabidopsis Col-0 plants were analyzed by ultrahigh performance LC–Fourier transform-ion cyclotron resonance (FT-ICR)–MS. Following chromatogram integration and alignment, 3060 peaks, characterized by a retention time and an accurate m/z value, and corresponding to ∼229 profiled compounds (see Methods; Supplemental Figure 1), were obtained. Because these peaks are biochemically related, peak pairs with a mass and retention time difference corresponding exactly to the expected mass and polarity shift from well-known enzymatic conversions in secondary metabolism are expected to be present.

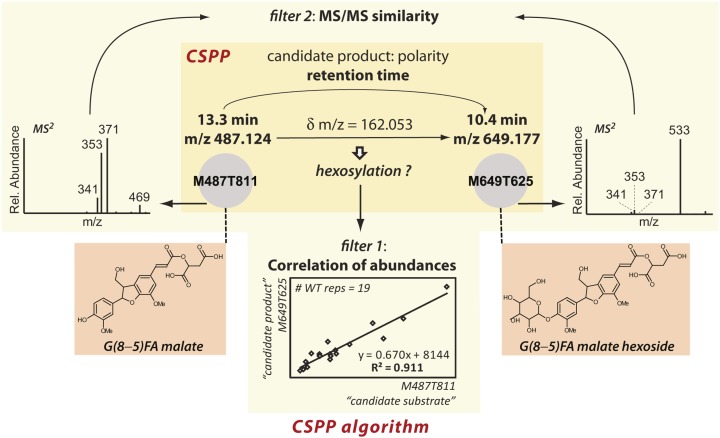
To test this assumption, we first compiled an arbitrary list of (bio)chemical conversions, of which some are expected to occur frequently in metabolism (the “true” conversions), whereas others occur rarely or not at all (the “false” conversions, see below; Table 1). Next, to obtain the CSPPs for each conversion, an algorithm was developed that used the following procedure: For each “substrate” peak, the list of 3060 peaks was queried to find “product” peaks for which the m/z value was equal to the m/z value of the “substrate” peak incremented by a mass equal to the mass change expected from the conversion. If such a peak pair was found, a CSPP was declared when the retention time of the “product” peak was smaller (conversions for which the product is more polar than the substrate) or larger (conversions for which the product is more apolar than the substrate) than that of the “substrate” peak (Figure 1; Supplemental Figure 2; see Methods for a detailed explanation of the CSPP algorithm). CSPPs were then concatenated into a network in which nodes and edges represent peaks and CSPP conversions. Statistical analysis of this CSPP network provided insight into its inherent metabolic network properties (see below; Figure 2). Subsequently, the validity of the “true” (bio)chemical conversions was assessed by comparison of the number of CSPPs presented in Table 1 with the number of pairs of chromatogram peaks obtained when the mass difference was systematically varied without taking the retention time into account (Table 1, Figure 3; Supplemental Figure 3). The latter method allows the relevant conversions for inclusion into the CSPP algorithm to be deduced from the data at hand. Finally, CSPP-based structural elucidation was performed via network propagation starting from known nodes (Figure 4). Whenever possible, structural elucidation of adjacent unknown nodes was aided by considering the Pearson correlation between the levels of both peaks across biological replicates and by MS fragmentation (MS²) spectral similarity matching (Figure 1). Information on all structurally characterized peaks is summarized in Supplemental Data Set 1 and Supplemental Figure 4. An overview of the profiled pathways is shown in Figure 5. Proposed structures were verified via MSⁿ ion trees, i.e., by a nested fragmentation approach in which MS² first product ions are further fragmented into MS³ second product ions.

Table 1. (Bio)Chemical Conversions for CSPP Network Generation.

Nr	Short	Con	m/z Dif	Elua	#CSPP	P.C.
1	Box	β-Oxidation	26.016	1	97
2	Qui	Quinate	174.053	1	102
3	Shi	Shikimate	156.042	1	103
4	Tar	Tartarate	132.006	1	108
5	Cul	Coumaryl alcohol	116.063	2	142
6	Mal	Malate	116.011	1	144
7	Rhab	Deoxyhexose	146.058	1	144	y
8	Col	Coniferyl alcohol	162.068	2	150
9	Cat	Catechol	136.016	2	151
10	Red	Reduction	2.016	1	152	y
11	Van	Vanillate	150.032	2	154
12	Syr	Syringate	180.042	2	156
13	Phb	Hydroxybenzoate	120.021	2	160
14	Caf	Caffeate	162.032	2	163
15	Dql	Dimethoxyquinol	152.047	2	165
16	Hql	Hydroxyquinol	108.021	2	169
17	Cou	Coumarate	146.037	2	169
18	Sil	Sinapyl alcohol	192.079	2	171
19	Iso	Isoprenylation	68.063	2	173
20	Val	Vanillyl alcohol	136.052	2	173
21	Fer	Ferulate	176.047	2	174
22	Pen	Pentose	132.042	1	182	y
23	Pcl	Protocatechus alcoholc	122.037	2	183
24	Pbl	Hydroxybenzyl alcohol	106.042	2	185
25	Cal	Caffeyl alcohol	148.052	2	194	y
26	Syl	Syringyl alcohol	166.063	2	213
27	Sin	Sinapate	206.058	2	217	y
28	Qul	Quinol	92.026	2	225
29	Sun	Syringyl	226.084	2	245	y
30	Hyd	Hydration	18.011	1	254
31	Gun	Guaiacyl	196.074	2	290	y
32	Gly	Glycerol	74.037	3	292	y
33	Oxy	Oxygenation	15.995	1	318	y
34	Ace	Acetylation	42.011	3	328
35	Hex	Hexose	162.053	1	341	y
36	Mth	Malate_hexosed	46.042	3	346	y
37	Met	Methylation	14.016	2	493	y
38	Mox	Methoxylatione	30.011	3	532	y

Nr, number; Short, shorthand naming; Con, conversion; m/z Dif, m/z difference; Elu, elution behavior of product peak versus substrate peak; #CSPP, number of CSPPs obtained for the conversion; P.C., prominent conversion (based on peak pair generation); y, yes.

^aElution behavior: 1, product elutes earlier; 2, product elutes later; 3, not known.

^bShorthand name is based on rhamnose. When the shorthand name is underlined or italics, > or ≤225 CSPPs were obtained for the conversion, respectively. Conversions written in italics are expected to occur to a lesser extent in Arabidopsis secondary metabolism. Conversions written in bold do not represent a true (bio)chemical conversion but are associated with a structural moiety that is often observed among the profiled metabolites.

^cThis conversion can also be the addition of a methoxyquinol.

^dHydroxycinnamoylmalate and hydroxycinnamoylhexose can be transesterified.

^eMethoxylation is often observed in phenylpropanoid metabolism, yet occurs by a separate oxygenation and methylation enzymatic reaction.

Figure 1.

Overview of the CSPP Algorithm.

A CSPP is defined based on a particular mass difference and retention time order, yet the CSPP algorithm computes the Pearson product-moment correlation coefficient and the MS² spectral similarity as well, which can be used as additional filters.

[See online article for color version of this figure.]

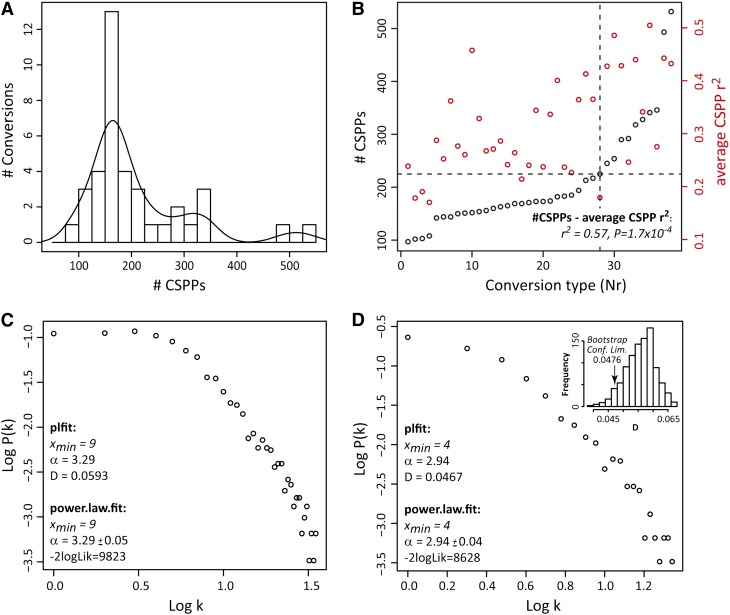
Figure 2.

CSPP Distribution Properties.

(A) Histogram of CSPP number. The curve represents a Gaussian kernel density function (weight = 40).

(B) CSPP number and average Pearson correlation coefficient versus the conversion type. (Bio)chemical conversions were ordered with increasing CSPP number (see Table 1, Nr). The dashed lines indicate the knot from which the CSPP number per conversion increases more steeply and all conversions represent well-known enzymatic reactions. A Pearson correlation coefficient was computed for each CSPP between its “substrate” and “product” levels (based on the MS ion current signal) across biological replicates. The correlation coefficients obtained for all CSPPs belonging to the same conversion were then averaged. The positive association between these average Pearson correlations and the number of CSPPs was also evaluated via a Pearson correlation (see r² and P values inserted in the plot).

(C) and (D) Node connectivity distribution of CSPP networks. Log-log plot of network node connectivity distribution involving all reactions (C) and log-log plot of network node connectivity distribution involving only the “high CSPP number” conversions (D). The accuracy of the fit to a power law distribution for the log-log plots in (C) and (D) was computed via the plfit (D statistic) and power.law.fit (-2logLik) functions in R (see Methods). The significance of the better accuracy obtained for the log-log plot in D was tested via bootstrapping (inset; see Methods). -2logLik, −2 times the logarithm of the likelihood; Conf. Lim., one-sided confidence limit; D, Kolmogorov-Smirnov goodness-of-fit statistic; k, node connectivity or the number of edges a node possesses. α and x_min are estimates for the power law function parameters.

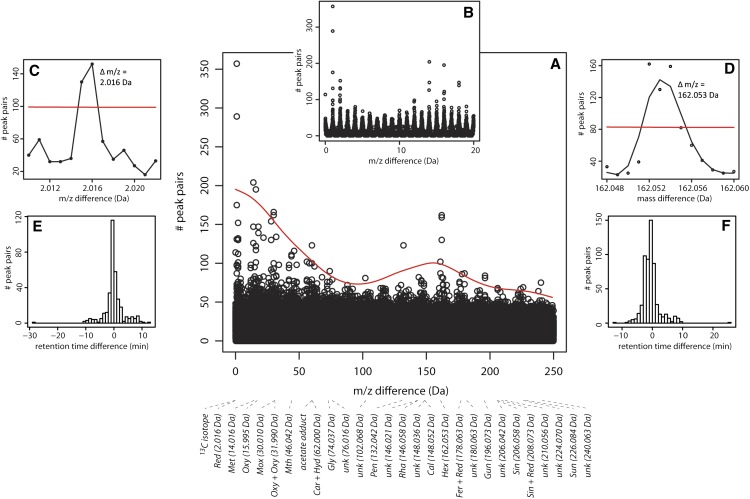
Figure 3.

Peak Pair Generation.

The number of chromatogram peak pairs for a particular mass difference, up to precisely three decimals, was computed. The mass differences varied between 0.001 and 250.000 D; thus, 250,000 mass differences were considered.

(A) Manhattan plot showing the number of peak pairs (y axis) versus the mass difference (x axis).

(B) Manhattan plot with mass differences ranging from 0 to 20 D.

(C) and (D) Expansion of Manhattan plot showing the mass difference region for reduction (C) and for hexosylation (D).

(E) and (F) Distribution of the number of peak pairs versus retention time difference between both peaks of the peak pair. Plots are given for mass differences corresponding to reductions (E) and hexosylations (F). The curved line in (A) and straight lines in (C) and (D) represent the minimum number of peak pairs necessary to consider the mass difference relevant for inclusion as a CSPP conversion type (see Supplemental Methods for further explanation).

[See online article for color version of this figure.]

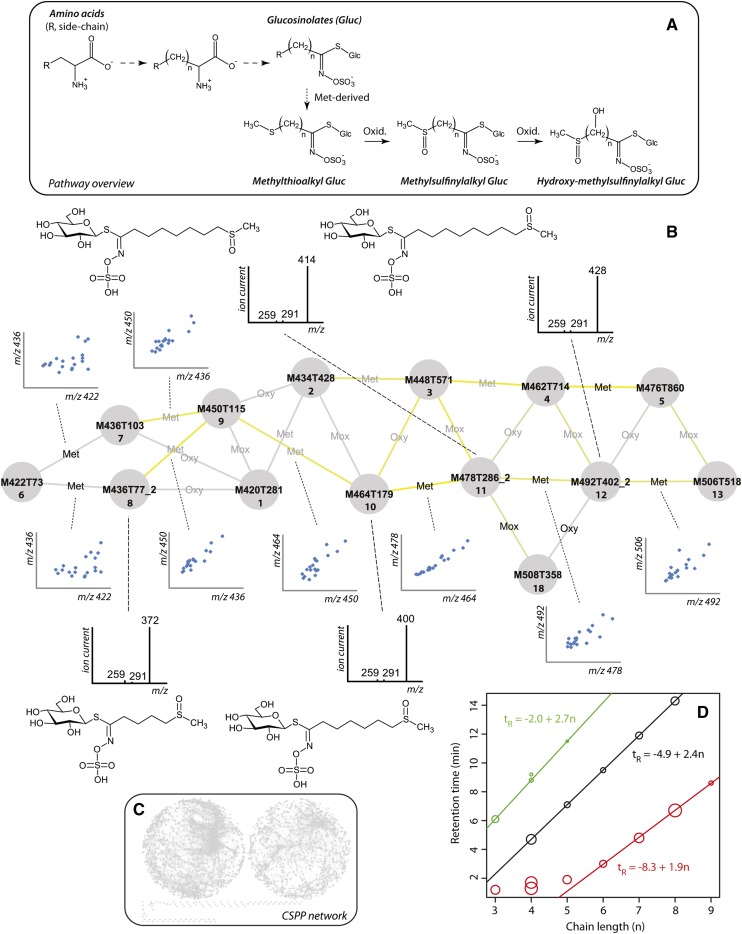
Figure 4.

CSPP Analysis of Aliphatic Glucosinolates.

(A) Pathway overview. Full arrows represent enzymatic reactions, whereas dashed arrows represent multiple enzymatic conversions. Dotted arrows indicate the various compound classes.

(B) Nodes and edges represent chromatogram peaks and (bio)chemical conversions (see Table 1 for conversion types). Node labels are based on the XCMS integration and alignment algorithm. Whenever the similarity between the MS² spectra of candidate substrate and product exceeds 0.8, the edge label is black. The outer left node, M422T73, represents glucoiberin 6. Only methylthioalkyl and methylsulfinylalkyl glucosinolates are included. The color brightness of the edge reflects the Pearson product-moment correlation coefficient between the levels of the CSPP “substrate” and “product” (blue and yellow represent a negative and positive correlation). Inserted are plots showing the covarying abundance of “substrate” and “product” for some of the conversions and MS² spectra of some of the peaks.

(C) Overview of the complete CSPP network: The network on the right is mainly composed of the ¹³C isotopes that are accompanying the base peak in LC-MS chromatograms.

(D) Retention time versus alkyl chain length. Black, red, and green circles represent methylthioalkyl, methylsulfinylalkyl, and Leu-derived glucosinolates, respectively. Circle size corresponds to the mean abundance of the glucosinolate in wild-type leaves, following rescaling of the abundance as log(ion current/10000). Linear models were calculated using the lm function in R version 2.13.1.

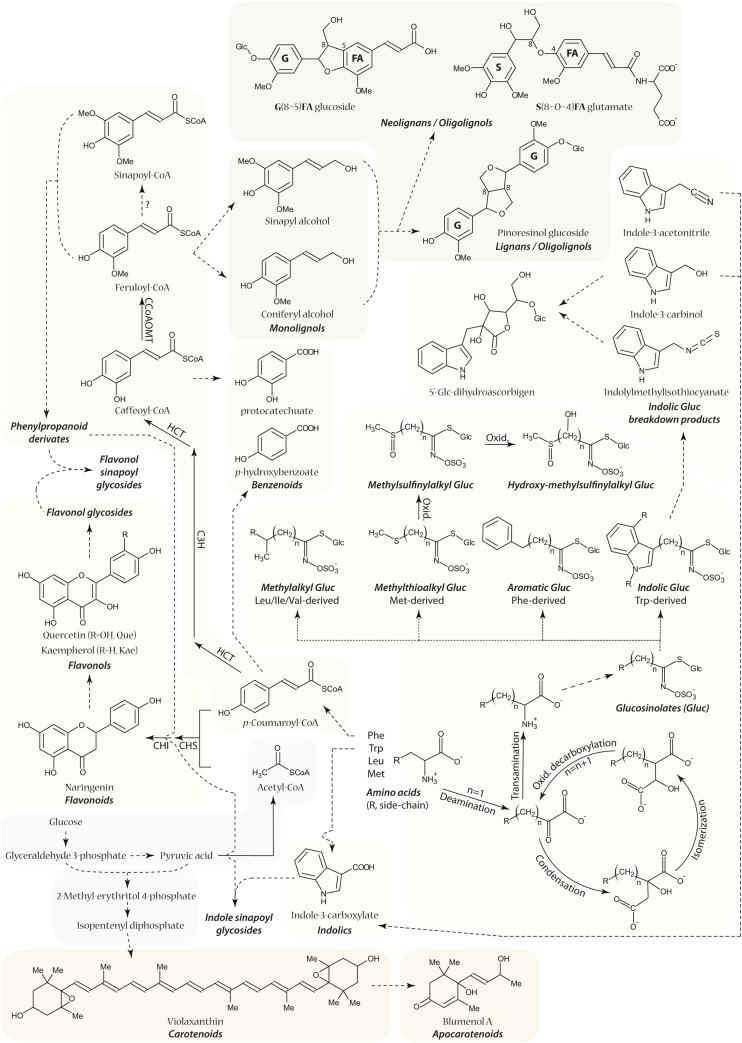
Figure 5.

Overview of the Profiled Pathways.

Full arrows represent enzymatic reactions, whereas dashed arrows represent multiple enzymatic conversions. Dotted arrows indicate the various compound classes. ?, in vivo conversion not demonstrated; C3H, cinnamic acid 3-hydroxylase; CCoAOMT, caffeoyl-CoA O-methyltransferase; CHI, chalcone isomerase; CHS, chalcone synthase; HCT, p-hydroxycinnamoyl-CoA:quinate/shikimate p-hydroxycinnamoyl transferase; Oxid., oxidation.

[See online article for color version of this figure.]

CSPP Network Statistical Analysis

The likelihood with which a CSPP reflects a metabolic conversion can be derived from the number of CSPPs that are obtained with a random selection of both well-known “true” (bio)chemical and “false” erroneous conversions (Table 1). These conversions had to be chosen a priori to allow a valid statistical analysis and to determine the number of false positive CSPPs (see below). Among the “true” biochemical conversions were enzymatic reactions that prevail in secondary metabolism such as methylation and oxygenation, and, because many phenolics were expected (D’Auria and Gershenzon, 2005), phenolic derivatizations, for example, the condensation of organic acids or saccharides with phenolics and chemical conversions arising from radical coupling of monolignols leading to (neo)lignans. For the “false” conversions, the masses of various aromatic moieties that are characteristic for the structures of flavonoids and (neo)lignans, e.g., quinol, but that do not arise directly from a chemical or enzymatic addition or condensation reaction, were chosen. Additionally, “pseudo” erroneous conversions were considered as well, i.e., enzymatic reactions that were not expected to occur frequently in Arabidopsis secondary metabolism, such as isoprenylation. In total, this (bio)chemical conversion list contained 38 reactions and yielded 7958 CSPPs (Table 1; see Methods).

CSPP Number Distribution

Depending on the type of conversion, between 97 and 532 CSPPs were obtained. By dividing this range into 19 classes (x axis), a histogram of the number of conversions (y axis) in each class was made (Figure 2A). Clearly, the histogram was not normally distributed but showed a bi- or multimodal distribution, demonstrating that the conversions could be partitioned into at least two groups. The largest group was represented by the mode at ∼150 to 175 CSPPs and, by considering the underlying normal distribution, the number of CSPPs for the 29 conversions comprising this normal distribution ranged between ∼50 and ∼250. Most of these conversions (Table 1, italics) were a priori not expected to occur frequently in secondary metabolism in Arabidopsis leaves (e.g., isoprenylation or quinol addition) (D’Auria and Gershenzon, 2005). Except for glycerol addition (Gly, Table 1), the eight conversions with more than 250 CSPPs are well known in Arabidopsis secondary metabolism, such as methylation (Met, Table 1) or hexosylation (Hex, Table 1). Thus, these data indicate that mass differences for which high numbers of CSPPs are found are more likely to be associated with true biochemical conversions.

Correlation of CSPP Candidate Substrate and Product Peak Abundances

The partitioning of the conversion types into two groups arises from Figure 2B as well; when ordering all 38 conversion types presented in Table 1 by their CSPP number-based rank (x axis, Nr in Table 1), and plotting this versus the number of CSPPs (y axis), a segmented linear function was obtained with a knot at 200 to 225 CSPPs. Assuming that levels of secondary metabolic pathway intermediates might be mutually more highly correlated than those with the rest of metabolism (see Discussion and Supplemental Methods), higher correlations are expected for CSPPs representing true (bio)chemical conversions than for those associated with false conversions. Therefore, across biological replicates, the Pearson product-moment correlation coefficients betweenthe MS ion current–based abundances of both “substrate” and “product” peaks for each CSPP were computed. Next, the average was computed of the correlations obtained for all CSPPs within each conversion type. These average correlation coefficients are displayed in Figure 2B. As can be observed, the average correlation coefficient increases from left to right in Figure 2B, i.e., conversions with a higher number of CSPPs represent more highly correlated CSPPs as well. In fact, a significant association (Pearson r² = 0.57, P = 1.7 × 10⁻⁴) existed between the average Pearson correlation coefficient for each conversion type and its number of CSPPs. The dichotomy in both plots (A and B) shown in Figure 2 supports the notion that the group of conversions with the higher number of CSPPs (“high CSPP” group) is enriched in CSPPs that have a true biochemical background than the group of conversions with lower CSPP numbers (“low CSPP” group). Additionally, these data supported the use of correlations to filter CSPPs representing true (bio)chemical conversions from the total list.

CSPP Network Topology

Subsequently, metabolic networks were made by concatenating “substrate”-“product” peak pairs, one based on the total number of CSPPs presented in Table 1, and one based on the “high CSPP” group only. In a metabolic network in which the edges and nodes represent enzymatic reactions and metabolites, the number of connections per node, i.e., the node connectivity, follows a scale-free (power law) rather than a random distribution (Jeong et al., 2000). This implies that few nodes are highly connected whereas the majority are scarcely connected. For the CSPP networks, the connections are based partially on CSPPs having a biochemical origin and partially on CSPPs that arise when two peaks have, purely by chance, a mass and retention time difference corresponding with that of a biochemical conversion. The latter can be regarded as “random” CSPPs. Therefore, the node connectivity of CSPP networks is expected to be a mixture distribution, i.e., a composite of a random and a scale-free distribution based on the presence of “random” and “biochemical” CSPPs. The higher the fraction of “biochemical” CSPPs, the more the underlying scale-free distribution will prevail in the mixture distribution profile. This should be the case for the network of the “high CSPP” group (high CSPP network) compared with that of the network containing all conversion types (full network). In agreement, based on the likelihood ratio (-2logLik) and Kolmogorov-Smirnov goodness-of-fit (D value) tests, the topology of the high CSPP network was more accurately modeled by a scale-free distribution (see log-log plots in Figures 2C and 2D) than that of the full network. Based on bootstrapping results, a one-sided 95% confidence interval for the D value was constructed in the case of the high CSPP network. This showed that the probability of obtaining a D value as low as 0.0467 (Figure 2D) when drawing a subnetwork from the full network was <5%, underscoring the significantly better power law fit of the high CSPP network. Therefore, the CSPP network topology provides further support that a substantial number of CSPPs represent true biochemical conversions.

In conclusion, all analyses indicated that, when compared with “false” conversions, “true” (bio)chemical conversions generally had (1) more CSPPs (at least 200 CSPPs in this study; Figure 2A), (2) higher correlations between the abundances of “substrate” and “product” peaks for each CSPP across biological replicates (Figure 2B), and (3) a CSPP network node connectivity distribution that more accurately fitted a scale-free distribution, characteristic of the node connectivity distribution of metabolic networks (Figures 2C and 2D).

Retrieving the Prominent Conversions from Metabolomic Data

Independent of the information retrieved from the CSPP networks discussed above, a more in-depth analysis of the mass differences that prevailed among all possible pairs of the 3060 peaks was performed. To this end, all 250,000 highly resolved mass differences between 0.001 and 250 D were considered (Figures 3A to 3D; see Methods). This showed that, except for hydration (Hyd) and acetylation (Ace), the above described a priori chosen “true” biochemical conversions were all among the frequently encountered mass differences (P.C. in Table 1). The numbers of peak pairs for the mass differences corresponding to a hydration and an acetylation were just below the computed threshold (see Methods for the threshold computation algorithm). Other common mass differences were either combinations of the a priori chosen list of “true” conversions or the corresponding conversion types were unknown (indicated as “unk” in Figure 3A). Subsequently, for each of the common conversions, the distribution of the retention time differences between the peaks of each peak pair was analyzed (Figures 3E and 3F; Supplemental Figure 3). Continuous distributions were obtained in which the center of mass was clearly in the expected direction, i.e., toward a negative or positive retention time difference for conversions in which the “product” peak is more polar or apolar than the “substrate” peak, respectively. However, these distributions tailed somewhat toward a positive or negative retention time difference, respectively, thus including zero retention time difference. For example, the center of mass was negative for hexosylation (Figure 3F), yet the right tail of the distribution extends beyond a retention time difference of 0. Other examples are shown in Supplemental Figure 3. This is a consequence of peak pairs being rendered by in-source fragmentation of compounds and supports the need for a minimum retention time difference within the CSPP algorithm. However, based on the retention time difference distribution, a minimum retention time difference could not be defined for any of the conversion types. Therefore, the minimum retention time difference for each conversion was set to be equal to the width of a chromatographic peak, i.e., 0.2 min.

Including a MS² Spectral Similarity Search Algorithm

The MS² spectra of peaks representing similar compounds are often highly similar (Figure 4) (Justesen, 2000; Morreel et al., 2004; Fabre et al., 2007). Consequently, in addition to the correlation coefficient between the peak abundances, MS² spectral matching can be regarded as a second optional filter to decide whether or not a CSPP is associated with a true biochemical conversion. Therefore, whenever the MS² spectra of “substrate” and “product” were available, similarity matches between the MS² spectra were calculated (see Methods). MS² spectral similarity matching avoided structural misinterpretations (Supplemental Methods). Thus, although CSPPs refer to pairs of compounds that have a mass difference and elution behavior characteristic for a (bio)chemical conversion, the full CSPP algorithm calculates also the correlation coefficient and the MS² spectral similarity.

Use and Validation of the CSPP Network to Aid in Structural Characterization of Unknown Metabolites

For structural characterization, a CSPP network was built based on the “high CSPP” group conversion types (underlined, Table 1) supplemented with those conversion types that had a high number of peak pairs (see P.C. in Table 1). To obtain all nodes that represent compounds of the same biochemical class, the same strategy was followed as used in automated gene and protein function annotation (Watson et al., 2007; Loewenstein et al., 2009; Klie et al., 2012). Given the CSPP network, first a subnetwork on nodes representing known compounds of the biochemical class of interest was extracted (together with the incident edges). Then, for each of the nodes in a so-obtained subnetwork, a breadth-first-search rooted on the nodes was conducted throughout the full network to transfer biochemical class annotation (based on the correlation coefficient and/or MS² spectral similarity thresholds; see legend in Supplemental Data Set 1), and the newly annotated nodes were included in the subnetwork. This approach for biochemical class annotation was iteratively repeated until all representative compounds for the biochemical class were traced from the full network. Structural characterization of the compounds represented by the nodes in the so-obtained final subnetwork was then performed based on the conversion labels of the adjacent edges and the structures represented by their connected nodes.

We evaluated this network propagation approach based on the major types of glucosinolates, i.e., the methylthioalkyl and the methylsulfinylalkyl glucosinolates. Glucosinolate biosynthesis can be divided into three phases (Figure 4A). In the first phase, the precursor amino acid is chain-elongated via methylene insertions (each leading to a mass shift identical to that of a methylation reaction). This phase is followed by the conversion of the amino acid to the glucosinolate structure. In the final phase, secondary modifications such as oxygenations produce the various glucosinolate classes. When Met is the precursor amino acid, the second phase leads to the methylthioalkyl glucosinolates that might then be further oxidized to the methylsulfinylalkyl glucosinolates (Sønderby et al., 2010). Therefore, only edges representing methylations and oxygenations (Oxy, Table 1) had to be considered. The subnetwork for the aliphatic glucosinolates was obtained as explained above: Starting from the node representing glucoiberin or 3-methylsulfinylpropyl glucosinolate, which is a small glucosinolate (compound 6; Figure 4B; number nomenclature and structures are presented in Supplemental Data Set 1 and Supplemental Figure 4), the network was propagated by selecting the edges representing methylations and oxygenations (Figure 4B). In the so-obtained subnetwork, strongly correlated CSPPs were predominantly observed for methylations (Figure 4B, yellow edges), representing the methylene insertions. This was verified by plotting the “substrate” versus the “product” levels (Figure 4B). Moreover, all glucosinolates in the subnetwork showed highly similar MS² spectra that still allowed the methylthioalkyl and the methylsulfinylalkyl glucosinolates to be distinguished. Structural characterization of the peaks associated with the various nodes was straightforward with this overall method.

The methylthioalkyl and the methylsulfinylalkyl glucosinolates in Arabidopsis represent two homologous series in which the members have an alkyl chain that can range from 3 to 11 methylene units (Halkier and Gershenzon, 2006). Plotting the retention time versus the alkyl chain length of all members within a series revealed a linear relationship except for a few very early eluting compounds (Figure 4D). This elution behavior corresponds exactly with expectations from gradient reversed phase LC (Jandera et al., 2003). Using the parameter estimates of the obtained linear models, the retention times of other members within each glucosinolate series that might have been missed upon chromatogram integration and alignment were calculated. Based on these estimated retention times, no additional members were observed in the chromatograms, confirming that all aliphatic glucosinolate peaks present in the chromatograms were picked up by the XCMS-based peak integration and the subsequent CSPP algorithm. This underscores the sensitivity and veracity of the whole procedure (Figure 4D).

To disclose all glucosinolates present in the CSPP network, all “true” conversion types were taken into account during network propagation and edges were retained whenever their associated correlation coefficient and/or MS² spectral similarity score surpassed their threshold values (see legend of Supplemental Data Set 1). In addition to the Met-derived glucosinolates, Leu-, Trp-, and Phe-derived glucosinolates could also be traced via the CSPP networks, leading to the structural annotation of 28 glucosinolates in Arabidopsis leaves (Supplemental Data Set 1). Interestingly, the MS² spectra of some glucosinolates showed a sulfinylmethane loss of 64 D as the major fragmentation pathway (Cataldi et al., 2010), cataloguing them as methylsulfinylalkyl-derived glucosinolates. However, their accurate masses indicated the presence of an additional hydroxyl substituent. This hydroxyl group was present on the alkyl chain rather than on the glucosinolate core structure because characteristic first product ions for the latter moiety were clearly observed at m/z 259 and often also at m/z 291 and 275 (Fabre et al., 2007; Rochfort et al., 2008). In Supplemental Data Set 1, these five compounds are more specifically referred to as hydroxy-(methylsulfinyl)-alkyl glucosinolates. Screening the CAS database revealed that, except for one of them, these compounds have never been documented in the plant kingdom before. These results illustrate the usefulness of CSPP networks to pick up new biochemical classes of metabolites.

The same network propagation method was used to derive subnetworks for other classes of secondary metabolites. In addition to the glucosinolates, 15 flavonols, 22 phenylpropanoid derivatives, 63 oligolignols/(neo)lignans, three benzenoids, four apocarotenoids, and eight indolics were encountered among a total of 145 structures that were characterized with the CSPP networks (Supplemental Data Set 1 and Supplemental Figures 5 and 6; Figure 5). Consequently, 60% of the 229 profiled compounds were annotated/characterized. Based on the CAS database, 61 of the characterized structures have never been described in plants (Supplemental Methods). An overview of the profiled pathways is shown in Figure 5.

The postulated structures based on the information from the curated CSPP networks (i.e., networks obtained by removing edges in which the associated correlation coefficient or MS² spectral similarity did not surpass the considered threshold; footnote in Supplemental Data Set 1) were further verified by a combination of MS² library searching and de novo MSⁿ structural elucidation (see Methods) whenever possible. Additionally, chemical synthesis (Supplemental Figure 7) was performed to authenticate the structures of the neolignans G(8–O–4)FA Glu 78 and 84 (Supplemental Methods). Furthermore, structural authentication was possible for 5′-O-β-d-glucosyl dihydroascorbigen 137 by comparison with tandem mass spectrometry data recorded by Montaut and Bleeker (2010) (Supplemental Methods and Supplemental Figure 8). Noticeably, for the latter three compounds for which a full authentication was possible, the proposed structures were confirmed.

DISCUSSION

In this study, using information on the mass and polarity differences between the substrate and product of a predefined set of (bio)chemical conversions, an MS-based metabolomics approach for the high-throughput structural characterization of the many unknown metabolites was developed. This cheminformatics algorithm generates CSPPs, each representing a pair of peaks having a mass difference and an elution order that corresponds with those expected for a particular biochemical conversion. When the resulting CSPPs are integrated into a network, structural knowledge of certain nodes aids the structural interpretation of subsequent nodes. Thus, similar to a Sudoku puzzle, the more nodes that are known, the more “unknown” nodes that can be tentatively annotated. Aside enhancing the structural characterization, this method also allowed searching particular classes of compounds and to define new enzymatic reactions (Supplemental Methods).

In metabolomics, four structural elucidation levels for a peak have been proposed: “identified,” “structurally annotated,” “structurally characterized,” or “unknown” (Sumner et al., 2007). In LC-MS, peak identification requires confirmation with a standard having the same elution and MS spectral characteristics or the recording of a high quality NMR spectrum of the isolated component. NMR yields information on the neighboring hydrogen and/or carbon atoms from which the molecular structure, including stereochemical information, can be deduced. However, due to its low sensitivity, coupling NMR to LC is troublesome, and compound purification is a prerequisite. Alternatively, to enable a high-throughput structural elucidation approach, other spectroscopic methods, e.g., MS, should be used. Although firm identification by MS is not possible without spiking of a standard, the MS fragmentation spectrum of the peak might match with a spectrum present in a MS library, enabling a structural annotation. Even in the absence of a library, the MS spectral details are often sufficient for a structural characterization. In this study, a less stringent definition of structural annotation and characterization was adopted: Here, “structural annotation” refers to structural elucidation based on both the CSPP network and MSⁿ data, whereas “structural characterization” implies the use of only CSPP network information. In order to obtain a chemical formula, structural characterization is constrained to the use of a highly accurate MS, e.g., via FT-ICR-MS, yet the CSPP algorithm can be implemented using low resolution MS. The strength of structural characterization with the CSPP algorithm was clearly underscored by the predictions and assignments of G(8–O–4)FA Glu 78 and 84 for which the structures were confirmed by spiking synthesized standards.

Combining the CSPP Algorithm with Correlation Analysis Reduces the Number of False Positives

The CSPP method is based on the biochemical relationships between the profiled peaks so that at least a fraction of the CSPPs are expected to represent true (bio)chemical substrate/product combinations. To verify whether this was indeed the case, a list of (bio)chemical conversions containing fictitious conversions, e.g., quinol addition, and conversions that are expected to occur infrequently or not at all in Arabidopsis metabolism, e.g., isoprenylation, was assembled (Table 1). The latter conversions yielded between 50 and 250 CSPPs with an average of 161 CSPPs (“low CSPP” group conversions; Figures 2A and 2B), which can be regarded as an estimate for the number of false positives for each conversion. Almost all of the (bio)chemical conversions that do occur in Arabidopsis metabolism provided more than 250 CSPPs (“high CSPP” group conversions). This agrees with a reported study by Iijima et al. (2008) showing that certain mass differences are biologically more relevant than others based on the distribution of mass differences between tomato metabolites profiled by LC-FT-ICR-MS. On average, 344 CSPPs were obtained for a “high CSPP” group conversion. This yielded an average chance of 47% [=(161/344)*100] for obtaining a false positive, illustrating the necessity of combining the CSPP network with additional filters such as the correlation coefficient calculated from the abundances of the “substrate” and “product” peaks in biological replicates and the MS² spectral similarity.

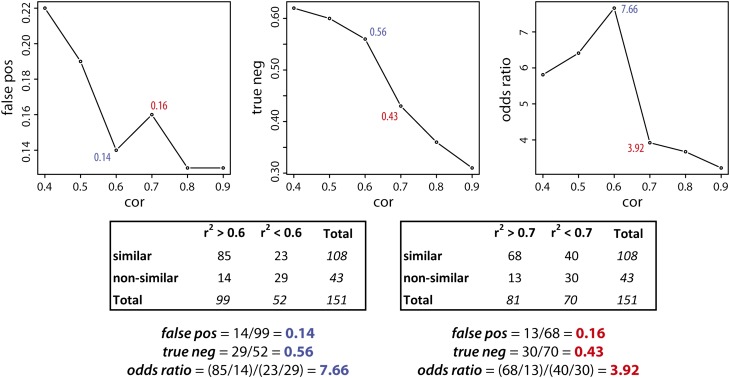
The additional use of correlations requires that a suitable correlation coefficient threshold is chosen. In metabolomics studies, metabolite-metabolite correlation networks are often made using only the very highly correlated metabolites (Pearson |r²|>0.8) to restrict the number of edges in the network. For example, 4,680,270 edges would have been computed from our set of 3060 peaks. Because the CSPP networks are based on a priori defined biochemical conversions, they contain much fewer connections. For example, in this study, 7650 edges emerged from 38 considered conversions. Therefore, a much less stringent correlation threshold can be used. The most appropriate correlation threshold can be estimated based on the data obtained from the MS² spectral similarity matching (see Methods). Whenever the “substrate” and “product” in a CSPP have similar MS² spectra, they usually have similar molecular structures (Rasche et al., 2012; Rojas-Cherto et al., 2012), conferring a high probability that the CSPP represents a “true” metabolic reaction. Therefore, the MS² spectral similarity is a measure for judging the likelihood that a CSPP for which a moderate to high correlation coefficient was obtained represents a “true” metabolic reaction. By considering only those CSPPs that were obtained with the “high CSPP” type conversions and for which a MS² spectral similarity was computed (151 CSPPs in total), the number of CSPPs in which the MS² spectra of “substrate” and “product” are similar or nonsimilar can be counted. In Figure 6 (left plot), the probability of a false positive is plotted for various correlation coefficient thresholds (computations are illustrated for r² > 0.6 and r² > 0.7 in Figure 6). Above a correlation coefficient threshold of 0.6, 85 CSPPs belonged to the “MS² spectrally similar group,” whereas only 14 CSPPs belonged to the “MS² spectrally nonsimilar group.” From this perspective, by selecting only CSPPs from the “high CSPP” group conversions and, furthermore, only those that are associated with moderate to high correlation coefficients, the chance on a false positive drops to 14% [=14/(85+14)*100]. The association of higher correlation coefficients with higher MS² spectral similarities is further strengthened by regarding the low-correlated CSPPs (r² < 0.6) in which the absence of a MS² spectral similarity prevailed (23 and 29 CSPPs belonged to the “MS² spectrally similar group” and the “MS² spectrally nonsimilar group,” respectively; Figure 6). This is reflected in the odds ratio of 7.66, which indicates that the chance that a highly correlated CSPP will belong to the “MS² spectrally similar group” rather than to the “MS² spectrally nonsimilar group,” is more than 7 times higher than that for a low-correlated CSPP (Figure 6, right plot). It should be stressed that, in the discussion above, MS² spectral similarities are used to assess the validity of including correlation coefficients as a filter to select CSPPs that are more likely associated with “true” biochemical conversions. Logically, adding the MS² spectral similarity itself as a second filter will, in combination with the correlation coefficient, diminishes the chance of a false positive even more (Figure 1) (Rasche et al., 2012; Rojas-Cherto et al., 2012). However, calculating the chance of a false positive using the CSPP algorithm with the inclusion of both filters is impossible as it would need the unambiguous structural identification of all characterized molecules.

Figure 6.

Effect of the Correlation Coefficient Threshold as a Filter for CSPP Selection.

CSPPs obtained from the “high CSPP” group conversions for which a MS² spectral similarity was computed were selected (151 CSPPs). CSPPs for which the “global common” (see Methods) was at least 2 or having a “global similarity” above 0.8 (see Methods) were classified as “MS² spectrally similar.” Other CSPPs were “MS² spectrally nonsimilar.” They were further classified as “high correlation” CSPPs whenever their associated correlation coefficient was higher than the threshold; otherwise, they were annotated as “low-correlation” CSPPs. This cross-tabulation was performed for different correlation coefficient thresholds (cor) and used for computing the chance on a false positive for the “high correlation” CSPPs (false pos), the chance on a true negative for the “low-correlation” CSPPs (true neg), and the odds ratio (see Discussion for explanation).

CSPP Networks Do Not Show a Small World Behavior

A more in-depth analysis of the number of false positive CSPPs obtained with various correlation thresholds provides information on the magnitude of the correlation coefficients associated with secondary biochemical conversions. Lowering the correlation threshold from 0.9 to 0.7 (Figure 6, left plot) increases the number of false positive CSPPs and thus lowers the odds ratio (Figure 6, right plot). Remarkably, when the correlation threshold is set at 0.6 rather than 0.7, a considerable increase in the odds ratio is observed. This odds ratio jump reflects the improved classification of low-correlated (r² < 0.6) CSPPs as true negative CSPPs (Figure 6, middle plot). Obviously, there is still a large number of moderately correlated (0.6 < r² < 0.7) CSPPs that belong to the “MS² spectrally similar” group and thus have a high probability of representing true biochemical reactions. Evaluating correlation thresholds from 0.6 to 0.4 did not substantially change the fraction of true negative CSPPs among the CSPPs with a correlation below the threshold, but the number of false-positive CSPPs increased considerably, leading to a decrease of the odds ratio. This data suggests that most biochemically valuable CSPPs are moderately to highly correlated. A more in-depth classification of the latter CSPPs based on the extent that they reflected a biochemical conversion is given as Supplemental Methods.

Correlations among metabolite abundances arise when environmental changes lead to metabolite abundance fluctuations that in their turn affect the complex regulation of metabolism. However, initial metabolome experiments (Roessner et al., 2001) as well as simulation studies (Steuer et al., 2003; Müller-Linow et al., 2007) have shown that correlations do not necessarily reflect the pathway architecture. More specifically, profiling studies of mainly primary metabolites (Roessner et al., 2001) have shown that most metabolite pairs have low correlation coefficients and only a few metabolite pairs are highly correlated. Therefore, the moderate to high correlation coefficients observed in the CSPP network could be associated with the biochemical nature of the profiled compounds that were all secondary metabolites. In the early plant metabolomics literature, highly positive correlations were observed between the abundances of metabolites that are in chemical equilibrium (Roessner et al., 2001). However, such an explanation does not hold for the highly correlated CSPPs, as all “high CSPP” group conversions represent irreversible reactions. Alternatively, highly correlated CSPPs could arise when the abundances of the candidate substrate and product are controlled by the same enzymatic reaction(s) (Camacho et al., 2005). In the latter case, if control is shared by a few enzymatic reactions, the coresponse of the candidate substrate and product abundances to an altered reaction rate should lie in the same direction for each of the controlling metabolic steps (Supplemental Figure 9, left plot) (Camacho et al., 2005). If the direction of the coresponse to at least one of the controlling reactions differs from those of the remaining controlling reactions, a moderate instead of a high correlation might still be observed (Supplemental Figure 9, right plot) (Camacho et al., 2005).

Another difference between the CSPP networks in this study and primary metabolic networks is the absence of negative correlations. Negative correlations emerge when the levels of two metabolites are controlled by mass conservation (Camacho et al., 2005), for example, when two metabolites are part of a moiety-conserved cycle or when they belong to different branches that compete for the same precursor. The predominance of moderate to high positive correlations together with the absence of negative correlations in our CSPP networks suggests that branches, cycles, and amphibolic reactions are less frequent in secondary than in primary metabolic networks. This lack of interconnectivity in the CSPP networks compared with primary metabolic networks can also be retrieved from the network diameter, i.e., the average shortest path calculated across all pairs of compounds. A network diameter of 24 was obtained for the CSPP network on which the structural characterization was based, i.e., the CSPP network that contained only the “high CSPP” group conversions together with the conversions having a high number of peak pairs. Furthermore, the diameter of the latter CSPP network did not change much when allowing only moderate to highly correlated edges (r² > 0.6, diameter = 23). These network diameters are far higher than those of (primary) metabolic networks (Jeong et al., 2000) that were between 3 and 4. This suggests that the small world character of primary metabolic networks, i.e., that any pair of metabolites can be linked via relatively short paths, cannot be extrapolated to secondary metabolic networks, although some caution is needed because many secondary pathway intermediates are not presented in the CSPP network. Nevertheless, the system biology information displayed by the CSPP network could not be retrieved from genome-based metabolic models as many enzymes operating in secondary metabolism are still unknown.

The newly described CSPP algorithm opens up a major avenue for the structural elucidation of the many unknowns in metabolomic experiments. Via network propagation, the structures of unknowns can be deduced from the structures of known precursors and can subsequently be used to aid in the structural elucidation of other unknowns that are connected in the network. The limited structural knowledge of the differential peaks in comparative profiling studies prohibits a clear understanding of the living system, a restriction that is largely overcome by the proposed CSPP method. By annotating peaks that differ in mass in agreement with a certain enzymatic conversion and taking into account (1) their retention time order, (2) the correlation between their abundances across biological replicates, and (3) their MS² spectral similarity, 60% of the compounds profiled by reversed phase LC-negative ionization MS of Arabidopsis rosette leaves could be structurally characterized. Moreover, the value of the method extends beyond the plant field and will also propel forward metabolomics in the human/animal field where the metabolome is heavily influenced by the microbiome and the nutritional composition.

METHODS

Growth Conditions and Extraction

Arabidopsis thaliana Columbia-0 seeds were randomly sown in trays (19 biological replicates). Following vernalization at 4°C in the dark for 48 h, plants were transferred to short-day-conditioned growth room (8 h light, 22°C, 55% relative humidity, 120 PAR). After 2 months, one rosette leaf from each plant with a length of ∼1 cm was randomly harvested and snap-frozen in liquid nitrogen. Following ball-milling with a Retsch mill (25 Hz) for 20 s, the homogenized plant material was extracted with 0.5 mL methanol. Of the supernatants, 0.4 mL was lyophilized and redissolved in 0.8 mL milliQ water/cyclohexane (1/1, v/v). From the water phase, 10 μL was used for phenolic profiling.

Metabolite Profiling

Extracts were analyzed with an Accela ultrahigh performance LC system (Thermo Electron) consisting of an Accela autosampler coupled to an Accela pump and further hyphenated to a LTQ FT Ultra mass spectrometer (Thermo Electron) consisting of a linear ion trap mass spectrometer connected with an FT-ICR mass spectrometer. The separation was performed on a reversed phase Acquity UPLC HSS C18 column (150 mm × 2.1 mm, 1.8 μm; Waters) with aqueous 0.1% acetic acid and acetonitrile/water (99/1, v/v, acidified with 0.1% acetic acid) as solvents A and B. At a flow of 300 μL/min and a column temperature of 60°C, the following gradient was applied: 0 min 1% B, 30 min 60% B, and 35 min 100% B. The autosampler temperature was 5°C. Analytes were negatively ionized with an electrospray ionization source using the following parameter values: spray voltage 3.5 kV, capillary temperature 300°C, sheath gas 40 (arb), and aux gas 20 (arb). Full FT-ICR-MS spectra between 120 and 1400 m/z were recorded (1.2 to 1.7 s/scan) at a resolution of 100,000. In parallel, four data-dependent MSⁿ spectra were recorded on the ion trap mass spectrometer using low resolution data obtained during the first 0.1-s period of the previous full FT-ICR-MS scan: A MS² scan of the most abundant m/z ion of the full FT-ICR-MS scan, followed by two MS³ scans of the most abundant first product ions and a final MS⁴ scan of the most abundant second product ion obtained from the base peak in the MS² spectrum. These MSⁿ scans were obtained with 35% collision energy. Using RecalOffline vs. 2.0.2.0614 (Thermo Electron), the full FT-ICR-MS scans were sliced from each chromatogram raw file and subsequently converted to netCDF with Xcalibur version 2.0 SR2 (Thermo Electron). Integration and alignment was performed with the XCMS package (Smith et al., 2006) in R version 2.6.1 using the following functions: xcmsSet (fwhm = 6, max = 300, snthresh = 2, mzdiff = 0.01), group (bw = 10, max = 300, mzwid = 0.01), retcor (method= “loess,” span = 0.2, family = “symmetric,” plot type = “mdevden”). Following retention time correction, a second peak grouping was performed: group (bw = 8, max = 300, mzwid = 0.01). This process resulted in 3060 integrated peaks. It should be stressed that the number of peaks does not reflect the number of compounds. Each compound is represented by multiple peaks: Besides the base peak, peaks representing isotopes and adducts and peaks due to in-source fragmentation of the compound show up in the chromatogram as well. Chemical formulae of compounds of interest were obtained with the Qual Browser in Xcalibur version 2.0 SR2. Instead of the pseudo-molecular ions of the compounds, all peaks were used for the CSPP algorithm. This avoids that the peak grouping algorithm, to define the compounds, introduces flaws into the CSPP network. Flaws can occur because (1) peaks belonging to two highly correlated, coeluting compounds would be grouped together and (2) the selection of the pseudo-molecular ion (i.e., the deprotonated compound) within the peak group can be erroneous.

Peak Grouping Procedure

Peaks associated with the same compound have the same retention time and their levels are highly correlated across chromatograms. The number of such peak groups can be regarded as an estimate for the number of profiled compounds; these were searched using a small range for the retention time window (varying from 1 to 6 s with the latter value representing half of the baseline peak width) and the Pearson correlation threshold (varying from 0.70 to 0.95) (Supplemental Figure 1). At a retention time window and a correlation threshold of 1 s and 0.8, an optimum was observed in the surface plot of Supplemental Figure 1D, which projects the co-optimization [(meanP/meanG)*P*G] of the number of peak groups (G = 229) and the number of peaks that could be assigned to a peak group (P = 2400) onto the retention time window and the correlation threshold. The 660 unassigned peaks are low-abundance peaks for which the m/z value was often not accurately determinable. Because G was one order of magnitude smaller than P, a correction factor (meanP/meanG) was added to the formula. Peak grouping was performed using an in-house-written script in R version 2.13.1.

CSPP Network Generation

A script was written in Perl to search for peaks that show mass and retention time differences corresponding with those of substrates and products of enzymatic conversions (Supplemental Figure 2). Central in the algorithm is the detection of all candidate product peaks (because multiple isomers might be present) that associate with a particular candidate substrate peak. In the article, candidate product and candidate substrate are annotated as “product” and “substrate.”

For each considered conversion, e.g., hexosylation, the “node” list of 3060 peaks, in which each row represented a peak, was ordered with increasing m/z (Supplemental Figure 2). Starting from the “substrate” peak i at m/z = mass_i, the m/z value of the theoretical hexosylation product was computed by adding 162.053 D (m/z = mass_i + 162.053). The list was then searched for peaks with the corresponding m/z value. Whenever a peak j was found at m/z = mass_j (mass_j = mass_i + 162.053 ± error with error equal to the chosen m/z window, i.e., 0.008 in this study), its retention time was considered. Given that a reversed phase column is used, the “product” peak is expected to elute before or after the “substrate” peak when the “product” is more polar or apolar than the “substrate,” respectively. In the case of hexosylation, the “product” is expected to elute earlier than its aglycone “substrate.” Thus, when the retention time of peak j was shorter than that of the “substrate” peak i (t_Rj<t_Ri ± error with error, i.e., 0.2 min in this study, equal to half of the chosen retention time window), it was annotated as a “product” peak. Both the “substrate” peak i and the “product” peak j were put in an “edge” file as a “hexosylation” CSPP pair. The abundance ratio between the “substrate” i and “product” j for each chromatogram of 19 biological repeats and their Pearson correlation coefficient across these chromatograms was computed and added to the “edge” file. In addition, the MS² spectral similarity results were as well added to the “edge” file (see below). The “node” file was then further searched for any other possible “product” peak associated with “substrate” peak i and the same CSPP annotation process was repeated. For the considered conversion, this central motif in the algorithm was executed iteratively by independently entering each peak as a “substrate” (1 ≤ i ≤ 3060). This process was conducted for each of the conversions listed in Table 1. For enzymatic conversion types where it was not possible to predict the retention behavior of the “product” peak versus the “substrate” peak, elution within the same retention time window (2 × error = 0.4 min) of both peaks was disabled. The latter is necessary to avoid the detection of “substrate”/“product” peak pairs that arise from in-source fragmentation. For example, partial fragmentation in the electrospray ionization of glycosylated compounds yields m/z peaks representing the glycosylated compound as well as the aglycone.

The output, a collection of peak pairs obtained for each of the conversions listed in Table 1, was then used as input in Cytoscape version 2.7.0 (http://www.cytoscape.org) to generate the CSPP network in which the nodes (representing peaks) and edges (representing CSPPs) were optimized with the Cytoscape spring embedded algorithm weighed by the Pearson product-moment correlation coefficient of the peak abundances across the biological replicates. To know whether two peaks might belong to the same compound, the peak group to which each peak belonged was also introduced in Cytoscape when constructing the CSPP network. Consequently, whenever a structure could be proposed for a peak, the corresponding node and all nodes associated with the same peak group were colored green to visually distinguish them from the not yet characterized nodes.

Inclusion of a MS² Similarity Search into the CSPP Algorithm

All MS² spectra from one wild-type chromatogram were sliced into a new raw file using RecalOffline version 2.0.2.0614 and further converted to a text (.txt) file using the file converter in Xcalibur version 2.0 SR2. Based on the m/z value and retention time of the precursor ion, all MS² spectra were then aligned with their corresponding peaks in the XCMS output file (using a retention time and m/z window of 0.6 s and 0.004 D). Whenever a CSPP was declared and a MS² spectrum was available for both the “substrate” and “product” peaks, a similarity match was calculated and added to the “edge” file.

The number of first product ions with an identical m/z value in both MS² spectra was computed (referred to as “common ions”) and the dot product (Stein and Scott, 1994) for these ions was calculated (referred to as “ion similarity” and varying between 0 and 1 for no match and a perfect match, respectively), using the same weights as used by MassBank (Horai et al., 2010). In addition, first product ions in both spectra were converted to neutral losses by taking the mass difference between each product ion and the precursor ion. The reason for considering neutral losses is that they can be informative for the presence of certain moieties. For example, in a hexosylated compound, fragmentation of the glycosidic bond yields a hexose neutral loss of 162 D. Other examples are the losses of 42, 44, 68, and 86 D, and 28 and 44 D in negative ionization mode that are characteristic for flavones and flavonols, respectively (Fabre et al., 2001). Additionally, compared with the collision-induced dissociation of methylthioalkyl glucosinolates, that of methylsulfinylalkyl glucosinolates is characterized by a loss of 64 D (Fabre et al., 2007; Rochfort et al., 2008). Also the different linkage types in lignin dimers can be annotated by their MS² neutral losses (Morreel et al., 2010). In our MS² spectral matching algorithm, the number of losses with an identical mass in both “neutral loss” spectra was counted (called “common losses”) and the dot product for these losses computed (called “loss similarity”) using the same procedure as for the MS² spectra. Finally, the “global common” represents the sum of the “common ions” and “common losses” with the restriction that if a particular ion/loss is found in common, then the corresponding loss/ion cannot be counted. A global match was computed by considering the dot products obtained for both the MS² spectra and the “neutral loss” spectra (called “global similarity”). In the “edge” file, the number of first product ions in the “substrate” and “product” MS² spectrum are displayed, as well as the number of first product ions and neutral losses that are in common. In addition, the dot product–based similarity of the MS² spectra and of the “neutral loss” spectra, and the global match result are shown.

Structural Annotation of Compounds

Compounds that have been identified previously in Arabidopsis and for which the MS² spectra and the relative elution behavior in reversed phase LC are well known (see references in Supplemental Methods and Supplemental Data Set 1) were taken as starting points (indicated by “ini” in Supplemental Data Set 1) to explore the CSPP network and structurally characterize other peaks. The rest of the peaks that served as starting points were structurally annotated by a combination of approaches. Their corresponding chemical formulae were searched in the CAS (https://scifinder.cas.org/) and the PubChem (http://pubchem.ncbi.nlm.nih.gov/search/search.cgi#) databases. Their corresponding MSⁿ spectra were searched in MassBank and in an in-house library and/or elucidated using MetFrag (Wolf et al., 2010), but also de novo based on literature data concerning MS fragmentation in the negative-ion mode (see footnote of Supplemental Data Set 1 and Supplemental Methods). MSⁿ fragmentation pathways were resolved based on literature data for the glucosinolates, flavonoids, and (neo)lignans/oligolignols. For the benzenoids/phenylpropanoids, a comprehensive gas-phase fragmentation study using various standards was performed (Supplemental Methods), enhancing their structural characterization (Supplemental Tables 1 and 2 and Supplemental Figure 8A). MSⁿ spectral elucidation of indolics and apocarotenoids (Supplemental Figures 8B and 8C) was aided by the MSⁿ analysis of purchased standards. The proposed structures of nonstarting point peaks that were characterized via the CSPP network were, when possible, verified by MSⁿ analyses (Supplemental Data Set 1 and Supplemental Figure 4) using the same strategy as mentioned above for starting point peaks.

Network Topology Statistics

Pearson correlations and the fitting of a power law distribution were performed in R version 2.13.1. For the distribution fitting, an “artificial” trait with 10,000 values was generated based on the frequencies of the different node connectivity values obtained from the network containing all CSPPs (full network, “real” trait contained 7958 values) and, separately, from a network (high CSPP network) based on solely the “high CSPP number” (bio)chemical conversions (conversions containing >225 CSPPs; see Table 1 and Results, “real” trait contained 3439 values). From both generated “artificial” traits, values equal to zero were subsequently excluded leading to “artificial” traits containing 8805 and 7188 values for the full and high CSPP networks. Because the latter network contained fewer CSPPs, the corresponding “artificial” trait contained less information and parameter estimation is expected to be less precise as compared with the full network. Modeling of a power-law distribution was performed using the plfit function for which the R source code was downloaded (http://www.santafe.edu/~aaronc/powerlaws/) (Clauset et al., 2009). In addition, using the x_min value estimated by the plfit procedure, the power.law.fit function in the igraph package was applied.

To determine whether the “high CSPP” network fitted a power-law distribution better than the full network, a one-sided 95% confidence interval for the Kolmogorov-Smirnov goodness-of-fit (D) statistic had to be constructed. This confidence interval was obtained via bootstrapping using the sample and plfit functions in R. In bootstrapping, a random sample is drawn from the “artificial” full network trait (8805 values) for which the D statistic is computed. This procedure was repeated 999 times after which the distribution of the D statistic can be plotted and the confidence interval determined. The ratio (=0.43) of CSPPs present in the high CSPP network (=3439 “real” values) versus those present in the full network (=7958 “real” values) determined the size of each bootstrap sample (=8805 * 0.43 = 3786). Samples were generated without replacement. This bootstrap strategy was pursued based on the lower information present in the high CSPP network and because the high CSPP network comprises a subset of the full network.

Peak Pair Generation

Mass differences that predominated among all possible peak pairs as well as the corresponding retention time difference distributions were determined and the corresponding plots (Manhattan plots and histograms; Figure 3) constructed with in-house-written R scripts using R version 2.13.1. Mass differences between 0.000 and 250.000 D with a precision of 0.001 D were considered. A threshold on the minimum number of peaks pairs had to be computed to determine which mass differences correspond to “true” (bio)chemical conversions occurring in metabolism. This threshold decision should take three properties of the Manhattan plot into account. (1) The number of peak pairs decreased with incrementing mass differences. (2) Regions are present that are enriched in mass differences having a high number of peak pairs. Most of these mass differences could only be reasoned to occur from the intervention of at least three different conversions. Properties (1) and (2) indicate that the threshold should be based on the local mass difference region. (3) In each nominal mass difference interval, the maximum number of peaks was observed at values close to unit mass differences. This is the consequence of the isotopic masses of oxygen (15.995 D), carbon (12.000 D), hydrogen (1.007 D), and nitrogen (14.003 D) that are all close to unit mass values. As a consequence, most of the computed number of peak pairs corresponded to erroneous mass differences and should not be taken into account for threshold computation. Thus, for each mass difference, the final threshold was chosen based on the maximum number of peak pairs (max) observed in a one-unit mass difference interval. A lognormal distribution was observed for all so-obtained max values.

For the reasoning above, the selection of the more prominent available mass differences corresponding to “true” (bio)chemical conversions was based on the following procedure: For each mass difference, the threshold was based on the logarithm of the maximum number of peak pairs (logmax) that was observed in the range of mass differences up to 1 D beyond the considered mass difference (e.g., when the considered mass difference was 14.000 D, the threshold was based on maximum number of peak pairs that was observed in the mass difference region between 14.000 and 15.000 D). The mean and sd of the logmax value across a mass difference range of 10 D was determined, a 95% confidence interval was computed at each mass difference, and the confidence limit of this logarithmic trait was back-transformed to obtain the threshold. In Figure 3, the smoothed threshold curve was obtained using the smooth.spline function (spar = 0.85) in R.

Synthesis of G(8–O–4)FA Glu

Compound S1 (Supplemental Figure 7) was obtained by alkaline hydrolysis from its parent methyl ester that was synthesized according to the method of Helm and Ralph (1992). Acetylation of S1 with acetic anhydride and pyridine was followed by an amidation with Glu hydrochloride in the presence of N,N'-dicyclohexylcarbodiimide and 4-dimethylaminopyridine produced compound S2. Hydrolysis of S2 with 1 M sodium hydroxide in 50% ethanol resulted in the target product, G(8–O–5)FA glutamate. The product contained two isomers, the chemical shifts for Glu moiety were the same and those for the rest of the molecular structure were different although they could not be assigned clearly for each isomer. ¹H NMR (acetone-d₆), δ_H, 2.02 to 2.25 (2H, m, G4), 2.47 (2H, m, G3), 3.46 to 3.62 (2H, m, A9), 3.55 to 3.72 (2H, m, A9), 4.35/4.42 (1H, m, A8), 4.67 (1H, m, G3), 4.90/4.91 (1H, d, J = 5.96 Hz, A7), 6.65/6.68 (1H, d, J =15.69 Hz, B8), 6.75/6.77 (1H, d, J = 8.12 Hz, A5), 6.85/6.89 (1H, dd, J = 8.12, 1.80 Hz, A6), 7.03/7.08 (1H, br-s, B6), 7.01/7.16 (1H, d, J = 1.80 Hz, B5), 7.09/7.11 (1H, d, J =1.0 Hz, A2), 7.22/7.17 (1H, d, J = 1.0 Hz, B2), 7.48/7.51 (1H, d, J =15.69 Hz, B7); δ_c, 27.88 (G4), 30.50 (G3), 52.19 (G2), 54.33 (A8), 56.10-56.24 (OMe), 61.86/62.06 (A9), 73.64/73.72 (A7), 85.72/87.35 (A8), 111.28/111.42 (A2), 111.64/111.75 (B2), 115.03/115.20 (A5), 117.94/118.33 (B5), 119.97/120.07 (B8), 120.42/120.50 (A6), 129.81/130.00 (B1), 133.68/134.05 (A1), 141.51/141.25 (B7), 146.62/146.77 (A4), 147.96/147.08 (A3), 151.14/151.71 (B4), 151.45/151.54 (B3), 150.84 (B4), 166.82 (B9), 173.44 (G1), 174.10 (G5).

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure 1. Peak Grouping Surface Plots.

• Supplemental Figure 2. CSPP Generation Algorithm.

• Supplemental Figure 3. Retention Time Difference Distributions.

• Supplemental Figure 4. Annotated Molecular Structures.

• Supplemental Figure 5. CSPP Subnetworks of Flavonoids and Phenylpropanoids.

• Supplemental Figure 6. CSPP Subnetwork of Highly Correlated CSPPs.

• Supplemental Figure 7. Synthesis of G(8–O–4)FA Glu.

• Supplemental Figure 8. Gas Phase Fragmentation Pathways of Simple Phenolics and Phenylpropanoids, 5′-O-β-d-Glucosyl Dihydroascorbigen, and Corchoionoside C Anions.

• Supplemental Figure 9. Effect of Shared Control on Correlation.

• Supplemental Table 1. MS² Spectra of Simple Phenolics.

• Supplemental Table 2. MS² Spectra of Monolignol-Related Compounds.

• Supplemental Data Set 1. Structurally Annotated Chromatogram Peaks.

• Supplemental References.

• Supplemental Methods.

Glossary

LC-MS

liquid chromatography–mass spectrometry

CSPP

candidate substrate-product pair

FT-ICR

Fourier transform-ion cyclotron resonance

MS

mass spectrometry