ResLog Plots as an Empirical Metric of the Quality of Cryo-EM Reconstructions

Abstract

Compared to the field of X-ray crystallography, the field of single particle three-dimensional electron microscopy has few reliable metrics for assessing the quality of 3D reconstructions. New metrics are needed that can determine whether a given 3D reconstruction accurately reflects the structure of the particles from which it was derived or instead depicts a plausible though incorrect structure due to coarse misalignment of particles. Here an empirical procedure is presented for differentiating between a reconstruction with well-aligned particles and a reconstruction with grossly misclassified particles. For a given dataset, 3D reconstructions are computed from subsets of particles with decreasing numbers of particles contributing to the reconstruction. A plot of inverse resolution vs. the logarithm of the number of particles (a “ResLog” plot) provides metrics for the reliability of the reconstruction and the overall quality of the dataset and processing. Specifically, the y-intercept of a regression line provides a measure of the relative accuracy of the particle alignment and classification, and the slope is an indicator of the overall data quality including the imaging conditions and processing steps. ResLog plots can also be used to optimize conditions for data collection and reconstruction parameters. Although resolution estimates can vary by method of calculation, ResLog-derived parameters are consistent whether calculated by Fourier shell correlation or Fourier neighbor correlation, or a new coordinate-based metric that serves as a yardstick for structures where atomic coordinates are available. ResLog plots could become part of a standard set of parameters to be included in 3D reconstruction reports.

Introduction

The field of three-dimensional electron microscopy is growing rapidly as the techniques are becoming increasingly mainstream. Along with this growth comes the need for reliable metrics for assessing the quality of the 3D reconstructions. The most widely accepted measurement of the quality of a 3D reconstruction is the resolution as estimated from the Fourier Shell Correlation (FSC) curve (Harauz and van Heel, 1986). The FSC curve is typically calculated by splitting a given single particle dataset into two halves, reconstructing the corresponding 3D volume, and calculating the correlation of Fourier coefficients of increasing spatial frequency shells. Resolution is then estimated by reporting the resolution at a point on the FSC curve, usually at FSC_0.5 or FSC_0.143 (Rosenthal and Henderson, 2003). The choice of FSC value has been exhaustively researched (Rosenthal and Henderson, 2003; Scheres and Chen, 2012; van Heel and Schatz, 2005), yet there is no clear consensus on what is the most accurate value to report. One source of controversy regarding FSC is that it is possible to produce a single particle refinement that converges on a 3D model with reasonable resolution but where the 3D model is completely artifactual. This problem arises from the fact that single particle refinements are strongly dependent on the ability to accurately classify particles relative to each other. This, in turn, depends on a variety of factors such as the initial model used for refinement, the shape of the molecule, the amount of noise in the data, etc. If the orientations of too many particles are inaccurately determined, this will distort the corresponding 3D reconstruction and can result in structures with artifactual features that could be interpreted as biologically relevant. What is needed is a metric that can be used to distinguish correct and incorrect 3D reconstructions.

One proposal for 3D reconstruction validation is the method of small angle tilts (Henderson et al., 2011; Rosenthal and Henderson, 2003). In this technique, two images are taken for every given particle: one of the untilted particle and one with the particle tilted 5-10°. The tilted and untilted particles are then aligned and classified separately. Their resulting respective Euler angles should be related by a simple geometric transformation that represents the imposed tilt. If they differ significantly from the expected value, this serves as a good indication that the resulting model is incorrect. There are usually at least a small number of outliers, representing particles that could not be accurately classified. There are three major difficulties with the small angle tilt method. The first is a bijective mapping must be defined between tilted and untilted particles. This often needs to be done manually which can be extremely time consuming. Secondly, beam-induced motion, which can be exaggerated with tilted images, can perturb particle orientation by several degrees (Brilot et al., 2012), confounding an attempt to assess quality through comparison of refined Euler angles to microscope tilt angles. Finally, since two images must be acquired, accumulated radiation damage can contribute to a decreased ability to align and classify the second image.

It has been shown that there is a linear dependence of spatial frequency (inverse resolution) on the logarithm of number of particles that go into a reconstruction (LeBarron et al., 2008; Rosenthal and Henderson, 2003; Stagg et al., 2008), a relationship that has been used to estimate the number of particles required for an atomic resolution reconstruction (LeBarron et al., 2008; Liao and Frank, 2010; Stagg et al., 2008). Here we show that the y-intercept of a plot of the log of the number of particles versus the spatial frequency corresponds to the average quality of the alignment of the particles and the slope of the plot corresponds to the overall quality of the data going into a reconstruction. We use the linear trend to compare subsets of particles that have been sampled for different EM or processing parameters. Finally we show that the value at the y-intercept can be used to distinguish correct from incorrect 3D reconstructions.

Results

We set out to determine the utility of plots of resolution vs. the log of number of particles (ResLog plots) in assessing the quality of 3D electron microscopy reconstructions. Our approach was to use samples that are well characterized and/or could be reconstructed to high-resolution to determine the parameters that contribute to the characteristic slope and y-intercepts of particular ResLog plots. To this end, we made ResLog plots of reconstructions of icosahedral adeno-associated virus DJ (AAV-DJ) (Lerch et al., 2012a) that we had previously determined to 4.5 Å resolution, AAV-DJ in complex with the disaccharide analog SOS (AAV-DJ/SOS) that was determined to 4.8 Å resolution (Xie et al., 2013), and GroEL (with D7 symmetry) that was determined to 6.4 Å at 120 keV and 7.0 Å at 300 keV. The ResLog plots were made by performing a 3D refinement with the full dataset of particles then randomly choosing subsets of particles and reconstructing a 3D volume using the previously determined Euler angles.

Resolution estimation by three different metrics produces similar ResLog plots

An accurate resolution measurement is a prerequisite for ResLog plots which are the foundation of our work. Resolution was calculated in a number of ways including FSC, Fourier neighbor correlation (Sousa and Grigorieff, 2007) (neither of which use atomic coordinates), and also by comparison to known x-ray structures. Use of the FSC curve has been controversial with several different threshold criteria proposed (Heel and Schatz, 2005). The spatial frequency at FSC_0.5 or FSC_0.143 are popular resolution metrics, with the caveat that the FSC curve itself can be shifted towards higher spatial frequencies due to artificial correlations in the noise spectrum, so called “noise bias” (Stewart and Grigorieff, 2004). Noise bias comes from correlated noise in the EM reconstructions; essentially due to alignment to noise instead of the features of individual particles. It is possible that increasing the number of particles in a single particle reconstruction might not necessarily increase the resolution of the resulting reconstruction, but instead might increase noise bias. The extent of noise bias depends strongly on the algorithms that are used for alignment, classification, and reconstruction and how they are used in a given refinement (Scheres and Chen, 2012; Stewart and Grigorieff, 2004). We used the same protocol for each of our reconstructions and expect them all to have similar levels of noise bias.

To assess the accuracy of our resolution measurement, we compared several different metrics for measuring the resolution of a reconstruction of the viral particle AAV-DJ (Lerch et al., 2012a). Resolution was estimated by FSC_0.143, FSC_0.5, and Fourier neighbor correlation at 0.5 and 0.143 as determined by the program Rmeasure (Sousa and Grigorieff, 2007) (Fig. 1A).

Fig. 1.

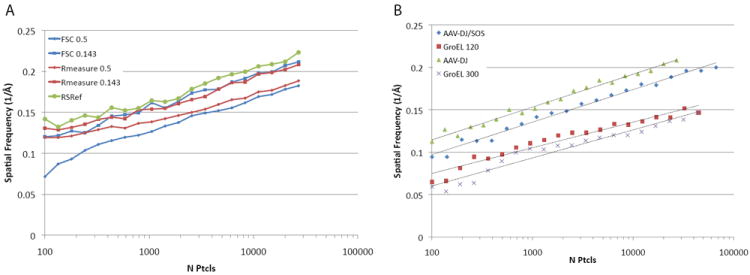
ResLog plots calculated using different resolution estimates and for different samples. A) Resolution estimated by AAV-DJ at FS_C0.5 and FSC_0.143 is compared against the Fourier neighbor correlation calculated by Rmeasure at 0.5 and 0.143, and using the resolution calculated by comparison against an atomic structure (RSRef). B) ResLog plots for four different samples: AAV-DJ, AAV-DJ/SOS, and GroEL all collected at 120 keV and GroEL collected at 300 keV.

Resolution was also estimated by a new approach that is possible in cases where an atomic model is also available. Density is calculated from the atomic coordinates, using a low-pass filter whose shape depends on a resolution parameter, d_c, that can be least-squares optimized for maximal agreement between the density of the reconstruction and atomic coordinates. The filter is a 5^th order (N=5) Butterworth function, giving a transfer function, H by which the Fourier transform of each atom’s scattering is multiplied. This, in turn, attenuates the high resolution signal which is a function of the reciprocal dimension in Fourier space (Chapman et al., 2013):

$$H(h)=1/\sqrt{1+{(h{d}_c)}^{2N}}$$ Equation 1

Here h is the reciprocal dimension in Fourier space, N controls the softness of the cutoff with a value of 5 used here and in other electron microscopy applications, and d_c is defined as in the signal processing field as the point where the power is halved (where H²/H₀² = 0.5). For closer compatibility with other electron microscopy measures of resolution, d_c is converted to d_0.5 quoted in this paper, where the amplitude drops to half, and is therefore more analogous to other measures of resolution in electron microscopy:

$$d_{0.5}=d_c/{(1/{0.5}^2-1)}^{1/2N}$$ Equation 2

There are important differences from the other measures of resolution. It is an estimate of where the raw signal falls, not of the signal-to-noise noise ratio. It is covariant with the envelope function – here it was estimated after correction of the map with EMBfactor (Fernández et al., 2008). It can be adversely affected by poor model quality or over-fitting if the coordinates have been flexibly fit into the reconstruction. The current resolution estimates were made using an unrefined homology model constructed from related crystal structures, but they differ little from those calculated with a model that had been flexibly fit into the EM reconstruction (Lerch et al., 2012b). Estimation using the homology model has a potential advantage over internal measures (FSC, Rmeasure), in that it represents bias-free cross-validation, because the atomic model and EM reconstruction have been obtained independently. To reiterate, no use was made of any atomic coordinates in obtaining the EM reconstruction, and by using an initial homology model rather than flexibly fit coordinates, the coordinates are not biased to the reconstruction. However, it is emphasized that even in the absence of bias, systematic differences compared to FSC and Rmeasure are expected, not only for the reasons discussed above, but because the new approach assesses resolution in real-space local to modeled atoms, excluding disordered components like solvent and nucleic acid (for a virus) that are averaged into a global reciprocal space measure. For ResLog assessment, it is not the absolute values that are important, but the change in resolution estimate with particle number. Nevertheless, high-consistency between the coordinate-derived estimate (hereafter called RSRef) and the FSC_0.143 and Rmeasure_0.143 attest to minimal noise bias in refinement of the AAV-DJ reconstruction (Fig. 1A).

ResLog plots of the AAV-DJ dataset with resolution estimates by FSC, Rmeasure and RSRef show that the plots are remarkably similar (Fig. 1A). ResLog plots for FSC_0.5, FSC_0.143, and RSRef are linear with the same slope and different y-intercepts. The Rmeasure plots match the FSC plots very closely past about 6,000 particles with a slight offset for the Rmeasure_0.5 plot. The offset at 0.5 is likely a consequence of the curve smoothing operation implemented in current versions of Rmeasure (Settembre et al., 2011). With fewer than 6,000 particles, the Rmeasure plots begin to diverge from linearity. This likely indicates that Rmeasure overestimates resolution below some threshold for noise at a given spatial frequency (Settembre et al., 2011). RSRef was used to generate resolution estimates that were free from known biases in the internal measures. While this might be considered an external gold-standard, it will be rare cases where an independently-derived atomic model will be available. High consistency between the ResLog plots calculated with different resolution estimators shows that, with care, either FSC or Rmeasure can satisfy the needs of ResLog just as well, when atomic coordinates are not available.

We next compared ResLog plots of different samples to determine if they all have linear trends and to determine if they have similar slopes and y-intercepts (Fig. 1B). The samples we compared were AAV-DJ, AAV-DJ bound to a disaccharide cofactor SOS (AAV-DJ/SOS), and GroEL. All the samples were collected at the same imaging conditions on the same microscope with the same camera: 120keV, 120,000x, on a Titan Krios. Additionally a second GroEL dataset was acquired with the same parameters except at 300keV. All the samples were processed identically with automated particle picking and CTF estimation in Appion (Lander et al., 2009). Initial particle alignment and classification were estimated by EMAN (Ludtke et al., 1999), and the resulting Euler angles were subsequently refined in Fourier space with Frealign (Grigorieff, 2007). ResLog plots of these samples were all linear but their slopes and y-intercepts differed. The two AAV samples had nearly identical slopes but AAV-DJ/SOS was shifted towards lower spatial frequencies. The 120keV GroEL sample had a higher y-intercept but slightly lower slope compared to the 300keV GroEL sample. Factors that might account for the differences in the slopes and intercepts for the different samples were then investigated.

ResLog trend reflects 3D reconstruction quality

Since AAV-DJ was our highest resolution reconstruction, we focused on these data in order to determine the factors that influence the ResLog trend. First we perturbed defocus estimation, Euler angles, and particle centering to determine how inaccuracies in those factors affect the ResLog trend. In order to determine if changes in the ResLog plots were significant, confidence limits were established by repeating the ResLog analysis 20 times on the unperturbed particles with different random particle subsets each time (Fig. 2, red squares). The estimated defocus for the particles was then perturbed by adding a value drawn from a Gaussian distribution with a mean of 0 and a standard deviation of 300 nm. This lowered the slope of the ResLog plot while the y-intercept was nearly unchanged (Fig. 2A, blue diamonds). Conversely, when the Euler angles for 50% of the particles were scrambled, the slope was unchanged but the y-intercept was shifted to lower spatial frequency (Fig. 2A, green triangles). Similarly when the Euler angles were scrambled for 75% of the particles, the y-intercept was shifted even lower (Fig. 2A, orange circles) and nearly all of the recognizable features in the AAV structure were gone (Fig. 2E). Perturbing the centering of the particles while leaving the Euler angles unchanged resulted in changes to both the slope and the y-intercept (Fig. 2B). With small perturbations to the centering (mean perturbation of 0 pixels with standard deviation of 1 pixel) the largest effect was a decrease in the slope with a small change in the y-intercept. With larger changes (mean perturbation of 0 pixels with standard deviation of 3 pixels), there is a large change in both the slope and the y-intercept. A similar trend was observed when Euler angles were perturbed by 0.5°, 1.0°, and 2.0° (Fig. S1). Note, in all cases, the particles were not refined further after the perturbations. These results suggest that the y-intercept reflects how well the particles are classified (how accurately the Euler angles could be estimated), and the slope reflects how much the average particle contributes to the resulting reconstruction. In other words, reconstructions with particles that are accurately classified will have higher y-intercepts than those with poorly classified particles, and reconstructions with accurately classified particles and high-quality data will have higher slopes than reconstructions with accurately classified particles and lower-quality data (i.e. due to poor microscope beam coherence, low DQE detector, inaccurate CTF estimation, thick ice, etc). The precision with which Euler angles can be determined is also reflected in the ResLog slopes. As long as the Eulers are close to the correct value the y-intercepts will be relatively high, and more precisely determined Eulers will have higher slopes than less precisely determined Eulers (Fig. S1). The interpretation of the slope as a reflection of the overall reconstruction B factor has been suggested before (Liao and Frank, 2010; Rosenthal and Henderson, 2003), and we show empirical evidence for the influence of CTF estimation, centering, and Euler angle determination on the B factor.

Fig. 2.

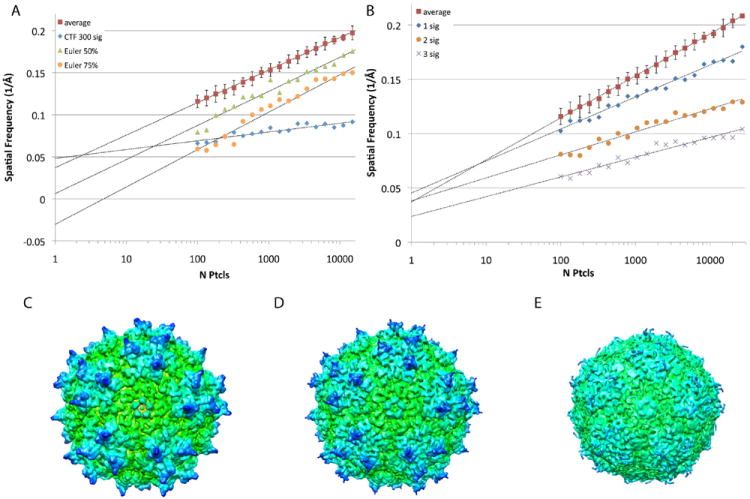
ResLog plots comparing the average ResLog trend (FSC_0.143) for AAV-DJ with samples with perturbed parameters. A) The ResLog plot for a reconstruction where the estimated defocus for the particles was perturbed randomly with a standard deviation of 300 nm (blue diamonds) had a lower slope than the unperturbed trend (red squares). The ResLog plots for a reconstructions with randomized Euler angles for 50% of the particles (green triangles) and 75% of the particles (orange circles) had similar slopes but lower y-intercepts compared to the unperturbed trend. B) ResLog plots for reconstructions where the particle origins had been perturbed randomly with a standard deviation of 1, 2, and 3 pixels had progressively lower slopes with increasing perturbation. C) Reconstruction of the unperturbed dataset filtered to 6.5 Å. D) Reconstruction (filtered to 6.5 Å) of the dataset where the Eulers for 50% of the particles were randomized. E) Reconstruction (filtered to 6.5 Å) of the dataset where the Eulers for 75% of the particles were randomized.

Shifting of the y-intercept towards lower spatial frequencies when the Eulers are perturbed suggests that it is an indicator of the average accuracy with which the particles in a given dataset can be aligned and classified. This led to the hypothesis that the ResLog trend could be used to distinguish correct models (models with accurate Euler angles for a substantial number of the particles) from incorrect models (models where the majority of the particles are not accurately aligned relative to each other). To test this, we randomized the Euler angles of the GroEL 120keV and the AAV-DJ datasets and classified the particles against incorrect initial models. With the GroEL dataset, we performed two different refinements because our first attempt converged back onto the correct structure. The incorrect refinements converged on ~9 Å (FSC_0.143) models that could be considered plausible in the absence of other information about the structure (Fig. 3). ResLog plots for the incorrect models showed the typical linear trend with greater than ~500 particles but deviated from linearity with fewer than 500 particles. The y-intercepts for the linear portion of the curve were substantially lower for the incorrect models compared to the correct models suggesting that the ResLog trend can be an empirical metric for determining whether a given 3D reconstruction is correct or results from grossly misaligned particles.

Fig. 3.

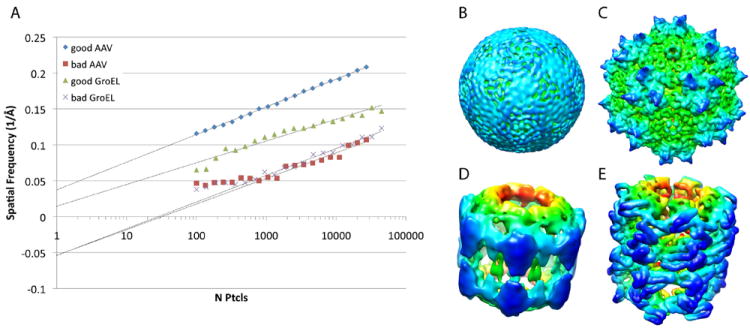
Comparison of correct and incorrect reconstructions. A) ResLog plots (FSC_0.143) for correct and incorrect reconstructions of AAV-DJ and GroEL. The ResLog trend for the incorrect reconstructions was fit based on the linear portion of the curve. B) Incorrect AAV-DJ reconstruction at 9 Å resolution by FSC_0.143. C) Correct AAV-DJ reconstruction at 9 Å by FSC_0.143. D) Incorrect GroEL reconstruction at 9 Å by FSC_0.143 E) Correct GroEL reconstruction at 9 Å by FSC_0.143.

Optimization of parameters by comparison to the ResLog trend

The optimal set of parameters for cryo-EM data collection and processing are sample dependent. For instance, two of the microscope parameters that most affect sample contrast are dose and defocus. Samples with doses greater than 1-5 e^-/Ų show beam-induced damage (Glaeser and Taylor, 1978), and samples collected with high defocus have been correlated with higher B-factors (Saad et al., 2001). On the other hand, limiting dose and defocus leads to increased noise and reduced contrast, both of which are critical for accurate particle alignment. There are many other such factors that can influence the quality of a reconstruction, and in any given dataset and refinement, there will be some number of particles with poor image quality and/or that were misclassified (i.e. have incorrect Euler angles). We hypothesized that these lower quality particles would correlate with microscope settings and refinement parameters.

Thus, we split the AAV-DJ dataset into multiple subsets based on microscope and refinement parameters in order to determine the optimal set of parameters for that dataset. Since resolution is dependent on the number of particles that go into a reconstruction, we compared the resolutions of each subset against the ResLog trend to determine if particular subsets were better or worse than the average randomly sampled subset of N particles.

Particles were split into subsets based on data collection or processing parameters and their corresponding reconstructions were compared against the average ResLog trend (Fig. 4). Subsets were judged to be significantly different from the average if their resolution values were more than 2 standard deviations away from the average of the 20 randomly sampled subsets with similar numbers of particles. Metadata directed subsets were generated in a number of ways: splitting by defocus, the grid square from which they were collected, confidence of CTF estimation, and other types of metadata. Since all of the metadata could not be reported in one graph, the results are shown in panels Figure 4 with 2 sets of metadata per graph. Subsets of particles that were 2 standard deviations away from the randomly sampled subsets are highlighted with their metadata ranges.

Fig. 4.

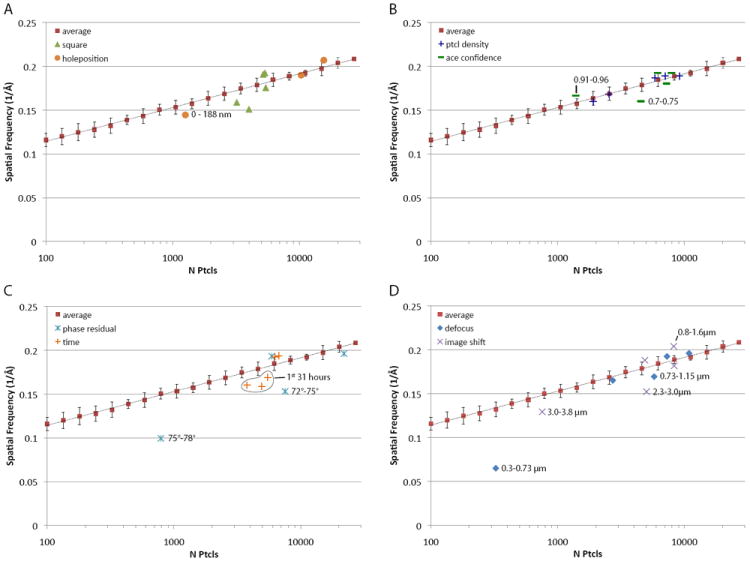
ResLog plots (FSC_0.143) comparing metadata directed subsets of particles against the average of randomly selected subsets. Samples that are outside of 2 standard deviations from the mean of the randomly sampled data are highlighted with their metadata range. A) Particles sampled by the grid square from which they derived (green triangles) and particles sampled by their position with respect to the center of the hole where they were located (orange circles). B) Particles sampled by particle density in the hole where they were located (blue crosses), and particles sampled by the confidence of the CTF estimation (green dashes). C) Particles sampled by their respective phase residual in the Frealign refinement (cyan stars), particles sampled by the time of day in which they were collected (orange crosses). D) Particles sampled by their estimated defocus (blue diamonds), and particles sampled by the image shift of the microscope while they were collected (magenta xs).

Previous observations suggested that factors like ice thickness, carbon thickness, and proximity to the edges of holes can influence the relative amounts of beam induced movement (Brilot et al., 2012; Glaeser et al., 2011). These factors are interdependent to some degree, so one cannot predict a priori what particles have the least movement. We split particles into subsets based on their proximity to the center of holes. This showed that the resolution of a reconstruction of particles in the subset that were 0-188 nm from the center of the 2000 nm diameter holes had significantly worse resolution than the average (Fig. 4A, orange circles) while those that were closer to the edges were indistinguishable from the average trend. It is likely that the particles closer to the edges of holes had less beam-induced movement perhaps because the ice was thicker in those areas.

Subsets were made of particles from the 5 different squares in which data were collected. Two of the subsets were significantly worse than the average (Fig. 4A, green triangles) for reasons that are not apparent. All 5 squares were from similar areas of the grid and had similar ice thicknesses (Fig. S2). One of the two had a crack in the carbon, but that area was excluded during hole picking; and the other subpar square had no apparent cracks. Moreover one of the better squares had many cracks (Fig. S2B). It is possible that the two subpar squares had high beam-induced motion perhaps due to poor adherence of the carbon film to the copper grid in those regions.

We used automatic CTF estimation with ACE (Mallick et al., 2005) to determine the defocus of micrographs. After estimating defocus, ACE reports a confidence value in the range 0-1 with higher numbers representing more accurate estimates of defocus. Particles were sorted into 5 subsets based on ACE confidence. The subset with the lowest confidence (0.7-0.75) was significantly worse than the average, and the subset with the highest confidence (0.9-0.96) was significantly better than the average (Fig. 4B, green dashes). This indicates that: 1) the ACE confidence value is a good indicator of the accuracy of defocus estimation, and 2) if particles are eliminated based on ACE confidence, one should balance the number of particles included in the reconstruction against degradation due to poor defocus estimation.

We hypothesized that the total number of particles per micrograph (the particle density) would affect the average particle quality: too few particles, and defocus estimation might be poor; too high and neighboring particles could cause misclassification. Surprisingly, sets binned by the number of particles per micrograph showed no significant differences from the average trend (Fig. 4B, blue crosses). It is noted, however, that this parameter is likely sample dependent as viral particles are easily centered and might be less susceptible than other samples to the effects of neighboring particles.

Phase residual is typically the metric by which particles are included or discarded in a Frealign reconstruction, where the cutoff to use is arbitrarily determined by the user. When split by phase residual, subsets with the highest phase residuals 75-78° and 72-75° were significantly worse than the average particles (Fig. 4C, light blue stars). Particles with phase residuals of 69-72° and 66-69° were slightly worse and slightly better than average respectively.

The quality of cryo-EM data collected over time tends to degrade due to ice contamination and other factors (Cheng et al., 2006). We split particles into 5 time-subsets beginning with the time from the start of data collection with the expectation that the first subsets would be better than the last. On the contrary, subsets from the first 31 hours of data collection were significantly worse than those from the last 21 hours (Fig. 4C, orange crosses). This result correlates with the time of acquisition of the worse-than-average squares described above since the two worse squares were the first acquired. It should be noted that this parameter is strongly microscope specific as the Titan Krios has an extremely low contamination rate relative to side entry microscopes, so the square-to-square variation might be the dominant factor in this case.

Particles were split into subsets by their estimated defocus value to determine the optimal range for single particle reconstruction. The range of defoci had a dramatic effect on the resolution of the particle subsets. Particles with defoci in the range 0.3-0.73 μm were 10 standard deviations worse than average (Fig. 4D, blue diamonds). Quality improved until defocus exceeded 1.15 μm defocus, whereupon no further differences were detected (Fig. 4D). Interestingly, particles with defocus as high as 2.0-2.4 μm showed no significant differences from the average. Other studies have suggested that high defocus is associated with a higher B-factor for individual images (Saad et al., 2001). However, this does not take alignment and classification into account. Our results demonstrate that particles with the lowest defocus were the worst in our dataset, and particles with the highest defocus were equivalent to the average randomly sampled particle.

The image shift value of the microscope is known to introduce off-axis coma in the corresponding images (Glaeser et al., 2011). The closer the images are taken to the coma-free axis, the more likely they are to be free from such aberration. Leginon, the automated software that we used to collect the data, navigates to the final acquisition target by image shift (Suloway et al., 2005). The magnitude of the image shift is dependent on how well the holes could be targeted by goniometer movements. The majority of the data have a range of image shift less than 2 μm, but some of the data have image shift as great as 4 μm. When split by image shift, subsets with 2.3-3.0 μm and 3.0-3.8 μm shift were significantly worse than the average (Fig. 4D, purple xs). Particles with 0.8-1.6 μm of image shift were significantly better than average, while particles with 1.6-2.3 μm image shift were indistinguishable from the average.

The particles that were significantly worse than average in the preceding analyses were eliminated, and the remaining particles were combined. ResLog analysis was then performed on the resulting set of exemplar particles (Fig. 5A). The ResLog trend for these particles was significantly better than the randomly selected particles with a slightly higher slope and substantially higher y-intercept. The map for the full exemplar set at 4.7 Å (Fig. 5C) was then compared to the map with all particles included at 4.5 Å (Fig. 5B), and the map for an equivalent number of randomly selected particles at 5.2 Å (Fig. 5D). The density in the exemplar map is more clearly resolved and has more connected densities along the peptide backbone than the randomly selected particles, but it is less detailed than when all particles are included. This indicates that elimination of suboptimal particles can improve the quality of a 3D reconstruction, but the suboptimal particles still contribute to a high quality reconstruction if enough of them are included.

Fig. 5.

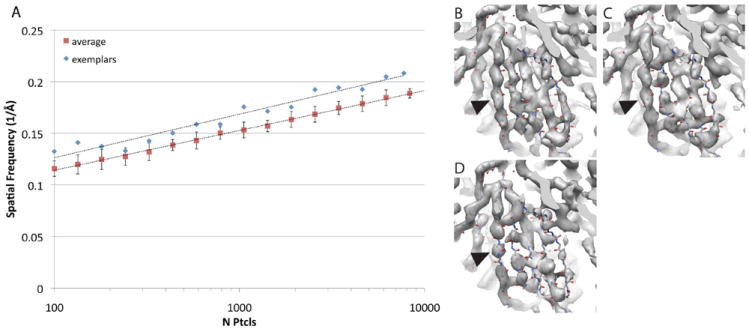
Comparison of exemplar AAV-DJ particles with randomly selected particles. A) ResLog plots (FSC_0.143) of particles with subpar particles removed (blue diamonds) compared to randomly removed particles (red squares). B) 4.5 Å resolution reconstruction from 29,024 particles. C) 4.7 Å reconstruction from 7727 exemplar particles. D) 5.2 Å reconstruction from 8313 randomly selected particles. All reconstructions are shown at the same contour level (5.4σ) together with a fitted atomic structure. Arrow heads indicate a region where the density is continuous for the 4.5 Å and 4.7 Å structure but discontinuous for the 5.2 Å structure.

Exemplar particles were similarly identified for the AAV-DJ/SOS dataset, and ResLog analysis was performed with both randomly selected and exemplar particles (Fig. S3). Again, the ResLog trend was substantially better for the exemplar particles with a slightly higher slope and substantially higher y-intercept compared to the randomly selected particles. This result compares favorably with the AAV-DJ optimization. Of note, the optimized AAV-DJ/SOS produced a reconstruction with the same resolution (4.8 Å) as when all the particles were included but with 1/3 of the particles.

Discussion

Here we have shown that ResLog trends are valuable for assessing the quality of single particle reconstructions, distinguishing correct from incorrect reconstructions, and for comparing subsets of particles. Unlike X-ray crystallography, the field of 3DEM has relatively few metrics for assessing the quality of 3D reconstructions. In some instances, the structures of the same complexes have been determined by different labs and have showed very different results (Jiang et al., 2002; Sato et al., 2004; Serysheva et al., 2003). New metrics such as the ResLog trend that report on the quality of EM reconstructions can help distinguish between such models. We suggest that analysis and reporting of ResLog trends could become a standard analysis that single particle reconstructions could include in their publications.

FSC is an excellent measure of the potential resolution of a reconstruction. However, as we and others have shown, artifacts due to noise bias (Scheres and Chen, 2012; Stewart and Grigorieff, 2004) and incorrect starting models can cause the FSC to report artifactual values for resolution. FSC alone is insufficient to assess the quality of a 3D reconstruction. There are numerous advantages of reporting ResLog trends as a metric of reconstruction quality. They are extremely easy to perform, can fit into any of the current 3D reconstruction workflows, and unlike the small angle tilt technique, require no additional data collection. Additionally, we have shown that the ResLog trend can distinguish correct from incorrect reconstructions. Our work has shown that a substantially negative y-intercept can help identify grossly incorrect reconstructions that might have other reconstruction metrics within acceptable bounds. At this point, it is unclear what an acceptable y-intercept value should be. It is clear that lower values are indicative of inaccuracies in particle classification, but as Henderson et al (Henderson et al., 2011) and others have shown, a substantial number of particles can be misclassified and the resulting reconstruction can still be accurately interpreted (Fig. 2). However, at some point the misclassified particles will overwhelm the correctly classified particles (Fig. 3). The ResLog trend can help identify 3D reconstructions that can be interpreted from those where artifacts overwhelm real features.

A quantitative mathematical description of the physical basis of the ResLog trend is not available. Nonetheless, qualitatively, one can induce that shifting a ResLog plot to the right is the same as lowering the y-intercept. This is essentially what happens when misclassified particles are added to a reconstruction. The misclassified particles do not contribute coherently to a reconstruction and in effect add particles without adding resolution. We interpret the slope of the ResLog plot as a reflection of the data quality and the precision with which particles can be classified. As long as particles can be correctly classified, higher quality data will have higher slopes than lower quality data. Likewise, accurately and precisely classified particles will give rise to higher slopes than accurately but imprecisely classified particles (Fig. S1). While there are any number of factors that can affect data quality, the advent of high DQE direct electron detectors that can track beam induced motion will almost certainly produce ResLog plots with substantially higher slopes than the data shown here. As ResLog analysis is applied increasingly, it is anticipated that a finer appreciation will build of what ResLog values are indicative of the threshold between interpretable and uninterpretable reconstructions. Of particular interest will be to compare the ResLog trends of asymmetric particles with those of the symmetrical particles shown here.

The interpretation of ResLog y-intercepts as an indication of classification accuracy and ResLog slopes as data quality is supported by ResLog plots of the four different samples on which we collected data. Viral particles are large, highly symmetrical, rigid, and have many features on which to align. One would expect that these would be the easiest to align, and indeed, these two datasets have the highest y-intercepts in our analysis. The slopes of the two datasets are also similar, which is unsurprising given that they were processed in the same way. The AAV-DJ dataset has a higher y-intercept than AAV-DJ/SOS. This is likely due to heterogeneous binding of SOS in the AAV-DJ/SOS dataset as complete SOS saturation could not be achieved with that sample. Incomplete occupancy likely causes some fraction of the particles to be misclassified.

Likewise, the two GroEL datasets have reduced y-intercepts compared to the viral particles. This is likely due to reduced relative alignability for this particle. Compared to AAV, GroEL is smaller and has a flexible apical domain. Both of these features likely contribute to particle misalignment. Furthermore the GroEL dataset at 300 keV has a reduced y-intercept compared to the 120 keV dataset. This is likely because the 300 keV particles have reduced low frequency contrast compared to the 120 keV particles due to poor performance of the CCD detector at 300 keV (Booth et al., 2006; Stagg et al., 2008). The lower slopes of the GroEL compared to the AAV datasets may be an indication of heterogeneity.

We have shown that ResLog plots can be used to compare subsets of particles in order to find the optimal parameters for cryo-EM data collection and reconstruction. The typical parameters for collecting cryo-EM data were determined by observation of diffraction spots on 2D crystals or by theoretical considerations (Glaeser and Taylor, 1978). Now we have the ability to optimize parameters not just for reciprocal space resolution for 2D images, but for those parameters that also produce the best alignment and classification and yield the best 3D reconstruction. For instance, with the defocus parameter, images taken closer to focus contain more high-resolution information. On the other hand close-to-focus images have less low frequency contrast than higher defocus images, which makes accurate classification more difficult. Even if the close-to-focus particles can be accurately classified, it may not be possible to accurately estimate the defocus, which is required for a high-resolution reconstruction. Moreover, one needs to optimize microscope and refinement parameters for each different type of sample. For instance, optimal dose, defocus, ice thickness, hole position, etc for viral particles are likely different than those for a smaller less symmetrical particle such as the spliceosome or ribosome. Additionally, the variables shown in Fig. 4 are not necessarily mutually orthogonal; i.e. they are likely all coupled to various degrees, but ResLog plots allow one to individually vary parameters and quantify the integrated impact on the quality of the overall reconstruction.

Our results suggest that the most important parameter for increasing the resolution of a 3D reconstruction is the number of particles. In our analyses there is no single subset of particles with a particular collection of processing parameters that has higher resolution than when all particles are included (Fig. 5B). However, the optimization information is very useful in directing data collection. For instance, if during data collection, the suboptimal parameters we determined here were avoided, the ultimate resolution of that resulting reconstruction would likely be better. In the future, it would be desirable to perform ResLog analysis on-the-fly, so that parameters varied in the early stages of data collection could be optimized using the partial data and fed back to the experiment to ensure that the data collection continues under optimal conditions for a given specimen.

Materials and Methods

Data collection and processing

Data were collected on an FEI Titan Krios equipped with a 4k × 4k pixel Gatan Ultrascan CCD camera. All data were collected at a nominal magnification of 120,000 X (corresponding to a pixel size of 0.65 Å/pixel) using Leginon (Suloway et al., 2005) with a dose of 15 e^-/Ų, and a range of nominal defocus from -0.8 to -3.0 μm. The AAV datasets were collected at 120 keV. One GroEL data set was collected at 120 keV and the other was collected at 300 keV. Data from different samples were processed as similarly as possible to each other using Appion (Lander et al., 2009). Particles were picked automatically using template matching. CTFs were estimated with ACE (Mallick et al., 2005). Euler angles were initially estimated using EMAN (Ludtke et al., 1999). Initial models were derived from the data themselves using EMAN’s starticos program for the viruses and startcsym for GroEL. The initial models were refined for a few rounds in EMAN and the resulting Euler angles were then were converted to the Frealign convention. Frealign (Grigorieff, 2007) was then used to refine the structures to convergence. The reconstructions were corrected for CTF phase flips and amplitude modulation. An inverse B-factor was applied to the volumes using EMBFactor (Fernández et al., 2008) after the refinement was completed. For the AAV-DJ dataset (Lerch et al., 2012a), 36,280 particles were collected in total, and 27,312 contributed to the 4.5Å final structure. For the AAV-SOS dataset (Xie et al., 2013), 94,123 particles were collected in total, and 70,725 contributed to the 4.8 Å final structure. For the GroEL 120 keV dataset, 61,704 particles were collected in total, and 49,476 contributed to the 6.4 Å final structure. For the GroEL 300 keV dataset, 60202 particles were collected in total, and 45,189 contributed to the 6.9 Å final structure. For the AAV-DJ data with a box size of 360 pixels, individual reconstructions took 5 hours to compute on a single 8 core computer.

Coordinate-based resolution estimate

The published atomic structure of AAV-DJ (Lerch et al., 2012b) had been refined against the cryo-EM reconstruction used here, using a flexible fitting procedure (Chapman et al., 2013). For the purposes of using an atomic model to estimate EM resolution, we were concerned that such a model might have been over-fit and become biased towards the EM reconstruction.

Thus, for the work described in this paper, instead of the published model, we used an unrefined homology model (described below) that had been obtained independently of the EM. (In retrospect, we found that the refined atomic structure gave similar ResLog plots, but it is the results with the homology model, free of the potential biases, that are presented.) The homology model was built from the crystal structures of AAV-2, -8 & -9 (DiMattia et al., 2012; Nam et al., 2007; Xie et al., 2002). AAV-DJ is the product of randomly shuffling elements of these three AAV variants (Grimm et al., 2008b). The homology model was constructed simply by merging the relevant parts of the superimposed serotype structures, then regularizing the stereochemistry where the constituent structures were spliced without any reference to the EM reconstruction.

The RSRef resolution estimate, d_0.5, comes from the refined resolution, d_c, of a low-pass filter (Equations 1 & 2) applied in the atomic density calculation (Chapman et al., 2013). It is optimized to minimize the least-squares differences between the density levels of the atomic model and the EM reconstruction, summed over grid points near atoms in an EM map that has been CTF and envelope-corrected. The map for the atomic model is calculated as the sum of densities from each atom, each a Fourier integral of electronic scattering factors from infinite to 4.5 Å resolution (the limit that had been imposed on the experimental reconstruction in EMBfactor sharpening (Fernández et al., 2008)), attenuated by the Butterworth low-pass filter (H(h)) in Equation 1. Grid points within 4.4 Å of any atom were used, and the contributions to overlapping density were considered for all atoms and icosahedrally-related symmetry equivalents up to a distance of 11 Å. The initial resolution estimate was set to 5.0 Å and refined to convergence, in all cases, within 5 cycles.

ResLog plots

ResLog plots were made by randomly rejecting particles from the final Frealign parameter file, with exponentially more particles rejected for each point on the plot. The sets of particles were then reconstructed and the resolution estimated using Fourier neighbor correlation (rmeasure), by the coordinate based metric described in the results, or by splitting into half-sets and calculating FSC curves. Individual reconstructions were calculated to the same resolution as the highest resolution as the reconstruction with all the particles. After resolution was calculated, plots were made of spatial frequency vs. the number of particles contributing to the reconstruction. Finally these points were fit to an exponential function of the form:

$$d=A\ln (N)⊣B$$

where d is the spatial frequency, N is the number of particles contributing to the reconstruction and A and B are constants.

The average AAV-DJ ResLog plot was made by repeating the ResLog analysis 20 times with randomly selected particles for each trial. For a subset of N particles, the average and standard deviation of the resolution of the 20 trials were calculated. The individual points in that ResLog plot show the average of the 20 trials. Subsets of particles that were chosen by their metadata parameters were judged to be significantly different than the average of the randomly selected particles if their resolution values were 2σ away from the average.

The plot with perturbed CTF was made by adding values to the estimated defocus where the values were drawn from a Gaussian distribution with a mean of 0 and a standard deviation of 300 nm. This simulated inaccuracy in the defocus estimation. The plots with randomized Euler angles were made by randomly choosing 50% or 75% of the included particles for a given point on the ResLog plot and randomizing their Euler angles. This simulated inaccurately classified particles. The plots with perturbed particle centering was made by shifting the particle origins by a number of pixels that was sampled from a Gaussian distribution with a mean of 0 and standard deviations of 1,2, and 3 pixels respectively for each of the individual plots. The plots with Euler angles perturbed by defined amounts were made by adding 0.5°, 1.0°, or 2.0° to one of the Euler angles for each of the particles.

Bad reconstructions

The bad reconstruction for AAV-DJ was made by randomizing the Euler angles, making a 3D reconstruction from the randomized Eulers, then performing a Frealign refinement against that model until convergence. The first attempt at a bad reconstruction of GroEL was made in the same way that AAV-DJ was. That refinement actually converged on the correct structure. We have observed that GroEL has a false minimum in 3D refinement where the top views are aligned but the side views are classified 90° from their proper position. Therefore, we turned our initial model 90° so that the 7 fold axis was lying where the 2 fold axis should be thereby causing the symmetry of the model to disagree with the symmetry imposed by the refinement. Then we refined the Euler angles to convergence with Frealign.

Subsets of particles split by metadata

The subsets of particles split by metadata were made by querying the Appion/Leginon database. Leginon and Appion record microscope and processing parameters for every particle in a refinement. The database was queried for the different parameters: image shift, time, defocus, etc., and subsets were made by dividing the particles into different bins by their metadata values. For instance, ACE confidence values ranged from 0.7-0.96 with a mean value of 0.84. The particles were split into 5 evenly spaced bins based on the ACE confidence (0.70-0.75, 0.75-0.80, 0.8-0.86, 0.86-0.91, 0.91-0.96). Subsets were made similarly for the other parameters.

Supplementary Material

01

Fig. S1 ResLog plots comparing the average ResLog trend (FSC_0.143) for AAV-DJ with samples with perturbed Euler angles. The Euler angles for each particle were perturbed by 0.5°, 1.0°, and 2° and ResLog plots were made for the resulting reconstructions.

02

Fig. S2. Images of the squares from which the data were acquired for the AAV-DJ data. A) Three squares that were indistinguishable from the average ResLog trend (Fig 4A). B) Two squares that were significantly different from the average.

03

Fig. S3. Comparison of exemplar AAV-DJ/SOS particles with randomly selected particles. A) ResLog plots of particles with subpar particles removed (blue diamonds) compared to randomly removed particles (red squares). B) 4.8 Å resolution reconstruction from 70,725 particles. C) 4.8 Å reconstruction from 20,580 exemplar particles. All reconstructions are shown at the same contour level (5.4σ). The regions shown in B) and C) are the same shown in Fig. 5.