Abstract
Acoustically-induced vibrations of the Tympanic Membrane (TM) play a primary role in the hearing process, in that these motions are the initial mechanical response of the ear to airborne sound. Characterization of the shape and 3D displacement patterns of the TM is a crucial step to a better understanding of the complicated mechanics of sound reception by the ear. In this paper, shape and sound-induced 3D displacements of the TM in cadaveric chinchillas are measured by a lensless Dual-Wavelength Digital Holography system (DWDHS). The DWDHS consists of Laser Delivery (LD), Optical Head (OH), and Computing Platform (CP) subsystems. Shape measurements are performed in double-exposure mode and with the use of two wavelengths of a tunable laser while nanometer-scale displacements are measured along a single sensitivity direction and with a constant wavelength. In order to extract the three principal components of displacement in full-field-of-view, and taking into consideration the anatomical dimensions of the TM, we combine principles of thin-shell theory together with both, displacement measurements along the single sensitivity vector and TM surface shape. To computationally test this approach, Finite Element Methods (FEM) are applied to the study of artificial geometries.
Keywords: Digital Holography, Middle-ear Mechanics, Shape and 3D Displacement Measurements, Sound-induced Response, Thin-shell Theory, Tympanic Membrane
1. Introduction
The Tympanic Membrane (TM) is an essential part of the vertebrates’ middle-ear. Its function as an acousto-mechanical transformer greatly increases the sensitivity of the ear to sound (Tonndorf and Khanna 1971). Despite the importance of the TM, the relationship between its structure and its sound-reception function is not fully understood. Current methodologies for characterization of TM function in the laboratory and clinic have limitations: time-averaged holography is qualitative rather than quantitative, laser-Doppler vibrometry is usually limited to single-point (or a series of single-point) measurements of mobility, and most measurement techniques only measure displacements along a single direction. Furthermore, none of the current clinical tools for diagnosis of hearing losses measure the shape of the TM, and the question of how shape affects function is an open experimental question (Lu 2012).
The shape of the TM has been measured by different optical techniques (e.g., Moiré interferometry: Decraemer et al. 1991, Dirckx & Decreamer 1989, 2003; Fringe projection: Liang 2009). However, the temporal resolution and sensitivity of such three-dimensional shape measurements are usually not sufficient to also accurately measure the sound-induced motions of the TM. The lack of an accurate tool for simultaneous measurements of shape and 3D vibrations of TM has been problematic. Conventional methods to measure the full-field 3D displacements of TM need at least three illumination or observation directions to realize three sensitivity vectors. In this paper, a new technique is proposed to determine the full-field 3D displacement components of the TM based on its shape and only 1D displacement measurements (Lu 2012, Rosowski et al. 2013). The shape of the TM is measured by a lensless Dual-Wavelength Digital Holography System (DWDHS) that uses a tunable near-infrared laser. Concurrently, 1D displacement measurements of acoustically-induced motion of the TM are obtained by stroboscopic holography with a single laser wavelength and parallel illumination-observation recording geometry. Decomposing the shape’s normal vector at each point on the surface of the TM into three orthogonal axes, combining the shape information with the 1D displacement at each point on the surface of the TM, and taking advantage of thin-shell theory principles, allow determination of the full 3D displacement at each point on the surface of the TM. Therefore, a single, compact otoscope system, could determine both the shape and 3D acoustically-induced displacement components of the TM.
2. Theoretical considerations
2.1. TM as a thin-shell
The shape, planar dimensions, and thickness of the TM vary amongst various vertebrate species (Decraemer and Funnell 2008). For human TM, Uebo et al. (1988) measured mean thickness values between 50 and 150 μm in several TMs of humans of different age. Ruah et al. (1991) measured thicknesses at different regions of several TMs of humans aged between two days and 91 years. For adults, the following mean thicknesses were found: at the pars flaccida, 80 to 600 μm; at the pars tensa, posterosuperior 100 to 500 μm, posteroinferior 20 to 200 μm, anterosuperior 50 to 340 μm, anteroinferior 30 to 430 μm; and at the umbo 820 to 1700 μm. Decraemer and Funnell (2008) measured thickness of the TM of three different species including cats, gerbils, and humans by confocal microscopy. For cats, the measured thickness was 12.5 to 60 μm ; for gerbils, 7 to 70 μm ; and for humans, 115 to 145 μm. Aernouts et al. (2012) measured thickness of the human TM by confocal microscopy with variations between 97 and 110 μm.
Can we think of the TM as a thin shell? According to plates and shells theories, and specifically by considering Kirchhoff’s assumptions (Love 1888), a shell can be considered thin if
Displacement at any point of the shell is small compared with the thickness of the shell.
Displacement at any point on the surface of the membrane is perpendicular to the middle surface of the membrane and remains normal to it during and after deformation.
There is no displacement tangent to the surface of the membrane.
The material of the shell is considered to be elastic, homogeneous, and isotropic.
Novozhilov (1964) developed an engineering criterion that classifies a shell as thin if the following condition is satisfied:
| (1) |
with h being the thickness of the shell and R its radius of curvature. In all of the references cited in this paper, except areas around the manubrium where the membrane is thicker and does not meet Eq.1, this ratio is much smaller than 0.05, so that we hypothesize that the TM can be modeled as a thin-shell and this is the basis for our approach.
2.2. Shape measurements by Dual-wavelength digital holography
A two-wavelength holographic contouring technique is applied to generate depth contours related to the geometry of the TM. The technique is based on the utilization of a coherent polarized light source with wavelength tuning capabilities (Furlong 2000). The technique requires acquisition of a set of optical amplitude and phase information at wavelength λ1, the reference state, as well as acquisition of a second set of amplitude and phase information at wavelength λ2, the deformed state. Interferometric depth contours, related to the geometry of the TM under investigation, are generated by speckle phase correlation of two sets of phase-stepped speckle intensity patterns.
The phase difference of the two corresponding sets of data Δϕ is given by,
| (2) |
where ϕ1 is the phase of the optical path length recorded at the first wavelength λ1, ϕ2 is the phase of the optical path length recorded at the second wavelength λ2, and OPL is the optical path length defined as the distance from the illumination point to an object point and to an observation point and Λ is the synthetic wavelength given by
| (3) |
From Eq.3, it is clear that the smaller the difference between the two wavelengths used the larger the synthetic wavelength and, consequently, the smaller the optical phase difference.
In two-wavelength contouring, the phase difference, Δϕ, is a discontinuous wrapped function varying in the interval [−π, π], thus phase unwrapping algorithms are applied to obtain a continuous phase distribution called the fringe-locus function, Ω(x,y), for calculation of the relative height of each point on the surface of the object Z(x, y) with
| (4) |
If the angle between illumination and the observation directions, θ, is zero then the distance between two consecutive contour lines is
| (5) |
2.3. Full-field 3-Dimensional displacement measurements
Conventional methods for measurement of 3-Dimensional displacements of objects by holographic interferometry use at least three illumination points or three observation points to define three sensitivity vectors. In our case, a new method is being developed in which utilizing measurements of the one-dimensional sound-induced displacements along the optical (z) axis together with the 3D decompositions of the shape information into surface normal vectors, the displacements in the other two orthogonal directions are calculated. By combining the measured displacement along the z-axis, with x and y axes normal vectors, displacement maps of the motion magnitude along the x- and y-axes are computed. Figure 1 illustrates the applied algorithm that we use in our approach to compute 3D displacement maps.
Fig.1.
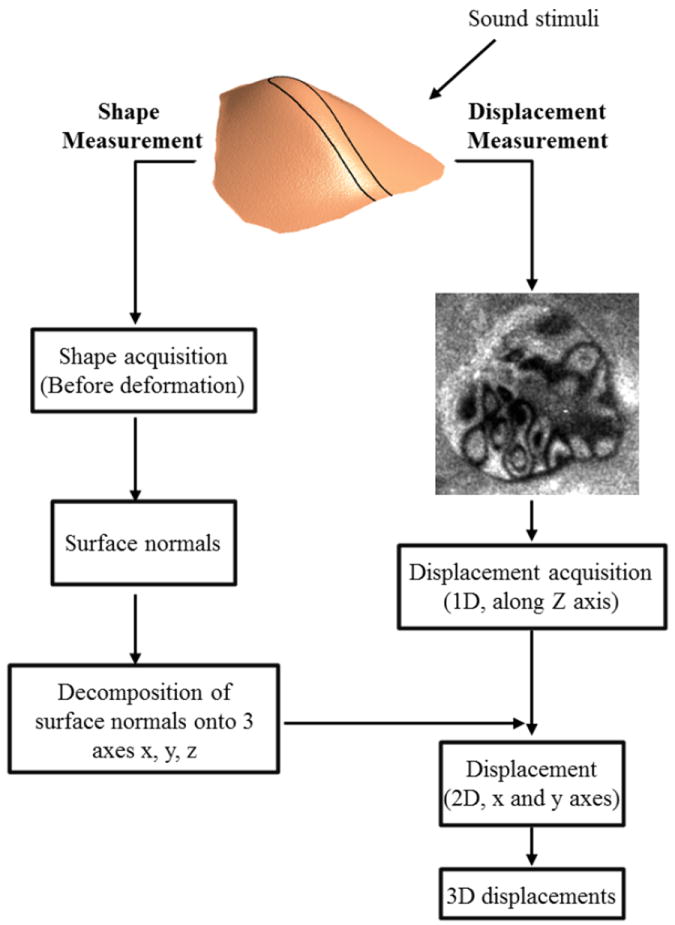
Algorithm used to extract 3D components of displacement by measurements of shape and one component of displacement.
Double-exposure stroboscopic mode is used for quantitative measurements of displacements between two loading states. In stroboscopic holography mode, the computed optical phase change, which is related to displacements by Eq.7, is based on the difference between measurements corresponding to two different stimulus phases, where the phases are defined by the pulsing of the ‘strobe switch’ (an Acousto-optic modulator capable of high-frequency switching) that is phase locked to the acoustic stimulus. In our measurements, the sinusoidal motion of the TM driven by a tone was determined from holograms of the TM that were gathered during ‘strobed’ laser pulse illumination at each of eight evenly spaced stimulus phases (Ø = 0, , , …, ). Each laser pulse has a duration of 5-10% of the period of the tonal stimulus. The result gives a difference between the two states in the form of a wrapped phase map. By considering our parallel illumination-observation experimental setup, only out-of-plane displacements along the optical axis can be measured. DWDHS records four images containing holographic patterns that result from the phase shifting of the reference beam (RB) in steps of multiples of , at both reference and deformed states. The intensities at each pixel measured by the camera at each of the four reference phase steps are I1,…,I4 in the reference state and in the deformed state. The optical phase difference between these two states is
| (6) |
which enables the measurements of out-of-plane displacement by
| (7) |
The hypothesis that the major components of acoustically induced displacements occur along the local surface normal of the TM, makes it possible to recover the two principal components of TM motion in the plane of the tympanic ring, and in a Cartesian coordinate system defined by the corresponding sensitivity vector, as shown in Fig.2. Specifically, single axis measurements, , together with the knowledge of shape normal vectors, , enable estimation of the two additional corresponding orthogonal components of displacement, and , with
| (8) |
| (9) |
Fig.2.
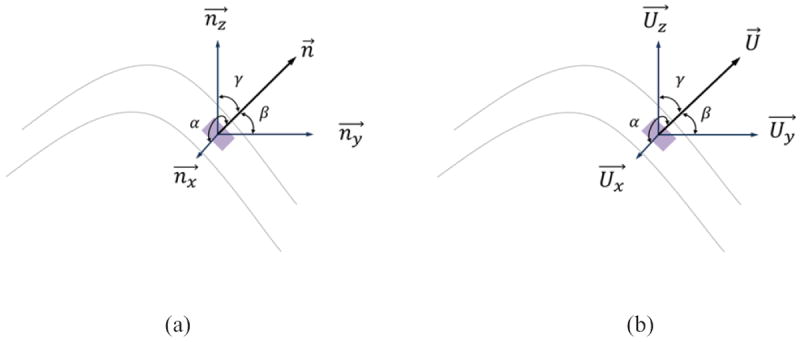
Decomposition of the surface normal vector and resultant displacement at one point: (a) is the surface normal vector and , and are decomposed components of along x, y and z axes; and (b) is the resultant displacement and , and are decomposed components of along x, y and z axes. α, β and γ are the angles between the direction of or and the x, y, z axes.
As illustrated in Fig.2, angles between displacement in x, y, z directions and the resultant displacement are the same as angles between the normal vectors in x, y, z directions and the normal vector.
2.4. Test of the proposed approach
In order to test our approach, an FEM modal analysis of an ideal semi-spherical membrane with physical properties similar to those of a TM is implemented and the results imported and processed in MATLAB. Figure 3 shows the test procedures while the geometry, mechanical properties, and modeling parameters incorporated into the FEA model analyses listed in Table 1.
Fig.3.
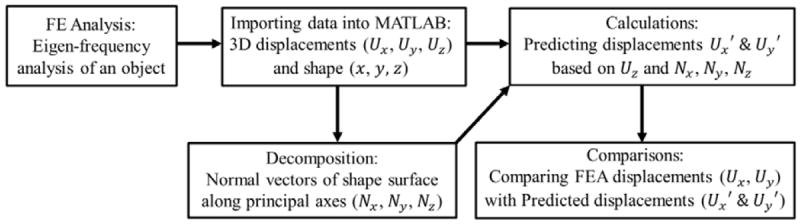
Procedure for testing our approach by FEM simulations.
Table 1.
Geometry, mechanical properties, and FEM parameters of the semi-spherical test object.
| Geometry | Mechanical properties | FEA parameters | |||
|---|---|---|---|---|---|
| Spherical radius | 2.5 mm | Young’s modulus | 115 GPa | No. of nodes | 15697 |
| Thickness | 17.8 μm | Poisson’s ratio | 0.33 | No. of elements | 7747 |
| Mass density | 8890 Kg/m3 | ||||
Boundary conditions: fully constrained along entire perimeter.
Outputs of the FEM modal analysis are the resultant displacement, as well as displacement along the x, y and z axes. By, for instance, taking the 4th mode of vibration for example, and by applying Eq.8 and Eq.9, the two additional displacements and are calculated and plotted in Fig.4.
Fig.4.
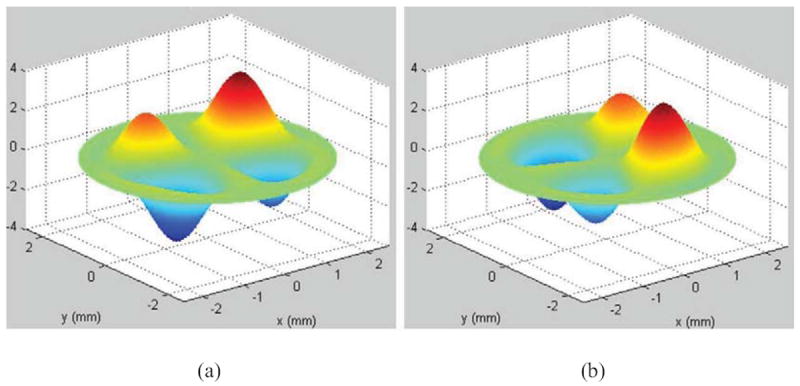
Computed x and y components of displacements obtained by applying our approach: (a) predicted displacement along x-axis ( ); and (b) predicted displacement along y-axis ( )
A significant criterion used in the testing of our approach is the computation of the differences between the displacements obtained from FEM analysis and the predicted components based on the thin-shell hypothesis. These differences are shown in Fig.5. Because of the nature of the eigenvectors provided by FEM, data from both FEM solutions and predictions are normalized.
Fig.5.
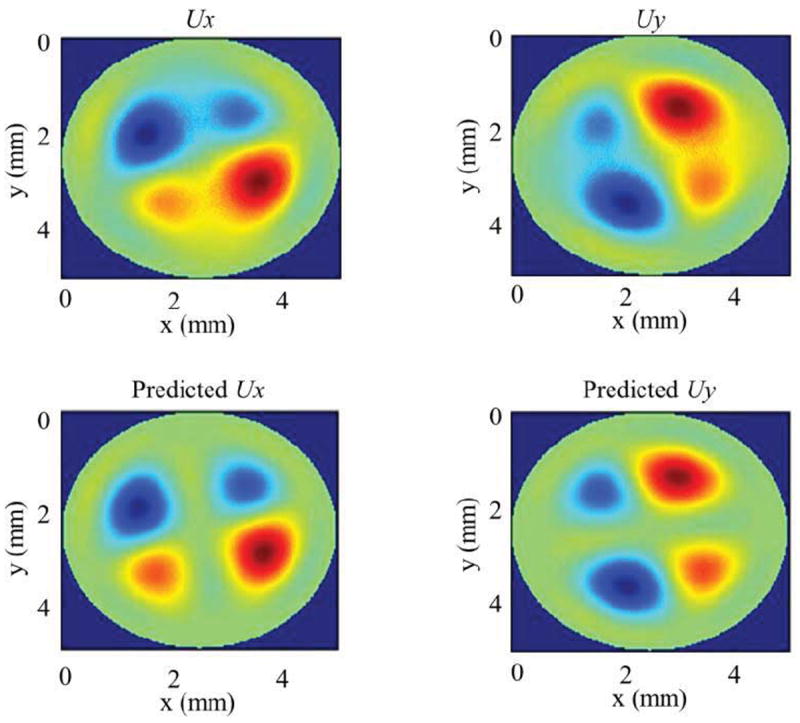
Comparisons of x and y components of displacements between FEM solutions (Ux and Uy) and predictions obtained by our approach after data normalization.
Table 2 shows the root mean square (RMS) and standard deviation (STD) of the differences between FEM and predicted displacements averaged over the surface for different modes of vibration after data normalization. The results show that the RMS difference and the standard deviation around the mean is less than 5%, which indicate that the predicted x and y displacement components obtained by our approach are well matched by the displacements obtained by FEM analysis.
Table 2.
RMS and STD of the difference between FEM solutions and predictions for different modes of vibration for the ideal semi-spherical test object.
| Difference | Mode 1 | Mode 2 | Mode 3 | Mode 4 | |
|---|---|---|---|---|---|
| x | RMS (%) | 3.08 | 3.52 | 3.18 | 0.71 |
| STD (%) | 3.10 | 4.18 | 2.91 | 0.90 | |
| y | RMS (%) | 3.11 | 3.38 | 3.52 | 0.71 |
| STD (%) | 3.12 | 3.07 | 4.30 | 0.91 | |
3. Experimental procedures
3.1. Digital opto-electronic holography system
The lensless Dual-wavelength Digital Holography System (DWDHS) consists of a Laser Delivery (LD), Optical Head (OH), and Computing Platform (CP) subsystems. The LD subsystem contains a tunable near-infrared diode laser in the range from 770nm to 789nm with central wavelength 779nm, an anamorphic prism pair, an acousto-optic modulator, a half-wave plate, and a fiber coupler assembly. The output of LD is delivered to the OH directly. The OH was designed using 3D optical ray tracing simulations in which selected components are rotated in specific angles to overcome reflection issues (TracePro 2012). A high-resolution digital camera with pixel size of 3.45μm by 3.45μm in OH is used for image recording at high-rates while the CP acquires and processes images in either time-averaged or double-exposure modes (Harrington et al. 2011). Figure 6 shows the major components of the DWDHS.
Fig.6.
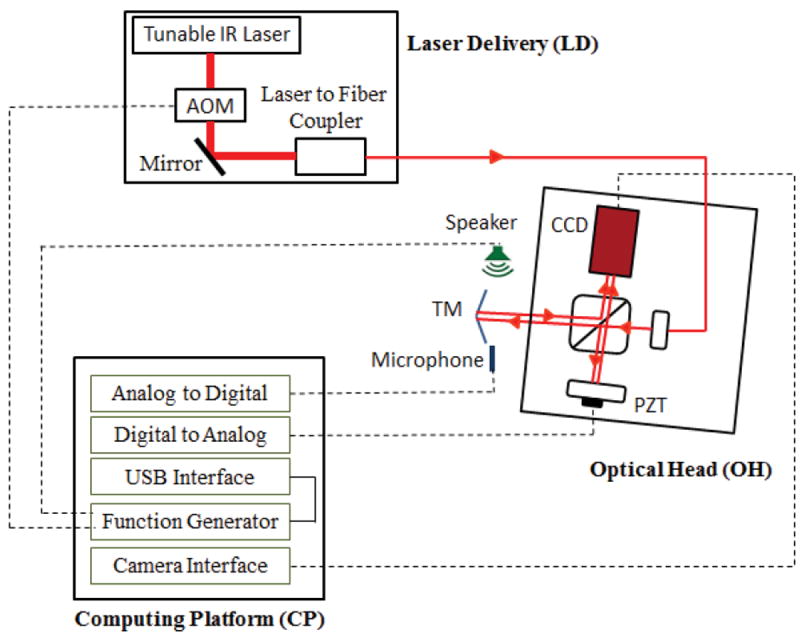
Schematic views of different subsystems of our DWDHS. Laser Delivery (LD) consists of an infrared tunable laser, acousto-optic modulator (AOM), mirror, and laser to fiber coupler; Optical Head (OH) which contains a modified Michelson interferometer; and Computing Platform (CP) to control the recording parameter such as sound-excitation level and frequency, phase shifting, synchronizations for stroboscopic measurements and all the acquisition parameters. The dashed lines are analog signal lines and digital control and sense lines.
3.2. Design of Optical Head (OH) subsystem
The OH subsystem is based on a Michelson optical configuration, shown in Fig.7. The input to the interferometer is a single mode polarization maintaining fiber terminated with an FC/APC connector that attaches to a collimator (C) producing a circular beam of 7.1 mm diameter. The collimated beam is directed to a non-polarizing broadband (700-1100 nm) beam splitter cube (BC) that splits the light into reference and object beams. A neutral density filter (NDF) and a linear polarizer (P) are embedded on the optical path of the reference beam to control the beam ratio; the ratio has an optimal value between 2 to 5 and depends on the reflectivity of the tested sample. NDF provides coarse adjustment and the P fine adjustment. There are no components in the optical path of the object beam, since we utilize lensless digital holographic methods. The reflected reference and object wavefronts are combined at the CCD sensor and a PZT is used for temporal phase shifting.
Fig.7.
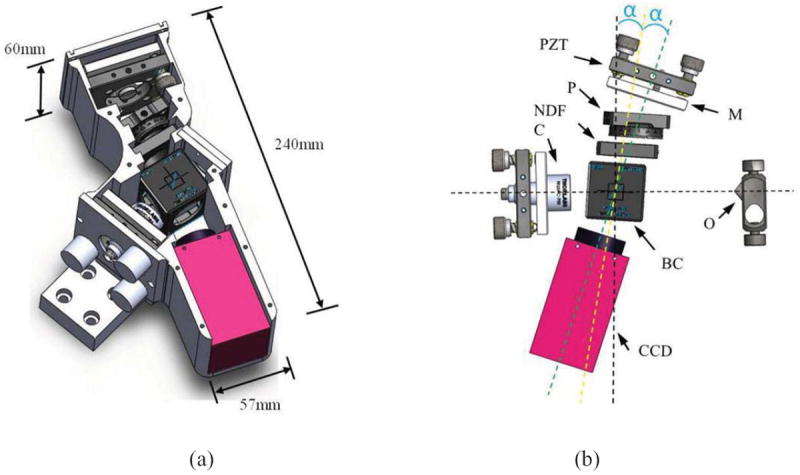
CAD models of the designed and implemented optical head: (a) assembled package showing characteristic dimensions; and (b) view showing its principal components. PZT: Piezoelectric Transducer, M: Mirror, P: Linear Polarizer, NDF: Neutral Density Filter, BC: Beam Splitter Cube, CCD: Digital Camera, C: Collimating lens with FC connector for optical fiber input, and O: Object.
In our initial OH configurations, we observed that the BC can introduce significant internal reflections that affect the quality of the reconstructed digital holograms. Therefore, the geometry of the interferometer was modified by applying rotations to some of the components within the optical path of the reference beam in order to identify a suitable optical configuration. In Fig.7, the original axis describing the location of all parts is shown by the vertical dotted line. The BC was rotated by an angle of α with respect to the vertical axis, and the mirror, M, and CCD camera were rotated by 2α in order to maintain the mirror and the camera parallel to each other. The angle α was changed from -18 to +18 in 2 degree increments. The resultant numerically reconstructed (Flores-Moreno et al. 2011, Furlong et al. 2013) digital holograms obtained after applying these rotations are shown in Fig.8. Selected images with interference fringes generated on a conical metal object for shape measurements are shown. Marks on the object were introduced to help numerical focusing of the object. While significant reflections degraded the holograms measured at α between +/- 18 degrees, good quality, low-reflection holograms were obtained at larger angles. By quantifying image intensity and contrast, it was determined that 14 degree was a suitable choice.
Fig.8.

Comparison of interferograms quality corresponding to different opto-mechanical configurations used during optimization of the OH by changing the incident angle of the BC. The configuration corresponding to 14 degree rotation was chosen in the final configuration.
3.3. Sound generation and measurement
In displacement measurement experiments, the TM is excited by a sound source. The sinusoidal output of the function generator was amplified by a unity gain power amplifier and used to drive a dynamic speaker coupled to an inverted horn. The narrow mouth of the horn was positioned about 8 cm away from the TM. A PCB Piezotronics (Depew, New York) pre-polarized ¼ inch microphone with a calibrated probe tube was positioned just at the edge of the TM to measure the sound pressure level. In the experiments sinusoidal sound stimuli varied in frequency from 414 to 10,000 Hz with levels between 70dB and 120dB SPL.
3.4. Sample preparation
The heads of chinchillas used in other physiological experiments were harvested from dead animals. The bilateral bullae were exposed and the bullar walls partially removed to expose the tympanic cavity. The cartilaginous ear canals were resected, and the bony external auditory canals were drilled away until at least 90% of the TM surface was visible (Rosowski et al. 2009, and 2013). When using laser imaging, it is essential that the surface upon which the beams are emitted is reflective enough to produce a good clean image. Due to the translucent nature of the TM, the surface of the membrane needs to be coated with a suitable material to increase the light reflection from the surface. While there are many chemical compounds that could be used to ‘paint’ the TM, most are unsuitable due to concerns and limitations regarding what is permissible for future use on the human TM (Goldish et al. 2010).
First, the coating must not be toxic, or cause any inflammation or irritation to the skin. Second, there must be a safe method for applying and removing the coating. Beyond health concerns, there are also concerns about what impact the coating will have on the results of the experiments. If the coating is too thick or too rigid, it may affect how the membrane vibrates, leading to incorrect measurements. Third, the coating needs to be highly reflective specifically within the wavelength region of the laser that is used during the experiments (780nm). Lastly, the coating needs to be evenly distributed on the membrane, as any large scale unevenness could alter the vibration patterns or the quality of the reflected light (Goldish et al. 2010). Based on the literature (Dirckx and Decraemer 1997) and the experience from physicians and researchers at the MEEI, zinc oxide (ZnO) was used as a paint. ZnO is commonly used in cosmetics is highly reflective and is soluble in weak acetic acid and easy removal from the membrane. Figure 9 shows a coated TM of a chinchilla subjected to the sound stimuli in a displacement measurement test.
Fig.9.
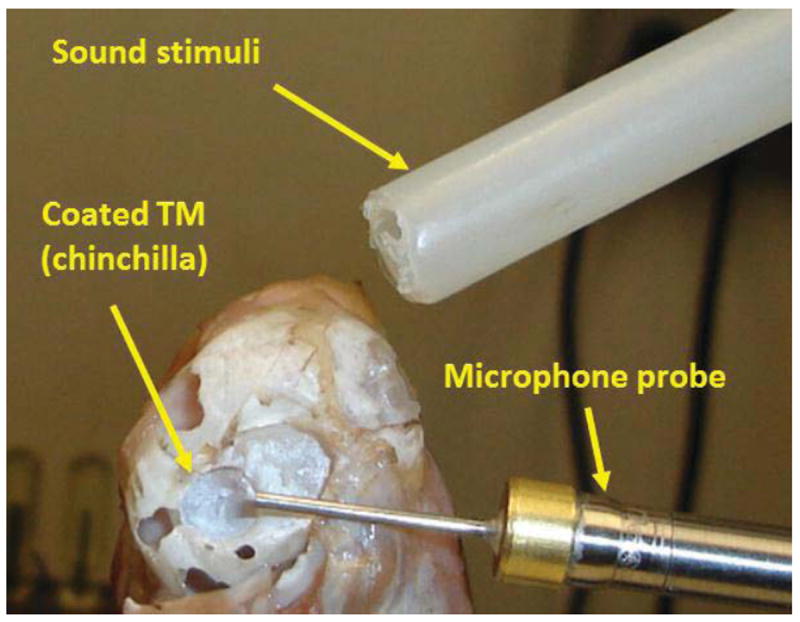
Chinchilla’s TM is coated with zinc oxide to increase light reflection. The TM is shown surrounded by the bone of the middle-ear wall. The placement of the tube conducting sound to the ear and the probe microphone are also illustrated.
4- Results
4.1. Shape and surface normal vectors
The shape of a chinchilla’s TM acquired by DWDHS and processed in MATLAB is shown in Figures 10 and 11. Figure 10 shows the masked and filtered wrapped optical phase of the shape of the TM obtained by dual-wavelength double exposure. In these experiments, the first exposure (reference state) obtained by a wavelength of 779.8 nm and the second one (deformed state) was captured at 780.2 nm. Applying Eq.3, the synthetic wavelength is 1.52 mm.
Fig.10.
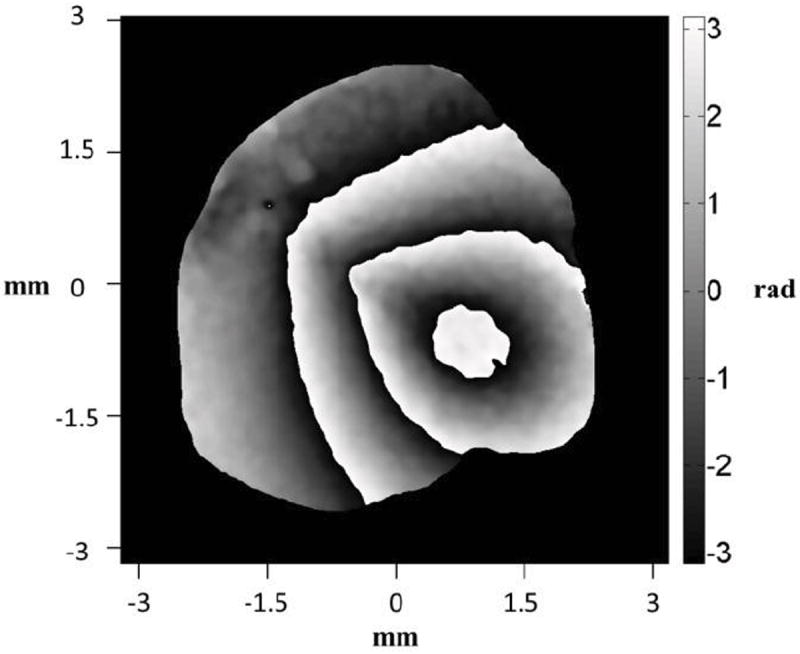
Masked and filtered wrapped optical phase of the shape of the TM, computed by lensless DWDHS (Rosowski et al. 2013).
Fig.11.
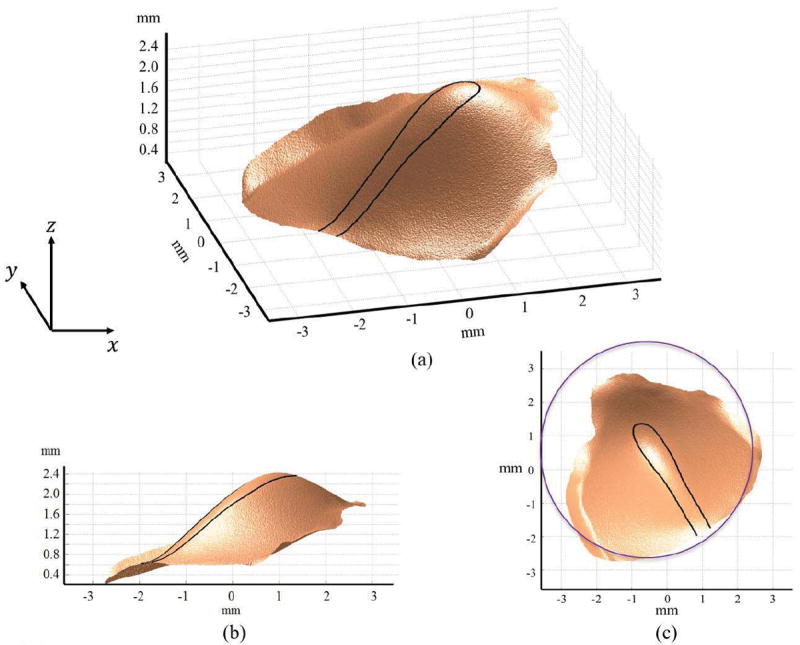
Measured shape of the TM of a chinchilla: (a) 3-Dimensional shape; (b) 2-Dimensional side view of the shape; and (c) 2-Dimensional top view of the shape; the outline of the entire tympanic ring is highlighted by a circle. The black outline shows the handle of the malleus (the manubrium). The umbo of the manubrium is at the apex of the TM cone.
Figure 11 shows the unwrapped scaled image of the optical phase that quantifies the shape of the lateral surface of the TM, where a ‘z’ value of 0 corresponds to the location of the bony rim that supports the TM and larger ‘z’ values code a deeper location within the ear. The outline of the handle of the malleus (the manubrium) embedded in the medial surface of the TM is also illustrated. The depth of the membrane (from the umbo to the rim) is about 2.4 mm and the diameter of the membrane is about 7mm. Because it is not possible to completely remove the bony canal that surrounds the TM, the image does not reconstruct the entire surface; this limitation is most severe at values of x ∈ (1:3) and y ∈ (−1: −3) which correspond to more ventral (inferior) portions of the TM.
The principal components of surface normal vector along three orthogonal axes are obtained by vector decomposition of the surface normal vector as shown in Figure 2.a. The results of this decomposition corresponding to the shape of the TM shown in Fig.11, are shown in Fig.12. Since the umbo is located at the apex of the TM cone, the surface at the umbo is nearly parallel to the TM ring and orthogonal to the observation direction that defines the z axis. Therefore, the normal vector at the umbo is dominated by its z-component (z-component near 1, and significantly small x and y components). Also note that cone-like shape of the TM and the near match between the z-projection and the axis of the cone yields z-components that are all positive, while the x- and y- components may be negative or positive depending on the spatial gradient of the membrane surface in x and y (Rosowski et al. 2013).
Fig.12.
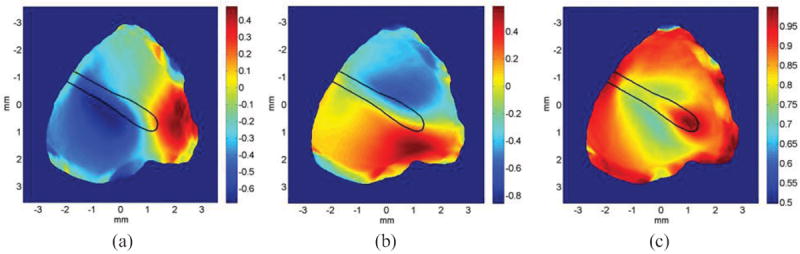
Principal components of surface normals along: (a) x-axis; (b) y-axis; and (c) z-axis (Rosowski et al. 2013). The black outline shows the handle of the malleus (the manubrium).
4.2. 1-D displacement measurements along one optical axis
Sinusoidal continuous sound stimuli were applied to the membrane and the displacements of the surface were recorded and computed at six frequencies of interest: 414Hz, 1,000Hz, 2,500Hz, 5,730Hz, 8,735Hz, and 10,000Hz with sound pressure levels between 100dB and 122dB SPL. The levels were selected to produce measurable sound-induced TM displacements.
Stroboscopic holography was used to measure TM motions. In stroboscopic holography, the acousto-optic modulator contained within the DWDHS, strobes the laser, so that the object and the CCD are illuminated by a series of brief pulses. Each pulse is 5-10% of the period of each cycle of the acoustic stimulus and within each camera frame the pulses are locked to a single phase of the stimulus cycle. Each camera image then represents the summed response to a large number of strobe impulses. To describe the variations in TM displacement with the phase of the stimulus, a holographic image (each calculated from four images with stepped optical phase of the reference beam) was gathered at each of eight stimulus phases of either 0°, 45°, 90° … 315° relative to the zero crossing of the sinusoidal voltage that drives the earphone (Cheng et al. 2010, Furlong et al. 2012).
Figure 13 shows out-of-plane (z-axis) displacements of the TM at different stimulus frequencies. The vibration patterns are categorized based on the sound excitation frequency. The vibrational pattern of 414 Hz is simple, which is characterized by one or two spatial maxima. The vibrational patterns of 1000 Hz and 2500 Hz are complex (Rosowski et al. 2009) characterized by multiple spatial maxima and minima separated by areas of small displacement. Above 4 kHz, the displacement patterns of chinchilla TM are ordered, characterized by many small areas of maximal displacement around the manubrium, with some order to the location of the maxima.
Fig.13.
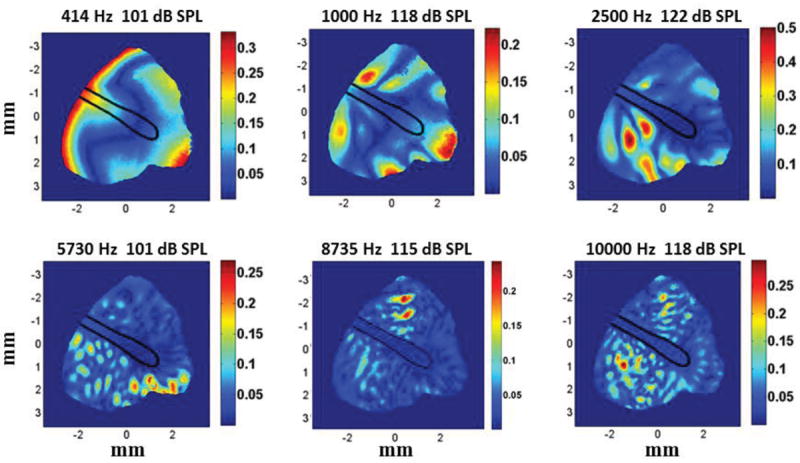
‘Out-of-plane’ or z–axis peak displacements measured at six different frequencies by DWDHS. Displacements are in the unit of μm (Rosowski et al. 2013).
4.3. Recovering the three components of displacement
By applying Eqs.8 and 9 and, the measured z-axis component of displacement (Uz), and taking advantage of the corresponding normal vectors extracted from the measured shape, the x-axis (Ux), y-axis (Uy) and resultant (Ures) components of displacement are calculated. To help identify the computed 3D components of displacement on the TM surface these displacements are overlaid on the measured 3D shape of the TM for one of the experiments in which a sound stimulus of 5,730Hz and 101 dB SPL sound level stimulates the TM, as shown in Fig.14, which demonstrates that the x and y components of displacement (Ux and Uy) are smaller than the out-of-plane component (Uz). The resultant displacement has a maximum value within the posterior-inferior quadrant of the TM.
Fig.14.

Principal components of displacement along three orthogonal axes of the TM as obtained by application of our approach. TM was subjected to sound stimuli of 5,730 Hz, and sound pressure of 101 dB SPL: (a) 3-D view; and (b) 2D top-view. The z axis corresponds to the lateral-medial direction with medial as positive that was defined by the longitudinal axis of the illuminating and reflected laser beam. The x direction is approximate to the rostral (anterior) - caudal (posterior) axis with rostral positive. The y direction is approximate to the dorsal (superior) - ventral (inferior) direction with ventral positive. Displacements are in the unit of μm.
5. Conclusions
We presented a new approach to measure 3D displacements of TM by combining shape information and 1D components of displacement. Shape and displacement measurements are carried out with a lensless DWDHS with shape measured in two-wavelengths mode and 1D displacements measured in single wavelength mode. The assumptions we used in our computation of the 3-Dimensional components of displacement from measured shape and 1D-displacments are based on considering the TM as a thin-shell, so that, the principal components of TM vibration are hypothesized to be parallel to the principal components of the normal vectors of the surface of the TM. This approach was tested using FEM models. Further testing of our approach will be performed in the next steps of this research, including the development of improved FEM models as well as direct measurements of x, y components of displacement by other digital holographic methods that involve speckle correlation and multiple sensitivity vectors. We expect that our efforts toward the development of methodologies for the concurrent measurement of shape and the three components of displacement vector will lead us to realize full-field-of-view tools for the effective study of middle-ear and some of its disorders.
Acknowledgments
This work was supported by the National Institute on Deafness and Other Communication Disorders (NIDCD) and the Worcester Polytechnic Institute, Mechanical Engineering Department. We would also like to acknowledge the support of all of the members of the CHSLT laboratories and particularly of Peter Hefti and Ellery Harrington.
References
- 1.Tonndorf J, Khanna SM. The Tympanic Membrane as a Part of the Middle Ear Transformer. Acta Oto-laryngologica. 1971;71(1-6):177–180. doi: 10.3109/00016487109125347. [DOI] [PubMed] [Google Scholar]
- 2.Lu W. MS Thesis. Mechanical Engineering Department, Worcester Polytechnic Institute; 2012. Development of a Multi-wavelength Lensless Digital Holography System for 3D Deformations and Shape Measurements of Tympanic Membranes. [Google Scholar]
- 3.Decraemer WF, Dirckx JJJ, Funnell WRJ. Shape and derived geometrical parameters of the adult, human tympanic membrane measured with a phase-shift moire interferometer. Hear Res. 1991;51:107–122. doi: 10.1016/0378-5955(91)90010-7. [DOI] [PubMed] [Google Scholar]
- 4.Dirckx JJJ, Decraemer WF. Phase shift moire apparatus for automatic 3-D surface measurement. Rev Sci Inst. 1989;60:3698–3701. [Google Scholar]
- 5.Dirckx JJJ, Decraemer WF. Moire topography for basic and clinical hearing research. Recent Res Devel Optics. 2003;3:271–296. [Google Scholar]
- 6.Liang J. MS Thesis. Mechanical Engineering Department; Oklahoma State University: 2009. Determination of the mechanical properties of guinea pig tympanic membrane using combined fringe projection and simulation. [Google Scholar]
- 7.Rosowski JJ, Dobrev I, Khaleghi M, Lu W, Cheng JT, Harrington E, Furlong C. Measurements of three-dimensional shape and sound-induced motion of the chinchilla tympanic membrane. Hear Res. 2013 doi: 10.1016/j.heares.2012.11.022. In-press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Decraemer WF, Funnell WRJ. Anatomical and mechanical properties of the tympanic membrane. In: Ars B, editor. Chronic otitis media Pathogenesis-oriented therapeutic management. 2008. pp. 51–84. [Google Scholar]
- 9.Uebo K, Kodama A, Oka Y, Ishii T. Thickness of normal human tympanic membrane. Ear Res Jpn. 1988;19:70–73. [Google Scholar]
- 10.Ruah CB, Schachern PA, Zelterman D, Paparella MM, Yoon TH. Age-related morphologic changes in the human tympanic membrane. Arch Otolaryngol Head and Neck Surg. 1991;117:627–634. doi: 10.1001/archotol.1991.01870180063013. [DOI] [PubMed] [Google Scholar]
- 11.Aernouts J, Aerts JRM, Dirckx JJJ. Mechanical properties of human tympanic membrane in the quasi-static regime from in situ point indentation measurements. Hear Res. 2012;290:45–54. doi: 10.1016/j.heares.2012.05.001. [DOI] [PubMed] [Google Scholar]
- 12.Love AEH. On the small free vibrations and deformations of elastic shells. Philosophical trans of the Royal Society. 1888;17:491–549. [Google Scholar]
- 13.Novozhilov VV. Theory of Thin Elastic Shells. 2. P. Noordhoff; Groningen: 1964. [Google Scholar]
- 14.Furlong C, Pryputniewicz RJ. Absolute shape measurements using high-resolution optoelectronic holography methods. Opt Eng. 2000;39(1):216–223. [Google Scholar]
- 15.TracePro. Lambda Research Corporation; Littleton, MA: 2012. [Google Scholar]
- 16.Harrington E, Furlong C, Rosowski JJ, Cheng JT. Automatic Acquisition and Processing of Large Sets of Holographic Measurements in Medical Research. Proc SEM. 2011;9999:219–228. [Google Scholar]
- 17.Flores-Moreno JM, Furlong C, Rosowski JJ, Harrington E, Cheng JT, Scarpino C, Mendoza SF. Holographic otoscopefor nano-displacement measurements of surfaces under dynamic excitation. Scanning. 2011;33:342–352. doi: 10.1002/sca.20283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Furlong C, Dobrev I, Rosowski JJ, Cheng JT. Assessing eardrum deformation by digital holography. SPIE News room, J Biomed Opt Med Imag. 2013 doi: 10.1117/2.1201212.004612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rosowski JJ, Cheng JT, Ravicz ME, Hulli N, Harrington EJ, Hernandez-Montes MS, Furlong C. Computer-assisted time-averaged holography of the motion of the surface of the tympanic membrane with sound stimuli of 0.4 to 25 kHz. Hear Res. 2009;253:83–96. doi: 10.1016/j.heares.2009.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Goldish S, Kunyz T, Lizewski C, Olecki D. Department of Mechanical Engineering. Worcester: Worcester Polytechnic Institute; 2010. Packaging and optimization of a digital holographic otoscope for clinical use. [Google Scholar]
- 21.Dirckx JJJ, Decraemer WF. Optoelectronic moire projector for real-time shape and deformation studies of the tympanic membrane. J Biomed Optics. 1997;2:176–185. doi: 10.1117/12.268966. [DOI] [PubMed] [Google Scholar]
- 22.Cheng JT, Aarnisalo AA, Harrington EJ, Hernandez-Montes MS, Furlong C, Merchant SN, Rosowski JJ. Motion of the surface of the human tympanic membrane measured with stroboscopic holography. Hear Res. 2010;263(1–2):66–77. doi: 10.1016/j.heares.2009.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Furlong C, Dobrev I, Harrington EJ, Hefti P, Khaleghi M. Miniaturization as a key factor to the development and application of advanced metrology systems. Proc SPIE (8413) 2012 doi: 10.1117/12.981668. 84130T-1:12. [DOI] [Google Scholar]


