Abstract
Despite an extensive literature, the “g” construct remains a point of debate. Different models explaining the observed relationships among cognitive tests make distinct assumptions about the role of g in relation to those tests and specific cognitive domains. Surprisingly, these different models and their corresponding assumptions are rarely tested against one another. In addition to the comparison of distinct models, a multivariate application of the twin design offers a unique opportunity to test whether there is support for g as a latent construct with its own genetic and environmental influences, or whether the relationships among cognitive tests are instead driven by independent genetic and environmental factors. Here we tested multiple distinct models of the relationships among cognitive tests utilizing data from the Vietnam Era Twin Study of Aging (VETSA), a study of middle-aged male twins. Results indicated that a hierarchical (higher-order) model with a latent g phenotype, as well as specific cognitive domains, was best supported by the data. The latent g factor was highly heritable (86%), and accounted for most, but not all, of the genetic effects in specific cognitive domains and elementary cognitive tests. By directly testing multiple competing models of the relationships among cognitive tests in a genetically-informative design, we are able to provide stronger support than in prior studies for g being a valid latent construct.
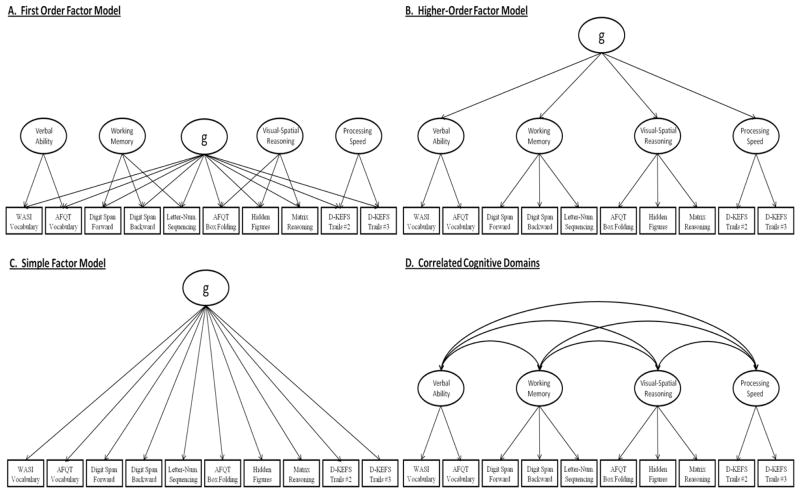
The construct of “g” has arisen from the observation that nearly all cognitive tests are correlated with one another, and when subjected to a principal component/factor analysis they load positively on the first principal component or factor (Deary, 2012). Since Spearman’s (1904) introduction of g, it has become a widely popular view that there is a general factor underlying all cognitive abilities, although alternative theories as to the structure and origin of the positive manifold for cognitive abilities have been proposed (Gustafsson, 1984). Here we examine four common models of the observed relationships among various cognitive tests, three of which include a g factor and one that does not (see Figure 1). All four models have received support in the literature. In some studies, they have been directly compared in traditional phenotypic analyses, but, to our knowledge, they have never all been directly compared against one another in the context of the classical twin design. Without direct comparison of all of these models, which is the best-fitting model for the relationships among cognitive tests cannot be determined. It is the first aim of the present study to directly compare all four of these models using multivariate applications of the twin design, and by doing so establish the best-fitting model for the genetic and environmental relationships among multiple cognitive tests.
Figure 1.
Competing theoretical phenotypic models explaining the relationships among cognitive tests
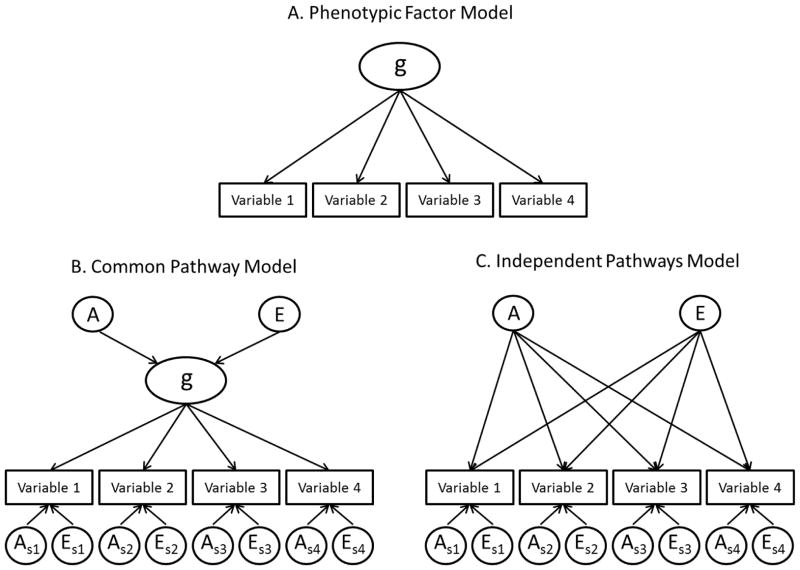
We also attempt to address whether g is indeed a valid latent construct. Although it may seem counterintuitive, finding a g factor at the phenotypic level does not necessarily mean that g is a valid latent construct. Validity can be conceptualized in numerous ways (Borsboom, Mellenbergh, & van Heerden, 2004). For the purposes of this study we argue that if g is indeed a valid latent construct, then both the genetic and environmental covariances among cognitive tests must be mediated through a single latent phenotype. In other words, it is not sufficient that the pattern of phenotypic relationships among cognitive tests supports a common latent phenotype. Rather, the genetic and environmental covariance that underlies the observed phenotypic relationships must also support that conclusion. If instead the genetic and environmental covariances are best represented by independent factors, and not a common latent phenotype, this would suggest that g is merely a psychometric phenomenon originating from the phenotypic correlations among elementary cognitive tests. This argument is illustrated in Figure 2.
Figure 2. Hypothetical phenotypic factor model and corresponding genetically informative factor models.
A = Additive genetic influences. E = Unique environmental influences. In order to simplify the figure, common environmental influences (C) are not presented. Parameters with a subscript notation represent variable specific genetic and environmental influences.
Figure 2A shows a hypothetical factor structure that is based solely on phenotypic information. Within the twin design the covariance among the same variables can be represented by either a common pathway model (Figure 2B) or an independent pathways model (Figure 2C) (Kendler, Heath, Martin, & Eaves, 1987; McArdle & Goldsmith, 1990), but it is not possible to know which will best represent the data with phenotypic analysis alone. If the common pathway model provides the best fit to the data then this suggests that the latent phenotype in the model is indeed a valid construct, as it serves to mediate the genetic and environmental covariance among the variables. In the independent pathways model, however, there is no latent phenotype, only independent genetic (A) and environmental (E) factors. Thus, the model does not support validity of the phenotypically derived factor. The key point here is that if the independent pathways model provides the best fit to the data, then it is not appropriate to calculate a heritability estimate (i.e., the proportion of the phenotypic variance attributable to genetic influences) for the phenotypically derived g factor. Put another way, if the independent pathways models is the best-fitting model, heritability estimates should only be calculated for the individual variables1.
Researchers who conduct phenotypic studies typically assume that factors such as g are valid latent constructs. Most likely, it goes unrecognized that this assumption requires that if the variables were examined in the context of the twin design the common pathways model would provide the best fit to the data. This assumption, however, is easily tested. It is the second aim of the present study to compare the common pathway and independent pathways models of the relationship among cognitive tests in order to determine if there is evidence in favor of g being a valid latent construct.
Competing Phenotypic Models of General Cognitive Ability
By far, the relationships among multiple cognitive tests are most frequently represented by a model with a hierarchical structure that includes a latent g factor, as well as specific cognitive domains. Although multiple terminologies have been used, we define the two primary competing hierarchical models as the “first-order factor model” and the “higher-order factor model” (see Figure 1A and 1B, respectively). Both models have been utilized extensively in the factor analytic literature (Carroll, 1993; Crawford, Deary, Allan, & Gustafsson, 1998; Gignac, 2008), and at times have been referred to as the direct hierarchical (first-order) and indirect hierarchical (higher-order) models of general cognitive ability (Gignac, 2008). Although both models make similar predictions regarding the covariance among cognitive tests, they are mathematically distinct from one another (Yung, Thissen, & McLeod, 1999) and fundamentally differ in how they define the role of g (Gignac, 2005). For instance, in the first-order factor model g is viewed as an independent latent factor that is directly associated with all elementary (measured) cognitive tests. Furthermore, specific cognitive domains are assumed to be uncorrelated with g and with one another. In contrast, in the higher-order factor model g is a superordinate latent factor that accounts for the correlation among specific cognitive domains. Thus, the association of g with elementary cognitive tests is assumed to be fully mediated through the specific domains in the higher-order factor model.
Given their differences, the first-order and higher-order models should be treated as competing hypotheses for the hierarchical structure of cognition, hypotheses that can be tested relative to one another. Many studies have merely assumed that either hierarchical model is the “true model”, and have failed to test whether one provides a better fit (i.e., representation of the data) over the other. Direct comparisons of these competing factor structures are, however, becoming more common. For instance, in a study utilizing the standardization sample for the WAIS-R, Gignac (2005) concluded that a first-order factor model provided a better fit to the data than a higher-order factor model. This finding has since been replicated with the WAIS-III (Gignac, 2006b), the French WAIS-III (Golay & Lecerf, 2011), the Multidimensional Aptitude Battery (Gignac, 2006a), and the WISC-IV (Watkins, 2010). Such results support the concept of g as a first-order or breadth factor rather than a higher-order superordinate entity (Gignac, 2008).
It is important to recognize that although the first-order and higher-order factor models are by far the most commonly used to represent the relationships among cognitive tests, there are additional, competing models that warrant consideration. We refer to the first of these as the “simple factor model” (see Figure 1C) in which all covariance between cognitive tests is accounted for by a single latent g factor, while specific cognitive domains are assumed not to be present. In many ways the simple factor model provides the closest resemblance to Spearman’s original construct, as individual differences on any given test are accounted for by the latent factor as well as by the residual influences that are specific to each individual test (not shown in Figure 1). Although not commonly tested, the simple factor model provides a critical gauge against which models of greater complexity can be compared.
Yet another alternative model for the relationships among cognitive tests is the “correlated cognitive domains model” (see Figure 1D) in which a latent g factor is not included. This model is in essence the antithesis of the simple factor model, as the two make opposing assumptions about the source of the covariance between tests and the existence of specific cognitive domains. While the positive manifold between cognitive tests has traditionally been interpreted as reflecting the presence of a true latent g factor, alternative theories exist which do not require g – for example Thomson’s bonds model (Bartholomew, Deary, & Lawn, 2009; Thomson, 1916) and the mutualism model (van der Maas, et al., 2006). The correlated cognitive domains model has often been found to provide fits to the data that are as good if not better than the hierarchical models. For example, although Bodin et al. (2009) concluded that there was a higher-order factor structure for WISC-IV, their correlated factors model fit the data equally well (Bodin, Pardini, Burns, & Stevens, 2009). Similarly, Dickinson et al. (2006) found that a six-correlated-factors model fit the data equally well as a six-factor model with a higher-order factor (Dickinson, Ragland, Calkins, Gold, & Gur, 2006). More recently, Holdnack et al. (2011) concluded that a seven-correlated-factor model without g and a five-factor model with g fit combined data from the WAIS-IV and WMS-IV equally well (Holdnack, Xiaobin, Larrabee, Millis, & Salthouse, 2011). Findings such as these argue for studying the correlated cognitive domains model alongside models that include a g factor. The correlated cognitive domains model, like the simple factor model, provides a critical indicator with which to gauge how well hierarchical models account for the relationships among cognitive tests. It should be noted, the correlated cognitive domains model can be differentiated from higher-order factor model only if four domains or more are examined.
The number of individual tests and cognitive domains shown in the models in Figure 1 are not intended to provide a comprehensive representation of the content of g. Our focus in this paper is on the factor structure, not the specific content. Studies of g may extend or reduce the number of tests and domains used while the fundamental structure of the model remains the same. Similarly, the higher-order model (Figure 1B) can be extended to include more than three strata, as in the case of the Verbal-Perceptual-Image Rotation (VPR) model (Johnson & Bouchard, 2005), while still representing g as a superordinate latent factor. What is important for purposes of this study is that such changes do not alter the basic structure of each model.
Applications of the Twin Design to the Study of General Cognitive Ability
Multivariate extensions of the classical twin design offer a unique opportunity to test specific hypotheses regarding the nature of the relationships among cognitive tests, and to test whether the g factor is indeed a valid latent construct. It is well established that there are substantial genetic effects on general and specific cognitive abilities, with estimates of the heritability varying between .30 and .80 (T. J. Bouchard, Jr. & McGue, 2003; Deary, Johnson, & Houlihan, 2009). Beyond the estimation of heritability, multivariate twin analyses allow for the covariance between variables to be decomposed into genetic and environmental components, thus enabling a much more comprehensive examination of the underlying relationships.
The twin design allows for a unique multivariate structure in which a latent phenotype is not modeled, but rather the genetic and environmental covariances are constrained into separate (independent) factors. This model is referred to as the biometric or independent pathways model (Kendler, et al., 1987; McArdle & Goldsmith, 1990). Figure 2C provides an example of the independent pathways model as it would be applied to the simple factor model. The model imposes genetic and environmental influences on the respective covariance estimates while simultaneously allowing variable-specific (i.e., residual) genetic and environmental influences. These genetic and environmental influences then act on each variable through separate, independent pathways. As a result, the covariance between any pair of variables can be accounted for by either the latent genetic or environmental influences. An advantage of the independent pathways model is that it allows for the genetic and environmental structure to be tested separately from one another. Thus, one is able to remain agnostic as to whether genetic and environmental influences adhere to the same covariance structure. In other words, the model does not require an overarching latent phenotype, but rather can account for the covariance via separate genetic and environmental factors that are independent of one another.
In contrast, the common pathway model assumes that the covariance among variables is accounted for by a single underlying latent phenotype, and that the genetic and environmental contributions to the observed covariance are accounted for by the genetic and environmental influences that operate through that phenotype (Kendler, et al., 1987; McArdle & Goldsmith, 1990). In other words, in the common pathway model the relationships among variables are accounted for by a single latent construct that has its own genetic and environmental influences (see Figure 2B). On its own, the latent factor derived from the common pathway model is essentially the same as the latent factor that is derived from standard phenotypic analyses. If the common pathway model provides a good fit to the data, then so too must the independent pathways model, as the ability to distinguish one from the other is based entirely on the collinearity of the factor loadings in the independent pathways mode. What is important is which model provides the best fit to the data; therefore, only when the fit of the common pathways model is tested against that of the independent pathways model is one able to empirically determine whether it truly provides the best representation of the data.
Phenotypic analyses are unable to test an independent pathways model; therefore they possess no empirical means of validating the constructs that are represented through traditional factor analysis. Testing the independent and common pathway models relative to one another is a unique aspect of the multivariate classical twin design. To our knowledge, only one prior twin study has used the comparison of the independent and common pathways models as a means of examining the validity of g. Utilizing data from a Japanese twin study, Shikishima and colleagues (2009) demonstrated that relationships between measures of logical, verbal, and visual-spatial abilities could best be represented by a common pathway model, and that the fit of this model was superior to that of an independent pathways model (Shikishima, et al., 2009). This study, while providing evidence consistent with g being a valid latent construct, with only three variables they could not test either hierarchical model (first-order or higher-order), nor could they differentiate their factor models from a model consisting only of correlated genetic and environmental influences.
In addition to Shikishima et al., several twin studies have examined the genetic and environmental relationships among multiple cognitive tests; however, none have leveraged the unique advantages of the twin design to the fullest possible extent. Higher-order genetic and environmental factor structures have been observed in several studies of children (Cardon, Fulker, Defries, & Plomin, 1992; Luo, Petrill, & Thompson, 1994; Petrill, Luo, Thompson, & Detterman, 1996). However, each time the preferred model of the genetic and environmental relationships was not been rigorously tested against other competing models, and a test for the validity of a latent g construct was not performed. Some twin studies have directly fit a latent g phenotype to cognitive data in the form of a common pathway model; however, in these cases the alternative independent pathways model of genetic and environmental relationships was not tested (Finkel, Pedersen, McGue, & McClearn, 1995; Johnson, et al., 2007; Petrill, et al., 1998; Petrill, Saudino, Wilkerson, & Plomin, 2001). Comparing the fit of alternative models of the genetic and environmental relationships was not the goal of these studies. If, on the other hand, one’s goal is to determine which model of the genetic and environmental relationships among cognitive tests best represents the data, it is necessary to directly compare model fits. In some cases the underlying genetic and environmental factor structures have been found to be different from the phenotypic factor structure and from one another (Kremen, et al., 2009; Petrill, et al., 1996; Rijsdijk, Vernon, & Boomsma, 2002), suggesting that each factor structure needs to be tested separately.
The Present Study
We utilized a multivariate application of the classical twin design to elucidate the genetic and environmental covariance structure among multiple cognitive measures, and formally test for the presence of a latent g factor. We first compared four distinct models (first-order factor model, higher-order factor model, simple factor model, and correlated cognitive domains– as presented in Figure 1) in order to determine which model provided the best representation of the data, and to establish whether the structure of the genetic and environmental covariance among the various tests were indeed the same. We then directly tested whether a latent g phenotype provided the best representation of the data (as represented by a common pathways model), or whether the observed covariance was better accounted for by independent latent genetic and environmental influences (as represented by an independent pathways model). To the best of our knowledge, no genetically-informative studies have directly tested all of these competing models against one another. Establishing the structure of the genetic and environmental covariance among cognitive tests, as well as addressing the validity of g represents an important step towards obtaining a better understanding of cognition, the processes that drive cognitive development, and the
Methods
Participants
Data were obtained as part of the Vietnam Era Twin Study of Aging (VETSA), a longitudinal study of cognitive and brain aging with a baseline in midlife (Kremen, et al., 2006). VETSA participants were recruited from the Vietnam Era Twin (VET) Registry, a nationally distributed sample of male-male twin pairs who served in the United States military at some point between 1965 and 1975. Complete descriptions of the VET Registry’s history, composition, and method of ascertainment have been provided elsewhere (Eisen, True, Goldberg, Henderson, & Robinette, 1987; Goldberg, Curran, Vitek, Henderson, & Boyko, 2002; Goldberg, Eisen, True, & Henderson, 1987; Henderson, et al., 1990). Although all VETSA participants are military veterans, the majority did not experience combat situations during their military service. Relative to U.S. census data, VETSA participants are similar to American men in their age range with respect to demographic and general health characteristics (Centers for Disease Control and Prevention, 2003). In 92% of cases, zygosity was determined by analysis of 25 microsatellite DNA markers obtained from blood samples. For the remainder of the sample zygosity was determined through a combination of questionnaire and blood group methods. Within the VETSA these two approaches demonstrated an agreement rate of 95%.
In all, 1,237 individuals participated in the first wave of the VETSA. To be eligible, participants had to be between the ages of 51 and 59 at the time of recruitment, and both members of a pair had to agree to participate. Participants traveled to either the University of California San Diego or Boston University for a day-long series of physiological, psychological, and cognitive assessments. In approximately 3% of cases, project staff traveled to the participant’s home town to complete the assessments. Study protocols were approved by the institutional review boards of both participating universities, and informed consent was obtained from all participants. The present analyses were based on data from 346 monozygotic (MZ) twin pairs, 265 dizygotic (DZ) twin pairs, and 12 unpaired twins for whom valid cognitive assessment data were obtained. The average age was 55.4 years (SD = 2.5), and the average years of education was 13.8 (SD = 2.1, Range = 8 to 20).
Measures
Ten measures were selected from the VETSA cognitive battery in order to assess four domains of functioning. We intentionally targeted cognitive domains that would parallel previous confirmatory factor analyses of cognitive tests, such as those conducted on various versions of the Wechsler intelligence scales (Canivez & Watkins, 2010; Golay & Lecerf, 2011; Watkins, 2010), as well as previous multivariate twin studies of cognition (Cardon, et al., 1992; Luo, et al., 1994; Petrill, et al., 1996). As noted, our focus is on factor structure rather than content; therefore, we selected domains that are non-controversial and widely accepted as relevant for inclusion in intelligence scales. Some domains such as episodic memory are more subject to debate as to their appropriateness for inclusion in intelligence scales, and were therefore not included in the present analyses. Care was taken to ensure that within a cognitive domain the selected variables correlated (at the phenotypic level) more strongly with one another than with cognitive tests from other domains.
Verbal ability was assessed by the Vocabulary subtest of the Wechsler Abbreviated Scale of Intelligence (WASI) (Wechsler, 1999), and the Vocabulary component of the Armed Forces Qualification Test (AFQT) (Uhlaner, 1952). The WASI Vocabulary subtest requires participants to define a series of increasingly difficult words, with more abstract definitions receiving greater weighting relative to more concrete definitions. The Vocabulary component of the AFQT (a timed paper-and-pencil test) requires participants to identify the correct synonym for a target word presented in a sentence from four multiple-choice options. The phenotypic correlation between these two tests was .57 (p<.01). Working memory was assessed by the Digit Span Forward, Digit Span Backward and the Letter-Number Sequencing subtests of the Wechsler Memory Scales (WMS-3) (Wechsler, 1997). In Digit Span tests, participants are read a series of numbers which they must then either repeat in the same order (Forward condition) or in the reverse order (Backward condition). In Letter-Number Sequencing participants are read a series of spans consisting of numbers and letters appearing in turn. These spans must then be repeated back in an unscrambled manner; numbers first in ascending order followed by letters in alphabetical order. The phenotypic correlations among these three tests ranged from .50 (p<.01) to .52 (p<.01). Visual-spatial reasoning was assessed by the Matrix Reasoning subtest of the WASI (Wechsler, 1999), the Gottschaldt Hidden Figures test (Thurstone, 1944) and the Box Folding component of the AFQT. In the Matrix Reasoning subtest the participant is asked to complete visually presented patterns that gradually increase in difficulty, by selecting from five possible solutions. The Hidden Figures test requires the participant to correctly identify a target figure that is embedded in a more complex two-dimensional design. In the Box Folding test, the participant is asked to correctly identify one of four cubes that can be made by folding a target pattern, or one of four patterns that can be made by unfolding a target cube (the test is evenly split between the two variations). In both variants, there is only one correct answer among the four alternatives. The phenotypic correlation between these three tests ranged from .52 (p<.01) to .63 (p<.01). Processing speed was assessed by the Number Sequencing and Letter Sequencing conditions (Conditions 2 and 3, respectively) of the Delis-Kaplan Executive Function System (DKEFS) Trail-Making test (Delis, Kaplan, & Kramer, 2000). Although the Trail Making test is traditionally used as a measure of executive functioning, Conditions 2 and 3 involve no set-shifting component (i.e., the participant is asked to sequence through only numbers or letters); thus, the conditions can be assumed to provide good indicators of psychomotor processing speed. The phenotypic correlation between these two tests was .60 (p<.01).
Statistical Analyses
In the classical twin design the variance of a trait can be decomposed into additive genetic influences (A), non-additive genetic influences that are due to genetic dominance or epistasis (D), shared or common environmental influences (C) (i.e., environmental factors that make twins similar to one another), and individual-specific or unique environmental factors (E) (i.e., environmental factors that make twins different from one another, including measurement error). Due to issues of model identification only three of these parameters can be assessed at any one time. When the degree of resemblance for a trait in MZ twins (cross-twin correlation) is less than twice that of DZ twins, non-additive genetic influences are assumed to be zero, resulting in what is widely referred to as the ACE model (Eaves, Last, Young, & Martin, 1978; Neale & Cardon, 1992). Under the ACE model additive genetic influences are assumed to correlate 1.0 between MZ twins because they generally share 100% of their genes, whereas DZ twins on average share 50% of their segregating genes, and are therefore assumed to correlate at least .50. Common environmental influences are assumed to correlate perfectly (1.0) between members of a twin pair regardless of the zygosity. Unique environmental influences, by definition, are uncorrelated between twin pairs. The ACE model does not account for the presence of gene-environment interaction or gene-environment correlation; thus, the latent variance components are assumed to be independent of one another (Jinks & Fulker, 1970). If such effects were present, estimates of the relative genetic and environmental influences can be biased in either positive or negative directions depending on the nature of the effect. The model also assumes the absence of assortative mating between the parents of twins, an effect that has been found to be prominent for measures of general cognitive ability (Bouchard & McGue, 1981). The presence of assortative mating is expected to increase the resemblance of DZ twins relative to MZ twins, resulting in an over estimation of common environmental effects for a trait and an underestimation of the heritability.
Multivariate twin analyses extend the univariate ACE model so as to further decompose the covariance between phenotypes into genetic and environmental components. This then allows for the estimation of genetic and environmental correlations between variables (representing the degree of shared genetic and environmental variance), as well as the testing of a variety of genetically- and environmentally-informed factor models. Carey (1988) has pointed out that although genetic correlations represent shared genetic variance, they do not necessarily indicate that the same genes are directly influencing the correlated phenotypes. Rather, they tell us that genetic influences on each phenotype are correlated. The latter, statistical pleiotropism, may or may not be due to the former, biological pleiotropism (Carey, 1988). Nevertheless, Carey does note that biological pleiotropism can be strongly inferred if the phenotypes are accounted for by additive genetic influences of many genes. Genome-wide association analyses of g have shown that this is indeed the case (Benyamin, et al., In Press; Davies, et al., 2011); as such it is also likely true that most underlying cognitive abilities are also highly polygenic underpinnings. Thus, it is a reasonable, although not certain, assumption that genetic correlations in the present study represent biological pleiotropism. Environmental correlations between phenotypes are subject to similar considerations; however, as with genetic influences, it is likely that each phenotype is influenced by multiple environmental factors that each contributes a small amount to the observed variance.
In order to elucidate the nature of the genetic and environmental covariance among the cognitive tests, we first fit a series of independent pathways models to the data (Kendler, et al., 1987; McArdle & Goldsmith, 1990). Four models, each reflecting one of our specific theoretical models (see Figure 1), were separately fit to the genetic and environmental covariance structures. The “first-order factor model” (Figure 1A) was fit as a five factor model, in which all variables were allowed to load onto one factor, while the remaining factors (conceptualized as specific cognitive domains) were constrained so that two to three variables loaded onto each. In this model the covariance between measured variables is accounted for by two sources: the g factor and the specific cognitive domain factors. The domain factors are also assumed to be orthogonal to one another. In order for this model to be identified, parameters leading to domains that included only two variables (i.e., verbal ability and processing speed) were constrained to be equal to one another within that domain. The “higher-order factor model” (Figure 1B) closely resembles the “first-order factor model”; however, in this case g is represented as a higher-order factor onto which the four domain-level factors directly load. This model assumes that g accounts for the correlation between specific cognitive domains and that its impact on elementary cognitive tests is fully mediated through the domain. In addition, each domain is also allowed to possess genetic and environmental influences that are independent of the other domains. The “simple factor model” (Figure 1C) was fit as a single factor independent pathway model. All eight measured variables load directly onto the g factor, and the g factor accounts for all genetic or environmental covariance among the variables. Finally, “correlated cognitive domains model” (Figure 1D) was fit as a four-factor model, each factor representing a specific cognitive domain, with the covariance between variables accounted for by the correlations between the domains. This model, as its name implies, requires no latent g factor. Common pathway models were subsequently used to test whether the genetic and environmental factor structures could be constrained into latent phenotypes (Kendler, et al., 1987; McArdle & Goldsmith, 1990). Although the common pathway model can algebraically be shown to be nested within the independent pathways model (Kendler, et al., 1987), for the present analyses the two are utilized as alternative representations of the data, and are therefore directly compared to one another.
All analyses were performed using the maximum-likelihood-based structural equation modeling software OpenMx (Boker, et al., 2011). Prior to model fitting, all variables were standardized to a mean of 0 and a variance of 1.0 in order to simplify the specification of start values and parameter boundaries. When necessary, variables were square-root or log transformed in order to normalize the observed distribution. Measures of processing speed (total time for completion of D-KEFS Trail Making Conditions 2 and 3) were reverse coded so that faster completion times correlated positively with all other cognitive tests. Evaluation of model fit was performed using the likelihood-ratio chi-square test (LRT), which is calculated as the difference in the −2 log-likelihood (−2LL) of a model relative to that of a comparison model. For the present analyses, the full ACE Cholesky was utilized as the comparison model for all models tested, as it is the most saturated representation of the genetic and environmental relationships among the variables. In addition to the LRT, we utilized the Bayesian Information Criterion (BIC) as a secondary indicator of model fit (Akaike, 1987; Williams & Holahan, 1994). The BIC indexes both goodness-of-fit and parsimony, with more negative values indicating a better balance between them, and has been found to outperform the commonly used Akaike Information Criterion (AIC) with regard to model selection in the context of complex multivariate models (Markon & Krueger, 2004).
Results
Table 1 provides the standardized variance components for each of the cognitive variables as derived from the full ACE Cholesky. Complete matrices of the cross-twin same trait and cross-twin cross-trait correlations separated by zygosity group are available in Supplemental Table 1. Heritability estimates ranged from .30 for Trail Making Number Sequencing condition (condition #2), to .65 for Hidden Figures. All heritability estimates were significantly different from zero based on the 95% confidence intervals. Estimates of common environmental influence ranged from .04 for Box Folding, to .19 for WASI Vocabulary. The estimates for WASI Vocabulary (C = .19), AFQT Vocabulary (C = .11), Digit Span Forwards (C = .12), Letter-Number sequencing (C = .17), and Matrix Reasoning (C = .18) were significantly different from zero based on the 95% confidence intervals. Phenotypic, genetic, and environmental correlations between all of the cognitive variables are presented in Supplemental Table 2. Significant phenotypic (rp) and genetic (rg) correlations were present among all of the variables (rp range = .14 to .65; rg range = .37 to .98). In contrast, only 7 of 45 common environmental correlations (rc) were found to be significantly greater than zero; these values ranged from .79 to .98. Unique environmental correlations (re) ranged from .00 to .37, with 22 of the 45 correlations proving to be significantly greater than zero.
Table 1.
Standardized variance components for individual cognitive tests
| A (95% CI) | C (95% CI) | E (95% CI) | |
|---|---|---|---|
| WASI Vocabulary | .46 (.29; .62) | .19 (.04; .34) | .35 (.30; .41) |
| AFQT Vocabulary | .39 (.24; .51) | .11 (.01; .24) | .50 (.44; .58) |
| WMS-3 Digit Span Forwards | .44 (.26; .57) | .12 (.01; .27) | .44 (.38; .52) |
| WMS-3 Digit Span Backwards | .33 (.16; .48) | .13 (.00; .29) | .54 (.48; .62) |
| WMS-3 Letter Number Sequencing | .36 (.17; .54) | .17 (.02; .35) | .47 (.40; .53) |
| AFQT Box Folding | .54 (.37; .63) | .04 (.00; .19) | .42 (.37; .49) |
| Hidden Figures | .65 (.53; .74) | .07 (.00; .18) | .28 (.24; .33) |
| WASI Matrix Reasoning | .36 (.18; .54) | .18 (.03; .34) | .46 (.39; .53) |
| DKEFS Trail Making Condition 2 | .30 (.16; .41) | .07 (.00; .20) | .63 (.55; .70) |
| DKEFS Trail Making Condition 3 | .32 (.14; .48) | .11 (.00; .27) | .57 (.49; .65) |
A = Additive Genetic Influences. C = Common/Shared Environmental Influences. E = Unique Environmental Influences. Estimates were derived from the full ACE Cholesky decomposition.
Given the small number of significant common environmental correlations, we tested whether all common environment covariance parameters could be fixed at zero. The resulting model provided a good fit relative the full Cholesky (LRT = 19.79, ΔDF = 45, p > .99) and produced a much lower BIC value (BIC = −48467.26). Moreover, all common environmental influences could be fixed to zero without a significant reduction in model fit (LRT = 21.29, ΔDF = 55, p > .99; BIC = −48530.11). Rather than drop common environmental influences from all subsequent multivariate models, we elected to keep the common environment freely estimated (i.e., common environmental influences would be allowed to correlate among the variables) and impose no specific factor structure on this aspect of the data. This allowed estimates of the genetic variance and covariance to remain unbiased by common environmental influences which exceeded 10% of the phenotypic variance for 7 of the 10 cognitive variables. In addition, this decision allowed us to avoid the likely ambiguous modeling fitting results that would have arisen from trying to fit a factor structure to limited covariance information.
Tests of the Genetic and Unique Environmental Factor Structures
Model-fitting results for tests of the genetic and unique environmental factor structures are presented in Table 2. Each factor structure was tested independently of the other; in other words, when the genetic factor structure was tested the unique environment remained estimated as a Cholesky. For the genetic structure, the simple factor model could be immediately dismissed as a viable explanation of the data, as it resulted in a significant change in model fit relative to the full Cholesky (LRT = 51.61, ΔDF = 35, p = .03). The three remaining genetic models all resulted in non-significant reductions in fit relative to the full Cholesky; however, the higher-order factor model demonstrated a clear advantage based on the BIC.
Table 2.
Model fitting results for tests of the genetic and environmental factor structures
| Model | −2LL | DF | LRT | ΔDF | p | BIC |
|---|---|---|---|---|---|---|
| ACE Cholesky | 29711.99 | 12108 | NA | NA | NA | −48197.50 |
| Additive Genetic Structure | ||||||
| First-Order “g” | 29729.19 | 12135 | 17.21 | 27 | .93 | −48354.03 |
| Higher-Order “g” | 29733.99 | 12139 | 22.00 | 31 | .88 | −48374.97 |
| Simple “g” | 29763.60 | 12143 | 51.61 | 35 | .03 | −48371.10 |
| Correlated Domains | 29731.83 | 12137 | 19.84 | 29 | .90 | −48364.27 |
| Unique Environment Structure | ||||||
| First-Order “g” | 29738.31 | 12135 | 26.32 | 27 | .50 | −48344.91 |
| Higher-Order “g” | 29740.78 | 12139 | 28.79 | 31 | .58 | −48368.18 |
| Simple “g” | 29814.17 | 12143 | 102.19 | 35 | <.01 | −48320.53 |
| Correlated Domains | 29734.47 | 12137 | 22.48 | 29 | .80 | −48361.62 |
−2LL = Negative 2 Log-Likelihood, DF = Degrees of Freedom, LRT = Likelihood Ratio Chi-Square Value; p = Significance of the LRT; BIC = Bayesian Information Criterion. All models are tested against the fit of the ACE Cholesky. For tests of the additive genetic structure, the common and unique environment remains estimated as a Cholesky structure. Similarly, for tests of the environmental structures, additive genetic elements and the untested environmental elements are estimated as Cholesky structures.
As with the additive genetic structure, the simple factor model was a poor fit for the unique environmental structure (LRT = 102.19, ΔDF = 35, p < .01). The three remaining factor structures each resulted in a nonsignificant change in fit relative to the full Cholesky; however, the higher-order factor model once again demonstrated a clear advantage over the other models based on the BIC value (−48368.18).
Testing for the Presence of Latent Phenotypes
Given that the higher-order factor structure provided the best fit for both the additive genetic and unique environmental influences, we proceeded to test whether a higher-order common pathway model could be fit to the data. We first simultaneously fit the higher-order factor models for both the additive genetic and unique environmental structures. As would be expected from the tests of the individual structures, the model resulted in a good fit relative to the full Cholesky (LRT = 57.63, ΔDF = 62, p = .63, BIC = −48538.81). We then tested whether the domain-level genetic and environmental factors could be collapsed into four latent phenotypes, while allowing the higher-order genetic and environmental factors to remain independent of each other (i.e., a combined independent and common pathways model). This model provided a direct test of whether latent cognitive domains could be assumed to be present, and served as an intermediate model between the previous higher-order independent pathways model and the final higher-order common pathway model. The model was a good fit relative to the Cholesky, and resulted in a BIC value that were lower than those of the of higher-order independent pathways model (LRT = 60.66, ΔDF = 68, p = .72, BIC = −48574.39). Finally, we fit a higher-order common pathway model in which domain level and higher-order genetic and unique environment factors were collapsed into latent cognitive domains and a latent higher-order g factor. The model was a good fit relative to the full Cholesky (LRT = 68.61, ΔDF = 71, p = .56), and resulted in the lowest BIC value of any model yet tested (BIC = −48585.74).
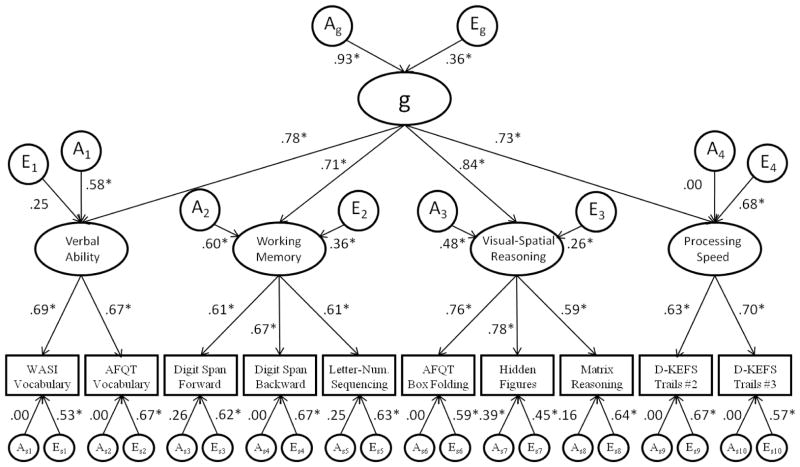
Standardized parameter estimates for the best-fitting model of the combined genetic and unique environmental factor structures (the higher-order common pathway model) are presented in Figure 3. The higher-order g factor was found to be highly heritable, as additive genetic influences accounted for 86% of the variance in the latent phenotype. The factor accounted for 60% of the phenotypic variance for the verbal ability domain, 51% of the variance for working memory, 71% of the variance for visual-spatial reasoning, and 53% of the variance for the processing speed domain. Each measured variable loaded significantly on the corresponding domain-level factor. Domain-specific genetic contributions to the phenotypic variance ranged from 0% for processing speed to 36% for working memory. The genetic influences specific to verbal ability, working memory, and visual-spatial reasoning were found to be significantly different from zero based on 95% confidence intervals. Unique environmental influences specific to each domain also demonstrated a wide range, accounting for little of the variance in verbal ability (6%) and visual-spatial reasoning (6.8%) and 46% of the variance in processing speed. At the level of the individual cognitive tests, variable-specific additive genetic influences contributed very little to the observed variance, most were less than 5%. The only significant variable specific genetic influences were observed for the Hidden Figures test, which accounted for approximately 15% of the variance. Variable-specific unique environmental influences ranged from 20% of the variance for Hidden Figures test to 45% of the variance for AFQT Vocabulary, Digit Span Backwards, and Letter Sequencing Condition of the D-KEFS Trail Making test.
Figure 3. Best-fitting model of the combined genetic and unique environmental factor structures.
A = Additive genetic influences. E = Unique environmental influences. Common environmental influences (C), although not presented here, are estimated as a Cholesky structure. Parameters with a subscript “s” notation represent variable specific genetic and environmental influences. Values are presented as standardized parameter estimates. Parameter estimates with an asterisk (*) are significantly greater than zero based on 95% confidence intervals.
Discussion
Although g is one of the most widely utilized and frequently discussed psychological constructs, tests of its underlying structure as well as its validity have been surprisingly incomplete in the extant literature. The results of the present study suggest that the best representation of the relationships among cognitive tests is a higher-order factor structure, one that applies to both the genetic and environmental covariance. The resulting g factor was highly heritable with additive genetic effects accounting 86% of the variance. These results are consistent with the view that g is largely a genetic phenomenon (Plomin & Spinath, 2002).
At first glance our finding of a higher-order structure to the relationships among cognitive tests may appear obvious, but it is important to recognize that the extensive literature on this topic includes few comparisons of competing models, and that in phenotypic studies that have compared competing models the first-order factor model has often proven to provide the best fit to the data (Gignac, 2005, 2006a, 2006b, 2008; Golay & Lecerf, 2011; Watkins, 2010). However, by directly testing all of the models against one another we were able to more firmly conclude that the higher-order factor model best represents the data.
This is the first genetically-informative study that has thoroughly tested alternative models of the relationships among cognitive tests against one another. In the twin studies we have reviewed (Cardon, et al., 1992; Finkel, et al., 1995; Luo, et al., 1994; Petrill, et al., 1996; Petrill, et al., 1998; Petrill, et al., 2001; Rijsdijk, et al., 2002), either a priori assumptions about the presence of the latent g phenotype were made or the fit of their models were not tested against the fits of other alternative models. Although it did not prove to be the best-fitting model in our study (as was the case in Shikishima et al, 2009), the independent pathways model was essential to establishing the validity of the latent g factor. The independent pathways model is unique in that it allows for an intermediate state between a model of correlated traits and one that allows for the presence of a true latent phenotype (i.e. the common pathway model). Such a state is entirely plausible from a biological perspective, and cannot be assessed with standard phenotypic analyses. Shikishima et al. (2009) did test the relative fit of both independent and common pathway models, but as they included only three cognitive variables they were not able to distinguish between the various alternative models that we examined.
Besides the presence of a latent g phenotype, we observed latent phenotypes at the specific cognitive domain level. As is shown in Figure 3, factor loadings from the specific domains onto the g factor were all comparable in magnitude (i.e., no factor loading was significantly different from any other), suggesting that from a “bottom-up” perspective each domain contributed relatively equally to the higher-order factor. However, from a strictly genetic perspective the relationships between the g factor and the specific domains were less uniform. Residual genetic influences accounted for none of the variance in the processing speed domain (0%), in contrast to other domains where residual genetic influences ranged from 23% to 36% of the variance. These domain-specific genetic influences indicate that there is substantially more to verbal ability, visual-spatial reasoning, and working memory than merely the genes that are common to all cognitive domains.
Contrary to many of the phenotypic studies that have directly compared competing models of general cognitive ability (Gignac, 2005, 2006a, 2006b, 2008; Golay & Lecerf, 2011; Watkins, 2010), the present results support a higher-order factor model over the first-order factor model. A likely explanation for the discrepant results may be found in the degree to which the cognitive variables selected for analysis correlated within and across specific domains. Many, if not most, of the previous phenotypic studies that have examined both the higher-order and first-order factor models utilized cognitive measures that easily load onto multiple cognitive domains with relatively similar weightings. Indeed, results from a confirmatory factor analysis for the French WAIS clearly demonstrate that equivalent loadings can be obtained if measured variables are reconfigured to load onto different domains (Golay & Lecerf, 2011). A battery in which elementary cognitive tests correlate equally well with tests from different domains as they do with tests from the same domain would seem likely to favor the first-order structure solution. On the other hand, the power to reject the first-order model is suggested to be very low (e.g., Maydeu-Olivares & Coffman, 2006). In many cases, first-order and higher-order models have very similar fit to the data and the factor loadings for the domain level and g-factor are very similar in these two models (see e.g., (Niileksela, Reynolds, & Kaufman, 2013). Nevertheless, the first-order model is less parsimonious than the higher-order model.
It should also be noted that the results of the present study may depend in part on the a priori criteria that were used to select the number and type of elementary cognitive tests and specific cognitive domains we examined. It has been shown that across different cognitive batteries, higher-order phenotypic factors that are assumed to represent g correlate very highly with one another (greater than .90), leading to the conclusion that g is highly stable across different methods of measurement (Johnson, Bouchard, Krueger, McGue, & Gottesman, 2004; Johnson, Nijenhuis, & Bouchard, 2008). It remains to be seen whether the structure of the genetic and environmental covariance among cognitive measures is affected by the chosen elementary cognitive tests and the number of indicators of specific cognitive domains.
Although we provide evidence in favor of g being a valid latent construct, it is still the case that we do not know if g is a causal individual differences construct with respect to specific cognitive abilities. If one interprets the higher-order common pathway model from a top-down perspective, it would seem to imply that g is indeed a causal individual differences construct. However, this model is not directional, and it can also be explained by models that do not include a g factor, such as the mutualism model (van der Maas et al 2006). In the mutualism model, g is an emergent property of the positive manifold among specific cognitive abilities rather than a construct that causes the relationships among cognitive abilities. On the other hand, we think it is still the case that, at another level, g can be viewed as a causal individual differences construct with respect to other phenomena. For example, evidence indicates that this is the case for a measure of g at age 20 in the VETSA sample and a measure of g at age 11 in the Lothian Birth Cohort. In both samples, findings strongly suggest that an early measure of g is a causal factor accounting for individual differences in several aging outcomes (Deary, Leaper, Murray, Staff, & Whalley, 2003; Franz, et al., 2011; Kremen, et al., 2007; Walker, McConville, Hunter, Deary, & Whalley, 2002; Whalley & Deary, 2001)—even if we do not fully understand the origins of g itself.
There are some potential limitations of the present study that warrant consideration. The all male, rather homogeneous composition of the VETSA sample limits our ability to generalize these findings to other populations. It is also possible that the observed magnitude of genetic influences and/or the underlying genetic and environmental covariance structure observed in the present sample could vary as a function of any number of socioeconomic factors. It has repeatedly been shown that socioeconomic factors sometimes influence the genetic and environmental determinants of cognition both during childhood and in adulthood (Hanscombe, et al., 2012; Kremen, et al., 2005; Tucker-Drob, Rhemtulla, Harden, Turkheimer, & Fask, 2011; Turkheimer, Haley, Waldron, D’Onofrio, & Gottesman, 2003); however, no studies have looked at whether socioeconomic factors influence the genetic and environmental relationships between cognitive measures. We must also acknowledge that the models examined in the present study are not a comprehensive summary of all competing models of the relationships among cognitive tests. For example, we did not test the fluid-crystallized model of intelligence (Cattell, 1963; Horn & Cattell, 1966), which contains two higher-order factors. Rather, we examined what we believed to be a set of reasonable hypotheses given the constraints of the data. The addition of more or different elementary cognitive tests might result in different numbers of domains, different content within the domains, or a different number of strata in the model. However, such changes do not in and of themselves alter the basic structure of the models presented in Figure 1, and are not really relevant to the question of whether g is a valid superordinate latent factor. For example, the VPR model (Johnson & Bouchard, 2005) was based on 42 tests and includes four strata rather than the three observed in the present study. With only ten individual tests, we were unlikely to be able to detect a fourth strata, but the VPR model is still a higher-order g model. Finally, it should be noted that although the present analyses utilize data from over 1,200 individuals, our power to distinguish between the models is probably weak. Thus, we must acknowledge that in a larger twin sample results may differ from what was obtained in the present study.
Conclusion
Results from the present study suggest that the well-established covariance among cognitive tests is indeed best accounted for by a true higher-order latent phenotype that is itself highly heritable. In testing multiple competing models, as well as leveraging the unique aspects of the classical twin design, this is the first study to rigorously examine alternative models of the relationships among cognitive tests, and formally test whether the g factor represents a true latent phenotype.
Supplementary Material
Table 3.
Model fitting results for tests of presence of latent phenotypes
| Model | −2LL | DF | LRT | ΔDF | p | BIC |
|---|---|---|---|---|---|---|
| ACE Cholesky | 29711.99 | 12108 | NA | NA | NA | −48197.50 |
| Higher Order IP Model | 29769.62 | 12170 | 57.63 | 62 | .63 | −48538.81 |
| Higher Order IP-CP Model | 29772.65 | 12176 | 60.66 | 68 | .72 | −48574.39 |
| Higher Order CP Model | 29780.60 | 12179 | 68.61 | 71 | .56 | −48585.74 |
−2LL = Negative 2 Log-Likelihood, DF = Degrees of Freedom, LRT = Likelihood Ratio Chi-Square Value; p = Significance of the LRT; BIC = Bayesian Information Criterion; IP = Independent Pathways Model; IP-CP = Combined Independent and Common Pathways Model; CP = Common Pathways Model. All models are tested against the fit of the ACE Cholesky. The common environment is estimated as a Cholesky in all models.
Highlights.
Testing g requires direct comparison of multiple models of general cognitive ability
Twin analyses can determine if a phenotypic g factor is a valid latent construct
A higher-order (hierarchical) latent g factor provided the best fit to the data
The underlying genetic structure supported g as a valid higher-order latent construct
Acknowledgments
The VETSA project is supported by grants from NIH/NIA (R01 AG018386, R01 AG018384, R01 AG022381, and R01 AG022982). Dr. Vuoksimaa also received independent support from the Academy of Finland (grant 257075) and Sigrid Juselius Foundation. The content of this paper is solely the responsibility of the authors and does not necessarily represent the official views of the NIA or the NIH. The Cooperative Studies Program of the U.S. Department of Veterans Affairs has provided financial support for the development and maintenance of the Vietnam Era Twin (VET) Registry. Numerous organizations have provided invaluable assistance in the conduct of this study, including: Department of Defense; National Personnel Records Center, National Archives and Records Administration; the Internal Revenue Service; National Opinion Research Center; National Research Council, National Academy of Sciences; the Institute for Survey Research, Temple University. This material was, in part, the result of work supported with resources of the VA San Diego Center of Excellence for Stress and Mental Health Healthcare System. Most importantly, the authors gratefully acknowledge the continued cooperation and participation of the members of the VET Registry and their families. Without their contribution this research would not have been possible. We also appreciate the time and energy of many staff and students on the VETSA projects.
Footnotes
There could also be cognitive domains summarizing subsets of the individual variables in each of these models. In that case, heritability estimates could also be calculated for cognitive domains in the independent pathways model, but there would still be no g factor.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akaike H. Factor analysis and AIC. Psychometrika. 1987;52:317–332. [Google Scholar]
- Bartholomew DJ, Deary IJ, Lawn M. A new lease of life for Thomson’s bonds model of intelligence. Psychological Review. 2009;116:567–579. doi: 10.1037/a0016262. [DOI] [PubMed] [Google Scholar]
- Benyamin B, Pourcain B, Davis OS, Davies G, Hansell NK, Brion MJ, Kirkpatrick RM, Cents RA, Franic S, Miller MB, Haworth CM, Meaburn E, Price TS, Evans DM, Timpson N, Kemp J, Ring S, McArdle W, Medland SE, Yang J, Harris SE, Liewald DC, Scheet P, Xiao X, Hudziak JJ, de Geus EJ, Jaddoe VW, Starr JM, Verhulst FC, Pennell C, Tiemeier H, Iacono WG, Palmer LJ, Montgomery GW, Martin NG, Boomsma DI, Posthuma D, McGue M, Wright MJ, Davey Smith G, Deary IJ, Plomin R, Visscher PM. Childhood intelligence is heritable, highly polygenic and associated with FNBP1L. Molecular Psychiatry. doi: 10.1038/mp.2012.184. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodin D, Pardini DA, Burns TG, Stevens AB. Higher order factor structure of the WISC-IV in a clinical neuropsychological sample. Child Neuropsychology. 2009;15:417–424. doi: 10.1080/09297040802603661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boker S, Neale MC, Maes HH, Wilde M, Spiegel M, Brick T, Spies J, Estabrook R, Kenny S, Bates T, Mehta PH, Fox J. OpenMx: An open source extended structural equation modeling framework. Psychometrika. 2011;76:306–317. doi: 10.1007/s11336-010-9200-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borsboom D, Mellenbergh GJ, van Heerden J. The concept of validity. Psychological Review. 2004;111:1061–1071. doi: 10.1037/0033-295X.111.4.1061. [DOI] [PubMed] [Google Scholar]
- Bouchard TJ, Jr, McGue M. Genetic and environmental influences on human psychological differences. Journal of Neurobiology. 2003;54:4–45. doi: 10.1002/neu.10160. [DOI] [PubMed] [Google Scholar]
- Bouchard TJ, McGue M. Familial studies of intelligence: a review. Science. 1981;212:1055–1059. doi: 10.1126/science.7195071. [DOI] [PubMed] [Google Scholar]
- Canivez GL, Watkins MW. Investigation of the factor structure of the Wechsler Adult Intelligence Scale - Fourth Edition (WAIS-IV): Exploratory and higher order factor analysis. Psychological Assessment. 2010;22:827–836. doi: 10.1037/a0020429. [DOI] [PubMed] [Google Scholar]
- Cardon LR, Fulker DW, Defries JC, Plomin R. Multivariate genetic analysis of specific cognitive abilities in the Colorado adoption project at age 7. Intelligence. 1992;16 [Google Scholar]
- Carey G. Inference about genetic correlations. Behavior Genetics. 1988;18:329–338. doi: 10.1007/BF01260933. [DOI] [PubMed] [Google Scholar]
- Carroll JB. Human Cognitive Abilities: A Survey of Factor-analytic Studies. Cambridge University Press; 1993. [Google Scholar]
- Cattell RB. The theory of fluid and crystalized intelligence: A critical experiment. Journal of Experimental Psychology. 1963;54:1–22. [Google Scholar]
- Centers for Disease Control and Prevention. Public health and aging: Trends in aging--United States and worldwide. MMWR CDC Surveillance Summaries. 2003;52:101–106. [Google Scholar]
- Crawford JR, Deary IJ, Allan KM, Gustafsson JE. Evaluating competing models of the relationship between inspection time and psychometric intelligence. Intelligence. 1998;26:27–42. [Google Scholar]
- Davies G, Tenesa A, Payton A, Yang J, Harris SE, Liewald D, Ke X, Le Hellard S, Christoforou A, Luciano M, McGhee K, Lopez L, Gow AJ, Corley J, Redmond P, Fox HC, Haggarty P, Whalley LJ, McNeill G, Goddard ME, Espeseth T, Lundervold AJ, Reinvang I, Pickles A, Steen VM, Ollier W, Porteous DJ, Horan M, Starr JM, Pendleton N, Visscher PM, Deary IJ. Genome-wide association studies establish that human intelligence is highly heritable and polygenic. Molecular Psychiatry. 2011;16:996–1005. doi: 10.1038/mp.2011.85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deary IJ. Intelligence. Annual Review of Psychology. 2012;63:453–482. doi: 10.1146/annurev-psych-120710-100353. [DOI] [PubMed] [Google Scholar]
- Deary IJ, Johnson W, Houlihan LM. Genetic foundations of human intelligence. Human Genetics. 2009;126:215–232. doi: 10.1007/s00439-009-0655-4. [DOI] [PubMed] [Google Scholar]
- Deary IJ, Leaper SA, Murray AD, Staff RT, Whalley LJ. Cerebral white matter abnormalities and lifetime cognitive change: a 67-year follow-up of the Scottish Mental Survey of 1932. Psychology and Aging. 2003;18:140–148. doi: 10.1037/0882-7974.18.1.140. [DOI] [PubMed] [Google Scholar]
- Delis DC, Kaplan E, Kramer JB. Delis-Kaplan Executive Function System Technical Manual. San Antonio: The Psychological Corporation; 2000. [Google Scholar]
- Dickinson D, Ragland JD, Calkins ME, Gold JM, Gur RC. A comparison of cognitive structure in schizophrenia patients and healthy controls using confirmatory factor analysis. Schizophrenia Research. 2006;85:20–29. doi: 10.1016/j.schres.2006.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eaves LJ, Last KA, Young PA, Martin NG. Model-fitting approaches to the analysis of human behavior. Heredity. 1978;41:249–320. doi: 10.1038/hdy.1978.101. [DOI] [PubMed] [Google Scholar]
- Eisen SA, True WR, Goldberg J, Henderson W, Robinette CD. The Vietnam Era Twin (VET) Registry: Method of construction. Acta Geneticae Medicae et Gemellologiae. 1987;36:61–66. doi: 10.1017/s0001566000004591. [DOI] [PubMed] [Google Scholar]
- Finkel D, Pedersen NL, McGue M, McClearn GE. Heritability of cognitive abilities in adult twins: Comparison of Minnesota and Swedish data. Behavior Genetics. 1995;25:421–431. doi: 10.1007/BF02253371. [DOI] [PubMed] [Google Scholar]
- Franz CE, Lyons MJ, O’Brien R, Panizzon MS, Kim K, Bhat R, Grant MD, Toomey R, Eisen S, Xian H, Kremen WS. A 35-year longitudinal assessment of cognition and midlife depression symptoms: the Vietnam Era Twin Study of Aging. American Journal of Geriatric Psychiatry. 2011;19:559–570. doi: 10.1097/JGP.0b013e3181ef79f1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gignac GE. Revisiting the factor structure of the WAIS-R: insights through nested factor modeling. Assessment. 2005;12:320–329. doi: 10.1177/1073191105278118. [DOI] [PubMed] [Google Scholar]
- Gignac GE. A confirmatory examination of the factor structure of the Multidimensional Aptitude Battery. Educational and Psychological Measurement. 2006a;66:136–145. [Google Scholar]
- Gignac GE. The WAIS-III as a nested factors model: A useful alternative to the more onventional oblique and higher order models. Journal of Individual Differences. 2006b;27:73–86. [Google Scholar]
- Gignac GE. Higher-order models versus direct hierarchical models: g as superordinate or breadth factor? Psychological Science Quartely. 2008;50:21–43. [Google Scholar]
- Golay P, Lecerf T. Orthogonal higher order structure and confirmatory factor analysis of the French Wechsler Adult Intelligence Scale (WAIS-III) Psychological Assessment. 2011;23:143–152. doi: 10.1037/a0021230. [DOI] [PubMed] [Google Scholar]
- Goldberg J, Curran B, Vitek ME, Henderson WG, Boyko EJ. The Vietnam Era Twin Registry. Twin Research and Human Genetics. 2002;5:476–481. doi: 10.1375/136905202320906318. [DOI] [PubMed] [Google Scholar]
- Goldberg J, Eisen SA, True WR, Henderson W. The Vietnam Era Twin Registry: Ascertainment bias. Acta Geneticae Medicae et Gemellologiae. 1987;36:67–78. doi: 10.1017/s0001566000004608. [DOI] [PubMed] [Google Scholar]
- Gustafsson JE. A unifying model for the structure of intellectual abilities. Intelligence. 1984;8:179–203. [Google Scholar]
- Hanscombe KB, Trzaskowski M, Haworth CM, Davis OS, Dale PS, Plomin R. Socioeconomic status (SES) and children’s intelligence (IQ): in a UK-representative sample SES moderates the environmental, not genetic, effect on IQ. PLoS One. 2012;7:e30320. doi: 10.1371/journal.pone.0030320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson WG, Eisen SE, Goldberg J, True WR, Barnes JE, Vitek M. The Vietnam Era Twin Registry: A resource for medical research. Public Health Reports. 1990;105:368–373. [PMC free article] [PubMed] [Google Scholar]
- Holdnack JA, Xiaobin Z, Larrabee GJ, Millis SR, Salthouse TA. Confirmatory factor analysis of the WAIS-IV/WMS-IV. Assessment. 2011;18:178–191. doi: 10.1177/1073191110393106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn JL, Cattell RB. Refinement and test of the theory of fluid and crystallized intelligence. Journal of Educational Psychology. 1966;57:253–270. doi: 10.1037/h0023816. [DOI] [PubMed] [Google Scholar]
- Jinks JL, Fulker DW. Comparison of the biometrical genetical, MAVA, and classical approaches to the analysis of human behavior. Psychological Bulletin. 1970;73:311–349. doi: 10.1037/h0029135. [DOI] [PubMed] [Google Scholar]
- Johnson W, Bouchard TJ. The structure of human intelligence: It is verbal, perceptual, and image rotation (VPR), not fluid and crystalized. Intelligence. 2005;33:393–416. [Google Scholar]
- Johnson W, Bouchard TJ, Krueger RF, McGue M, Gottesman II. Just one g: consistent results from three test batteries. Intelligence. 2004;32:95–107. [Google Scholar]
- Johnson W, Bouchard TJ, McGue M, Segal NL, Tellegen A, Keyes M, Gottesman II. Genetic and environmental influences on the Verbal-Perceptual-Image Rotation (VPR) model of the structure of mental abilities in the Minnesota study of twins reared apart. Intelligence. 2007;35:542–562. [Google Scholar]
- Johnson W, Nijenhuis JT, Bouchard TJ. Still just 1 g: Consistent results from five test batteries. Intelligence. 2008;36:81–95. [Google Scholar]
- Kendler KS, Heath AC, Martin NG, Eaves LJ. Symptoms of anxiety and depression in a volunteer twin population: The etiologic role of genetic and environmental factors. Archives of General Psychiatry. 1987;43:213–221. doi: 10.1001/archpsyc.1986.01800030023002. [DOI] [PubMed] [Google Scholar]
- Kremen WS, Jacobson KC, Panizzon MS, Xian H, Eaves LJ, Eisen SA, Tsuang MT, Lyons MJ. Factor structure of planning and problem-solving: a behavioral genetic analysis of the Tower of London task in middle-aged twins. Behavior Genetics. 2009;39:133–144. doi: 10.1007/s10519-008-9242-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kremen WS, Jacobson KC, Xian H, Eisen SA, Waterman B, Toomey R, Neale MC, Tsuang MT, Lyons MJ. Heritability of word recognition in middle-aged men varies as a function of parental education. Behavior Genetics. 2005;35:417–433. doi: 10.1007/s10519-004-3876-2. [DOI] [PubMed] [Google Scholar]
- Kremen WS, Koenen KC, Boake C, Purcell S, Eisen SA, Franz CE, Tsuang MT, Lyons MJ. Pre-trauma cognitive ability predicts risk for post-traumatic stress disorder: A twin study. Archives of General Psychiatry. 2007;64:361–368. doi: 10.1001/archpsyc.64.3.361. [DOI] [PubMed] [Google Scholar]
- Kremen WS, Thompson-Brenner H, Leung YJ, Grant MD, Franz CE, Eisen SA, Jacobson KC, Boake C, Lyons MJ. Genes, environment, and time: The Vietnam Era Twin Study of Aging (VETSA) Twin Res Hum Genet. 2006;9:1009–1022. doi: 10.1375/183242706779462750. [DOI] [PubMed] [Google Scholar]
- Luo D, Petrill SA, Thompson LA. An exploration of genetic g: Hierarchical factor analysis of cogntive data from the western reserve twin project. Intelligence. 1994;18:335–347. [Google Scholar]
- Markon KE, Krueger RF. An empirical comparison of information-theoretic selection criteria for multivariate behavior genetic models. Behavior Genetics. 2004;3:593–610. doi: 10.1007/s10519-004-5587-0. [DOI] [PubMed] [Google Scholar]
- McArdle JJ, Goldsmith HH. Alternative common factor models for multivariate biometric analyses. Behavior Genetics. 1990;20:569–608. doi: 10.1007/BF01065873. [DOI] [PubMed] [Google Scholar]
- Neale MC, Cardon LR. Methodology for genetic studies of twins and families. Dordrecht, The Netherlands: Kluwer Academic Publishers; 1992. [Google Scholar]
- Niileksela CR, Reynolds MR, Kaufman AS. An alternative Cattell-Horn-Carroll (CHC) factor structure of the WAIS-IV: age invariance of an alternative model for ages 70–90. Psychological Assessment. 2013;25:391–404. doi: 10.1037/a0031175. [DOI] [PubMed] [Google Scholar]
- Petrill SA, Luo D, Thompson LA, Detterman DK. The independent prediction of general intelligence by elementary cognitive tasks: genetic and environmental influences. Behavior Genetics. 1996;26:135–147. doi: 10.1007/BF02359891. [DOI] [PubMed] [Google Scholar]
- Petrill SA, Plomin R, Berg S, Johansson B, Pedersen NL, Ahern F, McClearn GE. The genetic and environmental relationship between general and specific cognitive abilities in twins age 80 and older. Psychological Science. 1998;9:183–189. [Google Scholar]
- Petrill SA, Saudino K, Wilkerson B, Plomin R. Genetic and environmental molarity and modularity of cognitive functioning in 2-year-old twins. Intelligence. 2001;29:31–43. [Google Scholar]
- Plomin R, Spinath FM. Genetics and general cognitive ability (g) Trends in Cognitive Science. 2002;6:169–176. doi: 10.1016/s1364-6613(00)01853-2. [DOI] [PubMed] [Google Scholar]
- Rijsdijk FV, Vernon PA, Boomsma DI. Application of hierarchical genetic models to Raven and WAIS subtests: a Dutch twin study. Behavior Genetics. 2002;32:199–210. doi: 10.1023/a:1016021128949. [DOI] [PubMed] [Google Scholar]
- Shikishima C, Hiraishi K, Yamagata M, Sugimoto Y, Takemura R, Ozaki K, Okada M, Toda T, Ando J. Is g an entity? A Japanese twin study using syllogisms and intelligence tests. Intelligence. 2009;37:256–267. [Google Scholar]
- Thomson GH. A hierarchy without a general factor. British Journal of Psychology. 1916;8:271–281. [Google Scholar]
- Thurstone LL. A factorial study of perception. Chicago: University of Chicago Press; 1944. [Google Scholar]
- Tucker-Drob EM, Rhemtulla M, Harden KP, Turkheimer E, Fask D. Emergence of a Gene x socioeconomic status interaction on infant mental ability between 10 months and 2 years. Psychological Science. 2011;22:125–133. doi: 10.1177/0956797610392926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turkheimer E, Haley A, Waldron M, D’Onofrio B, Gottesman II. Socieconomic status modifies heritability of IQ in young children. Psychological Science. 2003;14:623–628. doi: 10.1046/j.0956-7976.2003.psci_1475.x. [DOI] [PubMed] [Google Scholar]
- Uhlaner JE. Development of the Armed Forces Qualification Test and predecessor army screening tests, 1946–1950. PRB Report 1952 [Google Scholar]
- van der Maas HL, Dolan CV, Grasman RP, Wicherts JM, Huizenga HM, Raijmakers ME. A dynamical model of general intelligence: the positive manifold of intelligence by mutualism. Psychological Review. 2006;113:842–861. doi: 10.1037/0033-295X.113.4.842. [DOI] [PubMed] [Google Scholar]
- Walker NP, McConville PM, Hunter D, Deary IJ, Whalley LJ. Childhood mental ability and lifetime psychiatric contact: A 66-year follow-up study of the 1932 Scottish mental ability survey. Intelligence. 2002;30:233–245. [Google Scholar]
- Watkins MW. Structure of the Wechsler Intelligence Scale for Children--Fourth Edition among a national sample of referred students. Psychological Assessment. 2010;22:782–787. doi: 10.1037/a0020043. [DOI] [PubMed] [Google Scholar]
- Wechsler D. Manual for the Wechsler Memory Scale-Third Edition. San Antonio, TX: Psychological Corporation; 1997. [Google Scholar]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. San Antonio, Texas: The Psychological Corporation; 1999. [Google Scholar]
- Whalley LJ, Deary IJ. Longitudinal cohort study of childhood IQ and survival up to age 76. BMJ. 2001;322:1–5. doi: 10.1136/bmj.322.7290.819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams LJ, Holahan PJ. Parsimony-based fit indices for multiple-indicator models: Do they work? Structural Equation Modeling. 1994;1:161–181. [Google Scholar]
- Yung Y, Thissen D, McLeod LD. On the relationship between the higher-order factor model and the hierarchical factor model. Psychometrika. 1999;64:113–128. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.