A numerical study of blood flow using mixture theory

Abstract

In this paper, we consider the two dimensional flow of blood in a rectangular microfluidic channel. We use Mixture Theory to treat this problem as a two-component system: One component is the red blood cells (RBCs) modeled as a generalized Reiner–Rivlin type fluid, which considers the effects of volume fraction (hematocrit) and influence of shear rate upon viscosity. The other component, plasma, is assumed to behave as a linear viscous fluid. A CFD solver based on OpenFOAM^® was developed and employed to simulate a specific problem, namely blood flow in a two dimensional micro-channel, is studied. Finally to better understand this two-component flow system and the effects of the different parameters, the equations are made dimensionless and a parametric study is performed.

1. Introduction

Blood is a unique multi-component fluid whose composition is responsible for important rheological properties that are responsible for its vital physiological functions. Its primary constituents are flexible, discoid red blood cells (RBCs) (approximately 45% volume fraction) suspended within essentially Newtonian plasma (Robertson, Sequeira, & Kameneva, 2008). In the context of blood-wetted medical devices, the trafficking of RBCs within the plasma greatly contributes to both safety and efficacy. For example in oxygenators and artificial lungs, it is desirable for RBCs which are responsible for transport of oxygen and carbon dioxide, to efficiently interact with the artificial fibers that deliver and remove these gasses. In virtually all blood-wetted devices, it is usually undesirable for the blood to coagulate on the artificial surfaces. This phenomenon, known as thrombosis, is mediated by the platelets, a dilute constituent of blood which is in turn influenced by collisions with the RBCs. Therefore at the microscopic level, the distribution of RBCs is responsible for the distribution of platelets (Aarts, Steendijk, Sixma, & Heethaar (1986)). Accordingly the design of improved cardiovascular devices requires an accurate model of these phenomena. Conversely, the inadequacies of current models stifle our ability to design these devices with any confidence (Thompson, Loebe, & Noon, 2003). As a result, contemporary designs are based primarily on empiricism, and experimental trial-and-error.

It is known that in large vessels (whole) blood behaves as a Navier–Stokes (Newtonian) fluid (Fåhraeus, 1929; Fåhræus & Lindqvist, 1931; Fung, 1993, Chapter 3); however, in a vessel whose characteristic dimension is in the range of tens to hundreds of blood cells (e.g., for a diameter in the range of 20–500 microns) blood behaves as a non-Newtonian fluid, exhibiting shear-thinning, stress relaxation (Bagchi, 2007) and phase separation (Goldsmith, 1971). In larger vessels blood also exhibits shear thinning, particularly for shear rates below 100 s⁻¹. These non-Newtonian properties of blood are mainly attributed to the behavior of the RBCs: the aggregation and disaggregation of the RBCs as a function of shear rate; the deformability of the RBCs; and the alignment of the RBCs in response to extensional flow. Because of the fibrinogen and large globulins, RBCs aggregate and form rod-shaped stacks called rouleaux at low shear rate [see Popel and Johnson (2005) and Bäumler, Neu, Donath, and Kiesewetter (1999)]. This aggregation of the RBCs, which increases the blood viscosity is however reversed when the shear rate increases, causing their disaggregation. The volume fraction of RBCs (known as hematocrit) strongly influences all of the aforementioned phenomena. Increased packing of RBCs affects their collision frequency, and hence their ability to aggregate and to migrate within the flow field. Accordingly, the viscosity of the blood increases dramatically as the hematocrit increases (Chien, Usami, Taylor, Lundberg, & Gregersen, 1966, 1971; Pries, Neuhaus, & Gaehtgens, 1992). Likewise, the property of shear-thinning viscosity becomes weaker and eventually disappears as the hematocrit decreases (Brooks, Goodwin, & Seaman, 1970). The deformability of RBCs is also an important property which affects viscosity and cell trafficking. In capillaries, with sizes equivalent or smaller than that of RBCs, the deformability of RBCs allow them to fold and flex as they transport gasses through the vessel walls. In larger vessels or passages, the deformability of the RBCs allow them to become more streamlined, and aligned at high shear rates – thereby contributing to shear thinning (Chien, 1970). It should be acknowledged that, although the RBCs dominates the rheological properties of blood, other factors such as the plasma viscosity, white blood cells, etc. also play a role (Kameneva, Garrett, Watach, & Borovetz, 1998; Middleman, 1972; Rourke & Ernstene, 1930).

In the past several decades, investigations of blood flow in micro-scale channels have revealed several important phenomena due to the complex rheological properties of blood. In vessel of diameter ranging from approximately 0.05 to 1.5 mm, blood exhibits a thin layer adjacent to the wall that is depleted of RBCs (Marhefka et al., 2009). This phenomenon is known as the Fahraeus–Lindqvist effect (Fung, 1993). This depletion of RBCs near the wall causes the hematocrit of branch vessels to be depleted – a phenomenon known as plasma-skimming (Carr & Wickham, 1990; Krogh, 1921; Marhefka et al., 2009; Skalak, Ozkaya, & Skalak, 1989). Several early experiments related to blood cell margination were performed in tubes, such as Goldsmith’s seminal experiment in which he flash froze the flow to observe the concentration of cells to the center-line (Goldsmith, 1968), a great number of modern experiments are performed in microchannels of rectangular cross section. The reason for this is twofold: microchannels can be much more easily formed using photolithography, and secondly, parallel walls are much more amenable to microscopic measurements. The technology for visualizing flow in non-parallel (e.g. circular) cross sections is still in its infancy, and include micro PIV (Sugii & Okuda, 2005) and confocal PIV methods (Lima & Wada, 2006; Patrick, Chen, Frakes, Dur, & Pekkan, 2011). Furthermore, micro-channels have also been used in a variety of devices such as film oxygenators and recently, dialysis-like cell separators such as the one being developed by our group for treatment of malaria-infected blood. [see Kim, Massoudi, Antaki, and Gandini (2012)]. In summary, it is evident that blood flow at micro-scale exhibits more complex behavior and acts as a multi-component material, which cannot be described by a single phase model.

Motivated by the observation of these phenomena, various multiphase models for blood have been developed. The Immersed Boundary Method (IBM) combined with the Lattice Boltzman Method (LBM) has become a popular method for modeling deformation, cluster formation and collisions of RBCs [see Dupin, Halliday, Care, Alboul, and Munn (2007), Clausen, Reasor, and Aidun (2010) and Zhang, Johnson, and Popel (2009)]. An alternative method consists of the so-called two-fluid or Eulerian–Eulerian two phase model (Jung, Hassanein, & Lyczkowski, 2006). In tandem, over the past four decades, multiconstituent models have been developed for a variety of non-biologic fluids. Two methods in particular are based on first principles of continuum mechanics: the Mixture Theory (or the theory of interacting continua) [see Rajagopal and Tao (1995)] and the Averaging Method [see Ishii (1975)]. In this paper the Mixture Theory is applied as a basis for deriving a two-phase model for blood (Massoudi, Kim, & Antaki, 2012).

The Mixture Theory was first presented by Truesdell in 1957 (Truesdell, 1957) as a means of generalizing the equations and principles of the mechanics of a single continuum to include any number of superimposed continua. In a sense, it is a homogenization process in which each component is regarded as a single continuumand at each instant of time, every point in space is considered to be occupied by a particle belonging to each component of the mixture (Truesdell, 1984). In recent years it has been applied to a variety of applications such as fluid–solid particles, lubrication with binary-mixtures of bubbly oil, viscoelastic porous mixtures, swelling porous media with microstructure, reacting immiscible mixtures, polymeric solutions, growth and remodeling of soft tissues, ionized fluid mixtures, etc., (Massoudi, 2008). For review articles on this subject, see the papers by Atkin and Craine (1976a, 1976b) and Bowen (1976). Mixture Theory has also been used in a variety of biomechanics applications [see for example, Ateshian, Likhitpanichkul, and Hung (2006), Garikipati, Arruda, Grosh, Narayanan, and Calve (2004), Humphrey and Rajagopal (2002), Klisch and Lotz (2000), Lemon, King, Byrne, Jensen, and Shakesheff (2006) and Tao, Humphrey, and Rajagopal (2001)]. Because of its many desirable properties, Mixture Theory has been adopted for this study.

The paper is organized as follows. The kinematical variables and governing equations are introduced in Section 2 while the related constitutive equations are presented in Section 3. In Section 4, the effect of the various dimensionless parameters of our model is studied.

2. Governing equations

Let X₁ and X₂ denote the position of the bodies in the reference configuration (i.e., prior to mixing) belonging respectively to the plasma, treated as a fluid constituent, and the RBCs, treated as a solid. The motion of the two components can be represented as [see Johnson, Massoudi, and Rajagopal (1991)]

$${\mathit{x}}_1={\mathit{\chi }}_1({\mathit{X}}_1,t),{\mathit{x}}_2={\mathit{\chi }}_2({\mathit{X}}_2,t)$$ (1)

while the kinematical quantities associated with these motions take the expressions

$${\mathit{v}}_1=\frac{d_1{\mathit{x}}_1}{dt},{\mathit{v}}_2=\frac{d_2{\mathit{x}}_2}{dt}$$ (2)

$${\mathit{D}}_1=\frac{1}{2}\left(\frac{\partial {\mathit{v}}_1}{\partial {\mathit{x}}_1}+{\left(\frac{\partial {\mathit{v}}_1}{\partial {\mathit{x}}_1}\right)}^T\right),{\mathit{D}}_2=\frac{1}{2}\left(\frac{\partial {\mathit{v}}_2}{\partial {\mathit{x}}_2}+{\left(\frac{\partial {\mathit{v}}_2}{\partial {\mathit{x}}_2}\right)}^T\right)$$ (3)

where v is the velocity field, D is the symmetric part of velocity gradient, and $\frac{d_1}{dt}$ and $\frac{d_2}{dt}$ denote differentiation with respect to time holding X₁ and X₂ fixed, respectively. The bulk density field, ρ₁ and ρ₂, for these two components are

$${\rho }_1=(1-\varphi ){\rho }_{10},{\rho }_s=\varphi {\rho }_{20}$$ (4)

where ρ₁₀ and ρ₂₀ are the pure density of plasma, and the RBCs, in the reference configuration; ϕ is the volume fraction of RBCs, the hematocrit, where 0 ≤ ϕ < ϕ_max < 1. The function ϕ is represented as a continuous function of position and time, which takes a value between one and zero at any position and at anytime, with the extreme values of 1 and 0 depending upon whether one is pointing to a particle (RBCs) or to the liquid (plasma) at that position. That is, the real volume distribution content has been averaged, in some sense, over the neighborhood of any given position. It should be mentioned that in practice ϕ is never equal to one; its maximum value, generally designated as the maximum packing fraction, depends on the shape, size, method of packing, etc.

In the absence of thermo-chemical and electromagnetic effects, the governing equations consist of the conservation of mass, linear momentum and angular momentum. The equations of conservation of mass in the Eulerian form are [see Atkin and Craine (1976a, 1976b)],

$$\frac{\partial {\rho }_1}{\partial t}+\mathit{div}({\rho }_1{\mathit{v}}_1)=0$$ (5a)

$$\frac{\partial {\rho }_2}{\partial t}+\mathit{div}({\rho }_2{\mathit{v}}_2)=0$$ (5b)

where $\frac{\partial }{\partial t}$ is the derivative with respect to time and div is the divergence operator, while the equations of balance of the linear momentum are given by,

$${\rho }_1\frac{D^1{\mathit{v}}_1}{Dt}=\mathit{div}({\mathit{T}}_1)+{\rho }_1{\mathit{b}}_1+{\mathit{f}}_l$$ (6a)

$${\rho }_2\frac{D^2{\mathit{v}}_2}{Dt}=\mathit{div}({\mathit{T}}_2)+{\rho }_2{\mathit{b}}_2-{\mathit{f}}_l$$ (6b)

where in general for any scalar β, $\frac{D^{\alpha }\beta }{Dt}=\frac{\partial \beta }{\partial t}+{\mathit{v}}^{\alpha }·\nabla \beta$, α = 1, 2, and (for any vector w), $\frac{D^{\alpha }\mathit{w}}{Dt}=\frac{\partial \mathit{w}}{\partial t}+(\nabla \mathit{w}){\mathit{v}}^{\alpha }$, T₁ and T₂ stand for the Cauchy stress tensors, f_I represents the interaction forces (exchange of momentum) between the components, and b₁ and b₂ refer to the body force. T₁, T₂ and f_I will be given by the constitutive equations. The balance of the angular momentum implies that, in the absence of couple stresses, the total Cauchy stress tensor is symmetric. Once the individual (partial) stress tensors are derived (or proposed), a mixture stress tensor can be defined for blood as T_m = T₁ + T₂ (Green & Naghdi, 1967, 1968) where T₁ = (1 − ϕ) T₁₀ and T₂ = ϕT₂₀ so that the mixture stress tensor reduces to that of the plasma as ϕ → 0 and to that of the RBCs as ε → 0 [where ε = (1 − ϕ)]. T₂ may also be written as ${\mathit{T}}_2=\varphi \widehat{{\mathit{T}}_2}$, where $\widehat{{\mathit{T}}_2}$ may be thought of as representing the stress tensor in the reference configuration of the RBCs. Finally, for a complete study of a thermo-mechanical problem, not only in Mixture Theory, but in continuum mechanics in general, the Second Law of Thermodynamics has to be considered. In other words, in addition to other principles in continuum mechanics such as material symmetry, frame indifference, etc., the Second Law imposes important restrictions on the type of motion and/or the constitutive parameters [For a discussion of important concepts in constitutive equations of mechanics, we refer the reader to the books by Liu (2002) and Batra (2006)]. Since, there is no general agreement on the functional form of the constitutive relation and since the Helmholtz free energy is not known, a complete thermodynamical treatment of the model used in our studies is lacking.¹In the next section, we briefly discuss the constitutive models for both the plasma and the RBCs.

3. Constitutive equations

For closure of the governing equations of motion, Eqs. (5) and (6), we can see that constitutive equations are needed for the stress tensors of the plasma and the RBCs as well as the interaction forces. A complete constitutive relation for the stress tensor of the (whole) blood, not only must capture and describe the rheological characteristics of its different components, but also must include the biochemistry and the chemical reactions occurring. To date no such comprehensive and universal constitutive relation exists. As mentioned by Anand, Rajagopal, and Rajagopal (2005): “However, the numerous biochemical reactions that take place leading to the formation and lysis of clots, and the exact influence of hemodynamic factors in these reactions are incompletely understood.” In fact, the majority, if not all, of the papers published on blood characteristics either deal with the biochemistry of clot formation and other biochemical issues, ignoring completely the hemodynamic [see for example Kuharsky and Fogelson (2001)], or deal exclusively with hemodynamic or homeostasis and pay no attention to the biochemical reactions [see Sorensen, Burgreen, Wagner, and Antaki (1999)]. Anand and Rajagopal (2002) developed a model for blood that is capable of incorporating platelet activation. More recently, Rajagopal and colleagues (Anand, Rajagopal, & Rajagopal (2006, 2008)) have provided a framework whereby some of the biochemical aspects of blood along with certain rheological (viscoelastic) properties of blood are included in their formulation. We assume that blood is a two-component mixture, composed of the red blood cells (RBCs) suspended in a (platelet rich) plasma.

3.1. Plasma

We assume that the plasma behaves as a linear viscous fluid [see Massoudi and Antaki (2008)]

$${\mathit{T}}_1=[-p_1+{\lambda }_{1}tr{\mathit{D}}_1]\mathit{I}+2{\mu }_1{\mathit{D}}_1$$ (7)

where p₁ is the plasma pressure, μ₁ and λ₁ are the first and second coefficients of viscosity of the plasma, ‘tr’ is the trace operator, and I is the identity tensor. It is necessary to make sure that when the volume fraction of the RBCs equals ϕ_max, the effect of plasma should disappear from the equations. To ensure this, we assume,

$$p_1=p(1-\varphi ),{\lambda }_1={\lambda }_{10}(1-\varphi ),{\mu }_1={\mu }_{10}(1-\varphi )$$ (8)

where p is the pressure of the mixture, and λ₁₀ and μ₁₀ are the first and second (constant) coefficients of viscosity of the pure plasma.

3.2. RBCs

We model the RBCs as a generalized Reiner–Rivlin model proposed by Massoudi (2011), which exhibits a shear dependent viscosity and includes the effect of porosity,

$${\mathit{T}}_2=[{\beta }_1+{\beta }_{2}tr{\mathit{D}}_2]\mathit{I}+{\beta }_3{\mathit{D}}_2+{\beta }_4{\mathit{D}}_2^2$$ (9)

where β₁,β₂,β₃ and β₄, depend on the hematocrit ϕ; in addition, β₃, is also assumed to depend on the symmetric part of the velocity gradient, implying a shear rate dependent viscosity. Furthermore, based on the basic principle of Mixture Theory that when the hematocrit is equal to 0, the effect of the RBCs should disappear, the expressions for β₁,β₂,β₃ and β₄ as proposed by Massoudi and Antaki (2008) are,

$$\begin{array}{l}{\beta }_1=-p\varphi ,{\beta }_2={\beta }_{20}(\varphi +{\varphi }^2),\\ {\beta }_3(\varphi ,tr{\mathit{D}}_2)={\beta }_{30}({\mathrm{\Pi }}^{\alpha })(\varphi +{\varphi }^2),{\beta }_4={\beta }_{40}(\varphi +{\varphi }^2)\end{array}$$ (10)

where Π is related to the invariants of D₂; β₂₀, β₃₀ and β₄₀ are material parameters which, in general, need to be measured experimentally. In the present study, the shear-thinning effect is incorporated by applying a shear dependent viscosity model for the RBCs, as suggested by Yeleswarapu (1994),

$${\beta }_{30}=\left[{\mu }_{\infty }+({\mu }_0-{\mu }_{\infty })\frac{1+ln\left(1+k{\left(2tr{\mathit{D}}_2^2\right)}^{1/2}\right)}{1+k{\left(2tr{\mathit{D}}_2^2\right)}^{1/2}}\right]$$ (11)

where μ₀ and μ_∞ are the viscosities when the shear rate approaches zero and infinity, respectively, and k is the shear thinning parameter. It is known that in a vessel whose characteristic dimension is about the same size as the characteristic size of blood cells, blood behaves as a non-Newtonian fluid, exhibiting shear-thinning and stress relaxation. Thurston (1972, 1973) has pointed out the viscoelastic behavior of blood while stating that the stress relaxation is more significant for cases where the shear rate is low. It has also been reported that at low shear rates, blood seems to have a high apparent viscosity (due to RBC aggregation) while at high shear rates the opposite behavior is observed (due to RBC dis-aggregation) [see Anand and Rajagopal (2004) and Anand et al. (2005, 2006)]. A model which has been able to capture the shear-thinning behavior of blood over a wide range of shear rates is the one proposed by Yeleswarapu (1994) and Yeleswarapu, Kamaneva, Rajagopal, and Antaki (1998) which is a generalization of a three constant Oldroyd-B fluid. Thus, in a sense the model we are using here for the RBCs, is a viscoelastic shear-thinning fluid model where the viscosity is also a function of volume fraction.

3.3. Interaction forces

For the interaction forces, we use a simplified form of the constitutive equation proposed by Johnson, Massoudi, and Rajagopal (1990) and Massoudi (2003),

$${\mathit{f}}_I=A_1\nabla \varphi +A_{2}F(\varphi )({\mathit{v}}_2-{\mathit{v}}_1)+A_3\varphi {\left(2tr{\mathit{D}}_1^2\right)}^{-1/4}{\mathit{D}}_1({\mathit{v}}_2-{\mathit{v}}_1)$$ (12)

where the first term represents the force due to the density gradient (Muller, 1968); the second term is related to the (Stokes) drag force; and the third corresponds to the shear lift (or Saffman’s lift (Saffman, 1965, 1968)) force. Furthermore, A₁, A₂ and A₃ are related to material properties, F(ϕ) is called the hindrance function which comes from the generalization of the interaction force from a single particle (RBC) to an assembly of particles. It can be obtained from the empirical correlations of sedimentation of particles (see Johnson et al. (1990) and Drew (1976)),

$$A_2=\frac{9{\mu }_1}{2a^2},A_3=\frac{3(6.46){({\rho }_1{\mu }_1)}^2}{4\pi a}$$ (13)

where a is the radius of the particles (RBCs). Various forms of the hindrance function are available (see for example, Johnson et al. (1990), Batchelor (1972), Tam (1969) and Rourke & Ernstene (1930)),

$$F(\varphi )=\{\begin{array}{l}\varphi (1+6.55\varphi )\mathit{Batchelor}(\mathit{Drew})\hfill \\ \varphi \frac{4+3\varphi +3\sqrt{8\varphi -3{\varphi }^2}}{{(2-3\varphi )}^2}\mathit{Tam}\hfill \\ \varphi {(1-\frac{\varphi }{0.80145})}^{-3.2575}\mathit{Rourke}\mathit{and}\mathit{Ernstene}\hfill \end{array}$$ (14)

In this paper we use the relationship suggested by Drew (Batchelor).

4. Parametric study: flow of blood in a rectangular channel

In this section, in order to gain further insight into the nature and influence of the various terms in the two phase model we perform a parametric study. To achieve numerical stability, making it possible to select a wider range of parameters, we choose a special case of the function F (ϕ) above suggested by Bachelor (Drew). Moreover in order to save computational time, we reduce the geometry to 2-D, by assuming an infinitely deep channel (z direction as shown in Fig. 1). Hexahedral meshes of the micro-channel are generated by OpenFOAM^® (blockMesh) with 50 and 40 elements in x and y directions, respectively, and with the meshes refined near the walls. The velocity and the volume fraction fields are:

$$\{\begin{array}{l}{\mathit{v}}_1=v_{1x}(x,y;z){\mathit{e}}_{\mathit{x}}+v_{1y}(x,y,z;t){\mathit{e}}_{\mathit{y}}+v_{1z}(x,y,z;t){\mathit{e}}_{\mathit{z}}\hfill \\ {\mathit{v}}_2=v_{2x}(x,y,z;t){\mathit{e}}_{\mathit{x}}+v_{2y}(x,y,z;t){\mathit{e}}_{\mathit{y}}+v_{2z}(x,y,z;t){\mathit{e}}_{\mathit{z}}\hfill \\ \varphi =\varphi (x,y,z;t)\hfill \end{array}$$ (15)

Fig. 1.

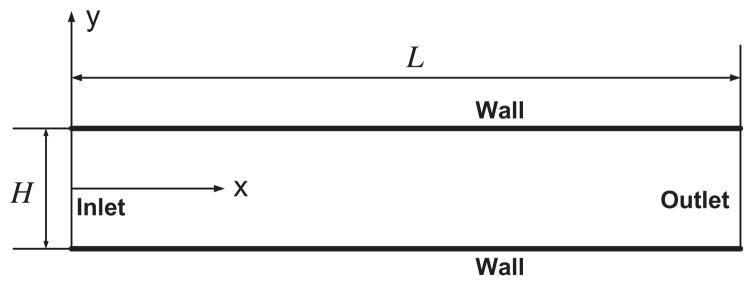
Schematic of the rectangular micro-channel, with infinite depth (z direction).

In a recent study, Wu, Aubry, and Massoudi (2013a) studied the flow of blood in a micro-channel. They used this particular geometry, since Patrick et al. (2011) had focused on a study where they measured the near-wall RBCs in a rectangular microchannel. Wu, Aubry, and Massoudi (2013b) were able to show that their numerical results, using the data available in literature, produced very good agreement with the experimental results of Patrick et al. (2011). In the current study, we will perform a parametric study using the dimensionless forms of the equations. We can see that the stress tensors and the interaction forces have many material parameters which need to be modeled. In the absence of any or limited experimental data, we have assumed very specific functions for some of these coefficients in the stress tensors and we have proposed some new ones for the interaction forces. Clearly, these choices would restrict the solution to the problem and clearly alternative choices are possible and they in turn may provide different answers. In our selection of the material coefficients, we have been guided by our previous studies in granular materials and blood flow.

4.1. Dimensionless governing equations

Substituting Eqs. (7), (9) and (12) into Eqs. (6a) and (6b), we obtain the two dimensionless momentum equations (here we have assumed that both phases are incompressible) which yield for the plasma phase,

$$\begin{array}{l}(1-\varphi ){\rho }_{10}\left[\frac{\partial {\mathit{V}}_1}{\partial \tau }+(\mathit{grad}{\mathit{V}}_1){\mathit{V}}_1\right]=(\mathit{grad}\varphi )P-(1-\varphi )\mathit{gradP}+\frac{2}{Re}[(-\mathit{grad}\varphi ){\mathit{D}}_1+(1-\varphi )\mathit{div}{\mathit{D}}_1]+\frac{{\rho }_{10}}{Fr}(1-\varphi ){\mathit{b}}_1\\ +C_1\mathit{grad}\varphi +C_{2}F(\varphi )({\mathit{D}}_2-{\mathit{D}}_1)+C_3\varphi {\left(2tr{\mathit{D}}_1^2\right)}^{-1/4}{\mathit{D}}_1({\mathit{D}}_2-{\mathit{D}}_1)\end{array}$$ (16)

and for the RBCs phase,

$$\begin{array}{l}\varphi {\rho }_{20}\left[\frac{\partial {\mathit{V}}_2}{\partial \tau }+(\mathit{grad}{\mathit{V}}_2){\mathit{V}}_2\right]=-(\mathit{grad}\varphi )P-\varphi \mathit{gradP}+[B_{31}(\varphi +{\varphi }^2)+B_{32}(\varphi +{\varphi }^2)\mathrm{\Pi }]\mathit{div}{\mathit{D}}_1+B_{31}[\mathit{grad}(\varphi +{\varphi }^2)]{\mathit{D}}_2\\ +B_{32}[\mathit{grad}(\varphi +{\varphi }^2)\mathrm{\Pi }+(\varphi +{\varphi }^2)\mathit{grad}\mathrm{\Pi }]{\mathit{D}}_2+R_4[\mathit{grad}(\varphi +{\varphi }^2)]{\mathit{D}}_2^2+R_4(\varphi +{\varphi }^2)\mathit{div}{\mathit{D}}_2^2\\ +\frac{{\rho }_{20}}{Fr}\varphi {\mathit{b}}_2-C_1\mathit{grad}\varphi -C_{2}F(\varphi )({\mathit{D}}_2-{\mathit{D}}_1)-C_3\varphi {\left(2tr{\mathit{D}}_1^2\right)}^{-1/4}{\mathit{D}}_1({\mathit{D}}_2-{\mathit{D}}_1)\end{array}$$ (17)

where

$$\begin{array}{l}{\mathit{V}}_1=\frac{{\mathit{v}}_1}{u_0};{\mathit{V}}_2=\frac{{\mathit{v}}_2}{u_0};{\mathit{x}}^{\ast }=\frac{\mathit{x}}{H};\tau =\frac{t{u}_0}{H}\\ {\rho }_{10}^{\ast }=\frac{{\rho }_{10}}{{\rho }_0};{\rho }_{20}^{\ast }=\frac{{\rho }_{20}}{{\rho }_0};{\mathit{b}}_1^{\ast }=\frac{{\mathit{b}}_1}{g};{\mathit{b}}_2^{\ast }=\frac{{\mathit{b}}_2}{g}\\ P=\frac{p}{{\rho }_0{u}_0^2};di{v}^{\ast }(·)=\mathit{Hdiv}(·);{\mathit{grad}}^{\ast }(·)=\mathit{Hgrad}(·)\\ {\mathit{D}}_1^{\ast }=\frac{1}{2}[{\mathit{grad}}^{\ast }{\mathit{V}}_1+{({\mathit{grad}}^{\ast }{\mathit{V}}_1)}^T];{\mathit{D}}_2^{\ast }=\frac{1}{2}[{\mathit{grad}}^{\ast }{\mathit{V}}_2+{({\mathit{grad}}^{\ast }{\mathit{V}}_2)}^T]\\ \mathrm{\Pi }=\frac{1+ln(1+K\mathrm{\Gamma })}{1+K\mathrm{\Gamma }};K=\frac{k{u}_0}{H};\mathrm{\Gamma }=\frac{H\stackrel{.}{\gamma }}{u_0};\stackrel{.}{\gamma }={\left[tr\left({\mathit{D}}_2^2\right)\right]}^{1/2}\end{array}$$ (18)

where H is a characteristic length, e.g., the distance between the two channel plates (y direction in Fig. 1), u₀ is a characteristic velocity, e.g., the inlet velocity, ρ₀ is a characteristic density, e.g., the plasma density, and x is the position vector. Moreover, the asterisks are dropped for simplicity. The following dimensionless numbers are then obtained,

$$\begin{array}{l}Re=\frac{{\rho }_0{u}_{0}H}{{\mu }_{10}};R_4=\frac{{\beta }_{40}}{{\rho }_0{u}_{0}H};Fr=\frac{u_0^2}{Hg}\\ K=\frac{k{u}_0}{H};B_{31}=\frac{{\mu }_{\infty }}{{\rho }_0{u}_{0}H};B_{32}=\frac{({\mu }_0-{\mu }_{\infty })}{{\rho }_0{u}_{0}H}\\ C_1=\frac{A_1}{{\rho }_0{u}_0^2};C_2=\frac{A_{2}H}{{\rho }_0{u}_0};C_3=\frac{A_3{H}^{1/2}}{{\rho }_0{u}_0^{1/2}}\end{array}$$ (19)

where Re is the Reynolds number of plasma, R₄ is related to the normal stress coefficient, Fr is the Froude number, K is a parameter related to the shear-thinning of the RBCs, B₃₁ and B₃₂ are related to the viscous effects of the RBCs (similar to the Reynolds number), C₁ is related to the coefficient of the force due to density gradients, C₂ is related to the drag coefficient, and C₃ is related to the lift coefficient.

In all cases in this study, we assume that a uniform volume fraction of the RBCs at the inlet equal to 0.45 and the inlet velocity of both RBCs and plasma is 1. The full set of boundary conditions² is summarized in Table 1. [See also Kim (2012).] Based on the mathematical model discussed above, using OpenFOAM^®, a two-component CFD solver was been developed. For a detailed description of the algorithm see Kim (2012) and Rusche (2002). We also assume that the first term in the interaction force, i.e. A₁, and the normal stress effect term, β₄₀, are zero; the effect of the body force, i.e. the gravity, is assumed to be negligible; thus we only consider the effect of the dimensionless parameters, Re, K, B₃₁, B₃₁, C₂ and C₃ hereafter.

Table 1.

Boundary conditions.

Boundary	Pressure	Velocity	Volume fraction
Inlet	Zero gradient	Uniform value	Uniform value
Outlet	Uniform value (0)	Zero Gradient	Zero gradient
Wall	Zero gradient	Uniform value (0)	Zero gradient

4.2. Numerical results

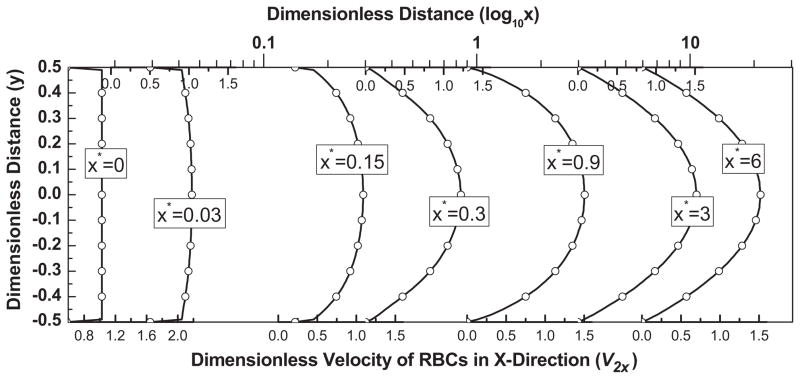
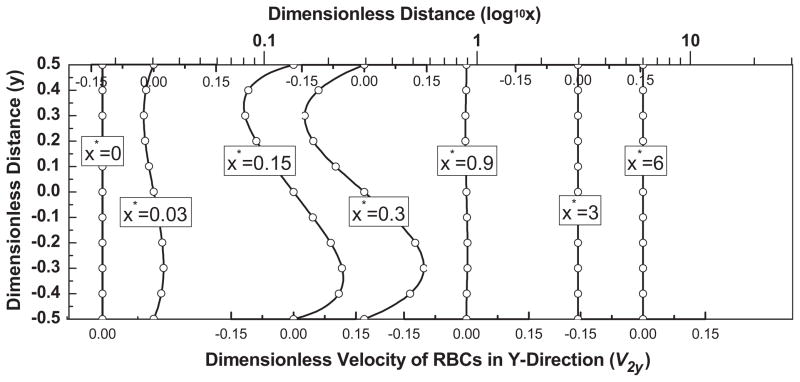
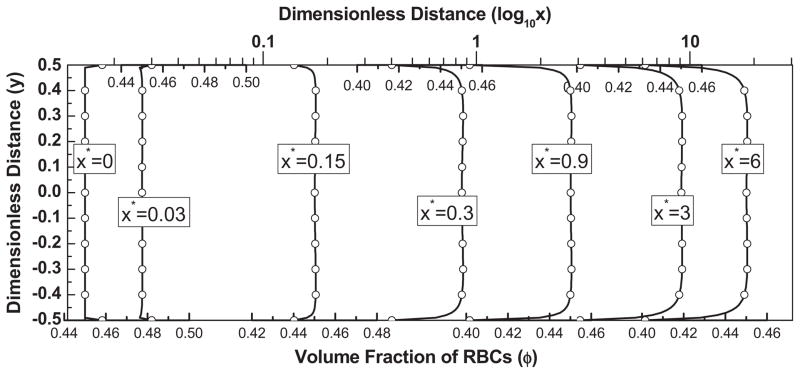
Figs. 2(a)–(c) show the velocity distributions in the x direction [v_2x] and y direction [v_2y] [see Eq. (15)] and the volume fraction of RBCs. Due to the large value of the drag force term, C₂, chosen in this case, the velocity profiles of the plasma and the RBCs coincide. From the observed development of velocity, we see that the flow becomes fully developed at approximately position x^*= 3 (i.e. x = 3H). Fig. 2b shows the corresponding y-velocity distribution of the RBCs at various downstream (x^*) locations. We observe that in the lower half of the channel the velocity is positive while in the upper half the velocity is negative, indicating that the RBCs migrate from the wall to the center of the channel. It also can be seen that near the inlet of the channel, influenced by the inlet boundary condition, the y velocity component is initially small and gradually increases due to the lift force, C₃, achieving a maximum value at approximately x^* = 0.3 and then returning to zero as the RBC distribution reaches equilibrium. The resulting volume fraction of the RBCs are provided in Fig. 2c, in which the development of a depletion layer is clearly visible.

Figure 2.

Fig. 2a. The streamwise (x) velocity distribution of RBCs at various streamwise locations, for the parameter values Re = 100, K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₂ = 10,000, C₃ = 3.

Fig. 2b. The y-velocity distribution of RBCs at various streamwise locations, for the parameter values Re = 100, K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₂ = 10,000, C₃ = 3.

Fig. 2c. The volume fraction distribution of RBCs at various streamwise locations, for the parameter values Re = 100, K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₂ = 10,000, C₃ = 3.

In the remainder of this section, we perform a parametric study, exploring the effect of various dimensionless parameters on the flow. All the numerical results shown in Figs. 3–8 are obtained for the case of the fully developed flow.

Figure 3.

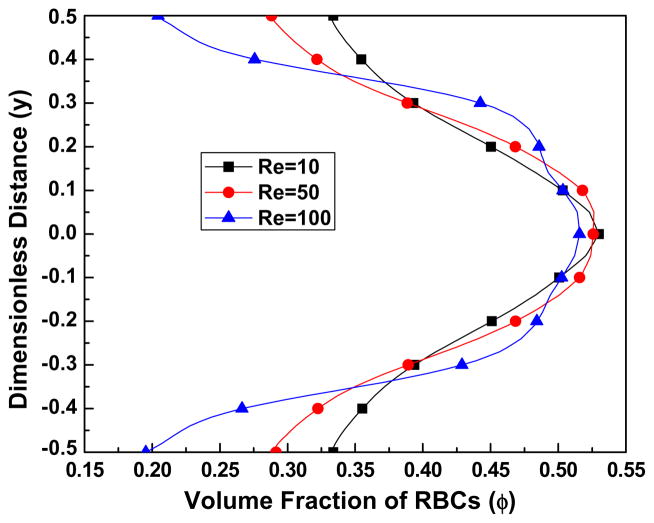
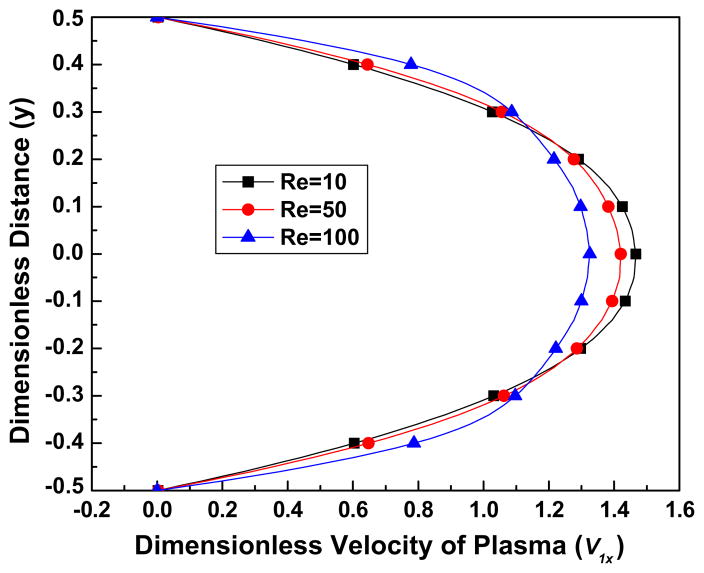
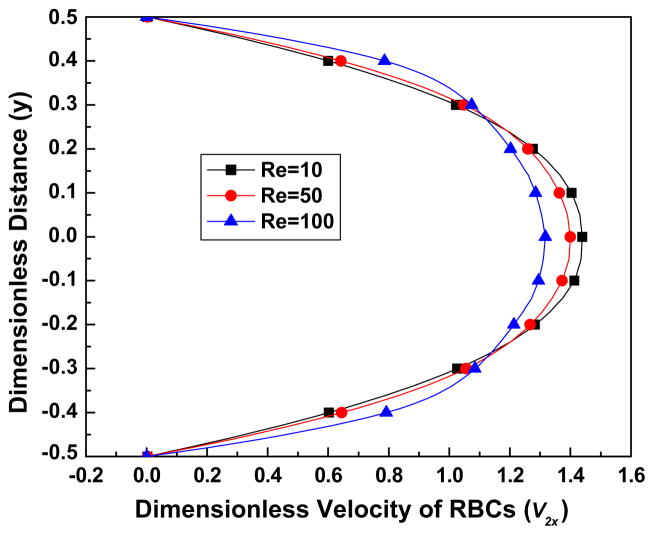
Fig. 3a. The effect of the Reynolds number Re on the volume fraction of RBCs, for the parameter values K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₂ = 10, C₃ = 3.

Fig. 3b. The effect of the Reynolds number Re on the streamwise (x) velocity of the plasma, for the parameter values K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₂ = 10, C₃ = 3.

Fig. 3c. The effect of the Reynolds number Re on the streamwise (x) velocity of RBCs, for the parameter values K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₂ = 10, C₃ = 3.

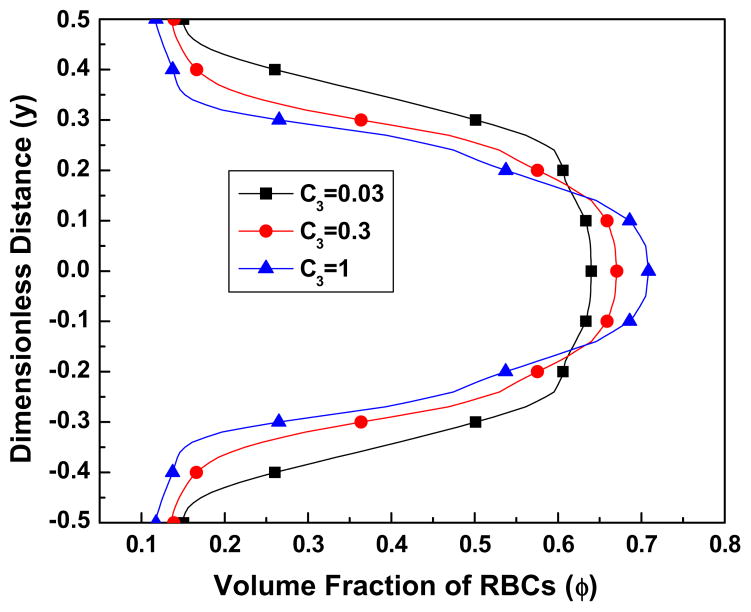
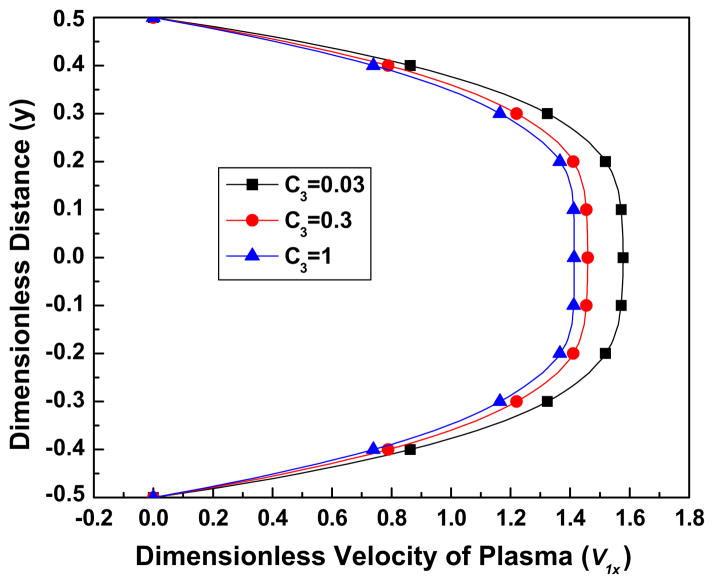
Figure 8.

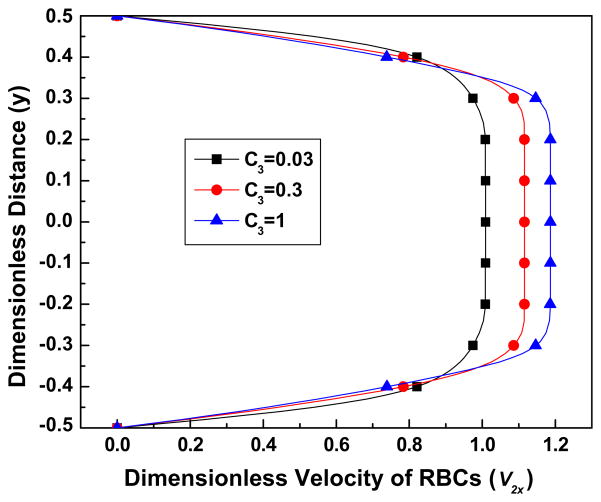
Fig. 8a. The effect of the parameter C₃ on the volume fraction of the RBCs, for the parameter values Re = 100, K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₂ = 0.1.

Fig. 8b. The effect of the parameter C₃ on the streamwise (x) velocity of the plasma, for the parameter values Re = 100, K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₂ = 0.1.

Fig. 8c. The effect of the parameter C₃ on the streamwise (x) velocity of the RBCs, for the parameter values Re = 100, K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₂ = 0.1.

4.2.1. Effect of Re

Fig. 3a shows the volume fraction distribution of the RBCs for different values of the Reynolds number Re. It can be seen that an increase of the Reynolds number accentuates the depletion phenomenon near the wall, which is consistent experimental observations of Lih (1969). Figs. 3(b) and(c) show the effect of the Reynolds number on the streamwise (x) velocity distribution of the plasma and the RBCs. Comparing these two figures we deduce that the velocity difference between the two phases is rather small. This could be attributed to the large value of the drag force term, C₂. These two figures also illustrate the effect of increasing values of the Reynolds number, for example through a decrease of the plasma viscosity, on the bluntness of the velocity profile.

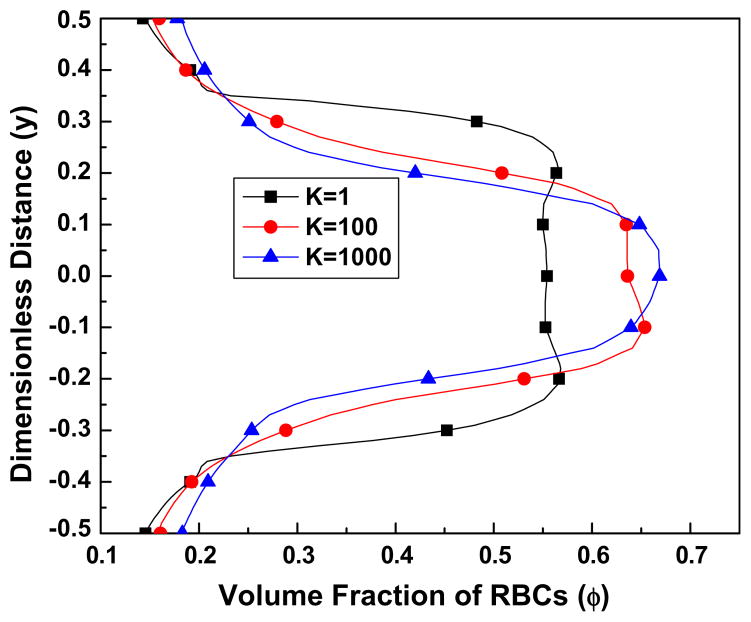
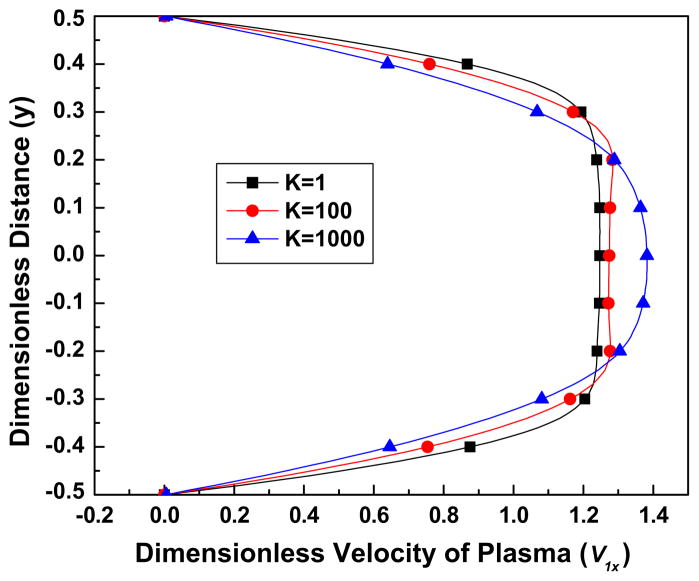
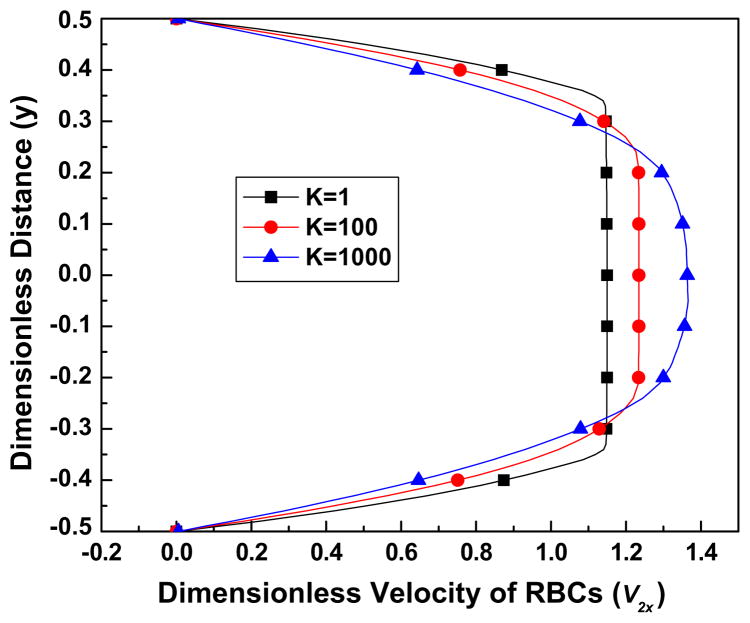
4.2.2. Effect of K, B₃₁ and B₃₂

Fig. 4a shows the volume fraction distribution of the RBCs as a function of the RBCs shear thinning parameter K. It can be seen that as K increases, the value of the volume fraction around the center line becomes larger. That might be related to the fact that for larger values of K a more parabolic velocity profile is obtained, implying a region of larger velocity gradient, see Figs. 4(b) and (c). Eq. (12) corroborates that the lift force, which causes the RBCs to migrate from the wall to the center line of the channel is positive and proportional to the plasma velocity gradient.

Figure 4.

Fig. 4a. The effect of the RBCs shear thinning parameter K on the volume fraction of RBCs, for the parameter values Re = 100, B₃₁ = 0.5, B₃₂ = 20, C₂ = 10, C₃ = 3.

Fig. 4b. The effect of the RBCs shear thinning parameter K on the streamwise (x) velocity of plasma, for the parameter values Re = 100, B₃₁ = 0.5, B₃₂ = 20, C₂ = 10, C₃ = 3.

Fig. 4c. The effect of the RBCs shear thinning parameter K on the streamwise (x) velocity of RBCs, for the parameter values Re = 100, B₃₁ = 0.5, B₃₂ = 20, C₂ = 10, C₃ = 3.

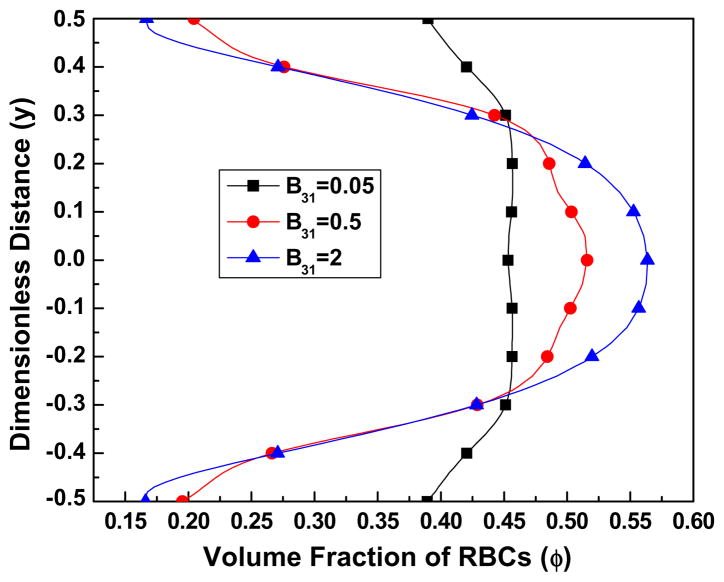
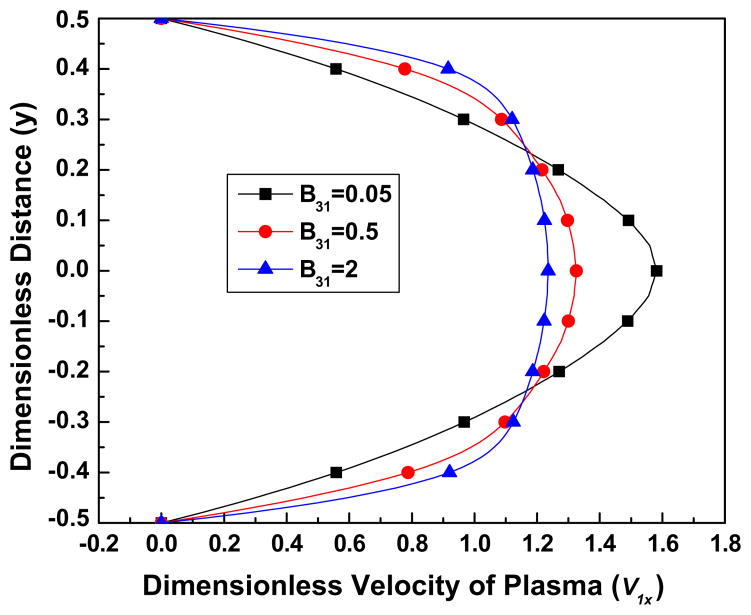
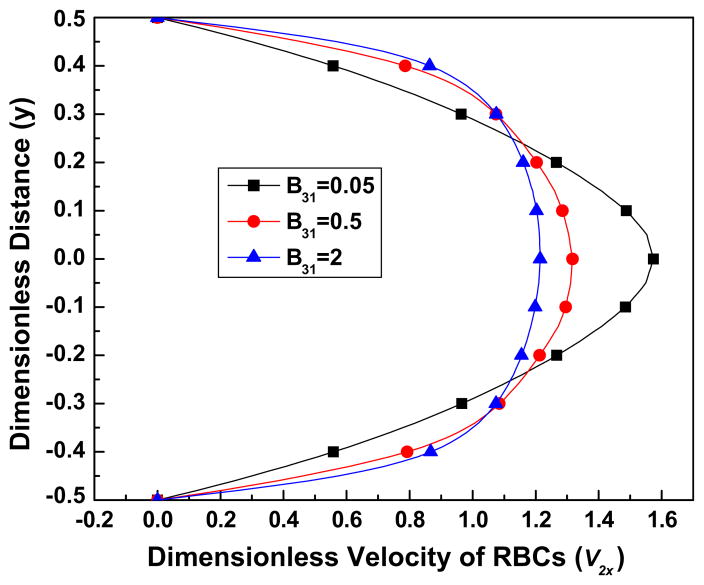
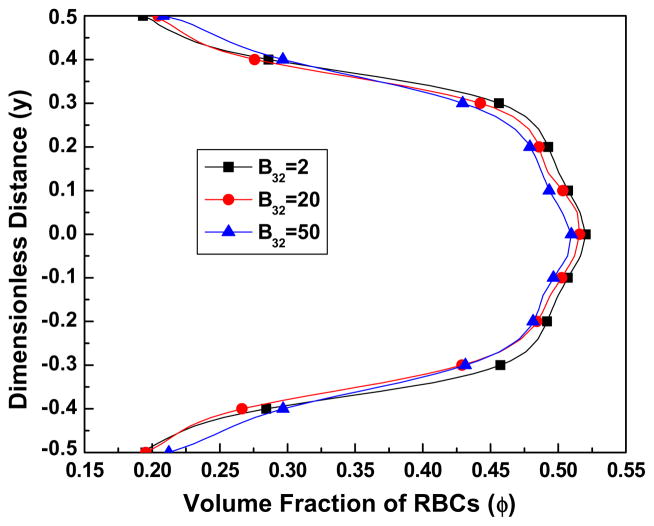
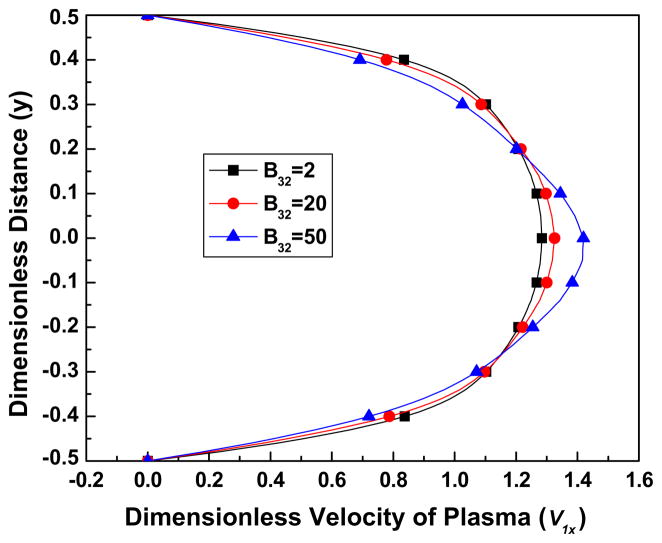
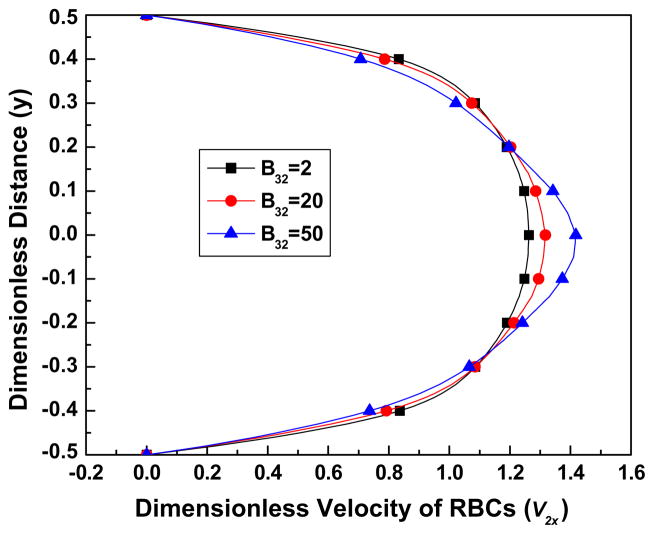
From Figs. 5(b) and (c), we can see that as the parameter B₃₁ decreases, the velocity profile loses its bluntness and becomes more parabolic. When K is very large, the viscosity of the RBCs is influenced more by B₃₁ rather than by B₃₂, and when B₃₁ is small, for example takes the value of 0.05, the viscosity of RBCs has the same order of the magnitude as the plasma viscosity in most parts of the flow ( $B_{31}=\frac{1}{Re}$). This implies that when B₃₁ is small the plasma influences the flow of the blood significantly. As B₃₁ increases, the velocity profiles deform to adopt a blunt shape. Fig. 5a shows the effect of B₃₁ on the volume fraction distribution of the RBCs. It can be seen that when B₃₁ has a small value, for example 0.05, indicating that the plasma viscosity is comparable to the viscosity of the RBCs, the volume fraction distribution is more uniform; however as B₃₁ increases, the distribution becomes less uniform. Fig. 6a shows the volume fraction distribution as a function of B₃₂ and demonstrates its negligible influence over the range of the values (2–50) studied here. Accordingly, Figs. 6(a) and (c) demonstrate negligible influence of B₃₂ on the velocity fields.

Figure 5.

Fig. 5a. The effect of the parameter B₃₁ on the volume fraction of RBCs, for the parameter values Re = 100, K = 1000, B₃₂ = 20, C₂ = 10, C₃ = 3.

Fig. 5b. The effect of the parameter B₃₁ on the streamwise (x) velocity of plasma, when Re = 100, K = 1000, B₃₂ = 20, C₂ = 10, C₃ = 3.

Fig. 5c. The effect of the parameter B₃₁ on the streamwise (x) velocity of RBCs, for the parameter values Re = 100, K = 1000, B₃₂ = 20, C₂ = 10, C₃ = 3.

Figure 6.

Fig. 6a. The effect of the parameter B₃₂ on the volume fraction of RBCs, for parameter values Re = 100, K = 1000, B₃₁ = 0.5, C₂ = 10, C₃ = 3.

Fig. 6b. The effect of the parameter B₃₂ on the streamwise (x) velocity of plasma, for parameter values Re = 100, K = 1000, B₃₁ = 0.5, C₂ = 10, C₃ = 3.

Fig. 6c. The effect of the parameter B₃₂ on the streamwise (x) velocity of the RBCs, when Re = 100, K = 1000, B₃₁ = 0.5, C₂ = 10, C₃ = 3.

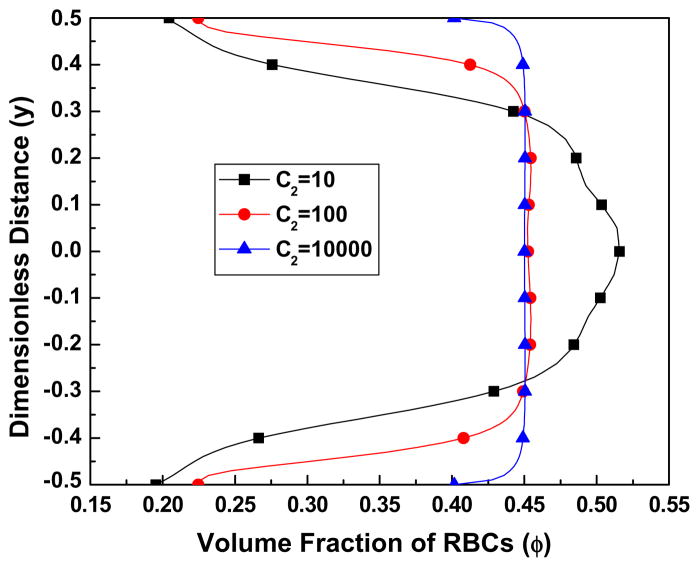
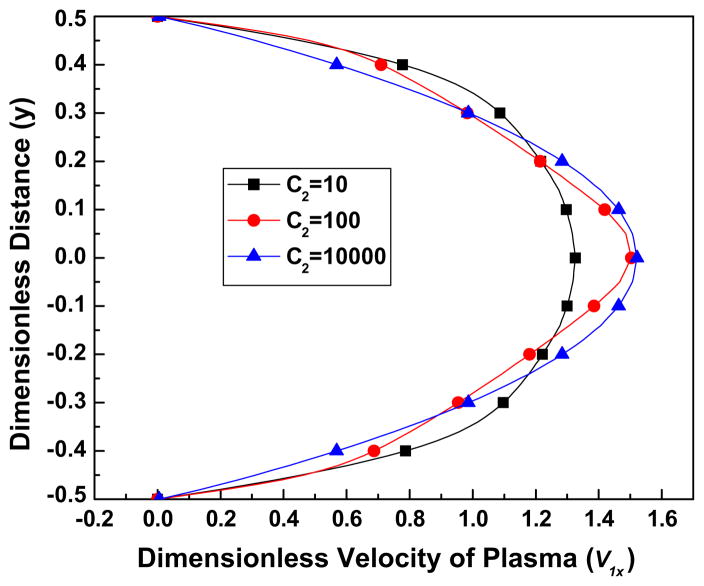
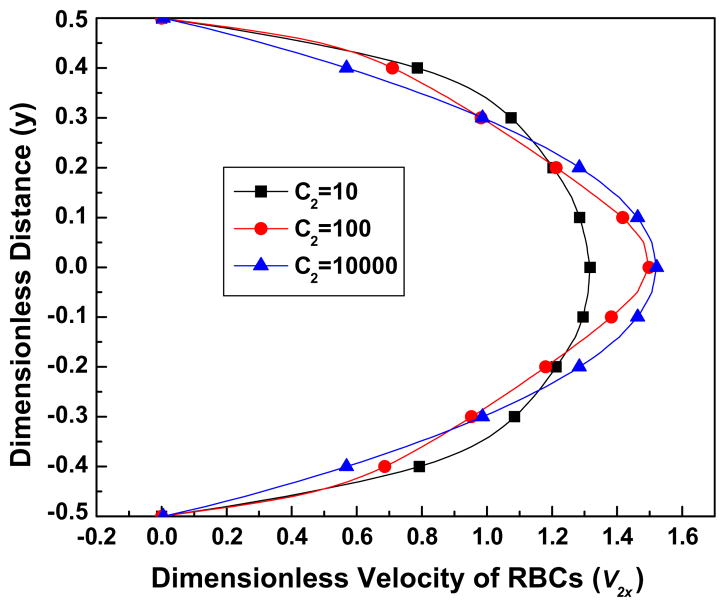
4.2.3. Effect of C₂ and C₃

Figs. 7(a)–(c) displays the effect of parameter C₂ on the volume fraction distribution and velocity profiles. With increasing C₂ by an order of magnitude from 10 to 100, it is seen that the volume fraction becomes dramatically blunter, and the velocity profiles less blunt. However additional increase of C₂, by 3 orders of magnitude does not have as much influence on the volume fraction or velocity fields. A slight decrease in velocity difference between the two components is also observed for increasing C₂, which leads to a smaller lift force, the main term causing the non-uniform distribution of the volume fraction of the RBCs, [see Eq. (12)]. The shape of the velocity field is inevitably related to the volume fraction: the more uniform the distribution of RBCs, the more uniform the viscosity distribution, [see Eq. (10)], and hence more parabolic the velocity field.

Figure 7.

Fig. 7a. The effect of the parameter C₂ on the volume fraction of RBCs, for parameter values Re = 100, K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₃ = 3.

Fig. 7b. The effect of the parameter C₂ on the streamwise (x) velocity of plasma, for the parameter values Re = 100, K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₃ = 3.

Fig. 7c. The effect of the parameter C₂ on the streamwise (x) velocity of RBCs, for the parameter values Re = 100, K = 1000, B₃₁ = 0.5, B₃₂ = 20, C₃ = 3.

Fig. 8a shows that as C₃ becomes larger more RBCs concentrate near the channel center line and the region of low volume fraction of the RBCs expands. This is understandable inasmuch as C₃ corresponding to a larger lift force causing the RBCs to migrate away from the wall to the center line of the channel. From Figs. 8(a) and(c), we observe that as C₃ increases, near the center line of the channel the velocity of the plasma decreases while the velocity of the RBCs increases, that is, there is a smaller velocity difference between the two components. This may be related to the higher values of the volume fraction near the center line which is caused by larger values of C₃. Indeed, a higher volume fraction of the RBCs leads to a higher drag force [see the Batchelor drag function in Eq. (14)] which, in turn, leads to a smaller velocity difference.

5. Conclusions

In this paper, a two-component flow of blood was formulated. The mathematical model was based on the framework of the Mixture Theory. A numerical solver was developed using OpenFOAM^®, and used to study a specific problem, namely the flow of blood in a micro-channel. A parametric study was performed, providing further insight into the model by giving additional information on the influence of the material properties. For example, varying the parameters B₃₁ and B₃₂ [see Eq. (11)] led to a wide range of shear dependent properties. Furthermore, by varying C₂ and C₃ (see Eq. (19), where C₂ is related to the drag coefficient, and C₃ is related to the lift coefficient) it was found that the interaction force has a strong influence on the RBCs. For certain value of C₂ and C₃, it was possible to show the RBCs depletion near the wall or plasma skimming (see Fig. 8a). We also notice that the parameters chosen in Fig. 8a might not be relevant to a physical problem, such as the flow of blood in a micro-channel. In order to overcome this, more accurate forms of the coefficients for the interaction forces are needed. Finally, it goes without saying that the model developed here is only appropriate for a healthy human, and it does not capture any blood disorder. To include the formation and growth of clots, and lysis of blood cells in blood, in general, the reaction–convection–diffusion equations are to be solved in conjunction with the balance laws for mass, linear and angular momentum, and energy (for each component). Although we have ignored the biochemical effects of blood in this paper, in principle, the theory is amenable to extension [see Anand et al. (2005)].