MATHEMATICAL MODELS OF CONTACT PATTERNS BETWEEN AGE GROUPS FOR PREDICTING THE SPREAD OF INFECTIOUS DISEASES

Abstract

The spread of an infectious disease is sensitive to the contact patterns in the population and to precautions people take to reduce the transmission of the disease. We investigate the impact that different mixing assumptions have on the spread an infectious disease in an age-structured ordinary differential equation model. We consider the impact of heterogeneity in susceptibility and infectivity within the population on the disease transmission. We apply the analysis to the spread of a smallpox-like disease, derive the formula for the reproduction number, ${\mathfrak{R}}_0$, and based on this threshold parameter, show the level of human behavioral change required to control the epidemic. We analyze how different mixing patterns can affect the disease prevalence, the cumulative number of new infections, and the final epidemic size. Our analysis indicates that the combination of residual immunity and behavioral changes during a smallpox-like disease outbreak can play a key role in halting infectious disease spread; and that realistic mixing patterns must be included in the epidemic model for the predictions to accurately reflect reality.

1. Introduction

The spread of infectious diseases depends upon contact patterns among people in the infected population. These contact patterns can help guide public health workers identify people at high risk of contracting an infection and where an outbreak can be effectively intercepted. Mathematical disease transmission models can be useful tools in understanding the complex dynamics between the population and disease transmission. The knowledge gained from these models can help improve the effectiveness of intervention strategies in slowing the spread.

A realistic model for the spread of an infectious diseases must take into account the mechanism of its transmission including the pattern of mixing among the population, the susceptibility within the population, the virulence of the infection, the probability of transmission per contact, and the changes in behavior in the affected population in response to an epidemic. The simplest mathematical models assume that the population mixes homogeneously, where it is equally likely that the disease can be transmitted between any two people, regardless of their age, where they live or work, or any other behavior traits that the individuals might have.

The assumption of a homogeneously mixing population is often sufficient to obtain general insights once an epidemic is well established in a population. However, there can be significant differences in the early stages of an epidemic and in the final epidemic size. In particular, homogeneous mixing can lead to an overestimation of the final epidemic size and the magnitude of the interventions needed to stop an epidemic [52]. For example, before smallpox was eradicated worldwide in the 1970s, smallpox vaccinations were routinely administered to the population; therefore, more than half of the U.S. population has received the smallpox vaccine, and recent studies have shown that some of these individuals may still have partial protection against smallpox [2, 13]. Because the vaccine itself carries potential health risks, the U.S. discontinued smallpox vaccinations in 1972 [7]. This protection should greatly reduce the number of severe and fatal cases of disease expected in a potential bioterrorist attack. Similarly, recent pertussis studies have shown that infection-acquired immunity against pertussis disease wanes after 4–20 years and protective immunity after vaccination wanes after 4–12 years [56]. Therefore, there are clear age-dependent differences in susceptibility that must be taken into account when developing models that will guide public health policy.

Mathematical models have demonstrated the importance of accounting for heterogenous mixing patterns in the population by using mixing functions or mixing matrices defined in compartmental and networks models [4, 26, 27, 30, 31, 35, 37, 57]. Techniques have been developed to incorporate non-random mixing into epidemic models, including proportional mixing (mixing between groups is proportional to the activity levels) [24, 46], restricted or preferred mixing (some contacts are chosen within a group and the rest are chosen proportionally) [34, 25, 46], and selective mixing (mixing between groups is based on desirability, acceptability, ad availability) [26, 38]. Network epidemic models have been used to investigate sequential partnership patterns [39], concurrency in relationships [39], the impact of various social biases on the spread of epidemics [16, 50], and other topics related to mixing [40]. Network and compartmental epidemic models have been used to model several infectious diseases; however, very few models have incorporated the impact of realistic mixing patterns in the presence of population heterogeneity.

Age-dependent risks and residual protection have been mostly neglected in the mathematical models proposed to guide response strategies for a smallpox outbreak [5, 14, 36, 41, 44], although some mathematical models of the dynamics of smallpox have incorporated the effects of residual immunity [23, 45]. Halloran et al. [23] used a stochastic simulation of smallpox in a community of 2,000 people in their efforts to compare mass vaccination versus ring vaccination under different scenarios. They concluded that ring vaccination would be more effective in the presence of preexisting immunity. However, their model divided the population into only two classes (with and without residual immunity), did not consider age-dependent risks, heterogeneous mixing, and behavioral changes in response to a disease outbreak. Nishiura et al. [45] used a deterministic model with a population of 1 million people to study the impact of long-lasting vaccine-induced immunity. They divided the population into three classes (never vaccinated, one vaccination, two vaccinations) and assumed homogeneous mixing; however, they did not incorporate age-dependent risks and behavioral changes. They observed that an epidemic could be greatly affected by the residual immunity within the population and that vaccination should be given in accordance to immunity level. Similarly, the recent 2009 H1N1 pandemic showed age-dependent risk; that is, people who received the 1976 swine flu vaccine had some protection against the virus [43]. Because many vaccinations are highly correlated to a persons age, these studies all support the need for models to incorporate age-dependent residual protection when predicting the disease dynamics within a population.

Responses to an infectious disease in a community can reduce morbidity and mortality; for example, significant changes in behavior among men who engage in sexual activity with men have been credited with decreases in prevalence of HIV/AIDS and other sexually transmitted diseases [22, 25, 28, 55]. Experiences with the severe acute respiratory syndrome (SARS) epidemic in 2003 and most recently, the 2009 H1N1 pandemic indicate that an outbreak of a deadly disease would generate dramatic behavioral changes [10, 47, 48, 17]. Del Valle et al. [11] used a deterministic model to study the effects of behavioral changes during a smallpox outbreak. They demonstrated that behavioral changes can have a dramatic impact in slowing an epidemic and reducing the total number of cases; however, they used homogeneous mixing and differences in susceptibility based on age were not incorporated.

We derived and age-structured model for transmission that combines the effects of age-dependent residual immunity with age-dependent mixing. We then compare the results of assuming different mixing patterns to determine the effects these assumptions have on the size and duration of epidemics. In our simulations, we assume that the population is closed (no immigration, births or natural deaths are considered, although we include disease-induced death) and that there is only one disease in operation.

Our simulations quantify how the different mixing assumptions lead to differences in the disease prevalence, the cumulative number of new infections, and the final epidemic size. We verify that reducing the number of contacts in the population slows the spread of the epidemic and observe that reducing the distribution of contacts also reduces the spread. That is, if people mix with a much smaller subset of the overall population, then the transmission rates are reduced.

We also quantify how the residual immunity to smallpox reduces the final epidemic size. We also observe that the age groups with high susceptibility are less affected by the mixing assumptions than those with less susceptibility. One implication of this result is that if smallpox vaccination becomes necessary, the smallpox vaccine should be given first to the most susceptible population groups. Defining the basic reproductive number, ${\mathfrak{R}}_0$, allows us to quantify the level of behavioral change required to control an epidemic. This can help guide public health officials in persuading the population to change their behavior by reducing their number of contacts or changing their contact patterns.

2. The mathematical model

2.1. Differential equations

We formulate the transmission dynamics model for a single outbreak of smallpox in a heterogeneously mixing population. We divide the population into three main epidemiological classes, susceptible (S), infected (I) and recovered (R) [29]. These classes are further divided into age groups with heterogeneous mixing, different susceptibilities, and infectiousness based on age and residual immunity from previous vaccinations. The infectious class is further divided into infectious stages, which allows us to take into account the differences in infectivity for diseases such as smallpox, i.e., latent or incubation period, prodromal period, and symptomatic or infectious period. We apply the model to a smallpox outbreak, and assume that the course of the outbreak is short compared with the life of an individual, therefore, births, aging, and natural deaths are not included.

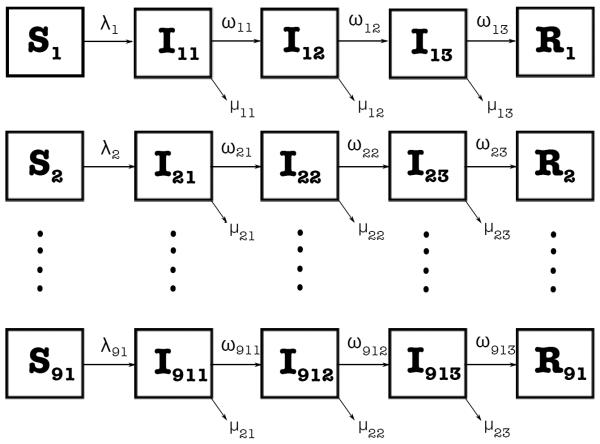
For our multi-group susceptible-infected-recovered (SIR) model with staged progression [29], we consider 91 age groups (n = 91) with 1-year intervals: 1, 2, 3, …, 90, 91 and 3 infection stages (m = 3; exposed (no symptoms), prodromic (early symptoms), and infectious (symptomatic)). Each 1-year interval corresponds to age groups, for example, group 1 corresponds to infants up to 1 year of age, group 2 corresponds to children between 1 and 2 years of age, and so on, except for group 91, which corresponds to all people aged over 90 years of age. Using the transfer diagram in Figure 1, we arrive at the following nonlinear system of differential equations:

$$\begin{array}{cc}\hfill & \frac{d{S}_i}{dt}=-{\lambda }_i\left(t\right)S_i\left(t\right),\text{for}1\le i\le n\hfill \\ \hfill & \frac{d{I}_{i1}}{dt}={\lambda }_i\left(t\right)S_i\left(t\right)-({\omega }_{i1}+{\mu }_{i1})I_{i1}\left(t\right),\hfill \\ \hfill & \frac{d{I}_{ik}}{dt}={\omega }_{i,k-1}{I}_{i,k-1}\left(t\right)-({\omega }_{ik}+{\mu }_{ik})I_{ik}\left(t\right),\text{for}2\le k\le m\hfill \\ \hfill & \frac{d{R}_i}{dt}={\omega }_{im}{I}_{im}\hfill \end{array}$$ (1)

where λ_i(t) is the force of infection (defined later in (3)); ω_ik is the relative rate of disease progression for a person in age group i and infection stage k; and μ_ik is the disease-induced relative death rate for age group i in infectious stage k. We define the total population size of each group i as

$$N_i=S_i+\sum _{k=1}^m{I}_{ik}+R_i.$$ (2)

Figure 1.

Schematic relationship for the multi-group SIR model with staged progression with 91 age groups and 3 infection stages. The arrows that connect the boxed groups represent movement of individuals from one group to an adjacent one. Susceptible individuals S_i of age i are infected at a rate, λ_i, and then progress through various infection stages at rates of disease progression, ω_ij, before entering the recovered state. Infected individuals die from the disease at a rate, μ_ij.

We define λ_i as the relative rate at which the susceptible population in age group i is infected and progresses to stage I_i1. We calculate this as the sum of the rate of disease transmission from each infected subgroup, I_jk, to the susceptible group, S_i. This means that a susceptible person in group i can be infected by an infected person in any group or infection stage. That is,

$${\lambda }_i\left(t\right)=\sum _{j=1}^n\sum _{k=1}^m{\lambda }_{ijk}\left(t\right).$$ (3)

Here, λ_ijk is the rate of disease transmission from the infected people I_jk in stage k of age group j to the susceptible individuals in age group i. We define λ_ijk in (3) as the product of the number of contacts per unit time that each individual in age group i has with age group j, γ_ij; the probability of disease transmission per contact between an infected in group j and a susceptible in group i (which is the product of the susceptibility α_i of someone in S_i, the infectivity ξ_jk, and the probability of transmission P_ij (defined later in (5)) based on the average duration of contacts between age groups i and j); and the proportion of contacts with the infected subgroup. That is,

$$\begin{array}{c}\hfill {\lambda }_{ijk}=\left(\begin{array}{c}\hfill \text{Number of}\hfill \\ \hfill \text{contacts per}\hfill \\ \hfill \text{unit time}\hfill \end{array}\right)\left(\begin{array}{c}\hfill \text{Probability of}\hfill \\ \hfill \text{disease transmission}\hfill \\ \hfill \text{per contact}\hfill \end{array}\right)\left(\begin{array}{c}\hfill \text{Proportion of}\hfill \\ \hfill \text{contacts that}\hfill \\ \hfill \text{are infected}\hfill \end{array}\right)\hfill \\ \hfill {\lambda }_{ijk}\left(t\right)=\left({\gamma }_{ij}\right(t\left)\right)\left({\alpha }_i{\xi }_{jk}{P}_{ij}\right)\left(\frac{I_{jk}\left(t\right)}{N_j\left(t\right)}\right),\hfill \end{array}$$ (4)

where we assume that the probability function P_ij follows a Poisson distribution given by

$$P_{ij}=1-e^{-\zeta T_{ij}},$$ (5)

where T_ij is the average duration of a contact of an individual from age group i with someone from age group j, and ζ is the mean number of transmission events per unit time (set in our simulations to 3 events per day [12]).

Summing over all the infection stages gives the force of infection from all infected individuals to the susceptible people in group i. Multiplying λ_i(t) by the number of susceptible individuals in age group i as in (1) gives the rate of change of new infected people in group i.

2.2. The basic reproduction number, ${\mathfrak{R}}_0$

The basic reproduction number is defined as the average number of secondary cases produced by one infected individual during the infected individual's entire infectious period assuming a fully susceptible population. In an epidemic model, the magnitude of ${\mathfrak{R}}_0$ determines whether or not an epidemic occurs. Typically, there is no epidemic if ${\mathfrak{R}}_0\langle 1$, but there is an epidemic if ${\mathfrak{R}}_0\rangle 1$. In a simple SIR model, where γ is the average number of contacts per unit time per individual, β the probability of transmitting the infection per contact, τ the mean duration of the infection period, and the basic reproduction number can be expressed by the following intuitive formula:

$${\mathfrak{R}}_0=\gamma \beta \tau .$$ (6)

However, since we are working with heterogeneous population, we use the “next-generation operator” approach [54] to find an expression for the basic reproduction number ${\mathfrak{R}}_0$. Note that we use a broad definition of susceptible individuals here that include partially susceptible individuals from prior vaccine campaigns. This is reasonable because we are not modeling current vaccination strategies that would create a separate vaccinated immune class; and all individuals in the population are susceptible, albeit with differential susceptibility.

We compute ${\mathfrak{R}}_0$ by linearizing system (1) around the disease-free steady state and by identifying conditions that guarantee growth in the infected classes. The disease-free steady state has I₁₁, I₁₂, I₁₃, I₂₁, I₂₂, I₂₃, …, I_91,1, I_91,2, I_91,3 equal to zero and positive values for the equilibrium number of susceptible individuals each group, $S_i^0\rangle 0$ for 1 ≤ i ≤ n. We denote the total equilibrium population of group i by $N_i^0$. The resulting 273 dimensional linearized system is of the form $\stackrel{.}{\mathbf{X}}=(\mathbf{F}-\mathbf{V})\mathbf{X}$, where

$$\mathbf{X}={\left[I_{11}{I}_{12}{I}_{13}\dots I_{91,1}{I}_{91,2}{I}_{91,3}\right]}^T,$$

The matrix, F, has nonzero entries in every column of rows 1, 4, 7, etc. and all zeros in rows 2, 3, 5, 6, 8, 9, etc. The entries in the 3 columns 3(j − 1) + 1, 2, 3 of row 1 + 3(i − 1) are

$$\frac{{\gamma }_{ij}{\alpha }_i{\xi }_{j1}{P}_{ij}}{N_j^0},\frac{{\gamma }_{ij}{\alpha }_i{\xi }_{j2}{P}_{ij}}{N_j^0},\frac{{\gamma }_{ij}{\alpha }_i{\xi }_{j3}{P}_{ij}}{N_j^0}.$$ (7)

The V matrix is block diagonal with 3 × 3 blocks of the form

$$\mathbf{B}=\left[\begin{array}{ccc}\hfill {\omega }_{j1}+{\mu }_{j1}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -{\omega }_{j1}\hfill & \hfill {\omega }_{j2}+{\mu }_{j2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -{\omega }_{j2}\hfill & \hfill {\omega }_{j3}+{\mu }_{j3}\hfill \end{array}\right],$$ (8)

which has an inverse of the form

$$\begin{array}{cc}\hfill {\mathbf{B}}^{-1}& =\left[\begin{array}{ccc}\hfill \frac{1}{{\omega }_{k1}+{\mu }_{k1}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{{\omega }_{k1}}{{\omega }_{k1}+{\mu }_{k1}}\frac{1}{{\omega }_{k2}+{\mu }_{k2}}\hfill & \hfill \frac{1}{{\omega }_{k2}+{\mu }_{k2}}\hfill & \hfill 0\hfill \\ \hfill \frac{{\omega }_{k1}}{{\omega }_{k1}+{\mu }_{k1}}\frac{{\omega }_{k2}}{{\omega }_{k2}+{\mu }_{k2}}\frac{1}{{\omega }_{k3}+{\mu }_{k3}}\hfill & \hfill \frac{{\omega }_{k2}}{{\omega }_{k2}+{\mu }_{k2}}\frac{1}{{\omega }_{k3}+{\mu }_{k3}}\hfill & \hfill \frac{1}{{\omega }_{k3}+{\mu }_{k3}}\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{ccc}\hfill \frac{1}{{\omega }_{k1}+{\mu }_{k1}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \frac{q_{k2}}{{\omega }_{k2}+{\mu }_{k2}}\hfill & \hfill \frac{1}{{\omega }_{k2}+{\mu }_{k2}}\hfill & \hfill 0\hfill \\ \hfill \frac{q_{k3}}{{\omega }_{k3}+{\mu }_{k3}}\hfill & \hfill \frac{q_{k3}∕q_{k2}}{{\omega }_{k3}+{\mu }_{k3}}\hfill & \hfill \frac{1}{{\omega }_{k3}+{\mu }_{k3}}\hfill \end{array}\right]\hfill \end{array}$$ (9)

with

$$q_{j1}=1,q_{j2}=\frac{{\omega }_{j1}}{{\omega }_{j1}+{\mu }_{j1}},q_{j3}=\frac{{\omega }_{j1}}{{\omega }_{j1}+{\mu }_{j1}}\frac{{\omega }_{j2}}{{\omega }_{j2}+{\mu }_{j2}}.$$ (10)

These q_jk factors are the proportion of infected individuals in the j age group that reach stage k. FV⁻¹ has zeros in the rows 2, 3, 5, 6, 8, 9, etc., so the eigenvectors must also have zeros in these rows 2, 3, 5, 6, 8, 9, etc. Thus, we can consider the 91 × 91 matrix consisting of the rows 1 + 3(i − 1) and columns 1+3(j−1) of FV⁻¹. This matrix E = FV⁻¹ will have ij entries given by

$${\mathbf{E}}_{ij}=\frac{{\alpha }_i{S}_i^0{\gamma }_{ij}{P}_{ij}}{N_j^0}\left(\frac{{\xi }_{j1}}{{\omega }_{j1}+{\mu }_{j1}}+\frac{{\xi }_{j2}{q}_{j2}}{{\omega }_{j2}+{\mu }_{j2}}+\frac{{\xi }_{j3}{q}_{j3}}{{\omega }_{j3}+{\mu }_{j3}}\right).$$ (11)

The basic reproduction number ${\mathfrak{R}}_0$ is the largest eigenvalue of the matrix E = FV⁻¹ [54]. We cannot obtain an explicit form of the ${\mathfrak{R}}_0$ for our general model (1). Therefore, ${\mathfrak{R}}_0$ is estimated numerically for a given set of parameter values and initial population size for the different mixing assumptions.

2.3. Contact patterns

The pattern of contacts between different age groups plays an essential role in determining the spread of disease. Several theoretical studies have developed mixing functions to account for heterogeneous mixing patterns [34, 6, 27]; however, very few studies have developed functions that mimic empirical studies [21]. In this paper, we use mixing patterns based on both empirical and theoretical studies to determine the impact that different mixing functions have on disease spread. Our study makes use of four different mixing models that we refer as normal mixing, reduced mixing, proportional mixing, and segregate mixing.

The force of infection λ_i is the relative rate at which susceptible people of age i acquire infection. In homogeneous mixing, a person's contacts are randomly distributed among all others in the population. One immediate implication of this assumption is that the force of infection is the same for all ages. However, in real populations the mixing in a population is heterogeneous and contacts are not random. For heterogeneous mixing, the forces of infection reflect the age-related changes in the degree of mixing and contact, within and among age groups, which are important factors for understanding disease spread. Furthermore, changes in behavior can alter the contact patterns in the population, which are also key in understanding disease spread.

We used the average number of contacts γ_ij, the susceptibility α_i, the infectivity ξ_jk, and the probability of transmission P_ij matrices to estimate the transmission rate β_ij for each mixing assumption. Here β_ij is defined as the transmission rate between a susceptible of age i with people in age j, which is the product of the average number of contacts, the susceptibility, the infectivity, and the probability of disease transmission; that is, β_ij = γ_ij × α_i × ξ_jk × P_ij.

2.3.1. Normal mixing

Definition 2.1. Normal mixing reflects the preferential mixing between the ages on a normal (typical) day in the absence of disease. The mixing function is generated from simulations based on empirical studies for the population of Portland, Oregon [12].

In normal mixing, the transmission matrix is estimated from empirical studies described in Del Valle et al. [12]. In short, we generated a synthetic population with demographic distributions drawn from census data and assigned activity patterns based on household travel surveys. From these two sets of information and land use data, we computed which individuals are together at the same location at the same time. The simulation keeps track of every single individual on a second-by-second basis and is therefore able to determine the contacts, including identities of those in contact, the location, the duration of the contact, and the nature of the activity where the contact took place. We calculated the total number of contacts, C_ij, generated over a typical day, and evaluated the average number of contacts, γ_ij, per person.

The normal contact matrix is formed by two blocks of mixing and a weak coupling between parents and their children. Glasser et al. [21] recently developed a function that can mimic the mixing patterns observed in these empirical studies.

2.3.2. Reduced mixing

Definition 2.2. For reduced mixing, we scaled the normal mixing matrix, described above, by multiplying it by a factor, 0 ≤ x < 1, to account for a reduction in the number of contacts.

People will make changes in behavior (e.g. reduce their number of contacts) in response to knowledge of an epidemic. These changes will not only reduce the number of contacts of the entire population, but also change the mixing patterns in the population. For example, if schools close, as a preventive measure to control an epidemic, the contact patterns of school children will change from children of their own age to their parents or family members.

For simplicity in the reduced mixing model, we incorporated behavioral changes by reducing the total number of contacts generated in the population, by multiplying the contact matrix C_ij by a desired factor, x. This approach keeps the same distribution of mixing in the population, while reducing the total number of contacts. In the numerical simulations presented here, we reduced the number of contacts by half.

While recognizing the crude introduction of behavioral changes into this model, this approach will serve as the foundation for later models that include validated behavioral changes in response to an outbreak. Note that the original version of the empirical studies presented here did not incorporate behavioral changes; however, new versions of the simulation now incorporate age-dependent behavior changes [53].

2.3.3. Proportional mixing

Definition 2.3. For proportional homogenous mixing, a potential contact is randomly selected from the entire population of Portland, which implies a greater probability of meeting people whose populations are larger.

We assume people in each age group behave the same way when selecting a contact, but have biases between age groups. In other words, mixing within each age group is assumed to be homogeneous but there is heterogeneous mixing among the age groups.

Models with varying populations must ensure that as the relative size of each group changes, the number of contacts between each group changes accordingly. One constraint on dynamically changing the number of contacts between groups is that the total number of contacts between two groups must be symmetric; that is, the total number of contacts between group i and group j must be equal to the total number of contacts between group j and group i. In multi-group models where an attempt is made to directly control the number of contacts formed between age groups, these balance conditions are usually artificially enforced, or the average number of contacts per individual per unit time is assumed to be constant.

Here, we use the heterogenous mixing approach developed in [27] to maintain the detailed balance for mixing between the age groups as their populations change. We present the proportional contact matrix, with the element in the i^th row and j^th column represented by d_ij. Thus, d_ij is the expected (desired) distribution of contacts that one has as a function of age, that is, d_ij is the preference that a person of age i has for contacts with a person of age j.

The contact matrix need not be symmetric (i.e., d_ij ≠ d_ji, when i ≠ j), but the probability of contact forming is symmetric since d_jid_ij = d_ijd_ji. Also, we note that there is no constraint on ${\sum }_{j=1}^n$ d_ij, which may be less than or greater than one.

We define a_i to be the preferred number of social contacts per unit time for a person in age group i. Assuming no preferences, the probability that a contact is with a person from age group j is $a_j{N}_j∕\left({\sum }_{k=1}^n{a}_k{N}_k\right)$ where N_j is the total population size of age group j defined in (2). This also characterizes the availability of contacts in age group j. Hence, the probability of a contact forming between individuals from age group i and age group j is $d_{ij}{d}_{ji}{a}_j{N}_j∕\left({\sum }_{k=1}^n{a}_k{N}_k\right)$.

We denote the total number of contacts per unit time of people in age group i with people in age group j by C_ij,

$$C_{ij}=d_{ij}{d}_{ji}\frac{a_j{N}_j}{\sum _{k=1}^n{a}_k{N}_k}{a}_i{N}_i=d_{ji}{d}_{ij}\frac{a_i{N}_i}{\sum _{k=1}^n{a}_k{N}_k}{a}_j{N}_j=C_{ji}.$$ (12)

Thus, the balance constraints are automatically satisfied as a natural consequence of the model. As the population size can change, the number of contacts with people in group j that one individual in group i can expect to have at time t is then,

$${\gamma }_{ij}\left(t\right)=\frac{C_{ij}\left(t\right)}{N_i\left(t\right)}=a_i{d}_{ij}{d}_{ji}\frac{a_j{N}_j\left(t\right)}{\sum _{k=1}^n{a}_k{N}_k\left(t\right)},$$ (13)

and the total number of contacts that an individual in group i has at time t is,

$${\gamma }_i\left(t\right)=a_i\left(\sum _{j=1}^n{d}_{ij}{d}_{ji}\frac{a_j{N}_j\left(t\right)}{\sum _{k=1}^n{a}_k{N}_k\left(t\right)}\right).$$ (14)

Definitions and units of the contact parameters are summarized in Table 1.

Table 1.

Parameter definitions and units used to describe the contact patterns.

Parameter	Description	Units
ζ	Mean number of transmission events per unit time	Time−1
dij	Desired distribution of contacts between age i and age j	1
aij	Preferred number of contacts per person per unit time	Time−1
Cij	Total number of contacts per unit time	People/Time
γ ij	Average number of contacts per person per unit time	Time−1
Pij	Probability of disease transmission per contact	1

To compare the proportional mixing matrix with the normal contact matrix, we matched the total of contacts of the proportionally mixing population with the total number of contacts of the normal mixing population as described in [12]. The adequate transmission rate matrix β_ij (Figure 3) is consistent with the age distribution of the population; that is, there are well-defined regions (shown by different colors) of adequate contacts, which are due to the age distribution of the population.

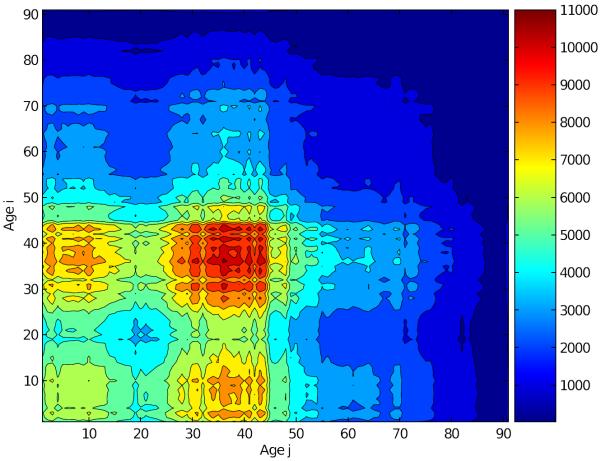
Figure 3.

Transmission rate matrix β_ij estimated using a proportionally mixing population. The transmission rate matrix is the average number of adequate contacts between a susceptible of age i with people of age j. Notice that the probability of transmission is determined by the size of the population in each age group.

In general, the population is more likely to have adequate contacts with people from the age groups with larger sizes (35–45 years) than with people from the age groups with smaller sizes (> 55 years), which is consistent with what we would expect for a proportionally mixing population.

2.3.4. Segregate mixing

Definition 2.4. For segregate mixing, we assume that people mix with people of the same age only.

We defined d_ij = 1 if i = j and d_ij = 0 otherwise. That is, each age group will have the same number of contacts but all their contacts will be with their own age group. Even though this type of mixing may not be realistic, this assumption allows us to determine whether the number of contacts or the heterogeneous mixing among the population are driving the epidemic.

3. Parameter estimation

The smallpox infection period is divided into three phases: exposed or incubation period, prodromal period, and infectious period. The incubation period for smallpox has been reported to be from 7 to 19 days, but the most common reported range is 10 to 14 days with a mean of 12 days [18, 49, 51]. Thus the latent phase has a relative rate of ω_i1 = 1/12. Afterward, smallpox patients experience a prodromal phase with symptoms such as fever, malaise, prostration, headache, backache, and vomiting. This period lasts for 2 to 4 days with a mean of 3 days [8, 18]. Therefore, the prodromal relative rate is ω_i2 = 1/3. Data on previous outbreaks show that patients have very low infectivity during the prodromal phase [14, 19, 42]. We assume that during both the exposed period and the prodromal period, individuals are non-infectious. Patients remain contagious for a period of approximately 14 to 17 days with a mean of 16 days [18, 32, 33]. Hence, we set the relative rate in the infectious phase as ω_i3 = 1/16 and the relative infectivity as 1. Once these patients recover, they have complete, permanent immunity.

The United States discontinued smallpox vaccinations in 1972 because the vaccine itself carries potential health risks [7]. Therefore, more than half of the U.S. native population has received the smallpox vaccine, and recent findings have shown that these individuals may still have partial protection against smallpox [2, 13]. Therefore, we assume that all individuals born after 1972 are completely susceptible to smallpox. Thus, the relative susceptibility of people between the ages of 1 and 40 is set to 1. We assume that individuals between the ages of 41 and 65 have partial immunity to smallpox and thus the relative susceptibility is set to 0.3 [13]. Furthermore, we assume that people between the ages of 66 and 80 have a relative susceptibility of 0.7, and people between the ages of 81 and above have a relative susceptibility of 0.9 due to their age-dependent risk of infection [13].

The relative death rate of smallpox varies, but is reported to be about 30% among unvaccinated individuals [18, 32, 33]. The fraction in the model that die from smallpox is μ_i3/(ω_i3 + μ_i3); setting this equal to 0.3 yields μ_ij = 0.0268. Smallpox deaths usually occurred 18 days or more after the onset of symptoms [32]. Therefore, we assume that the relative death rate for each infected stage is 0, 0, and 0.0268, respectively.

Recent estimates on the transmission of smallpox indicate that one infected person may infect three to six others [20]. Therefore, we set ζ = 3 so that ${\mathfrak{R}}_0$ would equal 3 for both the normal and proportional mixing matrices. However, for the reduced contact matrix, we multiplied the normal matrix by 0.5, resulting in ${\mathfrak{R}}_0$ equal to 1.5. Notice that by reducing the number of contacts by half, ${\mathfrak{R}}_0$ was also cut by half. This result provided an estimate of how much people must reduce their contacts in order to halt an epidemic. For example, if the number of contacts were reduced to less than one third, there would be no epidemic because ${\mathfrak{R}}_0$ would be less than one. For the segregate matrix, we used the normal contact matrix and grouped all the entries for each age group into the diagonal. This process resulted in different values of ${\mathfrak{R}}_0$ for each age group.

4. Results

We used a differential equation solver designed for multi-group SIR models with staged progression developed by Chitnis et al. [9] to examine the impact that the four mixing assumptions have on the final epidemic size and final susceptible population size for our model. All simulations assumed initial conditions of only susceptible individuals except for one infected individual in each age group in the incubation phase. We used the baseline parameters in Table 2 in our simulations and the synthetic population of Portland, Oregon, as the initial population for each age group.

Table 2.

Parameter definitions and values that fit the cumulative number of cases for the model.

Parameter	Description	Units	Baseline	Ref.
N	Initial population size	1	1,615,860	[12]
I i1	Initial infected population	1	91	Sec. 6
α i	Susceptibility of a person in Si for i = 1, ..40	1	1	[13]
α i	Susceptibility of a person in Si for i = 41, …, 65	1	0.3	[13]
α i	Susceptibility of a person in Si for i = 66, …, 80	1	0.7	[13]
α i	Susceptibility of a person in Si for i = 81, …, 91	1	0.9	[13]
ξ ik	Relative infectivity	1	k = (0, 0, 0.1)∀i	[14, 42]
ω ik	Relative rates of disease progression	Day−1	k = (1/12, 1/3, 1/16)∀i	[18]
μ ik	Relative death rate	Day−1	k = (0, 0, 0.0268)∀i	[18]

Table 3 summarizes the results of the epidemic size and final susceptible population size for the four mixing assumptions. The final epidemic size includes both the total number of recovered cases (shown in Figures 4, 5, 6, and 7) and the total number of people who died from the disease (not included in figures but given by D = N – (S + I)) at 120, 360, and 1,000 days after the introduction of smallpox into the population). One column in Table 3 identifies the basic reproduction number ${\mathfrak{R}}_0$ for each mixing assumption. The final day column represents the day when the number of cases reaches 99% of the final epidemic size, which is a measure of the length of the smallpox outbreak.

Table 3.

Cumulative smallpox cases at 120, 360, and 1,000 days for different mixing assumptions. Reducing the number of contacts by 50% (reduced mixing) decreases the final size for epidemic (normal mixing) by about 35%. and that the segregate mixing model epidemic takes off much faster than the other mixing assumptions. Although the normal and a proportional mixing models have the same ${\mathfrak{R}}_0$, the epidemic infects more people when there is proportional mixing.

Mixing Matrix	${\mathfrak{R}}_0$	Total Cases at			Final cases	Final daya
		120 days	360 days	1,000 days
Normal	3	33,460	1,317,460	1,321,590	1,321,590	324
Reduced	1.5	1,060	54,460	866,580	866,580	841
Proportional	3	56,760	1,429,100	1,429,660	1,429,660	280
Segregate		152,960	786,760	1,207,470	1,241,710	1325

^aDays from infection of index cases until outbreak is controlled (when the number of cases reaches 99% of the final epidemic size).

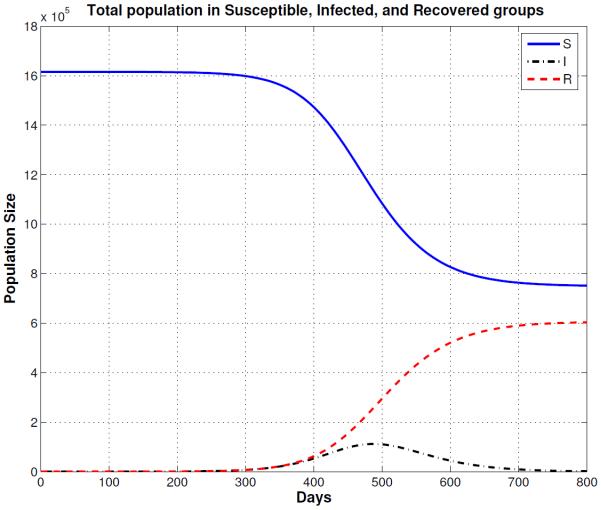
Figure 4.

Normal Mixing Epidemic: Solutions of the multi-group SIR model with staged progression for a normally mixing population. The figure shows the total susceptible (S), infected (I), and recovered (R) populations for a period of 500 days.

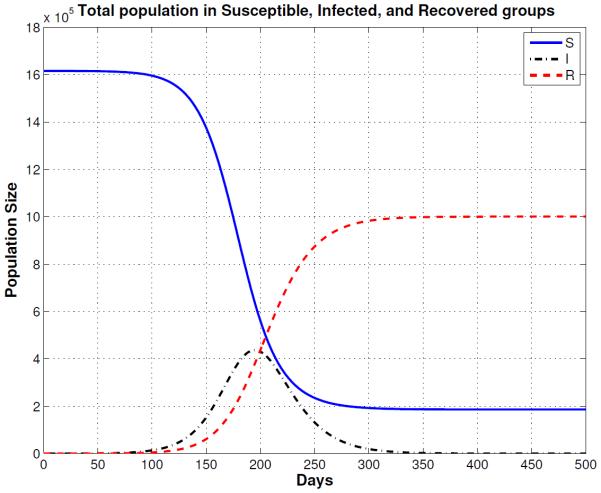
Figure 5.

Reduced Mixing Epidemic: Solutions of the multi-group SIR model for a population that reduces the number of contacts by 50% (reduced mixing). The smallpox outbreak starts much slower than the normal mixing population model (Figure 4) and the peak of the epidemic is delayed almost 200 days. Note that the epidemic is show for the first 800 days.

Figure 6.

Proportional Mixing Epidemic: Solutions of the multi-group SIR model for a proportionally mixing population start slightly faster than the model with normal mixing and the final epidemic size is larger.

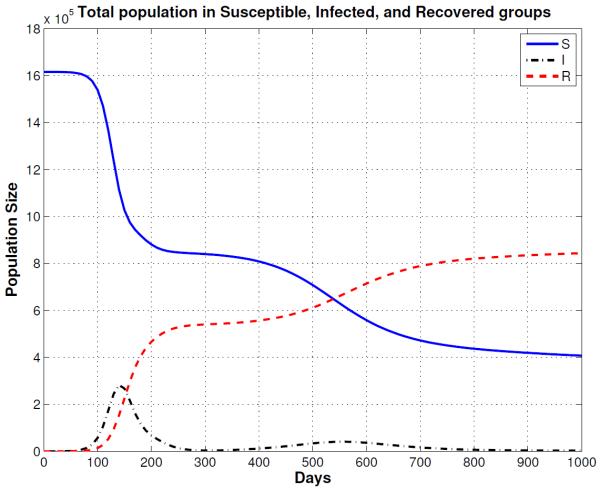
Figure 7.

Segregate Mixing Epidemic: Solutions of the multi-group SIR model for a segregate mixing population where people mix primarily with others their own age. There is an extremely rapid early burst of new infections, followed by a smaller delayed second epidemic. Note that this plot is for the first 1000 days of the epidemic.

The first entry in Table 3 shows the simulations results for normal mixing. With normal mixing, we obtained a cumulative total of 1,321,590 smallpox cases after 1,000 days and a final day of 324 days. However, when we assumed reduced mixing, which resulted in a smaller number of contacts per day, the number of cases was reduced to 866,580 and the final day was prolonged to 841 days. When proportional mixing is used, the number of smallpox cases increases to 1,429,660 and a final day is shorten to 280. The reason why the epidemic is shorten is because the mixing is assumed to be random so more people contract the disease faster. For segregate mixing, the number of smallpox cases further decreases to 1,207,470, but the final day is prolonged to 1,325. The total susceptible, recovered and disease prevalence for all mixing assumptions described in Table 3 are shown in Figures 4, 5, 6, and 7.

The differences in susceptibility of the different age groups causes the different age groups to be affected differently by the epidemic. Figure 8 shows the cumulative numbers of recovered cases, the susceptible population, and disease prevalence for age groups i = 20, 50, 65, and 85 for a normally mixing population. Age groups between 1 and 40 resemble the distributions shown in Figure 8, part A. Because the under 40 population has no residual immunity, they are affected by the disease than the rest of the population. Age groups between 41 to 61 and 66 to 71 resemble the distributions shown in Figure 8, part B, even though they had different susceptibilities. Age groups between 62 to 65 and 72 to 81 resemble the distributions shown in Figure 8, part C; notice that these age groups are the least affected by the disease. Finally, age groups between 82 and 91 resemble the distributions shown in Figure 8, part D.

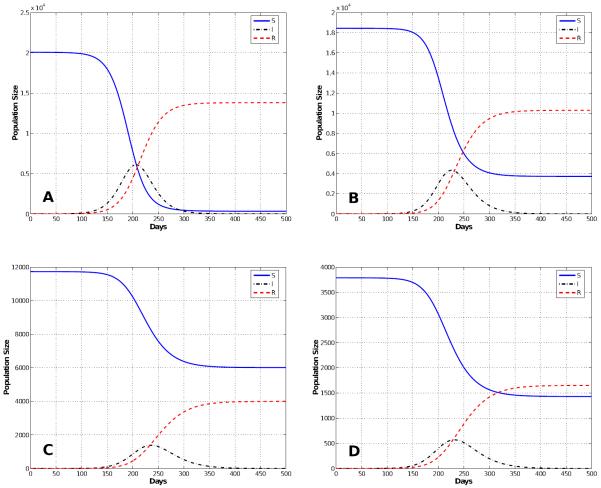
Figure 8.

Solutions of the multi-group SIR model with stage progression for a normal contact matrix for age groups 20 (A), 50 (B), 65 (C), and 85 (D). Notice the impact that partial immunity has on the final epidemic size on age groups < 41 years of age. The epidemic takes o faster in this age group and nearly all of the people are eventually infected. Because in a real epidemic there would certainly be significant behavior changes, this prediction illustrates why the behavior changes must be included before any model predictions are used to guide policy.

When the mixing among the population is reduced based on assumed behavioral changes, the number of total cases decreases dramatically. The cumulative numbers of recovered cases, the susceptible population, and the disease prevalence for some age groups are shown in Figure 9. Notice that the combination of residual immunity and behavioral changes plays a key role in halting the spread of the epidemic. In Figure 9, part A resembles the distributions of age groups 1–40; part B resembles the distributions of age groups 41–65; part C resembles the distributions of age groups 66–80; and part D resembles the distributions of age groups 81–91.

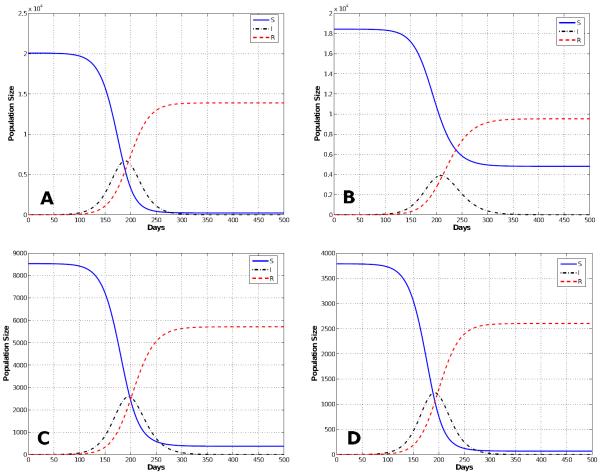
Figure 9.

Solutions of the multi-group SIR model with stage progression for a reduced contact matrix for age groups 20 (A), 50 (B), 65 (C), and 85 (D). Notice the impact that partial immunity has on the final epidemic size on age groups < 41 years of age.

When proportional mixing is assumed, all age groups are affected accordingly to their assumed susceptibility (Figure 10). Figure 10, part A resembles the distributions of age groups 1–40; part B resembles the distributions of age groups 41–65; Part C resembles the distributions of age groups 66–80; and Part D resembles the distributions of age groups 81–91. Since for segregate mixing ${\mathfrak{R}}_0$ is different for all age groups, the epidemic curves vary drastically for all age groups (Figure 11). Age groups between 1 and 40 are still the most affected (as seen with previous mixing assumptions) due to their lack of residual immunity (Figure 11, part A). Most age groups manage to maintain a large number of susceptible individuals at the end of the epidemic because of their present residual immunity (Figure 11, part B & D). However, there are a few age groups (> 60 years old) that avoid infection due to their ${\mathfrak{R}}_0$ being less than unity (Figure 11, part C).

Figure 10.

Solutions of the multi-group SIR model with stage progression for a proportional contact matrix for age groups 20 (A), 50 (B), 65 (C), and 85 (D). Notice the impact that partial immunity has on the final epidemic size on age groups < 41 years of age.

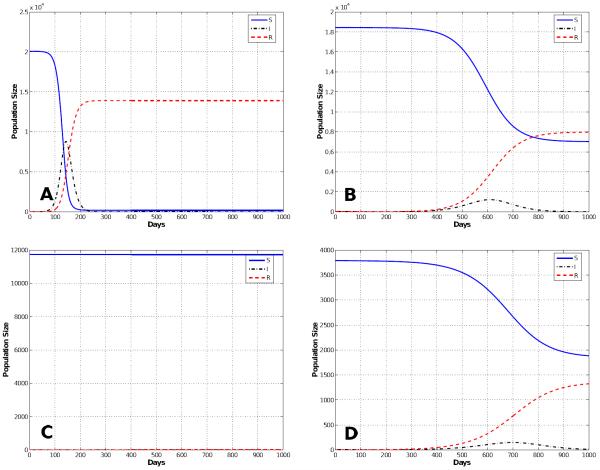
Figure 11.

Solutions of the multi-group SIR model with stage progression for a segregate contact matrix for age groups 20 (A), 50 (B), 65 (C), and 85 (D). Notice the impact that partial immunity has on the final epidemic size on age groups < 41 years of age.

5. Discussion

Assuming that a population is mixing homogeneously and has a homogenous susceptibility to a disease can often provide general insights into how a disease will spread. However, heterogenous differences in the susceptibility of a population and the contact mixing patterns within a population both affect the transmission of infectious diseases. When the population mixing patterns are correlated to the partial immunity of a population to an infectious disease, then including more realistic contact patterns within a population can lead to more accurate estimates of the effect of residual immunity on disease spread.

We investigated the impact of different mixing assumptions on outcomes related to epidemic spread in the presence of population heterogeneity. Four mixing scenarios were discussed: normal, reduced, proportional, and segregate mixing. Our results confirm and quantify the epidemiological picture proposed in previous works; that mixing assumptions have a great influence in the overall behavior of epidemic spreading and that residual immunity can play a key role in halting an epidemic such as smallpox.

We used an agent-based simulation model to generate mixing matrices and an age-structure differential equation model to model the spread of an infectious disease. Agent-based models are computational expensive and typically require a long time to run; however, they can include more detail than differential equation models. In contrast, differential equation models can run on a personal computer and are typically fast, but do not have the heterogeneity that agent-based models have. Although, the differential equation model stratified the population by age groups, we still assume homogeneous mixing patterns within each age group. This assumption will lead to different results than an agent-based model, which treats each person as an individual;. the homogeneous assumption will most likely over estimate the spread of a disease and lead to worse epidemics.

The numerical simulations in Section 4 show that proportional mixing, results in a greater number of new infections than does non-random mixing, even in the presence of residual immunity. With normal mixing, the total number of cases decreases and the final susceptible population size is larger. When moderate behavioral changes are introduced, the total number of cases is further reduced, compared to the normal mixing, and the final susceptible population size increases. We also observed that the disease affected specific age groups differently based on their assumed immunity and their mixing patterns within the population; that is, age groups with less residual immunity are more affected than age groups with higher immunity. One implication of these results is that those without prior smallpox vaccination should be vaccinated, if a smallpox vaccination campaign becomes necessary. Furthermore, we observed that for normal mixing, the probability of disease transmission among children is higher due to the frequency of their contacts; however, for proportional mixing, the probability of disease transmission is higher among young adults.

We studied an instance of segregate mixing to determine some of the factors that are driving the epidemic. Our results suggest that the heterogeneous mixing patterns have a greater impact on spreading the epidemic than does the number of contacts. Furthermore, we found that for this system, ${\mathfrak{R}}_0$ is proportional to the average number of contacts. Therefore, we can estimate the necessary reduction in contacts required to stop an epidemic.

Although parameter values were estimated using data, there is still uncertainty associated with their values. Consistent with other studies, we found that all the simulation results are highly sensitive to the number of index cases (initial infections) [11], the level of residual immunity assumed to be present in the population [45], and the value of the reproduction number [11] (results not shown here). We also found that the model is slightly sensitive to changes in the relative infectivity of the prodromal phase [19] (results not shown here). We also found that normal and reduced mixing populations were more sensitive to variations in the size and age distribution of the initially infected population than proportional mixing model [57] (results not shown here).

Our reduced behavior change model is unrealistic because of its simplicity. We reduced the number of all contacts by 50% to illustrate the importance that behavioral changes can have on the spread of an epidemic. In a real epidemic, the behavioral changes will not only reduce the number of contacts and intensity but will change the structure of the contact network. Because the model predictions are so sensitive to assumptions about the behavioral changes, these changes must be much better understood so they can be accurately included in the models. More data is needed to understand and predict the changes in behavior that a population will undertake in the presence of disease and uncertainty.

Another limitation of our study is the lack of intervention strategies. We were interested in investigating the effects of different mixing assumptions, therefore, for simplicity we did not include intervention strategies such as isolation, quarantine, and vaccination. Nevertheless, one must be aware that in the presence of a deadly disease like smallpox, many intervention strategies will take place that will further decrease the spread of the disease.

We conclude that for simulations of infectious diseases to be useful in guiding public health policy, they must consider the impact of heterogeneous mixing, residual immunity and behavioral changes. Residual immunity within the population as well as behavioral changes implemented in the affected population can greatly affect the final epidemic size and reduce the number of vaccinations needed during an outbreak. It is critically important to know the level of immunity in real populations from epidemiological studies and predict how the population will respond in the presence of an epidemic. The exact structure of the contact patterns in the general population is, to a large extent, still unknown; therefore, more research is needed to increase our understanding of the impact of human contact networks and human behavior on the spread of infectious diseases, and to assess the implications of this for the planning of public health policy.

Figure 2.

The total number of proportional contacts between age group i and j. The contact rates are defined by the elements of the n × n matrix, C_ij, where C_ij represents the total number of proportional contacts of all people of age i with people of age j per day. Note that the contacts between age group i and j is the same as between age group j and i, resulting in a symmetric graph.