Estimation and model selection of semiparametric multivariate survival functions under general censorship

Abstract

We study estimation and model selection of semiparametric models of multivariate survival functions for censored data, which are characterized by possibly misspecified parametric copulas and nonparametric marginal survivals. We obtain the consistency and root-n asymptotic normality of a two-step copula estimator to the pseudo-true copula parameter value according to KLIC, and provide a simple consistent estimator of its asymptotic variance, allowing for a first-step nonparametric estimation of the marginal survivals. We establish the asymptotic distribution of the penalized pseudo-likelihood ratio statistic for comparing multiple semiparametric multivariate survival functions subject to copula misspecification and general censorship. An empirical application is provided.

1. Introduction

Economic, financial, and medical multivariate survival data are typically non-normally distributed and exhibit nonlinear dependence among their component variables. A class of semiparametric multivariate survival models that has proven to be useful in modeling such data is the class of semiparametric copula-based multivariate survival functions in which the marginal survival functions are nonparametric, but the copula functions characterizing the dependence structure between the component variables are parameterized. More specifically, let X = (X₁, …, X_d)′ be the survival variables of interest with a d-variate joint survival function: F^o(x₁, …, x_d) = P(X₁ > x₁, …, X_d > x_d) and marginal survival functions $F_j^0(\cdot )(j=1,\dots ,d)$. Assume that $F_j^0(j=1,\dots ,d)$ are continuous. A straightforward application of Sklar's (1959) theorem shows that there exists a unique d-variate copula function C^o such that $F^0(x_1,\dots ,x_d)\equiv C^0\left(F_1^0\right(x_1),\dots ,F_d^0(x_d\left)\right)$, where the copula C^o(·) : [0, 1]^d → [0, 1] is itself a multivariate probability distribution function; it captures the dependence structure among the component variables X₁, …, X_d. This decomposition of the joint survival function leads naturally to the class of semiparametric multivariate survival functions in which the marginal survival functions are unspecified, but the copula function is parameterized: C^o(u₁, …, u_d) = C^o(u₁, …, u_d; α^o) for some parametric copula function C^o(u₁, …, u_d; α) and some value ${\alpha }^0\in \mathcal{A}$. As a multivariate survival function in this class depends on nonparametric functions of only one dimension, it achieves dimension reduction while maintaining a more flexible form than purely parametric survival functions. This class of semiparametric multivariate survival functions has been used widely in survival analysis, where modeling and estimating the dependence structure between survival variables is of importance. See Joe (1997), Nelsen (1999), Oakes (1989, 1994), Frees and Valdez (1998) and Li (2000) for examples of such applications.

A semiparametric copula-based multivariate survival model has two sets of unknown parameters: the unknown marginal survival functions $F_j^0,j=1,\dots ,d$, and the copula parameter α^o of the parametric copula function C^o(u₁, …, u_d; α^o). For complete data (i.e., data without censoring or truncation), Oakes (1994) and Genest et al. (1995) propose a two-step estimation procedure: in first step the marginal distribution functions $1-F_j^0,j=1,\dots ,d$ are estimated by the rescaled empirical distribution functions, in the second step the copula parameter α^o is estimated by maximizing the estimated log-likelihood function. For randomly right censored data, Shih and Louis (1995) independently propose the same two-step procedure, except that the Kaplan–Meier estimators of marginal survival functions are used in the first step. For a random sample of size n, Genest et al. (1995) establish the root-n consistency and asymptotic normality of their two-step estimator of α^o. For randomly right censored data, Shih and Louis (1995) derive similar large sample properties of their two-step estimator of αo under the assumption of bounded partial derivatives of score functions. Unfortunately, this assumption is violated by many commonly used copulas including the Gaussian copula, the Student's t copula, Clayton copula and Gumbel copula. In addition, Shih and Louis (1995) assume that the censoring scheme is i.i.d. random and the parametric copula function is correctly specified.

A closely related important issue in applying this class of semiparametric survival functions to a given data set is how to choose an appropriate parametric copula, as different parametric copulas lead to survival functions that may have very different dependence properties. A number of existing papers has attempted to address this issue. For complete data, we refer to Chen and Fan (2005, 2006a) for a detailed discussion of existing approaches and references. For bivariate censored data, existing work include Frees and Valdez (1998), Klugman and Parsa (1999), Wang and Wells (2000), Chen and Fan (2007), and Denuit et al. (2006). Frees and Valdez (1998) and Klugman and Parsa (1999) consider fully parametric models of bivariate distribution (or survival) functions, and they address model selection of parametric copulas and parametric marginals for insurance company data on losses and allocated loss adjustment expenses (ALAEs). The particular data set they use was collected by the US Insurance Services Office in which loss is censored by a fixed censoring mechanism and ALAE is not censored. Using various model selection techniques including AIC/BIC, Frees and Valdez (1998) select the Pareto marginal distributions and the Gumbel copula, while Klugman and Parsa (1999) select inverse paralogistic for loss marginal distribution, inverse Burr for ALAE marginal distribution and the Frank copula. Wang and Wells (2000), Denuit et al. (2006) and Chen and Fan (2007) consider model selection of semiparametric bivariate distribution (or survival) functions in which they do not specify marginals, but restrict the parametric copulas to be in the Archimedean family. In particular, Wang and Wells (2000) propose a model selection procedure for comparing copulas in the one-parameter Archimedean family, allowing for various censoring mechanisms, as long as a consistent nonparametric estimator for the bivariate joint distribution (or survival) function is available. Their selection procedure is based on comparing point estimates of the integrated squared difference between the true Archimedean copula and a parametric copula; the one with the smallest value of the integrated squared difference is chosen over the rest of the one-parameter Archimedean copulas. Denuit et al. (2006) apply Wang and Wells's (2000) procedure to copula model selection for the same Loss-ALAE data set studied in Frees and Valdez (1998). They use a nonparametric estimator of the bivariate distribution that takes into account the fixed censoring mechanism underlying the Loss-ALAE data. They examine four one-parameter Archimedean copulas (Gumbel, Clayton, Frank and Joe) and select Gumbel copula since it yields the smallest estimated integrated squared difference. Chen and Fan (2007) propose a model selection test for comparing multiple semiparametric bivariate survival functions by taking into account the randomness in the estimated integrated squared difference. However, their test is still only applicable to model selection of parametric copulas within the Archimedean family only. It is known that a one or two-parameter Archimedean copula family could be too restrictive to capture various dependence structures among multivariate variables. In addition, the semiparametric model selection procedures in Wang and Wells (2000), Denuit et al. (2006) and Chen and Fan (2007) require consistent nonparametric estimation of the joint distribution function and the limiting distributions are complicated. As a result, even for a parametric Archimedean copula family, these tests are difficult to implement for multivariate (higher than bivariate) data with general censorship.

In this paper we bridge the gap in existing work for estimating and selecting a semiparametric multivariate copula-based survival model by (i) allowing for data to be censored under various censoring mechanisms, (ii) using nonparametric estimation of marginal survival functions only, (iii) permitting any parametric copula specification, which may be misspecified, non-Archimedean, and its score function may have unbounded partial derivatives. For random samples without censoring, Chen and Fan (2005) already consider the Pseudo-likelihood estimation of copula parameters and Pseudo-likelihood ratio (PLR) model selection test for semiparametric multivariate copula-based distribution models, accounting for (ii) and (iii). In this paper, we extend their results to allow for general right censorship. In particular, we first establish the convergence of the two-step estimator of the copula parameter to the pseudo-true value defined as the value of the parameter that minimizes the Kullback-Leibler Information Criterion (KLIC) between the parametric copula induced multivariate density and the unknown true density. We then derive its root-n asymptotically normal distribution and provide a simple consistent asymptotic variance estimator by accounting for (i), (ii) and (iii). These results are used to establish the asymptotic distribution of the penalized PLR statistic for comparing multiple semiparametric multivariate survival functions subject to copula misspecification and general censorship. We also propose a standardized version of the test, whose limiting null distribution is easy to simulate. To illustrate the usefulness of our testing procedure, we apply it to copula model selection for the loss-ALAE data, taking into account the underlying censoring mechanism in the data and allowing parametric copulas to exhibit more flexible dependence structures than those in the Archimedean family. We find that the standardized test is generally more powerful than the non-standardized test.

The rest of this paper is organized as follows. Section 2 introduces the model selection criterion function and the two-step estimation of the copula dependence parameter. In Section 3, we study the large sample properties of the pseudo-likelihood estimator of the copula parameter allowing for independent but general right censorship and misspecified parametric copulas. In Section 4, we present the limiting null distributions of the (penalized) PLR test statistics for model selection among multiple semiparametric copula models for multivariate censored data. Section 5 provides an empirical application to the Loss-ALAE data set and Section 6 briefly concludes. All technical proofs are gathered into the Appendix.

2. Model selection criterion and parameter estimation

To simplify notation, we shall present our results for bivariate survival models only. Obviously, all these results have straightforward extensions to multivariate copula models for survival data with any finite dimension.

In the following we shall use (D₁, D₂) to denote the censoring variables. Thus under the right censorship, one observes (${\tilde{X}}_1$, ${\tilde{X}}_2$) = (X₁ ^ D₁, X₂ ^ D₂) and a pair of indicators, (δ₁, δ₂) = (I{X₁ ≤ D₁}, I{X₂ ≤ D₂}), where a ^ b = min(a, b) for real numbers a and b and I{·} is the indicator function. We assume that the censoring variables (D₁, D₂) are independent of the survival variables (X₁, X₂). Let $F_j^0\left(x_j\right)=P(X_j>x_j)$ denote the true but unknown marginal survival function of X_j for j = 1, 2. Suppose n independent (but possibly non-identically distributed) observations ${\left\{\right({\tilde{X}}_{1t},{\tilde{X}}_{2t},{\delta }_{1t},{\delta }_{2t}\left)\right\}}_{t=1}^n$ are available, where (${\tilde{X}}_{1t}$, ${\tilde{X}}_{2t}$) = (X_1t ^ D_1t, X_2t ^ D_2t) and (δ_1t, δ_2t) = (I{X_1t ≤ D_1t}, I{X_2t ≤ D_2t}). Denote $U_t=(U_{1t},U_{2t})=\left(F_1^0\right({\tilde{X}}_{1t}),F_2^0({\tilde{X}}_{2t}\left)\right)$.

2.1. Model selection criterion

Let $\left\{C_i\right(u_1,u_2;{\alpha }_i):{\alpha }_i\in {\mathcal{A}}_i\subset {\mathcal{R}}^{pi}\}$ be a class of parametric copulas with i = 1, 2, …, M. By Sklar's (1959) theorem, each parametric copula family i corresponds to a parametric likelihood $L_{i,n}\left({\alpha }_i\right)\equiv {\sum }_{t=1}^n{\ell }_i(U_{1t},U_{2t},{\delta }_{1t},{\delta }_{2t};{\alpha }_i)$, where

$${\ell }_i(u_{1t},u_{2t},{\delta }_{1t},{\delta }_{2t};{\alpha }_i)={\delta }_{1t}{\delta }_{2t}\log c_i(u_{1t},u_{2t};{\alpha }_i)+{\delta }_{1t}(1-{\delta }_{2t})\log \frac{\partial C_i(u_{1t},u_{2t};{\alpha }_i)}{\partial u_1}+{\delta }_{2t}(1-{\delta }_{1t})\log \frac{\partial C_i(u_{1t},u_{2t};{\alpha }_i)}{\partial u_2}+(1-{\delta }_{1t})(1-{\delta }_{2t})\log C_i(u_{1t},u_{2t};{\alpha }_i),$$

where $c_i(u_1,u_2;{\alpha }_i)=\frac{{\partial }^2{C}_i(u_1,u_2;{\alpha }_i)}{\partial u_1\partial u_2}$ is the density function of copula C_i(u₁, u₂; α_i).

In this paper, we are interested in testing whether a benchmark model (say copula model 1) performs significantly better than the rest of the copula models according to the KLIC. Let E⁰ denote the expectation with respect to the true probability measure. Define

$${\alpha }_{\mathit{in}}^{\ast }=\arg \underset{{\alpha }_i\in {\mathcal{A}}_i}{\overset{\max }{}}{n}^{-1}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t},{\delta }_{1t},{\delta }_{2t};{\alpha }_i\left)\right]$$

as the pseudo-true value that minimizes the KLIC between the i-th parametric copula family induced multivariate density and the unknown true density. To conclude that copula model 1 performs significantly better than the rest of the copula models calls for a formal statistical test, where the null hypothesis is:

$$H_0:\underset{i=2,\dots ,M}{\overset{\max }{}}{n}^{-1}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t},{\delta }_{1t},{\delta }_{2t};{\alpha }_{\mathit{in}}^{\ast }\left)\right]-{\ell }_1(U_{1t},U_{2t},{\delta }_{1t},{\delta }_{2t};{\alpha }_{1n}^{\ast })]\le 0,$$

meaning that none of the copula models 2, …, M is closer to the true model (according to KLIC) than model 1, and the alternative hypothesis is:

$$H_1:\underset{i=2,\dots ,M}{\overset{\max }{}}{n}^{-1}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t},{\delta }_{1t},{\delta }_{2t};{\alpha }_{\mathit{in}}^{\ast }\left)\right]-{\ell }_1(U_{1t},U_{2t},{\delta }_{1t},{\delta }_{2t};{\alpha }_{1n}^{\ast })]>0,$$

meaning that there exists a copula model from 2, …, M that is closer to the true model (according to KLIC) than model 1.

2.2. Two-step estimation

To construct a test statistic for the null hypothesis H₀ against the alternative H₁, we need estimates of $(U_{1t},U_{2t})=\left(F_1^0\right({\tilde{X}}_{1t}),F_2^0({\tilde{X}}_{2t}\left)\right)$ and ${\alpha }_{in}^{\ast }$ for i = 1, …, M.

For j = 1, 2, let ${\tilde{F}}_j(\cdot )$ be the Kaplan–Meier estimator of $F_j^0(\cdot )=P(X_j>\cdot )$:

$${\tilde{F}}_1\left(x\right)={\prod }_{{\tilde{X}}_{1\left(t\right)\le x}}{\left(1-\frac{1}{n-t+1}\right)}^{{\delta }_{1\left(t\right)}},$$

$${\tilde{F}}_2\left(x\right)={\prod }_{{\tilde{X}}_{2\left(t\right)\le x}}{\left(1-\frac{1}{n-t+1}\right)}^{{\delta }_{2\left(t\right)}},$$

where ${\tilde{X}}_{j\left(1\right)}\le {\tilde{X}}_{j\left(2\right)}\le \cdots \le {\tilde{X}}_{j\left(n\right)}$ are order statistics of ${\left\{{\tilde{X}}_{jt}\right\}}_{t=1}^n$ for j = 1, 2, and ${\left\{{\delta }_{j\left(t\right)}\right\}}_{t=1}^n(j=1,2)$ are similarly defined. Then under independent censoring, ${\tilde{F}}_j(\cdot )$ is consistent for $F_j^0(\cdot )$, j = 1, 2; see e.g., Lai and Ying (1991).

Given the definition of ${\alpha }_{in}^{\ast }$, a natural estimator for it is the pseudo-likelihood estimator ${\widehat{\alpha }}_{in}$:

$${\widehat{\alpha }}_{\mathit{in}}=\arg \underset{{\alpha }_i\in {\mathcal{A}}_i}{\overset{\max }{}}{n}^{-1}\sum _{t=1}^n{\ell }_i\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t}),{\delta }_{1t},{\delta }_{2t};{\alpha }_i),i=1,\dots ,M.$$

Since this estimation procedure involves the first-step nonparametric estimation of the marginal survival functions $F_j^0(\cdot )$, j = 1, 2, the estimator ${\widehat{\alpha }}_{in}$ is also called the “two-step” estimator.

Note that no assumption is made on the censoring variables (D_1t, D_2t) other than their independence with the survival variables (X_1t, X_2t). As a result, various censoring mechanisms are allowed, including the simple random censoring, fixed censoring, and of course no censoring. If the censoring variables are fixed at D_jt = +∞ for j = 1, 2, ${\widehat{\alpha }}_{in}$ becomes the estimator proposed in Genest et al. (1995). If the censoring variables (D_1t, D_2t) are i.i.d. with a continuous joint survival function, ${\widehat{\alpha }}_{in}$ becomes the estimator proposed in Shih and Louis (1995). Assuming that the parametric copula density c_i(u₁, u₂; α_i) is correctly specified and that log c_i(u₁, u₂; α_i) has bounded partial derivatives with respect to u₁, u₂, Shih and Louis (1995) establish the root-n asymptotic normality of ${\widehat{\alpha }}_{in}$ and provide a consistent estimator of its asymptotic variance for i.i.d. randomly censored data.

The censoring mechanism for the loss-ALAE data is non-random; ALAE is not censored and Loss is censored by a constant which differs from each individual to another. Results in Shih and Louis (1995) may not be directly applicable to this data set even under a correct specification of the copula function. Moreover, for model selection, we need to establish the asymptotic properties of the two-step estimator under copula misspecification. This will be done in the next section for a general censoring mechanism.

2.3. Penalized pseudo-likelihood ratio criteria

To test the null hypothesis H₀ against the alternative H₁, we use the PLR statistic:

$${\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})={\tilde{L}}_{i,n}\left({\widehat{\alpha }}_{in}\right)-{\tilde{L}}_{1n}\left({\widehat{\alpha }}_{1n}\right),i=2,\dots ,M,$$

where

$${\tilde{L}}_{i,n}\left({\widehat{\alpha }}_{\mathit{in}}\right)\equiv \frac{1}{n}\sum _{t=1}^n{\ell }_i\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t}),{\delta }_{1t},{\delta }_{2t};{\widehat{\alpha }}_{\mathit{in}}),i=1,\dots ,M.$$

In most applications, several parametric copula families are compared which may have different numbers of parameters. To take this into account, we follow the approach in Sin and White (1996) by adopting a general penalization of model complexity. Let Pen(p_i, n) denote a penalization term such that Pen(p_i, n) increases with p_i dim(${\mathcal{A}}_i$), decreases with n, and Pen(p_i, n)/n → 0. Then the penalized PLR statistic is

$$\begin{array}{cc}\hfill {\mathit{PLR}}_n({\tilde{F}}_1,{\tilde{F}}_2);{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})& ={\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})-\frac{\mathit{Pen}(p_i,n)-\mathit{Pen}(p_1,n)}{n}\hfill \\ \hfill & ={\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})+o_p\left(1\right).\hfill \end{array}$$

We note that Pen(p_i, n) = p_i corresponds to AIC, and Pen(p_i, n) = 0.5p_i log n corresponds to BIC criterion.

In many existing applications of copula models, AIC has been used to compare different families of parametric copula models. To be more specific, let

$${\mathit{AIC}}_i=-\frac{2}{n}\sum _{t=1}^n{\ell }_i\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t}),{\delta }_{1t},{\delta }_{2t};{\widehat{\alpha }}_{\mathit{in}})+\frac{2p_i}{n},i=1,\dots ,M.$$

Then the values of AIC_i for i = 1, …, M are compared; copula model 1 will be selected if AIC₁ = min{AIC_i : 1 ≤ i ≤ M} or equivalently if

$${\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})-\frac{p_i-p_1}{n}<0,i=2,\dots ,M.$$ (2.1)

Noting, however, that ${\mathit{PLR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{in},{\widehat{\alpha }}_{1n})$ (such as AIC_i) is a random variable, the fact that ${\mathit{PLR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{in},{\widehat{\alpha }}_{1n})<0$ for i = 2, …, M (or inequality (2.1) holds) for one sample ${\{{\tilde{X}}_{1t},{\tilde{X}}_{2t},{\delta }_{1t},{\delta }_{2t}\}}_{t=1}^n$ may not imply that copula model 1 performs significantly better than the rest of the models; it may occur by chance. As we will show in the next section, ${\mathit{PLR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{in},{\widehat{\alpha }}_{1n})=n^{-1}{\sum }_{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t},{\delta }_{t1},{\delta }_{2t};{\alpha }_{in}^{\ast })-{\ell }_1(U_{1t},U_{2t},{\delta }_{1t},{\delta }_{2t};{\alpha }_{1n}^{\ast }\left)\right]+o_p\left(1\right)$ for i = 2, …, M. To conclude that copula model 1 performs significantly better than the rest of the models we need to perform a formal statistical test for H₀ against H₁.

To test H₀, we have to take into account the randomness of the (penalized) PLR statistic. More precisely, we need to derive the asymptotic distributions of ${\widehat{\alpha }}_{in}$ and the test statistics under the null hypothesis. This will be accomplished in Sections 3 and 4 of this paper.

3. Asymptotic properties of the two-step estimator under copula misspecification

As mentioned in the previous section, asymptotic properties of the two-step estimator are established for randomly censored data in Shih and Louis (1995) under the assumptions that the parametric copula density correctly specifies the true copula density and that its score function has bounded partial derivatives. In this section, we will extend their results to a more general censoring mechanism and allow for misspecified parametric copulas whose score functions may have unbounded partial derivatives.

Recall that $\mathcal{A}\subset {\mathcal{R}}^p$ is the parameter space. For α, ${\alpha }^{\ast }\in \mathcal{A}$ we use ∥α − α*∥ to denote the usual Euclidean metric. To simplify notation, we now let

$$\ell (u_1,u_2;\alpha )={\delta }_1{\delta }_2\log c(u_1,u_2;\alpha )+{\delta }_1(1-{\delta }_2)\log \frac{\partial C\left(u_1\right),u_2;\alpha )}{\partial u_1}+{\delta }_2(1-{\delta }_1)\log \frac{\partial C\left(u_1\right),u_2;\alpha )}{\partial u_2}+(1-{\delta }_1)(1-{\delta }_2)\log C(u_1,u_2;\alpha ),$$

where c(u₁, u₂; α) is the density of the parametric copula C(u₁, u₂; α). Then the pseudo-true copula parameter value is ${\alpha }_n^{\ast }=\text{arg}{\max }_{\alpha \in \mathcal{A}}{n}^{-1}{\sum }_{t=1}^n{E}^0\left[\ell \right(U_{1t},U_{2t};\alpha \left)\right]$, and its two-step estimator is ${\widehat{\alpha }}_n=\text{arg}{\max }_{\alpha \in \mathcal{A}}{n}^{-1}{\sum }_{t=1}^n\ell \left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});\alpha )$.

Finally we denote

$${\ell }_{\alpha }(u_1,u_2;\alpha )=\frac{\partial \ell (u_1,u_2;\alpha )}{\partial \alpha },$$

$${\ell }_j(u_1,u_2;\alpha )=\frac{\partial \ell (u_1,u_2;\alpha )}{\partial u_j},(j=1,2),$$

$${\ell }_{\alpha \alpha }(u_1,u_2;\alpha )=\frac{{\partial }^2\ell (u_1,u_2;\alpha )}{\partial {\alpha }^2}\text{and}$$

$${\ell }_{\alpha j}(u_1,u_2;\alpha )=\frac{{\partial }^2\ell (u_1,u_2;\alpha )}{\partial u_j\partial \alpha }\text{for}j=1,2.$$

3.1. Consistency

The following conditions are sufficient to ensure the convergence of the two-step estimator ${\widehat{\alpha }}_n$ to the pseudo true value ${\alpha }_n^{\ast }$.

• C1
  • (i)
    The sequence of survival variables, ${\left\{\right(X_{1t},X_{2t}\left)\right\}}_{t=1}^n$ is an i.i.d. sample from an unknown survival function F^o(x₁, x₂) with continuous marginal survival functions $F_j^0(\cdot ),j=1,2$;
  • (ii)
    The sequence of censoring variables ${\{D_{1t},D_{2t}\}}_{t=1}^n$ is an independent sample with joint survival functions ${\left\{G_t\right(x_1,x_2\left)\right\}}_{t=1}^n={\left\{P\right(D_{1t}>x_1,D_{2t}>x_2\left)\right\}}_{t=1}^n$ and marginal survival functions ${\left\{G_{jt}\right(\cdot \left)\right\}}_{t=1}^n,j=1,2$;
  • (iii)
    The censoring variables (D_1t, D_2t) are independent of survival variables (X_1t, X_2t) and there is no mass concentration at 0 in the sense that ${\text{lim sup}}_{n\to \infty }{n}^{-1}{\sum }_{t=1}^n(1-G_{jt}(\eta \left)\right)\to 0$ as η → 0.
• C2
  Let $\mathcal{A}$ be a compact subset of ${\mathcal{R}}^p$. For every ∊ > 0,

  $$\underset{\alpha \in \mathcal{A}:\Vert \alpha -{\alpha }_n^{\ast }\Vert \ge ∊}{\overset{\lim \inf }{}}\frac{1}{n}\sum _{t=1}^n\left[E^0\right\{\ell (U_{1t},U_{2t};{\alpha }_n^{\ast }\}]-E^0\{\ell (U_{1t},U_{2t};\alpha )\left\}\right]>0.$$
• C3The true (unknown) copula function C^o(u₁, u₂) has continuous partial derivatives.
• C4
  • (i)
    For any (u₁, u₂) ∈ (0, 1)², ℓ(u₁, u₂; α) is a continuous function of $\alpha \in \mathcal{A}$
  • (ii)
    Let $L_t={\text{sup}}_{\alpha \in \mathcal{A}}\mid \ell (U_{1t},U_{2t};\alpha )\mid$ and $L_{t\alpha }={\text{sup}}_{\alpha \in \mathcal{A}}\mid {\ell }_{\alpha }(U_{1t},U_{2t};\alpha )\mid$ Then,

    $$\underset{K\to \infty }{\overset{\lim }{}}\underset{n\to \infty }{\overset{\lim \sup }{}}{n}^{-1}\sum _{t=1}^n{E}^0\left\{L_{t}I\right(L_t\ge K)+L_{t\alpha }I(L_{t\alpha }\ge K\left)\right\}=0;$$
  • (iii)
    For any η > 0, ∊ > 0, there is K > 0 such that $\mid \ell (u_1,u_2;\alpha )\mid \le K\mid \ell (u_1^{\prime },u_2^{\prime };\alpha )\mid$ for all $\alpha \in \mathcal{A}$ and all u_j ∈ [η, 1) such that $1-u_j\ge ∊(1-u_j^{\prime }),j=1,2$
• C5If ${\left\{X_{jt}\right\}}_{t=1}^n$ are subject to non-trivial censoring (i.e., D_jt ≠ ∞), then ${\tilde{F}}_j$ is truncated at the tail in the sense that for some ${\tau }_j,{\tilde{F}}_j\left(x_j\right)={\tilde{F}}_j\left({\tau }_j\right)$ for all x_j ≥ τ_j and lim inf n⁻¹ ${\sum }_{t=1}^n{G}_{jt}\left({\tau }_j\right)F^0\left({\tau }_j\right)>0$.

Note that in contrast to the censoring mechanism in Shih and Louis (1995) Condition C1(ii) allows the censoring variables ${\left\{\right(D_{1t},D_{2t}\left)\right\}}_{t=1}^n$ to be non-identically distributed. In addition, no assumption is made on the joint survival function G_t(x₁, x₂) of the censoring variables (D_1t, D_2t). Hence Condition C1(ii) includes the fixed censoring mechanism in which each survival variable (X_1t, X_2t) is censored at a pre-specified, fixed time (D_1t, D_2t) which may differ from one observation to another, in which case, the survival function G_t(x₁, x₂) is degenerate at (D_1t, D_2t). It also allows the variables X_1t and X_2t to have different censoring mechanisms, one random and the other fixed or one censored and the other uncensored. For example, the censoring mechanism for the Loss-ALAE data is such that Loss is censored by a fixed censoring mechanism and ALAE is uncensored. As a result, the observed variables ${\left\{\right({\tilde{X}}_{1t},{\tilde{X}}_{2t}\left)\right\}}_{t=1}^n$ may not be identically distributed and the identifiably unique maximizer ${\alpha }_n^{\ast }$ defined in Condition C2 may depend on n. Condition C5 is imposed to handle the possible tail instability of the Kaplan–Meier estimator, especially for non-identically distributed censoring times. The truncation can be achieved by simply using D_jt ∧ τ_j as the censoring variables. Thus, without loss of generality, we shall assume that D_jt ∧ τ_j are the censoring variables so that ${\tilde{X}}_{jt}\le {\tau }_j$. The simple truncation at τ_j can be changed to the more elaborate tail modification. We refer to Lai and Ying (1991) for the issue of tail instability and modification. Finally, because we allow the left tail of the copula to blow up as well, we shall set $\ell \left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});\alpha )=0$ whenever ${\tilde{F}}_j\left({\tilde{X}}_{jt}\right)=1$ for j = 1 or 2.

Proposition 3.1. Under conditions C1–C5, we have:

• (1)
  $$\Vert {\widehat{\alpha }}_n-{\alpha }_n^{\ast }\Vert o_p\left(1\right);$$
• (2)
  $$\frac{1}{n}\sum _{t=1}^n\ell \left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\widehat{\alpha }}_n)=\frac{1}{n}\sum _{t=1}^n{E}^0\left\{\ell \right(F_1^0\left({\tilde{X}}_{1t}\right),F_2^0\left({\tilde{X}}_{2t}\right);{\alpha }_n^{\ast }\left)\right\}+o_p\left(1\right).$$

Proposition 3.1(1) states that the two-step estimator ${\widehat{\alpha }}_n$ is a consistent estimator of the pseudo true value ${\alpha }_n^{\ast }$. If the censoring mechanism is random, then ${\alpha }_n^{\ast }={\alpha }^{\ast }$ which does not depend on n. In addition, if the parametric copula correctly specifies the true copula, then ${\alpha }^{\ast }={\alpha }^0$, where α^o is such that C(u₁, u₂; α^o) = C^o(u₁, u₂) for almost all (u₁, u₂) ∈ (0, 1)².

3.2. Asymptotic normality

Recall that $(U_{1t},U_{2t})=\left(F_1^0\right({\tilde{X}}_{1t}),F_2^0({\tilde{X}}_{2t}\left)\right)$. For j = 1, 2, we denote

$$W_j({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}};{\alpha }_n^{\ast })\equiv E^0\left[{\ell }_{\alpha j}\right(U_{1s},U_{2s};{\alpha }_n^{\ast }\left)I_j^o\right({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}}\left)\right({\tilde{X}}_{\mathit{js}})\mid {\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}}],$$

$$I_j^o({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}})\left({\tilde{X}}_{\mathit{js}}\right)\equiv -F_j^o\left({\tilde{X}}_{\mathit{js}}\right)\left[{\int }_{-\infty }^{{\tilde{X}}_{\mathit{js}}}\frac{\mathrm{d}{n}_{\mathit{jt}}\left(u\right)}{P_{n,j}\left(u\right)}-{\int }_{-\infty }^{{\tilde{X}}_{\mathit{js}}}\frac{I\{{\tilde{X}}_{\mathit{jt}}\ge u\}\mathrm{d}{\Lambda }_j\left(u\right)}{P_{n,j}\left(u\right)}\right],$$

with ${\Lambda }_j\left(u\right)\equiv -\log \left(F_j^0\right(u\left)\right)$ the cumulative hazard function of X_j, $N_{jt}\left(u\right)\equiv {\delta }_{jt}I\{{\tilde{X}}_{jt}\le u\}$ and dN_jt (u) = N_jt (u) − N_jt (u−), and $P_{n,j}\left(u\right)\equiv n^{-1}{\sum }_{k=1}^{n}P({\tilde{X}}_{jk}\ge u)=n^{-1}{\sum }_{k=1}^n{G}_{jk}\left(u\right)F_j^0\left(u\right)$.

Let Var⁰ denote the variance with respect to the true probability measure. The following conditions are sufficient to ensure the asymptotic normality of ${\widehat{\alpha }}_n$.

• A1
  • (i)
    C2 holds with ${\alpha }_n^{\ast }$ ∈ int(A*) for all n, where A* is a compact subset of $\mathcal{A}$;
  • (ii)
    $B_n\equiv -n^{-1}{\sum }_{t=1}^n{E}^0\left\{{\ell }_{\alpha \alpha }\right(U_{1t},U_{2t};{\alpha }_n^{\ast }\left)\right\}$ has all its eigenvalues bounded below and above by some finite positive constants;
  • (iii)
    ${\Sigma }_n\equiv n^{-1}{\sum }_{t=1}^n{\mathit{Var}}^0\left\{{\ell }_{\alpha }\right(U_{1t},U_{2t};{\alpha }_n^{\ast })+W_1({\tilde{X}}_{1t},{\delta }_{1t};{\alpha }_n^{\ast })+W_2({\tilde{X}}_{2t},{\delta }_{2t};{\alpha }_n^{\ast }\left)\right\}$ has all its eigenvalues bounded below and above by some finite positive constants;
  • (iv)
    ${\left\{{\ell }_{\alpha }\right(U_{1t},U_{2t};{\alpha }_n^{\ast })+W_1({\tilde{X}}_{1t},{\delta }_{1t};{\alpha }_n^{\ast })+W_2({\tilde{X}}_{2t},{\delta }_{2t};{\alpha }_n^{\ast }\left)\right\}}_{t=1}^n$ satisfies Lindeberg condition.
• A2Functions ℓ_αα(u₁, u₂; α) and ℓ_αj(u₁, u₂; α), j = 1, 2, are well-defined and continuous in $(u_1,u_2,\alpha )\in {(0,1)}^2\times \mathcal{A}$.
• A3
  • (i)
    $\mid {\ell }_{\alpha }(u_1,u_2;{\alpha }_n^{\ast })\mid \le q{\left\{u_1\right(1-u_1\left)\right\}}^{-a_1}{\left\{u_2\right(1-u_2\left)\right\}}^{-a_2}$ for some q > 0 and a_j ≥ 0 such that $\text{lim sup}{n}^{-1}{\sum }_{t=1}^n{E}^0\left[{\left\{U_{1t}\right(1-U_{1t}\left)\right\}}^{-1a_1}{\left\{U_{2t}\right(1-U_{2t}\left)\right\}}^{-2a_2}\right]<\infty$;
  • (ii)
    $\mid {\ell }_{\alpha j}(u_1,u_2;{\alpha }_n^{\ast })\mid \le \mathit{const}.{\left\{u_j\right(1-u_j\left)\right\}}^{-b_j}{\left\{u_k\right(1-u_k\left)\right\}}^{-a_k}$ for some b_k, a_k and j ≠ k such that $\text{lim sup}{n}^{-1}{\sum }_{t=1}^n{E}^0\left[{\left\{U_{jt}\right(1-U_{jt}\left)\right\}}^{{\xi }_j-b_j}{\left\{U_{kt}\right(1-U_{kt}\left)\right\}}^{-a_k}\right]<\infty$ for some ξ_j ∈ (0, 1/2).
• A4
  • (i)
    Let $L_{t\alpha j}={\text{sup}}_{\alpha \in \mathcal{A}}\mid {\ell }_{\alpha j}(U_{1t},U_{2t};\alpha )\mid$ and $L_{t\alpha \alpha }={\text{sup}}_{\alpha \in \mathcal{A}}\mid {\ell }_{\alpha \alpha }(U_{1t},U_{2t};\alpha )\mid$. Then,

    $$\underset{K\to \infty }{\overset{\lim }{}}\underset{n\to \infty }{\overset{\lim \sup }{}}{n}^{-1}\sum _{t=1}^n{E}^0\left\{L_{t\alpha j}I\right(L_{t\alpha j}\ge K)+L_{t\alpha \alpha }I(L_{t\alpha \alpha }\ge K\left)\right\}=0;$$
  • (ii)
    For any η > 0 and any ∊ > 0, there is K > 0, such that $\mid {\ell }_{\alpha }(u_1,u_2;\alpha )\mid +\mid {\ell }_{\alpha \alpha }(u_1,u_2;\alpha )\mid \le K\{\mid {\ell }_{\alpha }(u_1^{\prime },u_2^{\prime };\alpha )\mid +\mid {\ell }_{\alpha \alpha }(u_1^{\prime },u_2^{\prime };\alpha )\mid \}$ for all $\alpha \in \mathcal{A}$ and all u_j ∈ [η, 1) such that $1-u_j\ge ∊(1-u_j^{\prime })$, j = 1, 2.

Shih and Louis (1995) require bounded ${\ell }_{\alpha }(u_1,u_2;{\alpha }_n^{\ast })$ and ${\ell }_{\alpha j}(u_1,u_2;{\alpha }_n^{\ast })$ for j = 1, 2, however, this requirement is not satisfied by many popular copula functions such as Gaussian copula, t-copula, Gumbel copula and Clayton copula. Conditions A3 and A4 relax the boundedness requirement, and allow the score function and its partial derivatives with respect to the first two arguments to blow up at the boundaries. Similar conditions have been verified for Gaussian, Frank and Clayton copulas in Chen and Fan (2006b).

Proposition 3.2. Under conditions C1–C5 and A1–A4, we have: $B_n{\Sigma }_n^{-1∕2}\sqrt{n}({\widehat{\alpha }}_n-{\alpha }_n^{\ast })\to N(0,I_p)$ in distribution, where B_n and Σ_n are defined A1.

Proposition 3.2 extends Theorem 2 in Shih and Louis (1995) in two directions: (i) it allows for more general censoring mechanisms than the simple random censoring in Shih and Louis (1995), and (ii) it allows for the possibility that the parametric copula may not specify the true copula correctly. As a result, there are several differences between Proposition 3.2 and Theorem 2 in Shih and Louis (1995): First, since the censoring variables ${\{D_{1t},D_{2t}\}}_{t=1}^n$ may not be identically distributed, B_n and Σ_n may depend on n; Second, since the parametric copula may misspecify the true copula, the information matrix equality may not hold. Consequently, the asymptotic variance of $\sqrt{n}({\widehat{\alpha }}_n-{\alpha }_n^{\ast })$, $B_n^{-1}{\Sigma }_n{B}_n^{-1}$, can not be reduced to $[B_n^{-1}+n^{-1}{B}_n^{-1}{\sum }_{t=1}^n{\mathit{Var}}^0\{W_1({\tilde{X}}_{1t},{\delta }_{1t};{\alpha }_n^{\ast })+W_2({\tilde{X}}_{2t},{\delta }_{2t};{\alpha }_n^{\ast })\left\}{B}_n^{-1}\right]$ as in Shih and Louis (1995). For complete data, Proposition 3.2 reduces to that in Chen and Fan (2005).

To estimate the asymptotic variance $B_n^{-1}{\Sigma }_n{B}_n^{-1}$ of $\sqrt{n}({\widehat{\alpha }}_n-{\alpha }_n^{\ast })$, we let

$${\widehat{B}}_n=-n^{-1}\sum _{t=1}^n{\ell }_{\alpha \alpha }\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),({\tilde{F}}_2\left({\tilde{X}}_{2t}\right);{\widehat{\alpha }}_n),$$

$${\widehat{\Sigma }}_n=\frac{1}{n}\sum _{t=1}^n\left\{{\ell }_{\alpha }\right({\tilde{F}}_1\left({\tilde{X}}_{1t}\right),{\tilde{F}}_2\left({\tilde{X}}_{2t}\right);{\widehat{\alpha }}_n)+{\widehat{W}}_1({\tilde{X}}_{1t},{\delta }_{1t};{\widehat{\alpha }}_n)+{\widehat{W}}_2({\tilde{X}}_{2t},{\delta }_{2t};{\widehat{\alpha }}_n\left)\right\}{\left\{{\ell }_{\alpha }\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\widehat{\alpha }}_n);+{\widehat{W}}_1({\tilde{X}}_{1t},{\delta }_{1t};{\widehat{\alpha }}_n+{\widehat{W}}_2({\tilde{X}}_{2t},{\delta }_{2t};{\widehat{\alpha }}_n),\right\}}^{\prime },$$

with

$${\widehat{W}}_1({\tilde{X}}_{1t},{\delta }_{1t};{\widehat{\alpha }}_n)=\frac{1}{n}\sum _{s\ne t,s=1}^n{\ell }_{\alpha 1}\left({\tilde{F}}_1\right({\tilde{X}}_{1s}),{\tilde{F}}_2({\tilde{X}}_{2s});{\widehat{\alpha }}_n){\widehat{I}}_1^0({\tilde{X}}_{1t},{\delta }_{1t})\left({\tilde{X}}_{1s}\right),$$

$${\widehat{W}}_2({\tilde{X}}_{2t},{\delta }_2;{\widehat{\alpha }}_n)=\frac{1}{n}\sum _{s\ne t,s=1}^n{\ell }_{\alpha 2}\left({\tilde{F}}_1\right({\tilde{X}}_{1s}),{\tilde{F}}_2({\tilde{X}}_{2s});{\widehat{\alpha }}_n){\widehat{I}}_2^0({\tilde{X}}_{2t},{\delta }_{2t})\left({\tilde{X}}_{2s}\right),$$

in which for j = 1, 2,

$${\widehat{I}}_j^o({\widehat{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}})\left({\tilde{X}}_{\mathit{js}}\right)=-{\tilde{F}}_j\left({\tilde{X}}_{\mathit{js}}\right)\left[\frac{I\{{\tilde{X}}_{\mathit{jt}}\le {\tilde{X}}_{\mathit{js}}\}{\delta }_{\mathit{jt}}}{n^{-1}\sum _{k=1}^{n}I\{{\tilde{X}}_{\mathit{jk}}\ge {\tilde{X}}_{\mathit{jt}}\}}-\frac{1}{n}\sum _{k=1}^n\frac{I\{{\tilde{X}}_{\mathit{js}}\ge {\tilde{X}}_{\mathit{jl}}\}I\{{\tilde{X}}_{\mathit{jt}}\ge {\tilde{X}}_{\mathit{jl}}\}{\delta }_{\mathit{jl}}}{{\left[n^{-1}\sum _{k=1}^{n}I\{{\tilde{X}}_{\mathit{jk}}\ge {\tilde{X}}_{jl}\}\right]}^2}\right].$$ (3.1)

We note that an alternative expression for ${\widehat{I}}_j^0({\tilde{X}}_{jt},{\delta }_{jt})\left({\tilde{X}}_{js}\right)$ is:

$${\widehat{I}}_j^o({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}})\left({\tilde{X}}_{\mathit{js}}\right)=-{\tilde{F}}_j\left({\tilde{X}}_{\mathit{js}}\right)\left[\frac{I\{{\tilde{X}}_{\mathit{jt}}\le {\tilde{X}}_{\mathit{js}},{\delta }_{\mathit{jt}}=1\}}{{\widehat{P}}_{n,j}\left({\tilde{X}}_{\mathit{jt}}\right)}-\sum _{{\tilde{X}}_{\mathit{jl}}\le {\tilde{X}}_{\mathit{js}}}\frac{I\{{\tilde{X}}_{\mathit{jt}}\ge {\tilde{X}}_{\mathit{jl}}\}\Delta {\widehat{\Delta }}_j\left({\tilde{X}}_{\mathit{jl}}\right)}{{\widehat{P}}_{n,j}\left({\tilde{X}}_{\mathit{jl}}\right)}\right],$$

where ${\widehat{P}}_{n,j}\left(u\right)\equiv n^{-1}{\sum }_{k=1}^{n}I\{{\tilde{X}}_{jk}\ge u\}$,

$$\Delta {\widehat{\Delta }}_j\left(u\right)=\frac{I\left\{{\overline{Y}}_j\right(u)>0\}}{{\overline{Y}}_j\left(u\right)}d{\stackrel{‒}{N}}_j\left(u\right),{\overline{Y}}_j\left(u\right)=\sum _{k=1}^{n}I\{{\tilde{X}}_{\mathit{jk}}\ge u\},$$

$${\stackrel{‒}{N}}_j\left(u\right)=\sum _{k=1}^n{N}_{\mathit{jk}}\left(u\right),$$

in which $\Delta {\widehat{\Lambda }}_j\left(u\right)$ is so-called Nelson's estimator. This is because

$$\begin{array}{cc}\hfill \sum _{{\tilde{X}}_{\mathit{jl}}\le {\tilde{X}}_{\mathit{js}}}\frac{I\{{\tilde{X}}_{\mathit{jt}}\ge {\tilde{X}}_{\mathit{jl}}\}\Delta {\widehat{\Lambda }}_j\left({\tilde{X}}_{\mathit{jl}}\right)}{{\widehat{P}}_{n,j}\left({\tilde{X}}_{\mathit{jl}}\right)}& =\sum _{{\tilde{X}}_{\mathit{jl}}\le {\tilde{X}}_{\mathit{js}}}\frac{I\{{\tilde{X}}_{\mathit{jt}}\ge {\tilde{X}}_{\mathit{jl}}\}{\delta }_{\mathit{jl}}}{{\widehat{P}}_{n,j}\left({\tilde{X}}_{\mathit{jl}}\right)\sum _{k=1}^{n}I\{{\tilde{X}}_{\mathit{jk}}\ge {\tilde{X}}_{\mathit{jl}}\}}\hfill \\ \hfill & =\frac{1}{n}\sum _{l=1}^n\frac{I\{{\tilde{X}}_{\mathit{js}}\ge {\tilde{X}}_{\mathit{jl}}\}I\{{\tilde{X}}_{\mathit{jt}}\ge {\tilde{X}}_{\mathit{jl}}\}{\delta }_{\mathit{jl}}}{{\left[n^{-1}\sum _{k=1}^{n}I\{{\tilde{X}}_{\mathit{jk}}\ge {\tilde{X}}_{\mathit{jl}}\}\right]}^2}.\hfill \end{array}$$

By the consistency of the Kaplan-Meier estimators and ${\widehat{\alpha }}_n$, and by applying the law of large numbers to independent observations, we can the following result, which provides a consistent variance estimator.

Proposition 3.3. Under conditions C1–C5 and A1–A4, the asymptotic variance of $n^{1∕2}{\widehat{\alpha }}_n$ can be consistently estimated by ${\widehat{B}}_n^{-}{\widehat{\Sigma }}_n{\widehat{B}}_n^{-}$, where ${\widehat{B}}_n^{-}$ is the generalized inverse of ${\widehat{B}}_n$.

4. Pseudo-likelihood ratio test for model comparison

By applying Proposition 3.1(2) we immediately obtain the probability limit of the PLR statistic.

Proposition 4.1. Suppose for i = 1, …, M, the copula model i satisfies the conditions of Proposition 3.1. Then

$${\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})=\frac{1}{n}\sum _{t=1}^n{E}^0\left\{{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right\}+o_p\left(1\right),$$

where $U_{jt}=F_j^0\left({\tilde{X}}_{jt}\right)$ for j = 1, 2.

In the following, we adopt the convention that all the notations involving the copula function C(u₁, u₂; α) introduced in Section 3 are now indexed by a subscript i for i = 1, …, M to make explicit their dependence on the parametric copula model i. In addition, we define $U_t=(U_{1t},U_{2t})=\left(F_1^0\right({\tilde{X}}_{1t}),F_2^0({\tilde{X}}_{2t}\left)\right)$,

$$e_t={(e_{2t},\dots ,e_{\mathit{Mt}})}^{\prime },$$

$$e_{\mathit{it}}\equiv \left\{{\ell }_i(U_t;{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_t;{\alpha }_{1n}^{\ast })\right\}+\sum _{j=1}^2\left\{Q_{i,j}({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}};{\alpha }_{\mathit{in}}^{\ast })-Q_{1,j}({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}};{\alpha }_{1n}^{\ast })\right\},$$

where for i = 1, …, M and for j = 1, 2,

$$Q_{i,j}({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}};{\alpha }_{\mathit{in}}^{\ast })\equiv E^0\left[{\ell }_{i,j}(U_{1s},U_{2s};{\alpha }_{\mathit{in}}^{\ast })I_j^o({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}})\left({\tilde{X}}_{\mathit{js}}\right)\mid {\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}}\right].$$

It is easy to see that $\frac{1}{\sqrt{n}}{\sum }_{t=1}^n\{e_t-E^0(e_t\left)\right\}$ has the same asymptotic distribution as a multivariate normal random variable with mean zero and variance Ω_n, where

$${\Omega }_n=\frac{1}{n}\sum _{t=1}^n{E}^0\left[(e_t-E^0\{e_t\left\}\right){(e_t-E^0\{e_t\left\}\right)}^{\prime }\right]={\left({\sigma }_{\mathit{ik}}\right)}_{i,k=2}^M,$$

$${\sigma }_{\mathit{ik}}=\frac{1}{n}\sum _{t=1}^n{E}^0\left[(e_{\mathit{it}}-E^0\{e_{\mathit{it}}\left\}\right)(e_{\mathit{kt}}-E^0\{e_{\mathit{kt}}\left\}\right)\right].$$

It is easy to compute a consistent estimator ${\widehat{\Omega }}_n$ for Ω_n:

$${\widehat{\Omega }}_n=\frac{1}{n}\sum _{t=1}^n\left[\left({\widehat{e}}_t-\frac{1}{n}\sum _{s=1}^n{\widehat{e}}_s\right){\left({\widehat{e}}_t-\frac{1}{n}\sum _{s=1}^n{\widehat{e}}_s\right)}^{\prime }\right]={\left({\widehat{\sigma }}_{\mathit{ik}}\right)}_{i,k=2}^M,$$

$${\widehat{\sigma }}_{\mathit{ik}}=\frac{1}{n}\sum _{t=1}^n\left[\left({\widehat{e}}_{\mathit{it}}-\frac{1}{n}\sum _{s=1}^n{\widehat{e}}_{\mathit{is}}\right)\left({\widehat{e}}_{\mathit{kt}}-\frac{1}{n}\sum _{s=1}^n{\widehat{e}}_{\mathit{ks}}\right)\right],$$ (4.1)

where ${\widehat{e}}_t={({\widehat{e}}_{2t},\dots ,{\widehat{e}}_{Mt})}^{\prime }$ and for i = 2, …, M,

$${\widehat{e}}_{\mathit{it}}\equiv \left\{{\ell }_i\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\widehat{\alpha }}_{\mathit{in}})-{\ell }_1\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\widehat{\alpha }}_{1n})\right\}+\sum _{j=1}^2\left\{{\widehat{Q}}_{i,j}({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}};{\widehat{\alpha }}_{\mathit{in}})-{\widehat{Q}}_{1,j}({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}};{\widehat{\alpha }}_{1n})\right\},$$

in which

$${\widehat{Q}}_{i,j}({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}};{\widehat{\alpha }}_{\mathit{in}})=\frac{1}{n}\sum _{s\ne t,s=1}^n{\ell }_{i,j}\left({\tilde{F}}_1\right({\tilde{X}}_{1s}),{\tilde{F}}_2({\tilde{X}}_{2s});{\widehat{\alpha }}_{\mathit{in}}){\widehat{I}}_j^o({\tilde{X}}_{\mathit{jt}},{\delta }_{\mathit{jt}})\left({\tilde{X}}_{\mathit{js}}\right),$$

for i = 1, …, M and j = 1, 2 with ${\widehat{I}}_j^0({\tilde{X}}_{jt},{\delta }_{jt})\left({\tilde{X}}_{js}\right)$ given in (3.1).

Before we present the test statistics, we recall the following definition from Chen and Fan (2005): For model i ∈ {2, …, M},

Models 1 and i are generalized non-nested if the set $\left\{\right(v_1,v_2):c_1(v_1,v_2;{\alpha }_{in}^{\ast })\ne c_i(v_1,v_2;{\alpha }_{in}^{\ast }\left)\right\}$ has positive Lebesgue measure;

Models 1 and i are generalized nested if $c_1(v_1,v_2;{\alpha }_{1n}^{\ast })=c_i(v_1,v_2;{\alpha }_{in}^{\ast })$ for almost all (v₁, v₂) ∈ (0, 1)².

Given the definition of the pseudo true value ${\alpha }_{in}^{\ast }$, the closest $c_i(\cdot ;{\alpha }_{in}^{\ast })$ to the true copula c⁰ (according to KLIC) in a parametric class of copulas $\left\{c_i\right(\cdot ;{\alpha }_i):{\alpha }_i\in {\mathcal{A}}_i\}$ depends on the true (but unknown) copula. Hence it is not obvious a priori whether two parametric classes of copulas are generalized non-nested or generalized nested.

Remark 4.1. Define

$${\sigma }_{\mathit{ii}}^a\equiv \frac{1}{n}\sum _{t=1}^n{\mathit{Var}}^0\left[{\ell }_i\right(U_t;{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_t;{\alpha }_{1n}^{\ast }\left)\right].$$

It is obvious that if models 1 and i are generalized nested, then ${\ell }_i(U_{1t},U_{2t};{\alpha }_{in}^{\ast })={\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast })$ almost surely, e_it = 0 almost surely, and ${\sigma }_{ii}^a=0$. Following the proof of Proposition 3 in Chen and Fan (2005), we can show that if ${\sigma }_{ii}^0=0$ then models 1 and i are generalized nested, and σ_ii = 0. Therefore it is easy to test whether the models 1 and i are generalized nested by testing ${\sigma }_{ii}^a=0$, which may be done by using its consistent estimator:

$${\widehat{\sigma }}_{\mathit{ii}}^a=\frac{1}{n}\sum _{t=1}^n{\left[\left\{{\ell }_i\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\widehat{\alpha }}_{\mathit{in}})-{\ell }_1\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\widehat{\alpha }}_{1n})\right\}-{\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})\right]}^2.$$

See Chen and Fan (2005) for details.

The following proposition provides the basis for our tests. Note that we allow for some but not all of the candidate models i ∈ {2, …, M} to be generalized nested with the benchmark model 1.

Proposition 4.2. For i = 1, 2, …, M, assume that the copula model i satisfies conditions of Proposition 3.2 and that {e_it : t = 1, …, n} satisfies Lindeberg condition. If ${\Omega }_n={\left({\sigma }_{ii}\right)}_{i,k=2}^M$ is finite and its largest eigenvalue is positive uniformly in n, then:

• (1)
  $$\begin{array}{cc}\hfill & n^{1∕2}{\left[{\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})-n^{-1}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]\right]}_{i=2,\dots ,M}\hfill \\ \hfill & =\frac{1}{\sqrt{n}}\sum _{t=1}^n\{e_t-E^0(e_t\left)\right\}+o_p\left(1\right),\hfill \end{array}$$

  $$\begin{array}{cc}\hfill & \to {(Z_2,\dots ,Z_M)}^{\prime }\mathrm{in}\mathrm{distribution},\hfill \\ \hfill & \mathit{with}{(Z_2,\dots ,Z_M)}^{\prime }\sim N(0,{\Omega }_n).\hfill \end{array}$$
• (2)
  $${\widehat{\Omega }}_n={\Omega }_n+o_p\left(1\right).$$

Proposition 4.2 and the continuous mapping theorem imply

$$\underset{i=2,\dots ,M}{\max }{n}^{1∕2}\left\{{\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})-n^{-1}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]\right\}\to \underset{i=2,\dots ,M}{\max }{Z}_i.$$

Define

$$T_n\equiv \underset{i=2,\dots ,M}{\max }\left[n^{1∕2}{\mathit{LR}}_n\right({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n}\left)\right].$$

Proposition 4.2 implies that under the Least Favorable Configuration (LFC), i.e.,

$$n^{-1}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]=0\text{for}i=2,\dots ,M,$$

T_n → max_i=2,…,M Z_i in distribution. This allows us to construct a test for H₀. Suppose the largest eigenvalue of Ω_n is positive uniformly in n, then we will reject H₀ if T_n > Z_α, where Z_α is the upper α-percentile of the distribution of max_i=2,…,M Z_i.

The asymptotic power properties of this test against fixed alternatives and Pitman local alternatives follow immediately from Proposition 4.2 and are summarized in the following proposition.

Proposition 4.3. Suppose all conditions of Proposition 4.2 are satisfied. Then the test based on T_n is consistent against fixed alternatives of the form H₁ and has non-trivial power against local alternatives satisfying

$$\underset{i=2,\dots ,M}{\max }\underset{n\to \infty }{\lim }\left\{n^{-1∕2}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]\right\}>0.$$

Note that if the censoring mechanism is random, then the local alternatives in Proposition 4.3 can be written in the more familiar form:

$$\underset{i=2,\dots ,M}{\max }{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_i^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_1^{\ast }\left)\right]=K\frac{1}{\sqrt{n}},$$

for a positive constant K.

In general, the distribution of max_i=2,…,M Z_i is unknown, since the asymptotic variance Ω_n of (Z₂, #x2026;, Z_M) depends on ${\alpha }_{1n}^{\ast },\dots ,{\alpha }_{Mn}^{\ast }$. Following White (2000), one can use either “Monte-Carlo RC” p-value or “bootstrap RC” p-value to implement this test. As noted in Chen and Fan (2005), Hansen (2003), and Romano and Wolf (2005), the finite sample power of this test may be improved by standardization. In our empirical application, we have computed both “Monte-Carlo RC” p-value using

$$T_{\mathit{nS}}=\underset{i=2,\dots ,M}{\max }\left\{\frac{n^{1∕2}{\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})}{{\sqrt{\widehat{\sigma }}}_{\mathit{ii}}}{G}_b\left({\widehat{\sigma }}_{\mathit{ii}}\right)\right\},$$

and “bootstrap RC” p-value based on

$$T_{\mathit{nI}}=\max \left[\underset{i=2,\dots ,M}{\max }\left\{\frac{n^{1∕2}{\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})}{{\sqrt{\widehat{\sigma }}}_{\mathit{ii}}}{G}_b\left({\widehat{\sigma }}_{\mathit{ii}}\right)\right\},0\right],$$

where ${\widehat{\sigma }}_{ii}$ is a consistent estimator of σ_ii such as the one given in (4.1), b = b_n → 0 as n → ∞, and G_b(·) is a is smoothed trimming which trims out small ${\widehat{\sigma }}_{ii}$. The particular trimming function being used in our empirical study is

$$G_b\left(x\right)={\int }_{-\infty }^x{g}_b\left(z\right)\mathit{dz}=\{\begin{array}{c}0,x<b\hfill \\ {\int }_{-\infty }^x{g}_b\left(z\right)\mathit{dz},b\le x\le 2b\hfill \\ 1,x>2b\hfill \end{array}\phantom{\}}$$

where g_b(χ) = (b⁻¹g(b⁻¹ χ−1) and g(z) = B(a+1)⁻¹z^a(1−z)^a,z ∈ [0, 1] for some positive integer a ≥ 1, where B(a) = Γ(a)²/Γ(2a) is the beta function and Γ(a) is the Euler gamma function.

We note that the standardized tests T_nS and T_nI proposed here allow that some candidate models are generalized nested with the benchmark model, since the trimming $G_b\left({\widehat{\sigma }}_{ii}\right)$ in T_nS and T_nI removes the effect of generalized nested models (with the benchmark model) on its limiting distribution. By a minor modification of the proof of Theorem 7 in Chen and Fan (2005), we immediately obtain the following result:

Proposition 4.4. Suppose all conditions of Proposition 4.2 are satisfied. If b → 0 and nb → ∞, then under the null hypothesis H₀, the limiting distribution of T_nI is given by that of ${\max }_{i\in S_{NB}}(Z_i∕\sqrt{{\sigma }_{ii}},0)$, where

$$S_{\mathit{NB}}=\left\{\begin{array}{c}i\in \{2,\dots ,M\}:{\sigma }_{\mathit{ii}}>0\mathit{and}\hfill \\ n^{-1}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]=0\hfill \end{array}\right\}.$$

Proposition 4.4 implies that the asymptotic null distribution of T_nI depends on models that are generalized non-nested with the benchmark and satisfy

$$n^{-1}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]=0,$$

and hence is unknown. We propose the following bootstrap procedure to approximate the asymptotic null distribution of T_nI:

• Step1Generate a bootstrap sample by random draws with replacement from a consistent nonparametric estimator of the unknown joint distribution of (X_1t, X_2t) that takes into account the censoring scheme. Denote (${\tilde{F}}_1^{\ast }$, ${\tilde{F}}_2^{\ast }$, ${\tilde{\alpha }}_{in}^{\ast }$, ${\tilde{\alpha }}_{1n}^{\ast }$) as the bootstrap analogs of (${\tilde{F}}_1$, ${\tilde{F}}_2$, ${\tilde{\alpha }}_{in}$, ${\tilde{\alpha }}_{1n}$).
• Step2Compute the bootstrap value $T_{in}^{\ast }\equiv L{R}_n\left({\tilde{F}}_1^{\ast },{\tilde{F}}_2^{\ast };{\tilde{\alpha }}_{in}^{\ast },{\tilde{\alpha }}_{1n}^{\ast }\right)$ of $T_{in}\equiv L{R}_n({\tilde{F}}_1,{\tilde{F}}_2;{\tilde{\alpha }}_{in},{\tilde{\alpha }}_{1n})$, i = 2, …, M, and define its recentered value as $T_{inC}^{\ast }=T_{in}^{\ast }-T_{in}I(T_{in}\ge -a_n)$, where a_n → 0 is a small positive (possibly random) number such that $\sqrt{n}{a}_n\to \infty$.
• Step3
  Compute the bootstrap value of T_nI as

  $$T_{\mathit{nI}}^{\ast }=\underset{2\le i\le M}{\max }\left\{\frac{\sqrt{n}{T}_{\mathit{inC}}^{\ast }}{{\sqrt{\widehat{\sigma }}}_{\mathit{ii}}}{G}_b\left({\widehat{\sigma }}_{\mathit{ii}}\right),0\right\};$$
• Step4Repeat Steps 1–3 for a large number of times and use the empirical distribution function of the resulting values $T_{nI}^{\ast }$ to approximate the null distribution of T_nI.

We note that the above bootstrap procedure is very similar to that proposed in Chen and Fan (2005), except that in Step 1 we generate bootstrap samples from a consistent nonparametric estimator of the joint distribution that takes account of the censoring. For example, for bivariate random right censoring, we could sample from the bivariate Kaplan–Meier estimator; see Dabrowska (1989). See Davison and Hinkley (1997, page 85) for additional ways to generate bootstrap sample for censored data. The consistency of this standardized bootstrap RC test $T_{nI}^b$ could be established by a minor modification of the proof of Theorem 8 in Chen and Fan (2005).

Remark 4.2. Recall that

$${\mathit{PLR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})={\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})-\frac{\mathit{Pen}(p_i,n)-\mathit{Pen}(p_1,n)}{n}.$$

If ${\max }_{i=2},\dots ,M\left[\mathit{Pen}\right(p_i,n)-\mathit{Pen}(p_1,n\left)\right]∕\sqrt{n}\to 0$ (which is automatically satisfied with AIC and BIC), then

$${\mathit{PLR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})={\mathit{LR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})+o_p\left(n^{-1∕2}\right)\text{for}i=2,\dots ,M.$$

Therefore, penalization could be incorporated in the tests. Define

$$T_n^P=\underset{i=2,\dots ,M}{\max }\left[n^{1∕2}{\mathit{PLR}}_n\right({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n}\left)\right],$$

$$T_{\mathit{nS}}^P=\underset{i=2,\dots ,M}{\max }\left\{\frac{n^{1∕2}{\mathit{PLR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})}{{\sqrt{\widehat{\sigma }}}_{\mathit{ii}}}{G}_b\left({\widehat{\sigma }}_{\mathit{ii}}\right)\right\},$$

and

$$T_{\mathit{nI}}^P=\max \left[\underset{i=2,\dots ,M}{\max }\left\{\frac{n^{1∕2}{\mathit{PLR}}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})}{{\sqrt{\widehat{\sigma }}}_{\mathit{ii}}}{G}_b\left({\widehat{\sigma }}_{\mathit{ii}}\right)\right\},0\right].$$ (4.2)

Then we can conduct the test using $T_n^P$ (or $T_{nS}^P$ or $T_{nI}^P$) instead of T_n (or T_nS or T_nI).

5. An empirical application

In this section, we illustrate our testing procedure for the selection of multiple copula-based survival functions by using insurance company data on losses and ALAEs. The particular data set we use was collected by the US Insurance Services Office and has been analyzed in some detail in Frees and Valdez (1998), Klugman and Parsa (1999), and Denuit et al. (2006).

Two alternative approaches have been used in the literature to model multivariate survival data; that of the multivariate distribution function and that of the multivariate survival function. It is important to realize that in the context of semiparametric copula-based models, the copula in a semiparametric copula-based distribution function corresponds to its survival copula in the corresponding semiparametric survival function. To be specific, consider the bivariate case. Let (X₁, X₂) be the survival variables of interest with a joint survival function F^o(x₁, x₂) = Pr(X₁ > x₁, X₂ > x₂) and marginal survival functions $F_j^0(\cdot )$, j = 1, 2. Let H(x₁, x₂) denote the corresponding joint cumulative distribution function (cdf) with marginal distributions H_j(·), j = 1, 2. Assume that $H_1\equiv 1-F_1^0$ and $H_2\equiv 1-F_1^0$ are continuous. By the Sklar's (1959 theorem, there exists a unique copula function C_h such that H(x₁, x₂) ≡ C_h(H₁(x₁), H₂(x₂)), which in turn implies that the representation

$$F^o(x_1,x_2)\equiv C^o\left(F_1^o\right(x_1),F_2^o(x_2\left)\right),$$

holds where

$$C^o(u_1,u_2)\equiv u_1+u_2-1+C_h(1-u_1,1-u_2)$$

is itself a copula function, known as a survival copula. Hence the bivariate distribution function C_h(H₁(x₁), H₂(x₂)) and the bivariate survival function $C^0\left(F_1^0\right(x_1),F_2^0(x_2\left)\right)$, where $F_j^0(\cdot )$ is the survival function of H_j(·) and C^o is the survival copula of C_h represent the same model.

In Frees and Valdez (1998) and Klugman and Parsa (1999), fully parametric modeling of the joint distribution of the loss and ALAE has been examined; using various model selection techniques including AIC/BIC, Frees and Valdez (1998) select Pareto marginals and Gumbel copula, while Klugman and Parsa (1999) select inverse paralogistic for the loss, inverse Burr for ALAE and the Frank copula. Denuit et al. (2006) adopt a semiparametric distribution framework in which the marginal distributions of loss and ALAE are left unspecified, but their copula is modeled parametrically via a one-parameter Archimedean copula. Their model selection procedure is the same as that in Wang and Wells (2000) except that the joint distributions of loss and ALAE are estimated differently. They examined four one-parameter Archimedean copulas: Gumbel, Clayton, Frank and Joe, and select the same Gumbel copula as Frees and Valdez (1998). Compared with Denuit et al. (2006), we do not restrict the parametric copulas to be Archimedean. In addition, our test takes into account the randomness of the selection criterion. Chen and Fan (2005) have also studied this data set, but since their model selection test is applicable to uncensored data only, they restrict their analysis to the subset of 1466 complete data. We now apply our proposed test to the original censored data with 1500 data points.

The scatterplots for loss and ALAE presented in Frees and Valdez (1998) and Denuit et al. (2006) reveal positive right tail dependence between loss and ALAE: large losses tend to be associated with large ALAE's. This is because expensive claims generally need some time to be settled and induce considerable costs for the insurance company. Actuaries therefore expect positive dependence between large losses and large ALAE's. On the other hand, these plots do not reveal any visible left tail dependence between the two variables. As a result, it is not surprising that the Gumbel copula is chosen in Frees and Valdez (1998) and Denuit et al. (2006). To shed some light on the robustness of this result to the set of copula families being considered, we add three more copula families to the set considered in Denuit et al. (2006): Gaussian copula, survival Clayton, mixture of Clayton and Gumbel copulas; see Appendix B for expressions of these seven copulas and their partial derivatives. Survival Clayton has right tail dependence and the mixture of Clayton and Gumbel exhibits both left tail and right tail dependence unless the weights are degenerate. the Gaussian copula does not have tail dependence and is thus expected to fit poorly. They are included here in the set of copulas to see if the power of the test is adversely affected by the presence of poor copula candidates in the selection set.¹

To facilitate comparison, we also apply our tests to the subset of 1466 complete data. The results of the “Monte Carlo RC” test $T_n^P$ (using the AIC penalization factor) for the original censored data are presented in Table 1 and those for the subset of 1466 complete data are presented in Table 2, with 500,000 Monte Carlo repetitions. For each copula, we estimated its parameter(s) by the two-step procedure and computed the value of the AIC. To apply our model selection test we need to choose a benchmark model. In view of the existing results, we first use the Gumbel copula as the benchmark. For the Gumbel benchmark, we found the p-value of the test to be 1 with or without taking into account censoring. This provides strong evidence that none of the other six copulas performs significantly better than the Gumbel copula for the loss-ALAE data. This is consistent with the selection result based on comparing the values of the AIC only; Gumbel followed by mixture of Clayton and Gumbel, then by survival Clayton and then by Joe. The parameter estimates for the mixture of Clayton and Gumbel provide additional evidence in favor of the Gumbel copula; the estimates of the weight on Clayton are only 0.0003 when censoring is taken into account and 0.0002 when censoring is not taken into account. In addition, the estimates of the parameter in the Gumbel copula obtained by fitting the mixture of Clayton and Gumbel are very close to the estimates obtained by fitting the Gumbel copula alone for both the subset of complete data and the original censored data. To see if the test is sensitive to the choice of the benchmark model, we also used each of the remaining six copulas as the benchmark.

Table 1.

Monte Carlo p-values of the test for the original dataset subject to censoring.

Benchmark	p-value of	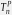p-value of	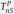AIC	2-step estimator
Gumbel	1.0000	0.9980	−0.1447	1.4428
Clayton	0.0015	0.0004	−0.0000	0.5152
Frank	0.0688	0.0394	−0.1009	0.0473
Joe	0.3968	0.2533	−0.1263	1.6466
Gaussian	0.1692	0.0724	−0.1125	0.4668
Survival Clayton	0.6295	0.4298	−0.1380	0.7825
Mix Clayton & Gumbel	0.9469	0.9794	−0.1420	(0.1505, 1.4433, 0.0003)

Table 2.

Monte Carlo p-values of the test for the subset without censoring.

Benchmark	p-value of	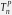p-value of	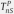AIC	2-step estimator
Gumbel	1.0000	0.9940	−0.2560	1.4254
Clayton	0.0037	0.0008	−0.1203	0.5098
Frank	0.1197	0.0834	−0.2160	0.0494
Joe	0.3530	0.1643	−0.2384	1.6105
Gaussian	0.2499	0.1442	−0.2286	0.4604
Survival Clayton	0.5570	0.3412	−0.2472	0.7440
Mix Clayton & Gumbel	0.9382	0.9590	−0.2530	(0.1572, 1.4256, 0.0002)

For each of the Tables 1 and 2, we present two versions of the Monte Carlo tests based on the non-standardized test, $T_n^P$, and the standardized test, $T_{nS}^P$, as described in Remark 4.2.² Comparing the first two columns in Tables 1 and 2, we see that both tests yield similar high p-values when the benchmark is either Gumbel or the mixture of Clayton and Gumbel; for all the other cases, the standardized test $T_{nS}^P$ yields significantly lower p-values than those of $T_n^P$. This indicates that the standardized version of the test is generally more powerful than the original non-standardized test.

Additionally, we present a bootstrap version of the test based on $T_{nI}^P$ (using the AIC penalization factor). We generate a bootstrap sample by random draws with replacement from a consistent non-parametric estimator of the bivariate joint distribution that takes into account the censoring scheme. For this loss-ALAE data set, we could draw bootstrap samples either from the bivariate Kaplan–Meier estimator of Dabrowska (1989), or from the estimator of Akritas (1994) and Denuit et al. (2006). Let $T_{nI}^{\ast ,P}$ be the counterpart of $T_{nI}^{\ast }$ for one bootstrap iteration, we write the re-centered bootstrap test statistic as $T_{nIC}^{\ast ,P}=T_{nI}^{\ast ,P}-T_{nI}^P\times I\{T_{nI}^P\ge -a_n\}$, where for simplicity we use the same parameter values (a, b_n, a_n) = (1, n^−1/2, 0:025n^−1/2 log log n) as those in Chen and Fan (2005). In this empirical application we use 100 bootstrap repetitions. The bootstrap p-values in Tables 3 and 4 overwhelmingly support the conclusion that the Gumbel copula fits the loss-ALAE data the best among the seven copulas we considered. This finding is consistent with existing results in the literature. The fact that the results in Tables 3 and 4 are so close to each other confirms the statement in Denuit et al. (2006) that the limited amount of censored points present in this Loss-ALAE data does not seem to affect the copula selection result.

Table 3.

Bootstrap p-values of the test for the original dataset subject to censoring.

Benchmark	p-value of	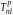AIC	Two-step estimate
Gumbel	1.0000	−0.1447	1.4428
Clayton	0.0000	−0.0000	0.5152
Frank	0.0000	−0.1009	0.0473
Joe	0.1010	−0.1263	1.6466
Gaussian	0.0517	−0.1125	0.4668
Survival Clayton	0.1414	−0.1380	0.7825
Mix Clayton & Gumbel	0.9900	−0.1420	(0.1505, 1.4433, 0.0003)

Table 4.

Bootstrap p-values of the test for the subset without censoring.

Benchmark	p-value of	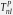AIC	Two-step estimate
Gumbel	1.0000	−0.2560	1.4254
Clayton	0.0000	−0.1203	0.5098
Frank	0.0000	−0.2160	0.0494
Joe	0.1052	−0.2384	1.6105
Gaussian	0.0202	−0.2286	0.4604
Survival Clayton	0.0909	−0.2472	0.7440
Mix Clayton & Gumbel	0.9963	−0.2530	(0.1572, 1.4256, 0.0002)

Finally, by comparing the bootstrap p-values in Tables 3 and 4 with the Monte Carlo p-values in Tables 1 and 2, we notice that the standardized “bootstrap RC” test is in general more powerful than the standardized “Monte Carlo RC” test, which in turn is more powerful than the non-standardized “Monte Carlo RC” test. Nevertheless, it is noteworthy that the standardized “bootstrap RC” test is computationally much more intensive than the standardized “Monte Carlo RC” test. For an AMD Athlon(tm) 64 Processor, 1.18 GHz and 384 Mb of RAM, for each benchmark case, the standardized “bootstrap RC” test (with 100 bootstrap replications) takes about 10,500 computer seconds, whereas the standardized “Monte Carlo RC” test (with 500,000 Monte Carlo repetitions) only takes about 350 computer seconds. Moreover, we are happy to see that the standardized “Monte Carlo RC” test and the standardized “bootstrap RC” test yield very similar rankings and lead to the same conclusion that the Gumbel copula fits the loss-ALAE data the best.

6. Conclusion

Many models of semiparametric multivariate survival functions are characterized by nonparametric marginal survival functions and parametric copula functions, where different copulas imply different dependence structures. In this paper, we first establish large sample properties of the two-step estimator of copula dependence parameter when the parametric copula function may be misspecified and when data may be subject to an independent but otherwise general right censorship. We then provide a penalized pseudo-likelihood ratio test for selecting among multiple semiparametric copula models for multivariate survival data. An empirical application to the famous Loss-ALAE insurance data set indicates the usefulness of our theoretical results.

Although our theoretical results allow for general right censoring scheme, we still assume that the data is independent and is subject to independent censoring. In some economic and financial applications, data could be serially dependent and may be subject to dependent censorship. The two-step estimator and its large sample properties have been extended to time series settings in Chen and Fan (2006a,b), but their results do not allow for any censoring. We shall extend the results in this paper to allow for time series and/or dependent censoring in another paper.

Appendix A. Technical proofs

We first introduce additional notation: $N_{\mathit{jt}}\left(x\right)={\delta }_{\mathit{jt}}I({\tilde{X}}_{\mathit{jt}}\le x)$, $J_{\mathit{jt}}\left(u\right)=I({\tilde{X}}_{\mathit{jt}}\ge u)$, $M_{\mathit{jt}}\left(x\right)=N_{\mathit{jt}}\left(x\right)-{\int }_{-\infty }^x{J}_{\mathit{jt}}\left(u\right)\mathrm{d}{\Lambda }_j\left(u\right)$ and ${\Lambda }_j\left(u\right)=-\log F_j^o\left(u\right)$ the marginal cumulative hazard function of X_j, j = 1, 2.

Lemma A.1. Suppose that Conditions C1 and C5 are satisfied. Then: (i) the marginal Kaplan–Meier estimators are uniformly strongly consistent: ${\sup }_{x\le {\tau }_j}\mid {\tilde{F}}_j\left(x\right)-F_j^o\left(x\right)\mid \to 0$ a.s. for j = 1, 2; (ii) they can be expressed as martingle integrals:

$$\begin{array}{cc}\hfill {\tilde{F}}_j\left(x\right)-F_j^o\left(x\right)=& -F_j^o\left(x\right){\int }_{-\infty }^x\frac{{\tilde{F}}_j(u-)}{F_j^o\left(u\right)}\frac{\sum _{t=1}^n\mathrm{d}{M}_{\mathit{jt}}\left(u\right)}{\sum _{t=1}^{n}I({\tilde{X}}_{\mathit{jt}}\ge u)}\hfill \\ \hfill & =-F_j^o\left(x\right){\int }_{-\infty }^x\frac{\sum _{t=1}^n\mathrm{d}{M}_{\mathit{jt}}\left(u\right)}{F_j^o\left(u\right)\sum _{t=1}^n{G}_{\mathit{jt}}\left(u\right)}+o_p\left(n^{-1∕2}\right),\hfill \end{array}$$

where o_p() is uniform in x ∈ [0, τ_j], for j = 1, 2.

Proof of Lemma A.1. Because of Condition C5, the risk set size in (−∞, τ_j] is of order n. Consequently, the uniform strong consistency is a special case of Theorem 3 of Lai and Ying (1991). The martingale integral approximation follows from formula (3.2.13) of Gill (1980) and the consistency of the Kaplan–Meier estimator.

Lemma A.2. Let ${\widehat{x}}_j=\inf \{x:{\tilde{F}}_j(x)<1\}$, j = 1, 2. There exists τ₀ > 0 such that for every ∊ > 0, there is an η > 0 such that

$$\underset{n\to \infty }{\text{lim inf}P}\left(\underset{{\widehat{x}}_j\le x\le {\tau }_0}{\text{inf}}\frac{1-{\tilde{F}}_j\left(x\right)}{1-F_j^o\left(x\right)}\ge \eta \right)>1-∊,j=1,2.$$

Proof of Lemma A.2. For notational convenience, subscript j 1, 2 will be omitted. By definition,

$$\tilde{F}\left(x\right)=\prod _{t:{\tilde{X}}_t\le x}\left(1-\frac{{\delta }_t}{\sum _{k=1}^n{J}_k\left({\tilde{X}}_t\right)}\right)\le \exp \left\{-{\int }_{-\infty }^x\frac{\sum _{k=1}^n\mathrm{d}{N}_k\left(u\right)}{\sum _{k=1}^n{J}_k\left(u\right)}\right\}.$$

The right-hand side is bounded by $1-\frac{2}{3}{\int }_{-\infty }^x\frac{{\sum }_{k=1}^n\mathrm{d}{N}_k\left(u\right)}{{\sum }_{k=1}^n{J}_k\left(u\right)}$, x ≤ τ₀ for suitably chosen τ₀, provided that ${\int }_{-\infty }^{{\tau }_0}\frac{{\sum }_{k=1}^n\mathrm{d}{N}_k\left(u\right)}{{\sum }_{k=1}^n{J}_k\left(u\right)}<-\log (2∕3)$, which holds for all large n. Thus,

$$1-\tilde{F}\left(x\right)+\frac{1}{n}\ge \frac{2}{3}\left\{\sum _{t=1}^{n}I(C_t\ge {\tau }_0)I(X_t\le x)+\frac{1}{n}\right\}.$$ (A.1)

By a theorem of van Zuijlen (1978, Theorem 1.1), for any ∊ > 0, there exists η such that

$$P\left\{\sum _{t=1}^{n}I(C_t\ge {\tau }_0)I(X_t\le x)+\frac{1}{n}\ge \eta \sum _{t=1}^{n}I(C_t\ge {\tau }_0)F^o\left(x\right)\right\}>1-∊.$$ (A.2)

Since $\lim \inf n^{-1}{\sum }_{t=1}^{n}I(C_t\ge {\tau }_0)>0$, it follows from (A.1), (A.2) and the fact that $1-\tilde{F}\left(x\right)\ge n^{-1}$ for all $x\ge \widehat{x}$ that the lemma holds.

Proof of Proposition 3.1. The main ideas here are to use the uniform consistency of the Kaplan–Meier estimator and the identifiability Condition C2. Write

$$\begin{array}{cc}\hfill n^{-1}& \sum _{t=1}^n\left\{\ell \right({\tilde{F}}_1\left({\tilde{X}}_{1t}\right),{\tilde{F}}_2\left({\tilde{X}}_{2t}\right);\alpha )-E^0[\ell \left(F_1^o\right({\tilde{X}}_{1t}),F_2^o({\tilde{X}}_{2t});\alpha )\left]\right\}\hfill \\ \hfill & =n^{-1}\sum _{t=1}^n\left\{\ell \right({\tilde{F}}_1\left({\tilde{X}}_{1t}\right),{\tilde{F}}_2\left({\tilde{X}}_{2t}\right);\alpha )-\ell (U_{1t},U_{2t};\alpha \left)\right\}+n^{-1}\sum _{t=1}^n\left\{\ell \right(U_{1t},U_{2t};\alpha )-E^0[\ell (U_{1t},U_{2t};\alpha )\left]\right\}.\hfill \end{array}$$ (A.3)

We first show that the first term on the right-hand side of (A.3) is of order o_p(1), uniformly in $\alpha \in \mathcal{A}$. Under Condition C5, ${\tilde{F}}_j\left(x\right)\ge {\tilde{F}}_j\left({\tau }_j\right)$, j = 1, 2, are bounded away from 0. By continuity of ℓ() on $(0,1)\times (0,1)\times \mathcal{A}$ and Lemma A.1, the first term, with summation over t such that both ${\tilde{F}}_1\left({\tilde{X}}_{1t}\right)$ and ${\tilde{F}}_2\left({\tilde{X}}_{2t}\right)$ are bounded away from 0, is of order o_p(1), uniformly in $\alpha \in \mathcal{A}$. i.e., for every η > 0,

$$\underset{n\to \infty }{\text{lim}}\underset{\alpha \in \mathcal{A}}{\text{sup}}{n}^{-1}\sum _{t=1}^n\mid \ell \left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});\alpha )-\ell (U_{1t},U_{2t};\alpha )\mid \times I({\tilde{X}}_{1t}\wedge {\tilde{X}}_{2t}\ge \eta )=0.$$ (A.4)

It remains to show that for every ∊ > 0, there exists η > 0 such that

$$P\left\{\underset{\alpha \in \mathcal{A}}{\text{sup}}{n}^{-1}\sum _{t=1}^n\mid \ell \left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});\alpha )I({\tilde{X}}_{\mathit{jt}}\le \eta )\mid \ge ∊\right\}\le ∊,j=1,2,$$ (A.5)

and

$$P\left\{\underset{\alpha \in \mathcal{A}}{\text{sup}}{n}^{-1}\sum _{t=1}^n\mid \ell \left(\right(U_{1t}),U_{2t};\alpha )I({\tilde{X}}_{\mathit{jt}}\le \eta )\mid \ge ∊\right\}\le ∊,j=1,2.$$ (A.6)

By Lemma A.2 and Condition C4(iii), there exists K > 0 such that

$$P\left\{\underset{\alpha \in \mathcal{A}}{\text{sup}}{n}^{-1}\sum _{t=1}^n\mid \ell \left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});\alpha )I({\tilde{X}}_{\mathit{jt}}\le \eta )\mid >K\underset{\alpha \in \mathcal{A}}{\text{sup}}{n}^{-1}\sum _{t=1}^n\mid \ell \left(\right(U_{1t}),U_{2t};\alpha )I({\tilde{X}}_{\mathit{jt}}\le \eta )\mid \right\}<\frac{∊}{3}.$$

Therefore, to show (A.5) and (A.6), it suffices to show that for any ∊* > 0, there exists η such that

$$P\left\{\mid n^{-1}\sum _{t=1}^n{L}_{t}I({\tilde{X}}_{\mathit{jt}}\le \eta )\mid \ge {∊}^{\ast }\right\}\le \frac{2}{3}∊,j=1,2.$$ (A.7)

By Condition C4(ii) and the Markov inequality, to show (A.7), we only need to show that for any K* > 0, there exists η such that

$$P\left\{\mid n^{-1}\sum _{t=1}^n{L}_{t}I(L_t<K^{\ast })I({\tilde{X}}_{\mathit{jt}}\le \eta )\mid \ge {∊}^{\ast }\right\}\le \frac{1}{3}∊,j=1,2.$$ (A.8)

But, again by the Markov inequality, the left-hand side of (A.8) is bounded by

$$\frac{K^{\ast }}{{∊}^{\ast }}{n}^{-1}\sum _{t=1}^{n}P\{{\tilde{X}}_{\mathit{jt}}\le \eta \}$$

which can be made arbitrarily small by Condition C1.

We next show that the second term is also of order o_p(1). By Condition C4(ii), it suffices to show that for every K > 0,

$$n^{-1}\sum _{t=1}^n\left\{\ell \right(U_{1t},U_{2t};\alpha \left)I\right(\max \{L_t,L_{\alpha t}\}\le K)-E^0[\ell (U_{1t},U_{2t};\alpha )I\left(\max \right\{L_t,L_{\alpha t}\}\le K)\left]\right\}$$

converges to 0 uniformly in $\alpha \in \mathcal{A}$. But this sequence converges to 0 a.s. for every α and has uniformly bounded derivatives over the compact set $\mathcal{A}$, and, therefore, the convergence must be uniform.

Proof of Proposition 3.2. The proof can be done by essentially combining the techniques of Shih and Louis (1995) and Chen and Fan (2005). A critical part is how to appropriately control the tail behavior.

By the mean-value theorem, we can linearly expand the pseudo-likelihood score function at ${\alpha }_n^{\ast }$ to get

$$\widehat{\alpha }-{\alpha }_n^{\ast }={\tilde{B}}_n^{-1}\frac{1}{n}\sum _{t=1}^n{\ell }_{\alpha }\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\alpha }_n^{\ast }),$$ (A.9)

where ${\tilde{B}}_n=\frac{1}{n}{\sum }_{t=1}^n{\ell }_{\alpha \alpha }\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\tilde{\alpha }}_n)$ for some ${\tilde{\alpha }}_n$ on the line segment between ${\alpha }_n^{\ast }$ and ${\widehat{\alpha }}_n$. Under Condition A4, we can apply the same argument for proving (A.5) to show that ${\sup }_{\alpha \in \mathcal{A}}{n}^{-1}{\sum }_{t=1}^n\mid {\ell }_{\alpha \alpha }\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});\alpha )I({\tilde{X}}_{\mathit{jt}}\le \eta )\mid$ is asymptotically negligible as η → 0. This in conjunction with Condition A2 and the consistency of ${\tilde{F}}_j$ and ${\widehat{\alpha }}_n$, implies that ${\tilde{B}}_n{B}_n^{-1}\to I_p$ in probability as n → ∞.

Again by the mean-value theorem,

$$\begin{array}{cc}\hfill \sum _{t=1}^n& {\ell }_{\alpha }\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\alpha }_n^{\ast })=\sum _{t=1}^n{\ell }_{\alpha }\left(F_1^o\right({\tilde{X}}_{1t}),F_2^o({\tilde{X}}_{2t});{\alpha }_n^{\ast })+\sum _{j=1}^2\sum _{t=1}^n{\ell }_{\alpha j}({\tilde{U}}_{1t},{\tilde{U}}_{2t};{\alpha }_n^{\ast })\left\{{\tilde{F}}_j\right({\tilde{X}}_{\mathit{jt}})-F_j^o({\tilde{X}}_{\mathit{jt}}\left)\right\}\hfill \\ \hfill & =D_{1n}+D_{2n},\hfill \end{array}$$ (A.10)

where (${\tilde{U}}_{1t}$, ${\tilde{U}}_{2t}$) lies on the line segment between (${\tilde{F}}_1\left({\tilde{X}}_{1t}\right),{\tilde{F}}_2\left({\tilde{X}}_{2t}\right)$) and (${\tilde{F}}_1^0\left({\tilde{X}}_{1t}\right),{\tilde{F}}_2^0\left({\tilde{X}}_{2t}\right)$).

By Lemma A.1,

$$D_{2n}=-\sum _{j=1}^2\sum _{t=1}^n{\ell }_{\alpha j}({\tilde{U}}_{1t},{\tilde{U}}_{2t};{\alpha }_n^{\ast })F_j^o\left({\tilde{X}}_{\mathit{jt}}\right)\times {\int }_{-\infty }^{{\tilde{X}}_{\mathit{jt}}}\frac{{\tilde{F}}_j(u-)}{F_j^o(u-)}\frac{\sum _s\mathrm{d}{M}_{\mathit{js}}\left(u\right)}{\sum _{s}I({\tilde{X}}_{\mathit{js}}\ge u)}.$$ (A.11)

Let $D_{2n}\left(\eta \right)={\sum }_{j=1}^2{D}_{2n,j}\left(\eta \right)$ denote the right-hand side of (A.11) with the summation restricted to those terms such that ${\tilde{X}}_{\mathit{jt}}\le \eta$ We next show that for some ∊_j > 0,

$$\mid n^{-1∕2}{D}_{2n,j}\left(\eta \right)\mid =O_p\left(1\right){(1-F_j^o(\eta \left)\right)}^{{∊}_j},j=1,2,$$ (A.12)

where O_p(1) is uniform over η > 0. For any ξ ∈ (0, 1), since

$$\begin{array}{cc}\hfill E^0& {\left\{{(1-F_j^o(x\left)\right)}^{-\xi ∕2}{\int }_{-\infty }^x\frac{{\tilde{F}}_j(u-)}{F_j^o(u-)}\frac{\sum _s\mathrm{d}{M}_{\mathit{js}}\left(u\right)}{\sum _{s}I({\tilde{X}}_{\mathit{js}}\ge u)}\right\}}^2\hfill \\ \hfill & \le E^0\left\{{\int }_{-\infty }^x{\left\{\frac{{\tilde{F}}_j(u-)}{F_0^j(u-)}\right\}}^2\frac{{\{1-F^o(u\left)\right\}}^{-\xi }}{\sum _{s}I({\tilde{X}}_{\mathit{js}}\ge u)}I(\underset{t}{\max }{\tilde{X}}_{\mathit{jt}}\ge u)\mathrm{d}{\Lambda }_j^o\left(u\right)\right\},\hfill \end{array}$$

it follows from Lenglart's inequality (Gill, 1980, Theorem 2.4.2) that

$$\begin{array}{cc}\hfill E^0& {\left\{{(1-F_j^o(x\left)\right)}^{-\xi ∕2}{\int }_{-\infty }^x\frac{{\tilde{F}}_j(u-)}{F_j^o(u-)}\frac{\sum _s\mathrm{d}{M}_{\mathit{js}}\left(u\right)}{\sum _{s}I({\tilde{X}}_{\mathit{js}}\ge u)}\right\}}^2\hfill \\ \hfill & =O_p\left(1\right){\int }_{-\infty }^x{\left\{\frac{{\tilde{F}}_j(u-)}{F_0^j(u-)}\right\}}^2\frac{{\{1-F^o(u\left)\right\}}^{-\xi }}{\sum _{s}I({\tilde{X}}_{\mathit{js}}\ge u)}I(\underset{t}{\max }{\tilde{X}}_{\mathit{jt}}\ge u)\mathrm{d}{\Lambda }_j^o\left(u\right)\hfill \\ \hfill & =O_p\left(1\right)n^{-1}{\int }_{-\infty }^x{\{1-F^o(u\left)\right\}}^{-\xi }\mathrm{d}\{1-F^o(u\left)\right\}\hfill \\ \hfill & =O_p\left(1\right)n^{-1}{\{1-F^o(x\left)\right\}}^{1-\xi },\hfill \end{array}$$ (A.13)

where O_p(1) is uniform in x and the second equality follows from Lemma A.2 and van Zuijlen (1978, Theorem 1.1). From (A.13), Lemma A.2 (with ξ = 2ξ_j) and Condition A3, we have, ignoring the right tail,

$$\begin{array}{cc}\hfill \mid n^{-1∕2}{D}_{2n,j}\left(\eta \right)\mid & =O_p\left(1\right)n^{-1}\sum _{t=1}^n{U}_{\mathit{jt}}^{{\xi }_j-b_j}{U}_{\mathit{kt}}^{-a_k}{(1-F_j^o(\eta \left)\right)}^{1-2{\xi }_j}\hfill \\ \hfill & =O_p\left(1\right){(1-F_j^o(\eta \left)\right)}^{1-2{\xi }_j}.\hfill \end{array}$$

Hence, (A.12) holds with ∊_j = 1 − 2ξ_j, j = 1, 2.

In view of (A.12), we can essentially pretend that ℓ_αj in (A.10) does not blow up at the tail. Therefore, (A.11) implies that for j = 1, 2,

$$\begin{array}{cc}\hfill D_{2n,j}& =-\sum _{s=1}^n\int \frac{n^{-1}\sum _{t=1}^n{\ell }_{\alpha j}({\tilde{U}}_{1t},{\tilde{U}}_{2t};{\alpha }_n^{\ast })U_{\mathit{jt}}I({\tilde{X}}_{\mathit{jt}}\le u)}{n^{-1\sum _{t=1}^{n}I(\tilde{X}\ge u)}}\mathrm{d}{M}_{\mathit{js}}\left(u\right)\hfill \\ \hfill & =-\sum _{s=1}^n\int \frac{n^{-1}\sum _{t=1}^n{E}^0\left\{{\ell }_{\alpha j}\right(U_{1t},U_{2t};{\alpha }_n^{\ast }\left)U_{\mathit{jt}}I\right({\tilde{X}}_{\mathit{jt}}\ge u\left)\right\}}{P_{\mathit{nj}}\left(u\right)}\mathrm{d}{M}_{\mathit{js}}\left(u\right)+o_p\left(n^{1∕2}\right).\hfill \end{array}$$ (A.14)

From (A.9)–(A.11) and (A.14), we see that ${\widehat{\alpha }}_n-{\alpha }_n^{\ast }$ is asymptotically a sum of independent zero-mean random vectors. Given Condition A1, Proposition 3.2 now follows from the standard multivariate central limit theorem for independent but non-identically distributed random variables.

Proof of Propositions 3.3. The consistency of the variance estimator clearly follows from the laws of large numbers, the consistency of the Kaplan–Meier estimator and of ${\widehat{\alpha }}_n$, when the possible “tail instability” is ignored. To control the tail behavior, we can applied the same techniques as in the proofs of Propositions 3.1 and 3.2. The details are omitted.

Proof of Proposition 4.2. For i = 1, …, M, by the definition of ${\widehat{\alpha }}_{\mathit{in}}$, we have

$$\sum _{t=1}^n{\ell }_{i,\alpha }\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\widehat{\alpha }}_{\mathit{in}})=0.$$

Hence,

$$\sum _{t=1}^n{\ell }_i\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\alpha }_{\mathit{in}}^{\ast })=\sum _{t=1}^n{\ell }_i\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\widehat{\alpha }}_{\mathit{in}})+\frac{1}{2}{({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}})}^{\prime }\sum _{t=1}^n{\ell }_{i,\alpha \alpha }\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\stackrel{‒}{\alpha }}_{\mathit{in}})({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}}),$$

where ${\stackrel{‒}{\alpha }}_{\mathit{in}}$ is between ${\alpha }_{\mathit{in}}^{\ast }$ and ${\widehat{\alpha }}_{\mathit{in}}$. By conditions C2–C5, A1–A4 and Proposition 3.2, we have

$$\frac{1}{2n}{({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}})}^{\prime }\sum _{t=1}^n{\ell }_{i,\alpha \alpha }\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\stackrel{‒}{\alpha }}_{\mathit{in}})({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}})=-\frac{1}{2}{({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}})}^{\prime }{B}_{\mathit{in}}({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}})+o_p(1∕n).$$

Hence,

$$\frac{1}{n}\sum _{t=1}^n{\ell }_i\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\widehat{\alpha }}_{\mathit{in}})=\frac{1}{n}\sum _{t=1}^n{\ell }_i\left({\tilde{F}}_1\right({\tilde{X}}_{1t}),{\tilde{F}}_2({\tilde{X}}_{2t});{\alpha }_{\mathit{in}}^{\ast })+\frac{1}{2}{({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}})}^{\prime }{B}_{\mathit{in}}({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}})+o_p(1∕n).$$

As a result, we get for all i = 2, …, M,

$$L{R}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})-\frac{1}{n}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]=A_{i,n}+D_{i,n}+o_p(1∕n),$$

where

$$\begin{array}{cc}\hfill A_{i,n}& \equiv L{R}_n({\tilde{F}}_1,{\tilde{F}}_2;{\alpha }_{\mathit{in}}^{\ast },{\alpha }_{1n}^{\ast })-\frac{1}{n}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]\hfill \\ \hfill & =\frac{1}{n}\sum _{t=1}^n\left\{\right[{\ell }_i(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast })]-E^0[{\ell }_i(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast })]+\sum _{j=1}^2\frac{1}{n}\sum _{t=1}^n[\left\{{\ell }_{i,j}\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_{1,j}(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right\}\times \left\{{\tilde{F}}_j\right({\tilde{X}}_{\mathit{jt}})-F_j^o({\tilde{x}}_{\mathit{jt}}\left)\right\}]+o_p(1∕\sqrt{n}),\hfill \end{array}$$

$$D_n\equiv \frac{1}{2}{({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}})}^{\prime }{B}_{\mathit{in}}({\alpha }_{\mathit{in}}^{\ast }-{\widehat{\alpha }}_{\mathit{in}})-\frac{1}{2}{({\alpha }_{1n}^{\ast }-{\widehat{\alpha }}_{1n})}^{\prime }{B}_{1n}({\alpha }_{1n}^{\ast }-{\widehat{\alpha }}_{1n}).$$

By Proposition 3.2, we have D_n = O_p(n⁻¹).

For generalized non-nested models, Using a proof similar to that of Proposition 3.2, we obtain:

$$\sqrt{n}\times A_{i,n}=\frac{1}{\sqrt{n}}\sum _{t=1}^n[e_{\mathit{it}}-E^0(e_{\mathit{it}}\left)\right]+o_p\left(1\right)=O_p\left(n^{-1∕2}\right),$$

hence $\sqrt{n}\times A_{i,n}$ converges in distribution to a $\mathcal{N}(0,{\sigma }_{\mathit{ii}})$. Therefore,

$$\sqrt{n}\left[L{R}_n({\tilde{F}}_1,{\tilde{F}}_2;{\alpha }_{\mathit{in}}^{\ast },{\alpha }_{1n}^{\ast })-\frac{1}{n}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]\right]$$

converges in distribution to a $\mathcal{N}(0,{\sigma }_{\mathit{ii}})$.

For generalized nested models, the term A_i,n becomes zero almost surely, we have

$$L{R}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})-\frac{1}{n}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]=D_{i,n}+o_p(1∕n),$$

where by Proposition 3.2, 2nD_i,n is distributed as a weighted sum of independent ${\chi }_{\left[1\right]}^2$ random variables.

Proof of Proposition 4.3. Note that

$$\begin{array}{cc}\hfill T_n& =\underset{i=2,\dots ,M}{\max }\left[n^{1∕2}L{R}_n\right({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n}\left)\right]\hfill \\ \hfill & =\underset{i=2,\dots ,M}{\max }\left[n^{1∕2}\left\{L{R}_n({\tilde{F}}_1,{\tilde{F}}_2;{\widehat{\alpha }}_{\mathit{in}},{\widehat{\alpha }}_{1n})-n^{-1}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]\right\}+n^{-1∕2}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]\right]\hfill \\ \hfill & \to \underset{i=2,\dots ,M}{\max }\left[Z_i+\underset{n\to \infty }{\text{lim}}\left\{n^{-1∕2}\sum _{t=1}{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{\mathit{in}}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]\right\}\right].\hfill \end{array}$$

Let

$$K_{in}=\underset{n\to \infty }{\lim }\left\{n^{-1∕2}\sum _{t=1}^n{E}^0\left[{\ell }_i\right(U_{1t},U_{2t};{\alpha }_{in}^{\ast })-{\ell }_1(U_{1t},U_{2t};{\alpha }_{1n}^{\ast }\left)\right]\right\}.$$

Then

$$\begin{array}{cc}\hfill P(T_n>Z_{\alpha })& \to P\left(\underset{i=2,\dots ,M}{\max }\{Z_i+K_{in}\}>Z_{\alpha }\right)\hfill \\ \hfill & \ge P\left(\underset{i=2,\dots ,M}{\max }{Z}_i+\underset{i=2,\dots ,M}{\max }{K}_{in}>Z_{\alpha }\right).\hfill \end{array}$$

For fixed alternatives, max_i=2,…,M K_in = +∞ and so P (T_n > Z_α) → 1. For local alternatives such that maxi=2,…,MK_in > 0,

$$P\left(\underset{i=2,\dots ,M}{\max }{Z}_i+\underset{i=2,\dots ,M}{\max }{K}_{in}>Z_{\alpha }\right)>P\left(\underset{i=2,\dots ,M}{\max }{Z}_i>Z_{\alpha }\right)=\alpha .$$

Hence lim_n→∞ P (T_n > Z_α) > α.

Appendix B. Expressions of copulas and their derivatives

In the Appendix B we describe the seven copulas and their derivatives that we have used in the empirical application Section 5.³ Let (X₁, X₂) be the lifetime variables of interest with joint survival function F^o(x₁, x₂) = Pr(X₁ > x₁, X₂ > x₂) and continuous marginal survival functions $F_j^o(x_1,x_2)=\mathrm{Pr}(X_1>x_1,X_2>x_2)$. Let H (x₁, x₂) denote the corresponding joint cumulative distribution function (cdf) with marginal distributions $H_j\equiv 1-F_j^o,j=1,2$. By the Sklar's (1959) theorem, there exists a unique copula function C_h on [0, 1]² such that

$$H(x_1,x_2)\equiv C_h\left(H_1\right(x_1),H_2(x_2\left)\right),$$

or equivalently

$$F^o(x_1,x_2)\equiv C^o\left(F_1^o\right(x_1),F_2^o(x_2\left)\right),$$

holds with

$$C^o(u_1,u_2)\equiv u_1+u_2-1+C_h(1-u_1,1-u_2),$$ (B.1)

where the copula function C^o() is sometimes called the survival copula (of C_h).

It is easy to see that, for any j ∈ {1, 2}

$$\frac{\partial C^o}{\partial u_j}(u_1,u_2)=1-\frac{\partial C_h}{\partial u_j}(1-u_1,1-u_2),$$ (B.2)

in fact, for any partial derivative of order k higher than 2 we have that

$$\frac{{\partial }^k{C}^o}{\partial u_{j_1}\dots \partial u_{j_k}}(u_1,u_2)={(-1)}^k\frac{{\partial }^k{C}_h}{\partial u_{j_1}\dots \partial u_{j_k}}(1-u_1,1-u_2),$$ (B.3)

where j_i ∈ {1, 2}. Note that this last equation implies that

$$c^o(u_1,u_2)=c_h(1-u_1,1-u_2),$$ (B.4)

where c^o and c_h are the copula densities associated to C^o and C_h, respectively.

Using relations (B.2)–(B.4), by replacing v_j = 1 − u_j in the expressions of partial derivatives of a copula C_h and its density c_h, we immediately obtain the expressions for the partial derivatives of the survival copula C^o and its density c^o. Therefore, in the following we only provide expressions for the partial derivatives of several copula functions C_h and their densities c_h that we have used in the empirical application.

Gumbel copula

The Gumbel copula and its density are given by

$$C_h(v_1,v_2)=\exp \{-{({(-\log (v_1\left)\right)}^{\alpha }+{(-\log (v_2\left)\right)}^{\alpha })}^{1∕\alpha }\},$$ (B.5)

and

$$c_h(v_1,v_2)=\frac{1}{C_h}\frac{\partial C_h}{\partial v_1}\frac{\partial C_h}{\partial v_2}{T}_1,$$

with T₁ = ((α − 1)(− log(C_h))⁻¹ + 1). Following Frees and Valdez (1998), we can express the partial derivative of C_h with respect to v_j, j = 1, 2, as

$$\frac{\partial C_h}{\partial v_j}(v_1,v_2)=\frac{C_h(v_1,v_2)}{v_j}{\left(\log \right(v_j)∕\log (C_h(v_1,v_2)\left)\right)}^{\alpha -1}.$$ (B.6)

Hence, a little algebra implies⁴

$$\frac{{\partial }^2{C}_h}{\partial {v_j}^2}={\left(\log \right(v_j)∕\log (C_h\left)\right)}^{\alpha -1}\left(\frac{\frac{\partial C_h}{\partial v_j}}{v_j}-\frac{C_h}{v_j^2}\right)+(\alpha -1)\frac{C_h}{\log \left(C_h\right)v_j^2}{\left(\log \right(v_j)∕\log (C_h\left)\right)}^{\alpha -2}-(\alpha -1)\frac{\log \left(v_j\right){\left(\log \right(v_j)∕\log (C_h\left)\right)}^{\alpha -2}}{v_j\log {\left(C_h\right)}^2}\frac{\partial C_h}{\partial v_j}.$$

The partial derivative of the copula density c_h with respect to v_j, j = 1, 2, is given by

$$\frac{\partial c_h}{\partial v_j}=-\frac{1}{C_h^2}{\left(\frac{\partial C_h}{\partial v_j}\right)}^2\frac{\partial C_h}{\partial v_i}{T}_1+\frac{1}{C_h}\frac{{\partial }^2{C}_h}{\partial {v_j}^2}\frac{\partial C_h}{\partial v_i}{T}_1+\frac{1}{C_h}\frac{\partial C_h}{\partial v_j}{c}_h{T}_1+\frac{1}{C_h}\frac{\partial C_h}{\partial v_j}\frac{\partial C_h}{\partial v_i}\frac{\partial T_1}{\partial v_j},$$

where

$$\frac{\partial T_1}{\partial v_j}=\frac{(\alpha -1){(-\log (C_h\left)\right)}^{-2}}{C_h}\frac{\partial C_h}{\partial v_j}.$$

Clayton copula

The Clayton copula and its density are given by

$$C_h(v_1,v_2)={(v_1^{-\alpha }+v_2^{-\alpha }-1)}^{-1∕\alpha },$$

and

$$c_h(v_1,v_2)=(1+\alpha )v_1^{-(1+\alpha )}{v}_2^{-(1+\alpha )}{(v_1^{-\alpha }+v_2^{-\alpha }-1)}^{-(1∕\alpha +2)}.$$

Hence the second order partial derivative of C_h with respect to v_j, j = 1, 2, is given by

$$\frac{{\partial }^2{C}_h}{\partial {v_j}^2}=(1+\alpha )\left(\frac{1}{C_h}{\left(\frac{\partial C_h}{\partial v_j}\right)}^2-\frac{1}{v_j}\frac{\partial C_h}{\partial v_j}\right),$$

where

$$\frac{\partial C_h}{\partial v_j}=v_j^{-(1+\alpha )}{(v_1^{-\alpha }+v_2^{-\alpha }-1)}^{-1∕\alpha -1}.$$

The first order partial derivative of the copula density c_h with respect to v_j, j = 1, 2, is given by

$$\frac{\partial c_h}{\partial v_j}=c_h\left(\frac{(1+2\alpha )}{C_h}\frac{\partial C_h}{\partial v_j}-(1+\alpha )∕v_j\right).$$

Frank copula

The Frank copula and its density are given by

$$C_h(v_1,v_2)=\frac{1}{\log \left(\alpha \right)}\log \left(1-\frac{(1-{\alpha }^{v_1})(1-{\alpha }^{v_2})}{1-\alpha }\right),$$

and

$$c_h(v_1,v_2)=\log \left({\alpha }^{-1}\right)\frac{{\alpha }^{v_1}{\alpha }^{v_2}}{1-\alpha }{\left(1-\frac{(1-{\alpha }^{v_1})(1-{\alpha }^{v_2})}{1-\alpha }\right)}^{-2}.$$

After some algebra, the second order partial derivative of C_h with respect to v_j, j = 1, 2, is given by

$$\frac{{\partial }^2{C}_h}{\partial {v_j}^2}=\log \left(\alpha \right)\left(\frac{\partial C_h}{\partial v_j}-{\left(\frac{\partial C_h}{\partial v_j}\right)}^2\right)$$

where

$$\frac{\partial C_h}{\partial v_j}={\left(1-\frac{(1-{\alpha }^{v_1})(1-{\alpha }^{v_2})}{1-\alpha }\right)}^{-1}\frac{(1-{\alpha }^{v_i}){\alpha }^{v_j}}{1-\alpha },$$

and the first order derivative of the copula density c_h with respect to v_j, j = 1, 2, is given by

$$\frac{\partial c_h}{\partial v_j}=\log \left(\alpha \right)\left(1-2\frac{\partial C_h}{\partial v_j}\right)c_h.$$

Joe copula

The Joe copula and its density are given by

$$C_h(v_1,v_2)=1-{({\stackrel{‒}{v}}_1^{\alpha }+{\stackrel{‒}{v}}_2^{\alpha }-{\stackrel{‒}{v}}_1^{\alpha }{\stackrel{‒}{v}}_2^{\alpha })}^{1∕\alpha }$$

and

$$c_h(v_1,v_2)={\stackrel{‒}{v}}_1^{\alpha -1}{\stackrel{‒}{v}}_2^{\alpha -1}{T}_2^{1∕\alpha -1}\left(\alpha -\frac{(1-\alpha )(1-{\stackrel{‒}{v}}_1^{\alpha })(1-{\stackrel{‒}{v}}_2^{\alpha })}{T_2}\right),$$

where ${\stackrel{‒}{v}}_j=1-v_j$ and $T_2={\stackrel{‒}{v}}_1^{\alpha }+{\stackrel{‒}{v}}_2^{\alpha }-{\stackrel{‒}{v}}_1^{\alpha }{\stackrel{‒}{v}}_2^{\alpha }$.

The second order partial derivative of the copula C_h with respect to v_j, j = 1, 2, is given by

$$\frac{{\partial }^2{C}_h}{\partial {v_j}^2}=(1-\alpha ){\stackrel{‒}{v}}_j^{\alpha -1}(1-{\stackrel{‒}{v}}_i^{\alpha })T_2^{1∕\alpha -1}\left(\frac{{\stackrel{‒}{v}}_j^{\alpha -1}(1-{\stackrel{‒}{v}}_i^{\alpha })}{T_2}-\frac{1}{{\stackrel{‒}{v}}_j}\right).$$

After some tedious algebra, the first order partial derivative of the copula density c_h with respect to v_j, j = 1, 2, is given by

$$\frac{\partial c_h}{\partial v_j}=(\alpha -1){\stackrel{‒}{v}}_i^{\alpha -1}{\stackrel{‒}{v}}_j^{\alpha -2}{T}_2^{1∕\alpha -1}(-1+{\stackrel{‒}{v}}_j^{\alpha }(1-{\stackrel{‒}{v}}_i^{\alpha }\left)T_2^{-1}\right)\times \left(\alpha -\frac{(1-\alpha )(1-{\stackrel{‒}{v}}_1^{\alpha })(1-{\stackrel{‒}{v}}_2^{\alpha })}{T_2}\right)+(1-\alpha )\alpha {\stackrel{‒}{v}}_i^{\alpha -1}{\stackrel{‒}{v}}_j^{2\alpha -2}(1-{\stackrel{‒}{v}}_i^{\alpha })T_2^{1∕\alpha -3}\times (-T2-(1-{\stackrel{‒}{v}}_j^{\alpha }\left)\right(1-{\stackrel{‒}{v}}_i^{\alpha }\left)\right).$$

Gaussian copula

The Gaussian copula and its density are given by

$$C_h(v_1,v_2)={\Phi }_{\alpha }\left({\Phi }^{-1}\right(v_1),{\Phi }^{-1}(v_2\left)\right),$$

where ϕ_α is the bivariate standard normal distribution with correlation α, Φ is the scalar standard normal distribution, and

$$c_h(v_1,v_2)=\frac{{\varphi }_{\alpha }\left({\Phi }^{-1}\right(v_1),{\Phi }^{-1}(v_2\left)\right)}{\varphi \left({\Phi }^{-1}\right(v_1\left)\right)\varphi \left({\Phi }^{-1}\right(v_2\left)\right)},$$

where ϕ is the density function of Φ, and ϕ_α is the density function of ϕ_α.

The second order partial derivative of the copula C_h with respect to v_j, j = 1, 2, is given by

$$\frac{{\partial }^2{C}_h}{\partial {v_j}^2}=-\left[{\int }_{-\infty }^{{\Phi }^{-1}\left(v_i\right)}\frac{{\Phi }^{-1}\left(v_j\right)-\alpha s}{2\pi {(1-{\alpha }^2)}^{3∕2}}\times \exp \left(-\frac{1}{2}\frac{{\Phi }^{-1}{\left(v_j\right)}^2-2\alpha {\Phi }^{-1}\left(v_j\right)s+s^2}{1-{\alpha }^2}\right)\mathrm{d}s\right]\varphi {\left(\Phi {\left(v_j\right)}^{-1}\right)}^{-2}+\frac{\partial C_h}{\partial v_j}\Phi {\left(v_j\right)}^{-1}\varphi {(\Phi \left(v_j\right){}^{-1})}^{-1}.$$

The first order partial derivative of the copula density c_h with respect to v_j, j = 1, 2, is given by

$$\frac{\partial c_h}{\partial v_j}=\left(\Phi {\left(v_j\right)}^{-1}-\frac{\Phi {\left(v_j\right)}^{-1}-\Phi {\left(v_j\right)}^{-1}\alpha }{1-{\alpha }^2}\right)\varphi {\left(\Phi {\left(v_j\right)}^{-1}\right)}^{-1}{c}_h.$$

Mixture copula

A mixture copula C_h(v₁, v₂; α), with its parameter α = (α₁, α₂, λ), is simply given by

$$C_h(v_1,v_2;\alpha )=\lambda C_h^1(v_1,v_2;{\alpha }_1)+(1-\lambda )C_h^2(v_1,v_2;{\alpha }_2),0\le \lambda \le 1,$$

where $C_h^1(v_1,v_2;{\alpha }_1)$ is one copula (such as the Clayton copula in our application) with its parameter α₁, and $C_h^1(v_1,v_2;{\alpha }_2)$ is another copula (such as the Gumbel copula in our application) with its parameter α₂. Then it is clear that the partial derivatives of C_h are simply the linear combination of the partial derivatives of the two copulas:

$$\frac{{\partial }^k{C}_h}{\partial v_j^k}=\lambda \frac{{\partial }^k{C}_h^1}{\partial v_j^k}+(1-\lambda )\frac{{\partial }^k{C}_h^2}{\partial v_j^k},j=1,2.$$