Influence of embedded fibers and an epithelium layer on glottal closure pattern in a physical vocal fold model

Abstract

Purpose

To explore the possible structural and material property features that may facilitate complete glottal closure in an otherwise isotropic physical vocal fold model.

Method

Seven vocal fold models with different structural features were used in this study. An isotropic model was used as the baseline model, and other models were modified from the baseline model by either embedding fibers aligned along the anterior-posterior direction in the body or cover layer, adding a stiffer outer layer simulating the epithelium layer, or a combination of the two features. Phonation tests were performed with both aerodynamic and acoustic measurements and high-speed imaging of vocal fold vibration.

Results

Compared to the isotropic one-layer model, the presence of a stiffer epithelium layer led to complete glottal closure along the anterior-posterior direction and strong excitation of high-order harmonics in the resulting acoustic spectra. Similar improvements were observed with fibers embedded in the cover layer, but to a lesser degree. Presence of fibers in the body layer did not yield noticeable improvements in glottal closure or harmonic excitation.

Conclusions

This study shows that the presence of collagen and elastin fibers and the epithelium layer may play a critical role in achieving complete glottal closure.

I. INTRODUCTION

An important feature of normal phonation is that the glottis remains closed for a considerable portion of one oscillation cycle. The glottal closure pattern (e.g., the speed and duration of glottal closure) is essential to the production of voice with harmonics at frequencies well above the oscillation frequency of the vocal folds (Stevens, 1998). In humans, it is often assumed that approximation of the vocal folds through arytenoid adduction is sufficient to achieve complete glottal closure in phonation. However, recent experiments using self-oscillating silicone-based physical models (Zhang et al., 2006a, 2009; Zhang, 2011; readers are referred to Kniesburges et al., 2011, for a comprehensive review of the use of physical vocal fold models in voice research) showed that isotropic (i.e., the material properties are the same along different directions) physical models often vibrated with incomplete glottal closure at onset despite the two vocal fold models being brought into contact at rest. During vibration, although the isotropic vocal fold models were able to move back towards glottal midline, the contact between the two vocal folds, if it happened at all, was brief and often occurred at the middle portion along the anterior-posterior (AP) direction. Due to this incomplete glottal closure, the produced sound was breathy in quality. This contrasts with human vocal folds which are able to vibrate with the glottis closed for a considerably long portion of the oscillation cycle at a large range of laryngeal conditions (van den Berg and Tan, 1959). In addition, the isotropic physical models often exhibited out-of-phase motion along the AP direction, particularly at the end of the closing phase of the oscillation cycle (Mendelsohn and Zhang, 2011; Zhang, 2011). In contrast, human vocal folds, at least the membranous portion, often move in-phase along the AP direction during normal phonation.

Our previous efforts to overcome these deficiencies of the isotropic physical model focused on reducing the static vertical and lateral deformation of the physical vocal fold model when subjected to the subglottal pressure. The underlying rationale was that reducing the mean glottal opening would shift the equilibrium position of vocal fold vibration towards the glottal midline and thus facilitate complete glottal closure. As a first attempt along this direction, Zhang et al. (2006b) used a vertical restraint applied to the lateral half of the superior surface of the vocal fold model, which significantly suppressed the vertical motion of the vocal fold model and facilitated complete glottal closure. As there is no obvious counterpart of this vertical restraint in human physiology, it was hypothesized that this restraining effect can be achieved through either stiffening the body layer, which presumably can be achieved by the contraction of the thyroarytenoid muscle, or increasing vocal fold stiffness along the AP direction, which can be achieved through the action of the cricothyroid muscle. This hypothesis was further explored in Zhang (2011), which showed that both mechanisms led to reduced mean glottal opening and increased production of high-order harmonic energy in the resulting sound spectra. Despite these improvements, glottal closure in these models was often brief with an almost-zero closed quotient (the fraction of the cycle that the glottis remains closed). Stiffening the body layer in an isotropic physical model also led to strong excitation of AP out-of-phase motion. More importantly, activation of these restraining mechanisms in humans requires strong contraction of laryngeal muscles, and thus are not effective in low-pitch low-intensity phonation conditions.

Thus, it seems that, in addition to laryngeal muscle activation, the human vocal folds have some inherent structural or material features that facilitate complete glottal closure during human phonation. Identifying these features of the vocal folds has the potential to significantly improve clinical management of voice disorders, and would also allow us to design physical models that are capable of producing more realistic vibration patterns. Some clues regarding what these structural features might be can be found in previous studies. Zhang (2011) showed that vocal folds with a higher stiffness in the AP direction due to vocal fold elongation improved glottal closure. A large AP-to-transverse stiffness ratio also suppressed the AP out-of-phase motion and thus led to a more in-phase medial-lateral motion along the AP direction during phonation (Zhang, 2011). Thus, it is possible that a naturally anisotropic vocal fold model is able to produce a relatively stronger medial-lateral motion and thus achieve complete glottal closure. Indeed, early studies by Hirano and Kakita (1985) showed that the vocal folds are at least transversely-isotropic, due to the presence of muscle fibers in the muscle layer, and collagen and elastin in the lamina propria. On the other hand, recent studies showed that a water-filled latex tube model of the vocal folds (Ruty et al., 2007) was able to achieve complete glottal closure and a considerably large closed quotient (Krebs et al., 2010). In humans, the epithelium is a very thin layer (about 50–80 μm thickness) with a Young’s modulus (about 100 kPa) much larger than the inner layers (Hirano and Kakita, 1985). Gunter (2003) showed that, for a given subglottal pressure, the maximum glottal opening decreased with increasing stiffness of the outer epithelium layer. Murray and Thomson (2012) showed that the combination of a stiff epithelium layer and an extremely soft cover layer led to an alternating convergent-divergent motion of the vocal fold motion. These suggest that the presence of the epithelium layer may also facilitate complete glottal closure.

Physical models with features approximating the collagen and elastin fibers and the epithelium layer have been developed in previous studies. For example, acrylic and polyester fibers were embedded in the surface layer of an otherwise linear two-layer silicone physical model (Shaw et al., 2012) to achieve vocal fold material nonlinearity. Titze and colleagues (Titze, et al. 1995; Chan and Titze, 1997) attached a silicone epithelium membrane onto a stainless steel flat surface and filled the air gap with fluids of varying viscosities to study the dependence of phonation threshold pressure on vocal fold viscosity and geometry. The latex membrane in the water-filled latex tube vocal fold model in Ruty et al. (2007) functioned equivalently as an epithelium layer. Recently, the effects of an epithelium layer and a ligament layer with fibers embedded along the AP direction on vocal fold vibration (e.g., medial surface profile and the vertical phase difference) were investigated in a multi-layer silicone vocal fold model (Murray and Thomson, 2012). However, these previous studies generally focused on other aspects of phonation, and the possible effects of the presence of a stiffer epithelium layer and embedded fibers on the glottal closure pattern and sound production have not been investigated.

The goal of this study was to investigate the possible influence of the epithelium and embedded fibers on the glottal closure pattern and sound production in an otherwise isotropic one-layer physical model. The use of a one-layer baseline model instead of a multi-layer baseline model as in previous studies (Zhang, 2011; Murray and Thomson, 2012) was to approximate the conditions of minimum laryngeal contraction and thus to focus this study on the effects of features inherent to the vocal folds (i.e., collagen and elastin fibers and the epithelium layer) rather than those induced by laryngeal muscle activation. We will show that adding a thin stiffer outer layer to an otherwise homogenous model led to complete glottal closure and more excitation of high-order harmonics. Similar improvement in the glottal closure pattern was also achieved with fibers embedded in the cover layer.

II. METHODS

The details of the experimental setup for phonation tests were described in previous studies (Zhang et al., 2006b; a; Zhang, 2011). As shown in. Fig. 1, the setup consisted of an expansion chamber (with a rectangular cross-section of 23.5×25.4 cm² and 50.8-cm long) simulating the lungs, an 11-cm-long straight circular PVC tube (inner diameter of 2.54 cm) simulating the tracheal tube, and a self-oscillating vocal fold model. The expansion chamber was connected upstream to a pressurized airflow supply through a 15.2-m-long rubber hose. To focus on the effects of vocal fold structural features on the glottal closure pattern, no vocal tract was used in this study to avoid possible source-tract interaction.

Figure 1.

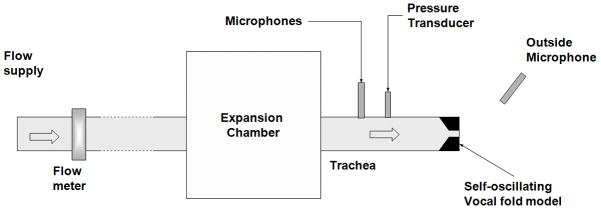
Schematic of the experimental set up.

Seven vocal fold models of identical geometry but different structural compositions were fabricated and used in this study. All vocal folds had a medial surface thickness of 2 mm, a lateral surface thickness of 9 mm along the inferior-superior direction, and a depth of 7.5 mm along the medial-lateral direction, as shown in Fig 2a. A one-layer isotropic model as used in previous studies (Thomson et al., 2005; Zhang et al., 2006a,b; Zhang, 2011) was used as the baseline model (M1), whereas models M2–M6 included a stiffer thin epithelium layer, or embedded fiber bundles, or both features (Table 1). The first six models (M1–M6) had a length of 17 mm along the AP direction. The M7 model was identical to M1, except for a reduced length of 12 mm. All models (M1–M7) were fabricated by mixing a two-component silicone compound solution (Ecoflex 0030, Smooth-on, Easton, PA) with a silicone thinner (Smooth-on, Easton, PA) at a 1:1:5 weight ratio. M1 to M6 models were made at the same time using the same mixture while the M7 model was made at a different time but with identical mixture ratio. The Young’s modulus of the fully cured mixture was measured to be about 2.5 kPa using an indentation method (Chhetri et al., 2011). Our previous experience showed that models of the same composition ratios but fabricated at different times were quite consistent in terms of the measured Young’s modulus which varied often less than 10%. The epithelium layer was added by evenly spreading three drops of a silicone mixture solution (Ecoflex 0030, weight ratio of 1:1, with a Young’s modulus of 60 kPa) over the surface of a baseline model. The thickness of the epithelium layers was about 130±20 μm, as measured after phonation tests using a digital microscope (Olympus DP70, Center Valley, PA) with 100x magnification. For each model with embedded fibers, a total of seven ultra gel-spun polyethylene fiber bundles (Ultra GSP thread, 50 denier, WAPSI, Inc. Mountain Home, Arkansas), each 4-mm long, were aligned along the AP direction at desired locations within the vocal fold model, as shown in Fig. 2b and 2c. Each fiber bundle had a diameter of 60 μm and a Young’s modulus in the order of 60 GPa as estimated from tensile tests. For models with fibers in the cover layer, the fiber bundles were first aligned in the mold before the silicone mixture solution was poured into the mold. For models with fibers in the body layer, the silicone compound solution was first poured to fill the bottom half of the mold and then the fiber bundles were added to the top of the half vocal fold model before the silicone compound solution was fully cured. Additional silicone compound solution (the same mixture solution as the bottom half) was then added to fill the top half of the mold. No pretension was applied to the fiber bundles and they were not fixed to the anterior or posterior ends. Before alignment, the fiber bundles were soaked in a silicone primer (Dow Corning, Midland, MI) and then dried for half an hour, in order to enhance bonding between the silicone rubber and the fiber bundles so that the fibers would not detach from the silicone rubber matrix during vibration. All models were cured at 75 °C for 1 hour after degassing and then two days in room temperature. As in previous studies, the fully-cured vocal fold models were then glued to a rectangular groove on the medial surface of two acrylic plates. The surface of the vocal fold model was further sprayed with a release agent (Ease Release 200, Smooth-on, Easton, PA) to prevent the two vocal folds from sticking to each other during vibration.

Figure 2.

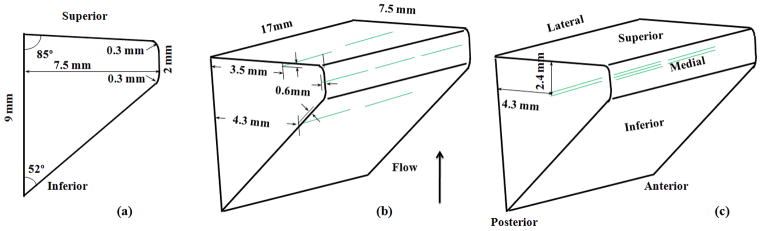
Sketch of a) the coronal cross sectional geometry of the vocal fold model and the three-dimensional vocal fold model with fibers (long dashed lines) embedded in b) the cover layer and c) the body layer. In Fig. 2b, two fiber bundles each were used at the superior and inferior locations and three bundles were used at the medial location. Seven fiber bundles were used in Fig. 2c.

Table 1.

Structural composition of the seven vocal fold models used in this study.

Model	M1	M2	M3	M4	M5	M6	M7
Epithelium	No	No	No	Yes	Yes	Yes	No
Fiber location	No fibers	Body	Cover	No fibers	Body	Cover	No fibers
Length (mm)	17	17	17	17	17	17	12

For each vocal fold model, the subglottal pressure was gradually increased in discrete increments from zero to about 20% above the phonation threshold pressure. At each step, with a delay of about 1–2 s after the flow rate change, the mean subglottal pressure (measured at 2 cm from the entrance of the glottis using a Baratron 220D pressure transducer), the mean flow rate (MKS 558A mass-flow meter), the subglottal acoustic pressure inside the tracheal tube (2 cm from the entrance of the glottis using a B&K 4182 probe microphone), and the outside acoustic pressure (about 20 cm downstream and about 30° off axis using a B&K 2669 microphone) were recorded for a 1-second period at a sampling rate of 50 kHz. The phonation threshold pressure, onset flow rate, and onset frequency were then extracted as the mean subglottal pressure, the mean flow rate, and the fundamental frequency at onset, as described in Zhang et al. (2006a). A high speed camera (Fastcam-Ultima APX, Photron Unlimited, Inc.) was used to record vocal fold vibration from a superior view at 2000 fps from which the glottal area waveform was extracted using a Matlab-based program.

III. RESULTS

Figure 3 shows the phonation threshold pressure and flow rate, the onset frequency, and the outside acoustic pressure at onset for all seven models. Adding a stiffer outer layer led to a significant increase in all four variables. In comparison, embedding short fibers in this study had a smaller effect.

Figure 3.

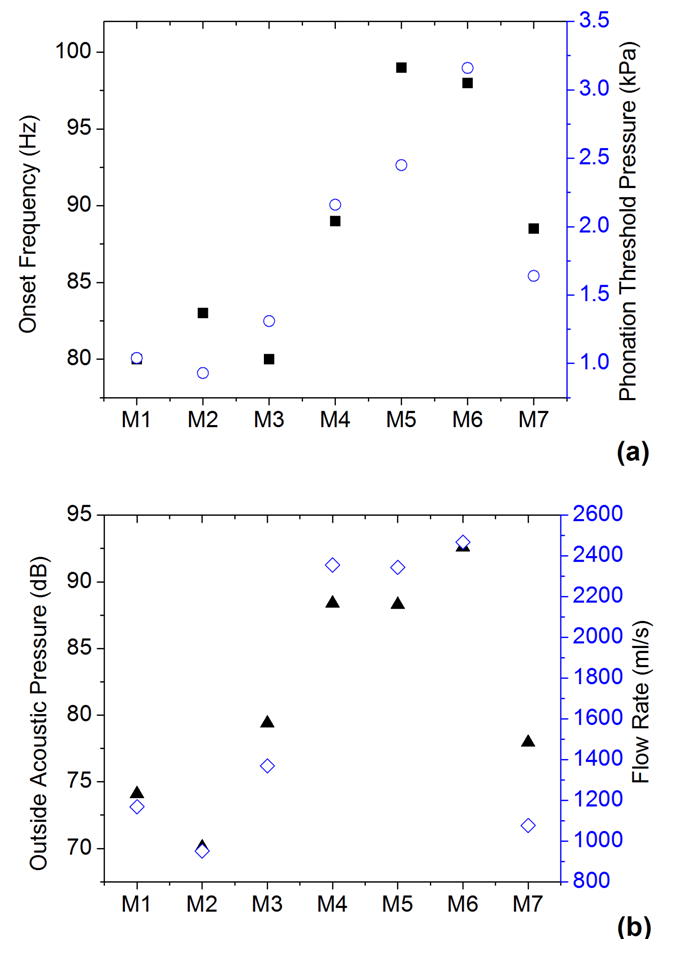
The phonation threshold pressure Pth (○), onset frequency F0 (■), onset flow rate (◇), and outside sound pressure amplitude (▲) at onset in the seven models.

Figure 4 shows superior-view images of the vocal folds at onset during one oscillation cycle for all seven models. The extracted glottal area waveforms are shown in Fig. 5. The baseline model M1 did not produce complete glottal closure, with a minimum glottal area of about 10 mm². Compared to the baseline model, embedding short fibers in the body layer did not reduce the minimum glottal area but noticeably reduced the maximum glottal opening area, and thus did not improve the closure pattern. Embedding fibers in the cover layer, however, allowed the glottis to reach complete closure (as indicated by the minimum glottal area of zero), although only briefly, and also led to an increased maximum glottal opening area. The most significant improvement in the glottal closure pattern was achieved by the addition of a stiffer outer layer in models M4–M6. Complete glottal closure was achieved in all three models with a stiffer outer layer (M4, M5, and M6), with or without fibers. The longest closure time was achieved in model M6, which had both the epithelium layer and fibers in the cover layer, with a closed quotient of 0.29, and decreased to 0.14 and 0.13 in M5 and M4, respectively.

Figure 4.

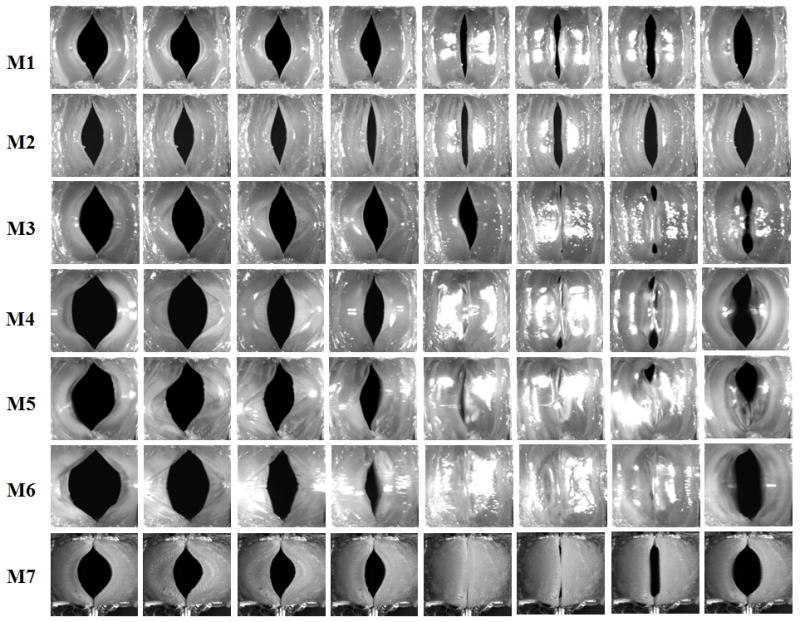
Superior-view images of the seven vocal fold models at equal intervals during one oscillation cycle.

Figure 5.

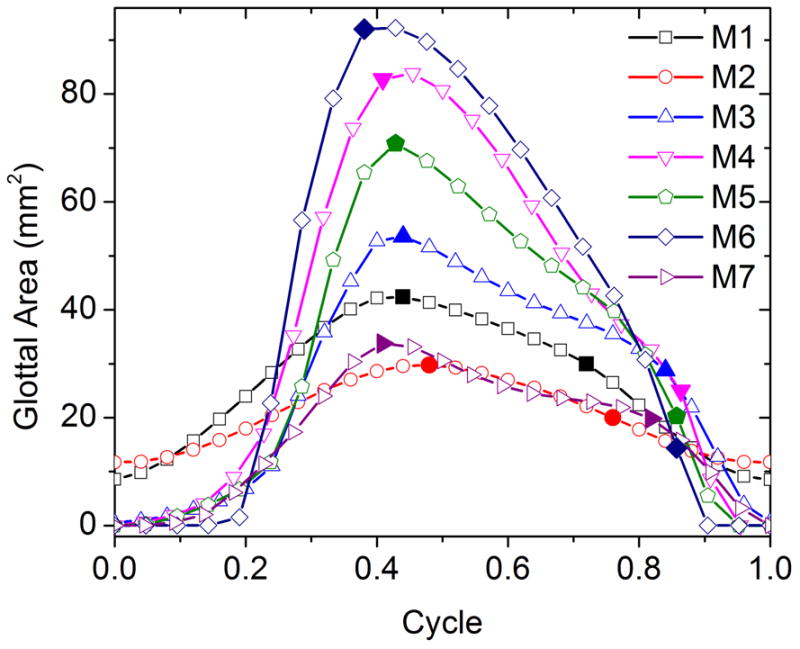
Glottal area waveforms extracted from the superior-view images in Fig. 4. The first solid symbol on each curve indicates the instant when the medial surface shape changed from convergent to divergent during glottal opening, and the second solid symbol indicates the instant when the medial surface shape changed from divergent to convergent during the closing phase.

The addition of the epithelium layer and fibers also led to changes in the transition pattern of the medial surface profile (from convergent, straight, and back to divergent) during one oscillation cycle. Figure 5 also shows the instants (solid symbols) at which the medial surface changed between divergent and convergent profiles. These transition instants were determined by manually stepping through consecutive frames and locating the frame in which a lower margin of the vocal folds first became either visible or hidden below the upper margin of the vocal folds. (Note that, because of prephonatory vocal fold deformation due to the applied subglottal pressure, the portion of the vocal fold surface between the observed upper and lower margins, or the actual medial surface, spanned a much larger vertical area than the predefined medial surface as indicated in Fig. 2.) All seven models had a convergent medial surface shape during glottal opening, and changed to a divergent medial surface around the moments of maximum opening. However, the transition from a divergent to a convergent medial surface shape occurred at a much later time during the closing phase for models M3–M6 than models M1 and M2. As the intraglottal pressure is generally lower or even negative for a divergent medial surface than for a convergent medial surface profile (Scherer et al., 2001), such late transition from a divergent to convergent medial surface profile may facilitate complete glottal closure.

For models with complete glottal closure, the vocal folds vibrated roughly in-phase along the AP direction, whereas notable out-of-phase motion along the AP direction was observed in models without complete closure. The phase difference in the medial-lateral motion between the middle part and the anterior/posterior edge for each model is illustrated in Fig. 6, which compares the time history of the superior-view images of two medial-lateral slices taken from the middle and the anterior quarter along the AP direction of the seven vocal fold models. For ease of comparison, the time-history plot for the anterior-quarter slice was flipped so that the medial edges of the two slices faced each other in each subplot. For models M3–M6 in which complete glottal closure was achieved, the vocal fold medial surface generally vibrated in a more in-phase pattern along the AP direction so that the entire vocal fold edge along the AP direction moved in and out towards the glottal midline together. In contrast, for models with incomplete glottal closure (M1 and M2), the vocal fold edge exhibited a noticeable out-of-phase medial-lateral motion along the AP direction, particularly during instants of glottal closure (indicated by the arrows in the figure). Specifically, the middle part moved towards the glottal midline when the AP edges were already moving away from the glottal midline, thus preventing complete glottal closure.

Figure 6.

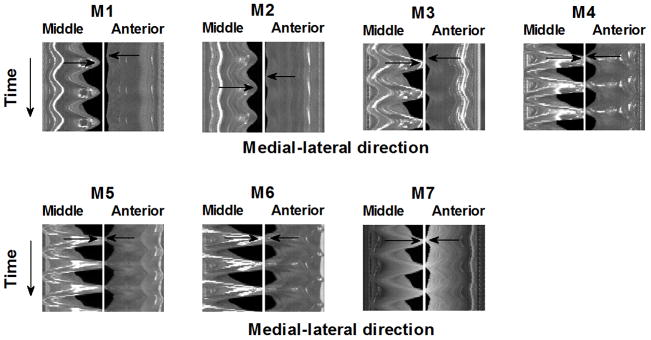
Comparison between the time history of the superior-view images of two medial-lateral slices taken from the middle and the anterior quarter along the anterior-posterior direction in the seven vocal fold models. The vertical position of the arrows indicate the instant of maximum medial excursion of the corresponding vocal fold slice, with the difference in the vertical position of the two arrows in each subplot indicating the degree of phase difference between the anterior and middle slices. The phase difference in the medial-lateral motion between the middle and the anterior slices was reduced in models M3-M7 compared to models M1-M2.

The same experiments were repeated four times using different sets of models with either dry powder or wet lubricant agents spread on the surfaces of the models. No qualitative difference in the glottal closure pattern was observed despite that these models were made at different times and of different surface conditions.

The fact that complete glottal closure was accompanied by a more in-phase motion along the AP direction suggests that suppression of the out-of-phase motion may facilitate complete glottal closure. To test this hypothesis, an additional experiment was performed using model M7, which was an isotropic vocal fold model identical to the M1 model except for a reduced length of 12 mm. Reducing vocal fold length along the AP direction shifts the AP out-of-phase motion to high-order eigenmodes and thus may suppress the occurrence of the AP out-of-phase motion during vibration (Zhang, 2011). This was confirmed in Fig. 6, which shows the medial surface moved almost in-phase along the AP direction in the M7 model. Figures 4 and 5 also show that the glottal closure in the M7 model was much improved from that of the M1 model, despite that both models were isotropic.

Figure 7 shows the spectra of the outside sound pressure at onset for seven models. In general, improvement in the glottal closure pattern led to more excitation of high-order harmonics in the outside sound spectra, comparing M3–M7 to M1–M2, and produced a brighter sound quality in models M3–M7. On the other hand, models with a large vibration amplitude also led to increased noise production, presumably due to the large flow rate.

Figure 7.

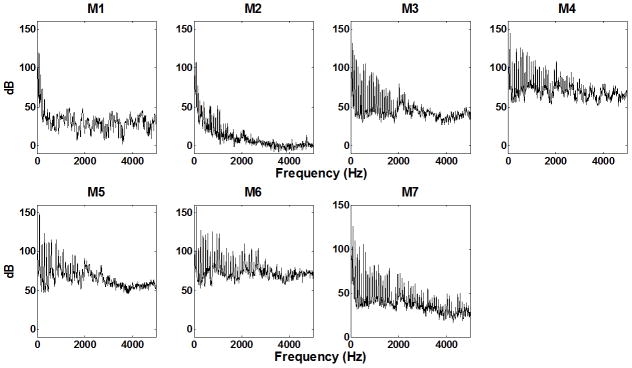
Spectra of the outside sound pressure slightly above onset in all seven models.

IV. DISCUSSION AND CONCLUSION

Although one-layer isotropic models often vibrated with incomplete glottal closure, this study showed that adding a stiffer outer layer or embedding fibers along the AP direction in the cover layer was able to produce complete glottal closure with a closed quotient as high as 0.29. Although the embedded fibers in the cover layer was less effective than the epithelium layer in this study, which was probably due to the small number of fibers used and the short fiber length, the improvement in the glottal closure pattern was achieved without noticeable increase in the phonation threshold pressure. In contrast, the presence of the epithelium layer was the most effective but also led to a significant increase in the phonation threshold pressure in models M4–M6. The stiffer outer epithelium layer used in this study had a thickness of about 130±20 μm, which was about twice of the reported thickness of the epithelium in human vocal fold (Hirano and Kakita, 1985). Thus, it is possible that the influence of the epithelium layer on the glottal closure pattern and the phonation threshold pressure in humans may not be as large as observed in this study.

Similar features of embedded fibers and a stiffer epithelium layer have been implemented earlier in Murray and Thomson (2012). In that study, although the presence of an epithelium layer and a fiber bundle (with and without pre-tension) led to a convergent-divergent motion of the vocal fold motion, the model did not appear to vibrate with complete glottal closure or a closed quotient as large as in the present study. Many factors may contribute to this difference in the glottal closure pattern. The epithelium layer and the fiber bundle in Murray and Thomson (2012) were made from a different softer material from that in the present study. The fiber bundle in Murray and Thomson (2012) was located further way from vocal fold surface compared with that in the present study, which, as indicated in our results in model M2, did not provide much improvement in achieving complete glottal closure. Lastly, it is important to note that the model used in Murray and Thomson (2012) was a multi-layer model, thus does not present a fair comparison to the one-layer model (other than the fibers and epithelium layer) of the present study.

Because complete glottal closure in models M4–M6 was accompanied by a significant increase in phonation threshold pressure, one may argue that the observed complete glottal closure in M4–M6 was due to the extremely high phonation threshold pressure in these models. However, in our previous experiments as well as in this study, increasing the subglottal pressure further beyond onset in the isotropic one-layer model led to almost proportionate increase in both the mean glottal area and the vibration amplitude, and thus still incomplete glottal closure. Figure 8 shows the equal-interval superior-view images of a M1 model (fabricated at a later time) during one oscillation cycle at five different subglottal pressures. The first condition corresponded to a subglottal pressure slightly above onset at 1.06 kPa, whereas the last condition was for a subglottal pressure of 2.17 kPa at which the model started to fracture due to collision. Compared to that at onset, the minimum glottal opening decreased only slightly with increasing subglottal pressure. The main effect of increasing subglottal pressure was to increase the vibration amplitude of the vocal fold in the middle portion along the AP direction. High subglottal pressures also led to a left-right asymmetric vibration pattern (Figs. 8d–8e). Further increase in the subglottal pressure beyond 2.17 kPa led to model damage due to extremely large vibration amplitude, thinning, and strong collision in the middle portion of the vocal fold model. The incomplete glottal closure in the M1 model at high subglottal pressures was in contrast to models M4–M6 which vibrated with complete glottal closure at comparable values of the subglottal pressure. Thus, the observed improvement in the glottal closure pattern in M4–M6 cannot be explained by the increase in phonation threshold pressure alone. The comparison between the M1 and M4 models also indicated that one function of the stiffer epithelium layer is to protect the soft inner layers of the vocal folds from extreme deformation and damage, as suggested in Murray and Thomson (2012).

Figure 8.

Superior-view images of the isotropic one layer model M1at equal intervals during one osscillation cycle. The mean subglottal pressure was a) 1.06 kPa (slightly above onset); b) 1.25 kPa; c) 1.46 kPa; d) 1.92 kPa; and e) 2.17 kPa.

Previous studies achieved improved glottal closure by stiffening the vocal fold body to restrain the mean deformation (Zhang 2006b, 2011), i.e. reduce the mean glottal opening for a given constant subglottal pressure. In this study, both the stiffer outer layer and the embedded fibers provided similar restraining effect. However, this restraining effect applied equally to both the mean glottal opening and the vibration amplitude, as shown in Fig. 9. Figure 9a shows the mean glottal opening area and the glottal vibration amplitude (estimated as half of the peak-to-peak value of the glottal area waveform in Fig. 5) for all seven models. Figure 9b shows the mean glottal area normalized by the phonation threshold pressure (the time-averaged subglottal pressure at onset) and the glottal vibration amplitude normalized by the subglottal acoustic pressure (the fluctuating component of the subglottal pressure). Although the glottal vibration amplitude increased at a higher rate than the mean glottal area with the addition of a stiffer outer layer or embedded fibers in the cover layer, Fig. 9b shows that, while the presence of an epithelium layer and the fibers reduced the mean glottal opening for a given mean subglottal pressure, it also reduced the vocal fold vibration amplitude for a given amplitude of the subglottal acoustic pressure. This suggests that restraining the prephonatory vocal fold deformation alone is not enough to achieve complete glottal closure.

Figure 9.

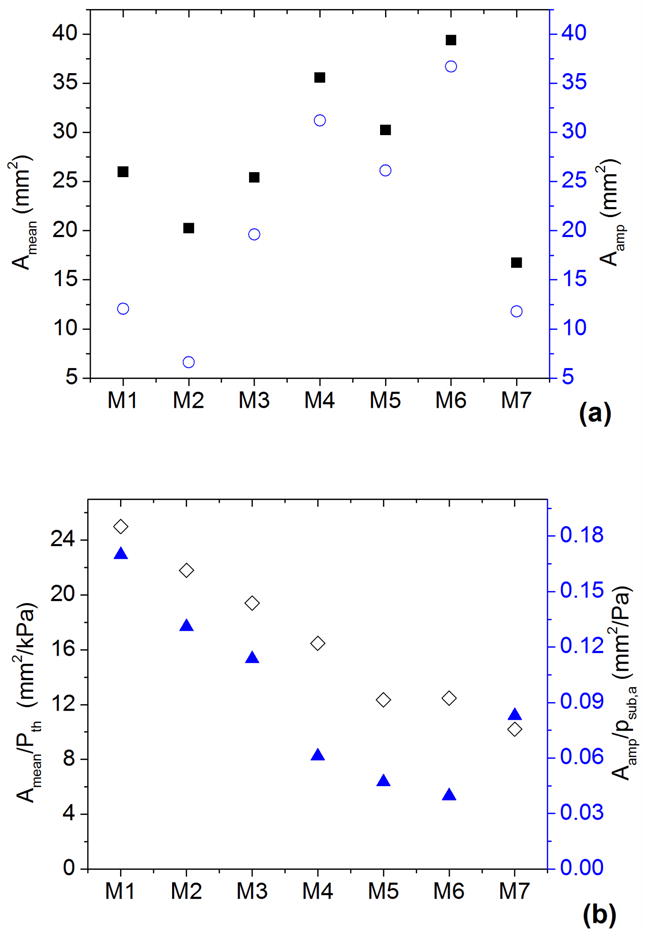
a) The mean glottal opening area (■) and the glottal area amplitude (○; estimated as the half of the peak-to-peak value of the glottal area waveform); b) the mean glottal opening area normalized by the phonation threshold pressure (◇) and the glottal vibration amplitude normalized by the subglottal acoustic pressure (▲).

Since phonation generally occurs as two or more vocal fold eigenmodes (i.e., resonances of the vocal fold structure) are synchronized (Zhang et al., 2007; Zhang, 2010), it is possible that both structural modifications significantly changed the eigenmodes of the vocal fold in a way that alters the fluid-structure interaction and energy transfer from airflow to the vocal folds. For example, the results from the M7 model seems to indicate that suppression of the AP out-of-phase motion, particularly during the closing phase, facilitates complete glottal closure. The suppression of the AP out-of-phase motion and the occurrence of a more in-phase motion would also enhance flow modulation and may increase sound production efficiency. Further investigation of the eigenmode synchronization pattern in the presence of the out-of-phase eigenmodes or in vocal folds of different structural features is required to further elucidate the mechanisms underlying the observation of this study. Such an improved understanding of the mechanisms underlying complete glottal closure would provides a theoretical foundation based on which better diagnosis and treatment of various voice disorders can be achieved.

Although no vocal tract was used in the experiments reported in this study, no obvious changes in the glottal closure pattern (e.g., the minimum and maximum glottal area) were observed in our preliminary experiments when a uniform vocal tract model was attached to the vocal fold model. The presence of the vocal tract did however lead to increased harmonic production in the output sound spectra, which occurred for all models and was presumably due to the acoustic resonances of the vocal tract tube. Nevertheless, a systematic investigation using different vocal tract shapes is justified and the acoustic effects of the vocal tract and possible source-tract interaction will be addressed in a separate study. Lastly, we note that the results reported in this study were based on one particular physical model and one specific geometry. Although we anticipate that the general observations of this study will remain qualitatively the same, future studies using different physical models and vocal fold geometry are required to confirm and generalize the findings of this study to human phonation.