Structure and flexibility of the tropomyosin overlap junction

Abstract

To be effective as a gatekeeper regulating the access of binding proteins to the actin filament, adjacent tropomyosin molecules associate head-to-tail to form a continuous super-helical cable running along the filament surface. Chimeric head-to-tail structures have been solved by NMR and X-ray crystallography for N- and C-terminal segments of smooth and striated muscle tropomyosin spliced onto non-native coiled-coil forming peptides. The resulting 4-helix complexes have a tight coiled-coil N-terminus inserted into a separated pair of C-terminal helices, with some helical unfolding of the terminal chains in the striated muscle peptides. These overlap complexes are distinctly curved, much more so than elsewhere along the superhelical tropomyosin cable. To verify whether the non-native protein adducts (needed to stabilize the coiled-coil chimeras) perturb the overlap, we carried out Molecular Dynamics simulations of head-to-tail structures having only native tropomyosin sequences We observe that the splayed chains all refold and become helical. Significantly, the curvature of both the smooth and the striated muscle overlap domain is reduced and becomes comparable to that of the rest of the tropomyosin cable. Moreover, the measured flexibility across the junction is small. This and the reduced curvature ensure that the super-helical cable matches the contours of F-actin without manifesting localized kinking and excessive flexibility, thus enabling the high degree of cooperativity in the regulation of myosin accessibility to actin filaments.

1. Introduction

The actin-binding protein tropomyosin is a coiled-coil present on thin filaments in virtually all eukaryotic cells [1,2]. By associating head-to-tail it forms a continuous cable along the length of the actin-based filaments, thus conferring increased thin filament rigidity and protection against filament severing proteins [1–6]. In smooth and striated muscles, tropomyosin also cooperatively regulates myosin’s association with the actin subunits of the thin filament and hence the myosin cross-bridge cycle and contraction [2–5,7]. In striated muscle, this regulation is controlled by interactions of tropomyosin with troponin and, in turn, by troponin binding Ca²⁺ [7]. In smooth muscles, tropomyosin interactions may be modulated similarly by caldesmon and calponin [8].

Despite the large number of tropomyosin isoforms, amino acid sequences of the coiled-coils are typically conserved [9,10]. Thus, tropomyosin variants are likely to bind to F-actin filaments by much the same well-characterized electrostatic mechanism [11]. While the specific positioning of tropomyosin on F-actin depends on the Coulombic interaction complementarity of residue pairs at the interface between actin and tropomyosin, the actual binding strength of a single tropomyosin molecule with F-actin is very low (reviewed in [4]). Its binding is augmented by head-to-tail tropomyosin polymerization with itself, forming a superhelical cable spiraling around the actin filament that prevents the detachment of tropomyosin from F-actin [2,3,5,6,10]. While the corresponding head-to-tail linkage is a universal attribute of all tropomyosin isoforms, the overlap structure appears to differ widely among the different family members [6,10,12,13]. In fact, the C-terminal tropomyosin sequences are not well conserved, and hence, head-to-tail complex formation is isoform-specific. For example, C-terminal sequence divergence is likely to be responsible for the different head-to-tail polymerization kinetics of smooth and striated muscle tropomyosin [6,9,10,12,13]. In fact, electron microscopy studies suggest that the smooth muscle junctional complex is more stable and less flexible than its skeletal muscle counterpart [14].

To date, no high resolution structures characterize the head-to-tail connection of full-length tropomyosin. However, the overlap structure for short C- and N-terminal sequences of tropomyosin have been determined after splicing them onto non-native peptides known to stabilize coiled-coils. These chimeric adducts form four-coiled complexes with an eight to fifteen residue overlap [6,12,13]. In this nexus, the partially opened C-terminal coiled-coil encloses the tight N-terminal coiled-coil, (see Figs 1a and 1b) [6,12,13]. Both the smooth and the striated muscle adducts display a near 90° rotation (i.e., twist around the longitudinal central axis) of the C-terminal coiled-coil fragment relative to the N-terminal coiled-coil fragment. In addition, the coiled-coil axis of the N-terminal fragments is not aligned with that of the C-terminal fragment, but instead they are angled relative to each other. This bend (or curvature) angle ω is 12.4° in the smooth muscle nexus and 19.6° in the striated muscle nexus. This is significantly more curved than the curvature angle of canonical tropomyosin on F-actin, which is 8.6° degrees (over a comparable length)[18]. Whether or not the presence of non-native protein adducts affects the twist and the curvature of the synthetic overlap domains is uncertain.

Fig. 1.

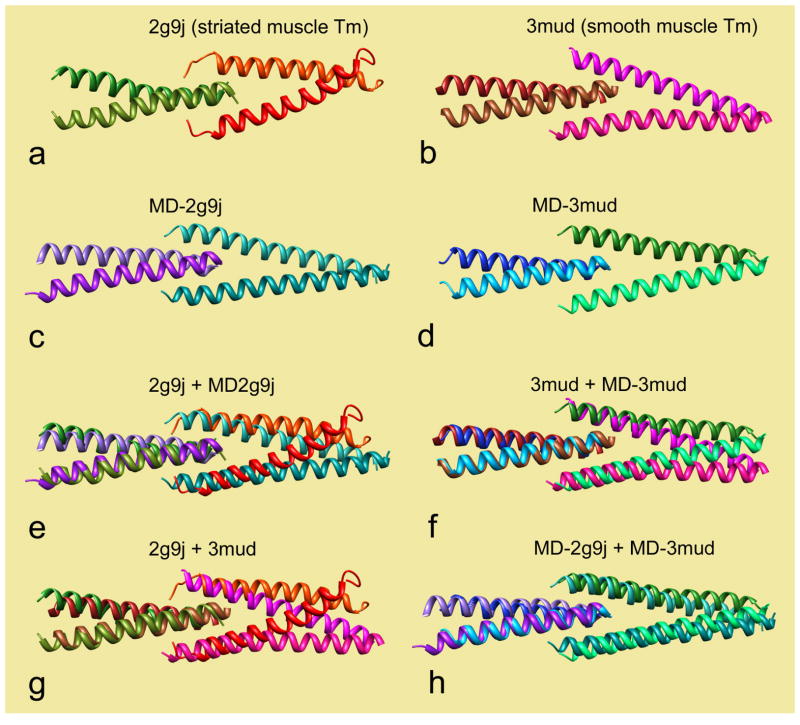
Tropomyosin head-to-tail overlap domains. (a, c) striated muscle structures, (a) chimera from NMR, (c) native domain, averaged from MD. (b, d) smooth muscle structures, (b) crystal structure of chimera, (d) native domain, averaged from MD. In each panel, N-terminal residues are on the left, C-terminal residues are on the right. (e–h) superimposition of structures, after aligning the left pair of chains, superimposing: (e) a + c, (f) b + d, (g) a + b, (h) b + d. Graphics and alignment done with Chimera [19].

In the present study, we use Molecular Dynamics to assess the effect of the non-native adjuncts on the overlap structure. In the X-ray crystal and NMR structures of the smooth and striated muscle overlap domains, the non-native residues were replaced by native tropomyosin sequences. Our study shows that the opening of the C-terminal coiled-coil and the orthogonal twist angle is maintained in the fully native overlap domain, although the helical content of unfolded chains is restored. In contrast, the curvature angle of both the smooth and the striated muscle overlap domain is reduced in the native structures compared to that in the chimeric structures. The average curvature (~9.4°, see Table 1) is similar to the curvature found along the rest of actin-bound tropomyosin. The curvature variance (i.e. the flexibility) is modestly greater for the striated tropomyosin overlap domain than for the corresponding smooth tropomyosin overlap, which is consistent with data from electron microscopy also showing that the overlap domains of striated muscle have a greater variance in curvature angle [14].

Table 1.

Geometry of the overlap domain during Molecular Dynamics.

Tropomyosin Source	Number of residue pairs in overlap	Distance covered by overlapping residues	Twist angle of C- vs. N-terminal fragments (θ)1	Curvature C- vs. N-terminal fragments (ω)1,2	Dynamic persistence length of overlap3
Striated Muscle	10	13.5 Å	90.6 ± 2.5°	9.3 ± 4.8°	342 nm
Smooth Muscle	9	12.0 Å	85.7 ± 2.4°	9.6 ± 3.8°	546 nm

¹Values for average ± standard deviation.

²An F-test shows that the two standard deviations are significantly different from each other (P<0.001).

³Measured over a 12 Å distance.

2. Methods

2.1 Reference models for MD simulations

Initial reference models for the striated and smooth muscle α-tropomyosin isoform head-to-tail overlap domains were based on NMR and crystal structures. In PDB ID code 2g9j (conformer model-1) [6], residues 1 to 14 from the N-terminus of rat striated muscle tropomyosin had been spliced onto last 18 residues of the leucine zipper coiled-coil forming sequence of GCN4, while residues 251 to 284 from the C-terminus of rat striated muscle tropomyosin were spliced onto GCG residues to stabilize the latter. In PDB 3mud [13], residues 1 to 29 from the N-terminus of chicken smooth muscle tropomyosin were fused to residues 215 to 257 of human microtubule-associated protein EB1, while residues 248 to 284 of C-terminus were fused to residues 2 to135 of human DNA repair protein XRCC4 protein. In the work reported here, we replaced the non-tropomyosin residues with native sequences to build two 40-residue-long C- and N-terminal fragments of the coiled-coil. We used native acetylated N-terminal methionine residues instead of the amino acid mimetics [6,13] employed in the PDB structures.

2.2 Molecular Dynamics

The reference models were energy minimized [11] and Molecular Dynamics simulations performed in explicit solvent including 150 mM NaCl at 300° K, using NAMD version 2.6 [15] and the CHARMM27 force field [16,17] as previously described [11,18]. Analysis was carried out after discarding the first 4 to 5 ns of MD, ensuring that the variance of the measurements had stabilized [11].

2.2 Analysis

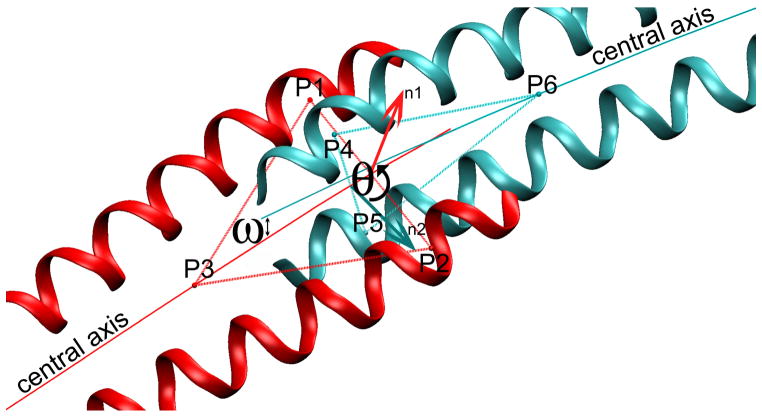
The junction twist angle (θ) between the C-terminal and the N-terminal coiled-coil fragments was computed as the angle between two planes, each constructed to contain the end of the respective fragment (see Fig. 2). Each plane was defined by three points (p₁p₂p₃ and p₄p₅p₆). At the C-terminus, points p₁ and p₂ were centered between residues 279 to 281 on each of the two α-helical chains, and p3 at the center of the coiled-coil between residues 267 to 273 (residues 1–3 were not included to avoid any effects of helix unraveling on the measurement of θ). Similarly at the N-terminus, p4 and p5 were centered between residue 4 to 6 on each α-helical chain, and p6 at the center of coiled-coil residues 12 to18. The angle θ was then obtained from the normal vector of each plane, n1 and n2, as

Fig. 2.

Schematic diagramming the calculation of twist and curvature for intersecting coiled-coils (see Methods for details). The orientation of the two triangular planes (P1,P2,P3 and P4,P5,P6) define the twist angle θ of the termini, and the respective central axes define the bending angle ω of the junction.

$$cos(\theta )=\frac{n_1·n_2}{\Vert n_1\Vert \Vert n_2\Vert }\text{for}0<\theta <\pi .$$

The curvature of the overlap domain was quantified by determining the angle ω between the respective central axes of the C- and N-terminal coiled-coils fragments (see Fig. 2).

The number of overlapping residues in the head-to-tail domain were counted by eye in Chimera [19] and also quantified by measuring the overlap between the central axes of the C- and N-terminal parts using Twister [20]. Persistence length was calculated as described previously [18]. Buried surface areas were calculated as in [13].

3. Results

3.1 General features of the MD structures

Molecular Dynamics simulations were initiated on models of the striated and smooth muscle α-tropomyosin head-to-tail overlap domains derived from pdb structures, here with native sequences in place of protein adducts previously used (see Methods). Both the striated and smooth muscle structures remained intact during MD runs performed in explicit water. The smooth muscle domain remained fully coiled over the 30 ns interval (compare Fig. 1b,d). Neither unfolding of individual helices nor separation of the adjoining chains in the 4-helix nexus occurred during MD. Although terminal residues of the NMR-based striated muscle domain are unfolded in the PDB (Fig. 1a), they became fully α-helical within the first 5 ns of simulation. The simulation period was extended to 270 ns, but the terminal residues remained helical throughout (Fig. 1c).

The average MD structures of both striated and smooth muscle head-to-tail domains are slightly curved, consistent with previous observations made on EM images of smooth and striated muscle tropomyosin dimers and oligomers [14]. Both average structures have a tight N-terminal coiled-coil inserting into the partially separated coils of the C-terminus (Fig. 1c,d). The relative twist angle (θ, Fig. 2) between the N-terminal and C-terminal pairs of chains at the overlap interface stayed very close to the initial 90° value, with little variance in the twist angle (Table 1). Kinking, dislocation, swiveling or longitudinal sliding were not observed.

3.2 Overlap domain length

Once the ends of the striated muscle structure formed helices during MD, the overlap complex straightened with a juxtaposition of 10 N- and C-terminal residues in the overlap over a length of ~13.5 Å. The smooth muscle structure also straightened during MD, but to a lesser degree. It became shorter than it is in the X-ray structure, with overlapping residues extending over ~12 Å (Table 1). These changes resulted in a 25% increase in the “buried surface” area of the striated muscle overlap domain (to 2299 Ų) and in a small increase (4%) for the smooth muscle domain (to 2113 Ų). The buried surface in both consists of a comparable high percentage of non-polar interaction (78% in each).

3.3 Overlap domain curvature

Curvature of the head-to-tail overlap domains was assessed by calculating the average bending angles from the MD trajectories (Table 1, see Methods). The bending angle was modestly greater for the smooth muscle overlap domain (9.6°) than for the striated muscle one (9.3°), and, in turn, each of these values was slightly higher than corresponding ones for the full molecule (8.6° over comparable distances) determined previously [11,18]. These bending angles, particularly in the case of the striated muscle overlap, were considerably smaller than those for the chimeric PDB structures (19.6°, striated muscle; 12.4°, smooth muscle), indicating that on average the overlap structures of both isoforms straightened during MD of the fully native domains.

3.4 Overlap domain flexibility

Variance in head-to-tail domain curvature, i.e., the deviation of the bending angle from its mean during MD, measures flexibility of the overlap domain. The standard deviation of the bending angle (4.8°) for the striated muscle overlap was significantly greater than that for the smooth muscle one (3.8°)(P < 0.001) (Table 1). These values equate to dynamic persistence lengths of 342 vs. 546 nm, gauging flexural rigidity, i.e. material properties of the striated and smooth muscle overlap domains [18,21]. (N.B., a high dynamic persistence length signifies a low flexibility.) Thus, even though on average the smooth muscle overlap is slightly more curved than the striated muscle one is, it still is significantly stiffer, as also was suggested by EM observations on purified tropomyosin samples [14]. Interestingly, the stiffness of the four-coiled nexus domain is similar to that of the rest of two-coiled tropomyosin, which has a dynamic persistence length of 423 nm [18].

3.5 Comparison of solution and MD overlap structures

The overlap curvature along the MD structure of smooth muscle tropomyosin and the corresponding region of the crystal structure (Fig. 1f) [13] are slightly different (9.6° vs. 12.4°), possibly due to modest effects of crystal packing distortions, which are not factors in MD. In contrast, the curvature of the NMR structure of the striated muscle overlap [6] differs considerably from that of the corresponding MD structure (19.6° for pdb 2g9j/Model 1 vs. 9.3° for the MD average). The dissimilarity of the NMR vs. the MD and crystallographic models is highlighted in Figure 1e. Note that an overlap curvature of ~20° would lead to an uncharacteristic divergence of tropomyosin away from the actin surface. The striated muscle NMR structure is also much more curved than the smooth muscle crystal structure of the (Fig. 1g). However, after MD, the smooth and striated muscle overlap domains converge onto a very similar structure (see Fig. 1h). Taken as a whole, these results suggest that the curvature of the NMR structure is exaggerated, which may be a result of perturbations caused by the leucine zipper segment in the chimera used for NMR.

4. Discussion

Previous MD studies showed that on average the curvature of superhelical tropomyosin closely matches the helical contours of F-actin [11,18]. Additional molecular modeling and EM studies indicated that this superhelical conformation maximizes electrostatic contacts between tropomyosin and successive actin subunits along the filament, thus stabilizing tropomyosin on F-actin [11]. In contrast, these and other studies of isolated tropomyosin and single tropomyosin molecules on F-actin also revealed coiled-coil splaying and rotation of the exposed terminal residues at the tips of tropomyosin [2,22]. Indeed, the localized divergence from a canonical superhelical structure at the ends of the molecule may provide the conformational diversity necessary for the terminal helices to make the specific head-to-tail interactions that allow polymerization on the actin filament [22]. The present work shows that once the tropomyosin cable is assembled, then the intrinsic flexibility of the terminal domains diminishes. Thus, together with the rest of tropomyosin, the terminal segments of the molecule become semi-rigid. The present simulations also demonstrate that the curvature and the flexibility of the head-to-tail overlap domain are almost the same as those of the other parts of F-actin-bound tropomyosin. This near equivalence ensures that the polymerized tropomyosin molecules can behave as an unbroken cable with mechanical properties that essentially are continuous along the actin filament.

In the current and earlier studies, we directly monitored the local and global flexural rigidity of tropomyosin by quantifying bending variance about the coiled-coil’s central axis. In parallel studies, we and others have also evaluated the impact of changes in the local coiled-coil radius on tropomyosin curvature [2,18,23]. These studies showed that there is no obvious correlation between alterations in the radial dimensions of tropomyosin and bending variance, i.e. between local conformational variance and coiled-coil flexibility. Rather, the correlation between radius and curvature is delocalized [18,23]. Similarly, the connection between tropomyosin flexibility and fluctuations measured for the radial or axial separation of hydrophobic core residues is unclear [24], since these parameters have not been shown to be directly related to tropomyosin’s local bending or twisting modulus.

Our analysis indicates that the head-to-tail curvature of smooth and skeletal muscle α-tropomyosin is close to that of the rest of the molecule. It is consistent with previous electron microscopy showing that the striated muscle overlap nexus is less rigid than the smooth muscle one [14]. However, this deficit is compensated in striated muscle by the additional presence of troponin-T which binds over and stiffens the overlap region [14]. Hence, extra flexibility between adjoining tropomyosins does not appear necessary for optimal actin-tropomyosin binding, and therefore, contrary to expectation, for effective cooperative thin filament activation. Indeed, even though isoform specific terminal sequences determine tropomyosin-tropomyosin head-to-tail assembly kinetics, the overall angular geometry and flexibility of the overlap domain appears to be designed to preserve the continuity of the super-helical cable shape as it forms on F-actin.

Highlights.

• Head-to-tail linkage is required for tropomyosin cable formation on F-actin.

• Molecular Dynamics of tropomyosin overlap domains were carried out.

• N- to C-terminal coiled-coils face each other at an orthogonal angle.

• The bending angle of the overlap domain and the rest of the molecule is comparable.

• This curvature ensures tropomyosin assembly as an uninterrupted cable on F-actin.