GPU-based High-Performance Computing for Radiation Therapy

Abstract

Recent developments in radiotherapy therapy demand high computation powers to solve challenging problems in a timely fashion in a clinical environment. Graphics processing unit (GPU), as an emerging high-performance computing platform, has been introduced to radiotherapy. It is particularly attractive due to its high computational power, small size, and low cost for facility deployment and maintenance. Over the past a few years, GPU-based high-performance computing in radiotherapy has experienced rapid developments. A tremendous amount of studies have been conducted, in which large acceleration factors compared with the conventional CPU platform have been observed. In this article, we will first give a brief introduction to the GPU hardware structure and programming model. We will then review the current applications of GPU in major imaging-related and therapy-related problems encountered in radiotherapy. A comparison of GPU with other platforms will also be presented.

1. Introduction

Radiation therapy has experienced rapid developments over the past a few decades. A number of novel technologies have been introduced into routine clinical practice. Behind these developments sit a significant number of computationally intensive tasks, such as 3D/4D tomography reconstruction, high spatial/temporal resolution image processing, inverse treatment planning, and Monte Carlo radiation dose calculations. On one hand, these sophisticated problems are usually associated with large data sets and/or complicated numerical algorithms. On the other, it is highly desirable to solve those problems in a timely fashion, e.g. in minutes or sometimes even in (near) real time, to meet the clinical demands of a high throughput or to facilitate new treatment modalities such as on-line adaptive radiation therapy. The conflicts between these two aspects have clearly posted great challenges to the time-critical and resource-limited clinical environment and thus there exists a high demand on computation powers.

During the last decade, the performance of personal computers increased dramatically. The technical innovations in the first few years of the new millennium were focused to produce processors with an ever-increasing clock speed, as predicted by the Moore’s Law (Moore, 1965). This advancement was very convenient for the user, since any code written on an older and slower CPU experienced an obvious speedup on a newer and faster processor. Yet, the situation changed recently. The increase of clock speed hits its bottleneck due to inherent technical limitations, especially with respect to energy consumption and heat emission of a processing chip. To continue boost computation powers, another approach was employed where several processing units are replicated on one chip. These homogenous units operate in parallel, leading to increased performance. Thus, modern computers are not only getting fast, but wider!

One particular example of the massively parallel architecture is graphics processing unit (GPU). Originally designed to handle computer graphics operations, a GPU comprises thousands of processing units on a single chip, which translates into a tremendous amount of processing capabilities. Lately, GPU has been employed to solve challenging scientific problems in, for example, physics, mathematics, chemistry, and biology. It has also become a platform alternative to the conventional CPU that was used to solve the problems in radiation therapy.

GPUs are particularly attractive for medical problems in radiotherapy for the following reasons, making them favorable for a clinical environment, e.g. a typical cancer clinic. First, GPU offers a high computing power suitable for radiotherapy problems. In fact, most radiotherapy problems can be formulated in a massive fine-grained fashion and often a set of relatively simple tasks are carried out independently on each subset of the underlying clinical data, e.g. on the voxels of a discretized patient geometry. This fact naturally supports GPU-based parallelization. Second, the computation power of GPUs is appropriate for medical physics problems in radiotherapy. The sizes of clinical problems are usually at an intermediate level. Apart from very few exceptions, they are much smaller in size than those challenging problems in fundamental sciences, e.g. in astronomy, fluid dynamics, or computational biology. While problems of those kinds are usually taken out on large distributed clusters of CPUs, problems in medical physics may not benefit much from distributed computing due to the relatively small size and hence large communication overhead. In contrast, GPU is more suitable in this regard. Third, GPU provides the advantage of having high performance computing with convenience and low cost. Compared to a cluster, they are easy to maintain and access. The continuing demands from computer game industry also significantly reduce the costs of GPU cards. It is usually orders of magnitudes lower in price to deploy a GPU facility compared to a CPU cluster with a similar processing power.

On the other hand, GPU also holds several disadvantages compared to CPU. First, the hardware architecture of the GPU makes it extremely suitable for data parallel problems, but not so for task parallel problems. Depending on the problems of interest, careful design of the algorithm considering the nature of GPU architecture is needed to achieve a high performance. Second, GPU is a relatively new platform. Most convenient libraries used extensively for CPU computing do not have GPU counterparts yet. Hence, it requires a large amount of work to code almost everything from scratch, increasing the difficulty to maintain code optimality and the chances of making errors. These issues have posed a significant amount of challenges for the developers and researchers who are actively seeking for GPU solutions.

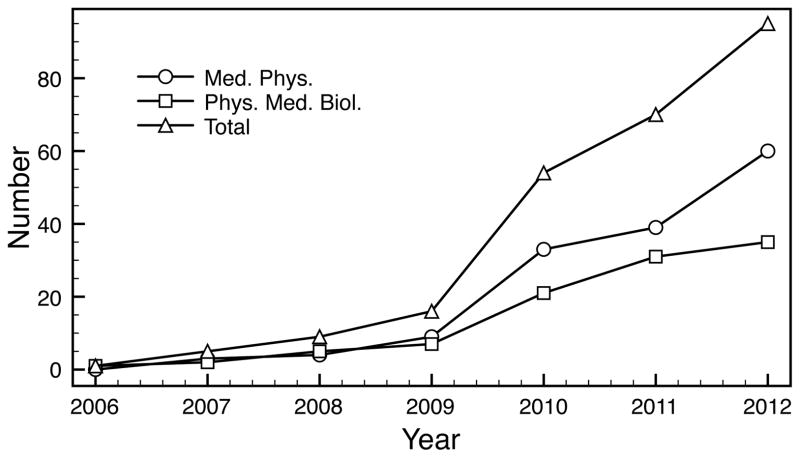
Since its introduction to medical physics, developing GPU-based solutions for those computationally demanding problems have been an active research topic. A number of algorithms have been developed particularly in a GPU-friendly form, leading to dramatically accelerated processing speeds in a wide spectrum of problems, ranging from imaging-related problems to therapy-related ones. This fact can be reflected by the number of publications related to the applications of GPU in medical physics. For instance, Figure 1 depicts the number of research articles published in Medical Physics and Physics in Medicine and Biology since 2006 that contain the word “GPU” in the title or abstract. The monotonically increasing trend, especially the jump from 2009 to 2010, clearly demonstrates the research interest on this topic. Arguably speaking, employing GPU has become a standard and typical approach to accelerate computation tasks in medical physics.

Figure 1.

The number of GPU-related research articles published in Physics in Medicine and Biology and Medical Physics in recent years.

After a few years of successful use of GPUs in medical physics, there is a need for a review article on this important topic. Not only will such an article summarize the current status of developments, it will also offer an opportunity to look back into the development path, to rethink those encountered problems, and to look into the future of this potent computational platform. Although one review article on GPU-based high-performance computing in medical physics was published in 2011 (Pratx and Xing, 2011a), given the vast development of GPU hardware, algorithms, and implementations recently, it is necessary to have another article to systematically review the current status of GPU applications in a wide spectrum of radiotherapy problems. It is also of critical importance to perform in-depth discussions regarding the techniques behind each problem, as well as the success, challenges, and potential solutions.

With this objective in mind, this article will provide a comprehensive review regarding GPU technology in radiotherapy physics. Because of the wide applications of GPUs, particularly in image processing field, it is infeasible to cover all the topics available in literature. Trying to cover all topics would also inevitably hinder the depth of each topic review. Hence, we will limit the scope of this article only to major imaging and therapy problems encountered in radiotherapy. In the rest of this paper, we will first give a general introduction about GPU hardware structure and programming model. We will then present a systematical review of the applications of GPU in a set of radiotherapy problems. The algorithm structure will be analyzed with emphases on the compatibility with GPU. Potential problems and solutions will also be discussed. A comparison of GPU with other platforms will be presented in Section 5. Finally, Section 6 concludes this article with discussions on relevant issues.

2. Graphics Processing Unit

A graphics-processing unit (GPU) is a specialized electronic hardware in a computer system. Although it was designed originally to conduct computations regarding image processing and to facilitate the processing of graphics information, GPU has recently been utilized to handle those computational tasks originally accomplished on CPU, leading to the so-called general-purpose computing on graphics processing unit (GPGPU). In this section, we will provide an overview about the GPU’s hardware structure, as well as its programming language and computation model.

2.1 Hardware

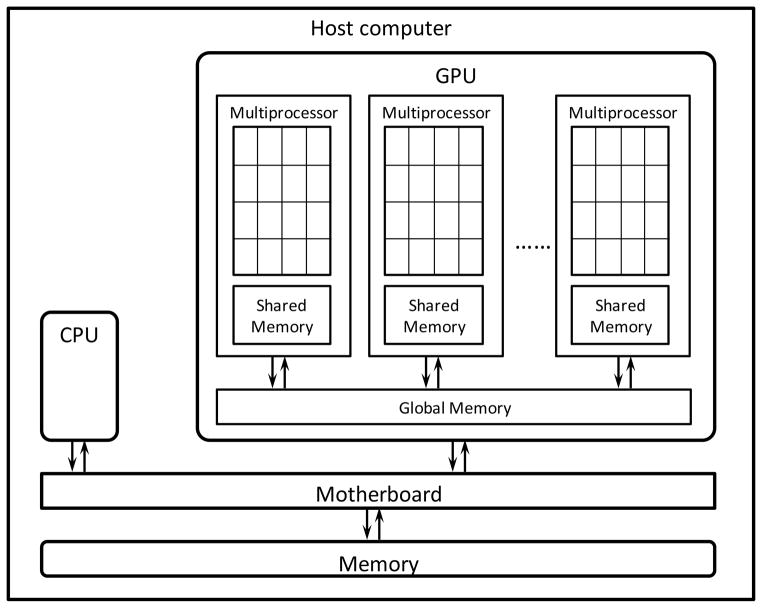
A typical hardware configuration of a computer workstation containing a GPU is shown in Figure 2. In such a system, GPU usually presents as an individual card plugged onto the PCI-express port on the workstation’s motherboard. It has access to the computer memory space via the PCI-express bus. In this structure, the GPU is termed a “device”, while the rest of the system is called “host”.

Figure 2.

Illustration of hardware structure of a workstation containing a GPU.

While GPUs from different manufactures have different design specifications, they share some common architectural characteristics. Here we only briefly present the hardware structures pertaining to the understanding of GPU programming.

The most distinct feature of a GPU compared to a conventional CPU is that it contains a large number of processing units called stream processors. These processors are physically grouped into a set of multi-processors. Each stream processor has a relatively low clock speed compared to CPU. However, the large amount of processors available on a GPU card lead to a much higher cumulative computational power.

As for the memory structure, different types of memory spaces exist on a GPU card, which have different characteristics and can be used in computations accordingly. First of all, analogous to RAM in a CPU workstation, there is global memory on the graphics card accessible to all processors, up to several gigabytes in current GPU configurations. The bandwidth of this memory is relatively low compared to other types of memories. Moreover, this is the only memory space accessible from the host computer. Three different types of memory can be allocated in the global memory: linear memory, arrays, and constant memory. Among them, linear memory is the most common one and can be read or written directly by the stream processors. Arrays are allocated and initialized from the host. After that, it is bounded to the so-called texture, which can be read only from all stream processors with the advantages of multi-dimensional spatial locality cache and hardware supported linear interpolations. Constant memory can be allocated and initialized from the host. They are readable from each stream processor with cache. Second, on each multiprocessor, there is a memory space called shared memory that offers a space accessible to all processors inside the multiprocessor. It usually serves as a user-managed cache space between each processor and the global memory. Visiting the shared memory is fast. Finally, each stream processor has a certain amount of registers (not shown in Figure 2), which provide memory spaces required in the computations on each particular processor. The specific sizes and bandwidths of these memory spaces vary depending on brands and generations.

2.2 SIMD programming model

GPU executes a program in a single-instruction-multiple-data (SIMD) fashion. Here we use NVIDIA GPU’s terminology to explain this concept. In GPU-based parallel processing, a special function called kernel is launched on GPU with a number of copies and each copy is termed a thread. These kernel threads are grouped into a number of blocks, which are then enumerated and distributed to multiprocessors for execution. A multiprocessor executes threads in groups of 32 parallel threads termed a warp. Inside a warp, a common instruction for all threads is executed at a time. If threads within a warp diverge at a certain point due to a conditional branch, e.g. an if-else statement, the warp serializes each branch path, while putting all other threads in idle. When all paths are enumerated, the threads converge back and continue the executions.

To illustrate how the GPU executes a program in parallel, we provide a simple example that approximates the π value by Leibniz formula $\pi ={\sum }_{i=0}^{\infty }\left(\frac{1}{4i+1}-\frac{1}{4i+3}\right)$. Conventional CPU code loops over the summation for a predefined large number of N times and accumulate the results. For the GPU-based computation, the principle of code execution is illustrated in Figure 3. After allocating a linear space data[] on GPU to hold each term in the series, a GPU kernel is launched. As opposed to a CPU function that runs in a single copy, a number of N copies of the kernel are launched, each indexed by a thread id i = 0,1, …, N − 1. Depending on the id, the thread will compute only one term in the series and place the result in the corresponding location of data[]. After all threads finish, the results stored in data[] is transferred back to CPU and a summation is conducted, yielding the π value. On a modern GPU, several thousands of threads are executed concurrently. Different GPU threads always follow the same execution path but with different data, which is fully compliant with the SIMD programming mode, leading to a high computational efficiency. It is worth mentioning that we provide this example only for the purpose of illustrating the principle. It is by no means the optimal implementation. For instance, advanced summation scheme can be conducted on GPU as well to improve efficiency.

Figure 3.

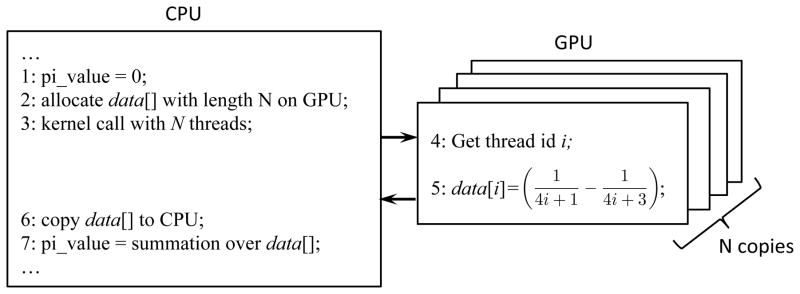
Illustration of GPU-based computation of π using Leibniz formula.

2.3 Programming languages

Widespread adoption of GPU for scientific computing requires user-friendly programming languages or APIs (Application Programming Interface). Over the years, a set of APIs has been developed to facilitate this purpose.

Among them, CUDA (Compute Unified Device Architecture) is a parallel computing platform created by NVIDIA to support the programming of its own GPUs. It offers developers the capability to program GPUs using typical programming languages, e.g. C, and Fortran. With years of developments, a set of libraries useful to scientific computing have become available, such as CURAND for random number generator, CUSPARSE for sparse matrix manipulations, and CUBLAS for linear algebra operations. These libraries greatly facilitate many scientific programming tasks by offering high efficiency implementations of frequently used functions. A number of plug-in modules have also been built on top of CUDA to provide GPU interfaces inside other computational environment, such as MATLAB and Mathematica.

Unlike CUDA that specifically supports NVIDIA GPUs, OpenCL (Open Computing Language) is an emerging framework for GPU programming. Because of its cross-platform capability, OpenCL has received a lot of attentions recently and is experiencing rapid developments. Not only does it support GPUs from different vendors, it also enables programming across heterogeneous platforms consisting of both CPUs and GPUs. Compared to CUDA, OpenCL is relatively at its early development stage and the support for scientific computing is relatively incomplete. It is also an active research topic to study if there is any efficiency compromise due to the portability (Fang et al., 2011; Weber et al., 2011; Kakimoto et al., 2012; Pallipuram et al., 2012; Su et al., 2012).

There are also a few other programming languages/APIs. Examples include Cg (C for graphics) developed by NVIDIA in collaboration with Microsoft, HLSL (High-level shader language) by Microsoft, Sh by the University of Waterloo Computer Graphics Lab, and Brook by the Stanford University graphics group, etc..

2.4 Performance considerations

Although GPU possesses a tremendous computational power, it has to be utilized in an appropriate fashion to fully exploit its capability. In practice, its SIMD programming model, as well as some limitations on memory, determines that some algorithms are suitable for GPU programming, while others attain inherent conflicts with this platform. It is therefore of top priority to understand GPU’s programming model and limitations, when designing an algorithm.

First, the SIMD programming model indicates that only when all 32 threads inside a warp have the same execution path can we attain the full efficiency of execution. This condition, however, is hardly met in real problems, and hence the so-called thread divergence problem occurs, limiting the overall program efficiency. It is worth emphasizing that thread divergence occurs only within a warp; different warps execute independently regardless of whether they are executing common or disjoint code paths.

In general, the means of parallel computation are categorized into Task Parallelization and Data Parallelization. The SIMD programming fashion of a GPU dictates that it is suitable for data parallelization. An example in this category include vector and matrix operations, as different GPU threads can process different matrix entries in the same operational fashion but with different data. In contrast, it is quite difficult to achieve high speed-up factors for task parallelization tasks, where different threads can follow different instruction path throughout the algorithm. Examples include Monte Carlo particle transport simulations, where the probabilistic nature of the code requires if-else statements all over the places. In practice, the programmer can essentially neglect the problem of thread divergence for the purpose of program correctness. However, substantial performance gain can be realized by carefully designing algorithm and implementations to maximally avoiding the thread divergence problem. Arguably speaking, eliminating thread divergence is the first priority issue in GPU-based parallel processing to fully take advantage the power of a GPU.

The second issue is related to GPU memory. GPU kernels are always accompanied with frequent visits to GPU memory, and the memory throughput critically determines the overall efficiency. As such, it is important to minimize data, particularly large data, transfer between the CPU and the GPU, where the bandwidth is much lower than that inside the GPU. It is also necessary to minimize visits to global memory, which has much lower bandwidth compared to other types of memories. In contrast, it is desirable to properly use other types of memory spaces, e.g. shared memory and texture, to improve memory access speed, to avoid redundant visits, and to improve memory visit locality. Moreover, a GPU tends to hide the memory latency by concurrently executing programs on some of the multi-processors while having others performing memory operations. Carefully designing a program to balance computation and memory visiting to keep GPU’s processors busy is hence another effective way to ensure optimal utilizations of GPU.

Another problem that one could encounter in parallel programming is the memory-writing conflict. While it is legitimate to have two GPU threads read from the same memory address concurrently, writing to the same address at the same time leads to unpredicted results. Hence, when there is possibility of concurrent writing from different threads, it is the programmer’s responsibility to foresee this issue and employ appropriate schemes to enforce result integrity. In most scenarios, some type of serialization of the writing operations, e.g. using atomic functions, is needed. This serialization apparently compromises the parallel capability of a GPU, reduces the efficiency, and thus should be used minimally.

There are also other issues that one would consider for code optimization. For instance, small kernel is preferred to save register usage. When threads may have different path length, it is better to organize the execution order among threads to simultaneously execute threads with similar lengths. One would also like to minimize the use of arithmetic instructions with low throughput: using intrinsic functions instead of regular functions, whenever the accuracy is tested unaffected.

In short, it requires tremendous efforts to fully optimize a GPU code and to maximize its performance. Depending on the way of coding, performance for a given problem may differ by an order of magnitude or even more. Yet, code optimization is usually problem-specific. This poses the most challenging problem when developing GPU-based applications.

2.5 GPU cards

Before we start discussing applications of GPUs in various radiotherapy physics problems, we would like to summarize the main properties of those GPU cards employed by different researchers. Providing the specifications of these GPUs will approximately give indications about the performance of each GPU cards, which will facilitate the cross-comparisons of efficiency among different implementations of a given problem. Yet, one needs to keep in mind that the real performance of a GPU code depends on many factors. In addition to those listed in Table 1, the speed is also critically impacted by the occupancy of the GPU processors, the memory access patterns, etc.. There is no practical way to compare different implementations on different GPUs in a completely fair fashion.

Table 1.

Specifications of GPUs used in research projects reviewed in this article.

Vendor	GPU		Number of cores	Clock speed (GHz)	Memory (MB)	Memory bandwidth (GB/s)	Processing power (GFLOPS)
NVIDIA	GeForce	7600 GS	12	0.4	256	22.4	N/A1
		8800 GTX	128	1.3	768	86.4	518
		9500 GT	32	1.4	512	25.6	134
		GTX 280	240	1.3	1024	142	933
		GTX 295	2×240	1.2	2×8962	112	1788
		GTX 480	480	1.4	1536	177	1345
		GTX 570	480	1.4	1280	152	1405
		GTX 580	512	1.5	1536	192	1581
		GTX 590	2×512	1.2	2×1536	164	2488
	Tesla	C1060	240	1.3	4096	102	933
		C2050	448	1.15	3072	144	1288
		C2070	448	1.15	6144	144	1288

¹Processing powers of GeForce 7600GS is not available in literature to our knowledge.

²This card and GTX 590 has dual GPUs, indicated by the 2× notation here. The processing power refers to the total power of the two GPUs.

Table 1 summarizes all the GPU cards employed in the research works reviewed in this article. A few interesting facts can be observed. First, NVIDIA clearly dominates the applications of GPUs in radiotherapy physics computations. It is surprising that all the research projects reviewed in this article utilizes NVIDIA GPUs. Second, only two series of GPUs are used, namely GeForce series and Tesla series. GeForce series belong to the so-called consumer-grade graphic cards, which are mainly used to support graphics processing tasks in desktop computers. It gains popularity in research community primarily due to its wide availability and low cost-to-performance ratio. On the other hand, Tesla series are NVIDIA’s dedicated general purpose GPU cards manufactured specifically for scientific computing purposes. While the price of a Tesla card is usually several times higher than a GeForce card with a similar processing power, a Tesla card has the advantages of error-correcting-code (ECC)-protected memory and availability of models with higher memory sizes, critical for many scientific computing tasks. The efficiency of processing double-precision float numbers is also much higher than that of the GeForce series.

3. Imaging-related problems

Imaging is one of the most important aspects of modern radiation therapy, where high quality images of the patient are generated for the purposes of treatment planning and guidance. The size of the problems in this category is usually large, especially when it comes to 4D problems. Yet, they are usually parallelization friendly, in that the entire task can be naturally broken down to small operations at pixel/voxel level. Hence, generally speaking, GPUs are suitable for the parallel processing of these problems. In the following subsections, we will cover problems including ray-tracing calculations, Monte Carlo photon transport in diagnostic energy range, analytical/iterative 3D/4D cone beam CT reconstructions, and image registrations, etc..

3.1 Ray-tracing

Ray tracing refers to the evaluation of radiological path length along a given x-ray line. This method is fundamental to many problems in radiotherapy, such as Digital Radiograph Reconstruction (DRR), iterative cone beam CT reconstruction (CBCT), and radiation dose calculations. The efficiency of ray-tracing algorithm hence largely impacts the overall performance of those problems. Physically, a ray-tracing algorithm numerically computes a line integral g = ∫_L dl μ (x) of the x-ray attenuation coefficient μ(x) along a straight line L. Since it usually requires the computations of g repeatedly for different ray lines, it is straightforward to parallelize the algorithm on a GPU platform by simply having each GPU thread compute the value of one line. Considerable speed-up factors can thus be obtained due to the vastly available GPU threads.

In practice, the evaluation of the line integral is carried out in the form of numerical discrete summation, and depending on the specific scheme the implementation varies. The most widely used algorithm for ray-tracing calculation is Siddon’s algorithm (Siddon, 1985), where the integral is approximated by g(u) = Σ_j Δl_j μ(x_j) with Δl_j being the line segment length of L intersecting with a voxel j and the summation is over all the voxels that L passes. On the GPU implementation, an improved version of Siddon’s algorithm (Jacobs et al., 1998) has been employed, which avoids the sorting operations required by the original Siddon’s method. In particular, Folkerts et al. (2010) has implemented the improved Siddon’s algorithm on an NVIDIA Tesla C1060 GPU card. It was reported that the average computation time was 30 ms for an image resolution of 512×384 and a volumetric CT data resolution of 512×512×104. The same algorithm was also implemented by Greef et al. (2009) for radiation dose calculations, where the calculation was accelerated by a factor of up to 10 using an NVIDIA GTX280 card.

This simple strategy of parallelization based on ray lines causes thread divergence during run time due to different ray lengths, which hinders the computational efficiency. Recent researches have been devoted to further improve the performance by maximally avoiding this issue. Chou et al. (2011) developed a multithread implementation scheme in which multiple threads in a warp wewe employed to handle the computations associated with a set of adjacent rays simultaneously. This approach eliminated the thread divergence within a warp and hence improved efficiency. Other techniques employed in this paper included the optimization of thread block size and the maximization of data reuse on constant memory and shared memory. The computation time was shortened to 11 ms for a case with volume resolution of 512³ and image resolution of 512² on an NVIDIA C1060 GPU card. Xiao et al. (2012) tried to convert conditional statements in the ray-tracing algorithm into simple arithmetic and logic operations to avoid thread divergence caused by the conditions. The algorithm was applied in a collapsed-cone convolution/superposition dose calculation algorithm using an NVIDIA GTX 570 card, where about 2 times speed-up was observed compared to the original simple implementation on GPU.

Another typical approach of discretizing the line integral is tri-linear interpolation (Watt and Watt, 1992). In such a scheme, the x-ray path is divided into a set of intervals of equal length Δl labeled by j and the linear attenuation μ(x_j) at the midpoint of each interval is computed via tri-linear interpolation of the underlying voxel data. j is then approximated by the sum over all intervals Σ_j Δl μ(x_j,E). Because of the interpolation nature behind this algorithm, the generated DRR is smoother than that from the Siddon’s algorithm. In terms of implementation, the same parallelization scheme, namely one GPU thread per x-ray line, can be used for this method. GPU’s texture memory also offers highly efficient interpolations via its hardware. Wu et al. (2009) has implemented this algorithm for the purpose of patient alignment, and a reduction of computation time for at least an order of magnitude has been reported compared to the CPU implementation using an NVIDIA GeForce 8800 GTX card. Yet, this method is generally slower than the Siddon’s algorithm due to the additional required operations of interpolations (Folkerts et al., 2010).

Another algorithm called Fixed Grid algorithm was recently proposed (Folkerts et al., 2012) aiming at the maximal reduction of the thread divergence, while using interpolation to render smooth images. The basic idea is to resample the volume data such that the projection is always along one of the principal direction of the grid. The projection is then conducted by tracing rays through each layer of voxels perpendicular to the projection direction. Because each ray traverses the same number of layers with the same operations, thread divergence is avoided. It only requires 2D interpolation during rotation and ray-tracing, reducing computational burden. Using an NVIDIA C1060 card, a speed up of 2.2 times compared to the Siddon’s algorithm on the same GPU has been observed.

Wobbled Splatting algorithm has also been implemented on GPU (Spoerk et al., 2007), where each voxel is projected in the prospective geometry, during which the focal spot or the voxel location is randomly perturbed to reduce aliasing artifacts. The implementation is voxel parallel, in that each voxels is projected by a GPU thread. The voxel values at each detector pixel are then summed up using alpha blending, a functionality of the GPU for image rendering. An NVIDIA GeForce 7600 GS card helps to achieve a reduction of rendering time by about 70%–90% compare the same algorithm on CPU.

3.2 Monte Carlo photon transport in diagnostic energy range

One problem with the aforementioned ray-tracing approach for DRR calculations is that only the primary component corresponding to the x-ray attenuation process is considered. In reality, scatter component also exists in an x-ray projection image due to the scattered photons detected at pixels. The realistic computation of a projection image calls for Monte Carlo (MC) simulations of the photon transport process. In addition, other tasks, such as accurately computing radiation dose from CT scans, also require photon transport simulations using MC methods. Since a large number of photons are needed to get a reliable result from the MC method, GPU can be of great help to significantly improve the computational efficiency.

Conventional wisdom dictates that MC-based particle transport is highly parallelizable, as particles can be simply distributed to different processing units and transporting them is expected to be independent. Yet, this fact does not hold for the SIMD structure of GPU. In fact, because particle transports at different threads are statistically independent, the instructions could be very different at any moment of the execution, causing the aforementioned thread divergence problem. Moreover, the random visit to GPU’s memory also poses challenges to achieve high efficiency.

Badal and Badano first implemented the photon transport process on a GPU platform (Badal and Badano, 2009). In their code named MCGPU, a number of GPU threads were launched to transport a set of photons simultaneously, one for each photon. The photon transport followed the same physics of PENELOPE (Salvat et al., 2009). A maximum 27-fold speed up factor has been observed using an NVIDIA GeForce GTX 295 dual-GPU card compared to the Intel Quad Cor 2 CPU at 2.66 GHz.

GPU-based photon transport was also studied by Jia et al. (2012d) with a focus on computing radiation dose received by a patient in a CT/CBCT scan, yielding a code called gCTD. While gCTD still used one thread per photon scheme, the transport process was optimized for GPU programming. An efficient sampling method of particle scattering angle was invented to replace the rejection method used in many other CPU-based photon transportation code. Moreover, gCTD supported the simulation of CT/CBCT scanners to a high level of realism, including the modeling of source spectrum and fluence map etc.. It was observed that gCTD is about 76 times faster than EGSnrc in a realistic patient phantom case and the radiation dose to a patient in a CBCT scan can be computed in ~17 sec with less than 1% relative uncertainty using an NVIDIA C2050 card.

Another package called gDRR was later developed by Jia et al. (2012c) for accurate and efficient computations of x-ray projection images in CBCT under clinically realistic conditions. In addition to the same MC simulation module used in gCTD, gDRR also contained a polyenergetic DRR calculation module using the incremental Siddon’s algorithm. Smoothing of the scatter signal generated by MC simulations was also supported and the noise signal was computed as well. On an NVIDIA GTX580 card, the computation time per projection was up to ~100 sec depending on the image resolutions, majority of which came from MC photon transport. This computation time was much shorter than the corresponding CPU time (usually hours).

3.3 Analytical CBCT reconstruction

CBCT (Jaffray et al., 1999; Jaffray et al., 2002) has been widely used in radiation therapy to provide image guidance. The reconstruction problem, namely to compute the volumetric image data based on x-ray projections obtained at various projection angles, is one of the central topics. The current clinical standard algorithm is filtered back projection, also known as FDK algorithm (Feldkamp et al., 1984). Because of the simplicity of this algorithm and its suitability for GPU-based parallelization, it is one of those algorithms in radiation therapy that was first implemented on the GPU platform. In this algorithm, there are three main steps: 1) multiplying each projection pixel by a factor determined by the geometry, 2) convolving the projection with a ramp filter, and 3) backprojecting the filtered projections along the CBCT x-ray lines. In this process, the first step can be easily implemented using one GPU thread per pixel, the second one can be accelerated by GPU-based convolution operations (Podlozhnyuk, 2007) or fast Fourier transformation (FFT), and the last one is performed in a voxel parallel manner, i.e., one GPU thread per voxel. The filtered data at the projection location of each voxel, which is not necessarily on the pixel grid, is needed in the third step. Hence, 2D interpolation is necessary, which can be accomplished by GPU-supported hardware bi-linear interpolation.

Because there is a large body of literatures on this topic, we only list a few representative ones here. Among the three key steps of the FDK algorithm, the backprojection step is the most time consuming. In light of this observation, this step has been ported to GPU (Sharp et al., 2007; Xu and Mueller, 2007; Noel et al., 2010), while the filter part was conducted on the CPU side using FFT. Okitsu et al. (2010) implemented the entire FDK algorithm on GPU, where the filtering part is accomplished by a direct summation. For another image modality called digital tomosynthesis, whose reconstruction formula is identical to that for CBCT, GPU has also been applied. The most computationally intensive backprojection part was first ported to GPU (Yan et al., 2007; Yan et al., 2008) and then the filtering part was later realized via GPU-based FFT using the CUDA library CUFFT (Park et al., 2011).

3.4 Iterative (4D)CT/CBCT/DTS reconstruction

Iterative approaches form another category of algorithms to solve the reconstruction problem. Due to its better image quality and potential to reduce required measurements and hence the associated radiation dose, it has attracted a lot of attentions recently.

Compared to the analytical reconstruction approach, in which the volumetric data is obtained via a closed form expression, iterative methods reconstruct the data in an iterative manner and in each iteration step, the solution is updated according to a certain algorithm. By nature the iterative reconstruction approach is a sequential operation, and the focus of acceleration is to parallelize the computations within each iterative step. In a CBCT reconstruction problem, there are data in two domains, namely projection domain and solution image domain. A projection operator relates them. The key to accelerate an iterative reconstruction process is to speed up the computations of the mapping between the two domains.

Several classical iterative algorithms for the CBCT reconstruction problem were first implemented on GPU. In general, these algorithms update the solution by iterating three steps: 1) forward projecting the current solution, 2) estimating correction factors based on the computed and the actual projections, and 3) backprojecting the correction term to update the solution. The step 1) is a DRR calculation and can be parallelized in the way mentioned previously. The step 3) is accelerated in a voxel parallelization akin to that in an analytical reconstruction. Algorithms that have been successfully implemented on GPU include simultaneous algebraic reconstruction technique (SART) (Mueller et al., 1999; Mueller and Yagel, 2000; Xu and Mueller, 2005) and expectation maximization (EM) (Xu and Mueller, 2004, 2005). The implementation was further refined by properly grouping a subset of ray-lines (OS-SART), leading to a better performance (Xu and Mueller, 2004; Xu et al., 2010).

Recently, Compressive Sensing (CS) (Candes et al., 2006; Donoho, 2006) based iterative reconstruction methods have demonstrated its tremendous power to restore CBCT images from only a few number of projections and/or projections at high noise levels. Accelerating algorithms of this type has become a major focus due to the potential benefit of imaging dose reduction. Compared to those classical iterative reconstruction algorithms, CS-based ones incorporate prior knowledge regarding the reconstructed image property and hence pose strong assumptions about what the solution should look like. As such, some steps enforcing the image properties, called regularization steps, exist in addition to those in a classical iterative reconstruction method. These regularization operations usually stem from image processing techniques. Because they act in the volumetric image domain, voxel parallelization can be utilized.

Among a number of different methods, Total Variation (TV) is the most popular one, which assumes that the solution image is piece-wise constant. Sidky et. al. first implemented the TV regularization step on GPU (Sidky and Pan, 2008; Bian et al., 2010). A gradient descent method was used in their implementation and the evaluation of the gradient was particularly suitable for GPU parallelization due to the independence of operations at each voxel. Later, the full reconstruction process was implemented on GPU. Specifically, Xu and Mueller (2010) inserted the TV minimization in each iteration of their OS-SART loop. Jia et. al. treated the reconstruction as an optimization problem in which the objective function contained both a least-square term to enforce the projection condition and a TV term to regularize the image (Jia et al., 2010b; Jia et al., 2011c). A GPU-friendly backprojection method was invented, and multi-resolution reconstruction technique was employed. All of these techniques considerably shortened the computation time to the scale of minutes on an NVIDIA C1060 card. A generalization of the TV function, called edge-preserving TV, was proposed by Tian et al. (2011b) to weight the TV term using adaptively determined spatially varying factors in order to prevent edge smoothing. Similar speed was observed. In addition, as opposed to enforcing the projection condition and the regularization in two alternative steps, Park et al. (2012) treated the two terms together and solved the problem with the Barzilai-Borwein algorithm. An improved efficiency was reported using an NVIDIA GTX 295 card. It needs to be mentioned that due to the algorithm nature, the computation time critically depend on many factors, such as image/projection resolution, iterative steps, stopping criteria etc.. The resulting image quality also varies accordingly. While GPUs greatly help reduce the computation time from hours to minutes, it is hard to compare the absolute efficiency of different GPU implementations in an objective manner.

Other types of regularization techniques have also been developed. Originated from image processing, bilateral filter is an edge-preserving non-linear filter that weights voxels similar in both the intensity and the special domain. This filter was used by Xu et. al. in their reconstruction framework together with the OS-SART algorithm (Xu and Mueller, 2009; Xu and Mueller, 2010). A more general form of this filter, non-local-means was also utilized by the same group (Xu and Mueller, 2010), where the weighting factors were obtained by comparing patches centering at each voxel, rather than the voxels themselves. Finally, another type of regularization method was invented based on the assumption that the reconstructed image has a sparse representation under the tight wavelet-frame basis (Jia et al., 2011a). The reconstructed image was found to maintain sharper edges compared to the classical TV method, and the reconstruction speed was not sacrificed. This algorithm was also implemented on a quad-GPU system recently (Wang et al., 2013). The frequent forward and backward x-ray projections were accelerated by distributing tasks corresponding to different projection angles among GPUs. A parallel-reduction algorithm was employed to accumulate data from all GPUs. The regularization step was achieved by having each GPU processing a sub-volume. Another acceleration factor of 3.1 was reported with two NVIDIA GTX 590 cards, each containing two GPUs.

Notably, with the greatly improved reconstruction speed, one can perform systematical studies involving a large number of CBCT reconstructions that were previously forbidden by the low computational efficiency. Yan et al. (2012) conducted a comprehensive study between the image quality and radiation dose in the low-dose CBCT problem using the TF model. Thousands of reconstructions were conducted in the study, leading to the conclusions that the dose can be reduced safely to a large extent without losing image quality and there exists an optimal combinations of the number of projections and the dose per projection for a given dose level.

CBCT generates a volumetric image of the patient body. Yet, when it comes to lung or upper abdomen area, respiratory motion blurs the image. To overcome this problem, 4D-cone beam CT (4DCBCT) was invented (Sonke et al., 2005), where a set of volumetric images are reconstructed, one corresponding to a respiratory phase. The extra temporal dimension in this problem inevitably increased the computational loads. One straightforward approach of 4DCBCT reconstruction is to restore image at each phase individually. The aforementioned GPU-based CBCT reconstruction algorithms are then trivially applicable.

Recently, it has drawn ones attention that utilizing the image correlations among different phases can greatly facilitate the reconstruction process, e.g. enhance image quality and improve convergence speed. In practice, this is realized by reconstructing all phases simultaneously using iterative algorithms, whereas image processing tasks at each phase using information from other phases are conducted frequently during the iteration process. The additional image processing costs, as well as the simultaneous reconstruction nature, call for GPU implementations. Because of the nature of image processing, these steps are typically parallelization friendly, where GPU threads process different voxel simultaneously.

A temporal non-local means (TNLM) method was developed by Jia et. al., where image content from the next and the previous phases are borrowed to enhance image quality. This method was first implemented in 4DCT context by Tian et al. (2011a) to reconstruct a transverse slice of a patient. It was then further refined in order to gain enough speed to solve the 4DCBCT problem (Jia et al., 2012b), where volumetric image reconstructions are needed. Algorithm implementation was fine tuned, so that the complexity was reduced from O(N³) to O(3N), where N is the number of voxels in each spatial dimension. It also employed a more coalesced memory access scheme to improve efficiency. About 1 min per phase reconstruction time has been reported using an NVIDIA C1060 card. Another algorithm in this category used spatial-temporal tensor framlet (Gao et al., 2012). In this approach, the four-dimensional tensor product of wavelet frame was applied to the spatial and the temporal dimensions. The matrix-vector operation in this method made it suitable for GPU parallelization. A total computation time of less than 10 min was reported when using an NVIDIA C2070 card.

3.5 Deformable registration

Deformable image registration (DIR) is another important problem in radiotherapy. It gains a lot of attentions recently in the context of adaptive radiotherapy, where DIR serves as a critical tool to establish voxel correspondence between planning CT and daily CT/CBCT in order to facilitate automatic segmentation and dose accumulation. Yet, the computation of DIR is usually intensive for high-resolution 3D images. The ill-pose nature of this problem requires complicated iterative algorithms with a large number of iteration steps to yield acceptable results. On the other hand, DIR is a perfect data-parallelization task, where deformation vectors at voxels can be computed almost independent of each other at each iteration step. This fact places GPU at a unique position to accelerate the problem.

The most widely explored DIR algorithm on the GPU platform is Demons (Thirion, 1998). Its popularity is mainly due to its simplicity and suitability for GPU parallelization. Specifically, the Demons algorithm has a closed form expression regarding how the deformation vector is updated at each iteration step based on the image intensities. The vector computation is local at each voxel, making the parallelization straightforward. Sharp et al. (2007) implemented this algorithm on an NVIDIA 8800 GPU using Brook, yielding 70 times acceleration compared to a CPU-based computation. An independent study was also conducted by Kim et al. (2007) using Cg and by Samant et al. (2008) using CUDA. Later, a systematic study was conducted by Gu et al. (2010) who implemented six different variants of the Demons algorithm on GPU. While the vector update formula are difference among these variants, the GPU code structure and parallelization scheme remain the same. A comprehensive study was conducted to compare these different versions. Recently, Gu et al. (2013) also generalized this algorithm into a contour-guided deformable image registration (CG-DIR) version, where the registration is performed in accordance with user specified organ contours. This is realized by regularizing the objective function of the original Demons algorithm with a term of intensity matching between the contour pairs. Because of the same algorithmic structure, the GPU implementation remains the same. The computation time is 1.3–1.6 times longer than that of the original Demons on the same GPU card.

Another challenging problem within the DIR regime is inter-modality registration. Of particular interest is CT-CBCT registration due to its potential applications in adaptive therapy. Aiming at this problem, Zhen et al. (2012) developed an algorithm named Deformation with Intensity Simultaneously Corrected (DISC). Under the Demons algorithm iterative structure, DISC performed an intensity correction step in each Demons iteration step to modify the CBCT image intensities to match intensities between CT and CBCT. The intensity correction of a voxel in CBCT was achieved by matching the first and the second moments of the voxel intensities inside a patch around the voxel with those on the CT image. This step was easily parallelizable due to the independence of processing among voxels. It took about 1 min to register two images of a typical resolution using an NVIDIA C1060 card. The much longer time compared to the original Demons on GPU was ascribed to the time-consuming intensity correction step, where complicated evaluations of statistical moments were performed.

3.6 2D/3D registration and one-projection CBCT

Another form of registration problem encountered in radiotherapy is the so-called 2D/3D registration, where a rigid or deformed vector field is determined in 3D image volume, such that the projected image under CBCT geometry matches 2D measurements. Problems as such are generally difficult, because of the nonconvex nature of the registration problem. Moreover, a big computation challenge comes from the repeated computations of forward or backward projections. Yet, similar to that in CBCT reconstruction problem, these two operations are suitable for GPU parallelization. Wu et al. (2009) first investigated the rigid 2D/3D registration problem with a focus on comparing different registration metrics for patient positioning in radiation therapy treatments. GPU-based DRR calculation was used to generate forward projections, where a speed up of ~50 was seen using an NVIDIA GeForce 8800 GTX card and the absolute computation time was reduced by an order of magnitude.

Li et. al. studied the deformable 2D/3D registration problem, with an attempt to reconstruct a volumetric 3D image corresponding to the 2D projection image by restoring the vector field between the target volume image and a reference CT image (Li et al., 2010; Li et al., 2011). An optimization problem was formed, in which the desired vector field would minimize the difference between the computed forward projection and the measured one. A gradient-based algorithm was employed to solve this problem, each iteration of which contained a multiplication of the forward projection matrix and a multiplication of its transpose. These operations were accelerated by GPU via a sparse matrix multiplication scheme (Bell and Garland, 2008). Other operations were vector-vector operations that were trivially parallelized on GPU. A high computational efficiency has been achieved on an NVIDIA C1060 card with an average run time of ~0.3 second, very promising for real time volumetric imaging.

3.7 Other image processing problems

Besides the aforementioned specific imaging problems, GPU has also been used to solve other image processing problems pertain to radiotherapy. The first example is denoising, namely removing noises from a given image. One of its applications in radiotherapy is to reduce noise levels in CBCT projection images acquired in low dose scans so as to improve the reconstructed CBCT image quality. As such, a 3D anisotropic adaptive filter has been developed (Maier et al., 2011). The most computationally demanding part in this algorithm was FFT, which was accelerated using JCUDA, the Java language of CUDA to enable GPU based FFT calculation. Other steps in the algorithm were easily parallelizable at pixel level, and the implementation was straightforward. With an NVIDIA C1060 GPU card, a 8.9-fold speed up compared to CPU implementation was achieved, which reduced the computation time from 1336s down to 150 s.

Image segmentation problem has also been accelerated using GPU. Zhuge et al. (2011) implemented a fuzzy connectedness-based segmentation algorithm on a GPU platform. In this algorithm, one of the sub-problems computed affinity between every pair of voxels in an image, which characterized the fuzzy relation between the two voxels. Because of the independence of the computation among different voxel pairs, GPU implementation was straightforward. Although another sub-problem requires Dijkstra’s algorithm, which was, however, not suitable for GPU, overall speed-up factors of 10~24 times were achieved on an NVIDIA C1060 GPU card over the CPU implementation, because of the dramatic acceleration in the first sub-problem.

4. Treatment-related problems

Treatment related tasks constitute another category of computationally intensive tasks in radiation therapy. Examples include radiation dose calculation, treatment plan optimization, and dose comparison. Because of the intensive computation nature, GPU has also been widely employed to solve problems here. We will discuss these applications in this section.

4.1 Non-MC dose calculations

Dose calculation plays a central role in radiotherapy. Its success dictates the entire clinical practice of radiotherapy treatment, ranging from pre-treatment planning to post-treatment verification. Classical correction-based methods are not computationally challenging enough to demand the utilizations of GPUs. More advanced model-based calculation methods can greatly benefit from GPU accelerations.

Popular model-based non-MC dose calculation algorithms are superposition/convolution (SC) algorithms and pencil beam (PB) algorithms. Both algorithms split a broad beam into small beamlets, and compute the total dose as a summation over dose from all the beamlets. SC and PB differ in how they handle the beamlet dose contributions. For SC-type algorithms for photon dose calculations, its basic idea comes from a physical picture of dose deposition, namely the total energy released per mass (TERMA) at each voxel is deposit to surrounding voxels through generated secondary particles. Hence, in an SC algorithm, TERMA is first computed via a ray-tracing algorithm along each ray line and final dose is obtained by a superposition-type operation to spread out the TERMA to nearby voxels. PB type algorithms, on the other hand, are phenomenological descriptions of the dose deposition. A quantity along the ray line is first calculated to characterize the overall dose variation along the depth direction, e.g. build-up in photon cases and Bragg peak in proton cases. This quantity is then spread out in planes perpendicular to the ray line via a certain kernel. Overall, the two types of algorithms attain very similar algorithmic structures that consist of two stages. The first stage involves computing quantities along the ray line, while the second one is 2D or 3D convolution or superposition type operations. Both steps are parallelizable and GPU-friendly.

SC type algorithm was first implemented on GPU by Jacques et al. (Jacques et al., 2008; Jacques et al., 2011; Jacques et al., 2010). In this implementation, an inverse TERMA calculation algorithm was invented by ray-tracing from each voxel back to the source to avoid discretization artifacts and memory writing conflicts occurred in forward ray-tracing TERMA calculations. It was also fully parallelized with a large degree of cache reuse. In the superposition stage, an inverse kernel formulation was employed where each voxel gathers dose contributions from surrounding voxels, enabling voxel-based parallelization and avoiding memory-writing conflicts. A multi-resolution superposition algorithm was used to reduce the algorithm complexity and mitigate the star artifacts due to finite number of angular discretization directions. A kernel tilting strategy was also implemented to account for slight direction change of the dose-spread kernel at each beamlet, improving calculation accuracy. On top of these, performance was optimized for CUDA, such as optimizing occupancy, synchronizing thread blocks, and using shared memory. A speed-up of over 100 over the highly optimized Pinacle (Philips, Madison, WI) implementation was observed on an NVIDIA GTX280 card, where the absolute computation time was about 1 second per plan. Later, Hissoiny developed another implementation of the SC algorithm on GPU (Hissoiny et al., 2010). Special function unit on the GPU was utilized to accelerate the computations of intrinsic functions, e.g. exponential function, using dedicated hardware. A larger number of ray directions were employed compared to the previous implementation by Jacques et al.. To further boost the computational efficiency, a multi-GPU solution was also developed, where the dose calculation array was split between GPUs. An overhead was observed due to the initial data loading to all the GPUs, as well as the final accumulation of results. Using the same GPU card, NVIDIA GTX280, acceleration ratios of 27.7~46 times were observed compared to an Intel Xeon Q6600 CPU for TERMA calculations and up to 900 times for the convolution step. The overall 3D dose calculation time was about 2.8 sec/beam. Using two GeForce 8800GT cards, another factor of up to 1.6 were achieved. SC type algorithm was also employed by Lu (2010) and up to ~16 times acceleration factor was reported in real clinical cases using an NVIDIA GTX295 card compared to a cluster with 56 2.66GHz CPUs.

As for the PB algorithms, Gu et al. (2009) first implemented an finite-size pencil beam (FSPB) algorithm on GPU, where the 2D dose spread kernel was modeled using a set of error functions. The algorithm sequentially computed dose from each beam angle. For each beam, a ray-tracing operation was first launched, in which each GPU thread built a lookup table of radiological depth as a function of physical depth for each beamlet. A second stage of dose spread was performed in a voxel-parallel fashion, where a voxel looped over all the beamlets nearby to accumulate contributions from each of them. A speed-up factor of ~400 times were achieved for the dose calculation part using an NVIDIA C1060 card. However, it was also discovered that data communication time between CPU and GPU was comparable to dose calculation time, reducing the speed-up factor to ~200. The implementation was also tested on other GPU cards and the computation time for GTX285, C1060, and S1070 were almost identical, and were over seven times shorter than that on a low end GeForce9500 card. Later, the algorithm was further improved to incorporate 3D density correction (Gu et al., 2011a). A different kernel function form was utilized with parameters fitted for different materials. Better accuracy was observed, whereas implementation structure remained unchanged.

Another dose calculation algorithm, Fluence-convolution broad-beam (FCBB) was proposed by Lu et. al. in his non-voxel-based broad-beam framework in Tomotherapy treatment planning system (Lu, 2010; Lu and Chen, 2010). The algorithm reversed the two steps seen in the aforementioned CS or PB algorithms. It first conducted a convolution in the 2D fluence map domain using a lateral spread function and then ray-tracing with radiological distance and divergence correction. In terms of GPU implementation, the ray-tracing part was handled by launching multiple GPU threads simultaneously, akin to the strategy in a CS or PB algorithm. While there was no direct report of acceleration ratio of this calculation by using GPU, when the algorithm was embedded in the treatment plan optimization process, up to 3 times overall speed up was achieved using an NVIDIA GTX295 card compared to a Tomotherapy cluster with 56 2.66GHz CPUs, which translated to ~150 times compared to a single GPU (Lu, 2010).

Dose calculations for proton therapy using PB approach became available on GPU recently (Fujimoto et al., 2011). The algorithm structure was very similar to that in the FSPB model. The implementation aimed at speeding up the 2D dose spreading part, since it dominated the computation time in CPU. As such, a voxel-parallel approach was employed to accumulate dose from each beamlet. Frequently used error function values were pre-computed and stored in tables. Performance was improved by using this table lookup approach. The new algorithm showed 5–20 times faster performance using an NVIDIA GeForce GTX 480 card in comparison with the Intel Core-i7 920 processor.

4.2 Monte Carlo dose calculations

Monte Carlo (MC) simulation is considered as the most accurate dose calculation method due to its capability of faithfully capturing real physical interaction processes. Because of the statistical nature of this method, a large number of particle histories are needed in one simulation to yield a desired precision level. Despite the vast developments in computer architecture and the increase of processor clock speed in recent years, the efficiency of currently available full MC dose engines is still not completely satisfactory for routine clinical applications. Recently, a lot of efforts have been spent on the developments of GPU-based MC dose engines. Yet, because of complicated particle transport physics, as well as sophisticated parallelization scheme required to achieve a decent speed up, GPU-based MC is arguably the hardest problem among those reviewed in this article. To date, a set of MC dose calculation codes have become available. They differ from each other in terms of the level of physics employed, the functionality supported, and the code optimization approaches.

The idea behind an MC simulation is simple: tracking particle propagation according to physical models. It was the conventional wisdom that MC is extremely parallelization friendly, as different computing unit can handle different particle transport independently. This is indeed the case for CPU cluster based MC simulations, where almost linear speed-up has been observed with respect to the number of processors (Tyagi et al., 2004). Nonetheless, the SIMD programming mode of a GPU and the randomness behind a MC simulation create such a big conflict that it is very hard to achieve high efficiency in MC dose calculation. In fact, Jia et al. (2010a) developed the first GPU-based MC dose calculation package gDPM, where all GPU threads were treated as if they were independent computational units, each tracking the entire history of a source particle as well as all the generated secondary particles. Despite hundreds of threads available on a GPU card, only 5.0~6.6 times speedup was observed.

There are two types of GPU thread divergence that one may encounter in a MC simulation for dose calculation, i.e. due to the different particle transport physics for different types of particles (type I), and due to the randomness of the particle transport process (type II). Hissoiny et al. (2011a) developed an MC dose calculation package, GPUMCD, where it was proposed to separate simulations of electrons and photons to remove the type I thread divergence. By smartly placing the particles to be simulated into two arrays holding electrons and photons separately and having the GPU to simulate particles in only one array at a time, a considerable amount of speed up was achieved. It only took ~ 0.3 s to simulate 1 million electrons or 4 million photons in water for monoenergetic beams of 15 MeV using an NVIDIA GTX 480 card. Another 1.9 times acceleration was further achieved with dual NVIDIA C1060 cards compared with single C1060 card. GPUMCD was developed based on existing physics extracted from other general purposed MC packages, and its accuracy was established when comparing with EGSnrc (Kawrakow, 2000). This package was later extended to support more functionalities, including brachytherapy dose calculation (Hissoiny et al., 2011b) and photon/electron transport in magnetic fields (Hissoiny et al., 2011c).

Later, in the second version of gDPM, Jia et al. (2011b) utilized the same strategy to separate transports of particles of different types and found a dramatic acceleration. Speedup factors of 69.1 ~ 87.2 were observed against a 2.27GHz Intel Xeon CPU processor using an NVIDIA C2050 card. The development of gDPM v2.0 also emphasized on its clinical practicality by integrating various key components necessary for dose calculation in radiotherapy plans. An IMRT or a VMAT plan dose calculation using gDPM can be achieved in 36.1~39.6 sec with a single GPU card with less than 1% average uncertainty. Multi-GPU implementation of gDPM has also been developed, achieving another speed-up factor of 3.98~3.99 compared to a single GPU using a 4-GPU system. Recently, the third version of gDPM was released with the capability of loading source particles from a phase space file (Townson et al., 2013), permitting dose calculations with realistic linac models.

Another MC simulation package for photon-electron transport, GMC, has also been developed (Jahnke et al., 2012) based on the electromagnetic part of the Geant4 MC code (Agostinelli et al., 2003). It aimed at alleviating the type II thread divergence problem. An electron trajectory in a simulation consists of a large number of small steps separated by voxel boundaries or discrete interaction sites. As opposed to having a GPU kernel simulating a full trajectory of an electron as in GPUMCD and gDPM, a GPU kernel in GMC transported an electron by only one step. Such a kernel was repeatedly invoked to move the electron forward. Compared with the CPU execution of Geant4 on a 2.13GHz Intel Core2 processor, a speed-up factor of 4860 was reported on an NVIDIA GTX 580 card. This enormously large speed-up factor can be partly ascribed to the slow Geant4 simulations on CPU.

Meanwhile, GPU-based MC simulations for proton dose calculations also become an active research topic. Kohno et al. first developed a simplified MC method (SMC) for proton dose calculations employing simplified physics (Kohno et al., 2003; Kohno et al., 2011). The dose deposition was determined by a water equivalent model (Chen et al., 1979) based on the measured depth-dose distribution in water. Multiple Coulomb scattering of the proton was also modeled. This simple model made it compatible with GPU’s SIMD structure, where each GPU thread independently performed the same instructions but using different data according to the current proton status. High speed shared memory was utilized in the implementation. A speed-up factor of 12~16 compared to CPU implementation has been observed in real clinical cases and it only took 9~67 seconds to compute dose in a clinical plan with acceptable uncertainty on an NVIDIA Tesla C2050 GPU.

Another GPU-friendly MC simulation strategy is track-repeating (Li et al., 2005) and is employed by Yepes et. al. in proton dose calculations (Yepes et al., 2009; Yepes et al., 2010). In this strategy, a database of proton transport histories was first generated in a homogeneous water phantom using an accurate MC code such as Geant4 (Agostinelli et al., 2003). For dose calculation in a patient case, the track-repeating MC calculated dose distributions by selecting appropriate proton tracks in the database and repeated them with proper scaling of scatter angles and track lengths according to the patient body materials. This method was computationally efficient, as it avoided the sampling of physical interactions on the fly. It also attained a computation mode compatible with the SIMD model, since each GPU thread essentially performed the same operations at all the time, i.e. repeating a track. In practice, a 1% precision can be accomplished in less than 1 minute with a dual GPU system equipped with Geforce GTX 295 GPUs, a speedup factor of 75.5 with respect to the same CPU-based implementation.

The first full MC dose calculation package for proton therapy was developed by Jia et al. (2012a), which tracked protons according to realistic physical process on the fly, each with a GPU thread. The accuracy of gPMC has been established by comparing the dose calculation results with those from TOPAS/Geant4 (Perl et al., 2012), a golden standard MC simulation package for proton nozzle simulations and dose calculations. With respect to the efficiency, it took only 6~22 sec to simulate 10 million source protons to yield ~1% relative statistical uncertainty on an NVIDIA C2050 GPU card, depending on the phantoms and the energy. One interesting issue discussed by Jia et. al. was that there existed a memory writing conflict problem when using GPU for MC dose calculations (Jia et al., 2012a). Specifically, when two threads happen to deposit dose to a voxel at the same time, a memory writing conflict occurs and the energy depositions have to be serialized in order to obtain correct results. Even though this memory writing conflict occurs also in photon dose calculations (Jia et al., 2010a; Jia et al., 2011b), it is exacerbated in the context of proton beams, because protons travel almost along a straight line and protons in a beam marches in a synchronized fashion, leading to a high possibility of memory writing conflicts. Hence, computation time dramatically increases, as field size decreases. A multi-dose counter technique is recently proposed to mitigate this problem (Jia et al., 2013). By allocating multiple dose counters and assigning each dose deposition event randomly to a counter, the probability of the writing conflict is reduced, improving computational efficiency.

4.3 Treatment optimization

The ultimate goal of radiation oncology is to deliver a prescribed amount of radiation dose to tumorous targets while sparing surrounding normal tissues. Compared to conventional trial-and-error forward planning process, advanced inverse planning strategies offer a more effective way of designing plans. The large computational burden in this problem demands high computational powers, especially in the context of adaptive radiotherapy (Yan et al., 1997), where it is critical to solve the optimization problem in a timely fashion. Hence, GPU has also been brought into this context to accelerate the problems.

While the available optimization models are ample, the basic principles behind them are quite similar. In short, an objective function is first defined to quantify the quality of the dose distribution as a function of the decision variables, e.g. fluence map, according to some clinical considerations. By convention, the minimum of this objective function indicates the best plan quality. A certain kind of optimization algorithm is then employed to solve this optimization problem. As analytical approach for solving this type of questions is very rare, iterative algorithms are usually utilized. In this process, evaluation of dose distribution based on the current solution variables is the dominant part in terms of complexity, and acceleration on this part is the main research focus.

Men et al. (2009) conducted the first investigation regarding the use of GPU for fluence map optimization (FMO) problem. The objective function in this work is a simple quadratic function. A dose deposition matrix D is first generated using the aforementioned FSPB model (Gu et al., 2009), whose element at i, j represents the dose to the voxel i from the beamlet j at its unit intensity. With this matrix, a dose distribution given the current fluence map x is simply Dx. In essence, the computational bottleneck in this optimization problem become matrix vector multiplications. In fact, the matrix D is sparse, as each beamlet only contributes to a small subset of all voxels. This sparsity property has been utilized in the GPU implementation, where the matrix was stored in a compressed sparse row (CSR) format and a sparse matrix-vector multiplication function (Bell and Garland, 2008) optimized for the GPU platform was employed. One complication in this strategy is that, the CSR format is only suitable for the computation of Dx. However, a multiplication with D^T was needed in the optimization algorithm when evaluating gradient of the objective function. Men et. al. simply stored both D and D^T on GPU, both in CSR format, and use them when necessary, which apparently increased the memory burden. On an NVIDIA Tesla C1060 GPU card, the achieved speedup factor was 20–40 without losing accuracy, compared to the results obtained on an Intel Xeon 2.27 GHz CPU. A problem for a typical nine-field prostate IMRT case can be solved with in 2–3 seconds.

Based on this development, the same group also investigated a direct-aperture optimization (DAO) problem (Men et al., 2010a), where beam apertures and intensities were directly obtained. The objective function was again, taken as a quadratic form and was solved by a column generation algorithm (Men et al., 2007). At each iteration, a subproblem was first solved to determine an aperture shape based on the objective function gradient at each beamlet, and a subsequent master problem computed the intensity of each determined aperture. For the sub-problem, the gradient evaluation was handled in the same way as in the above FMO problem. The determination of the aperture shape was carried out by an algorithm that searched each MLC row, which was parallelized by assigning one row to each GPU thread. After the aperture was determined, the dose deposition matrix for the aperture was inferred based on the involved beamlets. It, as well as its transpose, was again stored in the CSR format, and the aperture intensity was determined in the master problem using quadratic optimization, where the same sparse matrix functions were called.

The same column generation method was also utilized to solve VMAT optimization problem (Men et al., 2010b). Yet, modifications of the algorithm were made to accommodate special constraints in this problem. First, only one aperture can be added to a beam angle subject to the restrictions posted by neighboring apertures due to maximum leaf-travelling speed constraints. This was handled in the sub-problem, where each GPU thread searches for leaf positions of the designated MLC leaf row with this constraint considered. Second, beam intensity should vary smoothly among beam angles. A smoothness term was hence added to the objective function, and was addressed in the master problem. An extremely high efficiency has been achieved, such that it took 18~31 seconds on NVIDIA C1060 GPU to generate a plan, in contrast to the computation time of 5~8 minutes on an Intel Xeon 2.27 GHz CPU. Lately, Peng et al. (2012) refined the algorithm and developed improved schemes to handle more realistic hardware constraints in a rigorous fashion. However, the structure of the GPU-implementation remained the same. Computation time of 25~55 sec on an NVIDIA C1060 card was reported to generate a clinical realistic VMAT plan of high quality.

Another optimization approach, called non-voxel-based broad-beam (NVBB) framework, was developed by Lu (2010). This algorithm directly optimized with respect to machine parameters. It computed the dose corresponding to the current machine parameters using the aforementioned FCBB algorithm (Lu and Chen, 2010), and hence eliminated the necessity of storing the dose deposition matrix. During the iteration process, a more accurate SC-based dose calculation was frequently performed to compensate any inaccuracy introduced by the FCBB algorithm. Because the whole algorithm involved repeated dose calculations, the calculations greatly benefit from GPU. Using a single NVIDIA GTX295 card, it was found that the NVBB optimization process for real clinical cases was speed up by up to ~16 times versus the one on a CPU cluster with 56 CPUs of 2.66GHz.

4.4 Gamma-index calculation

Gamma-index (Low et al., 1998; Low and Dempsey, 2003) is a useful utility in radiotherapy for dose comparison. The computational intensive nature makes this metric clinically only applicable in 2D dose comparison cases. Recently, Gu et al. (2011b) first utilized GPU to substantially improve the computational efficiency, especially for 3D gamma-index calculations. The basic idea behind this implementation was the geometric interpretation of the gamma index (Ju et al., 2008), where the gamma index at a dose point on a reference dose grid is regarded as the minimum distance from this dose point to the surface formed by the test dose distribution. Because of the independence between gamma index evaluations at each dose point, it is natural to parallelize the computation with each thread for a dose grid point. A radial pre-sorting technique was also invented to group the computations for voxels with similar gamma index values together. This strategy ensured that concurrently launched GPU threads had similar lifetime, avoiding losing computational efficiency due to few long-living threads. It was found that the gamma-index calculations can be finished within a few seconds for 3D cases on one NVIDIA Tesla C1060 card, yielding 45~75 times speed-up compared to that on Intel Xeon CPU. Later, Persoon et al. (2011) conducted a similar study, and the texture memory was utilized to improve memory access efficiency. Acceleration factors of ~60 times were observed in phantom and patient cases using an NVIDIA Tesla C2050 card compared to Intel Xeon 2.66GHz CPU.

5. GPU vs. other architectures

5.1 Other typical architectures

As discussed in this article, using GPU is a cost efficient method to implement very fast solutions. However, there are alternative processor architectures that have been used to build computer systems. The most prominent alternative is to exploit the capabilities of a modern CPU.

Algorithms for the CPU have been developed since the early days of modern radiation therapy (Webb, 1989). In those days, GPUs or similar parallel architectures have not become popular. Serial processors dominated the market while the industry was focused on steadily improving the clock cycle speed and functionality of the processors. This trend has changed in the last decade due to a number of technical limitations. Nowadays, high performance is achieved on account of their ability to process instructions in parallel on several levels. Modern CPUs consists of multiple cores that are replicated together with a dedicated L2-Cache on the processor die. Each core comprises both, a set of “classic” integer and float pointing processing units and a unit for processing wide data in a SIMD fashion, like GPUs do. Thus, CPUs are suited to solve serial, latency-oriented algorithms on the one hand, while it is possible to achieve a much higher performance by exploiting its parallel architecture. Several works have shown the parallel performance capabilities of the CPU. Shackleford et al. (2010) found a speedup factor of only 1.88 comparing a GPU implementation with an optimized multi-threaded CPU implementation for a B-spline registration algorithm. Cabello et al. (2012) achieved a speedup of 2.5 for a 3D PET reconstruction implementation. Hofmann et al. (2011) even could not get any performance benefit using the GPU. In the field of treatment planning, there are only a few publications that investigate the full performance of a single CPU. Weng et al. (2003) investigated a vectorized implementation of an MC code for radiotherapy treatment planning dose calculation. He could achieve a speedup of 1.5 using an early version of the SSE extension on CPUs compared to using the conventional float point unit. Ziegenhein et al. (2013) showed that IMRT treatment planning based on a quadratic objective function with pre-calculated dose influence data is a strong memory bound problem on the CPU. He optimized the implementation on CPU and achieved over 90% of the theoretical peak performance of the CPU-based planning system.

To yield a shorter runtime for a given problem, multiple CPUs are often configured within one computer system. These systems could comprise 2, 4 or 8 processors which all share a common main memory. Bangert et al. (2012) showed that the IMRT planning algorithm introduced by Ziegenhein et al. (2013) scales on these shared memory systems, which achieved clinical planning time of about 1 second. Configuring a system with more than 8 processors is not possible with common off-the-shelf CPU hardware. More parallel processing resources can be employed by interconnecting many of these shared memory systems via a fast network. Usually, in these cluster configurations, each node comprises only 2 or maximally 4 CPUs for economic reasons. Lu (2010) mentioned a therapy planning framework for Tomotherapy on such a distributed system. He introduced a non-voxel based approach on GPUs that was compared to a commercial voxel based algorithm on a 14-node cluster with 56 CPUs.

Some recent publications have also investigated the benefit of using cloud computing for solving coarse-grained parallel problems in radiation therapy. Cloud computing (Armbrust et al., 2010) has the advantage that computational resources are provided “on-demand”. Keyes et al. (2010) first ported dose calculations into a cloud environment and the computation time was explained by a theoretical model, demonstrating the efficiency improvement using multiple nodes. Poole et al. (2012) found that the computation time decreases approximately with 1/n, where n was the number of parallel machines used. The simulation cost was found to be optimal when n was a factor of the total simulation time in hours. Pratx and Xing (2011b) achieved a similar result by porting an MC321 MC package to a cloud environment using MapReduce technique. They found a 1258x speedup on 240 cluster nodes compared to a single threaded MC program. In addition, this work showed that cloud computing based on MapReduce technique was fault tolerant: Even if 50% of the nodes were shut down, the cloud is able to compensate for that and delivers the correct results.

In addition to CPUs, we would like to mention field-programmable gate arrays (FPGAs) as another alternative architecture for high-performance computing. As the name suggests, FPGAs contain fully configurable logic blocks. In contrast to conventional processors, no additional software is needed, and the configurable logic implements the desired algorithm itself. This leads to a high computing performance with low energy consumption and allows for a very short response time to I/O interfaces. The potential of FPGAs was illustrated in the work of Luu et al. (2009) for implementing a MC simulation of light absorption for photodynamic cancer therapy. The authors reported a speedup of 28x compared to an Intel Xeon 5160 server processor. In another work, Pasciak and Ford (2008) present an MC electron transport simulation for microdosimetry and radiation biology on FPGAs. They claimed a speed-up of more than 500 for a test case that simulates an electron pencil beam incident on cell nuclei.

5.2 Comparisons of GPU with other architectures

The most popular architecture for tackling radiation therapy problems is the CPU. The key features of a GPU and a CPU are listed in Table 2 on the examples of NVIDIA’s K20 and Intel’s Xeon E5-2687W server processor. While the GPU is a massively parallel architecture employing thousands of arithmetic cores, the CPU comprises only a few of them. This pays off in performance. The theoretical single precision performance of a GPU is about 3950 GFLOPS (giga floating point operations per second) while the CPU only achieves 486 GFLOPS. On the memory side, professional GPUs are equipped with a fast GDDR memory, although the size is limited to a few GBs. In contrast, a CPU can be configured with several hundred GB of memory. The clock speed of the GPU is relatively low in order to limit the power consumption of this device. Therefore the energy efficiency is 12 times better.

Table 2.

Comparing high-end products of CPU and GPU.

	#Cores	Clock Speed (GHz)	Memory Size (max) (GB)	Efficiency (GFLOPS/Watt)	Memory Bandwidth (GB/s)	Single Precision Performance (GFLOPS)	Double Precision Performance (GFLOPS)
Intel Xeon E5-2687W	8	3.1/3.8	750	1.4	51.2	486	243
NVIDIA GPU K20	2688	0.732	6	16.80	250	3520	1170

By comparing the raw specifications of GPUs and CPUs, one can see that the GPU is approximately 8 times (for computation-bound algorithms) and 5 times (for memory-bound problems) faster than the CPU. These numbers reflect the theoretical comparison between the two platforms in terms of computational capability. In other words, if there were an algorithm that is suitable for both the GPU and the CPU platform, and it is implemented in an optimal manner on both of them, the expected efficacy gain on GPU should be very close to the above-mentioned numbers. Nonetheless, it is very rare, if not impossible, to find such an algorithm. In fact, apart from some extreme cases, e.g. MC particle transport, many problems in radiotherapy are very GPU-friendly. There usually exist some natural ways to break the computations into small pieces, e.g. according to voxels or pixels. This fact allows a straightforward implementation on GPU, which typically does not require deep level tuning of the GPU code to achieve a decent speed up comparing to a simple CPU implementation. It is true that carefully optimizing on the CPU side will also improve the code efficiency there. Yet, the required effort is typically not less than optimizing a GPU code, and the CPU code optimization also demands for the knowledge about the chip and memory structure, which a typical medial physics researcher does not have.

A CPU cluster consists of multiple computer systems that are connected to each other via a fast network. A fully equipped cluster is relatively expensive compared to a shared memory system or a GPU and has to be maintained by a professional. Furthermore, most of the cluster resources are not used all the time. It is believed that the utilization of clusters employed in data centers ranges from 5% to 20% on average (Rangan, 2008; Siegele, 2008). This is because a computer cluster at a service center is installed for a certain (estimated) peak workload. Real-world average workloads are often smaller by a factor 2 to 10 (Armbrust et al., 2010), so that cluster resources are idle for a significant amount of time. Moreover, unlike problems in fundamental sciences, radiotherapy problems are typically of intermediate sizes. When putting them on a cluster, the data communication overhead may occupy a significant portion of the total execution time, limiting the potential to achieve high efficiency.

Cloud computing overcomes the low-utilization drawback of a cluster by its “pay-as-you-go” policy. The user pays for time and the number of nodes that are requested. However, the data communication overhead still remains. The available work (Keyes et al., 2010; Pratx and Xing, 2011b; Poole et al., 2012) showed that cloud computing is feasible for a MC dose calculation. This was possible, because the MC dose calculation is an embarrassingly parallel computing problem, in which inter-CPU data communication is very minimal. In contrast, it is unlikely for problems that employ a more complex communication scheme to largely benefit from the apparent infinite scaling in the cloud.

6. Discussions and Outlook

In retrospect, GPU has been employed in a wide spectrum of radiotherapy physics problems and great success has been achieved in terms of accelerating those computationally challenging problems. Despite its short history, the achievements are significant. The observed efficiency, as well as the maintained accuracy, holds a great potential to bring those previously computationally unaffordable tasks to routine clinical practice. Nonetheless, we also keep in mind that GPU technology is still at its infant stage. Challenges and opportunities co-exist. Before the conclusion of this paper, we would like to discuss a few points regarding the future of this novel emerging technology in radiation therapy.

6.1 Further requirements

Single-precision vs double-precision float point data

First of all, almost all of the works discussed in this article used single-precision float point data type to represent rational numbers. This is mainly because GPU has better support for single-precision operations than double-precision ones in terms of efficiency. Take a widely used NVIDIA Tesla C1060 card as an example, its double-precision processing power is only 77.8 GFLOPS, less than one tenth of the single-precision processing power of 933.1 GFLOPS. This fact originates from the main function of GPU, namely computer graphics, for which single-precision is sufficient to render high-quality images. Nevertheless, when GPU enters the scientific computing regime, the relatively low precision becomes a concern. Especially in some problems where repeated operations may amplify small errors caused by machine precision, double-precision float number is of high desire. Examples include MC dose calculations, where small amount of dose is deposited for billions of times, and solving a large linear system in an iterative manner, where the final result precision is governed by machine precision due to the inherent properties of the problem (Golub and van Loan, 1996). On the other hand, it is encouraging to observe that more and more GPU cards have increasingly improved double-precision capability. Although the difference in processing power between the two precisions is still large, it is not as astonishing as it was, especially for those GPUs designed for scientific computing purpose. In a recent NVIDIA K10 GPU card, the double-precision processing power is about one quarter of that of single-precision (1.17 Tflops vs 4.11 Tflops). Given this fact, it will be feasible to develop some computation tools with double-precision, particularly for those tasks whose resulting precision may be critically dependent on the machine precision.

Further increase of efficiency

Another desire along the road of GPU adventure is to keep improving computational efficiency. In general, it is quite straightforward to port an existing CPU algorithm onto GPU and achieve acceleration to a certain degree. It is, nonetheless, quite hard to write a high-efficiency code that fully exploit the potential of a GPU. The latter requires understandings of the GPU architecture and programming mode, which allows for an optimization at a fine-grain level. Unfortunately, most of the researchers in radiotherapy who are currently developing GPU codes are not trained in this regard. It hence necessary to team up with computer science experts, particularly GPU experts, to develop highly optimized codes.

As for practical ways of improving code efficiency, they are apparently problem-specific. We have to analyze the algorithm structure in order to determine the corresponding GPU implementation. Here we only list a few general rules that one should keep in mind. (1) Design GPU-suitable algorithms. Algorithm acceleration is arguably the most effective way of boosting computational efficiency. While there are usually many algorithms conquering a given problem, selecting the one with a suitable structure for the SIMD processing mode of a GPU is important to achieve the best performance. In light of the dramatically different processing modes between CPU and GPU, it is also implied that some algorithms abandoned previously on CPU due to inferior performance may find its way on GPU. Hence, one has to specifically consider the GPU structure at the algorithm design stage. A good example is radiation dose calculation. While MC simulations encounter its own conflicts with the GPU’s SIMD mode, solving Boltzmann transport equation (Gifford et al., 2006) may be a good alternative due to the full matrix operations, which are particularly favored by GPU. (2) Reducing thread branching problem. This issue is and will remain the central problem given the specific hardware structure and SIMD mode of GPUs. Effective solutions vary among problems. It ranges from smartly coding to avoid if-else statements to changing the whole simulation scheme to force synchronization among threads. (3) Memory usage. Memory usage is another important aspect in GPU-based parallelization that potentially limits the performance. It is hence critical to understand the properties of each type of memory spaces on a GPU card and utilize them in an optimal fashion. For instance, a beginner tends to put all the data in the global memory. A small modification of binding data to texture memory would improve access efficiency by utilizing data caching. Sharing data among GPU threads is another effective approach to remove redundant data access. A good example is convolution operation of an image, where threads processing neighboring pixels share the use of common pixel data. Putting data in GPU shared memory effectively reduces the total number of memory visits to the slow global memory (Podlozhnyuk, 2007). Memory writing conflict is sometimes encountered in parallel processing. Designing algorithms to eliminate this issue is hence critical to avoid efficiency loss. For example, an inverse kernel formulation is employed in SC dose calculations for this purpose (Jacques et al., 2008; Jacques et al., 2011; Jacques et al., 2010). In addition, writing small GPU kernels is sometimes helpful, as large kernel would run out available register space on a GPU processor and directing those variables into global memory space will inevitably reduce the code efficiency considerably.

Multi-GPU also gradually came into the scene recently as another way to further boost computation efficiency, which adds one more layer of parallelization on top of the one within each GPU. Given the low cost of GPU cards and the feasibility of placing up to four cards in a workstation box, multi-GPU is practical. The parallelization among GPUs is very similar to conventional CPU-cluster-based processing. Hence, the programming can be handled by, for example, message passing interface (MPI) (Dongarra et al., 1994), where each CPU thread controls a corresponding GPU and inter-GPU data communication is conducted through the CPU. Lately, CUDA version 4.0 added a new feature to support multi-GPU parallelization by allowing universal addressing. This eliminates the need of explicit control of inter-GPU data transfer. However, the total number of GPUs supported in this scheme is limited. Similar to CPU-cluster based parallel processing, the efficiency gain from the multi-GPU system critically depends on the overhead associated with inter-GPU data communication. Among the very limited number of research projects on multi-GPU system, MC is the one that achieves easy accelerations. An almost linear speed up with respect to the number of GPU has been observed by Hissoiny et al. (2011a) and by Jia et al. (2011b). On the other hand, it may not be quite straightforward to accelerate calculations on other topics. In a recent paper reporting CBCT reconstruction using multiple GPUs, the data communication is found to occupy a relatively large amount of total computation time, limiting the advantages of multi-GPU (Wang et al., 2013). In short, the strength and weakness of multi-GPU is very similar to that for a CPU-cluster. Only when data communication overhead is small can we expect a large efficiency gain. It is a future topic to investigate the feasibility of using multi-GPU system for other problems in radiotherapy physics.

Portability

In terms of programming environment, CUDA developed by NVIDIA currently dominates the applications of GPU in scientific computing, such that majority of the works reviewed in this paper was developed in CUDA. Other languages/APIs employed by researchers include shadder, Cg, etc., developed by different vendors to specifically program their own GPUs. While these languages have fine controls of the associated hardware system, the developed applications based on them are hardly compatible with GPUs from different vendors. This fact poses large hardware dependence of the developed applications and limits their practicality. To a large extent, the nature of specific hardware and software dependence impedes the adoption of GPU technology into clinical practice, since vendors of clinical software are very often reluctant to tie their products to a specific hardware and software configurations. Recently, cross-platform programming language, e.g. OpenCL, gradually came into the scene and has attracted a great amount of attention. The supports of GPUs from different vendors, multi-CPUs, or even heterogeneous computing with combined CPU and GPUs make them very attractive in terms of developing hardware-independent solutions. Studies regarding the performance of OpenCL compared to other APIs yield controversial conclusions. While some of them indicate efficiency in OpenCL is hindered by the portability gain (Weber et al., 2011; Kakimoto et al., 2012; Pallipuram et al., 2012), others show that the comparisons are mostly unfair, and OpenCL gives comparable performance as long as all factors are considered for a fair evaluation (Fang et al., 2011; Su et al., 2012). It is hence interesting to keep track the developments of OpenCL, which may have a significant potential in achieving both portability and efficiency.

6.2 Clinical implementations

Despite the ample research developments in the past few years, clinical application of GPU in routine practice is few and far between. Besides the short history of GPU, this fact can also be ascribed to the following reasons. (1) Clinic-oriented software development. It is the ultimate objective to apply the developed tools in real clinical environments. Yet, very often the software is too complicated to be used by a normal user. For instance, some tools rely on fine-tuning of patient-specific parameters to yield a good result, which apparently unrealistic in some busy clinical workflow. Developing robust and easy-to-use software with the aim of clinical usage is of primary importance. (2) Clinical validations. The efficiency and accuracy of the available applications are usually only reported by the developers through publications. Systematic validations in clinically realistic contexts are hence needed to further test the benefits of these projects, their capabilities, as well as the limitations. Collaborative efforts are needed to draw fair conclusions. (3) System integration. The developed software is usually a single piece in a long chain of a clinical workflow. It is of importance to integrate it into the entire system to allow for clinical uses. As such, friendly and safe interface of the software is critical. Meanwhile, clinical software vendors are expected to play a key role in the clinical implementation process. Opening up interface with GPU-based applications will greatly facilitate this work. Nonetheless, GPU, as a special accelerator at its early age, has not received wide recognitions from vendors yet.

All of these issues call for serious efforts, combined from vendors, researchers, and clinical users to conduct high-quality implementations and comprehensive validations of GPU-based algorithms to permit the adoption of these potentially impactful researches in clinic.

6.3 Clinical impacts

Last, but not least, we believe that GPU will eventually find its fit into clinical practice of radiotherapy physics. It is apparent that GPU is capable of improving computational efficiency in a variety of problems. However, we believe the gains will be beyond merely efficiency. In fact, accompanied with its high efficiency, GPU will allow physicians and physicists in radiation therapy using more advanced but computationally intensive tools for better imaging, planning, and treatment accuracy. It will empower us with capabilities to accomplish tasks that were previously computationally prohibitive. It will also free us from limited computational power and facilitate novel developments. All of these aspects will potentially lead to measureable or even paradigm-shifting impacts. Here, we only list three example problems at the frontier of radiotherapy physics that may largely benefit from GPU-based processing.

The first example is low-dose CBCT reconstruction using iterative algorithms. Conventional analytical reconstruction algorithms (Feldkamp et al., 1984) requires high quality x-ray projection data acquired at a large number of directions, yielding too much radiation exposure to patients. Despite the great promise of iterative CBCT reconstruction in terms of dose reduction, the associated high processing time, e.g. hours, due to the repeated forward and backward projection operations makes these approaches clinically infeasible. The greatly reduced computation time using GPU, particularly multiple GPUs, have led to processing time similar to that of the analytical reconstruction algorithm, e.g. tens of seconds. This clears one of the most significant obstacles for the clinical introduction of iterative CBCT reconstruction, which will potentially offer a much safer image guidance technique to radiation therapy.

Another example is online adaptive radiation therapy (ART) (Yan et al., 1997). Because of inter-fraction anatomical variations, e.g. tumor shrinkage in response to radiation treatment, the treatment plan designed before the treatment course may lose its optimality as the treatment continues. It is desirable to frequently re-optimize the treatment plan according to the up-to-date patient anatomy. The technical challenges behind this idea is extremely large, especially for online ART, where a treatment plan should be designed in minutes, while the patient is laying on a treatment couch awaiting for the treatment. A sequence of operations, including image reconstruction, registration, dose calculation, optimization and quality assurance, are to be accomplished within this short scale of time. The recent developments of SCORE (SuperComputing Online Replanning Environment) system shed a light to this problem (Gautier et al., 2013). By integrating a series of GPU-based applications, all of these tasks are accomplished in a few minutes. Even though there is still a long way to go before SCORE is clinically adopted, online ART is likely realized with the aid of GPU technology.

Last, interactive treatment planning has also been proposed recently. Conventional treatment planning is a process iterating between a dosimetrist and a physician. A dosimetrist is involved in this process mainly due to the long process necessary to design a treatment plan and a physician cannot spend his valuable time to play with plan optimizations. It is, however, desirable to have the physician directly conduct the planning, as it is he who will evaluate the plan quality and make clinical decisions. The proposed interactive planning process enables a physician to interactively modify the plan. The underlying GPU system adjusts the plan to accommodate the physician’s specifications and display updated results in real time. This intriguing technology will potentially dramatically change the current treatment planning process.

In summary, GPU has offered us tremendous computational power to tackle problems that were conventionally considered too challenging to be solved. Its suitability for medical physics in radiotherapy and the great potential has generated ample research enthusiasm. While technical and clinical challenges remain to be conquered in this venture, we believe that GPU will play a critical role in the advancements of radiotherapy in near future.