Resonance Assignment of the NMR Spectra of Disordered Proteins Using a Multi-Objective Non-Dominated Sorting Genetic Algorithm

Abstract

A multi-objective genetic algorithm is introduced to predict the assignment of protein solid-state NMR spectra with partial resonance overlap and missing peaks due to broad linewidths, molecular motion, and low sensitivity. This non-dominated sorting genetic algorithm II (NSGA-II) aims to identify all possible assignments that are consistent with the spectra and to compare the relative merit of these assignments. Our approach is modeled after the recently introduced Monte Carlo simulated annealing (MC/SA) protocol, with the key difference that NSGA-II simultaneously optimizes multiple assignment objectives instead of searching for possible assignments based on a single composite score. The multiple objectives include maximizing the number of consistently assigned peaks between multiple spectra (“good connections”), maximizing the number of used peaks, minimizing the number of inconsistently assigned peaks between spectra (“bad connections”), and minimizing the number of assigned peaks that have no matching peaks in the other spectra (“edges”). Using six solid-state NMR protein chemical shift datasets with varying levels of imperfection that was introduced by peak deletion, random chemical shift changes, and manual peak picking of spectra with moderately broad linewidths, we show that the NSGA-II algorithm produces a large number of valid and good assignments rapidly. For high-quality chemical shift peak lists, NSGA-II and MC/SA perform similarly well. However, when the peak lists contain many missing peaks that are uncorrelated between different spectra and have chemical shift deviations between spectra, the modified NSGA-II produces a larger number of valid solutions than MC/SA, and is more effective at distinguishing good from mediocre assignments by avoiding the hazard of suboptimal weighting factors for the various objectives. These two advantages, namely diversity and better evaluation, lead to a higher probability of predicting the correct assignment for a larger number of residues. On the other hand, when there are multiple equally good assignments that are significantly different from each other, the modified NSGA-II is less efficient than MC/SA in finding all the solutions. This problem is solved by a combined NSGA-II/MC algorithm, which appears to have the advantages of both NSGA-II and MC/SA. This combination algorithm is robust for the three most difficult chemical shift datasets examined here and is expected to give the highest-quality de novo assignment of challenging protein NMR spectra.

Introduction

Resonance assignment of solid-state NMR (SSNMR) spectra of uniformly or extensively labeled proteins is a prerequisite for full structure determination (Comellas and Rienstra, 2013; Luca et al., 2003; McDermott, 2009). A set of 2D and 3D magic-angle-spinning (MAS) correlation experiments have now been well established on model proteins with high structural order (Böckmann et al., 2003; Castellani et al., 2002; Franks et al., 2005; Igumenova et al., 2004) and have been applied to structurally unknown proteins (Loquet et al., 2012; Wasmer et al., 2008). However, for disordered membrane proteins (Hong et al., 2012; Li et al., 2008) and fibrous proteins (Tycko, 2011), and for ordered but large proteins (Bertini et al., 2010; Shi et al., 2009), resonance overlap, protein motion and disorder still present significant challenges to SSNMR-based structure determination.

In general, NMR spectra with broad linewidths and resonance overlap can have more than one assignment solution. Moreover, certain segments of the protein can be conformationally polymorphic and hence can give rise to multiple peaks per atom. Manual assignment is usually ineffective for identifying all possible assignments in this type of experimental spectra. While various automated solution NMR resonance assignment programs have been reported, the majority of these programs were intended to rapidly assign a large number of cross peaks in multiple high-resolution 2D, 3D and 4D spectra (Baran et al., 2004; Bartels et al., 1996; Buchler et al., 1997; Hyberts and Wagner, 2003; Leutner et al., 1998; Moseley et al., 2001; Schmidt and Guntert, 2012). Only a few automated solution NMR assignment programs so far directly address the issue of assignment ambiguity and missing peaks (Coggins and Zhou, 2003; Olson and Markley, 1994).

To assign SSNMR MAS spectra, which usually have lower resolution than solution NMR spectra, Tycko and coworkers recently introduced a Monte-Carlo simulated-annealing (MC/SA) program (Hu et al., 2011; Tycko and Hu, 2010). This program searches for all allowed sequential assignments that are consistent with the amino acid types attributed to each recorded spin system and that are within the linewidths of the peaks. A generalized MC/SA algorithm, MCASSIGN2, optimizes the assignment by maximizing a score function S, which is defined to reward good connections (N_g) between different spectra and the number of used peaks (N_u), and to penalize bad connections (N_b) and “edge” assignments (N_e). The good, bad and edge connections have been defined in the original papers; briefly, they designate assignments of a residue that have consistent chemical shifts between different peak lists (good connections), that have mismatched chemical shifts between different peak lists (bad connections), and that either miss the peak in one of the spectra or cannot be tested for consistency because the neighboring residue’s peaks are missing (edges). The S score encapsulates these four objectives through four user-defined weighting factors, w₁-w₄:

$$S=w_1{N}_g-w_2{N}_b-w_3{N}_e+w_4{N}_u.$$ (1)

The MC/SA algorithm searches for all possible assignments that satisfy the peak lists within the specified linewidths, evaluates the goodness of each assignment in terms of S, and improves the solutions in the direction of maximum S. Solutions with N_b= 0 are considered valid, while solutions with N_b ≠ 0 violate the data and should be discarded by the user.

The MC/SA algorithm has been successfully applied to not only model proteins with microcrystalline order but also amyloid proteins with intrinsic disorder (Hu et al., 2011; Hu et al., 2011; Tycko and Hu, 2010), and is found to be effective in preventing assignment solutions to be trapped in a local optimum. However, the algorithm also has some weaknesses. First, MC/SA is not efficient in finding many different solutions because each run yields one assignment and there is no mechanism to prevent independent runs from giving the same results. Thus, a large number of runs are needed to obtain sufficiently diverse solutions. More importantly, the S score turns the inherently multi-objective problem into a single-objective problem, which can eliminate some good solutions while retaining inferior ones. Because the single score depends on the choice of the weighting factors, if the weighting factors are not chosen optimally for a specific dataset, the algorithm may end up with some invalid solutions or solutions that are not the best. For example, if we use the standard recommended maximum values of w₁ = 10, w₂ = 20, w₃ = 3, and w₄ = 1, two assignments with (N_g, N_b, N_e, N_u) values of (66, 1, 31, 82) and (64, 0, 34, 81) would have scores of 629 and 619, so the search process will attempt to change the second assignment towards the first to reach a higher score and thus move away from the valid (N_b= 0) solution. Although this problem can be ameliorated by changing the weighting factors, for example by increasing w₂ to penalize bad connections, the choice of the weighting factors requires prior knowledge of the protein structure and chemical shifts.

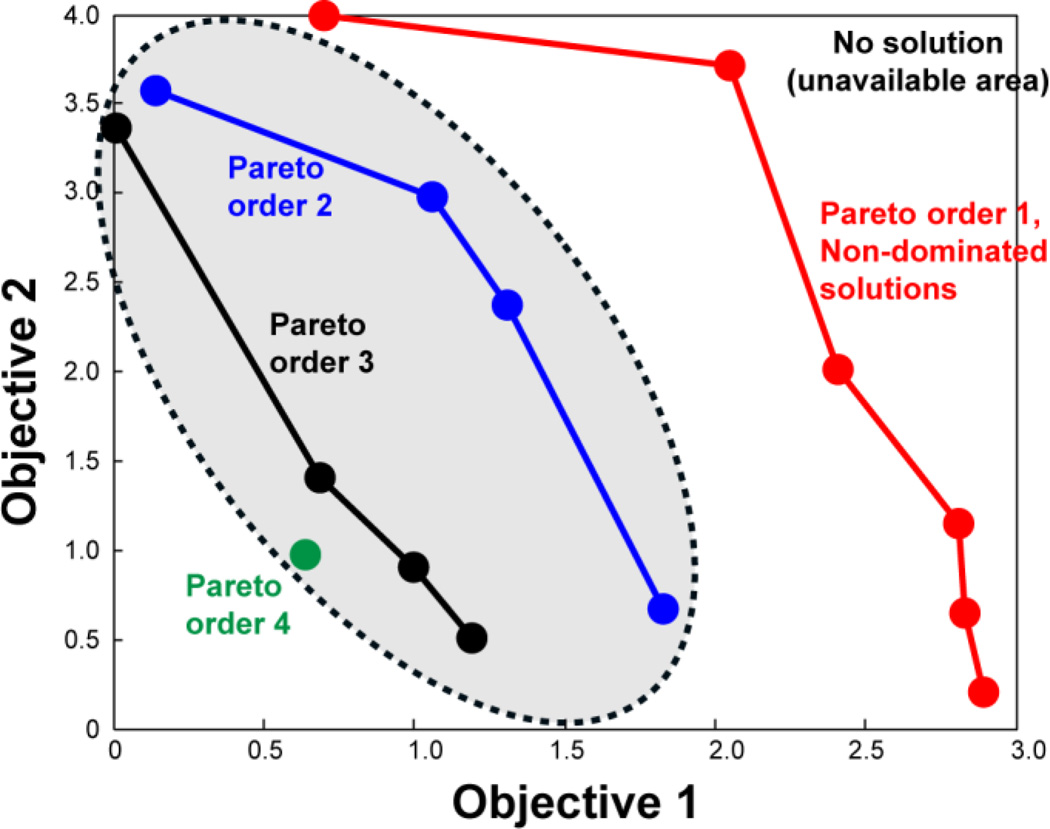
In general, the presence of multiple objectives in an optimization problem should produce multiple optimal solutions. In engineering and computer science, these multiple optimal solutions are known as Pareto-frontier solutions or Pareto-order-1 solutions (Deb et al., 2002). A number of multi-objective evolutionary algorithms (MOEAs) have been developed in the last decade to find as many Pareto-frontier solutions as possible (high diversity), in as short a time as possible (fast convergence speed), and in a single simulation run (Knowles and Corne, 2000). To better reflect the multi-objective nature of NMR resonance assignment, we now adapt and improve one of the widely used MOEAs, the non-dominated sorting genetic algorithm II (NSGA-II) (Deb et al., 2002). NSGA-II is a fast and “elitist” genetic algorithm that produces a large spread of solutions and has fast convergence towards the Pareto frontier in various problems. An “elitist strategy in the evolution process refers to the fact that the best individuals are always chosen for the next iteration step. Fig. 1 illustrates the principle of the non-dominated sorting approach to find different Pareto orders, using a dual-objective problem as an example. The statement that solution B is dominated by solution A means that no objective value of B is better than A, and at least one of the objective values is worse for B than for A. Conversely, the statement that a solution B is not dominated by solution A means that at least one objective value of B is better than A, or all objective values are equal between B and A (while the two solutions still remain distinct in content). Non-dominated sorting searches for solutions that are not dominated by any other solutions, which are Pareto-order-1 solutions. In Fig. 1, 6 solutions have Pareto-order 1, and are equally optimal. Pareto-order-2 solutions are only dominated by the Pareto-frontier solutions and can be found after the Pareto-frontier solutions are removed from the search pool. Pareto-order-3 solutions are only dominated by Pareto-order-2 and Pareto-order- 1 solutions, and so on.

Figure 1.

Principle of NSGA-II and Pareto orders for multi-objective optimization. Four Pareto orders in a two-objective maximization problem are illustrated. Shaded area contains the dominated solutions.

The standard NSGA-II algorithm works in the following way (Deb et al., 2002). First, a group of N distinct individuals (e.g. assignments) are randomly generated as the parent population P₀. Each individual in P₀ is evaluated for its “fitness”; those with lower Pareto order or better “fitness” will have a higher probability to transfer their “genes” to the next generation. From the parent generation, N₁ individuals (N₁ ≤ N) are chosen based on the fitness and changed using crossover and mutation operators (see Supplementary Information) to create a new set of N individuals that are different from each other and from those in the parent population P₀. These new individuals constitute the offspring generation Q₀. The parent and offspring populations are combined to create 2N individuals, which are sorted according to their Pareto order, and the “crowding distances” between them are calculated. The N individuals with the lowest Pareto orders and maximal crowding distances are chosen to form a new generation P₁. This process is repeated until the generation number reaches the specified number. Thus, by design, NSGA-II requires all individuals of the population to be different. The number of comparisons required to sort individuals into different Pareto orders scales as BN², where B is the number of objectives.

In this paper, we introduce a modified NSGA-II algorithm and a combined NSGA-II/MC algorithm for resonance assignment of protein NMR spectra. We test these two algorithms and compare their performances with MC/SA using published SSNMR protein chemical shift datasets with varying degrees of imperfection. Compared to manual assignments, the automated assignment strategies described here aim at generating a complete set of assignment solutions that are consistent with the data, and analyzing these solutions to obtain the probabilities of the assignments. Thus, we compare MC/SA and the two NSGA-II based algorithms on both the “correctness” and “completeness” of the possible assignment solutions. For high-quality peak lists, we find that all algorithms perform similarly well. But for difficult datasets containing missing peaks, large numbers of residues, and non-negligible chemical shift deviations between multiple spectra, the modified NSGA-II and the combination NSGA-II/MC algorithm show significant advantages in assignment diversity and accuracy over the MC/SA algorithm. In the three most difficult datasets, the combination algorithm consistently shows excellent and stable performances, and is thus most promising for de novo assignment of challenging protein MAS NMR spectra.

Methods

The NSGA-II and combination NSGA-II/MC programs are written in Fortran 95. The input for the two programs, similar to the MCASSIGN2 program, includes the amino acid sequence, peak lists of different spectra, and a connection table that specifies the relative residue number of the chemical shifts from different spectra. The sequence file contains the single-letter amino acid code of the protein sequence. The peak lists contain all the correlated chemical shifts observed in each spectrum and the corresponding half-widths at half maximum. In the Supplementary Information the peak lists for all six protein datasets (Tables S1-S7) used in this work are provided. The first line of each peak list gives the total number of peaks (i.e. the number of rows in the table) and the number of chemical shift columns. Values larger than 2000 indicate no chemical shifts; these entries are left blank in Tables S1-S7 for clarity. The last numerical column indicates peak degeneracy, which is unity here but can be a larger number to represent overlapped peaks. The last column of the peak lists contains the possible residue types. We use the PLUQ algorithm that we developed recently (Fritzsching et al., 2013) to predict amino acid types as well as their likely secondary structures based on the PACSY protein chemical shift database (Lee et al., 2012). The secondary structure is denoted as C for coil, S for β-strand, and H for helix. NSGA-II still works without the secondary structure information, but its use allows the user to check whether an assignment is reasonable based on whether a sufficiently long segment of residues show the same secondary structure motif.

The connection table describes how the residue numbers from different spectra are shifted relative to each other. Our connection table differs slightly from that of MCASSIGN2, by giving one column for each peak list. Table 1 shows an example of a connection table for two peak lists, NCACX and NCOCX, where each list contains 3 chemical shift columns, N, CA and CB, in that order. The three rows of the connection table refer to the three chemical shifts. The first 2 columns of the table give the identity of the two peak lists, which is 1 for NCACX and 2 for NCOCX. The next two columns refer to the chemical shift columns in each peak list, and are (1 2 3). The 5^th and 6^th columns give the residue shift indices. By default, the residue number is defined with respect to the CA atom. We set the indices to (0 0 0) for NCACX in the 5^th column. Since the NCOCX spectrum gives inter-residue cross peaks whose CA and CB chemical shifts belong to the i^th residue while the ¹⁵N chemical shift belongs to the i+1^th residue, the NCOCX indices in the 6^th column are (1 0 0). If a CONCX peak list is included, and the three chemical shifts are N, CA, and CO, then the indices would be (0 0 –1) for the CONCX peak list.

Table 1.

Connection table for an NCACX peak list (1) and an NCOCX peak list (2), each with three chemical shift columns: N, CA, and C•

3
1	2	1	1	0	1
1	2	2	2	0	0
1	2	3	3	0	0

The two NSGA-II based programs also constrain the residue of every atom to be within the input sequence, in order to correctly treat the assignment of N- and C-terminal residues in inter-residue correlation spectra. The C-terminal residue cannot contribute any cross peaks in the NCOCX spectrum due to the lack of the next ¹⁵N atom, so any assignment of the NCOCX peak list that contains the C-terminal residue is a bad connection. Similarly, any peak in the CONCA spectrum assigned to the N-terminal residue is a bad connection. This penalty of the N- and C-terminal residue assignment prevents some trivial wrong assignments.

To test the performance of NSGA-II and the combination algorithm, we used the ¹³C and ¹⁵N chemical shifts of four proteins: GB1 (Franks et al., 2005), HET-s (BMRB 11064) (Wasmer et al., 2008), sensory rhodopsin (BMRB 18595) (Shi et al., 2011) and HNP-1 (Zhang et al., 2010). For the first three proteins, we created input NCACX and NCOCX peak lists by modifying the reported chemical shifts randomly by 0.3–0.4 ppm. For HNP-1, the chemical shifts were directly read off from the 3D NCACX and NCOCX spectra. The HNP-1 peak lists are imperfect, because the 3D spectral linewidths are not very narrow (FWHM 0.6–2 ppm), and 2D ¹³C-¹³C correlation spectra were not consulted in generating the peak lists.

For MC/SA simulations, 100 independent runs were conducted for each dataset. The ranges of the weighting factors are 0–10 for w₁, 0–20 for w₂, 0–3 for w₃, and 0–1 for w₄. The number of simulated-annealing steps (N_S) during which the weighting factors vary is 20, except for the case of GB1 with random and independent deletion of 20% of the peaks, where N_S was set to 30. The number of assignment change (N_a) per simulated-annealing step is 10⁶.

For NSGA-II simulations, the number of individuals in each generation (i.e. group number) was 100. N_S denotes the number of lucky-ratio variations (see below) and was set to 20. The number of generations (N_a) per lucky ratio is 10⁴. The total number of generations is the product of N_S and N_a and is thus 2×10⁵. The results of 1 run containing 2×10⁵ generations of 100 distinct individuals are shown.

The combination NSGA-II/MC simulations were conducted for the three most difficult datasets, which are GB1 with random and independent peak deletion, sensory rhodopsin, and HNP-1. N_S was set to 20, the number of MC attempts per step was 10⁴ for HNP-1 and 10⁵ for GB1 and sensory rhodopsin, and the number of NSGA-II attempts per step was 10³.

For 100 runs of MC/SA, all results with N_b = 0 (i.e. valid solutions) are evaluated. Among these only a subset of results are distinct. We report the number of valid solutions (N_total) and the number of distinct solutions for each case. The modified NSGA-II and the combination algorithm produce 100 valid and distinct solutions in one run. Among these, Pareto-order-1 solutions are chosen based on four criteria, (N_g, N_b, N_u, S₀), as described below.

We compare the predicted assignments with the “true assignment” obtained manually or from the original BMRB data. When the highest-probability predicted assignment for a peak differs from the “true assignment”, we call it a “mis-assignment”. Since the input chemical shift lists used for automated assignments are purposefully made incomplete to mimic the situation of missing peaks in the spectra due to protein motion or broad linewidths, such “mis-assignments” are partly a result of the imperfect peak lists. However, even with the imperfect peak lists, the two NSGA-II based algorithms are more robust than MC/SA, in that they find the manual assignment with higher probabilities. This is due to the diversity of the solutions found by the genetic algorithm and the better evaluation process by the multi-objective optimization protocol.

The assignments are analyzed in terms of the probability p_top that the top assignment for each residue is found within N_total valid solutions:

$$p_{\mathit{\text{top}}}=\frac{N_{\mathit{\text{top}}}}{N_{\mathit{\text{total}}}}$$ (2)

where N_top is the number of times the top assignment is found. This p_top is compared to the probability that the true assignment is found.

Resonance assignment using NSGA-II

1. The modified NSGA-II

Our NSGA-II method is modified from the original method to tailor to the needs of protein NMR resonance assignment. The evolution process adopts four criteria, (N_g, N_b, N_u, S), where S is a composite score that implicitly accounts for edge assignments:

$$S=r_{\mathit{\text{lucky}}}*rand+(1-r_{\mathit{\text{lucky}}})*(10N_g-20N_b-3N_e+N_u).$$ (3)

Here r_lucky is a lucky ratio and rand is a random number, the product of which gives a “lucky number”. For each individual (i.e. possible assignment), a random number is generated. If an individual has a high “lucky number”, then S may be sufficiently high that this solution can become one of the Pareto-frontier solutions even if the other criteria values are not optimal. The solutions with the best N_g, N_b, and N_u values but worse S score still remain in the Pareto frontier because no other individuals can dominate these values. This strategy reduces the possibility that NSGA-II is trapped in a local optimum. The value of the lucky ratio is allowed to change from 0 to 1 between each of the N_S steps. A larger lucky ratio means the evaluations of the individuals are more dependent on their “luck” and less dependent on their real fitness.

There are many ways to define r_lucky. We chose a Gaussian function

$$r_{lucky}=e^{-\frac{1}{10}{(n_s-N_s/2+2)}^2.}$$ (4)

where n_s is the step counter and N_S is the number of lucky-ratio variations, which is 20. At the beginning and end of the evolution, r_lucky is close to 0, thus the original NSGA-II is conducted. In the middle of the evolution, when n_s is near 8, the lucky ratio is close to 1, which allows more random variation of the solutions. The Gaussian function is centered at n_s = 8 instead of 10 to better revert the simulations to the original NSGA-II by the end of the evolution. r_lucky is defined in this way so that the competition between individuals is more intense (small r_lucky value) at the beginning of the evolution to quickly converge to good results, less intense (large r_lucky value) in the middle of the evolution so that the group members have a higher probability to escape local optima, and more intense again at the end of the evolution so that the solutions are evaluated mainly on their fitness rather than luck. When r_lucky = 0, the score becomes

$$S_0=10N_g-20N_b-3N_e-N_u.$$ (5)

and the four criteria become (N_g, N_b, N_u, S₀).

Table 2 shows an example of the advantage of these four criteria for comparing the relative merit of assignment results. If the standard MC/SA criteria of (N_g, N_b, N_e, N_u) are used for non-dominated sorting, then solutions A, B and C will have the same Pareto order. However, among these three results, C has much lower N_g and N_u values than A and B, indicating fewer peaks that are consistently assigned between spectra and fewer used peaks. These poor N_g and N_u values are compensated by a low N_e value, which makes C a non-dominated solution. But N_g is usually more important than N_e, since edges can be valid due to molecular motion. So C is effectively an incomplete assignment and should be considered inferior to A and B. On the other hand, solutions A and B both have high and identical N_g values but slightly different N_e and N_u values. Either result can be the true assignment and should be considered equally good. The choice of (N_g, N_b, N_u, S₀) as the four evaluation criteria achieve the purpose of keeping A and B in Pareto-order 1 while sorting C as dominated by A and B.

Table 2.

Comparison of the objective values and scores of three hypothetical solutions using the original and modified NSGA-II. S₀ is calculated using Eq. (5).

	Ng	Nb	Ne	Nu	Pareto order	S0	Modified Pareto ordera
A	66	0	38	86	1	632	1
B	66	0	42	88	1	622	1
C	58	0	20	80	1	600	2

This example also illustrates the point that not all assignments that are valid (i.e. N_b = 0) have the same merit. The MC/SA algorithm does not have a mechanism to discard inferior solutions. After 100 MC/SA runs many valid but poor assignments can be generated that reduce the confidence of assignment prediction, as we found for HNP-1 and the most imperfect of three GB1 datasets.

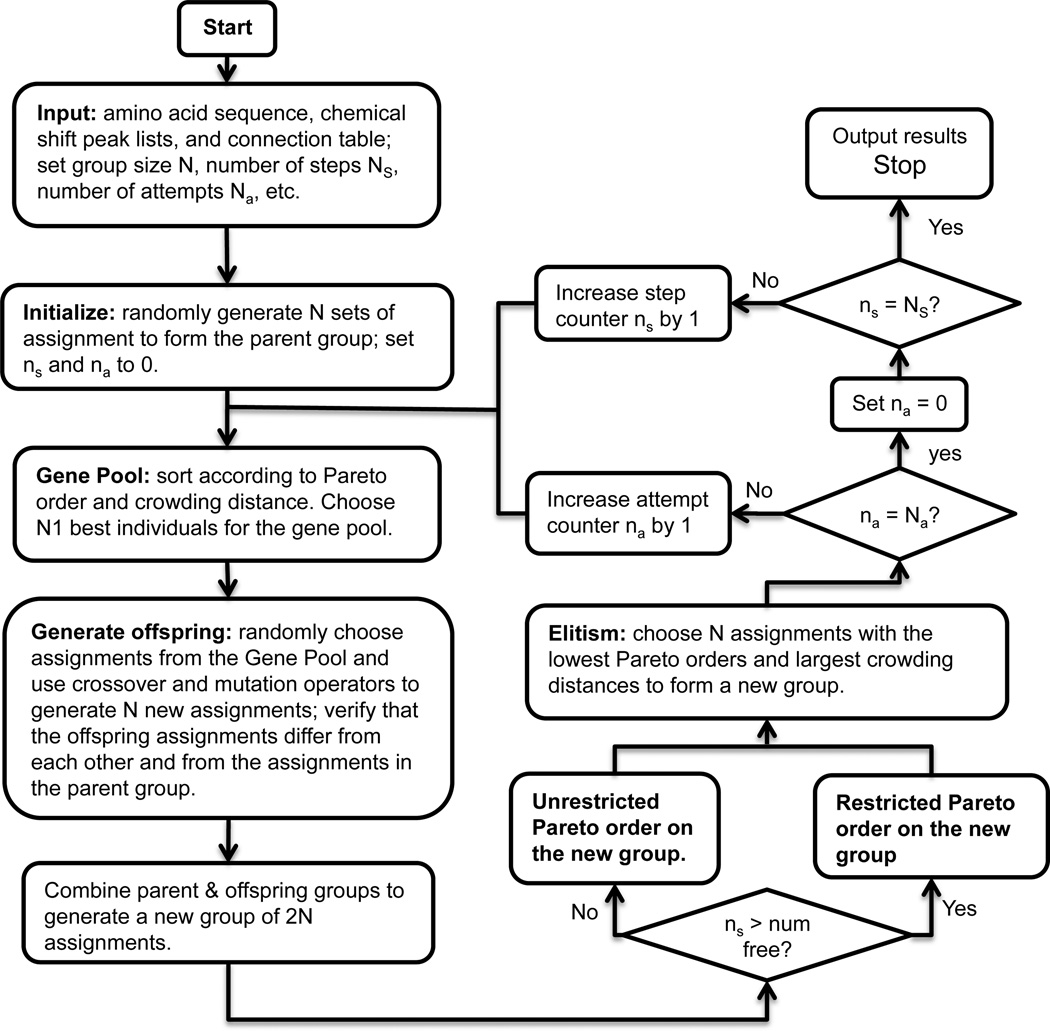
Fig. 2 shows a flowchart of the modified NSGA-II. Two points are noteworthy. First, to make changes to the parent generation, we use a crossover operator, which uses two individuals to generate two offspring, and a mutation operator, which uses one parent to generate one offspring. Second, in the final group of solutions, all results with N_b ≠ 0 will be discarded because they directly contradict the measured chemical shifts. So during the final step of evolution, we use a restricted Pareto-order strategy that makes all solutions converge to N_b = 0. If solution A has an N_b value larger than that of solution B, then A is dominated by B; but if A and B has the same N_b value, then the dominance relationship depends on the values of the other objectives. In this way, the final results will rapidly converge to N_b = 0. This restricted Pareto-order strategy is only used in the final few (typically 2) steps of evolution, while the rest of the evolution process involves unrestricted sorting of the Pareto order. The parameter “num_free” (0 ≤ num_free ≤ N_S) denotes the number of steps involving unrestricted sorting of Pareto orders. When n_s > num_free, the restricted sorting of Pareto order is used.

Figure 2.

Flowchart for the modified NSGA-II resonance assignment method.

2. The combination NSGA-II/MC algorithm

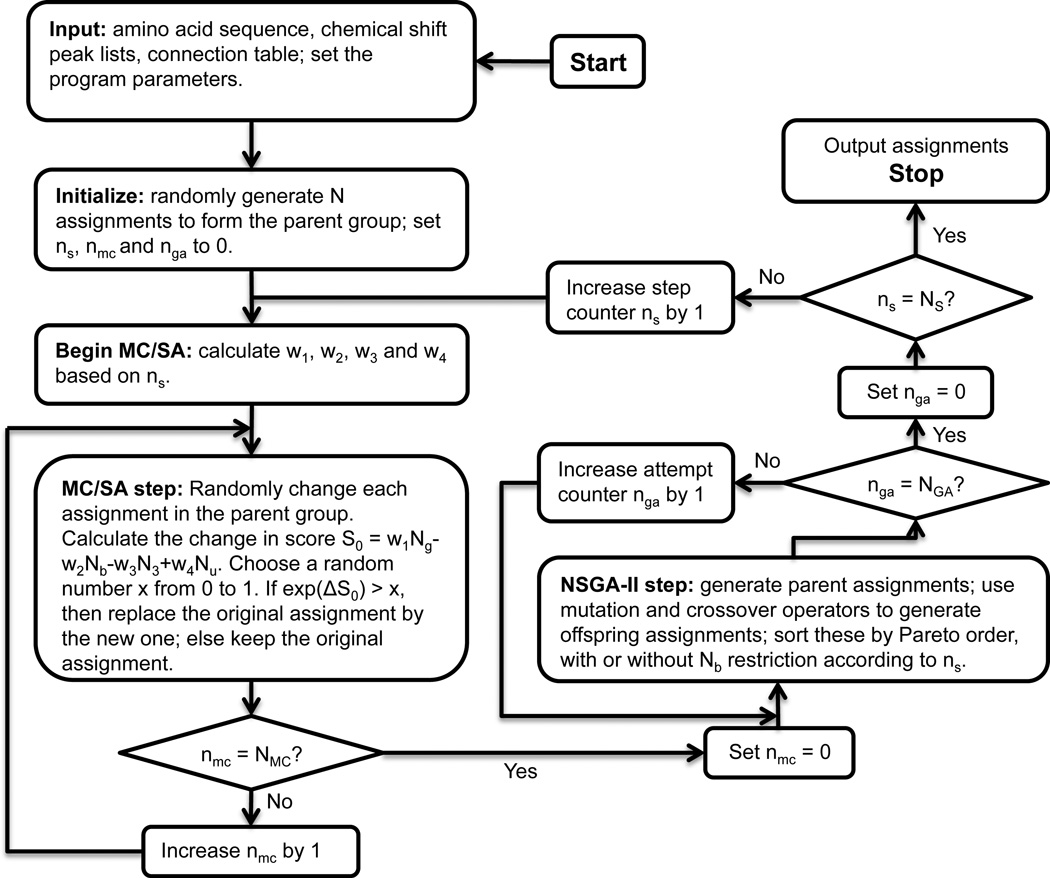
When multiple good assignments are quite different from each other, NSGA-II can be trapped into one of the good solutions and may not find all others. To address this issue, we developed a combination NSGA-II/MC algorithm (Fig. 3). Here, in each of the N_S steps of evolution, each individual first has N_MC Monte-Carlo attempts, where the score defined in Eq. 1 is used to evaluate the fitness. Subsequently, N_GA attempts of NSGA-II is used to make these group members compete with each other. The best individuals, as judged by (N_g, N_b, N_e, N_u), have their “genes” pass into the next generation. Thus, the Monte-Carlo process gives each individual opportunity to evolve and allow them to jump out of local optima, while the NSGA-II process makes the group of individuals rapidly converge to Pareto-frontier solutions. When N_MC is set to 0, the program reverts to the modified NSGA-II; if N_GA is set to 0, then the program reverts to the MC/SA algorithm but with 100 distinct solutions in one run. Different attempt numbers can be tested. Based on our experience, N_MC = 10⁴ – 10⁵ and N_GA = 10³ work well.

Figure 3.

Flowchart for the combination NSGA-II/MC resonance assignment method.

Results and Discussion

1. GB1 with consecutive deletion of 20% of the residues’ chemical shifts

The 56-residue GB1 is one of the best microcrystalline proteins for developing multidimensional SSNMR techniques due to the extensive literature of Rienstra and coworkers (Franks et al., 2008). We used the chemical shifts published in reference (Franks et al., 2005) for the assignment tests here. Fictitious NCACX and NCOCX peak lists were generated by adding a random deviation of 0.3 – 0.4 ppm onto the reported chemical shifts. The complete GB1 data have 56 and 55 peaks in the NCACX and NCOCX lists, respectively, and can be assigned readily using both NSGA-II and MC/SA (data not shown). Thus, we increased the difficulty level by removing some of the peaks. The choice of deleted peaks is designed to mimic realistic situations where peaks can be missing due to protein motion. As a first example, we deleted the peaks for the three loops in GB1, which span residues 9–12, 20–22, and 38–41 (Fig. S1a). Such loop residues are often dynamic and can thus escape detection in cross-polarization (CP) based experiments at moderate temperatures.

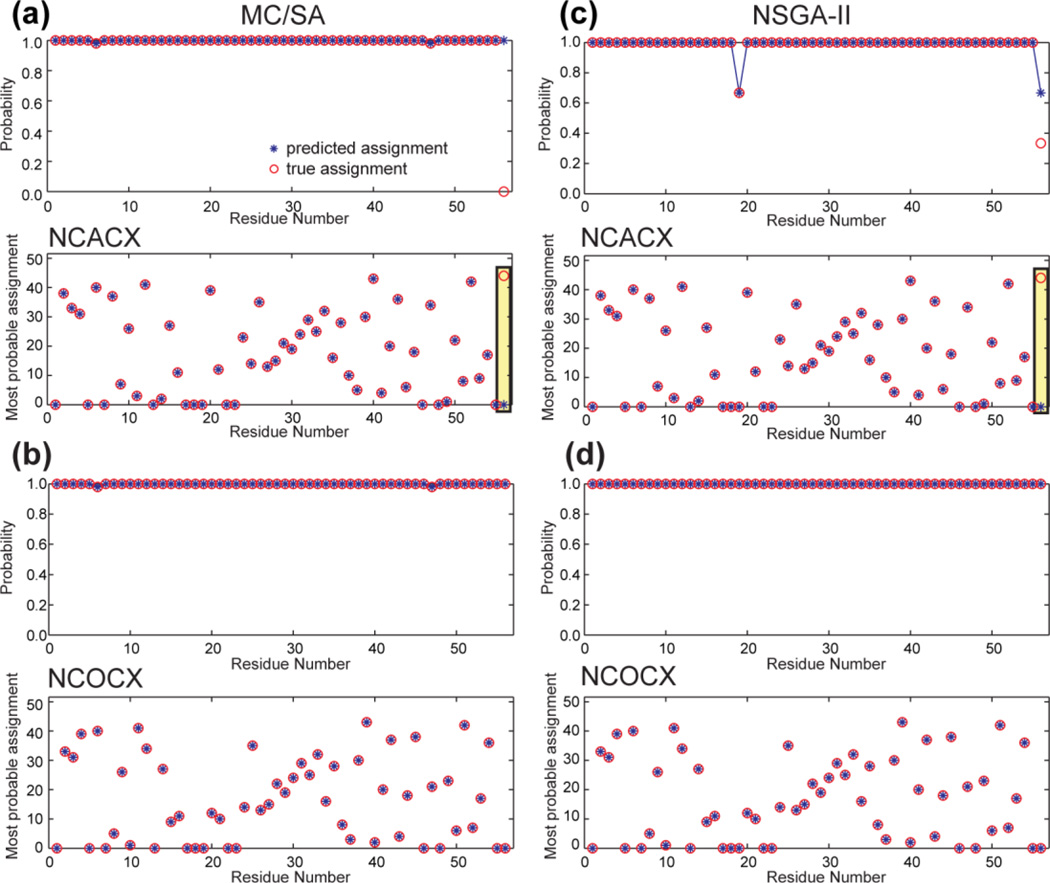
Fig. 4 compares the performance of MC/SA and modified NSGA-II. All 100 runs of MC/SA gave valid results, among which 2 solutions are distinct. 99 results gave (N_g, N_b, N_e, N_u) values of (85, 0, 7, 89), while one solution gave (84, 0, 9, 89). The two solutions differ from each other at residues M1, K10 and E42: the first solution has assignment for M1 and E42 but no assignment for K10, while the second solution has assignment for M1 and K10 but null assignment for E42. Q2 and W43 show peaks in both spectra, so the assignment of M1 and E42 can find good connections. Thus, missing the assignment of E42 in the second solution reduces N_g by 1. In comparison, G9 and T11 peaks have been deleted from the lists, so the assignment of K10 cannot be proved to be either right or wrong, which leads to a higher N_e value for the second solution.

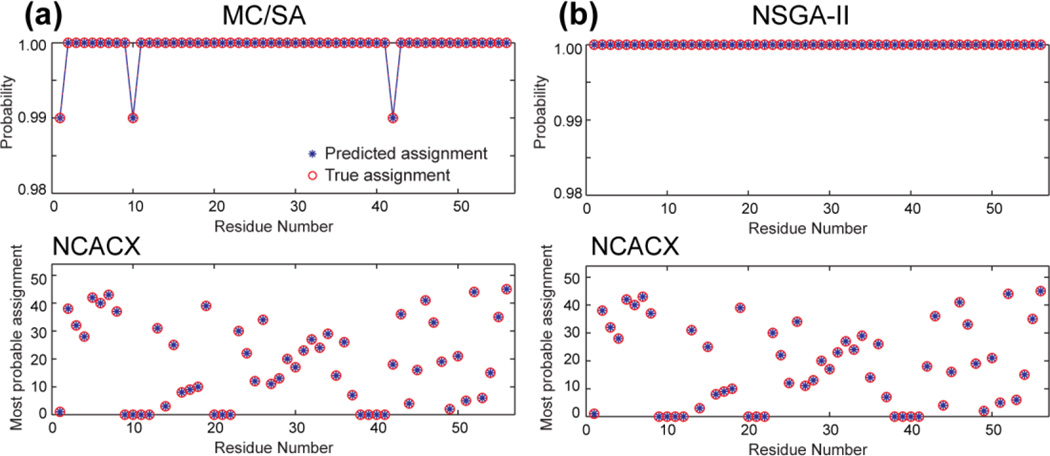
Figure 4.

Resonance assignment of GB1 with consecutive deletion of 20% of the peaks. Only the NCACX assignment is shown; the NCOCX prediction is similar. (a) MC/SA generated 100 valid results containing 2 distinct solutions. (b) Modified NSGA-II produced a single Paratoorder- 1 solution. The top panels show the probability of the top assignment of each residue, and the bottom panels show the peak number of the most probable assignment. The probability and peak number of the predicted assignment (blue stars) are compared with those of the true assignment (red circles). Note the y-axis scale of the probabilities covers a very small range of 98–100%, indicating that both algorithms have very high assignment probabilities, and both methods are 100% accurate in the most probable predictions.

From one run of modified NSGA-II, we obtained a single Pareto-frontier solution, which is the majority solution found by MC/SA. Non-dominated sorting identified the second solution as inferior. This case, while simple, shows that when a protein contains a small number of dynamic segments that do not give signals, as long as the rest of the protein gives reliable chemical shifts that are consistent among multiple spectra, the assignment is straightforward and not more difficult than for a fully detected protein. Both MC/SA and modified NSGA-II predicted the correct assignment well, but NSGA-II showed a slight advantage of sorting the valid solutions according to the Pareto order.

2. GB1 with random deletion of 20% of the residues’ peaks

We next examined the case where the missing peaks are randomly distributed in the protein sequence and thus cause many more edge assignments. This situation could arise from low sensitivity of the sample, line broadening of certain residues by conformational disorder, intermediate-timescale motion, or chemical exchange. We randomly chose 12 residues (1, 5, 7, 13, 17, 18, 19, 22, 23, 46, 48, and 55) in GB1 and deleted their peaks in both the NCACX and NCOCX lists.

Fig. 5 shows the results of MC/SA and modified NSGA-II simulations. Surprisingly, both methods produced good assignments, with only one “mis-assigned” residue in the NCACX dataset. MC/SA found 3 distinct solutions out of 100 valid results: 96 results are identical, with (N_g, N_b, N_e, N_u) values of (78, 0, 16, 86), while 4 results have N-values of (77, 0, 14, 84) and contain 2 distinct solutions. We call solution (78, 0, 16, 86) A and the other two solutions B and C. Comparing A and B, A assigned I6 while B did not. Between A and C, A assigned D47 while C has no assignment for D47. Thus, among the three solutions, A is the most complete assignment. However, A has only 86 used peaks out of 87 total. The missing peak is that of the C-terminal residue E56 in the NCACX spectrum. Since T55 is deleted and the C-terminal residue does not give signals in the NCOCX spectrum, the assignment of E56 increases the edge number by 1 without adding a good connection, thus worsening the score. Thus, the assignment of E56 is eliminated as long as MC/SA chooses (78, 0, 16, 86) as a better solution than a possible solution with N-values (78, 0, 17, 87). Fig. 5a shows that the correct E56 assignment is never predicted by MC/SA.

Figure 5.

Resonance assignment of GB1 with random deletion of 20% of the peaks. The deleted peaks come from the same residues between the NCACX (a, c) and NCOCX (b, d) lists. (a, b) MC/SA generated 100 valid results containing 3 distinct solutions. (c, d) Modified NSGA-II found 3 Parato-order-1 solutions. Both methods have one “mis-assignment” in the NCACX dataset and have correct assignment of all NCOCX peaks.

In comparison, NSGA-II gave 3 Pareto-frontier results within 100 distinct solutions. Two Pareto-order-1 solutions have N-values of (78, 0, 18, 87), one of which is the correct assignment. The other solution switched the E56 and E19 assignments because these two residues both have no neighboring peaks due to deletion and no NCOCX peaks. The third solution is the same as solution A from MC/SA. In contrast to MC/SA, NSGA-II gives these three results the same merit or Pareto order, thus predicting the correct assignment of E56 with 33.3% of the probability (Fig. 5b).

This test shows that even when many residues are not detected in the spectra, as long as the same residues have missing peaks in different spectra, the rest of the protein can still be assigned relatively well using both NSGA-II and MC/SA.

3. GB1 with random and uncorrelated deletion of 20% of the peaks in multiple datasets

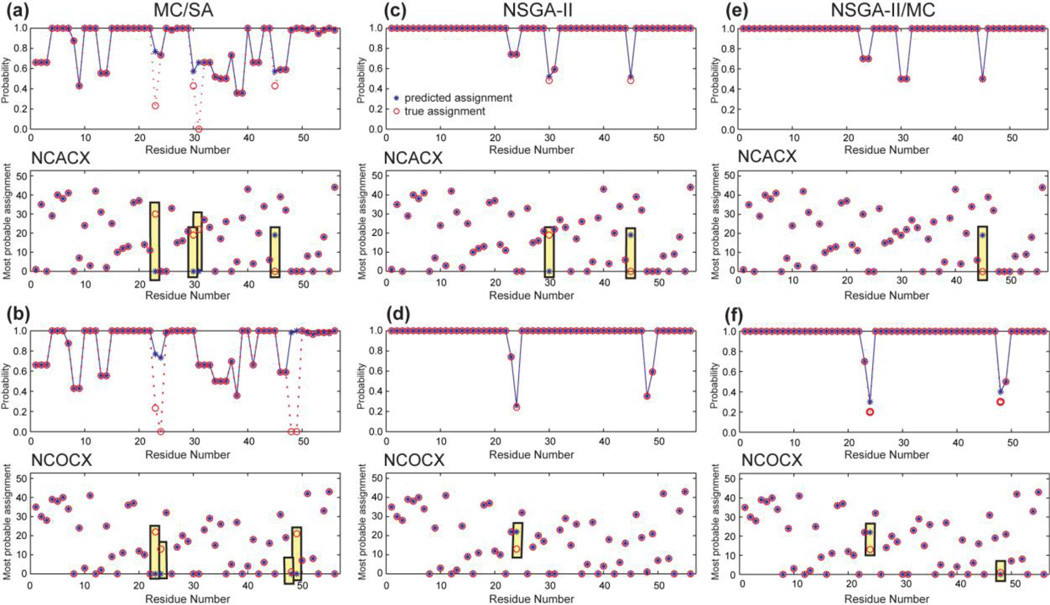
Peaks can be missing or broadened in an uncorrelated fashion between multiple spectra, due to resonance overlap with different residues, incorrect grouping of peaks during manual peak picking, or suboptimal experimental conditions. To mimic this situation, we randomly deleted 20% of the peaks in the NCACX and NCOCX peak lists, but the deleted peaks do not come from the same residues (Table S3). All three algorithms were employed for this case, and the results are shown in Fig. 6 and the N-values are listed in Table 3.

Figure 6.

Resonance assignment of GB1 with random and independent deletion of 20% of the peaks, which do not come from the same residues between the NCACX (a, c, e) and NCOCX (b, d, f) datasets. (a, b) MC/SA found 56 valid results, among which 43 are distinct. 4 residues are “mis-assigned” for each dataset. Various residues have low probabilities for the top assignment, some of which are nevertheless correct. (c, d) Modified NSGA-II found 54 Parato-frontier solutions with 2 and 1 “mis-assignments”. (e, f) The combination algorithm found 80 Paratoorder- 1 solutions with 1 and 2 “mis-assignments”.

Table 3.

Assignment results of GB1 with 20% randomly and independently deleted residues. S₀ is calculated using Eq. (5). Bold indicates rows that contain the true assignment.

Method	# of evaluated Results	Ng	Nb	Ne	Nu	S0	# of results	# of distinct solutions
MC/SA	56 valid results (out of 100 runs)	65	0	34	82	630	6	5
		65	0	35	83	628	9	6
		64	0	32	80	624	1	1
		64	0	33	81	622	9	6
		64	0	34	81	619	10	10
		64	0	35	82	617	3	3
		63	0	31	79	616	8	3
		63	0	32	79	613	1	1
		63	0	33	80	611	7	6
		62	0	29	77	610	1	1
		63	0	34	80	608	1	1
NSGA-II	54 Pareto- frontier results (out of 100 valid results)	65	0	35	83	628	4	4
		65	0	39	85	618	26	26
		65	0	41	86	613	20	20
		65	0	43	87	608	4	4
NSGA2/MC	80 Pareto- frontier results (out of 100 valid results)	65	0	35	83	628	4	4
		65	0	37	84	623	20	20
		65	0	39	85	618	32	32
		65	0	41	86	613	20	20
		65	0	43	87	608	4	4

MC/SA found 56 valid assignments among which 43 are distinct. The objective values of these 43 solutions are more divergent than the previous two test cases: for example, the number of good connections ranges from 65 to 62. The modified NSGA-II produced 100 valid and distinct results with 54 Pareto-frontier solutions, all of which have 65 good connections but differ in N_e and N_u. The combination NSGA-II/MC algorithm yielded 80 Pareto-order-1 solutions, with similar objective values as the NSGA-II results. Interestingly, most (41 out of 56) of the MC/SA solutions are dominated by the NSGA-II and combination results based on the (N_g, N_b, N_u, S₀) criteria.

Fig. 6 compares the predicted assignments by the three methods. For MC/SA, 4 residues are “mis-assigned” in each spectrum. For modified NSGA-II, the Pareto-frontier solutions have 2 “mis-assigned” residues for the NCACX list and only 1 “mis-assignment” for the NCOCX list. The accuracy of the combination NSGA-II/MC is similar to that of the modified NSGA-II.

In addition to higher accuracy, the NSGA-II and NSGA-II/MC results are more predictive of ambiguous residues: the “mis-assigned” residues have low prediction probabilities (20–50%) while the high-probability assignments are always correct (Fig. 6c-f). In comparison, MC/SA gave relatively high probabilities of 50–100% to the “mis-assigned” residues, while some correctly assigned residues have low prediction probabilities (Fig. 6a, b). This poor “judgment” can be traced to the treatment of edge assignment. Because the missing peaks do not match between the two peak lists, the already low value of w₃ (0–3) turned out to be still too high for this case. Table 3 shows that many MC/SA solutions compensate for low N_g and N_u values by having low N_e values, thus giving relatively high S₀ scores. Similar to the example in Table 2, it is more important to have many good connections and many used peaks than to strive for fewer edges. Indeed, when we set the maximum value of w₃ to 0, thus no longer penalizing edge assignments, then MC/SA gave more accurate predictions (data not shown). Of course, for de novo assignment, it is impossible to know whether missing peaks are correlated or uncorrelated between spectra, thus it is impossible to choose w₃ optimally. The modified NSGA-II algorithm avoids this dilemma altogether, since N_e is only one of the evaluation criteria, implicitly accounted for through S, thus NSGA-II can keep high-N_e outcomes as long as the other objectives have non-dominated values. As a result, the two NSGA-II methods gave high prediction probabilities for the correctly assigned residues and low probabilities for the “misassigned” residues, making the probability a reliable indicator of the true assignment.

4. HET-s

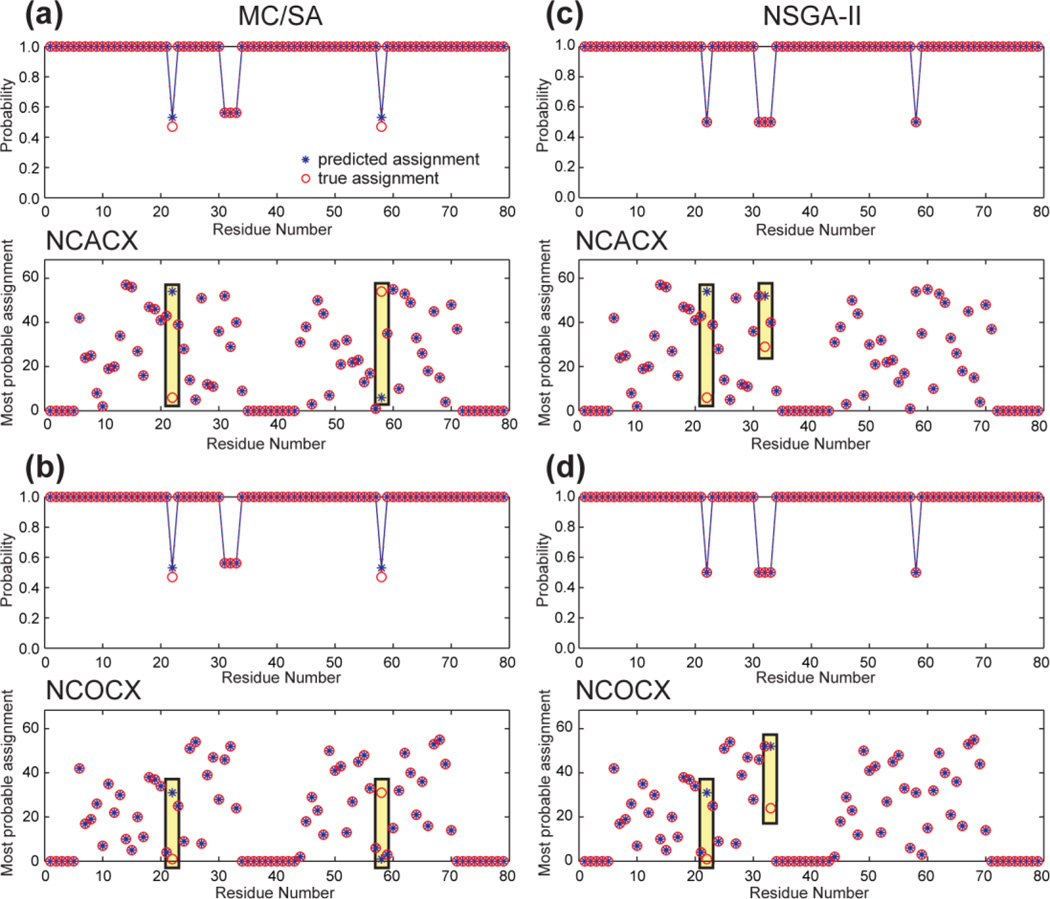
We next predicted the assignment of the amyloid protein HET-s, using the chemical shifts in the BMRB entry 11064 to generate the fictitious NCACX and NCOCX peak lists. There are 57 peaks in NCACX and 55 peaks in NCOCX. No chemical shifts are available for residues 1–5 and 35–42 in the original dataset.

Fig. 7 compares the MC/SA and modified NSGA-II results. Both algorithms performed similarly well, with only 2 “mis-assigned” residues in each dataset by both methods. MC/SA yielded 98 valid results that contain 4 distinct solutions, while NSGA-II yielded 4 Pareto-frontier results that are identical to the MC/SA predictions. All four results have N-values of (110, 0, 4, 112). The “mis-assigned” residues are correctly reflected by their low prediction probabilities. R22 and R58 have low probabilities because the ¹⁵N chemical shifts of R22 and V23 are similar to those of R58 and V59. The assignments of the Ala triplet, A31-A32-A33 are also ambiguous, as expected. Moreover, the ¹⁵N chemical shift difference between A31 and A33 and between A33 and L34 are within the linewidths. Thus the A31-A32 chemical shifts cannot be easily distinguished from the A32-A33 chemical shifts.

Figure 7.

Resonance assignment of HET-s (a, c) NCACX and (b, d) NCOCX spectra. (a, b) MC/SA found 98 valid results containing 4 distinct solutions. (c, d) Modified NSGA-II produced 4 Pareto-order-1 solutions. The two methods performed equally well, with only 2 “misassignments” in each dataset.

5. Sensory Rhodopsin

We next considered the assignment of a relatively large protein sequence to investigate how MC/SA and NSGA-II algorithms handle increased chemical shift overlap and the presence of identical residue pairs in the sequence. We chose the predominantly α-helical sensory rhodopsin (BMRB 18595), but truncated its size to the first 98-residues, which correspond to the first three transmembrane helices (Fig. S1b). The use of the chemical shifts of the entire 236- residue protein resulted in poor predictions by all methods (data not shown). The peak lists contained 87 spin systems in NCACX and 82 spin systems in NCOCX (Table S6).

MC/SA found 100 valid results with 33 distinct solutions, out of which the 23 highest-scoring results have N-values of (164, 0, 10, 169). The modified NSGA-II produced 8 Pareto-order- 1 solutions, all of which have the same N-values as the top MC/SA result. The combination program yielded 24 Pareto-order-1 solutions with the same N-values (Table 4). Additional runs of NSGA-II and the combination algorithm did not generate more Pareto-frontier solutions, suggesting that the 24 solutions are the complete set of Pareto-frontier solutions.

Table 4.

Assignment results of truncated rhodopsin using the three algorithms. S₀ is calculated using Eq. (5). Bold indicates rows that contain the true assignment.

Method	# of evaluated Results	Ng	Nb	Ne	Nu	S0	# of Results	# of distinct solutions
MC/SA	100 valid results (out of 100 runs)	164	0	10	169	1779	90	23
		163	0	10	168	1768	1	1
		163	0	12	169	1763	4	4
		162	0	12	168	1752	5	5
NSGA-II	8 Pareto-frontier results (out of 100 valid results)	164	0	10	169	1779	8	8
NSGA2/MC	24 Pareto-frontier results (out of 100 valid results)	164	0	10	169	1779	24	24

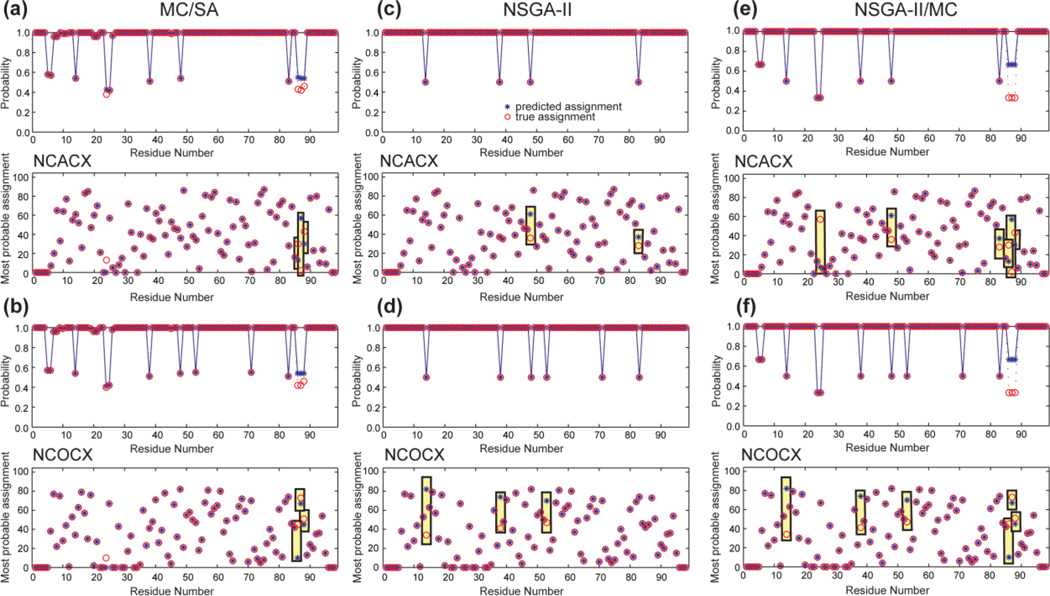
It is noteworthy that MC/SA found more solutions than modified NSGA-II for this case. The reason is that among the 24 Pareto-frontier solutions, some results are very different from the others, with three or more residues having different assignments. NSGA-II appears to be less efficient in finding all these divergent solutions when they have equal merit, while the combination algorithm, by incorporating a MC search, overcomes this limitation and finds the largest number of Pareto-frontier solutions among the three methods.

Fig. 8 shows that the three methods predicted ambiguous assignments for similar residues. The common ambiguous residues include G14, L38, G48, A53, A71, and L83. The ¹⁵N chemical shifts of G14-M15 are very similar to those of G48-L49, making the G14 and G48 assignments interchangeable. For the same reason, the assignment of L38 (L38-V39) and L83 (L83-L84) are ambiguous. The ¹³C chemical shifts of residues A53 and A71 overlap nearly completely, and their neighboring residues also have similar ¹⁵N chemical shifts (A53-M54 and A71-R72), which resulted in a 50% assignment probability for each residue. Additional ambiguities in the MC/SA assignment and the combination assignment result from the presence of several identical residue pairs, such as S5-L6, S24-L25, and S86-L87 (Table S8).

Figure 8.

Resonance assignment of the first 98 residues of sensory rhodopsin. (a, c, e) NCACX dataset. (b, d, f) NCOCX dataset. (a, b) MC/SA generated 100 valid results containing 33 distinct solutions. (c, d) Modified NSGA-II generated 8 Pareto-frontier solutions. The two methods showed similar accuracy. (e, f) Combination NSGA-II/MC found 24 Pareto-frontier solutions, thus showing the highest diversity among the three methods.

6. HNP-1

The above test cases used literature chemical shifts that have been randomly modified and partially deleted. To test the assignment programs starting from manual peak picking, we used the 3D NCOCX and NCACX spectra of HNP-1, a human antimicrobial protein (Zhang et al., 2010). Soluble HNP-1 has typical linewidths of ~0.5 ppm for ¹³C and ~1 ppm for ¹⁵N, which are intermediate between the linewidths of the most crystalline proteins and the most disordered proteins. Manual peak picking gave 27 peaks in the NCACX list and 25 peaks in the NCOCX list (Table S7). Chemical shifts from 2D CC and 3D CCC spectra, which were also used in the original manual assignment (Li et al., 2010), are not consulted in creating the peak lists. In addition, a small number of chemical shifts do not match well between the two 3D NCC spectra, which would cause edge assignments. These imperfections are intentionally left in the peak lists in order to test the robustness of the three assignment algorithms.

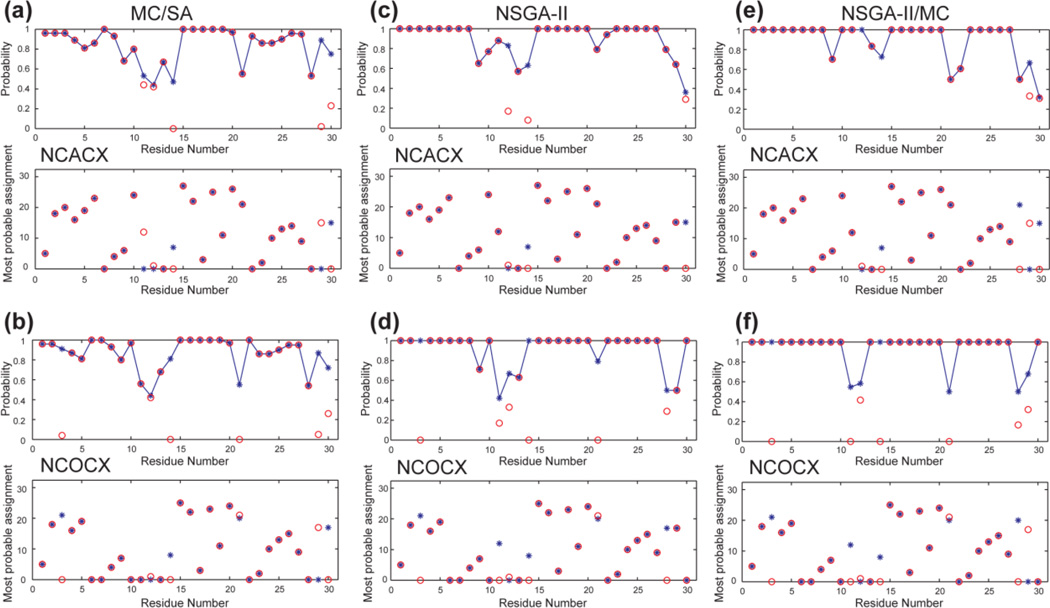
Fig. 9 compares the assignment results of the three methods. MC/SA found 100 valid results, among which 52 are distinct, while NSGA-II and the combination algorithm found 100 and 84 Pareto-frontier solutions, respectively. All three methods indicate significant numbers of residues with ambiguous assignment, but MC/SA showed the highest ambiguity: only 14 and 16 peaks were assigned with > 90% probabilities (Table 5), while the two NSGA-II based algorithms predicted 20–25 peaks with >90% probabilities. Among the high-probability predictions, the fraction of correct assignment, by comparison with the manual assignment, was high (92–100%) for all methods: the correctly assigned peaks among the high-probability predictions are 14 and 15 for MC/SA and 20–23 for the two NSGA-II methods. Interestingly, this investigation suggests that the original manual assignment (Zhang et al., 2010) may be ambiguous at the C5-R6 junction because of the high number of Cys residues (6) in this small protein (30 residues). Thus, a few “mis-assignments” by the computational algorithms may actually be correct or at least cannot be definitively shown to be wrong. If we consider the most probable predictions for all residues, then the number of correctly assigned residues increases to 24 and 25 for MC/SA, which is comparable to the numbers of correctly assigned residues by the two NSGA methods (Table 5). However, for de novo assignment, assignment probability will be the only indicator of the reliability of the assignment, thus the low probabilities of the MC/SA predictions are detrimental. This limitation is traced to the suboptimal balance between multiple criteria in the single-score optimization. Table 6 indicates that MC/SA kept many solutions with low N_e but also low N_g and N_u values, while the two NSGA methods retained some higher-N_e solutions because they also have high N_g and N_u values, which gave better predictions of the truly ambiguous residues. Thus, the attempt to reduce the edge number again interferes with high-quality assignment, similar to the case of GB1 with random and independent deletions.

Figure 9.

Resonance assignment of HNP-1. (a, c, e) NCACX data. (b, d, f) NCOCX data. (a, b) MC/SA found 100 valid assignments containing 52 distinct solutions. (c, d) Modified NSGA-II found 100 Pareto-order-1 results. (e, f) Combination NSGA-II/MC produced 84 Pareto-order-1 results. All three methods show ambiguous predictions, but more residues are correctly predicted with high (>90%) probabilities by NSGA-II and the combination algorithm than by MC/SA.

Table 5.

Number of high-probability assigned residues and correctly assigned residues of HNP-1 using the three algorithms.

Method	# of assignments with >90% probabilities	# of correct assignments within the > 90% probability solutions	# of correct assignments within the most probable predictions
MC/SA	14 in NCACX	14 in NCACX	25 in NCACX
	16 in NCOCX	15 in NCOCX	24 in NCOCX
NSGA-II	20 in NCACX	20 in NCACX	27 in NCACX
	23 in NCOCX	21 in NCOCX	24 in NCOCX
NSGA-II/MC	22 in NCACX	21 in NCACX	25 in NCACX
	25 in NCOCX	23 in NCOCX	23 in NCOCX

Table 6.

Assignment results of HNP-1 using the three algorithms.

Method	# of evaluated Results	Ng	Nb	Ne	Ne Nu	S0	# of results	# of distinct solutions
MC/SA	100 valid results (out of 100 runs)	40	0	10	46	416	64	19
		40	0	11	46	413	5	5
		40	0	12	47	411	1	1
		40	0	13	47	408	4	4
		40	0	14	48	406	1	1
		39	0	9	44	407	10	7
		39	0	10	45	405	5	5
		39	0	11	45	402	6	6
		39	0	12	46	400	3	3
		38	0	11	44	391	1	1
NSGA-II	100 Pareto-frontier results (out of 100 valid results)	40	0	11	46	413	59	59
		40	0	15	48	403	41	41
NSGA-II/MC	84 Pareto-frontier results (out of 100 valid results)	40	0	11	46	413	20	20
		40	0	13	47	408	44	44
		40	0	15	48	403	20	20

7. Computation times

These assignments were run on a 2.9 GHz Intel Core i7 MacBook Pro laptop computer with 8 GB of memory. The computation time of MC/SA mainly depends on the number of simulated annealing steps N_S and the number of attempts per step N_a, while the size of the protein has little effect. For NSGA-II, the number of generations, the protein size, and the group number all have significant influences on the computational time. Table 7 shows that for a short sequence such as HNP-1, a full NSGA-II run took only 9 minutes, while for the 98-residue truncated rhodopsin, the computational time rose to 19 minutes.

Table 7.

Computation times of the three algorithms on the four test proteins on a 2.9 GHz Intel Core i7 MacBook Pro.

Method	GB1 (56 residues)	HET-s (79 residues)	HNP-1 (30 residues)	Rhodopsin (98 residues)
MC/SA (20 steps)	25 min	25 min	25 min	25 min
NSGA-II	13 min	16 min	9 min	19 min
NSGA-II/MC	19 min	-	2 min	23 min

For moderate-sized proteins, NSGA-II is faster than MC/SA because the former is a multi-thread algorithm while MC/SA is single-threaded. In NSGA-II, all group members evolve and optimize together, thus speeding up the convergence. However, for longer sequences, NSGA-II requires more computer memory, since NSGA-II is designed to search for different results. Whenever a new solution is generated, the program must compare it with all other solutions. The time cost of this step depends on the sequence length and the group size, hence the NSGA-II computation time increases more rapidly with the sequence length than MC/SA.

Conclusion

The analysis shown here indicates that for high-quality protein chemical shift datasets such as GB1 with consecutive deletion of residues and HET-s, both MC/SA and the modified NSGA-II predict the assignment similarly accurately. However, when a significant number of peaks are missing from the spectra, the chemical shifts deviate between spectra, and the protein sequence is long and thus contains multiple identical residue pairs, the modified NSGA-II and the combination algorithm find more diverse assignments than MC/SA and have better predictive powers about the residues with ambiguous assignments. The high probabilities for the correctly assigned residues are important for identifying core domains in proteins that can be unambiguously assigned. The better performance of NSGA-II results from the fact that the multi-objective optimization strategy is able to identify and discard inferior (although valid in a limited sense, i.e. N_b = 0) solutions by not relying on weighting factors, which cannot be optimized since the type of spectral imperfection is difficult to know without assignment. We find the weighting factor for the edge assignment can be especially influential in the assignment outcome: both the case of GB1 with random and uncorrelated deletion and the HNP-1 case indicate that edge peaks should not be overly penalized. Since edge assignments can be justified for some spectra but reflect poor assignment for others, multi-objective optimization is the only approach to handle edges appropriately.

When there are many equally good assignments that are quite different, as in the case of sensory rhodopsin, MC/SA can be more efficient in finding these results than the modified NSGA-II. In this case, the combination NSGA-II/MC algorithm overcomes the limitation of NSGA-II and is found to be best among the three algorithms.

Other than protein motion and resonance overlap induced by conformational heterogeneity, another cause of assignment ambiguity is the existence of the same residue pairs, which tend to cause multiple possible assignments, as seen in sensory rhodopsin. Thus, not surprisingly, proteins that contain repetitive stretches of sequences are inherently difficult to assign. Even when two residue pairs are not the same, as long as the ¹⁵N chemical shifts of residues k and k+1 are similar to those of residues p and p+1, and the residue type of k and p are the same, then the assignments of residues k and p are still interchangeable, if only NCACX and NCOCX spectra are used. This degeneracy can be removed if additional 3D spectra such as CONCX are measured.

Overall, the combination NSGA-II/MC algorithm shows the most stable and good performance in all three most challenging datasets (GB1 with random and uncorrelated peak deletion, sensory rhodopsin and HNP-1). Thus we expect the combination algorithm to be the most promising to apply to de novo assignment of structurally unknown proteins.

The multi-objective optimization strategy shown here can be applied to other automated assignment programs to improve their performances. For example, the ssFLYA program (Schmidt and Guntert, 2012) evaluates assignments in terms of the completeness and the chemical shift values with respect to given shift statistics. These attributes are combined with weighting factors into a scoring function. A multi-objective optimization strategy should also be useful for this ssFLYA algorithm by finding a more complete set of Pareto frontiers with the optimized attribute values.