At the bench: the key role of PK–PD modelling in enabling the early discovery of biologic therapies

Abstract

Pharmacokinetic–pharmacodynamic (PK–PD) modelling is already used extensively in pre-clinical and clinical drug development to characterize drug candidates quantitatively, aid go/no-go decisions and to inform future trial design and optimal dosing regimens. Less well known, although arguably as powerful, is its application at the earliest stages of drug development, at target selection and lead selection, where these same techniques can be used to predict and so bring forward drug candidates with the necessary characteristics or, for unachievable requirements, allow the abandonment of the programme for the minimum spend of time and cost. We consider three examples that illustrate the power of the application of modelling at this early stage. We start with the simple case of determining the optimal characteristics for a monoclonal antibody against a soluble ligand with its application to the investment decision for the development of best-in-class compounds. This is extended to the more complex situation of the target protein having an endogenous, inhibitory binding protein. We then illustrate how using physiologically-based pharmacokinetic modelling enables the appropriate engineering and testing of biological therapeutics for optimal PK–PD characteristics. These examples illustrate how a minimal investment in modelling achieves orders of magnitude better returns in choosing the correct targets, mechanism of action and candidate characteristics to progress to clinical trials, streamlining drug development and delivering better medicines to patients.

Introduction

In recent times the integrated and systematic implementation of pharmacokinetic−pharmacodynamic (PK–PD) modelling from the pre-clinical to post-marketing stages of drug development, under the paradigm of Model-Based Drug Development (MBDD) [1–3] has been proposed as one means of improving pharmaceutical R&D productivity [4]. These publications postulate that application of traditional compartmental and more mechanistic translational PK−PD models to integrate all available non-clinical and clinical data on a drug candidate with prior data on competitor medicines can provide a powerful tool to guide early and objective investment decisions on candidate projects, based on their comparative safety/efficacy profile.

A natural extension of these conclusions is the question of whether such mathematical models can be used to help guide decisions even earlier within the medicine R&D life cycle, to the design of the drug candidates themselves. In silico design of small and large molecule candidates for optimal interaction with the target protein and even for safety is now de rigeur within industry [5,6]. Well-documented mathematical models also exist to predict the absorption, distribution, metabolism and elimination (ADME) properties of small molecule drug candidates based on structure and to predict oral absorption based on in vitro properties [7,8]. However, few examples exist within the literature on the application of combining these techniques within an in silico drug design paradigm, especially for biologics. In this paper we seek to address this less-appreciated application of MBDD and to highlight the work being undertaken at the earliest stages of drug development, prior to the beginning of animal in vivo testing of candidate medicines. We will use three case studies, based on our experience, to illustrate the power of applying modelling and simulation to determine design parameters that optimize the in vivo PK–PD performance of biologic drug candidates and focus resources on technologies most likely to result in well-differentiated medicines.

Example 1: optimal antibody design

Mager & Jusko [9] have previously presented a general PK–PD model for drugs demonstrating a target-mediated drug disposition. A schematic of this model and the more complex variant considered in example 2 is shown in Figure 1. This form of model was employed by Meno-Tetang & Lowe for the interaction of the monoclonal antibody Xolair® (omalizumab) with its IgE target [10]. This model described both the individual and the population PK well, demonstrating the sufficiency of this description as a model for Xolair® PK–PD. Moreover, the model parameters could be identified using total Xolair® PK data and free and antibody-bound IgE data from a phase 1 study in 16 atopic asthma patients. These estimated values were comparable with those that would be expected from the literature. PK parameters were similar to those of a typical IgG1 monoclonal antibody in man, the clearance of IgE was within the range of values in the literature and the estimate for the in vivo affinity (K_d) was close to the in vitro measured value. Thus the Mager & Jusko/Meno-Tetang & Lowe model system provides a minimal, mechanistic description of the interaction of an anti-IgE monoclonal antibody with its target.

Figure 1.

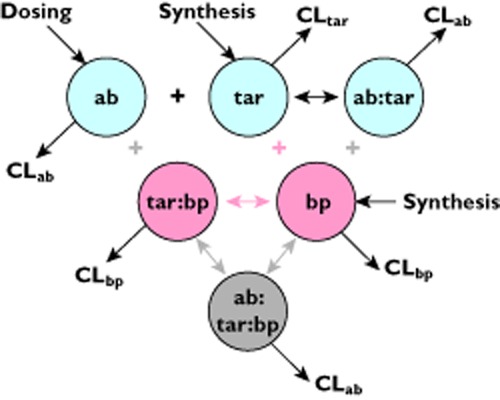
A schematic of the antibody-target interaction models considered in examples 1 and 2. The simplest model considered in example 1 consists of those components in light blue: the antibody (ab), the target (tar) and the complex formed by the association of the two (ab:tar). As a first approximation the clearance of the complex is assumed to be equal to that of the antibody. Example 2 considers the introduction of an endogenous binding protein (bp) for the target, adding the components in pink describing the binding protein (bp) and the target-binding protein complex (tar:bp). In this scheme binding of either the antibody or the binding protein precludes the binding of the other, indicating a competitive mechanism of action for the antibody. A non-competitive mechanism of action is considered by adding in the grey component of the antibody-target-binding protein complex (ab:tar:bp), made the association of either free antibody with target-binding protein complex, or antibody-target complex with free binding protein

Two important conclusions can be drawn from this. Firstly, that this model description is sufficient to describe the PK–PD of a range of monoclonal antibodies directed against soluble targets. The PK can be substituted with that specific for the antibody of interest or, as we will argue below, with those of a generic antibody. Moreover, the dynamics of any constitutively expressed protein can be approximated by a constant production and first order clearance employed in the model. In the absence of information contradicting such a simple treatment of the target, which we will consider some cases of later, this model then describes the PK–PD of any soluble target for the substitution of the appropriate target-specific parameters. Secondly, if the parameters for the model could be assumed a priori, rather than by fitting to trial data, then simulation of the model can be used to predict the PK–PD of the monoclonal antibody and its target ahead of clinical trials.

A corollary of this second conclusion is particularly powerful. It is not necessary to produce the antibody in order to make accurate predictions of the clinical PK–PD. Given that the kinetics of the potential therapeutic antibody will be similar to those of an antibody in its class, the most sensitive parameters of the model are the kinetics of the target and the affinity of the antibody for the target. With knowledge of the target kinetics, which are independent of the targeting antibody and may therefore be derived from other sources, one can assume typical antibody PK and then use model simulation to identify what characteristics the antibody should have in order to achieve the desired clinical PK–PD.

As an example, suppose that we are considering using an antibody to target a soluble ligand whose kinetics are consistent with the mechanisms described by the Meno-Tetang & Lowe model. For therapeutic efficacy the levels of the target must be suppressed to below 10% of its baseline level. The antibody has the typical small volume of distribution and long half-life of IgG1 kinetics. As a first approximation we will assume that the antibody-ligand complex is cleared at the same rate as the free antibody. From a base case of requiring 100 mg of antibody dosed every 4 weeks to achieve the required suppression of the target, Figure 2 shows the sensitivity in the required dose as a function of each of the parameters of the model.

Figure 2.

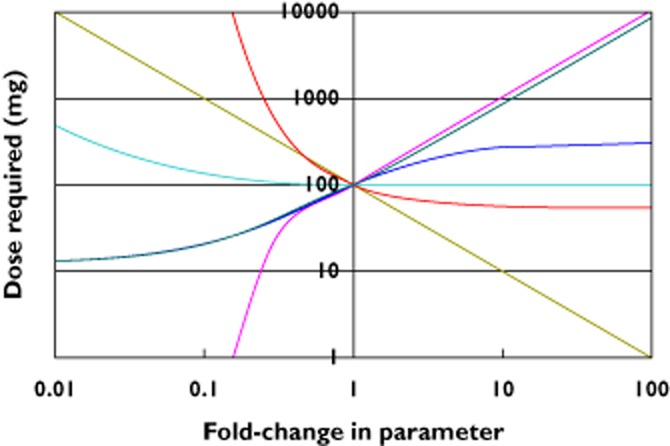
A spider plot of the dependency of the predicted clinical dose for each of the model parameters. The central point assumes that the antibody has typical IgG1 PK of a half-life of 21 days and volume of distribution of 70 ml kg⁻¹. It binds with an affinity of 10 pm to its target, which has a turnover half-life of 1 h with a baseline concentration of 10 pm. A subcutaneous dose of 100 mg every 4 weeks is required to maintain 90% suppression of the target under these conditions. The plot shows how that required dose varies for, and thus demonstrates the sensitivity to, each of the model parameters, such as how the dose is particularly sensitive to an enhanced clearanceof the antibody (decreased half-life). , antibody half-life; , complex half-life; , target half-life; , k_on; , K_d; , target concentration

Figure 2 demonstrates that the most critical factor for an antibody therapy to avoid the requirement for a large dose, which would render it unviable as a therapy due to a combination of cost and patient convenience, is the half-life of the antibody. Antibodies should therefore be of the isotype IgG1, 2 or 4 and be fully human to minimize the risk of quicker clearance and neutralizing immunogenicity. Antibody mutations in the Fc-binding region that promote longer than typical half-lives [11] may further mitigate this risk but, under the circumstances of this example extended PK exposure will not lead to significant reductions in the required dose.

Thereafter, the key determinants of the required dose are the target half-life, its baseline concentration and the antibody affinity for the target. The first two determine the total amount of target that must be bound by antibody and the linear dependency of these on dose is obvious: 10 times faster target clearance, means 10 times faster production to maintain baseline levels, or 10 times higher levels will require 10 times as much antibody. The risk posed by an abundant or quickly-turned over target may be mitigated with a high affinity antibody but only to a limited extent. The reason for this asymmetry in the dependence on the affinity of the antibody is the same as that for the antibody half-life as the amount of target that needs to be bound sets a minimum antibody dose requirement. Even a therapeutic with irreversible binding to the target and zero clearance will fail when out-numbered by the target.

More than a mere model artefact, this illustrates the fundamental importance of knowing the target clearance and level in disease. If that minimum dose is in excess of what would be required for a viable therapy – high cost-of-goods, unable to be formulated for a sub-cutaneous dose or of no worthwhile improvement on competitor drugs – then the project can be stopped. Establishing the target clearance at the target selection stage and modelling to determine the minimum dose could avoid distant phase 2 trials that fail due to insufficient interaction with the target or because there is no difference from the competition.

If an antibody therapy remains viable then the model defines the lead requirements. Necessary and sufficient PK, affinity and binding rates are defined on clear, quantitative criteria along with the expected dose, ensuring as much as possible that a lead is capable of testing the target hypothesis in clinical trials.

Example 2: target specificity

The turnover model applied to Xolair® by Meno-Tetang & Lowe [10] may not be applicable to targets with more complex mechanisms. One common complication can be the occurrence of an endogenous binding protein for the target, such as IL-1Ra for IL-1beta [12] or IL-18BP for IL-18 [13]. The binding protein inhibits the target but also changes its kinetics, typically reducing the clearance of bound target, and, as the target kinetics are a critical factor in the design requirement of the optimal antibody, must be taken into account. The additional binding interaction can be captured mathematically and if the values of additional parameters are known then the model can be extended to describe this more complex system with the optimal antibody parameters determined in the same way.

However, this system allows us to pose an additional and much more interesting question to that of the optimal affinity: is it better to have an antibody that binds only the target or that also binds target-binding protein complex? For this example we will assume that same parameter values as for the simpler example considered above, where the target has a half-life of 1 h and the affinity of both antibodies is 10 pm. As such, the dose required for 90% suppression of the target in the absence of a binding protein is 100 mg s.c. every 4 weeks. We assume that the binding affinity between the target and the binding protein is also 10 pm. The target-binding protein complex will be cleared with a much longer half-life of 2 days, which would be consistent with the binding protein taking the target above the molecular weight limit for renal elimination. (In this model, the half-life of the binding protein itself was also taken to be 2 days, although it is interesting to note that this parameter has no bearing on the model output, result not shown.)

Figure 3 plots the required dose for 90% suppression of the (free) target for both mechanisms of action of the antibodies, for increasing levels of the binding protein. For relatively low levels of binding protein only a small fraction of the target is bound, making little difference to its kinetics and the mechanisms are of equivalent potency. For increasing concentrations of the binding protein the potency of the antibodies diverges, with the non-competitive antibody (i.e. that which binds both the target and target bound to the binding protein) requiring lower doses to achieve the required suppression, while the competitive antibody requires slightly larger doses. This may seem counter-intuitive as one may expect that antibody bound to the target-binding protein complex is wasted and one should need to dose higher to compensate. Instead, consider that the most sensitive driver of the required dose is, as demonstrated in Figure 2, the turnover of the target. For a non-competitive antibody, the compound target of (target + target-binding protein complex) has a decreasing turnover as more target is bound to the binding protein. Only when the levels of binding protein grow sufficiently large that the compound target levels deplete the antibody does the dose requirement cease reducing. Conversely, a competitive antibody may be expected to be independent of the binding protein. However, increasing levels of target bound to the binding protein require a higher target production rate, and therefore turnover rate, to maintain the observed free target level. This increased turnover rate then leads to increasing dose requirements for this antibody mechanism as binding protein levels increase.

Figure 3.

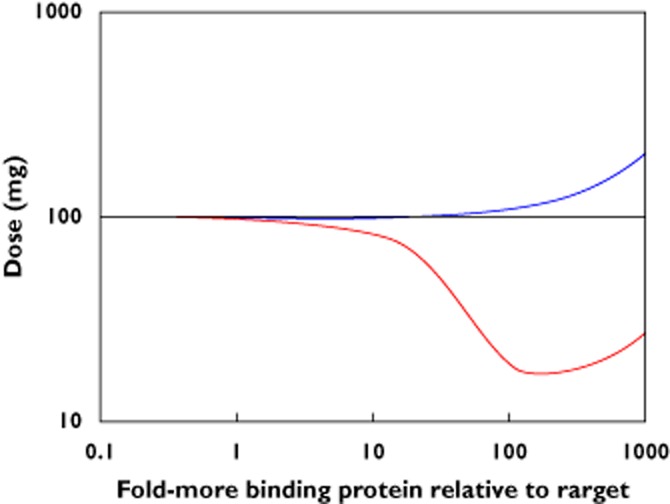
The change in the required dose of antibody for increasing levels of target binding protein depends on whether the antibody competes or not for the target with the binding protein. Using the base-case parameters from example 1, a subcutaneous dose of 100 mg of the antibody of either mechanism is required to maintain 90% suppression of the target when levels of a binding protein for the target arenegligibly low. The required dose changes as levels of this binding protein increase: the dose decreases for an antibody that also binds the target and binding protein complex but increases for an antibody that competes with the binding protein. , competitive; , non-competitive

This example further emphasises the need to characterize the intended target in order to make the most informed decision on the design of a therapeutic antibody, a binding protein could have a significant bearing on this. In general, and as our example illustrates, if the effect of the binding protein on the target is low then the two mechanisms are equally potent and so lead antibodies can be selected on other criteria (cross-reactivity to toxicology species, stability, patentability). The relative benefits will depend on the kinetics of the target and binding protein but may be considerable. In the example for the 100-fold greater level of binding protein, choosing the inferior mechanism comes at a penalty of requiring a five-fold larger dose (or a 20-fold higher affinity, not shown) to achieve the same suppression of the target.

Example 3: Physiologically-based PK modelling to enable optimal therapeutic engineering

A number of new and exciting biologic formats are continuously emerging to fulfil therapeutic niches. As these formats are being developed with a specific application in mind, mathematical modelling, especially physiologically-based PK (PBPK) modelling, can be used to (i) assess the likelihood the format will fulfil its intended purpose and (ii) design and interpret animal studies to confirm their potential. Two such examples were recently presented by Niederalt et al. [14] and Bergmann et al. [15].

The former involved the use of a PBPK model to help in the design of pH-dependent target binding (PHB) antibodies [16]. A physiological-based model was built with a mechanistic description of the distribution of antibody in the plasma and discrete organs. This model then allows the prediction of the effect of altering the FcRn binding characteristics of the antibody by virtue of this explicit consideration of the FcRn in cellular uptake and recycling. These antibodies bind their target with high affinity at physiological pH and low affinity at endosomal pH, so the antibody is recycled efficiently through the neonatal Fc receptor (FcRn) salvage pathway and the target is guided towards endosomal degradation, thus allowing a single antibody molecule to neutralize multiple target molecules. Niederalt et al. [14] showed that a complex relationship between physiological and endosomal affinities and the in vivo potency exists for these molecules. The optimal combination of these affinities was a function of various factors including the endogenous concentration of the target, its endogenous turnover rate and antibody kinetics. For example, the potency increases as the affinity at extracellular pH is high and decreases as that at endosomal pH is less. However, these affinities typically change together and therefore higher extracellular affinities are associated with higher endosomal affinities, rendering the recycling process inefficient. Lower extracellular affinities would result in lack of binding in the first place. A quantitative understanding of all the processes is invaluable in then guiding future experiments to optimize affinities for such compounds.

Similarly, Bergmann et al. [15] used a mechanistic model of serum albumin disposition to evaluate half-life extension of therapeutics by conjugating to serum albumin mutants with higher affinity to the FcRn receptor than endogenous albumin. An interesting finding from the model is that transgenic mice models, commonly used to evaluate PK behaviour of such mutants, may be limited in their ability to predict human half-life extension due to competing murine serum albumin, whereas cynomolgus monkeys, which do not suffer from this limitation, are a better in vivo model for assessing half-life extension.

These two examples illustrate that the development of novel technologies to overcome existing PK–PD limitations of biologics can greatly benefit from a systematic quantitative understanding of the targeted PK–PD profile, design goals for the format, and testing and confirmation strategy. It should, however, be pointed out that available in vitro methodology for generating data to inform the models are not always adequate. Therefore it is important to account for the uncertainty in the predictions prior to decision-making.

Conclusions

We have used three examples to illustrate the utility of applying the principles of PK–PD modelling at the earliest opportunities in the discovery and development of biologic therapies. These simulations were used to address some of the most common questions in medicine and technology projects, including:

1. to assess whether a potential receptor/ligand is feasible as a target for therapeutic intervention using available antibody technologies,

2. whether the PK–PD characteristics of existing medicines can be improved upon to obtain best-in-class compound,

3. to identify gaps in our knowledge of the PK–PD behaviour of the system of interest and prioritize experiments to bridge these gaps and

4. to assess the utility of a particular PK–PD enhancement technology and experimental techniques to confirm the enhancement.

These resulted in objective, quantitative outputs that reflected the uncertainties in the knowledge of the system. For example, on a project, a difference in the turnover of the target antigen by 10-fold would result in an increase of the antibody dose by 10-fold, potentially leading to an unfeasible dose. Therefore, antigen turnover (and concentration) was identified as an important parameter to measure prior to lead optimization investment. Similarly, a switch to PHB antibodies, and not affinity increase, was predicted to reduce the clinical dose by two-fold on a particular project.

The models used in these simulations are more complex than standard PK–PD models and fall under the umbrella of quantitative systems pharmacology (QSP) models [17,18]. QSP models' predictive ability and portability across compounds is due to a mechanistic approach that separates the ‘system’ and ‘drug’ parameters. Development of these models presents different challenges from standard PK–PD models. They are not usually calibrated with compound data prior to use – analyses may take place before the compounds themselves are produced – and therefore they contain greater uncertainty in the projections. A systematic sensitivity analysis (Figure 2) is often required to clarify the impact of uncertainty in model assumptions. Furthermore, the identified key system parameters (biomeasures) have to be measured in analytical systems, for which investment in sophisticated bioanalytical techniques may be required. This can be a challenge to resource from a project which is focussed on advancing a specific candidate through drug development milestones and, therefore, a convincing argument on the need for data to calibrate a model of the underlying system is required.

Apart from these investments, for a comprehensive implementation of model-based drug discovery, a change in the research culture is also required from a process of developing and characterizing potential drug candidates in the hope of finding one that is good enough to progress to one in which the aim is building a comprehensive understanding of the disease and target system, from which the characteristics for an ideal therapy can then be derived [19,20].

In this paper we have presented examples from the earliest phases of biologic drug discovery and development that demonstrate how a relatively trivial investment in modelling can produce critical information on the expected success or failure of drug projects. Millions of dollars and years of time are saved by the identification of projects that will never be viable. That investment can instead be made in projects with a better chance of success bringing forward optimally-designed lead candidates.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare no support from any organization for the submitted work, BA and MP are employees of MedImmune plc and no other relationships or activities that could appear to have influenced the submitted work.