Covariate effects and population pharmacokinetics of lamivudine in HIV-infected children

Abstract

Aim

Lamivudine is used as first line therapy in HIV-infected children. Yet, like many other paediatric drugs, its dose rationale has been based on limited clinical data, without thorough understanding of the effects of growth on drug disposition. Here we use lamivudine to show how a comprehensive population pharmacokinetic model can account for the influence of demographic covariates on exposure (i.e. AUC and C_max).

Methods

Data from three paediatric trials were used to describe the pharmacokinetics across the overall population. Modelling was based on a non-linear mixed effects approach. A stepwise procedure was used for covariate model building.

Results

A one compartment model with first order elimination best described the pharmacokinetics of lamivudine in children. The effect of weight on clearance (CL) and volume of distribution (V) was characterized by an exponential function, with exponents of 0.705 and 0.635, respectively. For a child with median body weight (17.6 kg), CL and V were 16.5 (95% CI 15.2, 17.7) l h⁻¹ and 46.0 (95% CI 42.4, 49.5) l, respectively. There were no differences between formulations (tablet and solution). The predicted AUC(0,12 h) after twice daily doses of 4 mg kg⁻¹ ranged from 4.44 mg l⁻¹ h for children <14 kg to 7.25 mg l⁻¹ h for children >30 kg.

Conclusions

The use of meta-analysis is critical to identify the correct covariate-parameter relationships, which must be assessed before a model is applied for predictive purposes (e.g. defining dosing recommendations for children). In contrast to prior modelling efforts, we show that the covariate distribution in the target population must be considered.

WHAT IS ALREADY KNOWN ABOUT THIS SUBJECT

• Lamivudine is recommended as first line therapy in HIV-infected children.

• Previous investigations on the pharmacokinetics of lamivudine have been performed on small populations or consisted of somewhat large groups within narrow age ranges.

• In most cases, the impact of developmental growth on systemic exposure was assessed in subsets of the paediatric population, by covariate analysis using a fixed correlation between pharmacokinetic parameters and demographic factors.

WHAT THIS STUDY ADDS

• Identification of the correct covariate–parameter relationships is crucial to predict drug exposure accurately across different age groups in the population.

• Covariate stratification should be considered to prevent hidden biases in the covariate model describing the effects of developmental growth on pharmacokinetics in children.

• Body weight was found to be the best descriptor of changes in systemic exposure. It significantly affected lamivudine clearance and volume of distribution.

• Based on the current dosing regimen, predicted steady-state exposures showed a slight increase with increasing body weight. Given that lamivudine is given in combination with other antiretroviral agents, such differences are unlikely to be clinically relevant.

• There were no differences in the pharmacokinetics of lamivudine after administration of the solid or liquid dosage form (i.e. tablet or solution).

Introduction

Lamivudine (3TC) is a nucleoside reverse transcriptase inhibitor (NRTI) widely administered as the nucleoside backbone in combination with highly active antiretroviral therapy to HIV-infected children. Lamivudine's mechanism of action is based on the competitive inhibition of the HIV reverse transcriptase. It is phosphorylated to an active metabolite that competes for incorporation into viral DNA. According to the latest WHO guidelines [1], lamivudine is administered as paediatric first line therapy in combination with abacavir (ABC), with either a non-nucleoside reverse transcriptase inhibitor (NNRTI) or a protease inhibitor (PI). In fact, given its excellent record of efficacy, safety and tolerability in HIV-infected children lamivudine is contained in practically all recommended combinations in paediatric antiretroviral therapy. In addition, it is a frequent component of fixed dose, including low cost, drug combinations.

Lamivudine is rapidly absorbed after oral administration and it is excreted primarily in the urine as unchanged drug [2–6]. The intracellular triphosphate has a long half-life of 16 to 19 h, as compared with the plasma lamivudine half-life of 5 to 7 h [7]. Lamivudine is currently administered to HIV-infected children based on body weight according to the dose of 8 mg kg⁻¹ day⁻¹ for children lighter than 14 kg, 150 mg day⁻¹ from 14 to 21 kg, 225 mg day⁻¹ from 21 to 30 kg and 300 mg day⁻¹ thereafter, all given twice a day.

Over the last years, various attempts have been made to describe the effect of developmental growth on the pharmacokinetics of antiretroviral drugs in children. Tremoulet et al. performed an extensive population pharmacokinetic analysis in infants between 3 days and 3 years [8]. Burger et al. also investigated the influence of age on lamivudine pharmacokinetics in HIV-infected children, showing that in children of 6 years of age and younger, the recommended dose of 4 mg kg⁻¹ twice daily led to exposure levels lower than those observed in children ≥7 years of age and adults [9]. These findings have prompted additional evaluation of the effects of developmental growth on the pharmacokinetics of lamivudine. In this context, focus has been given to the use of allometric models to characterize the effect of body weight on clearance. Bouazza et al. described the covariate effects in a large group of children (n = 580) aged between 2 days and 18 years [10], whilst Zhang et al. developed a population pharmacokinetic model in young children between 0.5 and 4.5 years [11]. In all these studies, either small populations (i.e. group size) or narrow age ranges (i.e. population inclusion criteria) were used or the relationship between parameter and covariate was fixed a priori.

Bearing in mind the impact of covariate selection on the dose rationale when dealing with small datasets, we propose the use of a model-based meta-analysis for the evaluation of covariate effects on systemic exposure. Here we analyze data from three groups of HIV-infected children who received daily doses of lamivudine as part of a standard HIV protocol, focusing on the requirements for 1) accurately assessing the correlation between demographic covariates and pharmacokinetic parameters and 2) balance in the covariate distribution across the groups, without relying on a priori assumptions about the parameter–demographic covariate correlation.

Given the need for a scientifically driven dose rationale in paediatric diseases [12], it can be anticipated that the correct identification of influential covariates on drug disposition is essential when a population pharmacokinetic model is used for simulations and dosing recommendation purposes [13–15]. Dosing recommendations should be therefore obtained without introducing bias due to factors such as unbalanced distribution of the covariates, or due to the small sample size available for data analysis. Such a bias may result in suboptimal dosing across different groups in the population and consequently lead to increased risk of toxicity or reduced efficacy. Thorough understanding of the correlation between the demographic covariates and pharmacokinetic parameters is still required to assess the implications of developmental growth on drug exposure and, as a consequence, on the efficacy of lamivudine.

Methods

Patients and samples

This investigation was a retrospective pooled analysis of data obtained from three studies: PENTA (Paediatric European Network for the Treatment of AIDS) 13; PENTA 15 and ARROW (AntiRetroviral Research fOr Watoto). The primary objectives of these studies were to compare the pharmacokinetics of once daily vs. twice daily lamivudine regimens in HIV type-1-infected children. PENTA 13 and PENTA 15 were conducted in European children aged from 2–13 years and from 3 months–3 years, respectively. The ARROW study was conducted in Uganda with children aged 3–12 years.

The studies have been conducted in full conformance with the principles of the Declaration of Helsinki and with the local laws and regulations concerning clinical trials. The protocol and the informed consent documents for each study have been formally approved by the relevant research ethics committee of each clinical site and by a national ethics body.

In total data from 77 paediatric patients were available (19 from PENTA 13 study [16], 18 from PENTA 15 study [17] and 40 from the ARROW trial [18]). The analysis population consisted of male and female patients across the age range between 3 months and 13 years (median age 5.79 years), and weight between 7.43 and 61.3 kg (median weight 17.6 kg). Demographic details are summarized in Table 1. In total 1184 blood samples were available for pharmacokinetic modelling, with nine samples below the quantification limit.

Table 1.

Summary of demographic characteristics

	PENTA 13	PENTA 15	ARROW	Full population
Subjects	19	18	40	77
Male	9	9	16	34
Female	10	9	24	43
Median age (years)	5.7	1.9	7.5	5.7
Minimum (years)	2.1	0.4	3.5	0.4
Maximum (years)	12.8	2.8	12.5	12.8
Median weight (kg)	21.7	11.7	20.1	17.6
Minimum (kg)	12.5	7.4	14	7.4
Maximum (kg)	61.3	16.1	30	61.3
Creatinine clearance (ml min−1)	81.7	59.9	63.8	95.5
Minimum (ml min−1)	41.2	31.9	50.4	31.9
Maximum (ml min−1)	199.5	87.5	168.3	199.5
Ethnicity	17 black, 2 others	14 black, 4 others	40 black	71 black, 6 others

Assay of lamivudine

For the PENA13 and PENTA15 studies, plasma concentrations of lamivudine were determined by high performance liquid chromatography assay with u.v. detection (HPLC-UV) with a lower limit of quantification (LLOQ) of 0.015 mg l⁻¹ [19]. For the ARROW study, the high performance liquid chromatography assay was used in conjunction with a tandem mass spectrometry detection (HPLC-MS/MS) method, which had a LLOQ of 0.0025 mg l⁻¹.

Population pharmacokinetic analysis

The pharmacokinetic analysis was split into two steps:

1. Development of the population pharmacokinetic model using a subset of two studies (PENTA 13 and PENTA 15 studies) to allow for an initial assessment of model stability and predictive performance.

2. Integrated pharmacokinetic analysis of the patient data from all three studies, followed by model validation, as implemented by standard graphical and statistical methods.

Model building

Non-linear mixed effects modelling was performed in nonmem version 6.2 (Icon Development Solutions, USA) [20]. Model building criteria included: (i) successful minimization, (ii) standard error of estimates, (iii) number of significant digits, (iv) termination of the covariance step, (v) correlation between model parameters and (vi) acceptable gradients at the last iteration [21].

Fixed and random effects were introduced into the model in a stepwise manner. Inter-individual variability in pharmacokinetic parameters was assumed to be log-normally distributed. The parameter value of an individual i (post hoc value) is therefore given by the following equation:

in which θ_TV is the typical value of the parameter in the population and ηi is assumed to be a random variable with zero mean and variance ω². Residual variability, which comprises measurement and model error, was described with a proportional error model. This means for the j^th observed concentration of the i^th individual,the relation Y_ij:

where F_ij is the predicted concentration and ε_ij the random variable with mean zero and variance σ². W is a proportional weighing factor for ε.

Goodness of fit was assessed by graphical methods, including population and individual predicted vs. observed concentrations, conditional weighted residual vs. observed concentrations and time, correlation matrix for fixed vs. random effects, correlation matrix between parameters and covariates and normalized predictive distribution error (NPDE) [22]. Comparison of hierarchical models was based on the likelihood ratio test. A superior model was also expected to reduce inter-subject variability and/or residual error terms.

Covariate analysis

Continuous and categorical covariates were tested during the analysis. The relationship between individual pharmacokinetic parameters (post hoc or conditional estimates) and covariates was explored by graphical methods (plot of each covariate vs. each individual parameter). Relevant demographic covariates (body weight, age, height, creatinine clearance) were entered one by one into the population model (univariate analysis). Given that different lamivudine formulations were administered in the trials, formulation was also treated as a covariate. After all significant covariates had been entered into the model (forward selection), each covariate was removed (backward elimination), one at a time. The model was run again and the objective function recorded. The likelihood ratio test was used to assess whether the difference in the objective function between the base model and the full (more complex) model was significant. The difference in – 2log likelihood (DOBJF) between the base and the full model is approximately χ² distributed, with degrees of freedom equal to the difference in number of parameters between the two hierarchical models. Because of the exploratory nature of this investigation, for univariate analyses, additional parameters leading to a decrease in the objective function of 3.84 were considered significant (P < 0.05). During the final steps of the model building, only the covariates which resulted in a difference of objective function of at least 7.88 (P < 0.005) were kept in the final model.

Model validation

The validation of the final model was based on graphical and statistical methods. Given the importance of the validation procedures for the subsequent use of a model for simulation purposes, in this study we applied a wide range of diagnostic methods to assess the accuracy of the parameter estimates and the predictive performance of the model. First, a bootstrap procedure was performed in PsN v2.30 (University of Uppsala, Sweden) [23]. Bootstrap was used to identify bias, stability and accuracy of the parameter estimates (standard errors and confidence intervals (CIs)). PsN does so by generating a set of new datasets by sampling individuals with replacement from the original dataset, and fitting the model to each new dataset. Subsequently, parameter estimates were used to simulate plasma concentrations in paediatric HIV patients with similar demographic characteristics, dosing regimens and sampling scheme as in the original clinical studies. Mirror plots were then generated to evaluate the variance–covariance structure of the parameters in the model, which is reflected by the degree of similarity between the original fit and the pattern obtained from the fitting of the simulated data sets using the final pharmacokinetic model.

In addition to the graphical analysis, posterior predictive checks were performed using the area under the plasma concentration vs. time curve (AUC) and peak plasma concentration (C_max) as a measure of model performance. AUC and C_max values were calculated non-compartmentally by the trapezoidal method from simulations of 1000 data sets with the same demographic characteristics, dosing regimens and sampling schemes as in the original clinical studies.

The distribution of model-predicted AUC and C_max values was presented as geometric mean, lower and upper boundaries of the 95% CIs and compared with the findings from non-compartmental analysis in the two clinical studies. Model performance was assessed by the location of the original estimates across the predicted distribution (histograms).

Results

Population pharmacokinetic modelling

The results shown in this paper are derived from the analysis of the combined datasets from three studies. A one-compartment pharmacokinetic disposition model with first-order absorption was fitted to the plasma concentration vs. time data from the three populations. Inter-individual variability was identified for CL, V and K_a. In all three studies used in our investigation the patients received lamivudine according to once and twice daily dosing regimens. Therefore inter-occasion variability on CL and K_a was included in the model to quantify potential differences in parameter estimates between the two dosing regimens. The residual error was described using a combined model including a weighting factor for the variance estimate, which resulted in a better fit of the data as compared with a simple combined error model. CL and V were found to increase with body weight. An exponential function best described the correlation between these pharmacokinetic parameters and body weight. The exponent for the effect of weight on CL was 0.705 and the exponent for the effect of weight on V was 0.635.

It should be pointed out that both body weight and age showed an influence on lamivudine clearance and volume of distribution. However, based on the magnitude of the changes in objective function (i.e. statistical criteria used for model building), body weight was found to be more influential than age on lamivudine pharmacokinetics. In addition to the statistical criteria, graphical diagnostics were used to assess the goodness of fit (see Figure S1 supplementary material for details). Although concentrations below the quantification limit were present at time 0 and 24 h, the predicted mean concentrations did not significantly differ from the observed mean concentrations (0.081 mg l⁻¹ vs. 0.098 mg l⁻¹ at time 0 h and 0.059 mg l⁻¹ vs. 0.061 mg l⁻¹ at 24 h after dose).

Model validation

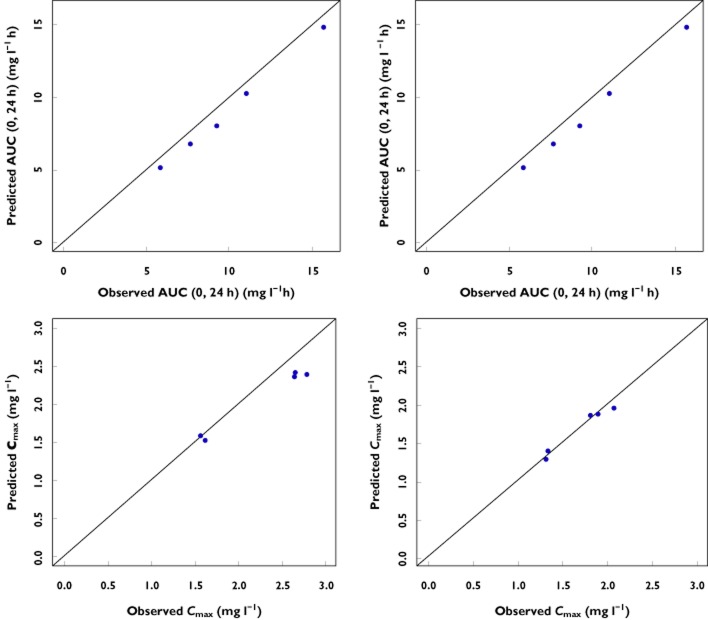
The validation procedure has been performed for twice daily and once daily data separately to ensure accurate characterization of the data irrespective of the dosing regimen. The visual predictive check (VPC) indicated model stability and absence of significant bias in the estimates for fixed and random effects. Bootstrapping was also performed as part of the validation procedure. All runs carried out (n = 500) were successful. As shown in Table 2, the final parameter estimates and their confidence intervals were very similar to the original fitting. Given that few patients between 3 to 24 months of age were included in the analysis (n = 11), scatter plots of observed vs. model predicted AUC and C_max for these subjects are shown to illustrate model performance in young children (Figure 1).

Table 2.

Summary of pharmacokinetic parameter estimates obtained from the final model. Results from the initial model built using data from PENTA 13 and PENTA 15 studies are not shown

Parameter	Notation	Population estimate*	%CV	Bootstrap mean (95% CI)
Clearance (CL)
CL/F = θ1 × (BW/med)∧ θ5
(intercept) l h−1	θ1	16.5	3.8	16.5 (15.2, 17.7)
(exponent)	θ5	0.705	14.9	0.701 (0.498, 0.911)
Volume (V)
V/F = θ2 × (BW/med)∧ θ6
(intercept) l	θ2	46.0	3.7	46.0 (42.4, 49.5)
(exponent)	θ6	0.635	14.0	0.625 (0.461, 0.809)
Absorption rate constant (Ka) 1 h−1	θ3	3.68	15.9	3.86 (1.92, 5.43)
ALAG1 h	θ4	0.755	4.5	0.755 (0.658, 0.851)
Weighing factor in $ERR	θ7	−2.69	14.7	−2.73 (−4.13, 1.24)
Interindividual variability
ηCL/F variance	ω1	0.0684 (26%†)	30.3	0.065 (0.032, 0.104)
ηV/F variance	ω2	0.0368 (19%†)	52.8	0.035 (0.009, 0.06)
ηKa variance	ω3	0.438 (66%†)	37.8	0.44 (0.098, 0.777)
Inter-occasion variability
OCCCL	ω5	0.073 (27%‡)	27.2	0.072 (0.024, 0.121)
OCCKa	ω7	0.53 (72%‡)	42.5	0.52 (0.173, 0.886)
OCCV	ω9	0.04 (20%‡)	32.73	0.039 (0.011, 0.069)
Residual error
Additive error mg l−1	σ1	0.005 (7%)	21.48	0.005 (0.002, 0.007)

^*Population parameter point estimates for the full one-compartment model are presented along with the %CV and 95% CI from a non-parametric bootstrap.

^†Value in parentheses represents the interindividual variability of the PK parameters calculated as the square root of ω × 100%.

^‡Value in parentheses represents the inter-occasion variability of the PK parameters calculated as the square root of the ω × 100%.

Figure 1.

Scatter plots of observed vs. model predicted AUC(0,24 h) (top panels) and C_max (bottom panels) for children younger than 24 months. Left panels depict children from 0 to 12 months, whereas children from 12 to 24 months are shown on the right panels

The predictive performance of the model in subsequent simulations was deemed critical to achieve the objective of our analysis. To this purpose, mirror plots were used to assess whether the variance and covariance structures have been well characterized (Figure 2). Mirror plots explore whether model parameters can accurately replicate the findings in the original study, enabling therefore further assessment of the covariate effects on dosing regimen and dose recommendations.

Figure 2.

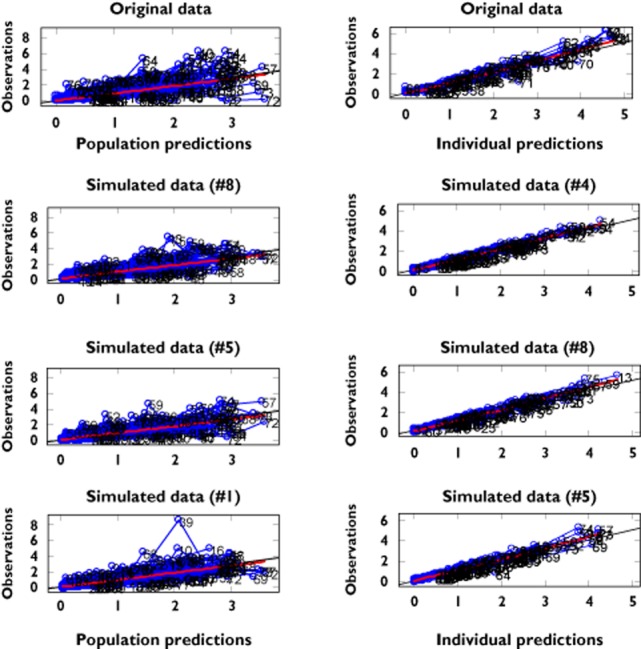
Mirror plots. Each panel shows the goodness of fit for the original data set (first on the top) and three randomly selected simulated data sets. On the left panel the mirror plots depict population predictions vs. observations. On the right panel the mirror plots depict individual predictions vs. observations

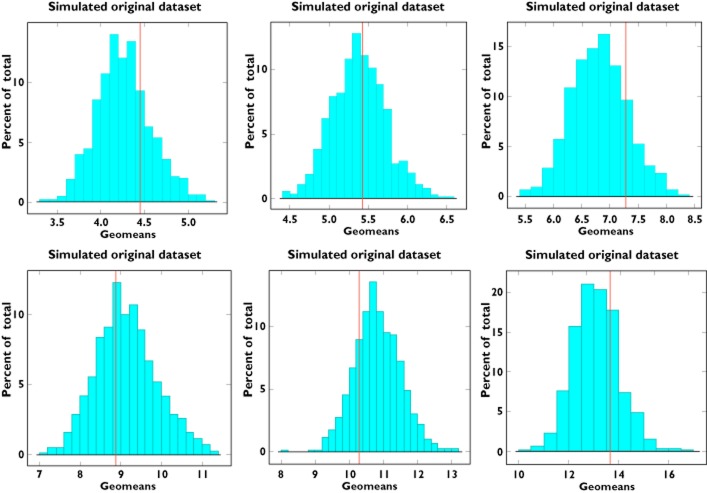
To complete the validation, a graphical summary of model performance across different weight ranges was used to assess the predicted distribution for the variable of interest [AUC (0,τ)]. As shown in Figure 3, the predicted AUC distribution encompasses the exposure observed in the original dataset.

Figure 3.

Distribution of the model-predicted area under the plasma concentration vs. time curve [AUC(0,∞)] (1000 replicate trials) compared with the original dataset. The left panels show AUC(0,∞) predictions for children weighing less than 14 kg, middle panels show AUC (0,∞) predictions for children from 14 to 21 kg and right panels show AUC(0,∞) predictions for children weighting more than 21 kg. These weight boundaries were defined according to the dosing recommendations available in the approved label. Predictions for twice and once daily doses are depicted in the upper and lower panels, respectively. The solid red line represents the geometric mean of the observed AUC(0,∞) in the three sub-groups for each dosing regimen. AUC(0,∞) = AUC(0,12 h) for twice daily and AUC(0,24 h) for once daily dosing

Discussion

Pharmacokinetic model for the paediatric population

A model-based approach has been applied in our study to describe the pharmacokinetics of lamivudine in HIV-infected children across a wide age range. A one-compartment model with first-order absorption was found to best describe lamivudine pharmacokinetics, which is consistent with previous studies in adults and children [5, 8]. In our analysis body weight was the only covariate found to influence lamivudine apparent clearance and volume of distribution, which is also in agreement with earlier investigations [5, 8, 10]. However, differently from the study in adults, creatinine clearance was not found to have an effect on lamivudine apparent clearance, probably because its effect was confounded by body weight, and patients were likely to have normal renal function. Apparent clearance estimates in our study were very similar to the literature findings in children (16.5 vs. 16.9 l h⁻¹). In addition, it was not possible to find a significant effect of the formulation on relevant pharmacokinetic parameters or to estimate a relative bioavailability of the two formulations. Similar results were reported previously by Bouazza et al. [24], whereas Kasirye et al. [25] showed in a study with 19 children (aged between 1.8 and 4 years) that lamivudine exposure was 55% higher after administration of the solid dosage form (i.e. tablet) as compared with the liquid formulation. Such differences may be partly due to dose approximation with the scored tablet as compared with the precise dose administration of the solution.

Identification of covariates in lamivudine pharmacokinetics in children

Our meta-analysis using three groups of HIV-infected children (see Table 1) included model building and validation steps to ensure predictive performance in subsequent applications of the model, as for example in clinical trial simulations. In contrast to common practice, an integrated analysis of the full population was performed after preliminary model-building based on a subset of the full population. Such a method was chosen to assess model stability and confirm the selection and magnitude of the effect of influential covariates. This approach can be particularly useful in paediatric studies, given the difficulties in identifying the correct demographic covariates, which are often highly correlated with each other [13, 14, 26]. Given that a wrong decision in covariate selection may affect future dosing recommendations, special attention should be paid to covariate model building. As shown in a previous study, the stepwise approach commonly used for covariate selection may introduce selection and omission bias in the model when the dataset used during the analysis is small [27]. In fact, in small datasets the distribution of the covariates may not allow identification of a correlation between the covariate and the pharmacokinetic parameters.

In our analyses, the initial lamivudine model accurately predicted the pharmacokinetic profiles of the group which was not used for initial model building (results not shown). The same parameter–covariate correlations were identified when the model was re-evaluated using the full paediatric population. It is important to point out that the correlation between clearance and body weight was exponential (Figure 4). For example, the apparent clearance had a median value of 9.33 l h⁻¹ for a child weighing 10 kg. It increased to 16.55 l h⁻¹ in children whose weight was 20 kg, but only increased by an additional 1.27 l h⁻¹ in children of 30 kg (17.82 l h⁻¹).

Figure 4.

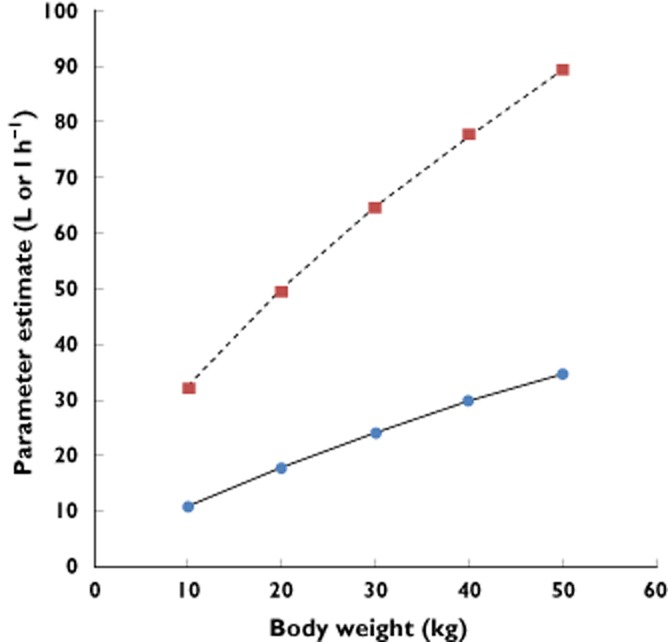
Non-linear increase in clearance () and volume of distribution () of lamivudine as a function of body weight. One of the main implications of such a pattern in drug disposition is the need to assess carefully changes in exposure when dosing regimens are defined on a mg kg⁻¹ basis. It is also clear from these curves that unbalanced distribution of the covariate can lead to model misspecification

A separate analysis of the data from the ARROW trial (age range 3 to 12 years) was also performed and a one-compartment model with first-order absorption and elimination was identified to describe best this subset of data. Very interestingly, none of the demographic covariates available was found to be significantly correlated with the pharmacokinetic parameters. Furthermore, diagnostic measures, such as the VPC of the model, were not able to show any inaccuracy or bias in model-based predictions of the data (Figure 5). These results suggest that the model could be used subsequently for dosing recommendation purposes. However, its use would yield incorrect model-based predictions in a different population since the correct parameter–covariate relationship was not identified during covariate model building. This finding strongly underlines the importance of an integrated data analysis and the risk of inaccurate covariate selection when only a part of the full population is available for analysis.

Figure 5.

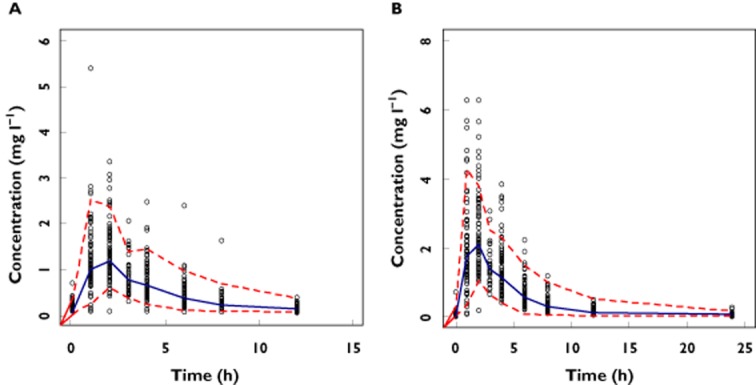
Visual predictive check (VPC) of the population model for lamivudine using only the data from the ARROW trial. The dots represent observed concentrations, whereas the dotted line represents the 95% CI of the simulated values. The solid blue line represents the median of the simulated profiles. Splitting of the data sets based on dosing regimen reveals that approximately 95% of the dots lie within the expected boundaries for both twice daily (A) and once daily (B) dosing. These results suggest absence of bias and accurate model performance irrespective of dosing regimen

The limited availability of demographic information does not imply that the proposed dosing regimen is inaccurate. The data we have used reflect the information available in a typical study protocol in HIV-infected children. On the other hand, we acknowledge that given that not only differences due to body size are relevant across wide age ranges, extrapolation of these findings to babies and infants may be inappropriate. Also maturation and potentially external factors may affect covariate–parameter correlations. Unfortunately, we could not explore the effects of renal function in the current study. Patient showing varying degrees of renal function would have enabled a more mechanistic description of the elimination of lamivudine. There are various examples in which large discrepancies in exposure are observed in the target population when doses are selected using information on the covariate effect observed in a subgroup (e.g. linezolid) [28]. Previous investigations with lamivudine have shown a prolonged half-life in children immediately after birth, with elimination increasing with renal function. Published figures based on clearance normalized by body weight (i.e. assuming linear correlation between parameter and covariate) show clearance values of 0.19–0.25 l h⁻¹ kg⁻¹ on day 1 up to 0.32–0.40 l h⁻¹ kg⁻¹ after 1 week of life, as compared with 0.53 l h⁻¹ kg⁻¹ in older children [29, 30]. Based on these findings dosing recommendation of 2 mg kg⁻¹ twice daily has been proposed for neonates. Although non-compartmental methods have been used in the aforementioned publications, these figures are considerably lower than the estimates we have obtained for clearance, which would be approximately 0.93 l h⁻¹ kg⁻¹ if we incorrectly apply the same normalization method.

Limitations of current approaches in paediatric dosing

Many examples are available in the literature of population pharmacokinetic analyses based on less than 40 patients [31–34]. In such small populations an unbalanced covariate distribution may lead to the identification and selection of wrong covariate–parameter relationships and, in turn, to wrong model-based predictions when applying the model to a different population (i.e. extrapolation). Many experts in paediatric pharmacology claim to be able to define the type and magnitude of the effect of a covariate on pharmacokinetic parameters. However they do not take into account that the parameter–covariate correlation may be biased by the covariate distribution in that particular group of children and as such should not be used in a different population. In these circumstances, one should talk about a data-driven approach, in the sense that the model is able to describe correctly the data (as shown in our analysis by the visual predictive check in Figure 5), but is not able to predict correctly the variable of interest in a different population. It is also worth mentioning that such a hidden bias is not addressed by simply increasing the sample size as often is the case in the pooled analysis of patients undergoing therapeutic drug monitoring. Meta-analyses should therefore be the preferred method in paediatric pharmacokinetics to avoid model misspecification and consequently expose children to suboptimal drug concentrations or to a higher risk of toxicity. When sufficient paediatric data are not available, one should consider overcoming the limitations of small populations by incorporating prior information from pharmacokinetic parameters in adults and include them in the model, as suggested by Cella et al. [12]. There are also other research groups, who choose not to use pharmacokinetic modelling for the analysis for drug exposure and dose selection in children. Instead, they prefer to rely solely on non-compartmental analysis, ignoring the issues highlighted above. The use of a model-based approach presents significant advantages compared with non-compartmental analysis, which cannot be overlooked from a scientific and ethical point of view.

Clinical implications of an integrated population analysis for accurate dosing recommendation

Given that drug exposure drives efficacy, it should be clear that model misspecification may lead to incorrect dosing recommendations. The identification of the correct covariate–parameter relationships is therefore crucial to predict drug exposure accurately across different groups in the paediatric population. Yet, this issue is further compounded by current prescription practices. The role of covariate–parameter correlations is apparently even more important when exploring changes in dosing regimen. For instance, we could not investigate the effect of obesity in this population. However, given the low lipophilicity of lamivudine (which is water soluble), we anticipate no major impact of obesity on its pharmacokinetics. It is conceivable that doses based on lean body mass might be required for very obese patients, as drug distribution and metabolism would not increase proportionally to total body weight.

How to dose a drug in children remains a very debatable subject. Whereas normalization of the dose by body weight makes prescription easy and reduces the risk for prescription errors, deriving dose recommendations without a thorough understanding of drug disposition in children has been proven to be unsafe and harmful [35]. Clearly, the effect of developmental growth on pharmacokinetics is a nonlinear phenomenon and as such it can be best described by a model-based approach. However, modelling and simulation techniques should be used with caution. Too little attention has been paid so far to the implications of unbalanced covariate distributions on pharmacokinetic analyses, as shown by the elevated number of examples available in the literature. We are fully aware of the challenges in performing paediatric trials and in collecting clinical data in children. These difficulties must not prompt us to neglect the problems caused by small datasets, which may lead to the wrong dose selection. The use of meta-analyses, i.e. combined datasets from available clinical trials in children, is strongly encouraged to avoid erroneous predictions of the paediatric dose.

Limitations in our approach

It is important to mention that lamivudine plasma concentrations represent a limited marker of drug exposure, as it is the intracellular lamivudine triphosphate metabolite that becomes pharmacologically active. Unfortunately adequate sampling for determination of intracellular concentrations of nucleoside transcriptase inhibitor triphosphate is logistically and technically difficult [36]. Furthermore the volume of blood needed to measure intracellular lamivudine triphosphate concentrations with current technology makes serial sampling impractical for paediatric patients.

In conclusion, the clinical relevance of a pharmacokinetic model depends on the generalizability of the covariate model across the overall population. Here we have shown that covariate effects may be under or overestimated if the available data do not support accurate identification of the correlation between parameters and covariates. Unbalanced distribution of covariates may result in hidden bias and yield inaccurate dosing recommendations in children. In addition, our work shows that the concept of pharmacokinetic bridging has been met for lamivudine, in that the dosing corrected by body weight does account for developmental growth, yielding comparable systemic exposure throughout the population older than 3 months of age.

Conflict of Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare CP had support from PENTA-LABNET and GlaxoSmithKline for the submitted work. ODP and KA are employed by GlaxoSmithKline, as indicated in their affiliations. WZ, DB, EJA and MD declare no conflict of interest. There are no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years and no other relationships or activities that could appear to have influenced the submitted work.

We thank all the children, families and staff from the centres participating in the PENTA 13, PENTA15 and ARROW studies. We acknowledge the MRC Clinical Trials Unit, London, UK and INSERM SC10, Paris, France for conducting the studies.

PENTA is a Co-ordinated Action of the European Commission (EC), supported by the Sixth Framework contract LSHP-CT-2006–018865 and Fifth Framework Program contract QLK2-2000-00150. PENTA activities are also supported by the PENTA Foundation and PENTA LABNET (EC Seventh Framework contract 201057). Financial support for PENTA 13 and 15 was also received from GlaxoSmithKline, UK.

Supporting Information

Additional Supporting Information may be found in the online version of this article at the publisher's web-site.

Figure S1

(A) Goodness of fit (left). Left upper panel shows the population prediction (PRED) vs. observed concentration values (DV). Right upper panel shows individual predictions (IPRE) vs. observed concentration values (DV). Left lower panel shows conditional weighted residuals (CWRES) vs. population predictions (PRED). Right lower panel shows conditional weighted residuals (CWRES) vs. time (TIME). Solid red line represents the identity line. (B) Visual predictive check (VPC) of the population PK model for lamivudine (right). The dots represent observed concentrations; the dotted red lines represent the 95% CI of the simulated values. The solid blue line represents the median of the simulated profiles. The VPC of the data following twice daily (left) and once daily (right) dosing shows that, approximately 95% of the dots lie within the expected boundaries. These results indicate that model predictions encompass the observed data accurately irrespective of the dosing regimen