Changes in Cytoplasmic Volume are Sufficient to Drive Spindle Scaling

Abstract

The mitotic spindle must function in cell types that vary greatly in size, and its dimensions scale with the rapid, reductive cell divisions that accompany early stages of development. The mechanism responsible for this scaling is unclear, because uncoupling cell size from a developmental or cellular context has proven experimentally challenging. Here we combined microfluidic technology with Xenopus egg extracts to characterize spindle assembly within discrete, geometrically defined volumes of cytoplasm. Reductions in cytoplasmic volume, rather than developmental cues or changes in cell shape, were sufficient to recapitulate spindle scaling observed in Xenopus embryos. Thus, mechanisms extrinsic to the spindle, specifically a limiting pool of cytoplasmic component(s), play a major role in determining spindle size.

Organelles and other intracellular structures must scale with cell size in order to function properly. Maintenance of these dimensional relationships is challenged by the rapid and reductive cell divisions that characterize early embryogenesis in many organisms. The cellular machine that drives these divisions, the mitotic spindle, functions to segregate chromosomes in cells that vary greatly in size, while also adapting to rapid changes in cell size. The issue of scale is epitomized during Xenopus embryogenesis, where a rapid series of divisions reduces cell size 100-fold - from the 1.2 mm diameter fertilized egg to approximately 12 μm diameter cells in the adult frog (1). In large blastomeres, spindle length reaches an upper limit that is uncoupled from changes in cell size. As cell size decreases, however, a strong correlation emerges between spindle length and cell size (2). Although this scaling relationship has been characterized in vivo for several different organisms, little is known about the direct regulation of spindle size by cell size or the underlying mechanism(s) (2–4). Spindle size may be directly dictated by the physical dimensions of a cell, perhaps through microtubule-mediated interaction with the cell cortex [i.e. boundary sensing; (5–7)]. Alternatively, cell size could constrain spindle length by providing a fixed and finite cytoplasmic volume and, therefore, a limiting pool of resources such as cytoplasmic spindle assembly or length-determining components [i.e. component limitation; (8, 9)]. Lastly, mechanisms intrinsic to the spindle could be actively tuned in response to systematic changes in cytoplasmic composition occurring during development [i.e. developmental cues; (10, 11)].

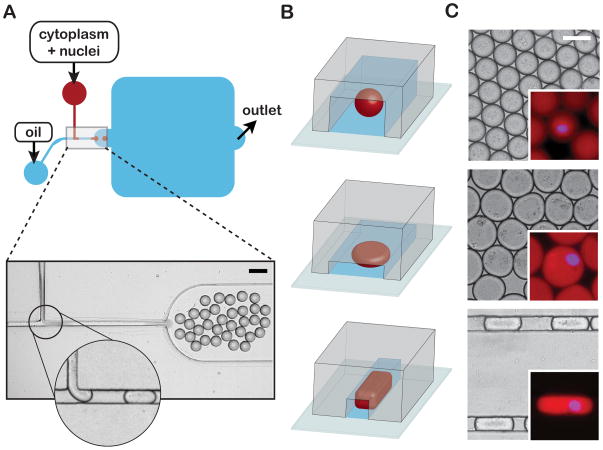
To elucidate the responsible scaling mechanism(s), we developed a microfluidic-based platform to confine spindle assembly in geometrically defined volumes of Xenopus egg extract (12). Interphase extract containing Xenopus sperm nuclei was induced to enter mitosis and immediately pumped into a microfluidic droplet-generating device prior to nuclear envelope breakdown and the onset of spindle assembly. At the same time, a fluorinated oil/surfactant mixture was pumped into the device through a second inlet. These two discrete, immiscible phases merged at a T-shaped junction within the device to produce stable emulsions of extract droplets in a continuous oil phase (Fig. 1, A and C). Changing the T-junction channel dimensions and relative flow rates of the two phases enabled us to tune droplet volume. Droplet shape could be controlled independently by changing the geometry and dimensions of the device’s collection region. In this way, we were able to produce three distinct geometries; spheres, flattened discs, and axially elongated “slugs” (Fig. 1, B and C). Following encapsulation, nuclei size and shape resembled that of their unencapsulated counterparts (Fig. 1C), suggesting that the process of droplet-generation did not appreciably perturb nuclear morphology.

Fig. 1.

Microfluidic encapsulation of nuclei in cytoplasmic volumes of defined size and shape. (A) Top panel - Simplified schematic of a PDMS microfluidic device featuring a classic T-junction droplet generator and collection reservoir (blue rounded-square). An extract phase containing nuclei (red) is continuous until sheared off into droplets by the oil/surfactant phase (blue). Bottom panel - a representative image of droplet generation at a standard T-junction. The magnified inset shows a formed droplet moving toward the collection reservoir and another about to be sheared from the extract phase (see Movie S1). Scale bar = 100 μm. (B) Alternative droplet shapes result from changing the collection reservoir geometry: spheres (top panel), flattened disks (middle panel) and elongated slug-shaped droplets (bottom panel). (C) Representative micrographs of spheres, discs, and slugs contained within reservoirs/channels. Scale bar = 50 μm. Insets: Magnified images of droplets encapsulating “cycled” interphase sperm nuclei. Nuclear DNA was stained with DAPI to access nuclear morphology (blue) and soluble tubulin (pseudo-colored red, labeled with Atto-488) was used to visualize droplet boundaries. All droplets are approximately isovolumetric. Inset scale bar = 50 μm.

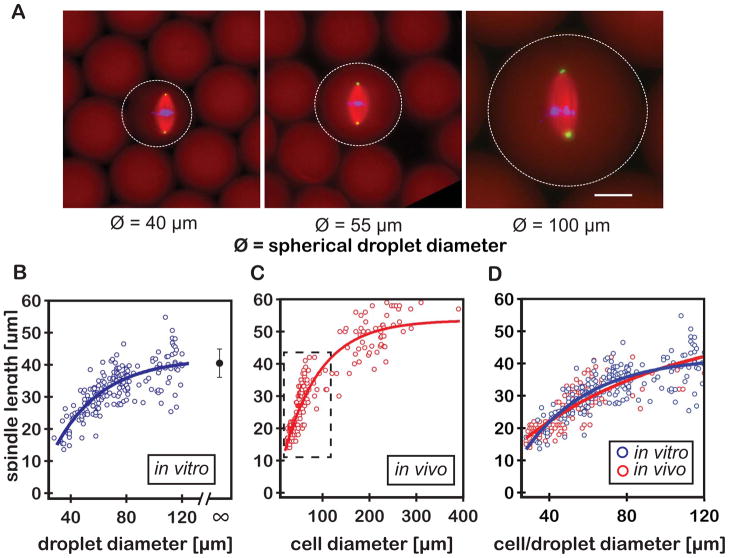
To examine the relationship between steady-state spindle length and cytoplasmic volume, interphase nuclei were encapsulated within spherical droplets ranging in diameter from 20–120 μm. Bipolar spindle assembly was observed in droplets of greater than ~30 μm diameter, permitting measurements of spindle length using fluorescence microscopy (Fig. 2, A and B). Spindles exhibited isometric scaling, so we used the single metric of spindle length to serve as a reasonable proxy for spindle “size” (Fig. 2A). This also allowed direct comparisons with previously published scaling data in which length was the only reported spindle dimension. These measurements defined two distinct regimes that described the relationship between spindle length and droplet diameter: in droplets with diameters larger than ~80 μm, spindle length was relatively constant, reaching an upper limit similar to the average spindle length found in unencapsulated extract (~40.5 ± 4.4 μm), whereas in smaller droplets, spindle length scaled almost linearly with droplet diameter (Fig. 2B).

Fig. 2.

Developmental spindle scaling can be recapitulated in vitro in the absence of developmental cues or a functional cell cortex. (A) Representative fluorescent images of spindles assembled in spherical extract droplets of various sizes. Spindles were labeled by adding fluorophores to the extract prior to droplet formation; tubulin to visualize microtubules (pseudo-colored red, labeled with Atto-488), DAPI to visualize DNA (blue), and directly labeled antibodies against NuMA to visualize spindle poles (pseudo-colored green, Atto-568 α-NuMA). Dashed circles indicate droplet boundaries as visualized by the extent of soluble labeled tubulin. Scale bar = 25 μm. (B) Spindle length plotted as a function of encapsulating droplet diameter (blue open circles, n=96 spindles). The single black circle indicates the average spindle length in unencapsulated extract (mean +/− SD; n=81 spindles). (C) Spindle length at metaphase plotted as a function of cell size during early (stage 8 to 9) Xenopus embryo development (red open circles, adapted from (2)). (D) Comparison of spindle scaling in vitro and in vivo (blue and red open circles, respectively; with corresponding fits). Each data set was fit using a three-parameter equation that assumes asymptotic growth (solid lines in Fig. 2, B to D; fig. S1 and S2).

These results shared remarkable similarity with spindle scaling observed during Xenopus development, particularly in the linear scaling regime (2) (Fig. 2, C and D). Within their respective scaling regimes, asymptotic growth fits to the in vivo and in vitro data sets were statistically indistinguishable (solid lines in Fig. 2, B to D; fig. S1 and S2), suggesting that our in vitro system recapitulated the scaling observed in vivo. Scaling was observed in droplets ranging in diameter from ~30 to 80 μm, corresponding to cell sizes typical of Stage 8 and Stage 9 of Xenopus development (Fig. 2D), a temporal window that encompasses the mid-blastula transition and the onset of zygotic transcription (13, 14). Because Xenopus egg extracts are effectively static in a developmental context, changes in cytoplasmic composition that might affect scaling in the intact embryo do not occur in our system (e.g. (15)). Thus, developmental cues can be eliminated as a potential model for the spindle scaling observed in these droplets, leaving the two remaining hypothetical mechanisms, component limitation and/or boundary sensing.

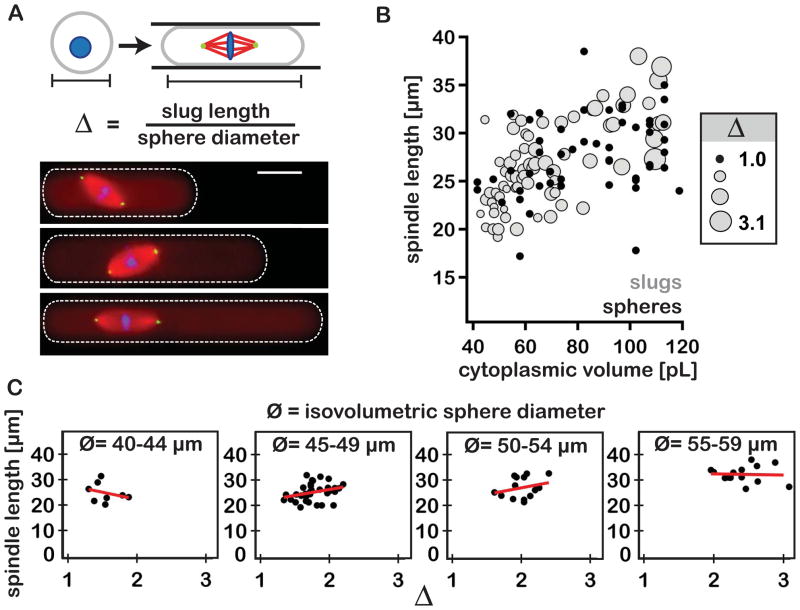
A boundary sensing mechanism predicts that changing the physical dimensions of the encapsulating droplet, while holding droplet volume constant, should impact spindle length. To test this model, the lengths of spindles assembled in spheres were compared to those assembled in longer, isovolumetric slugs. Employing slugs as opposed to flattened spheres allowed spindle assembly to be restricted in two of three dimensions over a broader aspect ratio range (Fig. 3A). To ensure that encapsulated spindle lengths could vary in response to changes in droplet shape, slugs used in these experiments were generated by geometrically confining spheres ranging in diameter from 40–60 μm (the approximate midpoint of the scaling regime; Movie S2). Differences in spindle lengths for these two extract droplet geometries were statistically indistinguishable (Student’s t-test, p = 0.2 for all slug and sphere data between 40–60 μm). Furthermore, spindle length remained relatively constant despite three-fold increases in slug length over a narrow range of cytoplasmic volumes (Fig. 3, B and C, fig. S3). Collectively, these results opposed the predictions of a boundary sensing model for spindle length regulation and suggested that cytoplasmic shape was not likely a major determinant of spindle length.

Fig. 3.

Reductions in cytoplasmic volume account for the spindle scaling observed in vitro. (A) Top panel – cartoon depicting the transformation of spherical droplet into an isovolumetric slug, and the calculation of extent of elongation (Δ). Bottom panel - fluorescent images of representative spindles assembled in slugs of increasing Δ. Fluorophores were added to the extract as described in Fig. 2. (B) Graph shows spindle length plotted as a function of droplet cytoplasmic volume. For shaded markers (grey circles, n=71 spindles), marker size is proportional to the ratio of slug long axis length over the diameter of an isovolumetric sphere (i.e. extent of elongation, denoted as Δ). Solid markers (black circles) represent data derived from spherical droplets (i.e. Δ=1, n=96 spindles). (C) Plots of spindle length as a function of extent of elongation under near-isovolumetric conditions (i.e. binned by isovolumetric sphere diameter, Ø). Linear trend lines (red) exhibit variable slopes indicating a lack of a constant relationship between the two measurements.

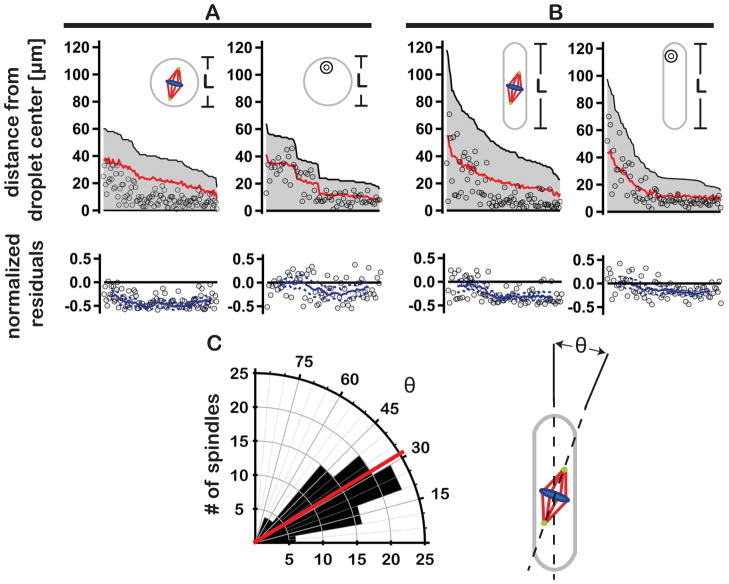
Through a variety of different mechanisms, spindles in vivo demonstrate a remarkable ability to correctly position themselves near the cell center prior to the onset of anaphase and cytokinesis. (16–20). Each implicitly requires the spindle be able to “sense” its position relative to cellular boundaries. In the absence of boundary sensing, spindle position within a cell (or a confining extract volume) is expected to be random. To test this prediction, we plotted spindle position relative to the volumetric centers of confining spheres and slugs (Fig. 4, A and B). In both geometries, spindles tended to localize toward the droplet center, to a greater extent than expected for uniform random positioning (Fig. 4, A and B; Movies S3). This trend was more pronounced in smaller droplets (Fig. 4, A and B residual plots). In contrast, the positions of encapsulated polystyrene beads aligned more closely with average random positions (Fig. 4, A and B residual plots; figs. S1 and S2 and Movie S4). This suggested that the weak convective flows observed in some slugs were likely not responsible for spindle centering (e.g. see Movie S5). The distribution of spindle orientations relative to the slug long axis was found to be 31 ± 16° (Fig 4C), indicating that, like in cells, a spindle is more likely to align parallel to the long-axis of its enclosure (21), even in the absence of a cortical membrane and associated pulling forces. Indeed, peripheral spindle microtubules extend well beyond the spindle proper, effectively increasing its size (22). Perhaps these peripheral microtubules exert pushing forces against droplet boundaries resulting in centering (23). Alternatively, spindle proximity to a droplet boundary might influence the distribution of forces generated by microtubule-associated motors pulling against the bulk cytoplasm (19, 24). Thus, a boundary sensing mechanism might indeed work to affect spindle position, but contributes little, if at all, to determining spindle length.

Fig. 4.

Spindles exhibit non-random positioning in spheres and slugs. (A) Plots show the positions of spindles (left panel) and polystyrene beads (right panel) within spherical droplets. Black lines in each of the plots reflect the distance between the droplet center and its most distal edge (L/2, shown schematically in insets). Open circles indicate the positions of spindles/beads in relation to the droplet center. Red lines depict the average absolute displacement of spindles/beads expected for uniform random positioning (see supplementary material). Corresponding residual plots show the normalized difference between the center-to-center position of the spindle or bead and the theoretical random position. Solid blue lines represent the moving average of residual values (with upper and lower 95% confidence intervals indicated by dashed blue lines). (B) As in A, spindle and bead positions in axially elongated slugs. (C) Spindle orientation in slugs. Left panel - polar histogram plot showing the angle θ between the interpolar spindle axis and the long axis of the confining slug (red line indicates the average orientation angle; n = 89 spindles). Right panel – cartoon depicting the determination of angle θ.

Collectively, our data indicate that changes in cytoplasmic volume are sufficient to account for the spindle scaling as it occurs in vivo (2). By eliminating alternative hypothetical models, the data support a scaling mechanism in which a limiting pool of cytoplasmic component(s) regulates spindle length (8, 11). In large droplets or cells, like in unbounded extract, spindle length appears to be constrained by mechanisms intrinsic to the spindle (2, 25). Once cytoplasmic volume is reduced to a critical threshold, components become limited, which produces smaller spindles. This process serves as a passive, yet robust way for cells to control the size of their spindles and possibly other internal structures.