Generalized Dynamic Factor Models for Mixed-Measurement Time Series

Abstract

In this article, we propose generalized Bayesian dynamic factor models for jointly modeling mixed-measurement time series. The framework allows mixed-scale measurements associated with each time series, with different measurements having different distributions in the exponential family conditionally on time-varying latent factor(s). Efficient Bayesian computational algorithms are developed for posterior inference on both the latent factors and model parameters, based on a Metropolis Hastings algorithm with adaptive proposals. The algorithm relies on a Greedy Density Kernel Approximation (GDKA) and parameter expansion with latent factor normalization. We tested the framework and algorithms in simulated studies and applied them to the analysis of intertwined credit and recovery risk for Moody’s rated firms from 1982–2008, illustrating the importance of jointly modeling mixed-measurement time series. The article has supplemental materials available online.

1 Introduction

Multiple co-evolving time series or data streams consisting of either discrete (binary, categorical and counts) or continuous outcomes are ubiquitous in many applications areas. An effective approach of jointly modeling mixed-measurement time series and thus sharing information is essential to characterizing the dependence among the variables and can improve prediction and interpolation across missing data regions. In this paper, we propose generalized Bayesian dynamic factor models for jointly modeling mixed-measurement time series. Efficient computational algorithms are also developed for Bayesian inference and prediction.

There has been a rich history of jointly modeling mixed outcomes involving binary, categorical and continuous variables, using either underlying Gaussian models (Muthen (1984)) or generalized latent trait models (GLTM) that specify GLMs for each response with shared latent factors (Moustaki and Knott (2000) and Dunson (2000)). Underlying Gaussian models assume categorical manifest variables arise by thresholding normal underlying variables. This leads to substantial computational simplifications, as algorithms for Gaussian latent factor models can be easily adapted. However, the price to be paid for computational efficiency is lack of modeling flexibility in that categorical variables will be assigned probit models and count variables cannot be naturally accommodated. Although substantial flexibility can be gained through using mixtures of underlying Gaussian models (Yang and Dunson (2010)), there is an associated price in terms of computational and modeling complexity.

The GLTM framework represents a compromise in that it is much more flexible than the underlying Gaussian framework, while maintaining a simple parametric form. For example, counts can be characterized via Poisson log-linear models, and categorical variables via logistic regressions. Dunson (2003) applied GLTMs to dynamic modeling of mixed scale multivariate longitudinal data, specifying GLMs for each variable. Time-varying Gaussian latent factors were included, assuming a discrete Markov model. However, substantial computational challenges result outside of the underlying Gaussian framework. In particular in Bayesian analysis, one can no longer specify conditionally-conjugate priors and implement simple Gibbs sampling algorithms. Although adaptive rejection sampling can be used within Gibbs samplers, the sampler chains are commonly poorly behaved due to high posterior dependence in the model parameters leading to slow mixing (Ghosh and Dunson (2009)). Such problems are particularly prevalent in dynamic factor models. Therefore, latent factor models with distributions in the exponential family are much more challenging computationally than the underlying normal model class.

When it comes to multivariate time series analysis, the literature has focused primarily on joint models for multiple time series with normal (or conditionally normal) observations. Latent factor models, among other multiple time series analysis approaches, are useful tools for both dimension reduction and characterizing dependency between multiple time series (Anderson (1963) and Hamann et al. (2005)). In the absence of mixed-measurement data, the latent time-varying factors can be analyzed using either principal component analysis in an approximated dynamic factor framework (see e.g. Stock and Watson (2002), Bai (2003), Bai and Ng (2002), Zhang et al. (2012) and Mohamed et al. (2008)), frequency domain methods (Boashash (2006)), or filtering and smoothing techniques as in the state-space framework (Aguilar and West (2000) and Jungbacker and Koopman (2008)). Alternatively, Zhang and Nesselroade (2007) used an underlying Gaussian variable approach to jointly model multiple categorical time series. However, little effort has been made to jointly model mixed-measurement time series.

Motivated by providing a flexible and computationally efficient framework for mixed-measurement time series analysis, we propose the use of generalized Bayesian dynamic factor model. The framework allows mixed scale measurements in different time series, with the different measurements having distributions in the exponential family conditional on time-specific dynamic latent factors. Efficient computational algorithms for Bayesian inference are also developed, which, as shown later, can be easily extended to mixed-measurement time series with missing values and/or mixed-frequency. Briefly, a Metropolis Hastings algorithm with adaptive proposals is developed to efficiently obtain posterior samples of time-varying latent factors. The algorithm is based on a Greedy Density Kernel Approximation (GDKA) via a mixture of normal distributions and further combined with the forward filtering backward sampling algorithm. In addition, parameter expansion with latent factor normalization is proposed to improve the efficiency of sampling model parameters. These steps are further embedded in a higher-level MCMC sampler, which gives efficient updating, improved inference, and prediction.

We introduce the general framework of Bayesian dynamic factor modeling for mixed-measurement time series in Section 2. Section 3 describes computational algorithms developed for Bayesian inference on both latent factors and model parameters. Section 4 applies the model and algorithms to simulated data sets. In section 5 the model is applied to jointly modeling corporate default risk, bond recovery rates and business cycles. Section 6 contains a discussion of the model and results.

2 Proposed Modeling Framework

Consider p mixed-measurement time series y_t = {y_it} (i = 1, …, p, and t = 1, …, T), with y_it denoting the value of the i^th time series at time point t, and the points assumed to be equally-spaced. Each time series can have a different measurement scale, so, for example, y_1t may be binary, y_2t a count and y_3t continuous. We follow the setting of Dunson (2003) and jointly model the mixed-measurement time series y_t via m common latent dynamic factors η_t = (η_t1, …, η_tm)′ (t = 1, …, T) and time series-specific observed covariates z_it.

Conditional on a factor path (η₁, …, η_T), the observation y_it is modeled as coming from a distribution in the exponential family with canonical parameter θ_it:

$$y_{it}~f_i({\theta }_{it},{\phi }_i).$$ (2.1)

The canonical parameters are defined by a generalized linear model linked to the latent factors and observed covariates:

$$h_i({\theta }_{it})={\alpha }_i+z_{it}^{\prime }{\beta }_i+{\mathrm{\Lambda }}_i{\eta }_t,$$ (2.2)

where h_i(·) is the link function for the i^th time series, α_i is the intercept term, z_it is a b × 1 vector of observed covariates at time t, β_i is a b × 1 parameter vector, η_t is m × 1 latent factor vector at time t, and Λ_i is 1 × m factor loading vector. Let $\mathrm{\Lambda }={[{\mathrm{\Lambda }}_1^{\prime },\dots ,{\mathrm{\Lambda }}_m^{\prime }]}^{\prime }$ denote the factor loading matrix. Considering identifiability of factors, Λ is lower-triangular with positive elements on the diagonal.

For simplicity in exposition, a stationary VAR(1) vector autoregressive process is assumed for the equally spaced m-dimensional factor η_t (2.3). However, the methods are easily modified to place arbitrary Gaussian process priors on continuous time factors to accommodate unequally-spaced and mixed-frequency time series. For example, a simple yet flexible choice corresponds to the Ornstein-Uhlenbeck (O-U) process prior (Barndorff-Nielsen and Shephard (2001)).

Considering the identifiability of latent factors, the covariance matrix of η₁ is set to I_m, and mean is set to 0 (in this paper, N(mean, precision) is used in this paper to represent Normal distributions), and we let

$$\begin{array}{l}{\eta }_1~N(0,I_m)\\ {\eta }_t=A_{\eta }{\eta }_{t-1}+{\epsilon }_t,{\epsilon }_t~N(0,{\mathrm{\sum }}_{\eta }^{-1}),t=2,\dots ,T\\ \text{where}{\mathrm{\sum }}_{\eta }={\mathrm{\Phi }}_{\eta }^{-1}=I_m-A_{\eta }{A}_{\eta }^{\prime }\end{array}$$ (2.3)

Conditional on the factor path (η₁, …, η_T), the covariates z_1:T and all other model parameters Θ, the observations y_1:T are independent of each other, which implies that the likelihood is of the form

$$f({\mathbf{y}}_{1:T}\mid {\eta }_{1:T},{\mathbf{z}}_{1:T},\mathrm{\Theta })=\prod _{t=1}^T\prod _{i=1}^{m}f(y_{it}\mid {\eta }_{1:T},{\mathbf{z}}_{1:T},\mathrm{\Theta })$$ (2.4)

Further combined with the Bayesian computational algorithms explored in the next section, the model allows missing data on a subset of the time series and/or mixed-frequency.

3 Computational Algorithms for Bayesian Inference

For Bayesian computation in dynamic generalized latent trait models, Dunson (2003) proposed to use one-at-a-time Gibbs updates with adaptive rejection sampling (ARS) to sample from the full conditional posterior distributions of the model parameters and latent factors. There are several problems that arise with this approach. First, ARS can be slow as many sampling and updating steps are needed. Second, due to high posterior dependence in the unknowns, one-at-a-time Gibbs samplers tend to be very slow to converge and mix. This is particularly the case as the number of time points increases, with computation becoming completely infeasible for moderate to large T. To address these problems, we propose a Metropolis Hastings algorithm with adaptive proposals, which relies on a Greedy Density Kernel Approximation (GDKA) via mixture of normal distributions, to efficiently draw samples of latent factors in a block. For efficient updating of model parameters, parameter expansion techniques are proposed and combined with latent factor normalization to improve mixing.

3.1 Sampling Latent Factors – Background

Posterior computation in latent factor time series models shares many characteristics with similar issues in state-space models, where sequential filtering and backward sampling (FFBS) using Monte Carlo is pivotal. In the absence of mixed-measurement data, when smoothing distributions of the states do not have closed forms, computational techniques based on sequential Monte Carlo (Liu and West (2001)), particle filtering and using approximated distributions have been proposed for non-linear and non-Gaussian state-space models (see e.g. Harrison and Stevens (1971), Sorenson and Alspach (1971), Alspach (1974) and more recently Ravines and Schmidt (2007)). Stroud et al. (2003) further proposed to jointly update all unobserved states by using a Metropolis Hastings proposal that approximates the exact conditional posterior. Closer to our perspective is the recent work of Niemi and West (2010), who proposed adaptive mixture approximations by matching moments for the smoothing distributions in non-linear state-space models. However, most of the these algorithms are not designed for cases with multidimensional mixed-measurement response data, in which presence of multiple exponential family distributions of data makes sequential approximation of smoothing distributions more computationally challenging, especially when missing data exist.

In this paper, we proposed a fast and efficient Greedy Density Kernel Approximation (GDKA) to the smoothing distributions via mixtures of Gaussian kernels. The GDKA needs to be performed for each filtering step and chooses mixture Gaussian backward sampling distributions. Assuming the approximations are reasonably accurate, Metropolis Hastings steps based on the approximated mixture of normal distributions as proposals (the actual proposal distributions are based on the mixtures of normals approximation, modified to have heavier tails) jointly update latent factors efficiently.

3.2 Sampling Latent Factors – Approximating Filtering Distributions

Let α_t(η_t) denote the forward filtering function at time t

$${\alpha }_t({\eta }_t)=f({\eta }_t\mid {\mathbf{y}}_{1:t})$$

We have the recursive relationship between time t and t+1

$${\alpha }_{t+1}({\eta }_{t+1})\propto \left[\int {\alpha }_t({\eta }_t)f({\eta }_{t+1}\mid {\eta }_t)d{\eta }_t\right]·f(y_{i,(t+1)},\forall i\mid {\eta }_{t+1})$$ (3.5)

For simplicity of exposition, we focus on the case η_t is one-dimensional. Clearly, the computational bottleneck is that α_t(η_t) does not have an analytic form with mixed-measurement time series, making it infeasible to perform filtering and smoothing. To tackle this, we propose to use a Greedy Density Kernel Approximation (GDKA) to approximate the forward filtering functions α_t(η_t) over a compact domain Ω via mixtures of K Gaussian kernels:

$${\alpha }_t({\eta }_t)\approx \sum _{k=1}^K{w}_{tk}N({\eta }_t;{\mu }_{tk},{\phi }_t),w_{tk}\ge 0.$$ (3.6)

Suppose there are N_t pairs of $\{{\alpha }_t({\eta }_t^{(i)}),{\eta }_t^{(i)}\}(i=1,\dots ,N_t)$ over domain Ω available compromising a training set, and let ${\mathrm{\Gamma }}_t={({\mathrm{\Gamma }}_t^{(1)},\dots ,{\mathrm{\Gamma }}_t^{(N_t)})}^T$ be a N_t × 1 vector with ${\mathrm{\Gamma }}_t^{(i)}\propto {\alpha }_t({\eta }_t^{(i)})$. Then GDKA via a mixture of K Gaussian kernels has the form:

$${\widehat{\mathrm{\Gamma }}}_t^{(i)}=\sum _{k=1}^K{w}_{tk}exp\left(-\frac{{\phi }_t}{2}{\left|\right|{\eta }_t^{(i)}-C_{tk}\left|\right|}^2\right),\text{where}{w}_j\ge 0$$

where C_tk (k = 1, …, K) are centers (means) of Gaussian kernels, and φ_t is the Gaussian precision, which are set to be the same for all K kernels. Letting H_t denote the distance matrix with $H_{t,i,k}=exp\left(-\frac{{\phi }_t}{2}{\left|\right|{\eta }_t^{(i)}-C_{tk}\left|\right|}^2\right)$, (i = 1, …, N_t, k = 1, …, K), and w_t = (w_t1, …, w_tK)^T be a K ×1 vector of the weights, we can represent the fitting/approximation problem in the regression form:

$${\mathrm{\Gamma }}_t=H_t{\mathbf{w}}_{\mathbf{t}}+{\epsilon }_t$$ (3.7)

Given the means and variances of the Gaussian kernels, the best approximation can be achieved by minimizing the residual errors. The optimal weights are:

$${\widehat{\mathbf{w}}}_{\mathbf{t}}=\mathit{arg}\underset{{\mathbf{w}}_{\mathbf{t}}}{min}{\left|\right|{\epsilon }_t\left|\right|}^2;\text{subject}\text{to}:{\mathbf{w}}_{\mathbf{t}}\ge 0;$$ (3.8)

If we cannot be sure that H_t is well conditioned or even a full ranked matrix, a regularized least square solution is:

$${\widehat{\mathbf{w}}}_{\mathbf{t}}=\mathit{arg}\underset{{\mathbf{w}}_{\mathbf{t}}}{min}{\left|\right|{\epsilon }_t\left|\right|}^2+\alpha {\left|\right|{\mathbf{w}}_{\mathbf{t}}\left|\right|}^2;0<\alpha \ll 1;\text{subject}\text{to}:{\mathbf{w}}_{\mathbf{t}}\ge 0;$$ (3.9)

It is trivial to prove that with the non-negative constraints, the quadratic optimization problem always has a unique solution.

Clearly, specification of number of kernels used (K), choice of training pairs, Gaussian centers C_tk and Gaussian precision φ_t is critical for the approximation. In details, to form the training pairs, a grid of N_t equally-spaced α_t are chosen within a compact domain on which the density α_t(η_t) is above certain threshold. In our studies, we chose the threshold of α_t(η_t) to be > 10⁻³ relative to the mode of the filtering distribution (Note that the filtering distributions have to be uni-modal if the observations are assumed to be coming from distributions in the exponential family). Gaussian centers are chosen from the N_t training points α_t. Given equation (3.7), choosing a greedy set of K Gaussian centers from N_t values of α_t can be achieved using the forward-selection algorithm as in the variable selection settings in linear regression problems. For the value of K, in our preliminary simulation studies, we found that K = 20 provides reasonably good approximations to a variety of distributions based on our algorithm, so in all our studies, we chose K to be 20. A greedy search step is also included within GDKA to find a reasonable value of φ_t. A detailed step-by-step procedure for GDKA is shown in Section A (in the appendix), and an example is shown in Figure S1 to show the fine approximation.

With the approximated α_t(η_t), forward filtering can be conducted sequentially. Let ψ_t(η_t+1) = ∫ α_t(η_t)f(η_t+1|η_t)dη_t ∝ f(η_t+1|y_i1, …, y_i,t, ∀i) denote the one-step prediction function (the integral part in the filtering function). Then we have:

$$\begin{array}{l}{\psi }_t({\eta }_{t+1})\propto \sum _k{w}_k^{\ast }N({\eta }_{t+1};{\mu }_k^{\ast },{\phi }_k^{\ast }),\\ \text{where}{w}_k^{\ast }=w_{tk},{\mu }_k^{\ast }=A_{\eta }{\mu }_{tk},{\phi }_k^{\ast }=\frac{{\phi }_{tk}{\mathrm{\Phi }}_{\eta }}{{\phi }_{tk}+A_{\eta }^2{\mathrm{\Phi }}_{\eta }},\end{array}$$ (3.10)

with A_η, μ_η and Φ_η defined in (2.3), and w_tk, μ_tk, φ_tk from (3.6).

With the approximated closed-form ψ_t(η_t+1), we can evaluate α_t+1(η_t+1), generate N_t+1 training pairs $\{{\eta }_{t+1}^{(i)},{\alpha }_{t+1}({\eta }_{t+1}^{(i)})\}(i=1,\dots ,N_{t+1})$ and approximate α_t+1(η_t+1) using the same GDKA algorithm we used to approximate α_t(η_t), and obtain the updated filtering function α_t+1(η_t+1):

$${\alpha }_{t+1}({\eta }_{t+1})\propto \sum _k{w}_{t+1,k}N({\eta }_t;{\mu }_{t+1,k},{\phi }_{t+1,k})$$ (3.11)

The normalizing constant is not involved in the computation, and the nature of the recursion relationship implies that we can start with approximating α₁(η_t) ∝ π₀(η₁)L(η₁|y_i1, ∀i), and then proceed with sequentially approximating each α_t(η_t).

3.3 Sampling Latent Factors – Backward Sampling Distributions

Given the approximated filtering functions, backward sampling distributions π_t(·) (t = 1, …, T) can be approximated straightforwardly via π̂_t(·):

$$\begin{array}{l}{\widehat{\pi }}_T({\eta }_T\mid {\mathbf{y}}_{1:T})={\alpha }_T({\eta }_T)\propto \sum _k{w}_{Tk}N({\eta }_T;{\mu }_{Tk},{\phi }_{Tk}),\\ {\widehat{\pi }}_{t-1}({\eta }_{t-1}\mid {\eta }_t,{\mathbf{y}}_{1:T})\propto \sum _k{\stackrel{\sim }{w}}_{t-1,k}N({\eta }_{t-1};{\stackrel{\sim }{\mu }}_{t-1,k},{\stackrel{\sim }{\phi }}_{t-1,k}),\\ \text{where}{\stackrel{\sim }{w}}_{t-1,k}=w_{t-1,k}exp\left(\frac{A_{\eta }{\mathrm{\Phi }}_{\eta }{\mu }_{t-1,k}{\phi }_{t-1,k}[2({\eta }_t-{\mu }_{\eta })-A_{\eta }{\mu }_k^{(t-1)}]}{2({\phi }_k^{(t-1)}+A_{\eta }^2{\mathrm{\Phi }}_{\eta })}\right),\\ {\stackrel{\sim }{\mu }}_{t-1,k}=\frac{{\mu }_{t-1,k}{\mathrm{\Phi }}_{\eta }+A_{\eta }{\mathrm{\Phi }}_{\eta }({\eta }_t-{\mu }_{\eta })}{{\phi }_{t-1,k}+A_{\eta }^2{\mathrm{\Phi }}_{\eta }},\\ {\phi }_{t-1,k}={\phi }_{t-1,k}+A_{\eta }^2{\mathrm{\Phi }}_{\eta },\end{array}$$ (3.12)

with A_η, Φ_η defined in (2.3), and w_t−1,k, μ_t−1,k, φ_t−1,k from (3.6).

Given (3.12) the joint posterior distribution of all latent factors can be approximated by a sequential product of mixture of normals:

$$\widehat{\pi }({\eta }_{1:T}\mid {\mathbf{y}}_{1:T})\propto {\widehat{\pi }}_T({\eta }_T\mid {\mathbf{y}}_{1:T})\prod _{t=2}^T{\widehat{\pi }}_t({\eta }_{t-1}\mid {\eta }_t,{\mathbf{y}}_{1:T})$$ (3.13)

3.4 Sampling Latent Factors – Metropolis Hastings Updating

Using the approximated joint posterior distribution π̂(η_1:T |y_1:T ) of the latent factors as proposal distributions, sample paths of latent factors can be drawn from a Metropolis Hastings step. For practical reasons, the approximated joint posterior distribution π̂(η_1:T |y_1:T ) is further combined with a mixture of corresponding heavier-tailed Cauchy distributions π̃(η_1:T |y_1:T ), forming the proposal distribution g(η_1:T |y_1:T ) (as shown in (3.14)), to avoid irregular behaviors of the Markov chain in the tail region:

$$g({\eta }_{1:T}\mid \mathbf{y})=p_{\eta }\widehat{\pi }({\eta }_{1:T}\mid {\mathbf{y}}_{1:T})+(1-p_{\eta })\stackrel{\sim }{\pi }({\eta }_{1:T}\mid {\mathbf{y}}_{1:T})$$ (3.14)

where 0 ≪ p_η < 1 is the weight of the approximated joint distribution. p_η = 0.95 is used in all the following computations.

The Metropolis Hastings step in the (m + 1)^th iteration of the MCMC then proceeds by:

1. Generate the entire block of candidate values γ^m+1 for η = η_1:T from the proposal distribution ~ g(·), with g(·) following (3.14).

2. Accept the candidate and let η ^(m+1) = γ ^(m+1) with probability $min\left(1,\frac{\pi ({\gamma }^{(m+1)})g({\eta }^{(m)})}{\pi ({\eta }^{(m)})g({\gamma }^{(m+1)})}\right)$ where π(·) is the unnormalized posterior full conditional joint distribution of latent factors. η_1:T. Otherwise, let η ^(m+1) = η ^(m).

3.5 Sampling Model Parameters

For models with other parameters Θ in addition to the latent factors, the above latent factor sampler is applied at each stage of an MCMC algorithm that also includes steps for updating Θ. To reduce slow-mixing which is common in MCMC algorithms for latent factor models, we combine parameter expansion with latent factor normalization to induce default priors and improve computational efficiency for model parameters.

Parameter Expansion (PX) has been introduced as a useful approach for both introducing new families of prior distributions and improving computational efficiency (Liu and Wu (1999), Gelman (2004) and Kinney and Dunson (2007)). Ghosh and Dunson (2009) used parameter expansion in Bayesian Gaussian factor analysis to induce heavy-tailed priors for factor loadings and improve mixing of samplers simultaneously. In this paper, we extend the parameter expansion technique to the Bayesian dynamic factor model setting with mixed-measurement data. Basically, parameter expansion introduces a working model that is over-parameterized, and parameters in the working model are then transformed back to parameters in the inferential model.

Considering model (2.1)–(2.3) as our inferential model, we define the following working PX-factor model:

$$\begin{array}{l}{h}_i({\theta }_{it})={\alpha }_i^{\ast }+z_{it}^{\prime }{\beta }_i+{\mathrm{\Lambda }}_i^{\ast }{\eta }_t^{\ast },\\ {\eta }_1^{\ast }~N({\mu }_1^{\ast },{({\mathrm{\Psi }}_1^{\ast })}^{-1}),\\ {\eta }_t^{\ast }~N({\mu }_{\eta }^{\ast }+A_{\eta }^{\ast }{\eta }_{t-1}^{\ast },{({\psi }_{\eta }^{\ast })}^{-1}),\\ \text{where}{\mu }_{\eta }^{\ast }=(I-A_{\eta }^{\ast }){\mu }_1^{\ast },{\mathrm{\Psi }}_{\eta }^{\ast }={\mathrm{\Psi }}_1^{\ast }-A_{\eta }^{\ast }{\mathrm{\Psi }}_1^{\ast }{A}_{\eta }^{\ast \prime },\end{array}$$ (3.15)

where ${\mathrm{\Lambda }}_i^{\ast }$ is an unconstrained working factor loading matrix having a lower triangular structure, ${\eta }_t^{\ast }$ is an m×1 working latent factor vector, Ψ₁ = diag(ψ₁, …, ψ_m) is a diagonal covariance matrix, and ${\alpha }_i^{\ast }$ is the intercept term, with ${\alpha }_k^{\ast }=0$, for k ≤ m. $A_{\eta }^{\ast }=\text{diag}(A_1^{\ast },\dots ,A_m^{\ast })$ is a diagonal matrix of AR(1) coefficients, with $\mid A_1^{\ast }\mid <1$ to guarantee stationarity. Note that the PX-factor model is clearly over-parameterized, having redundant parameters in both the covariance matrix Ψ₁ and mean ${\mu }_1^{\ast }$.

In order to transform the working model parameters back to inferential model parameters, we let:

$$\begin{array}{l}{\lambda }_{jl}=\mathcal{S}({\lambda }_{ll}^{\ast }){\lambda }_{jl}^{\ast }{\psi }_l^{-1/2},{\eta }_t=S_d\left[{\mathrm{\Psi }}_1^{1/2}({\eta }_t^{\ast }-{\mu }_1^{\ast })\right],{\alpha }_i={\alpha }_i^{\ast }+{\mathrm{\Lambda }}_i^{\ast }{\mu }_1^{\ast },\\ A_{\eta }=A_{\eta }^{\ast },{\mu }_{\eta }=S_d\left[{\mathrm{\Psi }}_1^{1/2}\{{\mu }_{\eta }^{\ast }+(A_{\eta }^{\ast }=I){\mu }_1^{\ast }\}\right],\end{array}$$ (3.16)

where (x) = −1 for x < 0, (x) = 1 for x ≥ 0, and $S_d=\text{diag}\{\mathcal{S}({\lambda }_{ll}^{\ast })\}$. Then, instead of placing priors directly on α_i and Λ_i, with η_t~ N(0, I), we specify priors on α^*, ${\mathrm{\Lambda }}_1^{\ast },{\mu }_1^{\ast }$ and ${\mathrm{\Psi }}_1^{\ast }$ . In particular, we let

$$\begin{array}{l}{\lambda }_{jl}^{\ast }~N(0,1)\text{for}\text{all}\text{lower}\text{triangular}\text{elements},\\ {\psi }_l~\text{inv}-\mathrm{\Gamma }(a_l,b_l),\\ {\alpha }_i^{\ast }~N(0,{\phi }_{\alpha }),A_i^{\ast }~\text{Unif}(-1,1),{\mu }_1^{\ast }~N(0,{\mathrm{\Phi }}_B).\end{array}$$ (3.17)

Hence, in the one-factor case, we obtain

$$\begin{array}{l}{\mathrm{\Lambda }}_i=S({\mathrm{\Lambda }}_i^{\ast }){\mathrm{\Psi }}_1^{-1/2}{\mathrm{\Lambda }}_i^{\ast },{\eta }_t=S({\mathrm{\Lambda }}_i^{\ast }){\mathrm{\Psi }}_1^{1/2}({\eta }_t^{\ast }-{\mu }_1^{\ast }),{\alpha }_i={\alpha }_i^{\ast }+{\mathrm{\Lambda }}_i^{\ast }{\mu }_1^{\ast },\\ A_{\eta }=A_{\eta }^{\ast },{\mu }_{\eta }=S({\mathrm{\Lambda }}_i^{\ast }){\mathrm{\Psi }}_1^{1/2}\{{\mu }_n^{\ast }+(A_{\eta }^{\ast }-1){\mu }_1^{\ast }\}\end{array}$$ (3.18)

with priors

$$\begin{array}{l}{\mathrm{\Lambda }}_i^{\ast }~N(0,1)\text{for}\text{all}\text{lower}\text{triangular}\text{elements},\\ {\mathrm{\Psi }}_1~\text{inv}-\mathrm{\Gamma }(a,b),\\ {\alpha }_i^{\ast }~N(0,{\phi }_{\alpha }),A_i^{\ast }~\text{Unif}(-1,1),{\mu }_1^{\ast }~N(0,{\mathrm{\Phi }}_B)\end{array}$$ (3.19)

To efficiently draw samples of parameters from the inferential model, we draw samples from the working model, followed by a post-processing step to transform working-model draws back to the parameters in the inferential model.

3.6 Sampling Model Parameters – Latent Factor Normalization

Parameter expansion can greatly reduce the autocorrelation of factor loadings, however, it has limited effect on improving the mixing of other parameters (e.g. the intercept term, see Figure (S12)). To further improve computational efficiency, we combine latent factor normalization with parameter expansion in sampling the model parameters from the full conditional distributions. In detail, suppose ${\eta }_{1:T}^{\ast }$ is a realization of latent factors in model (3.15) with ${\eta }_t^{\ast }=({\eta }_{1,t}^{\ast },\dots ,{\eta }_{m,t}^{\ast })$, let η̃_t = (η̃_1,t, …, η̃_m,t)′ denote the normalized latent factors, with

$${\stackrel{\sim }{\eta }}_{i,t}=\frac{{\eta }_{i,t}^{\ast }-\mathit{mean}({\eta }_{i,1:T}^{\ast })}{\mathit{std}({\eta }_{i,1:T}^{\ast })},t=1,\dots ,T;i=1,\dots ,m.$$

Then in matrix form we have:

$${\stackrel{\sim }{\eta }}_t=\nu +\mathrm{\Delta }{\eta }_t^{\ast }$$ (3.20)

where ν is a m × 1 vector with ${\nu }_i=-\frac{\text{mean}({\eta }_{i,1:T}^{\ast })}{\text{std}({\eta }_{i,1:T}^{\ast })}$, and Δ is a m × m diagonal matrix with ${\mathrm{\Delta }}_{i,i}=\frac{1}{\text{std}({\eta }_{i,1:T}^{\ast })}$.

PX with Latent Factor Normalization Algorithm

Considering the working PX-factor model (3.15) and priors (3.17), given a realization of latent factors ${\eta }_{1:T}^{\ast }$, in order to obtain a sample of model parameter Θ = (α_i, Λ_i) (i = 1, …, p) from the full conditional distribution f(Θ|η_1:T ), we can first sample Θ̃ from the full conditional distribution using the normalized PX model (3.21) via normalized latent factors η̃_1:T (i = 1, …, m):

$$h_i({\theta }_{it})={\stackrel{\sim }{\alpha }}_i+z_{it}^{\prime }{\beta }_i+{\stackrel{\sim }{\mathrm{\Lambda }}}_i{\stackrel{\sim }{\eta }}_t,$$ (3.21)

with the induced priors (3.22) for the parameters of normalized PX-factor model derived from (3.17):

$$\begin{array}{l}{\stackrel{\sim }{\lambda }}_{jl}~N(0,{\mathrm{\Delta }}_{ll}^2)\text{for}\text{all}\text{lower}\text{triangular}\text{elements},\\ {\stackrel{\sim }{\alpha }}_i~N\left(0,{(1/{\phi }_{{\alpha }_i}+\sum _{l=1}^{min(i,m)}{v}_l^2/{\mathrm{\Delta }}_{ll}^2)}^{-1}\right).\end{array}$$ (3.22)

and transform Θ̃ to obtain a sample of Θ via the following transformations via (3.23).

$$\begin{array}{l}{\mathrm{\Lambda }}_i^{\ast }={\stackrel{\sim }{\mathrm{\Lambda }}}_i\mathrm{\Delta },\\ {\alpha }_i^{\ast }={\stackrel{\sim }{\alpha }}_i+{\stackrel{\sim }{\mathrm{\Delta }}}_i\nu .\end{array}$$ (3.23)

4 Simulation Examples

4.1 Mixed-Measurement Time Series

To access the efficiency of the algorithms, we first consider the simulation example jointly modeling a 3-dimensional mixed-measurement time series (D_t) consisting of Poisson counts (Y_t), continuous (Z_t) and binary responses (W_t), with T=50, 100, 150. 200 and 500 respectively (as shown in (4.24)). In each case, 10% of the data in each time series are randomly missing, allowing us to evaluate the model in dealing with missing values. The time-varying latent factors are modeled to follow an O-U process.

$$\begin{array}{l}{D}_t=[Y_t,Z_t,W_t],\\ Y_t~\mathit{Poiss}({\lambda }_t),Z_t~N({\mu }_t,1/{\sigma }_z^2),W_t~\mathit{Bernoulli}(p_t),\\ \text{where}log({\lambda }_t)=a+b{\eta }_t,{\mu }_t=c+d{\eta }_t,\mathit{logit}(p_t)=e+f{\eta }_t,\\ \text{and}d{\eta }_t=-\beta ({\eta }_t-\alpha )dt+\sigma {dW}_t\end{array}$$ (4.24)

We run the sampler for 10,000 iterations, discarding the first 2,000 iterations as burn-in. The results are later compared with those obtained by simply using WinBUGS or extended Kalman filters. Taking T=200 case as an example, we set the values of a–f to be 2, 2, 3, 2, 0.5 and 1 respectively, ${\sigma }_z^2=1$ and for the time-varying latent factors α = 0, β = 1 and σ = 1. The simulated time series are shown in Figure 1.

Figure 1.

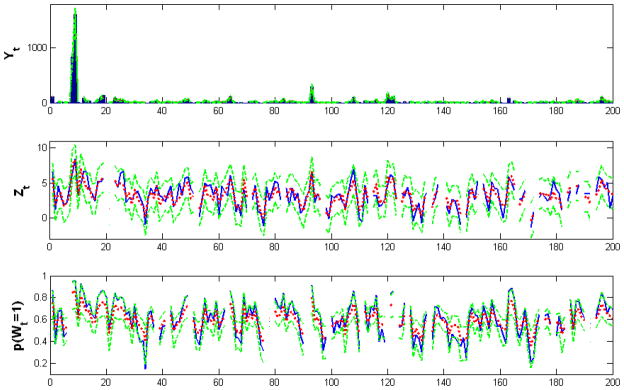
Illustration of simulated dataset and interval validation to show the model fitting. Solid lines (and the histogram for the first figure): simulated data. A 3-dimensional mixed-measurement time series D_t = [Y_t, Z_t, W_t] up to T=200 is simulated, where Y_t is count time series, Z_t is continuous and W_t is binary. 10% data in each time series are randomly missing.; dotted lines: posterior mean; dashed lines: 95% posterior C.I.

We introduce priors on the parameters in the PX working model as shown in (3.17). Specifically, half-Cauchy priors are placed on the variance components of latent factor autoregressions as recommened by Gelman (2006), while Inv-Gamma(0.01,0.01) priors are given to all other variances. To visualize the mixing the MCMC chain, trace-plots of the posterior samples of model parameters (intercepts and factor loadings shown in Figure 2) and latent factors (Figure 3) are shown.

Figure 2.

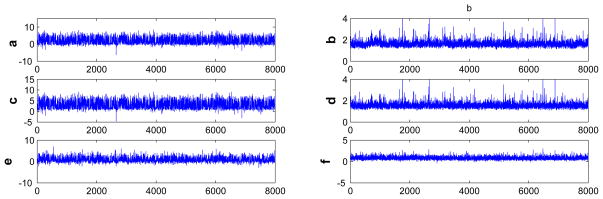
Traceplot of Posterior Samples of Model Parameters: Intercepts (a,c,e) and factor loadings (b,d,f) shown. The parameters are defined in (4.24).

Figure 3.

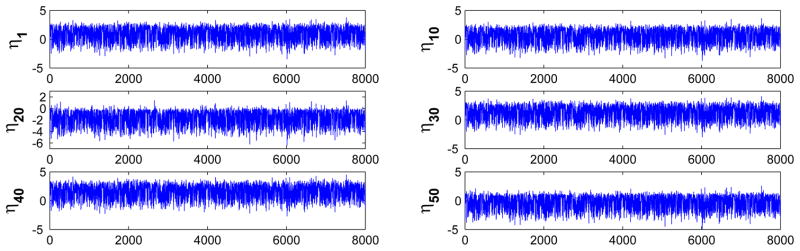
Traceplot of Posterior Samples of Latent Factors: Six time points shown. The latent factors are defined in (4.24).

A summary of effective sample size and sample autocorrelation of posterior samples are further listed in Table 1. A summary of effective sample size and sample autocorrelation of posterior samples are further listed in Table 1.We compare the mixing of our MCMC sampler with that of WinBUGS (Traceplots shown in Figure 4 and S2, and the summary of effective sample size and autocorrelation shown in Table S1), which is based on a Gibbs sampler and use of adaptive-rejection sampler or random-walk MCMC for full conditional distributions without closed forms. Our sampler relying on GDKA, parameter expansion and latent factor normalization leads to tremendous gains in the mixing of MCMC chains for both model parameters and latent factors. Furthermore, it is important to note that all three techniques contribute to improving the efficiency of the MCMC sampler, as not implementing one of them tends to give poor mixing of the chains for at least some model parameters (see e.g. Figure 6 and S12). Especially, we find that while Metropolis Hastings via GDKA is critical for latent factor filtering and sampling, parameter expansion substantially improves computational performance for factor loadings, and latent factor normalization helps the mixing of chains for other model parameters (e.g. intercepts).

Table 1.

MCMC Summary for T=100 and T=150 respectively shows improved mixing, compared to Table S1, which is obtained using WinBUGS. Using T=100 and T=150 as examples, in each case, 10000 posterior samples are drawn for each unknown with the first 2000 as burn-in. Effective sample size (ESS) and sample autocorrelation with lag 10 and 30 of the 8000 posterior samples are shown for selected parameters as representatives (c, d, η₁ and η₅₀ are defined as in (4.24)).

# of Time Points	T=100				T=150
Parameters	c	d	η1	η50	c	d	η1	η50
ESS	1815	6500	1875	1740	1905	6025	1982	1887
Autocorr-Lag 10	0.045	0.008	0.043	0.039	0.019	0.025	0.019	0.018
Autocorr-Lag 30	0.007	−0.005	0.012	0.009	−0.009	−0.005	−0.011	−0.013

Figure 4.

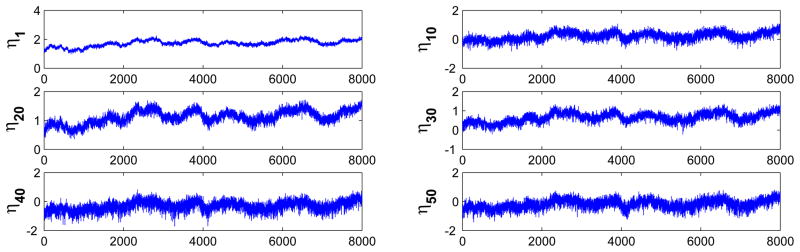
Traceplot Produced by WinBugs of Posterior Samples of Latent Factors. The traceplots are compared with those in Figure 3, also showing that our algorithm improve the mixing of the Markov Chain.

Figure 6.

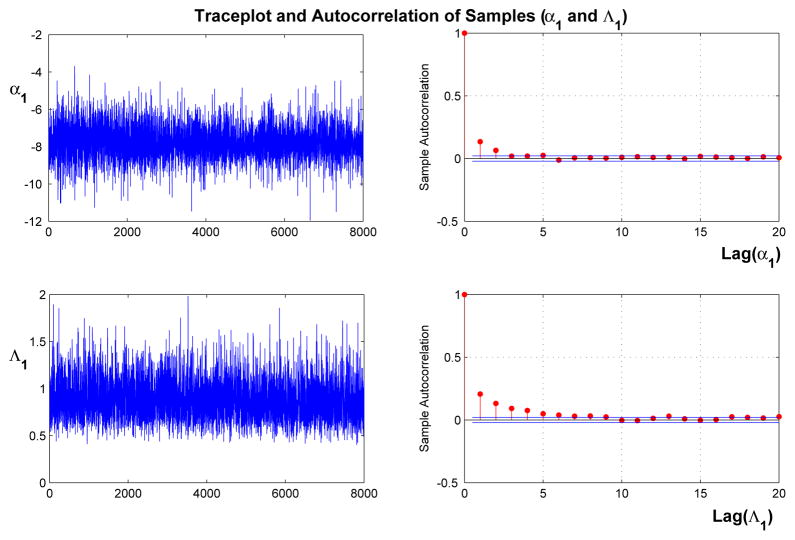
Traceplots and Autocorrelation Plots of Posterior Samples. Note that our modification can effectively reduce both the autocorrelation of factor loading matrix (Λ₁ as a representative here) and the intercept (α₁ as a representative) very well, as compared to those in Figure S12. α₁ and Λ₁ are defined in (5.27).

On the other hand, since extended Kalman filters have been used to approximate non-Gaussian filtering and sampling distributions using Laplace normal approximations, especially when the length of time series is not long, we compared the results of our method with those of Kalman filters with all simulated datasets. A comparison of acceptance ratio clearly shows that our sampler gave much better acceptance ratio, especially with increased length of the time series. Low acceptance rates of extended Kalman filter inevitably lead to MCMC inefficiency, illustrated by the increased autocorrelation and decreased effective sample size (a comparison between Table 1 and Table S1).

To show the model fitting, internal validations are performed, with posterior means and 95% confidence intervals (C.I.s) of the simulated time series shown in Figure 1.

The use of our MCMC sampler seems to provide a reasonable inference to the unknown quantities. Furthermore, the framework and computational algorithms allows missing values on a subsect of the time series. Figure S3 shows that the model gives good interpolations of missing data based on the posterior marginal distributions.

Efficient adaptive Metropolis Hastings via GDKA to sample time-varying latent factors is one of the key steps in our sampling scheme, and it is well known that the acceptance rates of Metropolis Hastings steps tend to decrease rapidly as the number of time points increases (Niemi and West (2010)). To evaluate this, we generated 100 simulated datasets for each T and look at the overall performance. Table 2 lists the acceptance rates of the Metropolis Hastings steps to sample latent factors using our sampling scheme, showing that the algorithm is efficient even for big time series with T=500, which has much higher acceptance ratio than extend Kalman filters. The accuracy of inference to unknown quantities is also further confirmed based on the 100 simulated datasets by checking whether the posterior estimates would recover the true values of model parameters under such a complex model, with Table S3 showing that in almost all cases the 95% posterior C.I.s cover the true values with all 100 simulated datasets.

Table 2.

Acceptance Ratio for the Metropolis-Hastings update with GDKA for latent factors compared with extended Kalman filters (E-KF). Mean, minimum and maximum acceptance rates based on 100 simulated datasets are shown. Note that our algorithm both has higher acceptance ratio and more stable performance with mixed-measurement observations with possible missing values.

T (# of Time Points)	50	100	150	200	500
GDKA (mean)	73.1%	59.4%	43.3%	30.4%	12.4%
(min)	70.3%	57.3%	40.6%	27.4%	8.1%
(max)	76.1%	61.3%	46.8%	33.1%	13.3%
E-KF(mean)	41.1%	25.3%	1.7%	~0	0
(min)	30.1%	14.1%	0%	0	0
(max)	43.3%	27.1%	7.7%	0.3%	0

Furthermore, it is worth mentioning that although we show that our algorithm updates latent factors in a single block and infers model parameters efficiently with relatively big time series (T=500), the performance of the proposed algorithm is expected to decrease with bigger time series. In those cases, a reasonable strategy could be combining our algorithm with the idea of block sampling scheme, where the big time series can be divided to a few blocks with T smaller than 500 and updated sequentially in each block, which will definitely help in problems with extremely big time series.

4.2 Mixed Discrete Time Series

Time series with discrete outcomes having a variety of measurement scales (count, binary, categorical) are also commonly collected in various fields of study. Discrete variables contain less information than continuous variables (Chin and Lee (2008)), so it is of great help to share information between time series with mixed discrete outcomes whenever it is possible.

In this simulation study, 4-dimensional time series D_t consisting of a mixture of binomial counts (Y_t and Z_t) and binary responses (W_t and V_t) up to time T are jointly modeled, as shown in (4.25). Similarly, 10% of the simulated data in each time series are randomly missing to evaluate the model in dealing with missing data.

$$\begin{array}{l}{D}_t=[Y_t,Z_t,W_t,V_t],\\ Y_t~\mathit{Bino}(N_y,p_t^{(y)}),Z_t~\mathit{Bino}(N_z,p_t^{(z)}),\\ W_t~\mathit{Bernoulli}(p_t^{(w)}),V_t~\mathit{Bernoulli}(p_t^{(v)}),\\ \text{where}\mathit{logit}(p_t^{(y)})=a+b{\eta }_t,\mathit{logit}(p_t^{(z)})=c+d{\eta }_t,\\ \mathit{logit}(p_t^{(w)})=e+f{\eta }_t,\mathit{logit}(p_t^{(v)})=g+h{\eta }_t,\\ \text{and}{\eta }_t=\gamma \eta t_{-1}+{\epsilon }_t,{\epsilon }_t~N(0,{\phi }_{\epsilon }).\end{array}$$ (4.25)

Taking T=100 case as an example, we set the values of a–h to be 0.5, 1, 1, −1.5, 1, −2, 0.5 and −3 respectively. An AR(1) autoregressive structure is applied to the time-varying latent factors, with γ = 0.368 and σ_ε = 0.658. The simulated time series are shown in Figure S4. Similarly, to obtain posterior samples, we run our MCMC sampler for 10,000 iterations, discarding the first 2,000 samples as burn-in. Again, the effective sample size and autocorrelation shown in Table 3 show good mixing of the Markov Chain, which is further illustrated by the trace-plots of intercepts, factor loadings (Figure S5) and latent factors (Figure S6). In addition, with T=100, the Metropolis Hastings step for latent factors update gives a good acceptance ratio of 56.1%.

Table 3.

MCMC Summary for T=100 (selected parameters shown) shows good mixing of the Markov Chain. 10000 posterior samples are drawn for each unknown with the first 2000 as burn-in. Effective sample size (ESS) and sample autocorrelation with lag 10 and 30 of the 8000 posterior samples are shown for selected parameters as representatives (a – h, η₁ and η₅₀ are defined as in (4.25)).

Parameters	a	b	c	d	e	f	g	h	η1	η50
ESS	5726	6449	5742	6488	5030	2659	4057	2043	5998	5710
Autocorr-Lag 10	0.007	0.008	0.009	0.011	0.012	0.029	0.017	0.029	−0.004	−0.005
Autocorr-Lag 30	0.001	−0.006	0.003	−0.002	0.007	0.013	0.011	0.018	0.013	0.014

Internal validations with posterior mean and 95% C.I. of the simulated time series are shown in Figure S7. Again, the framework provides good fit to the simulated data, which is reinforced by the missing data interpolation results shown in Figure S8.

4.3 Mixed-Measurement-Mixed-Frequency Time Series

Another challenge with mixed-measurement time series is that time series are often sampled at different frequencies. For example, some time series are observed every month or quarter while others are recorded every year. In empirical financial analysis, daily and intra-daily time series are also often readily available for analysis. To model the time series simultaneously, the literature and methodology have been focused on either aggregating the higher-frequency data to the lower frequency, or interpolating the lower-frequency data to the higher-frequency (Ghysels et al. (2005), Andreou et al. (2010) and Ghysels et al. (2007)). Neither of these is generally satisfactory. First of all, temporal aggregation loses information and may lead to poor prediction. Secondly, the approaches via data interpolation transform the mixed-frequency problem to a missing data problem, assuming that the model operates at the highest frequency of the time series, while data in the lower-frequency time series are periodically missing. However, commonly used interpolation methods generally do not efficiently and fully exploit the sample information, especially when massive missing data exist, which is very likely to occur when performing data interpolation in mixed-measurement-mixed-frequency time series analysis.

We apply our generalized dynamic factor model and computational algorithms to mixed-measurement-mixed-frequency time series analysis, in which the observed time series are simultaneously modeled via dynamic latent factors at specifically defined frequencies discussed later. Under this scenario, neither data aggregation nor interpolation is required in the inference or prediction, which improves the computational efficiency with mixed-frequency observations.

In detail, we treat the low-frequency time series as high-frequency time series with “missing data” and low “observed” frequency. For the p-dimensional mixed-measurement-mixed-frequency time series, let t be the time index of the highest frequency time series, and y_t = {y_it} (i = 1, …, p and t = 1, …, T), with observed frequencies ω = (ω₁ …, ω_p)′. Let ${\mathbf{y}}_{\mathbf{t}}^{\ast }={(y_{1t}^{\ast },\dots ,y_{pt}^{\ast })}^{\prime }$ be the corresponding ordered p-dimensional time series by descending frequency. Let ${\omega }^{\ast }={({\omega }_1^{\ast },\dots ,{\omega }_p^{\ast })}^{\prime }$, with ${\omega }_i^{\ast }(i=1,\dots ,p)$ denoting the highest common frequency from $y_{it}^{\ast }$ to $y_{pt}^{\ast }$. Then ${\mathbf{y}}_t^{\ast }$ can be modeled following (2.1), (2.2) and (2.3) via m common factors η_t = (η_1t, …, η_mt)′, with each latent factor η_it (i = 1, …, m) constructed to follow an AR(1) process with frequency ${\omega }_i^{\ast }(i=1,\dots ,m\le p)$. In particular, in the one-factor model case, ${\omega }_1^{\ast }$ is the highest common frequency of all observed time series.

In the following simulation study, we considered jointly modeling a 3-dimensional mixed-measurement-mixed-frequency time series y_t with observed frequency omega; = (3omega;₀, omega;₀, omega;₀)′ respectively (shown in (4.26)). The simulated data are generated through two common latent factors (η_t = (η_1t, η_2t)′) at the frequency of 3ω₀, and chosen in accordance with empirical applications to form multivariate mixed-measurement-mixed-frequency time series, where the first time series (Y_1t) can be considered as monthly recorded data, while the other two as quarterly recorded data. Specifically,

$$\begin{array}{l}{Y}_t={[Y_{1t}^{\prime },Y_{2t}^{\prime },Y_{3t}^{\prime }]}^{\prime },\\ Y_{1t}~\mathit{Bernoulli}(p_{1t}),Y_{2t}~N({\mu }_{2t},1/{\sigma }^2),Y_{3t}~\mathit{Bino}(N_3,p_{3t}),\\ \text{where}\mathit{logit}(p_{1t})=a_1+b_1{\eta }_{1,t}+c_1{\eta }_{2,t}\\ {\mu }_{2t}=a_2+b_2{\eta }_{1,t}+c_2{\eta }_{2,t}\\ \mathit{logit}(p_{3t})=a_3+b_3{\eta }_{1,t}+c_3{\eta }_{2,t}\\ \text{and}{\eta }_{i,t}={\gamma }_i{\eta }_{i,t-1}+{\epsilon }_{it};{\epsilon }_{it}~N(0,{\phi }_{{\eta }_i})\end{array}$$ (4.26)

The simulated data and latent factors up to T=90 are shown in Figure S9 (90 time points for Y_1t, and 30 time points observed for Y_2t and Y_3t). Again, analysis of posterior samples indicates good mixing the the Markov Chain (Table S2), and internal validation shows good fitting of the model to the simulated mixed-measurement-mixed-frequency data (Figure S10).

5 Intertwined Corporate Default, Recovery Rate and Business Cycle

It has been noted that corporate default rates and bond recovery rates on defaults are negatively correlated (Altman et al. (2005)). Since recovery rates play a critical role in pricing and risk models, treating recovery rates as either constant or a stochastic variable independent of default rates while neglecting inverse relationship leads to inaccurate estimation of the loss function and suboptimal capital allocation. Furthermore, according to the current Basel proposal, banks can opt to provide their own recovery rate forecasts for the calculation of regulatory capital (Creal et al. (2011)). Thus there is an immediate need for statistical models explaining the relationship between the corporate default risk and bond recovery rates (and probably some other credit risk indicators), which can be used in default prediction and credit risk modeling. Macroeconomic conditions, on the other hand, may affect both default and recovery rates (see e.g. Nickell et al. (2000)), where the number of defaults tends to increase with lower recovery rates in economic recessions (Altman et al. (2005)).

In this study, we apply the generalized Bayesian dynamic factor models to jointly modeling corporate default counts, bond recovery rates and business cycle indicators over time. Default counts are model by binomial distribution with the default probability modeled via logistic link function. Recovery rates, which are between 0 and 1, are modeled via logistic-Normal model. Unemployment rate is used as an indicator for business cycle. The relationship between them are modeled via shared common unobserved systematic risk factor(s).

5.1 Data

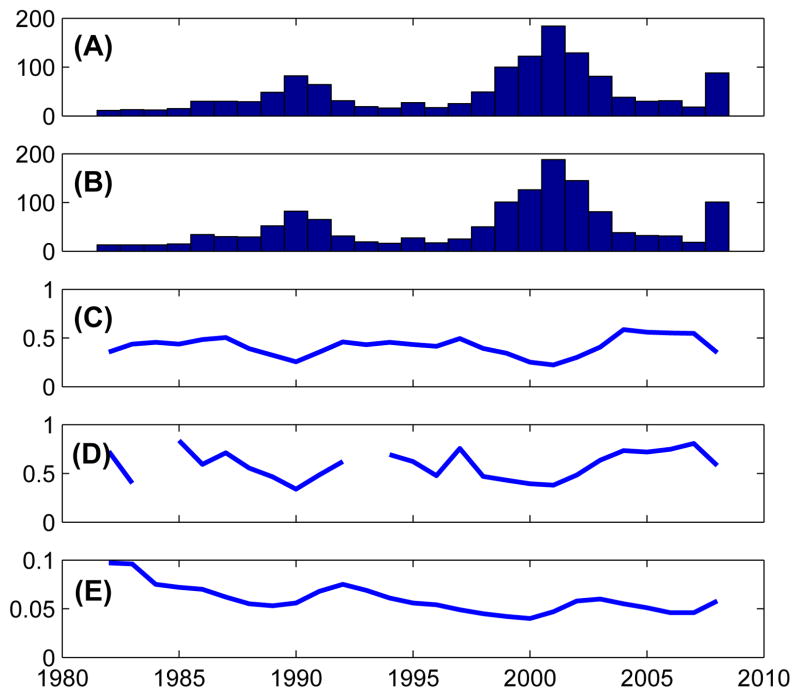
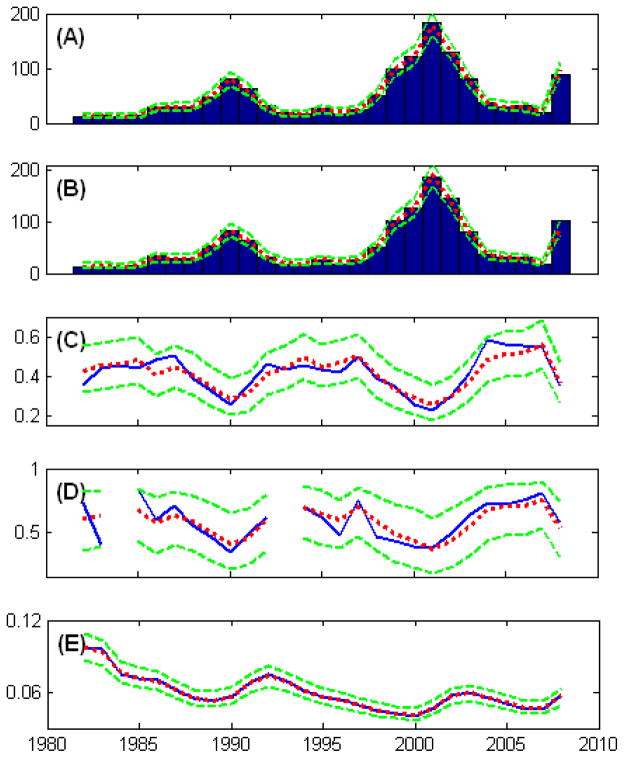
The 5 time series (shown in Figure 5) we have are annual recovery rates, corporate default counts and unemployment rate data from 1982 to 2008 (Latest public data obtained from Moody’s Default and Recovery Database), denoted as:

$${\mathbf{y}}_t=\{y_{it}\};(i=1,\dots ,5\text{and}t=1,\dots ,27)$$

where y_1t: annual default counts within investment-grade cooperates. y_2t: annual default counts within speculative-grade cooperates. y_3t: all-bonds annual recovery rates. y_4t: senior-secured bonds annual recovery rates. y_5t: annual unemployment rate of the United States.

Figure 5.

Data consisting of 5 Mixed-Measurement Time Series Shown. (A): Annual Default Counts: Speculative-Grade Cooperates. (B): Annual Default Counts: Investment-Grade Cooperates. (C): Annual Recovery Rates: All Bonds. (D): Annual Recovery Rates: Senior-Secured Bonds. (E): Annual Unemployment Rate.

5.2 Model Specification

Default counts are modeled as coming from binomial distributions. Recovery rates and unemployment rates are modeled as coming from logistic-Normal distributions. The inferential model is shown in (5.27). Default priors are placed on the corresponding parameter expanded working model.

$$\begin{array}{l}{y}_{1t}~\mathit{Bino}(N_{1t},p_{1t}),y_{2t}~\mathit{Bino}(N_{2t},p_{2t}),\\ \text{logit}(y_{3t})~N({\mu }_{3t},{\phi }_3),\text{logit}(y_{4t})~N({\mu }_{4t},{\phi }_4),\text{logit}(y_{5t})~N({\mu }_{5t},{\phi }_5),\\ \text{where}\text{logit}(p_{1t})={\alpha }_1+{\mathrm{\Lambda }}_1{\eta }_t,\text{logit}(p_{2t})={\alpha }_2+{\mathrm{\Lambda }}_2{\eta }_t,\\ {\mu }_{3t}={\alpha }_3+{\mathrm{\Lambda }}_3{\eta }_t,{\mu }_{4t}={\alpha }_4+{\mathrm{\Lambda }}_4{\eta }_t,{\mu }_{5t}={\alpha }_5+{\mathrm{\Lambda }}_5{\eta }_t,\\ \text{and}{\eta }_1~N(0,I_m),{\eta }_t~N(a_{\eta }{\eta }_t+b_{\eta },I_m),\mid a_{\eta }\mid <1\end{array}$$ (5.27)

The 5 time series are jointly modeled via one or two factor models, based on the previous studies showing that default counts and recovery rates are negatively correlated, and they may be further associated with but do not match business cycle. Inference of number of factors is based on comparing fit for the one and two factor models.

5.3 Results

We are interested in the inference of both parameters and latent factors, as well as the relationship between corporate default counts, bond recovery rates and business cycle.

In the one-factor model, the latent factor can be interpreted as credit risk within the period. We explore the posterior distribution of the unknowns using the algorithms discussed earlier. Two results show the efficiency of the MCMC sampler: Firstly, the acceptance ratio of latent factors in the Metropolis Hastings update is 81%. Secondly, parameter expansion and latent factor normalization promote the mixing of the Markov chain, and greatly improve the sampling efficiency (as shown in Figure 6), compared to those obtained via only parameter expansion (Figure S12) or WinBUGS (results not shown).

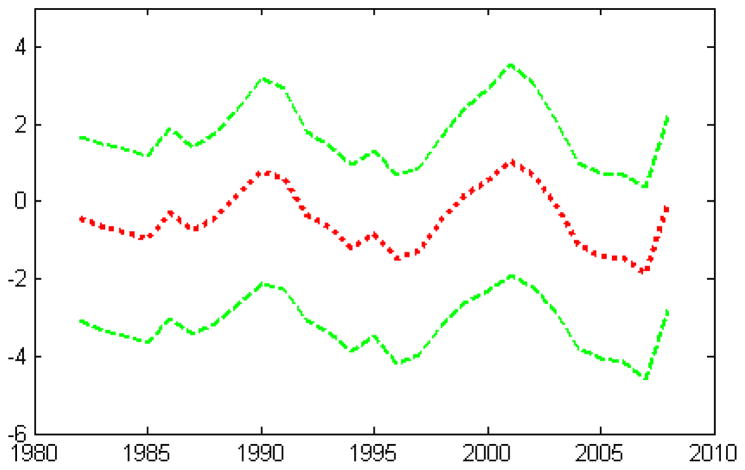
We constructed point and interval estimates of the credit risk factor within the period. This is shown in Figure 7. Clearly, the figure shows that credit pressure peaks around 1990, 2001 and 2008, which are all well-known financial crises.

Figure 7.

1982–2008 Credit Pressure Reconstruction. Dotted line: posterior mean of the credit risk factor, and dashed lines: 95% posterior C.I.

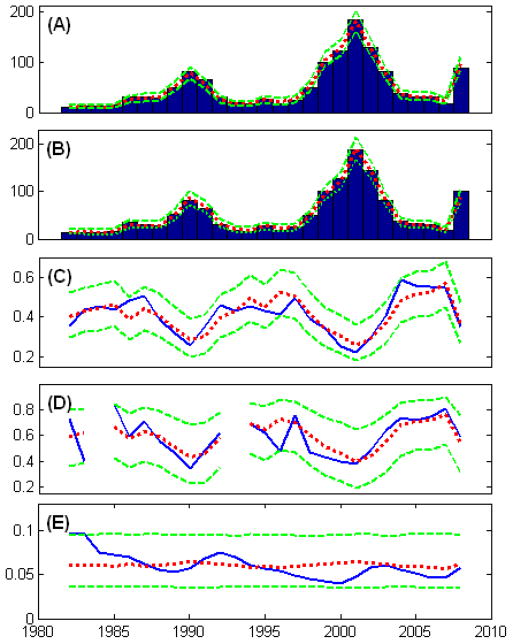
Furthermore, Figure 8 shows the fitting of the model to the data, with posterior retrospective mean and 95% intervals shown with dotted lines and dashed lines respectively. Note that the fitting of annual recovery rates and default counts are good under the one-factor setting (The fitting of recovery rate for senior-secured bonds seems not as good as others, indicating the possibility of existence of additional factors. Two-factor model gives a better fit, as shown later), indicating that a common credit risk factor may be used to model the inverse relationship between them. Fitting of unemployment rate data, however, is not as good, indicating the idea that business cycle, though may be related to credit cycle, have effects from additional latent factors.

Figure 8.

Model Fitting using One-Factor Generalized Dynamic Factor Model. The solid lines (and the histograms for the first two panels) show real historical data, the dotted lines indicate posterior means and the dashed lines show posterior 95% C.I. (A): Annual Default Counts: Speculative-Grade Cooperates. (B): Annual Default Counts: Investment-Grade Cooperates. (C): Annual Recovery Rates: All Bonds. (D): Annual Recovery Rates: Senior-Secured Bonds. (E): Annual Unemployment Rate.

In comparison, we also fit the data with a two-factor model, with the two factors chosen to be corresponding to the speculative-grade-cooperate default counts and unemployment rates time series, which can be considered as representing the credit risk factor and the business cycle factor. Again, we have high acceptance rates for the two latent factors (83% and 78% respectively) and the model fitting is shown in Figure 9. Clearly, the two-factor model gives improved fitting for unemployment data and senior-secured bonds recovery rate data, but has trivial improvement on others. This indicates that default and recovery risk, though related to, is not solely determined by the business cycle.

Figure 9.

Model Fitting using Two-Factor Generalized Dynamic Factor Model. The solid lines (and the histograms for the first two panels) show real historical data, the dotted lines indicate posterior means and the dashed lines show posterior 95% C.I. (A): Annual Default Counts: Speculative-Grade Cooperates. (B): Annual Default Counts: Investment-Grade Cooperates. (C): Annual Recovery Rates: All Bonds. (D): Annual Recovery Rates: Senior-Secured Bonds. (E): Annual Unemployment Rate.

Furthermore, we specifically looked at the posterior distributions of factor loadings to obtain a better understanding of the relationship between the time series (Histograms of posterior samples of factor loadings shown in Figure S11 and the posterior summaries are shown in Table 4). Table 4 clearly shows that default counts (the first and second times series) and bond recovery rates (the third and fourth time series) have strong negative correlation in terms of the credit risk factor (factor one), with the factor loadings of the first factor being strictly positive for default counts and strictly negative for bond recovery rates, at the 95% confidence level. In addition, we are not sure if unemployment rate is strongly correlated with default counts or bond recovery rates, although there is some weak evidence showing that default counts may be negatively associated and bond recovery rates may be positively associated with unemployment rates. This further demonstrates that systematic default and recovery risk does not coincide with business cycle risk, which is consistent with the related findings in Das et al. (2007), Bruche and Gonzlez-Aguado (2010) and Creal et al. (2011).

Table 4.

Posterior Summary of Factor Loadings Λ_ij (i = 1, …, 5 and j = 1, 2) in the Two-Factor Model, where Λ_ij is the factor loading of the jth factor for the ith time series (Λ₁₂ = 0).

Factor Loadings	Mean	Medium	SD	95% HPD C.I.
Λ11	1.312	0.927	1.957	[0.478,3.127]
Λ21	1.322	0.936	1.986	[0.503,3.195]
Λ22	−0.0828	−0.0717	0.0808	[−0.225,0.035]
Λ31	−0.592	−0.422	0.842	[−1.424,−0.172]
Λ32	0.0642	0.0547	0.0735	[−0.038,0.196]
Λ41	−0.683	−0.497	1.076	[−1.706,−0.128]
Λ42	0.119	0.104	0.131	[−0.033,0.383]
Λ51	0.0586	0.0440	0.115	[−0.077,0.213]
Λ52	0.219	0.186	0.159	[0.099,0.454]

6 Discussion

This paper proposes the use of Bayesian generalized dynamic factor models for jointly modeling mixed-measurement time series, and efficient computational algorithms are developed. The proposed framework allows mixed-scale measurements associated with each time series, with different measurements having different distributions in the exponential family, and thus provides a more flexible framework for multivariate time series analysis. Although our illustration examples are based on specific k-factor models, the broader question of inference on the number of factors and model selection in (generalized) factor analysis, especially in the mixed-measurement observation framework, is interesting and challenging. Reversible jump MCMC algorithms can be used to allow for model uncertainly (Lopes and West (2004) and Lopes et al. (2011)). Alternatively, sparse spike-and-slab priors were proposed to induce sparsity in the factor loading matrix (see e.g. West (2003) and Carvalho et al. (2008)). More recently, non-parametric infinite factor models were introduced using either a multiplicative gamma process shrinkage prior on factor loadings (Bhattacharya and Dunson (2011)) or Indian-Buffet Process (IBP) prior on the factor loading matrix (Knowles and Ghahramani (2010)). However, translating these non-parametric approaches to the generalized dynamic factor model framework with mixed measurement is challenging and as yet unexplored.