Standardization of Blood Growth Hormone Levels Measured by Different Kits Using a Linear Structural Relationship

Abstract

Accurate and reliable determination of blood growth hormone level is essential in the diagnosis and treatment of short stature children. However, measured levels differed considerably among measurement kits available in Japan until 2003. Therefore, standardization of the measured values was attempted by measuring growth hormone levels in a sample of healthy adult individuals every year using the different kits. A standardization equation was developed for each kit through linear structural relationship with the mean values of the used kits and measured values in each kit as random variables. A Pearson’s correlation coefficient between the mean values of all kits and the measured values from each kit was also obtained. Sources for the marked discrepancies amongst the measured values in the different kits were also explored. The obtained values for slopes and intercepts in the equations varied considerably, but the standard values obtained from these equations after the measured values for each kit were transformed into standard values served well as the standard. The standard solutions in the respective measurement kits were found to be the source of variability in the measured values among the kits.

Introduction

Growth hormone is administered to short-stature children with growth hormone deficiency. Diagnosis of these patients relies on accurately measuring the levels of growth hormone in the blood and changes therein using a provocation test. However, values obtained using the different kits available in Japan have always differed considerably, to an extent that could affect a proper clinical judgment regarding growth hormone therapy. Therefore, the need for standardization of the measured levels was perceived and from 1991 to 1997 standardization was conducted by linear regression of the measured levels for kit as an independent variable, and the mean of the levels measured by several kits as a dependent variable (1). Using the regression line for each kit, the measured level was converted into a "standard" value to be used in the diagnosis and judgment of therapeutic eligibility.

The use of linear regression for this situation, however, is theoretically incorrect. Since both the measured levels for each kit and the mean of the measured levels by several kits are considered to be random variables, the model used should be a linear structural relationship with random errors in both variables (2). This point was raised in 1998 in committee at the Foundation for Growth Science, Japan and thereafter standardization was performed by linear structural relationship. The equations obtained were thereafter employed to standardize the levels measured by the various kits. These standardized values were taken as authorized values in applying for the use of growth hormone in therapy, which is controlled by committee at the Foundation for Growth Science, Japan (1).

In this paper, the methods and the results of the above-mentioned standardization are presented, together with an analysis of the possible sources of difference in the measured values among the measurements kits.

Subjects and Methods

Study samples and measurement kits

The study was carried out every year from 1998 to 2003. Blood samples were obtained with informed consent from healthy adult volunteers who were hospital staff. Blood specimens were collected from each individual for a growth hormone- releasing provocation test; blood was drawn before the test, and 15, 30, 60, 90 and 120 min after provocation. The serum specimens were kept at –20 °C prior to testing.

The measurement kits studied were the following: immunoradiometric assay kits made by Eiken Chemical Co., Ltd. (Eiken IRMA) and Daiichi Radioisotope Labs., Ltd. (Daiichi IRMA); an immunoenzymometric assay kit from Tosoh Co., Ltd. (Tosoh IEMA); chemiluminescence enzyme immunoassay kits from Japan DPC Corp. (DPC CLEIA), Hitachi Kasei Co., Ltd. (Hitachi CLEIA), Beckman Coulter, Inc. (Beckman CLEIA) and Yatoron Co., Ltd. (Yatoron CLEIA); chemiluminescence immunoassay kits from Sumitomo Pharmaceuticals (Sumitomo CLIA) and Kyowa Medex Co. Ltd. (Kyowa CLIA).

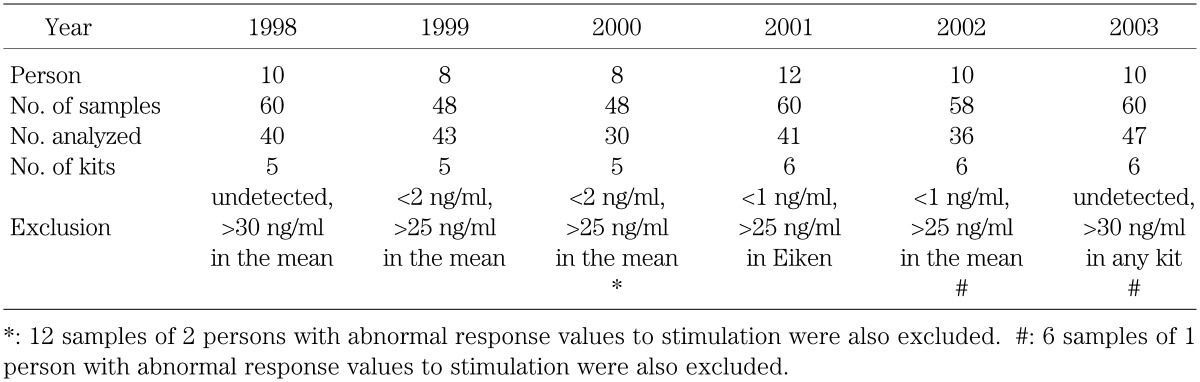
The details for the number of specimens measured, number of kits used, and exclusion criteria employed in each year are summarized in Table 1. In addition, from 2000 to 2003, a standard solution prepared from human recombinant growth hormone (rhGH) was included to explore the sources of difference in measured values among the kits. For this purpose a rhGH preparation for clinical injection was used in 2000, and rhGH prepared by the Japan Chemical Research Pharmaceuticals Co, Ltd which was calibrated to the No.88/624 standard provided by the WHO was used in the other years.

Table 1. The number of specimens, measurement kits, and exclusion criteria.

Calculation of linear structural relationship

Equations for standardizing measured values were obtained using the following linear structural relationship: Y = α + βf(x) + ε; X = f(x) + δ; covariance (f(x), ε) = covariance (f(x), δ) = covariance (ε, δ) = 0. Here, the mean of the values from several kits was assigned as Y and the value for each kit was assigned to X in each equation. Both Y and X had error terms, ε and δ, respectively. The covariance of the three pairs in the above equation was set to 0 signifying that these terms were mutually independent. It is noted here that the linear structural equation is reduced to linear regression if δ is zero.

Calculation was done by the CALIS procedure of the SAS software (3). Product-moment correlation coefficients, which have error terms in both variables, between the mean of the kits and the value for each kit were also calculated using CALIS.

Results

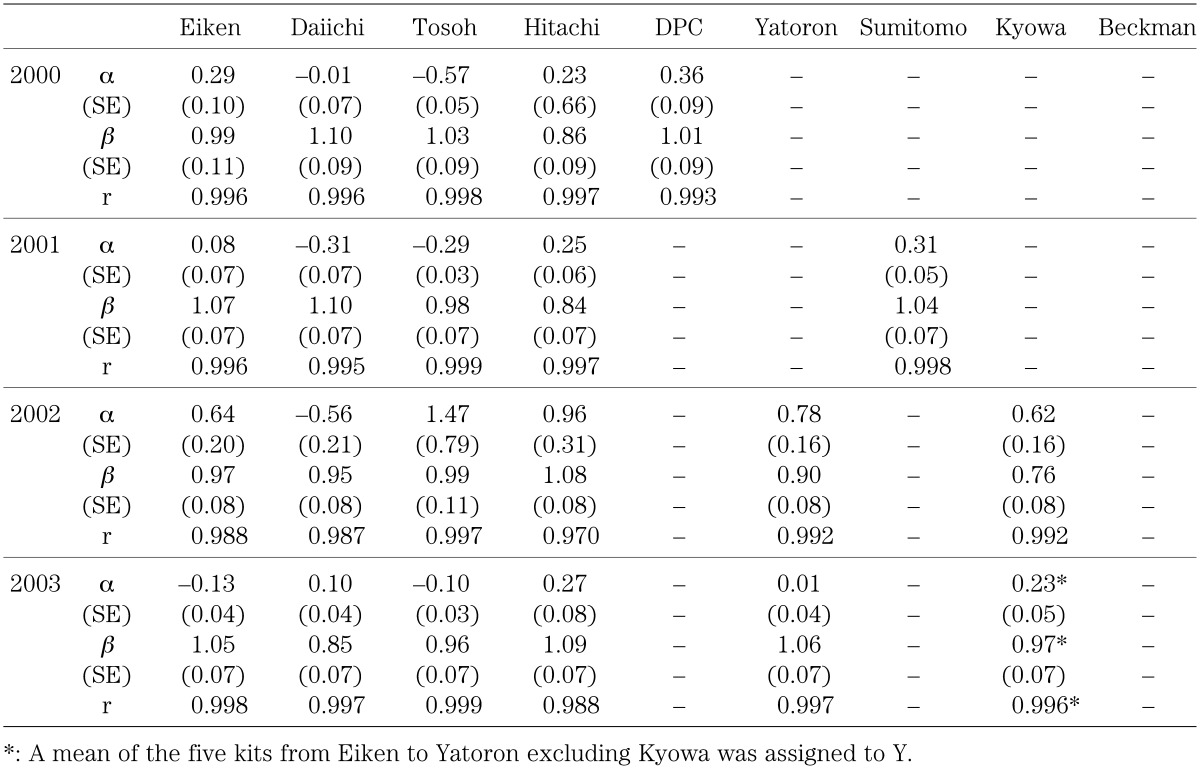
Table 2 shows the linear structural relationship and the correlation coefficient for values measured in 1998–2003. Standard errors (SE) for the slope β and the intercept α of the equation are also shown. The slope and the intercept differed considerably among the kits. The results for 2000–2003 using the rhGH standard solution are shown in Table 3. These results also show considerable differences between the slopes and intercepts among the kits, however, the slope and the intercept remained fairly stable from year to year for the same kit. The standard errors for the slope and intercept were quite small for all kits in each year, and correlation was quite high. The value for the same specimen could differ as much as two-fold between kits with the highest and lowest slope values. The slope in all the kits became closer to 1 with the use of the rhGH standard solution. From these results, the differences in the measured values among the kits were ascribed largely to the use of different standard solutions.

Table 2. Linear structural relationship: results using each standard solution in 1998∼2003.

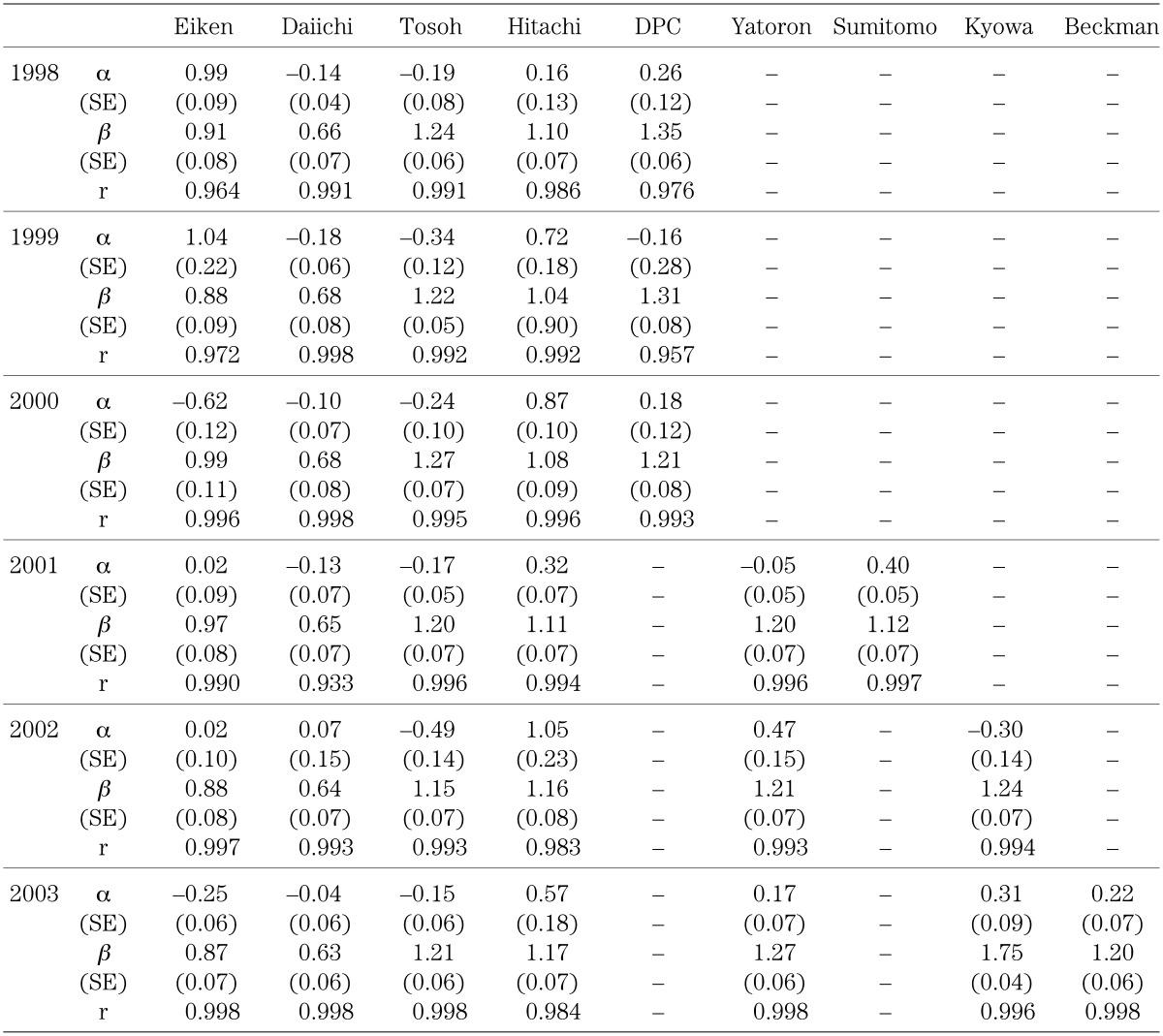
Table 3. Linear structural relationship: results using a standard solution prepared from human recombinant growth hormone (rhGH) in 2000∼2003.

Discussion

Using a linear structural relationship in comparing two measurement methods was precedented in the field of clinical chemistry in the 1970s (4, 5), and raised as an issue in Japan in 1986 (6). However, the theoretically incorrect analysis of linear regression remained in use. This study is one of only a few to apply linear structural relationship.

Our study, however, did have to overcome several problems in the analysis. First, the variable assigned to Y in the linear structural relationship was not a measured value of a given kit but the mean of several of the kits. Therefore, the variable of X was included in the variable Y as one of the numbers of the numerator of the mean, making the slope of the equation closer to 1 and the intercept closer to 0 than in those cases when a gold standard containing a true level of growth hormone was assigned to the variable Y. It is also theoretically incorrect to calculate correlation coefficients for the same reason. However, the distortion resulting from employing the mean value from several kits rather than a true value is expected to be small enough to justify using the results of the obtained equations in deciding on growth hormone therapy. In addition, no alternative methods for standardization were available which would have allowed linear regression to be used on a diluted gold standard for the dependent variable without an error term when a standard solution of a known level of growth hormone had been available. If a standard solution is available, use of linear regression is justifiable using its diluted samples for the dependent variable without an error term; but this was not the case. Therefore, the discrepancy between the linear structural relationship and linear regression methods can be significant in the standardization of blood growth hormone levels. Having said this, the results (data not shown) did indicate that the differences between the two methods in the slope and intercept were negligible for all the measurement kits. The differences were all in the order of below two decimal points in the slope and below three decimal points in the intercept. Therefore, although theoretically incorrect, the use of linear regression before 1998 should not have caused any serious errors in the diagnosis and judgment of growth hormone therapy.

There was a substantial difference in the measured values among the kits, as shown particularly by the slope values and to some extent by the intercepts. The difference was ascribed mainly to the difference in standard solutions employed in the different kits. This conclusion was supported by the following observations. First, the slope of the value measurements for a given a kit did not differ significantly from year to year, and the intercept was close to 0 in most kits. In addition, the standard errors of the slope and intercept were quite small in all of the kits. Therefore, the precision of the kit measurements, that is the variance of the repeated measurements, was not a major source of the variability. Second, the slope approached 1 and the intercept approached 0 in every kit when the same recombinant standard solution was employed, indicating the kit accuracy as a major source of the original difference among the kits. Thirdly, the correlation coefficient between the values measured with the kits’ own standard solutions and with the same standard solution was quite high in every kit. This further excluded precision as a possible source of variation among of the kits.

Detailed analyses on the sources of differences among kits using the same samples analyzed in this study have already been reported (7, 8). These reports ascribed the variability largely to the different standard solutions employed in the kits, and to a lesser extent to the variation of measurement in each kit, namely, rather large coefficients of variation. The latter may be explained by differences in the antibodies used in the kits or by the interassay variance of the kits.

The difference in the slope and intercept of the equations among the kits using the same standard solution became small enough to make conversion of the values with the equations unnecessary for the purpose of diagnosis and judgment in growth hormone therapy (7). Based on these results employment of rhGH calibrated to WHO standard as the standard was proposed. This will lead to consistent values without using different equations for standardization. However, new difficulties arise; one is the setting of a new cut point below which administration of growth hormone is justified. A new cut point, 60% of the previous cut point, in a refined measurement was proposed by committee at the Foundation for Growth Science (8). This point needs to be assessed thoroughly with input from the medical community and the concerned organizations. Another difficulty is to secure methods which enable comparison of the new measurement values with previous values for research purposes. This can be achieved by creating equations by linear structural relationship between the new methods and the old methods.

Equations for standardizing values measured by various kits ceased to be used after 2005. This was made possible by a joint effort of the Foundation for Growth Science and the kit manufacturers in Japan. All kits now available in Japan will use rhGH or pituitary growth hormone calibrated to rhGH for their standard solutions. This action was based on the results of research including this report.