Estimating Podocyte Number and Density Using a Single Histologic Section

Abstract

The reduction in podocyte density to levels below a threshold value drives glomerulosclerosis and progression to ESRD. However, technical demands prohibit high-throughput application of conventional morphometry for estimating podocyte density. We evaluated a method for estimating podocyte density using single paraffin-embedded formalin-fixed sections. Podocyte nuclei were imaged using indirect immunofluorescence detection of antibodies against Wilms’ tumor-1 or transducin-like enhancer of split 4. To account for the large size of podocyte nuclei in relation to section thickness, we derived a correction factor given by the equation CF=1/(D/T+1), where T is the tissue section thickness and D is the mean caliper diameter of podocyte nuclei. Normal values for D were directly measured in thick tissue sections and in 3- to 5-μm sections using calibrated imaging software. D values were larger for human podocyte nuclei than for rat or mouse nuclei (P<0.01). In addition, D did not vary significantly between human kidney biopsies at the time of transplantation, 3–6 months after transplantation, or with podocyte depletion associated with transplant glomerulopathy. In rat models, D values also did not vary with podocyte depletion, but increased approximately 10% with old age and in postnephrectomy kidney hypertrophy. A spreadsheet with embedded formulas was created to facilitate individualized podocyte density estimation upon input of measured values. The correction factor method was validated by comparison with other methods, and provided data comparable with prior data for normal human kidney transplant donors. This method for estimating podocyte density is applicable to high-throughput laboratory and clinical use.

Pagtalunan et al. used the term podocyte density to describe the key relationship between podocyte number and glomerular tuft volume.¹ Model systems have proven the causative relationship between podocyte depletion (resulting from reduced podocyte number or dysfunction and/or glomerular enlargement) and glomerulosclerosis and progression to ESRD.^2–9 Groundbreaking kidney morphometric biopsy reports from type 1 and 2 diabetes, IgA nephropathy, and hypertensive kidney biopsies in humans support the concept that reduced podocyte number and density is associated with development of glomerulosclerosis and progression,^1,10–15 and strongly imply that podocyte density estimation could help guide clinical decision making.

The importance of avoiding simplistic podocyte counting strategies and using appropriate stereologic considerations for estimating podocyte number and density have recently been re-emphasized.^16–20 Optimal research methods for estimating podocyte density, such as the disector/fractionator approach, are too technically demanding for high-throughput use in laboratory work, drug testing by pharmaceutical companies, routine clinical biopsy readout, and automated biopsy analysis. We therefore assessed whether it might be feasible to use single formalin-fixed paraffin-embedded histologic sections to estimate podocyte density in biopsy samples with adequate accuracy and reproducibility. A similar approach for counting nuclei in tissue sections was suggested by Abercrombie in 1946.²¹

Results

Podocyte Nuclear Identification

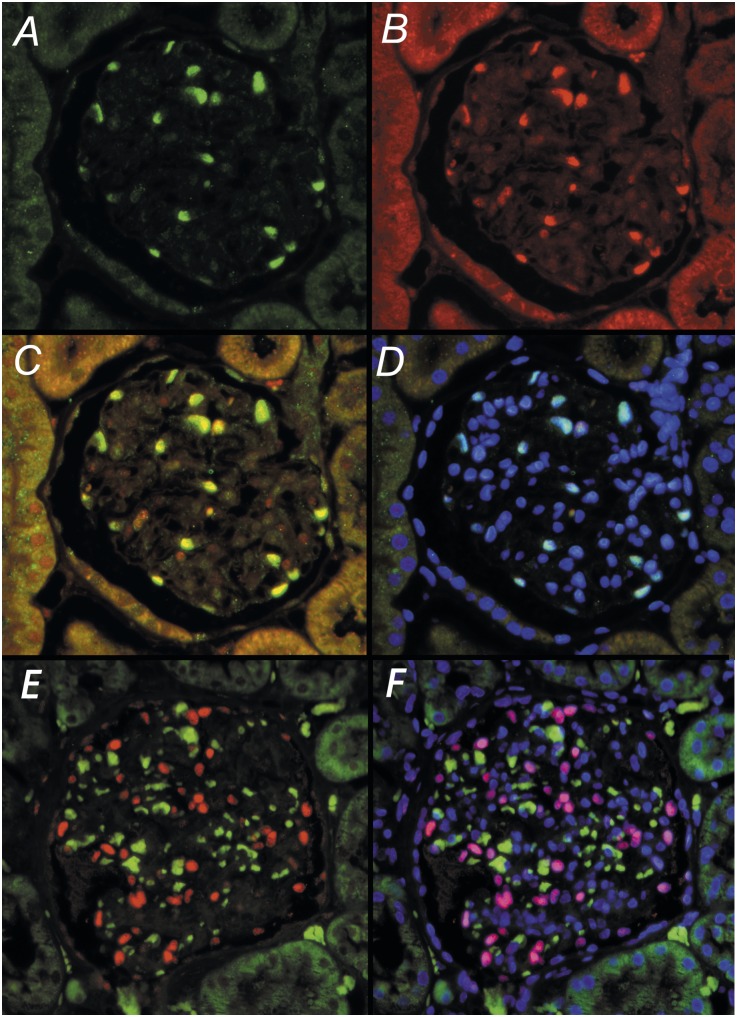
The transcription factor Wilms’ tumor-1 (WT1) is uniformly highly expressed in rodent podocyte nuclei,²² but may be less robustly expressed in formalin-fixed sections of human kidney. We therefore identified transducin-like enhancer of split 4 (TLE4), a transcriptional corepressor factor,²³ as an alternative podocyte nuclear marker. Confirmation that TLE4 colocalizes with WT1 in podocyte nuclei is shown in Figure 1, A–D. A commercially available TLE4 murine mAb can be used to identify podocyte nuclei in formalin-fixed human kidney sections (Figure 1E).

Figure 1.

TLE4 antibody identifies podocyte nuclei as identified by WT1 antibodies in glomeruli of formalin-fixed kidney. (A–C) In a rat glomerulus, WT1 green fluorescence (A) and TLE4 red fluorescence (B) colocalize within podocyte nuclei (C). (D) Nuclear localization is confirmed by blue DAPI fluorescence to give a merged pale blue signal. (E) In formalin-fixed human glomeruli, TLE4 (red fluorescence) merged with the green nonspecific fluorescence signal provides a robust marker of podocyte nuclei (red) that can be excluded from nonspecific signals arising from autofluorescence blood products in glomerular capillaries (green/orange). (F) Confirmation that the red TLE4 signal is in nuclei is shown by colocalization with blue nuclear DAPI to give shocking pink human podocyte nuclei. Original magnification, ×100.

Emersion-fixed kidney biopsies contain blood elements that remain within glomerular capillaries where they can cause nonspecific signals. Three-color immunofluorescence imaging is used in which the primary antibody directed against WT1 (or TLE4) is present in podocyte nuclei photographed in the red channel, nonspecific autofluorescence is photographed in the green channel, and 4′,6-diamidino-2-phenylindole (DAPI)–labeled nuclei photographed in the ultraviolet channel. Merging of these images results in shocking, pink podocyte nuclei easily distinguishable from nonpodocyte nuclei (blue), trapped red cells and blood clot (orange/green), and other autofluorescence structures (Figure 1F).

Correction Factor

Because podocyte nuclei are large in relation to section thickness, simply counting nuclear profiles overestimates true podocyte number by 200%–300% depending on section thickness and nuclear size. A correction factor (CF) can be applied to the nuclear count that compensates for both section thickness (T) and nuclear size/shape as estimated by the podocyte mean nuclear caliper diameter (D). D is defined as the averaged diameter of a randomly orientated structure viewed in a single dimension as illustrated in the upper panel of Figure 2. A simple equation was derived (see Concise Methods) to define the relationship between CF, T, and D, where CF=1/(D/T+1), similar to that reported by Abercrombie in 1946.²¹ Using this equation, the CF can be calculated for any section if tissue section thickness and the mean caliper diameter of the podocyte nuclei are known.

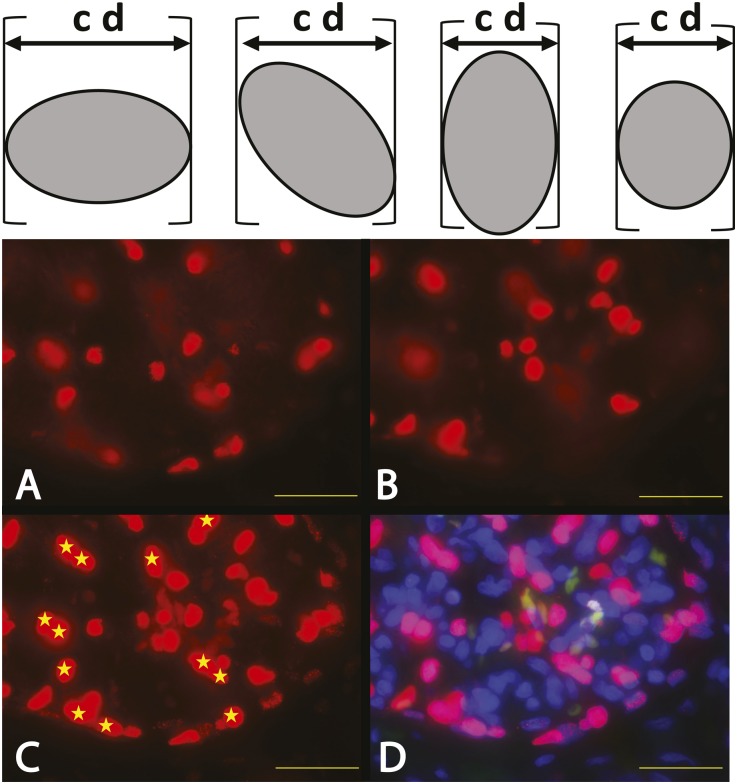
Figure 2.

Podocyte nuclear mean caliper diameter D direct measurements. In the upper panel, the caliper diameter (cd) for a randomly orientated asymmetric object is the distance between the edges of the object in any single dimension as shown by the calipers (brackets). (A–D) The images show part of a human glomerulus in a 20-μm–thick section of human kidney developed using TLE-4 antibodies to identify podocyte nuclei by red fluorescence. A and B show the top and bottom optical sections respectively of a z-stacked composite image shown in C and D. C shows the z-stack composite in the red channel only. D shows the same z-stack composite using the merged red (TLE-4), green (nonspecific autofluorescence), and blue (DAPI) channels to identify podocyte nuclei (shocking pink) and exclude nonspecific autofluorescence of erythrocytes (orange/green). Podocyte nuclei that are sharply in focus in the top (A) or bottom (B) optical sections are excluded from further analysis, leaving only those podocyte nuclei that cannot have been partially sectioned (shown by yellow stars) to be evaluated. The podocyte nuclear caliper diameter (D) of the starred nuclei can thereby be directly measured by tracing their outer boarders using calibrated imaging software program to estimate the mean caliper diameter of 100 consecutive nuclei. Scale bar, 32 μm.

Direct Measurement of the Mean Caliper Diameter D

Any attempt to directly measure D in a tissue section will be confounded by the nuclei at the edges of the section being partially cut off and, therefore, appearing smaller than their true size. To circumvent this problem, a collated stack of immunofluorescence photomicrographs was made by sequentially photographing through 15- to 20-μm–thick tissues to obtain a series of “optical sections” (Figure 2). This allows nuclei that appear at the top and bottom of the z-stack (i.e., nuclei that could have been sectioned at the upper surface or lower surfaces of the histologic section) to be identified and excluded from the nuclear size measurements. Thus, the mean caliper diameter of the remaining intact nuclei in the section can be traced and measured directly using calibrated imaging software. The measured mean podocyte nuclear caliper diameter values for D were as follows: 8.3±0.6 μm for humans (n=12), 7.1±0.4 μm for rats (n=10), and 6.9±0.4 μm for mice (n=10). D values for human podocyte nuclei were statistically larger than mouse or rat podocyte D values (P<0.01). Rat and mouse podocyte nuclear D values were not statistically different from each other. CF curves were plotted related to section thickness for each species as shown in Figure 3A. Table 1 provides a CF value for any section thickness based on the average mean caliper diameter of podocyte nuclei in humans, rats, or mice. However, the question remains as to whether or not D is a constant value or varies under physiologic or pathologic conditions. This question was evaluated in both human biopsies and rat model systems.

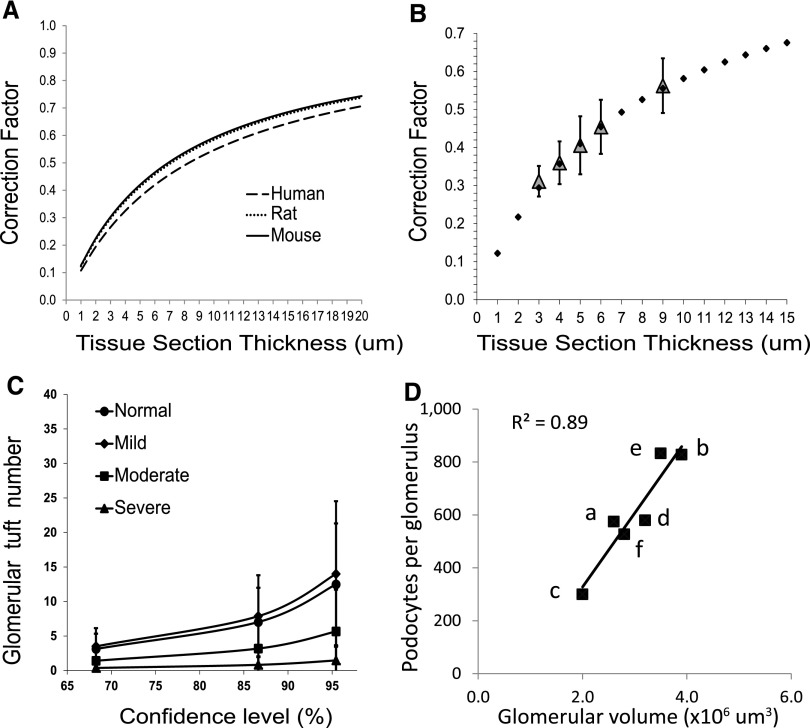
Figure 3.

(A) CF variation in relation to section thickness for each species. The curves for human podocyte nuclei (mean caliper diameter 8.3 μm), rat podocyte nuclei (mean caliper diameter 7.1 μm), and mouse podocyte nuclei (mean caliper diameter 6.9 μm) are shown in relation to section thickness (x-axis) and the CF (y-axis) as calculated using the equation CF=1/(D/T+1). Note that the curves for rat and mouse are almost superimposable and that even the difference in nuclear size between human and rodent podocytes changes the CF by a relatively small amount (<10%). (B) Observed CF reflects predicted CF. CF values for sections of different thicknesses are estimated by comparing the observed number of podocyte nuclei in a section with the known number of podocyte nuclei per glomerulus measured using the two-thickness method and confirmed by serial sectioning through whole glomeruli to count all podocytes in five tissue blocks from different rat kidneys. The values for the CF at each section thickness±1 SD are plotted in relation to the section thickness (gray diamonds). A CF curve calculated using the equation CF=1/(D/T+1) using mean podocyte nuclear caliper diameter measured for rat podocyte nuclei of 7.1 μm is shown for a range of tissue section thickness (closed diamonds) demonstrating that the measured CF values corresponded to the CF values derived from the equation over a wide range of section thicknesses. (C) Glomerular tuft number required to reliably estimate podocyte density. The graph shows the confidence limits (x-axis) and tuft sample size required (y-axis) to obtain a value for podocyte number within 5% of the true value (derived from a sample size of 50 glomerular tufts). Data are from rats that have >90% of normal (n=15), mild (60%–89% of normal; n=10), moderate (30%–59% of normal; n=8), and severe (<30% of normal; n=9) podocyte depletion. Less than eight tuft profiles are required to arrive at a value within 5% of the measured value with 90% confidence for any level of podocyte depletion. (D) Published data for podocyte number per tuft and glomerular volume for donor kidneys varies 2- to 3-fold, as shown in Table 3. For kidney transplant donors, there are large differences in the estimated glomerular volume and podocyte number per tuft between different reports. However, when plotted against each other, there is a strong correlation between glomerular volume and podocyte number per glomerulus, indicating that the relationship between these two variables (podocyte density) does not vary much between different methods. The letters in D correspond to the following references: a, Pagtalunan et al. (1997)¹; b, Steffes et al. (2001)¹¹; c, Lemley et al. (2002)¹³; d, White et al. (2002)¹²; e, Dalla Vestra et al. (2003)¹⁴; and f, Venkatareddy et al. (current report).

Table 1.

CF table for human, rat, and mouse podocyte nuclei according to tissue section thickness

Section Thickness (μm)	Human CF	Rat CF	Mouse CF
1	0.11	0.12	0.13
2	0.19	0.22	0.22
3	0.27	0.3	0.3
4	0.33	0.36	0.37
5	0.38	0.41	0.42
6	0.42	0.46	0.47
7	0.46	0.5	0.5
8	0.49	0.53	0.54
9	0.52	0.56	0.57
10	0.55	0.58	0.59
11	0.57	0.61	0.61
12	0.59	0.63	0.63
13	0.61	0.65	0.65
14	0.63	0.66	0.67
15	0.64	0.68	0.68

Values for CF were derived using the equation CF=1/(D/T+1) and the measured mean nuclear caliper diameter values for D from human (8.3 μm), rat (7.1±0.4 μm), and mouse (6.9±0.4 μm) podocyte nuclear mean caliper diameters.

Relationship between the Apparent Mean Podocyte Nuclear Caliper Diameter in Histologic Sections and the True Mean Caliper Diameter

Because a histologic section will cut through nuclear profiles at its edges, the apparent mean podocyte nuclear caliper diameter (d) underestimates the true mean podocyte nuclear caliper diameter (D) in proportion to tissue section thickness and podocyte nuclear size and shape. To describe these relationships, we derived a quadratic equation,

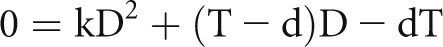where D is the true mean caliper diameter, d is the apparent mean caliper diameter, k is the podocyte nuclear shape coefficient, and T is the section thickness (Supplemental Methods). Simulation analysis was used to confirm that k accurately describes nuclear shape in the context used (Supplemental Methods). A value of 0.72 for k for podocyte nuclear shape was estimated using the quadratic equation under conditions in which both D and d were directly measured (Supplemental Methods). Podocyte nuclear shape (k=0.72) falls between a sphere (k=0.79) and either prolate or oblate ellipsoids of dimensions a=2b (k=0.66 or 0.68, respectively). Changes in podocyte nuclear shape that might theoretically occur under physiologic and pathologic conditions have minimal effect on the CF (Supplemental Methods).

To facilitate individualized estimation of D in a histologic section, a spreadsheet is provided in the Supplemental Material. The quadratic equation is solved using the quadratic formula

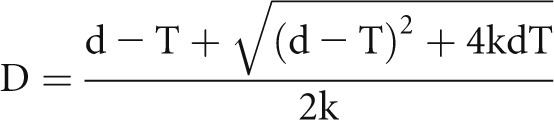that is embedded in the spreadsheet together with the CF equation, CF=1/(D/T+1), so that by inputting values for section thickness (T) and apparent mean caliper diameter (d), a value for D and, thereby, an appropriate CF for the section is calculated. Podocyte density is then calculated from the entered podocyte count and tuft area derived as shown in Figure 4.

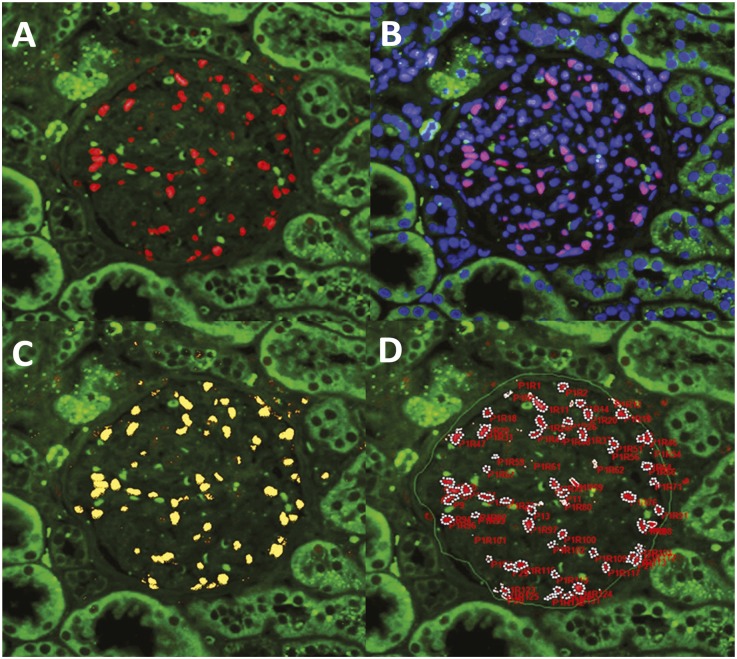
Figure 4.

Measurement of podocyte number and mean caliper diameter (d) using Image-Pro software. A glomerulus from a human kidney biopsy before implantation is shown processed for immunofluorescence imaging and photographed using the three-color system to identify podocyte nuclei (red TLE4) superimposed on blue DAPI (to give purple) as distinct from erythrocytes (green) (A). The red/green merged images are opened in the Image-Pro software (B), and a mask (yellow) is applied and adjusted to exactly cover red podocyte nuclei (C). Occasional TLE4-positive signals are present outside the glomerulus (e.g., at right of the glomerulus shown). An area of interest is drawn around the glomerular tuft (green line shown by arrows in D), and a number is automatically assigned to each masked structure. Overlapping nuclei are “split” using the software. All podocyte nuclei are then identified by clicking on them so that they become surrounded by white dots. Individual nuclear profile caliper diameters and the glomerular tuft area are automatically exported to an Excel file to give the podocyte nuclear number, mean podocyte nuclear caliper diameter (d), and glomerular tuft area. Original magnification, ×100.

D in Human Kidney Biopsies

Calibrated Image-Pro Premier software was used to measure apparent d and, thereby, to estimate true D in human kidney biopsies (see Figure 4). In biopsies obtained at the time of transplantation, D was 8.2±0.3 μm (n=10, coefficient of variation <5%). This value is similar to the true D of 8.3±0.6 μm that was directly measured in thick de-identified human kidney sections as outlined above. The D value measured in kidney allografts that were biopsied 3–6 months after transplantation (at which time kidney hypertrophy would have been expected to have occurred) was 8.4±0.4 μm (n=9) and was not significantly different from controls. In eight paired kidney transplant samples in which D was measured both immediately before implantation and 3–6 months after transplantation, D did not change significantly (8.2±0.2 versus 8.4±0.4; P=NS). A third group of kidney transplant biopsies with transplant glomerulopathy was evaluated in which the podocyte number was decreased from 567±123 to 295±137 podocytes per tuft (n=15; range, 71–467; P<0.001 compared with controls). The value for D from these biopsies was 8.3±0.7 μm and was not significantly different from control or 3-month biopsies. Individual values for D ranged from 6.8 to 9.6 μm. Therefore, in human biopsies, average nuclear caliper diameter did not change significantly under conditions of expected kidney hypertrophy and measured podocyte depletion, although there was considerable individual variation.

Estimation of D in Rat Kidneys under Physiologic and Pathologic Conditions

Apparent mean caliper diameter (d) was measured using WT1 immunofluorescence and manual tracing of each podocyte nuclear profile (n=100 per sample). The quadratic equation was then used to calculate D as described above. The results for sex, age, podocyte depletion in glomerular tufts, and kidney hypertrophy are as follows. Male and female rats weighing 100 g had D values of 7.5±0.4 μm and 7.1±0.3 μm, respectively (n=5 per group; P=NS). Rats aged 2 months (young) and 24 months (old) had D values of 6.9±0.4 μm and 7.5±0.3 μm, respectively (n=5 per group; P=0.05). To assess podocyte depletion in glomerular tufts, we used the hDTR rat model system to deplete podocytes by variable degrees as previously described.⁶ The resultant D values were as follows: nonpodocyte depleted glomeruli (>95% of normal), 6.9±0.3 μm; 10%–25% podocyte depletion, 7.5±0.4 μm; 26%–50% podocyte depletion, 7.5±0.2 μm; 51%–75% podocyte depletion, 7.1±0.2 μm; and >76% podocyte depletion, 7.0±0.5 μm. Therefore, depletion of podocytes per se did not significantly alter D values. Finally, we assessed 100-g rats before uninephrectomy and 1 week after uninephrectomy to induce kidney hypertrophy and found that their D values (6.7±0.3 and 7.7±0.5, respectively) were significantly different (n=5 per group; P<0.01).

In summary, there was no significant change in D values under conditions of podocyte depletion in both the rat model and human glomerular disease. An increase in D of approximately 10% was found in young versus old rat glomeruli and immediately after nephrectomy. In contrast, there was no significant increase in D for human biopsies in which the same kidney was biopsied at the time of transplantation and 3 months later.

Validation of the CF Method versus Published Methods

Two-Thickness and Serial-Sectioning Methods

The average podocyte number per glomerulus in five rat renal cortex samples was measured using both complete glomerular serial sectioning and the previously validated two-thickness method.²⁴ The values obtained (131±19 podocytes per glomerular tuft) were similar to those reported previously by us²⁴ and by Bai et al. using the disector fractionator method.²⁵ Additional sections of various thicknesses were then cut from these same blocks of kidney cortex and the average number of podocyte nuclei per tuft cross-section at each section thickness was counted (n=5 per thickness). Because the true average number of podocyte nuclei per glomerular tuft for each rat was known, we could then calculate the CF that would be needed to correct for overcounting at each section thickness. The CFs at various section thicknesses were as follows: 0.31±0.04 for 3 μm, 0.36±0.06 for 4 μm, 0.41±0.08 for 5 μm, 0.45±0.07 for 6 μm, and 0.56±0.07 for 9 μm. These data are plotted in Figure 3B as open triangles and could be superimposed onto the curve generated from the equation CF=1/(D/T+1) using the measured value for D of 7.1 μm for rat podocyte nuclei. These data demonstrate that the CF method provides the appropriate CF values over a wide range of section thicknesses.

Multiple-Thickness Method

This method (Figure 5, Table 2) uses podocyte nuclear counts at multiple section thicknesses to generate a slope whose characteristics give values for the CF. It independently generates a value for the mean caliper diameter. In this case, D is 7.2±0.1 μm for rat podocyte nuclei. This result independently validates the CF methodology and the thick-section method for estimating podocyte nuclear mean caliper diameter D.

Figure 5.

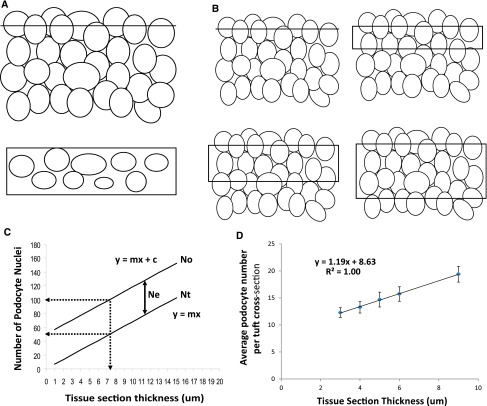
Validation of the CF method using a multiple section thickness approach. (A) A hypothetical collection of randomly arranged solids cut by an infinitely thin plane is shown, which when viewed from above (A, bottom) contains ellipsoid solids randomly sectioned at various levels that can be counted to give a value (Ne). (B) The image shows how as this plane becomes thicker, it increasingly includes more solids counted as the observed (apparent) total number (No). No will be the sum of the number of solids cut by the infinitely thin plane at the edge of the section (Ne) plus the number of solids that increases in direct proportion to the thickness of the section (Ntrue or Nt). Nt therefore=No–Ne at any section thickness. (C) This relationship is shown diagrammatically, where the value for the observed number of solids (No) increases linearly with section thickness (described by the equation y=mx+c where y is the number of solids observed, x is the section thickness, m is the slope of this relationship, and c is the value for Ne. The true number of solids (Nt) is given by No–Ne at any section thickness. The dotted lines show that at a section thickness equal to mean caliper diameter of 7.1 μm, the observed podocyte number would be approximately twice the true podocyte number (or CF=0.5). (D) Real data are presented that are derived from counting the average number of podocyte nuclei in rat glomerular sections from a range of section thicknesses to derive parameters for the equation y=mx+c. Using these parameters, values can be calculated for No, Ne, Nt, and CF as shown in Table 2.

Table 2.

Validation of the CF using the multiple section thickness method

Section Thickness (T) (μm)	Podocytes per Cross-Section (No) (n)	Podocytes per Nuclear Tuft (Nt) (n)	Extra Podocyte Nuclei (Ne) (n)	CF	D (μm)
3	12.3	3.6	8.7	0.29	7.29
4	13.3	4.8	8.5	0.36	7.12
5	14.7	6.0	8.7	0.41	7.32
6	15.7	7.2	8.6	0.46	7.17
9	19.4	10.7	8.6	0.55	7.24
Mean			8.6		7.23
1 SD			0.1		0.08

As the section thickness increases, the observed (apparent) number of podocytes per tuft cross-section (No) increases as shown in Figure 5, C and D. Figure 5C shows that the true podocyte number is given by y=mx, where x is the section thickness. From the slope of the line in Figure 5D, the value for m is 1.19. Therefore, the true number of podocyte nuclei per tuft (Nt) can be calculated for each section thickness as shown in Table 1 (Nt=1.19×T). The number of extra podocyte nuclei (Ne) counted in any glomerular cross-section due to nuclei bisected at the edge of the section (as illustrated in Figure 5A) is derived from No−Nt and, as expected, is a constant value whatever the section thickness (8.6±0.1 μm). The CF is given by Nt/No for any section thickness as shown in Table 1. The value for the mean caliper diameter of podocyte nuclei can be derived from the formula D=(1/CF−1)×T by substituting known values for the CF and section thickness T. The value for D derived for rat podocyte nuclei (7.2±0.1 μm) is not significantly different from the value directly measured in thick sections of 7.1±0.1 μm.

The Disector Method

This classic method favored by morphometrists relies on being able to accurately identify the nuclei that appear in an upper section (“top” nuclei) that do not appear in a lower section separated by a known distance.^17–21 We used neighboring 3-μm sections and WT1 immunofluorescence to identify podocyte nuclei that appeared in one section but not the other and vice versa. The proportion of top nuclei (Ntop) that do not appear in the adjacent section is the CF needed to correct the observed total podocyte nuclear count (No) to obtain the true value (CF=Ntop/No). The CF value obtained using this method was 0.32±0.02 for 3-μm sections (n=6), similar to the value derived using the CF method as shown in Table 1.

Human Kidney Biopsy Data Generated Using the CF Method Compared with Previously Published Data

The CF method applied to human donor kidneys before transplantation (n=10) gave values for mean podocyte density of 194±46 podocytes/10⁶ μm³, mean podocytes per glomerular tuft of 527±80, and mean glomerular volume of 2.8±0.6×10⁶ μm³. Table 3 shows these data compared with previously published data all derived from kidney transplant donor biopsies, which should, therefore, be comparable. The number of podocytes per tuft estimated by different investigators using different methods varies almost 3-fold and glomerular volume varies approximately 2-fold. Figure 3D shows that although different methods and investigators estimated a wide range of podocyte numbers per tuft and glomerular volume, there is a strong correlation (r²=0.89) if these variables are plotted against each other. This relationship, which is rather consistent between methods and investigators, is the podocyte density (number per volume). The CF method gives data that are comparable with these other reports.

Table 3.

Comparison of the CF method with previously published parameters all measured in kidney transplant donors

Reference	Biopsies (n)a	Glomerular Volume (×106 μm3)	Podocytes per Glomerular Tuft (n)	Podocyte Density (n/106 μm3)b
Pagtalunan et al. (1997)1	8	2.6	575	235
Steffes et al. (2001)11	20	3.8	828	218
Lemley et al. (2002)13	14	2.0	300	152
White et al. (2002)12	10	3.2	580	193
Dalla Vestra et al. (2003)14	20	3.5	833	263
Venkatareddy et al. (current report)	10	2.8	527	194
Mean		3.0	614	204
1 SD		0.7	224	41
Coefficient of variation (%)		23	37	20

Mean data are shown for comparison between methods.

^aBiopsies indicates the number of biopsies evaluated in each study. For the Steffes et al. publication,¹¹ only the group aged>20 years was used.

^bPodocyte density shows the data provided in the text/tables for each publication unless this was not calculated, in which case the data shown is for the number of podocytes per glomerular tuft divided by glomerular volume (for Steffes et al.¹¹ and Lemley et al.¹³). Note that there is a 2-fold variation in estimation of glomerular volume (coefficient of variation between methods = 23%) and almost a 3-fold variation in estimates of podocyte number per glomerulus (coefficient of variation between methods=37%). The podocyte density coefficient of variation between methods was 20%, showing that podocyte density is a relatively robust measurement between methodologies. Figure 3D plots the data for glomerular volume versus podocytes per glomerular tuft and shows that these parameters correlate highly between different methods (r²=0.89).

Discussion

There is now strong evidence from both model systems and humans to support the hypothesis that podocyte depletion relative to glomerular volume (captured by the term podocyte density) is the critical process driving glomerulosclerosis.^1–15 This report evaluates a single histologic section for high-throughput podocyte density estimation.

The CF method for podocyte density estimation requires podocyte nuclei to be clearly identified. WT1 antibodies have traditionally been used for this purpose,²² but, although WT1 is highly expressed by rodent podocyte nuclei, its expression may be less robust in some human histologic sections. We therefore identified TLE4 as an additional/alternative transcription factor easily detected in podocyte nuclei for human biopsy analysis. TLE4 was originally identified as an immature B-cell marker,²³ but B cells are rarely found in the glomerulus even under severe inflammatory conditions and are, therefore, not likely to significantly interfere with estimation of podocyte number/density.^26–28 At the same time, podocytes can lose expression of WT1 (and probably also TLE4) in the setting of altered phenotype, such as in HIV nephropathy²⁹ or FSGS caused by increased expression of microRNA-193a.³⁰ On the other hand, methods that rely on the podocyte unique structure and anatomic relationships for identification become less reliable in pathologic settings. Podocyte structure can change remarkably. Macrophages, T cells, fibroblasts, and parietal epithelial cells may occupy Bowman’s space and invade the tuft. Basement membranes can rupture and become reduplicated to further distort anatomic relationships. No method will be perfect in every circumstance so that podocyte density/number estimates must be evaluated within the constraints of the methodology used.

Once identified, podocyte nuclei must be counted in relation to the volume of the disc of glomerular tuft represented in the histologic section. The most important confounder is overestimation because podocyte nuclei are large in relation to routine section thickness so that they appear in more than one neighboring section. This commonly ignored fact gives rise to an error of 200%–300%, depending on section thickness. This problem can be addressed by using a CF that, in turn, depends on section thickness and nuclear size/shape as given by the equation CF=1/(D/T+1). T is the section thickness that is known or can be easily measured. D is the mean caliper diameter of podocyte nuclei that accounts for both nuclear size and shape. Values for D vary between humans (D=8.3±0.5 μm) and rodents (rat D=7.1±0.4 μm and mouse D=6.9±0.4 μm). Table 1 provides the CF for any section thickness that assumes the above values for D are constant under different physiologic and pathologic conditions.

The size of a cell nucleus is proportional to the size of the host cell (the “karyoplasmic ratio”).³¹ Both nuclei and cells increase in size immediately before cell division so that a significant part of this karyoplasmic relationship is due to increased DNA during cell division. Podocytes do not divide in situ although binucleate podocyte nuclei do rarely occur³²; thus, cell division is not a major factor determining podocyte nuclear size. Nuclei also increase in volume in relation to RNA transcription levels.³³ However, podocytes have limited capacity to hypertrophy to cope with glomerular volume increase⁵ and we found no increase in podocyte nuclear size in association with podocyte depletion either in model systems or humans. We did find that podocyte nuclear size was approximately 10% larger in old versus young rat glomeruli and under conditions of kidney hypertrophy immediately after nephrectomy. However, we found no significant increase in podocyte nuclear size in humans 3–6 months after kidney transplantation where hypertrophy would be expected to have occurred. Pagtalunan et al. reported that podocyte nuclear volume in Pima Indian patients with diabetes was significantly increased compared with kidney transplant donor controls.¹ We conclude that podocyte nuclear size appears to be quite constant within species under most circumstances. Furthermore, the CF method is not sensitive to moderate changes in nuclear size so that even a 10% difference in D would cause only a 6% change in estimated podocyte density. However, under some conditions, podocyte D might vary significantly, so this eventuality must be taken into account and further evaluated by focused studies in children and adults.

How could the CF method be utilized in practice? First, good-quality podocyte nucleus imaging is a sine qua non. Low-quality images will result in unreliable data. Second, a simple podocyte nucleus count done either manually or using imaging software must be corrected for podocyte mean nuclear caliper diameter and section thickness using Table 1. This corrected podocyte nuclear count is then related to the volume of the tuft discs in which they were counted (tuft area×section thickness) to provide a podocyte density estimate. To facilitate individualized podocyte density estimation for a section, we provide a working spreadsheet (Supplemental Material) in which the equations have been embedded. Entering four variables (section thickness [T], apparent podocyte mean caliper diameter [d], observed podocyte nuclear count [No], and tuft area in which podocyte nuclei were counted [A]) will automatically calculate a value for podocyte density.

In summary, design-based methods for estimating podocyte density may be theoretically preferable,²⁰ but they are also time-consuming and are often not possible on routine human pathology specimens. The CF method addresses the major sources of potential error. It is robust, simple to use, and utilizes commonly available technologies. Its limitations are easy to understand. Importantly, it can be applied to large numbers of glomeruli in a biopsy or kidney section. It is usable for archival pathologic biopsies and could be adapted for automated biopsy analysis. These assets will prove useful for further evaluation of the critical role that podocytes play in maintaining glomerular well-being.

Concise Methods

Kidney Sources

Rat, mouse, and human tissues were obtained under protocols approved by the University Committee on Use and Care of Animals (PRO00003841) and the Human Subjects Institutional Review Board (HUM00055525) of the University of Michigan. Human kidney was from de-identified surgical specimens (n=12) and from kidney biopsies obtained before implantation (n=11), 3–6 months after transplantation (n=12) as part of a routine surveillance strategy, and from patients with a pathologic diagnosis of transplant glomerulopathy (n=15). Rat models of podocyte depletion used for analysis included the hDTR Fischer344 model of controled podocyte depletion,^6,8 a Fischer344 aging model,⁵ a puromycin aminonucleoside model,⁸ and a partial nephrectomy model.⁸ Mouse kidney cortex was obtained from C57Bl6 mice aged 3 months.

Microscope and Camera

All microscopic work was performed with standard imaging equipment. We used an Olympus DP70 Digital Microscope Camera (Center Valley, PA) fitted onto a Leica DM IRB microscope (Deerfield, IL). The reflectors and filter cubes were standard as designated in the Leica Catalogue as A (ultraviolet imaging), L5 (green imaging), and N2.1 (red imaging). We used ×20 magnification/0.50 aperture (HC PL FLUOTAR) and ×63 magnification/1.32 aperture (HCX PL APO) lenses.

Podocyte Nuclear Identification

Rat sections were deparaffinized in fresh xylene, rehydrated, and incubated for 3 hours at 92°C in Retrieve-All Antigen Unmasking System 1: Universal pH8 solution (Signet Laboratories, Dedham, MA) for antigen unmasking. They were then blocked with 5% BSA for 1 hour and incubated overnight at 4°C with mouse mAb to WT1 (SC-7385 monoclonal IgG1; Santa Cruz Biotechnology, Santa Cruz, CA) at 1:30 dilution. Slides were washed twice in PBS for 5 minutes prior to incubation for 2 hours at room temperature with Cy3-conjugated AffiniPure goat anti-mouse IgG diluted at 1:200 (Jackson ImmunoResearch Laboratories, West Grove, PA). Slides were mounted using SlowFade Gold antifade reagent with DAPI (S36939; Molecular Probes, Eugene, OR). Glomerular profiles were imaged using red, green, and blue filters and merged as RGB and RG files. Podocyte counts were made from the RGB image while comparing it with the RG image visualized at the same time on parallel monitors. MS Paint and Windows Picture and Fax Viewer programs were utilized for image analysis and to mark podocyte nuclei. Screen brightness and contrast were optimized to enhance visibility of podocyte nuclear profiles. For human podocyte nuclear identification, mouse mAb to TLE4 (SC-365406 monoclonal IgG1; Santa Cruz Biotechnology) at 1:150 dilution was used in combination with, or instead of, WT1 antibody. For mouse podocyte nuclear identification, rabbit polyclonal antibody to WT1 (SC-192 polyclonal IgG; Santa Cruz Biotechnology) at 1:300 dilution was used. When required, an amplification step was utilized either by a cy3-labeled third antibody against the secondary antibody or by using a tyramide signal amplification kit (T20915; Molecular Probes).

Mean Podocyte Nuclear Caliper Diameter D Measurements

Paraffin-embedded blocks were sectioned at 15- to 20-μm thickness and sections were collected on glass slides. These slides were air dried, placed in a slide holding rack for vertical orientation, and incubated in an oven for 20 minutes at 60°C–65°C to melt excess wax. They were then deparaffinized overnight in fresh xylene and subsequently developed for Cy3 immunofluorescence using either WT1 antibody or TLE4 antibody as outlined above. Under oil immersion at ×63, glomerular profiles were optically sectioned beginning from their upper surface and progressing down to their lower surface at 1- to 2-μm steps to obtain a series of 10–15 photomicrographs captured under a red filter at 2040×1536 pixels using the above microscope. These images were merged to obtain a single stack image over which the nuclear measurements were made. A series of images were also obtained using a green filter and merged with the above stack to serve as a reference for eliminating erythrocytes present in the first red stack. WT1 (or TLE4) positive nuclei that had been sectioned at both upper and lower surfaces of the stack were identified and excluded from the analysis by marking as shown in Figure 2B so that only intact nuclei within the body of the stack of photomicrographs were evaluated. These merged images were imported onto the Metamorph Image System (Universal Imaging, Downington, PA), magnified ×200–300, and podocyte nuclear borders coming into sharp focus were traced. The software was calibrated by photographing an optical ruler at the appropriate magnifications and pixel densities used for capturing images. Once calibrated, the software was used to measure the caliper diameter measured in two axes (x-y) and reported as width and height. Thus the x-y caliper measurements are done on the z-projection of the stacked image. These data were logged onto an Excel spreadsheet and mean value was calculated as he mean nuclear caliper diameter (D). Optimum screen brightness and contrast were set and kept consistent between samples while tracing the nuclear borders. Fifty to 100 consecutive intact nuclei were evaluated for each tissue section. In some experiments, confocal microscopy was used but was found not to add significantly to precision and to take more time and expense.

Derivation of the CF Equation

We used the following terms to derive the CF=1/(D/T+1) equation. (1) Observed podocyte nuclear number (No) is the observed number of podocyte nuclei in a histologic section of thickness T. (2) The true podocyte nuclear number in a glomerular tuft section (Nt) is the true number of podocyte nuclei per glomerular tuft section of thickness T. (3) The excess podocyte nuclear number (Ne) is the difference between No and Nt, which is caused by counting podocyte nuclei that appear in more than one section. (4) The CF is the factor that multiplied by No gives Nt. (5) T is the tissue section thickness. (6) D is the mean caliper diameter of podocyte nuclei.

When tissue section thickness equals mean tangent (caliper) diameter (D) of the podocyte nucleus, then on average each nucleus will be sectioned once. Therefore, under these conditions, the true number (Nt) is 50% of the observed number (No). Or, when the tissue section thickness equals mean tangent diameter (D), the true number (Nt)=excess number (Ne)=0.5×the observed number (No).

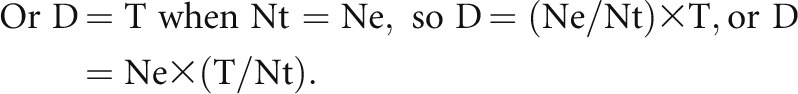Ne is a constant (see above), and T/Nt is also a constant for any section [y=mx, and x/y=1/m, which is a constant (Figure 5C)]. Therefore, the equation would hold good for any T and its respective Nt.

Because the observed podocyte nuclear number (No)=true number (Nt)+excess number (Ne), or Ne=No−Nt. By substituting Ne for (No–Nt),

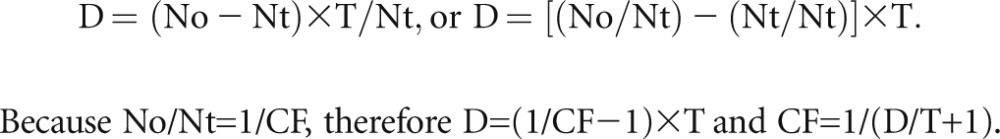A Quadratic Equation to Describe the Relationships between the True Mean Caliper Diameter (D), the Apparent Mean Caliper Diameter (d) in a Tissue Section, the Section Thickness T (or z), and a Podocyte Nuclear Shape Coefficient (k)

A quadratic equation was derived to describe the relationship between these variables of the form

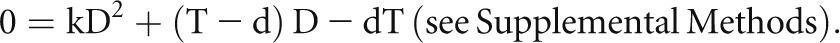This equation rearranged as k×D²+T×D–d×D–d×T=0 was used with free online software (http://www.algebrahelp.com/calculators/equation/completingthesquare/) in which data are entered in the format (k×D×D)+(T×D)−(d×D)−(d×T)=0 to calculate the shape coefficient k for podocyte nuclei (k=0.72±0.03) by substituting the true measured values for D (derived from the thick-section experiments) and the apparent values for d at different section thicknesses (Supplemental Methods). Simulation studies were performed to prove that k accurately describes the shape for podocyte nuclei in the context of tissue sections (Supplemental Methods). The quadratic equation solved for the true mean caliper diameter

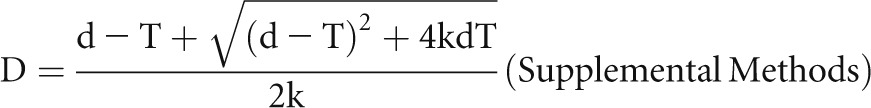was used to embed into the Supplemental Spreadsheet. By entering different values for k into the spreadsheet (k=0.79 for a sphere, k=0.66 for a prolate ellipsoid of dimensions a=2b, and k=0.68 for an oblate ellipsoid of dimensions a=2b) in the example shown, it can be seen that even large shape changes have a minor effect on the CF method for estimating podocyte density.

Estimation of D Using Image-Pro Software and the Quadratic Equation

Human kidney biopsy sections were developed for TLE4 antibody-mediated immunofluorescence (red), nonspecific autofluorescence (green), and DAPI (blue). Photomicrographs were made at 4080×3072 pixels as outlined above. The red-green double merged images were opened in Image-Pro (Figure 3B) and the three-color triple image was opened on another screen (showing podocyte nuclei as purple/pink due to superimposition of the red podocyte nuclear signal on the blue DAPI signal as shown in Figure 3A). A yellow mask was adjusted in Image-Pro to exactly cover the red podocyte nuclei as shown in Figure 3C. Overlapping podocyte nuclei were identified individually and “split” using the software. Individual podocyte nuclei were then identified by comparison of the image open in the Image-Pro software with the triple merged image (purple podocyte nuclei) by clicking on each nucleus so that it becomes circumscribed by white dots (Figure 3D). The mean caliper diameter of 100 consecutive nuclei from 3–10 glomeruli was measured, expressed in an Excel file, and adjusted from pixels to micrometers. The mean measured value for d from 100 nuclei was then converted to D using the quadratic equation as shown in the Supplemental Spreadsheet.

Measurement of Mean Nuclear Caliper Diameter (d) in Rat Cortex

Podocyte nuclei (n=100–200) contained within 10–30 glomerular profiles were photographed under oil immersion at ×63 magnification and 4080×3072 pixels through the section thickness at 2- to 3-μm steps using the above-described tri-color strategy. The merged images were imported onto the Metamorph Image System and caliper diameters of these profiles were measured as above. The mean was calculated and D was estimated for each condition using the quadratic equation (see Supplemental Methods).

Validations Using the Two-Thickness and Serial-Sectioning Methods

The two-thickness method, as described previously, was used, except that podocyte nuclei were identified using the tri-color fluorescence approach outlined above.¹⁵ For the serial-sectioning method, tissues were fixed overnight in 4% PFA, embedded in paraffin, and serially sectioned at 15- to 20-μm thickness. The blocks were thoroughly chilled before sectioning and only one section was collected at a time before returning the block into an ice bucket. These serial sections were developed for Cy3 immunofluorescence using WT1 antibody as outlined above. Using the above microscope and software, glomerular profiles that began to appear within a thick section were chosen and photographed at 1- to 2-μm steps under oil immersion. These glomerular profiles were then followed serially by imaging them in subsequent sections until the whole glomerulus had been imaged. Images were stacked and nuclei were counted on the final stack image for each section. The lowermost step image of one section was matched with the uppermost step image of its adjacent section to mark nuclei that were crossing between sections and eliminated from double counting. MS Paint software was utilized to mark the nuclei for analysis while Windows Picture and Fax Viewer was utilized on a parallel screen to view series of images back and forth within a stack to make judgments about overlapping or crossing nuclei. Light exposure and diaphragm aperture over the microscope were optimized for image quality.

Validation Using the Disector Method

Five rat kidney tissues were fixed overnight in 4% PFA, embedded in paraffin, and sectioned at 3-μm thickness to obtain a pair of adjacent sections that were developed for Cy3 immunofluorescence using WT1 antibody as outlined above. For each pair of sections, 8–15 pairs of glomerular profiles were photographed and analyzed using a dual screen monitor. Podocyte nuclear profiles that were present in one section, but missing from its adjacent section (nuclear tops), were counted. The average of nuclear tops (Ntop or Nt) divided by the average of observed count (No) in each pair of sections was calculated to obtain the CF.

Section Thickness Estimation

The distance between upper and lower edges of the section was directly measured under oil immersion using the calibrated caliper dial on a microscope.

Podocyte Nuclear Density

To obtain podocyte density, the counted podocyte nuclear number is corrected using the CF for the appropriate species (or individualized nuclear mean caliper diameter) and section thickness. The tuft volume in which these podocyte nuclei were counted is given by the area of each glomerular tuft profile (measured by tracing the edge of the tuft using calibrated Image-Pro or Metamorph software)×section thickness. Podocyte density is given by the corrected podocyte number/tuft volume. The inverse of podocyte density is the glomerular volume per podocyte (GV/P).

Measurement of Average Glomerular Volume

The method of Weibel and Gomez,³⁴ modified from Abbercrombie,²¹ was used. Transected glomerular tufts are assumed to be circular. Their areas are measured by tracing the outer aspect of each glomerular tuft using the calibrated Metamorph Imaging System. The average radius (r) for 50 consecutive transected tufts, or all the tufts in any kidney biopsy, is computed. The average maximal tuft radius (R) is calculated based on the Weibel monograph R=4/π×r.^35,36 The average GV is calculated as GV=4/3πR³.

Optimal Section Thickness for Analyses

Thicker sections contain more podocyte nuclei to be counted and require a smaller correction, and nuclear shape variation will have less effect. However, as sections become thicker, there is greater potential for podocyte nuclei to become superimposed on one another and thereby be obscured, and glomerular volume will tend to be overestimated. Sections that are 3–7 μm are satisfactory.

Number of Glomerular Profiles Required to Estimate Podocyte Nuclear Number per Tuft

hDTR transgenic rats were used to obtain kidney cortex in which podocytes had been depleted by variable amounts from 0% to 95%.⁶ Tissue sections from these rats were used to determine how many glomeruli were required to achieve various levels of probability of arriving at the same value as had been obtained for the estimate made from 100 consecutive glomerular profiles (Figure 4C). The most variation was found for glomeruli that had mild or moderate podocyte depletion. However, even in these groups, the number of glomeruli needed to arrive at a >90% approximation of the true value was ≤8 (Figure 4C). The average number of profiles present in human kidney biopsies was 17.3±9.6 (n=35).

Tissue Fixation and Dehydration

Tissue fixation and the dehydration steps for mounting light microscopic sections will alter tissue volume. These changes proportionally affect all components of the tissue in the section and are consistent between different samples. Therefore, comparisons between similarly fixed tissues will be valid, and estimates of podocyte density and number per tuft will not be affected by fixation. Values for in vivo podocyte density will be affected by fixation and dehydration steps. However, tissue volume will also be affected to a large extent by blood perfusion at normal BP and thus any ex vivo methodology will not reflect the true tissue volume.

Antibodies and Reagents

The following antibodies were used: mouse mAb to WT1 (SC-7385 monoclonal IgG1; Santa Cruz Biotechnology) at 1:30 dilution, rabbit polyclonal antibody to WT1 (SC-192 polyclonal IgG; Santa Cruz Biotechnology) at 1:254 dilution, mouse mAb to TLE4 (SC-365406 monoclonal IgG1; Santa Cruz Biotechnology) at 1:150 dilution, and Cy3-conjugated AffiniPure goat anti-mouse IgG diluted at 1:200 (Jackson ImmunoResearch Laboratories). SlowFade Gold antifade reagent with DAPI (S36939; Invitrogen Molecular Probes) was used as the mounting medium.

Statistical Analyses

All results were presented as means±1 SD. Differences among two groups was tested by the t test and by Kruskal–Wallis test between more than two groups. When the Kruskal–Wallis test result was significant, a Scheffe test was carried out for post hoc analysis. Correlations between parameters were compared by single-regression analysis. P<0.05 was considered statistically significant.

Disclosures

None.