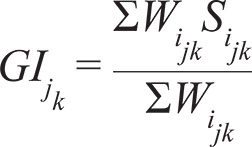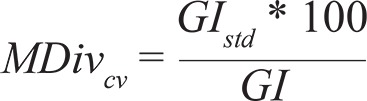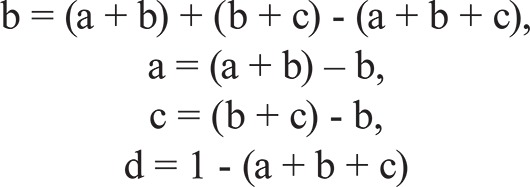Large-scale patterns in morphological diversity and species assemblages in Neotropical Triatominae (Heteroptera: Reduviidae)

Abstract

We analysed the spatial variation in morphological diversity (MDiv) and species richness (SR) for 91 species of Neotropical Triatominae to determine the ecological relationships between SR and MDiv and to explore the roles that climate, productivity, environmental heterogeneity and the presence of biomes and rivers may play in the structuring of species assemblages. For each 110 km x 110 km-cell on a grid map of America, we determined the number of species (SR) and estimated the mean Gower index (MDiv) based on 12 morphological attributes. We performed bootstrapping analyses of species assemblages to identify whether those assemblages were more similar or dissimilar in their morphology than expected by chance. We applied a multi-model selection procedure and spatial explicit analyses to account for the association of diversity-environment relationships. MDiv and SR both showed a latitudinal gradient, although each peaked at different locations and were thus not strictly spatially congruent. SR decreased with temperature variability and MDiv increased with mean temperature, suggesting a predominant role for ambient energy in determining Triatominae diversity. Species that were more similar than expected by chance co-occurred near the limits of the Triatominae distribution in association with changes in environmental variables. Environmental filtering may underlie the structuring of species assemblages near their distributional limits.

Biological diversity may be quantified in terms of both the species richness (SR) and variety of forms, e.g., the morphological diversity (MDiv) ( Roy & Foote 1997 ). Different morphologies may be associated with different functional aspects of ecological significance, including niche differentiation ( Gatz 1979 ), foraging niche and activity ( Gilber 1985 ) and diet diversity ( Collar et al. 2005 ). SR and phenotypic variation might depend on species interactions, environmental variability and random processes [for reviews, see Chesson (2000) , Hubbell (2001) and Venner et al. (2011) ]. A strong relationship between MDiv and SR associated with ecological factors may suggest a major role for niche partitioning ( Patterson et al. 2003 , Safi et al. 2011 ). However, the association between MDiv and SR remains controversial.

There is evidence to suggest that a variety of morphologies may be a positive function of the number of species [e.g., in fish ( Gatz 1979 ), mammals ( Shepherd & Kelt 1999 ) and birds ( Cumming & Child 2009 )] or taxonomic diversity [e.g., in plants such as Desmidiales ( Neustupa et al. 2009 )]. However, the spatial congruence between richness and morphological patterns may not be perfect, as in the case of certain mammals ( Stevens et al. 2006 , Arita & Figueroa 1999 ). A weak positive correlation between richness and MDiv has been reported in marine gastropods ( Roy et al. 2001 ) and a negative relationship has been observed in North American mammals ( Shepherd 1998 ). Discrepancies in the association between morphological and taxonomic diversity have been documented for evolutionary time scales in blastozoan echinoderms and trilobites ( Foote 1993 ). This evidence has led to the concept that although morphological and taxonomic diversity are non-independent estimators of biological diversity, they cannot be considered direct surrogates for one another.

Few of the aforementioned examples include invertebrates. For example, Diniz-Filho et al. (2010) did not find any reports that focused on morphological traits or MDiv related to SR in insects; analyses have been restricted to wing size/geographic range size ( Rundle et al. 2007 ), body size/abundance ( Siqueira et al. 2008 ) and body size/altitudinal and latitudinal patterns ( Brehm & Fiddler 2004 , Kubota et al. 2007 ). Here, we evaluate the congruence between spatial patterns of variation in Triatominae SR and MDiv at the continental scale in North and South America.

Members of the Triatominae (Heteroptera: Reduviidae) are insect vectors of Chagas disease and consist of 140 species, of which 128 are found in the Neotropics (6 of the 7 species of the Triatoma rubrofasciata complex are found only in Asia and six species of the genus Linchosteus are found in India) ( Schofield & Galvão 2009 ). The Neotropical triatomines show relatively high variability in body size, morphology and geographical range and inhabit diverse habitats ( Galíndez-Girón et al. 1998 , Bargues et al. 2010 , Patterson & Guhl 2010 ). Populations of T. infestans show large changes in their wing morphometrics associated with habitat type (e.g., structures associated with chickens vs. goat or pig corrals) ( Schachter-Broide et al. 2004 ). Triatomines have, with a few exceptions, an haematophagous feeding regime mainly based on the blood of birds and mammals ( Carcavallo et al. 1998b , Rabinovich et al. 2011 ). Our objective was to explain the large scale spatial patterns of MDiv and SR of Neotropical triatomine species in terms of environmental gradients to complement the analysis performed by Diniz-Filho et al. (2013) and account for the distribution and SR patterns of Triatominae. First, we addressed the issue of whether there is spatial congruence between MDiv and SR patterns. We then considered multiple environmental variables that could plausibly explain MDiv and SR patterns on a large geographical scale by exploring the role of the climate-productivity hypothesis and two (local and regional) versions of the heterogeneity hypotheses to account for MDiv and SR patterns, as follows.

(i) The climatic/productivity hypotheses [ sensu Field et al. (2009) ] explain how climate, acting either directly through physiological effects or indirectly through resource productivity or biomass, is the primary determinant of large-scale richness patterns. The water-energy hypothesis proposes the interaction between water and energy as fundamental to determining the capacity of environments to support a certain number of species and the productivity hypothesis assumes that an increase in primary productivity promotes an increase in the abundance of species at the consumer trophic level that may favour species coexistence [examples for insects include Hawkins et al. (2003) and Field et al. (2009) ]. Given that these mechanisms could also favour the coexistence of high morphological variety, we predict that SR and MDiv will increase with the total amount of water-energy available and/or in regions of high primary productivity.

(ii) The environmental heterogeneity hypothesis assumes that high spatial heterogeneity in any topographic, climatic or habitat component of the environment promotes high SR because resources are more readily subdivided in heterogeneous habitats, thereby leading to greater specialisation and the coexistence of a larger number of species ( Field et al. 2009 ). Phenotypic differentiation between populations and species may be directly caused by differences in the environments they inhabit and resources they consume, as differentiation is mediated through a mechanism of natural selection that pulls the phenotypic means of two or more populations toward different adaptive peaks ( Schluter 2000 ). This mechanism would result in greater functional diversity with increasing spatial and/or temporal environmental heterogeneity ( Safi et al. 2011 ). We predict that SR and MDiv will increase with climatic, habitat and topographic heterogeneity. We also explored the role of the presence of biomes and major rivers as regional features that could potentially contribute to SR and MDiv patterns. Specifically, major biomes may be associated with convergence in community structure (e.g., Holarctic mammals) ( Rodríguez et al. 2006 ) and major rivers may act as barriers that shape distributional patterns in vertebrate and invertebrate taxa ( Turchetto-Zolet et al. 2013 ); thus, the increased habitat heterogeneity near a major river may have an indirect influence on the diversity of triatomines.

Factors invoked in the statement of each aforementioned hypothesis are not necessarily independent and could theoretically interact as selective pressures to account for concurrent spatial patterns in terms of SR and MDiv. Nonetheless, the association between morphology and environment should not necessarily parallel SR-environment relationships due to the occurrence of random processes (e.g., genetic drift) and phyletic and developmental constraints upon evolutionary change that may also influence the phenotypes of species [see Gould and Lewontin (1979) for discussion and examples].

On the other hand, environmental filtering and species sorting may promote the persistence of only a narrow spectrum of traits under specific environmental conditions, leading to the coexistence of more similar species than expected by chance ( Keddy 1992 , Leibold 1998 ). Chase (2007) suggested that if only a small number of species could persist under harsh environmental conditions, this could eliminate (filter) a large proportion of the regional source species pool, leading to a higher similarity among communities. In contrast, as many species can tolerate benign environments, such conditions will result in considerable unpredictability in their species composition ( Chase 2007 ). In addition, the environment can enhance divergence for certain traits, thereby allowing for the coexistence of species that are more dissimilar than expected by chance ( Podani 2009 ). Here, we examined for the first time whether there are assemblages of Triatominae species that are more similar (or dissimilar) in their morphology than expected by chance and, if so, we determined whether they are associated with variations in environmental conditions.

MATERIALS AND METHODS

Data sources - A climatic and geographic database of 115 triatomine species (Supplementary data 1, Table SI ) was compiled (by author JR) from a public domain source ( Carcavallo et al. 1998a ) and digitised at a 0.1º x 0.1º resolution; this database was used for the analysis of species distribution ranges. From this database we selected 91 species for which we had additional morphological measurement data, which were compiled from Lent et al. (1998) . We divided the American continent occupied by triatomines into equal-area grid cells of 110 km x 110 km using an equal area Mollweide projection in ArcGis 9.2 ( ESRI 2007 ); coastal cells that included < 50% land surface were excluded, resulting in a grid of 2,023 cells. A species was recorded as present in each 110 km x 110 km grid cell if it was present in at least one of the original 0.1º x 0.1º coordinates. We estimated SR based on the same 91 species selected for in the analysis of MDiv by counting the number of species present in each 110 km x 110 km grid cell. Although it is well known that diversity-environment relationships are not scale-invariant, the 10,000 km ² resolution represents the minimum spatial scale at which the predominance of environmental predictors may account for diversity gradients ( Belmaker & Jetz 2011 ). Diniz-Filho et al. (2013) used this same grid size for a biogeographical analysis of triatomines and thus our scale selection allows for a direct comparison with that study.

TABLE SI. List of the 91 species studied.

Alberprosenia goyovargasi	Triatoma circummaculata
Belminus costaricensis	Triatoma costalimai
Belminus herreri	Triatoma delpontei
Belminus laportei	Triatoma dimidiata
Belminus peruvianus	Triatoma dispar
Bolbodera scabrosa	Triatoma eratyrusiforme
Cavernicola pilosa	Triatoma flavida
Dipetalogaster maximus	Triatoma garciabesi
Eratyrus cuspidatus	Triatoma gerstaeckeri
Eratyrus mucronatus	Triatoma guasayana
Mepraia spinolai	Triatoma guazu
Microtriatoma borbai	Triatoma incrassata
Microtriatoma trinidadensis	Triatoma indictiva
Panstrongylus geniculatus	Triatoma infestans
Panstrongylus guentheri	Triatoma lecticularia
Panstrongylus howardi	Triatoma lenti
Panstrongylus lignarus	Triatoma limai
Panstrongylus lutzi	Triatoma longipennis
Panstrongylus megistus	Triatoma maculata
Panstrongylus rufotuberculatus	Triatoma matogrossensis
Panstrongylus tupynambai	Triatoma mazzotti
Parabelminus carioca	Triatoma melanocephala
Parabelminus yurupucu	Triatoma melanosoma
Paratriatoma hirsuta	Triatoma neotomae
Psammolestes arthuri	Triatoma nigromaculata
Psammolestes coreodes	Triatoma nitida
Psammolestes tertius	Triatoma oliveirai
Rhodnius brethesi	Triatoma pallidipennis
Rhodnius dalessandroi	Triatoma patagonica
Rhodnius domesticus	Triatoma peninsularis
Rhodnius ecuadoriensis	Triatoma petrochii
Rhodnius nasutus	Triatoma phyllosoma
Rhodnius neglectus	Triatoma picturata
Rhodnius neivai	Triatoma platensis
Rhodnius pallescens	Triatoma protracta
Rhodnius paraensis	Triatoma pseudomaculata
Rhodnius pictipes	Triatoma recurva
Rhodnius prolixus	Triatoma rubida
Rhodnius robustus	Triatoma rubrovaria
Rhodnius stali	Triatoma ryckmani
Triatoma arthurneivai	Triatoma sanguisuga
Triatoma brasiliensis	Triatoma sinaloensis
Triatoma breyeri	Triatoma sordida
Triatoma bruneri	Triatoma tibiamaculata
Triatoma carcavalloi	Triatoma vitticeps
Triatoma carrioni

Morphology data - We used a total of 12 morphological descriptors, which are commonly used for the classification of triatomine species based on external morphology: (i) total length, (ii) pronotum width, (iii) abdomen width, (iv) anteocular-postocular ratio, (v) eye dorsal width/synthlipsis ratio, (vi) 2nd-1st antennal segment ratio, (vii) 3rd-1st antennal segment ratio, (viii) 4th-1st antennal segment ratio, (ix) 2nd-1st rostrum segment ratio, (x) 3rd-1st rostrum segment ratio, (xi) length head/pronotum ratio and (12) length/width of head ratio. Data were compiled from Lent et al. (1998) and the definition of variables and the measurement methodology were used according to Lent and Wygodzinsky (1979) . Measurements on five males and five females were averaged for each species, although fewer specimens were available in certain cases. The geographic distribution and morphological measurements for each of the 91 species are available from dx.doi.org/10.6084/m9.figshare.653959 .

Environmental variables - Climatic/productivity hypothesis - Actual evapotranspiration (AET) is a surrogate of primary productivity that has been used to study richness patterns in Triatominae ( Diniz-Filho et al. 2013 ). Data on AET were obtained from the Atlas of the Biosphere ( atlas.sage.wisc.edu/ ) at a resolution of 0.5º x 0.5º as described in Willmott and Matsuura (2001) . We projected the AET data onto the Mollweide projection to extract mean values for each 110 km x 100 km cell using ArcGIS 9.2 ( ESRI 2007 ).

As surrogates for the total amount of energy available, we used the following: (i) potential evapotranspiration (PET) extracted for each 110 km x 100 km cell from the agroclimatic database of the United Nations’ Food and Agriculture Organization via the software New_LocClim v. 1.10 ( Gommes et al. 2004 ) (available from: ftp://ext-ftp.fao.org/SD/Reserved/Agromet/New_LocClim/ ) and (ii) the mean annual temperature (T _mean ) obtained from the WorldClim v. 1.4 database at a resolution of 30 s ( Hijmans et al. 2005 ). Water availability was represented by the annual precipitation (PREC _annual ) as obtained from the WorldClim v. 1.4 database at a resolution of 30 s ( Hijmans et al. 2005 ). We projected the T _mean and PREC _annual data onto the Mollweide projection to extract a mean value for each 110 km x 100 km cell using ArcGIS 9.2 ( ESRI 2007 ).

The environmental heterogeneity hypothesis - We used the mean (Altitude _mean ) and standard deviation (Altitude _std ) in elevation as indicators of meso-climatic and topographic heterogeneity, respectively. Elevation data were obtained from the WorldClim v. 1.4 database at a resolution of 30 s ( Hijmans et al. 2005 ). Habitat heterogeneity was derived from ecoregions maps ( Olson et al. 2001 ) projected onto the Molleweide projection. We counted the number of ecoregions (ECO _numb ) in each 110 km x 110 km grid cell to estimate the habitat heterogeneity. Energy variation was represented by the inter-annual coefficient of variation in temperature (TEMP _cv ) as provided by Hay et al. (2006) . Variation in the water availability was represented by the inter-annual coefficient of variation in precipitation (PRECcv) and Colwell’s precipitation predictability index (CPI) ( Colwell 1974 ) calculated based on the average monthly precipitation. PRECcv was estimated from the 0.5º x 0.5º time series from 1901-2000 of the global gridded climatology data produced by the Climate Research Unit at the University of East Anglia, United Kingdon ( New et al. 1999 ) derived from interpolated meteorological station data. We projected the TEMP _cv , CPI and PREC _cv data onto the Mollweide projection to extract a mean value for each 110 km x 100 km cell using ArcGIS 9.2 ( ESRI 2007 ).

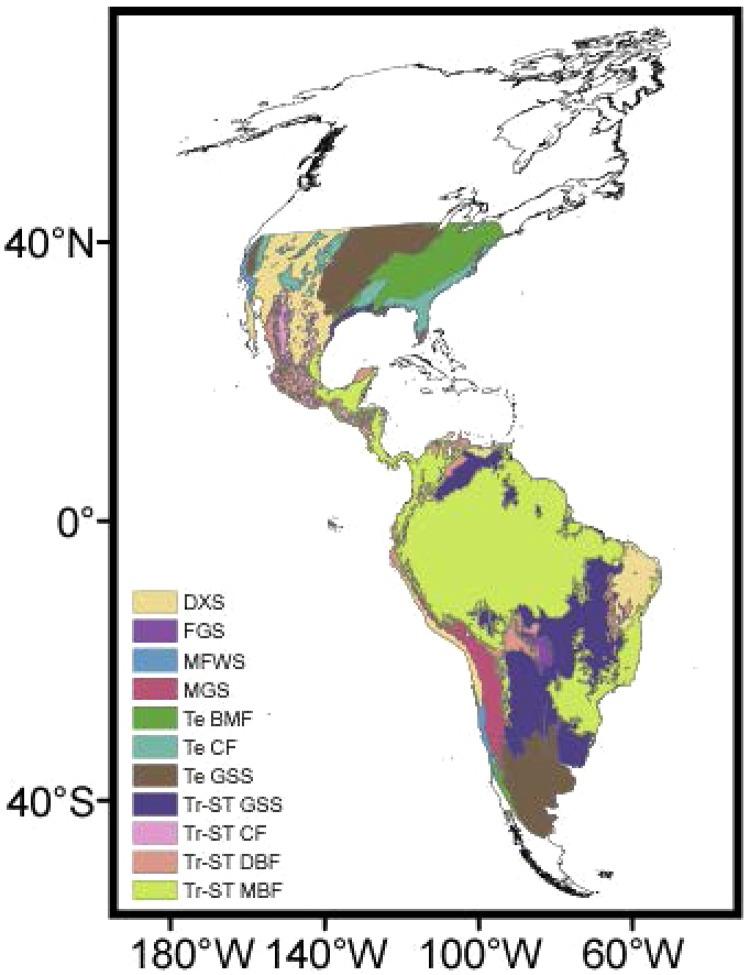
The geographic distribution of biomes was obtained from Olson et al. (2001) (Supplementary data 1, Fig. S1 ) and the minimum distance of each cell in the grid map to major rivers (River _dist ) was estimated from the ESRI Data & Maps Media Kit (Global Imagery Shaded Relief of North and South America included in ArcGis 9.2) projected onto the Molleweide system.

Fig. S1. : map of biomes used in the present analysis (Olson et al. 2001). Maps are in Molweide equal-area projection. DXS: deserts and xeric shrublands; FGS: flooded grasslands and savannas; MFWS: mediterranean forests, woodlands and scrub; MGS: montane grasslands and shrublands; Te BMF: temperate broadleaf and mixed forests; Te CF: temperate conifer forests; Te GSS: temperate grasslands, savannas and shrublands; Tr-ST CF: tropical and subtropical coniferous forests; Tr-ST DBF: tropical and subtropical dry broadleaf forests; Tr-ST GSS: trop and subt grasslands savannas and shrublands; Tr-ST MBF: tropical and subtropical moist broadleaf forests.

Estimation of MDiv - We estimated the mean MDiv in each grid cell using the mean Gower Index ( GI ) ( Gower 1971 ), which indicates the mean dissimilarity between pairs of coexisting species based on attributes measured on interval and ratio scales ( Podani & Schemera 2006 ). The GI _jk , which ranges from 0 (complete similarity between species pairs) to 1 (complete dissimilarity between species pairs), was calculated as:

where S _ijk is the partial similarity of a continuous variable (trait) i for the j-k pair of species and is defined as S _ijk =|X _ij – X _ik |/ [max{X _i } – min{X _i }] and W _ijk is the weight for variable i for the j-k pair. W _ijk = 0 if, for variable i , X _ij or X _ik have missing values. Otherwise, W _ijk = 1. In our calculations, we always used W _ijk = 1. The traits ( i ) were the 12 triatomine morphological descriptors.

For each cell, we computed GI _jk for each combination of species pairs and then summed the values of all pairs of species combinations and divided this number by the total number of species pairs in each cell to produce the GI and standard deviation ( GI _std ) of the GI. GI was our estimation of MDiv per cell and is independent of the number of species being compared; thus, the GI can be used to compare across grid cells with different SR values. We mapped the MDiv and the coefficient of variation in MDiv (MDiv _cv ), estimated as:

Phylogenetic effects should be taken into account in these types of analysis ( Harvey & Pagel 1991 ); however, few phylogenetic trees of Triatominae are available and these do not cover all of the 91 species studied herein. Even the partial lists of species analysed in the existing phylogenies are usually disjointed sets ( Carcavallo et al. 1999 ) and thus, we did not apply a phylogenetic comparative method.

Data analyses - Assessment of non-random species associations - To assess the existence of non-random species co-occurrence patterns at the local scale (i.e., for each of the 110 km x 110 km grid cells) for each level of observed SR, we simulated 10,000 random species assemblages by resampling species with replacements (bootstrap randomisation) from the total pool of 91 species. The probability ( Pr ) of each species to be resampled each time was proportional to its geographic range ( Pr = number of grid cells occupied by each species/number of total cells in the grid map) and the GI was calculated for each of the 10,000 random species assemblages. From the bootstrap randomisation we estimated a mean GI and the 0.025 and 0.975 quantiles for each grid cell with its corresponding richness value. GI values less than the 0.025 quantile indicated that the dissimilarity between pairs of coexisting species was lower than expected by chance, whereas GI values greater than the 0.975 quantile indicated that dissimilarity between pairs of coexisting species was larger than expected by chance and we interpreted these as evidence of a non-random association of species.

Assessment of environmental associations - The association between MDiv and environmental variables was assessed using a generalised linear model (GLM) without interactions and normality of error. A binomial distribution of errors was used to model the association between environmental variables and the presence/absence of significant structures in the organisation of species assemblages.

We used glmulti , an R package by Calcagno and Mazancourt (2010) , for automated multi-model selection to find the best subset of candidate environmental models supported by the data; this package is based on Akaike’s information criterion (AIC) ( Diniz-Filho et al. 2008 ). We applied the package’s default method (exhaustive screening of all candidate models) to find the best explanatory models from all possible unique models involving our list of environmental variables. Out of the total possible models obtained, we chose a subset of models where each predictor (or term) had a correlation of less than 0.8 from each other to reduce multicollinearity. From this subset, those models that differed by less than two AIC units from the model with the minimum AIC value were selected as the best subset of candidate models. The most parsimonious model (the one with the minimum number of predictors) was selected from that subset of best candidate models as the “final” model for biological interpretation.

The autocorrelation of variables across the geographic space is an inherent property of most ecological data and often complicates the statistical testing of hypotheses by standard methods; i.e., autocorrelation usually inflates type I errors and may result in model instability ( Diniz-Filho et al. 2003 ). We assessed the effects of the spatial structure of variables on the performance of our environmental models (Supplementary data 2).

Data analysis is complicated due to the difficulty in establishing a direct causal relationship between variables. It is difficult to disentangle whether any environmental variable associated with MDiv or SR is a direct driver of the spatial variation or if such an association is driven by a third variable that is also spatially structured ( Diniz-Filho et al. 2003 ). To partially overcome this problem, we conducted a partial regression analysis ( Borcard et al. 1992 ) of SR and MDiv (Supplementary data 3).

RESULTS

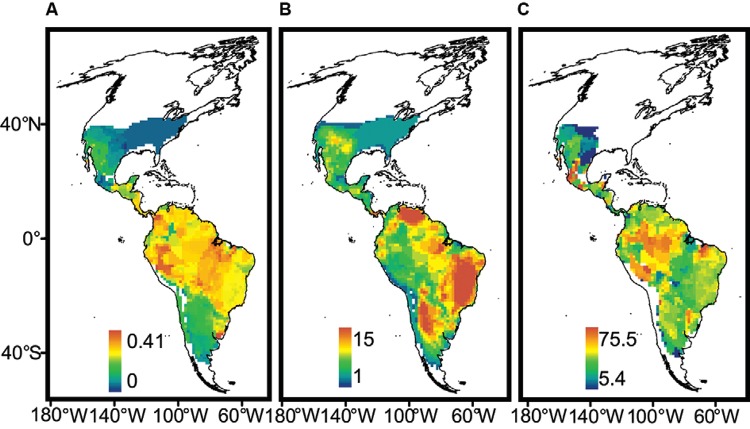
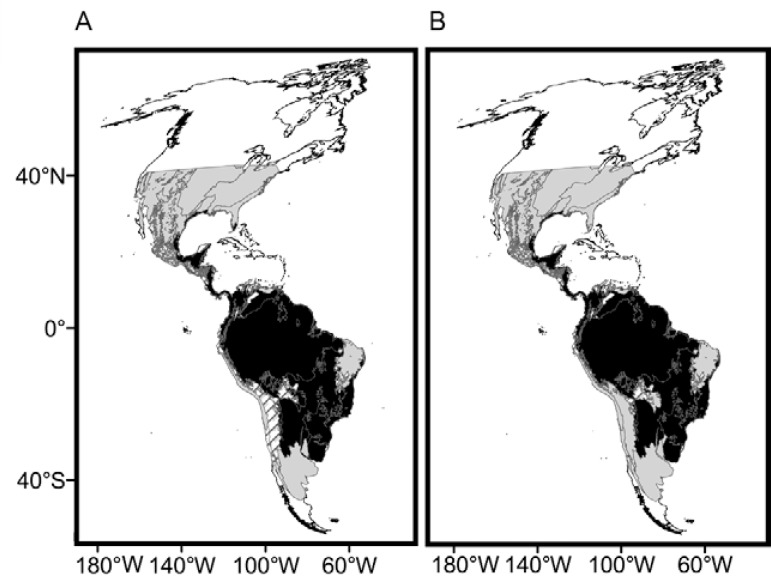
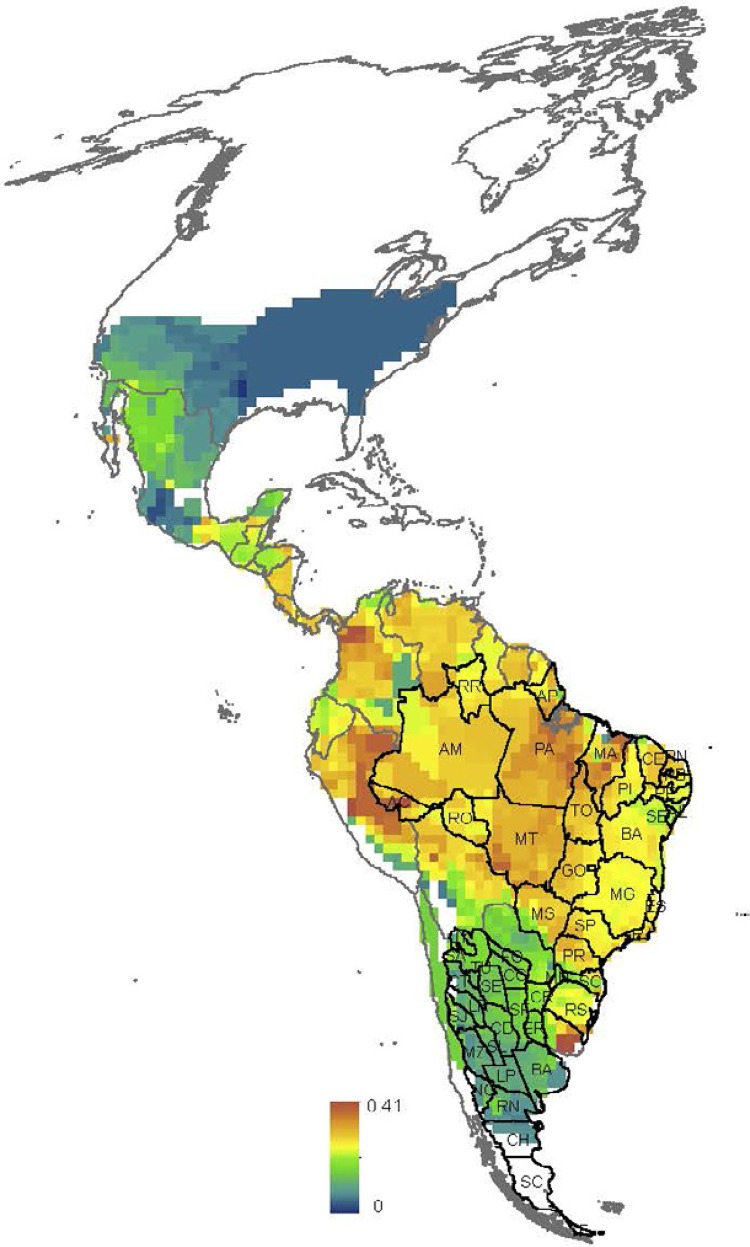
S patial variation in the MDiv and SR at the continental scale - Both SR and MDiv followed a latitudinal gradient, which suggests overall spatial congruence between these two facets of triatomine species diversity. However, SR increased in tropical savannahs and shrublands in South America ( Fig. 1B , Supplementary data 1, Fig. S1 ), showing peaks in central and northeastern Brazil, central and northwestern Argentina and northern latitudes of Venezuela. MDiv increased in the tropics and decreased in extra-tropical latitudes towards the northern and southern distributional limits of the Neotropical triatomines ( Fig. 1A ), showing localised peaks in restricted regions of Brazil, Colombia and eastern Peru and Uruguay. The high SR in subtropical latitudes in Argentina is associated with low MDiv and the same trend was observed at the limit between the southern USA and Mexico ( Fig. 1A , B , Supplementary data 4, Figs S5 , S6 ). The highest local variability in MDiv _cv ( Fig. 1C ) was observed within the Amazon Basin, coinciding with low SR and high MDiv (compare Fig. 1A-C ).

Fig. 1. spatial variation. A: morphological diversity (MDiv); B: species richness; C: coefficient of variation in MDiv. Scale units in A correspond to mean Gower index values, which run between 0 (maximum similarity) and 1 (minimum similarity), and in B to species number. Maps are in Mollweide equal-area projection.

Associations between MDiv, SR and environmental variables - The environmental models ( Table I ) accounted for a greater proportion of the variation in MDiv (R ² = 0.73) than in SR (R ² = 0.46). The MDiv data supported two environmental models as being equally likely and both models had T _mean as the most significant predictor ( Table I ). Although neither AET nor PREC _annual remained in either model, there was a tendency for MDiv to increase with an increase in the PREC _cv in Model 1 and precipitation predictability (CPI in both models, Table I ).

TABLE I.  Environmental models selected after the application of multi-model selection criteria to account for the geographic variation in morphological diversity (MDiv) and species richness (SR).

	MDiv
	Model 1			Model 2			SR
Environmental variables	b	p		b	p		b	p
Potential evapotranspiration	-	-		0.024	0.105		0.154	0.000
Mean annual temperature	0.477	0.000		0.467	0.000		-	-
Mean altitude	0.141	0.000		0.139	0.000		-	-
Mean precipitation	-	-		-	-		-0.295	0.000
Actual evapotranspiration	-	-		-	-		-	-
Colwell’s precipitation predictability index	0.163	0.000		0.173	0.000		-	-
Mean standard deviation altitude	0.098	0.000		0.109	0.000		0.103	0.000
Coefficient of variation in temperature	-	-		-	-		-0.392	0.000
Coefficient of variation in precipitation	0.025	0.008		-	-		-0.197	0.000
Number of ecoregions	-0.065	0.000		-0.068	0.000		-	-
Distance of each cell in the grid map to major rivers	-0.126	0.000		-0.124	0.000		-0.108	0.000
Deserts and xeric shrublands	-0.242	0.000		-0.240	0.000		-0.226	0.000
Flooded grasslands and savannas	0.370	0.002		0.364	0.003		-0.264	0.132
Mediterranean forests, woodlands and scrub	0.105	0.423		0.140	0.287		-0.840	0.000
Montane grasslands and shrublands	-0.093	0.355		-0.079	0.427		-0.436	0.000
Temperate broadleaf and mixed forests	-0.962	0.000		-0.968	0.000		-0.623	0.000
Temperate conifer forests	-0.855	0.000		-0.877	0.000		-0.663	0.000
Temperate grasslands, savannas and shrublands	-0.503	0.000		-0.498	0.000		-0.268	0.000
Tropical and subtropical grasslands savannas and shrublands	0.200	0.000		0.199	0.000		0.741	0.000
Tropical and subtropical coniferous forests	-0.319	0.000		-0.322	0.000		-0.505	0.000
Tropical and subtropical dry broadleaf forests	0.019	0.756		0.025	0.685		-0.127	0.136
Tropical and subtropical moist broadleaf forests	0.317	0.000		0.316	0.000		0.092	0.018
R 2	0.73			0.73			0.46

b : estimated beta regression coefficients; p : probability level; R ² : coefficient of determination of the whole model adjusted by degrees of freedom.

MDiv increased with Altitude _mean and high topographic heterogeneity (Altitude _std ), but decreased with high local habitat heterogeneity (ECO _numb ) and River _dist ( Table I ). SR tended to increase in hot and dry regions of the continent [characterised by high energy (PET) and low water availability (PREC _annual )], but decreased in sites with high variability in TEMP _cv , which is the strongest predictor of triatomine richness ( Table I ). The tendency for SR to increase in sites with low PREC _cv was weak ( Table I ). SR also increased in sites with high topographic heterogeneity (Altitude _std ) and decreased with River _dist ( Table I ), although the local habitat heterogeneity (ECO _numb ) did not remain in the final models.

The biomes were also significant predictors of the variation in MDiv and SR. Extra-tropical temperate biomes, desert habitats and coniferous forests were associated with low MDiv and SR. Tropical and subtropical grasslands, savannahs and shrublands as well as moist broadleaf forests were associated with high MDiv and/or SR. In the flooded savannahs and grasslands, low SR but high MDiv values were observed ( Fig. 2 , Table I ).

Fig. 2. association between biomes and morphological diversity (MDiv) (A) and species richness (SR) (B), resulting from the final best model selected (see Materials and Methods and Table I). Biomes associated with an increase in MDiv or SR, after controlling for other climatic variables (Table I), are shown in black. Biomes associated with a decrease in MDiv and SR are shown in gray. Biomes that do not show a significant association with MDiv and SR are shown in diagonal lines. Maps are in Mollweide equal-area projection.

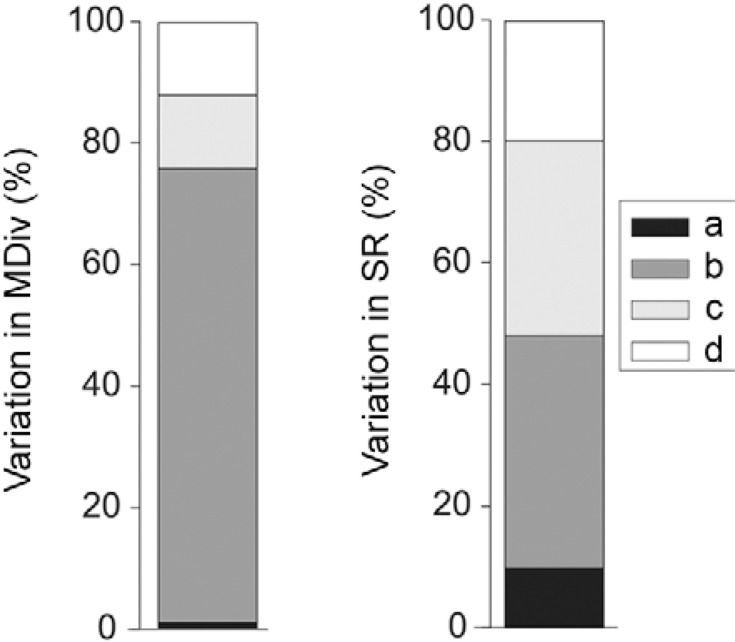
The low-to-moderate values for spatial autocorrelation that remained in the residuals of MDiv and SR indicated that the estimation of the regression coefficients was not seriously affected by the existence of spatial autocorrelation in our original data (Supplementary data 2, Fig. S2 ). The partial regression analysis revealed that a greater proportion of MDiv (66%) than SR (approximately 33%) was explained by spatially structured variation in the environmental variables. A lower proportion of the variation in MDiv (7%) and SR (13%) was explained by local environmental variation independent of space. Approximately 20% of the variation in SR was explained by spatially structured environmental variables that were not included in our models ( Fig. 3 ).

Fig. 3. partition of variation in morphological diversity (MDiv) and species richness (SR) a: local environmental effects independent of space; b: regional spatially structured environmental variation (i.e. shared variation between environment and space); c: spatial effects independent of environment; d: unexplained variation (see Supplementary data 2 for detailed explanations of methods and results).

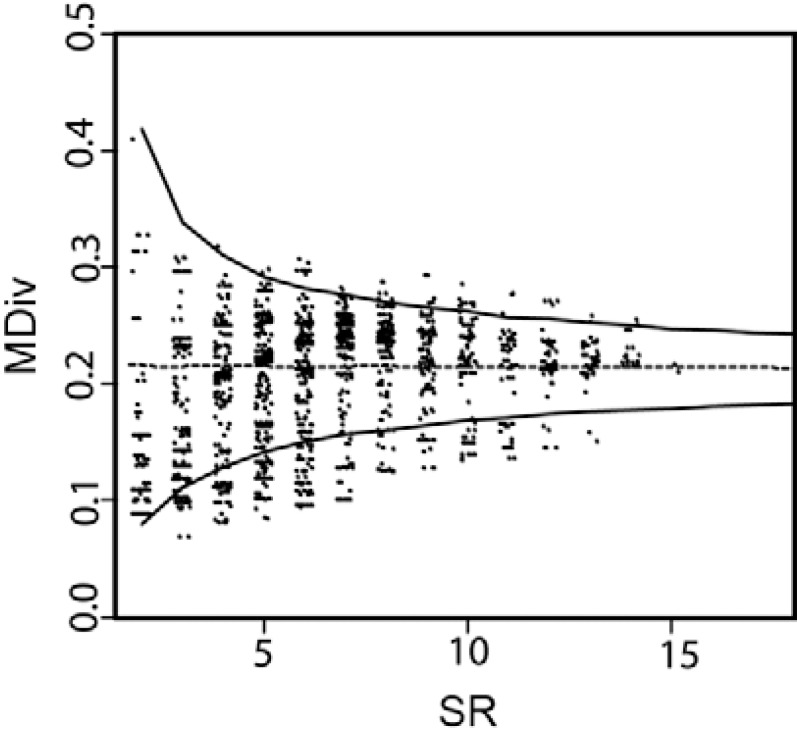
The structuring of MDiv in local (110 km x 110 km) species assemblages with different SR - The relationship between SR and MDiv examined in the absence of geographical context followed a funnel-like shape, suggesting greater variation in MDiv in low SR assemblages rather than high SR ones ( Fig. 4 ). MDiv values above the upper 0.975 or below the lower 0.025 quantiles (i.e., outside the limits of the lines shown in Fig. 4 ) suggested a non-random structuring, which appeared only in certain restricted regions across the continent ( Fig. 5 ).

Fig. 4. association between morphological diversity (MDiv) with species richness (SR). The broken line indicates the mean value in ecological diversity obtained after randomisation (see text). Upper and lower lines correspond to 0.025 and 0.0975 quantiles. Points enclosed within the upper and bottom lines correspond to observed values of mean Gower index ( GI ) as expected by chance. Points above the 0.025 and below the 0.0975 quantiles correspond to the observed mean GI values that identify statistically significant deviations from chance of the morphological similarities and dissimilarities, respectively.

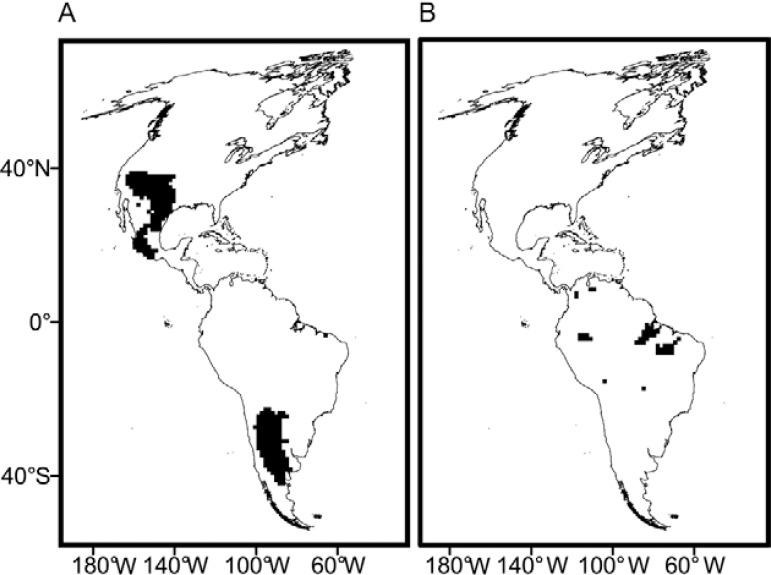
Fig. 5. geographic location of 110 km x 110 km cells with non-random species assemblages. A: morphological diversity (MDiv) lower than expected by chance; B: MDiv greater than expected by chance. Maps are in Mollweide equal-area projection.

The structure of MDiv in local species assemblages relative to environmental variables - Local assemblages composed of species more similar in MDiv than expected by chance were clustered in open habitats (grasslands, savannahs, deserts and shrublands). In South America, this area covered much of the biogeographical units known as the Monte Desert and the southern parts of the Chaco and Espinal in Argentina; in North America, the region overlapped with the majority of the Xerophytic province in México [see Cabrera and Willink (1980) for definitions of biogeographical units]. In general, these were regions of low MDiv and located towards the northern and southern limits of the distribution of triatomine species ( Figs 1 , 5 ). The species assemblages composed of those more dissimilar in MDiv than expected by chance occurred in closed habitats (moist broadleaf forest in the Amazonia), which harboured high MDiv and mainly corresponded to the central areas of the overall distribution of the Triatominae ( Figs 1 , 5 ).

Environmental variables were best associated with the occurrence of species that are morphologically more similar than expected by chance (McFadden’s pseudo r-squared for binomial regression models = 0.43) ( Table II ) than with the occurrence of species morphologically more dissimilar than expected by chance (McFadden’s pseudo r-squared = 0.15) ( Table II ).

TABLE II. Environmental models resulting from multi-model selection criteria to account for the presence of structure in the organisation of local species assemblages with respect to morphological diversity (MDiv).

	MDiv lower than expected by chance		MDiv greater than expected by chance
Environmental variables	b	p	b	p
Constant	-4.012	0.000	-5.389	0.000
Potential evapotranspiration	-0.556	0.001	-	-
Mean annual temperature	0.693	0.002	5.420	0.000
Mean altitude	-	-	-	-
Mean precipitation	-6.26	0.000	-	-
Actual evapotranspiration	-	-	-	-
Colwell’s precipitation predictability index	-2.712	0.000	-	-
Mean standard deviation altitude	0.552	0.006	-	-
Coefficient of variation in temperature	-	-	-	-
Coefficient of variation in precipitation	-5.628	0.000	-	-
Number of ecoregions	-	-	-	-
Distance of each cell in the grid map to major rivers	-	-	-2.033	0.011
Rho	0.43		0.15

b : coefficient that indicates the magnitude of the association; p : probability level; Rho: McFadden’s pseudo r-squared (between 0.2 and 0.4 are indicative of a very good fit).

In the GLM analysis, the assemblages with species that are more similar than expected by chance were associated with high T _mean , low PET and PREC _mean , low PREC _cv , low precipitation predictability (CPI) and high topographic heterogeneity (Altitude _std ) ( Table II ). However, after accounting for the effect of spatial autocorrelation in the data (Supplementary data 3, Fig. S3 ), the effect of T _mean was not statistically significant (Supplementary data 3, Table SII ).

DISCUSSION

Geographical patterns in MDiv and SR: are they spatially congruent? - The SR of Neotropical triatomines showed a latitudinal pattern of variation, in agreement with previous findings ( Rodriguero & Gorla 2004 , Diniz-Filho et al. 2013 ); MDiv also followed a latitudinal gradient, suggesting an overall spatial congruence between these two facets of species diversity. However, their spatial congruence is far from perfect; for example, there were regions in tropical and subtropical latitudes in Argentina and Brazil where peaks in SR were not paralleled by peaks in MDiv and the increase in SR observed at the limit between the southern USA and Mexico was not paralleled by an increase in MDiv.

Spatial incongruence between components of biodiversity has been previously reported for the taxonomic, functional and phylogenetic diversity of birds ( Devictor et al. 2010 ), SR and MDiv in gastropods ( Roy et al. 2001 ) and between richness and functional diversity in mammals ( Safi et al. 2011 ). To the best of our knowledge, this is the first study to elucidate this type of relationship in insects at the continental scale and we demonstrated that for the triatomines, SR and MDiv cannot be considered surrogates for one another.

The relationship between environmental factors and triatomine diversity - Our results offer only partial support for the idea that hypotheses of environmental factors previously invoked to account for the spatial variation in SR may also be extended to explain the variation in MDiv ( Meynard et al. 2011 ). The proportion of the spatial variation explained by environmental factors in triatomines was higher for MDiv than for SR patterns. After controlling for covariation with other environmental variables and regional effects (e.g., the presence of biomes and rivers), triatomine SR increased with a decrease in temporal variability in temperature (TEMP _cv ), whereas MDiv increased with an increase in T _mean . The predominance of these energy-related variables accounting for triatomine SR patterns is in agreement with the results of Diniz-Filho et al. (2013) regarding triatomine richness. Rodriguero and Gorla (2004) also analysed the species-energy hypothesis using 118 triatomine species and found that there was a positive monotonic relationship between SR and mean annual land surface temperature (which they used as a surrogate of available energy).

These data on Neotropical Triatominae are an exception to previous evidence suggesting that water or water-energy variables are strongly and positively associated with richness in warm climates ( Hawkins et al. 2003 ). SR was negatively associated with the total amount of PREC _annual and the temporal variability in PREC _cv and was not associated with AET, which contradicts the predictions of the productivity hypothesis. The stronger effect of ambient energy on triatomine SR is presumably mediated through physiological constraints that influence the geographic distribution of insects ( Addo-Bediakko et al. 2000 , Diniz-Filho et al. 2013 ).

In contrast to SR, we found that an increases in the temporal PREC _cv and predictability (CPI) promoted an increase in MDiv, indirectly supporting the notion that temporal environmental variation may induce phenotypic differentiation ( Schluter 2000 ) and an increase in functional diversity as observed in mammals ( Safi et al. 2011 ). Such environmental variability could result in temporal niche partitioning, thereby increasing the variation of biological traits across species ( Chesson & Huntly 1997 , Venner et al. 2011 ). However, the harshness of a variable environment may select against the coexistence of a high number of species [see Cohen (2004) for further discussion].

Our study confirms that topographic and habitat heterogeneity play secondary roles in accounting for species diversity gradients on a large geographic scale ( Field et al. 2009 ). On the other hand, large-scale differences in climatic, vegetation, physiognomy and soil conditions that influence the structuring of species assemblages across biomes ( Rodríguez et al. 2006 ) may underlie the regional associations of triatomine SR and MDiv with the presence of biomes.

The variety of “rules” in the structuring of triatomine species assemblages - The funnel-like relationship between triatomine SR and MDiv outside of a geographic context conforms well with similar results for other species, for which functional diversity was found to be independent of SR ( Laliberté & Legendre 2010 ). At the resolution used here, random species assemblages predominated (i.e., most of the MDiv values fell inside the 95% confidence interval under the null hypothesis of a random pattern). Nonetheless, the co-occurrence of species more similar (or dissimilar) in their morphology than expected by chance was observed in certain regions, also suggesting that the structuring of triatomine species assemblages at the continental scale might be governed by different underlying processes. Caution is needed when interpreting our results because the detection of structuring patterns may depend on the spatial scale of analysis ( Gomez et al. 2010 ) and size of the species pool used for randomisation ( de Bello 2012 ). One limitation in our study may be that we restricted our analyses to one spatial scale of resolution (110 km x 110 km) and used a single species pool involving the entire set of studied species. With these two potential limitations in mind, we consider the following alternative mechanisms that could provide an explanation for our results.

The co-occurrence of species that are more similar in their functional diversity than expected by chance has often been interpreted as evidence of environmental filtering acting at a regional scale within temperate latitudes ( Petchey et al. 2007 ). It is suggestive that the two triatomine assemblages with species more similar than expected by chance occur at two separate xeric regions in North and South America that share similar environmental conditions (high temperature and low precipitation) and biogeographic history ( Roig et al. 2009 ). These xeric environmental conditions may have filtered out from the regional source pool those triatomine species that have the morphological attributes to tolerate such xeric conditions ( Keddy 1992 , Chase 2007 ). This possibility is reinforced by Triatominae phylogenies ( Hypsa et al. 2002 , Silva de Paula et al. 2005 ) showing that, at least for the Triatomine tribe, there is a strong phylogenetic distinction between the northern and southern species of this genus.

Nonetheless, species that are more similar in their morphology than expected by chance and co-occur at a 110 x 110 km-scale might be segregated at the local scale. For example, 12 of the 16 Triatoma species of the North American assemblages are found in different habitats, including bat caves and shelters, cricetid nests, Edentata shelters, didelphid shelters, sciurid shelters and Galliformes nests ( Carcavallo et al. 1998c ). Similarly, 15 of the 17 triatomine species of the South American assemblages show an extremely large variety of relationships with habitats and associated fauna: bat caves and bat tree holes [e.g., Caviidae caves, Dasypodidae and Myrmecophagidae burrows, Didelphidae, Procyonidae, Echimidae, Phyllostomidae, Caviidae, Microcavia, Cricetidae, Muridae and Dasypodidae shelters, Passeriformes and Psittaciformes nests and Caviidae and Cricetidae nests ( Carcavallo et al. 1998c )], providing the potential for strong habitat segregation. Thus, although climate may promote the occurrence of assemblages composed of morphologically similar species at the regional scale, habitat and ecological interactions with other species may vary and these differences could be coupled with other demographic ( Medone et al. 2012 ), dietary ( Rabinovich et al. 2011 ) and physiological ( Pereira et al. 2006 ) differences among triatomine species to facilitate coexistence at a local scale.

The environmental variables used in our analyses could not account for the presence of species assemblages composed of taxa that are more dissimilar than expected by chance alone, which were mainly located in tropical and subtropical moist broadleaf forests. The small number of species assemblages with this type of structure and their scattered distribution within tropical areas further complicates interpretation of this pattern. However, coexisting species may be more different than expected by chance if a competition-based limiting similarity underlies the organisation of local species assemblages ( MacArthur & Levin 1964 ). It has been suggested that this limiting similarity could scale up to affect species co-occurrence patterns at a large geographic scale ( Davies et al. 2007 ); however, the role of competition was impossible to test given the scale of our analysis as well as the inherent comparative-descriptive nature of this type of study.

We conclude that Triatominae provide useful insight regarding patterns and processes associated with the structuring of MDiv of species on a large geographic scale. Our geographical analysis of MDiv has opened a new perspective for the study of triatomines and we propose that specialists in ecology, behaviour and physiology should look deeper into possible differences between triatomine species that may explain their co-occurrence at the geographical level.

Geographic patterns in Triatominae diversity and Chagas disease - In most Latin American countries, multiple initiatives have been implemented to control Chagas disease vectors based on entomological and epidemiological criteria ( Guhl 2009 ). In Brazil, the spatial distribution of mean mortality rates caused by Chagas disease per 100,000 inhabitants/year between 1999-2007 shows a clear concentration of municipalities with high mortality in the Central-West Region, including the Federal District, major parts of the state of Goiás and the so-called Triângulo Mineiro region of northwestern of the state of Minas Gerais and north of the state of São Paulo (SP); some areas of the states of Mato Grosso do Sul, Bahia (BA) and Tocantins are also affected and additional small high-mortality areas are found in the border between the state of Paraná and SP, in southern state of Piauí and in north-central regions of BA ( Martins-Melo et al. 2012a ). Our study showed that the heterogeneous and focal distribution of those areas of high mortality risk greatly overlapped areas of high SR in Brazil [compare Fig. 2 in Martins-Melo et al. (2012a) with Supplementary data 4, Fig. S5 ]. This may have important consequences for planning control actions. It has been observed that despite the recent elimination of the most important vector species in Brazil ( Triatoma infestans ), the spatial clusters of high mortality areas have remained relatively stable over time ( Martins-Melo et al. 2012a ). In addition, although certain Regions of Brazil (Central-West and Southeast) have seen a steady decline in mortality due to Chagas disease after efforts were concentrated to eliminate the primary vector T. infestans, in other regions (North and Northeast), a reduction in mortality rates required interventions to control other prevailing vectors ( Martins-Melo et al. 2012b ). Vector species of subtropical affinity (i.e., those whose geographical distributions largely encompass subtropical latitudes of South America: T. infestans, Triatoma brasiliensis, Triatoma sordida and Panstrongylus megistus ) tend to show extensive overlap with sites having high triatomine SR (Supplementary data 4, Fig. S7A-D ). Hence, in the absence of reliable information or underreporting of mortality data, areas of high triatomine SR could be considered preliminary indicator areas of high potential mortality risk within the subtropics of South America. In parallel with this reasoning, we suggest that in Argentina, the high-richness area encompassing the eastern portion of the provinces of Jujuy, Salta, Tucuman, Catamarca and La Rioja, the northeastern areas of San Luis province, the northwest part of Cordoba province, the eastern region of Santiago del Estero province and the borders between the provinces of Salta, Chaco and Formosa (Supplementary data 4, Fig. S5 ) deserve priority in the development of policies involving vector control.

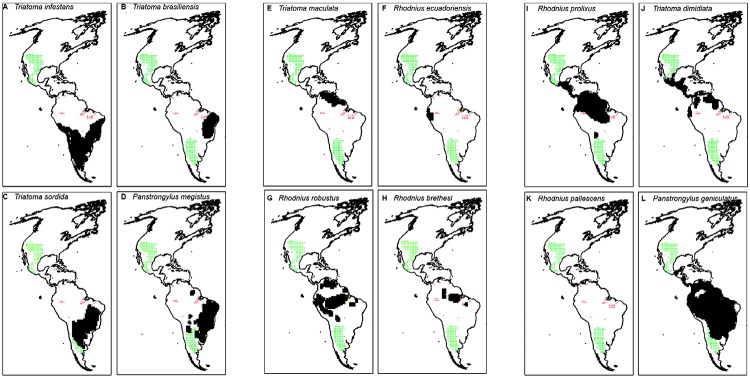
Within the tropics, there are regions of high triatomine SR in Venezuela, in Andean regions in Ecuador, Colombia and northern Peru and Brazil in the state of Pará close to the Amazon River mouth (Supplementary data 4, Fig. S5 ). However, there are only two vector species ( Triatoma maculate and Panstrongylus geniculatus ) of tropical affinity (i.e., those constrained to live within tropical latitudes of South and Central America) associated with high-richness regions (Supplementary data 4, Fig. S7E, L ); the remaining vectors of tropical affinity ( Rhodnius prolixus, Triatoma dimidiata, Rhodnius pallescens, Rhodnius ecuatoriensis, Rhodnius robustus and Rhodnius brethesi ) tend to overlap sites with low, intermediate and high SR in similar proportions (Supplementary data 4, Fig. S7F-K ). Thus, we predict that centres of high triatomine SR could be more closely associated with centres of high mortality risk in the subtropics rather than in the tropics of South America.

The geographic distributions of vector species are more variable with respect to their association with MDiv than with SR. The association of areas of high mortality risk identified in Brazil ( Martins-Melo et al. 2012a , b ) with patterns in MDiv is less clear because vector species of subtropical affinity tend to overlap a greater proportion of sites of intermediate MDiv (Supplementary data 4, Fig. S8A-D ). In contrast, the geographical distribution of vector species of tropical affinity is associated with sites of high MDiv (Supplementary data 4, Fig. S8F-K ). In addition, vector species of subtropical affinity are represented in assemblages of species that are more similar or dissimilar than expected by chance (Supplementary data 4, Fig. S9A-D ), whereas those of tropical affinity are represented in assemblages that are more dissimilar than expected by chance (Supplementary data 4, Fig. S9E-L ). Although the possible implications of these patterns remain to be elucidated in terms of the epidemiology of Chagas disease, the present study suggests that analyses of biogeographical patterns in Triatominae diversity may complement analyses of the spatial variation in epidemiological parameters ( Martins-Melo et al. 2012a , b ) in attempts to define strategies for vector control at a large spatial scale in the Neotropics.

Supplementary data 2

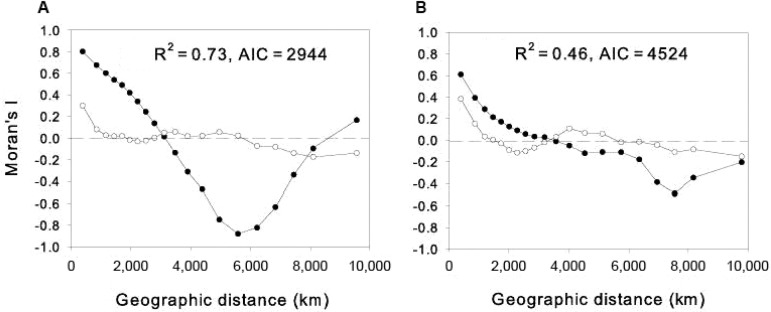
a: evaluation of the effect of spatial autocorrelation on the performance of environmental models fitted to morphological diversity (MDiv) and species richness (SR) - We checked the adequacy of the environmental models shown on Tables I (main text) to account for the geographic variation in MDiv and SR in the presence of spatial autocorrelation.

We elaborated spatial correlograms using Moran’s I coefficient to describe the magnitude of autocorrelation of MDiv and SR for different distance classes. Then, we examined the spatial patterns of autocorrelation in their residuals after the fit of the models shown on Table I. Independently of the pattern of autocorrelation in the original (predictors and response) variables, if no spatial autocorrelation is found in the residuals it can be concluded that the model had taken into account all spatial structure in the original data and that there was no statistical bias in the overall statistical analysis (Diniz-Filho et al. 2003).

The spatial correlogram for MDiv (Fig. S2A) showed a quadratic pattern that indicated the presence of positive autocorrelation up to c.3100 km, then the negative autocorrelation increased strongly to reach -0.8 at c.6200 km and then it progressively decreased to approach low values (i.e. between 0-0.2) at the largest distance classes. SR showed high positively autocorrelation (0.61) at the shortest distance class (c.400km), then the autocorrelation decreased up to c.4,000 km and then it increased again to reach -0.49 at c.7,500 km (Fig. S2B).

After model fit, the autocorrelation in the residuals of MDiv at the shortest distance classes (c.400 km) (Fig. S2A) decreases from 0.80-0.30 and decreases to < 0.1 for all subsequent distance classes up to c.7,400 km; the spatial autocorrelation increases again at distance classes > 8,000 km, although coefficients are never larger than 0.2 (Fig. S2A). Similarly, the autocorrelation in the residuals of SR decreases from 0.61-0.38 at the shortest distance classes and then remained between 0-0.15 for all subsequent distance classes (Fig. S2B).

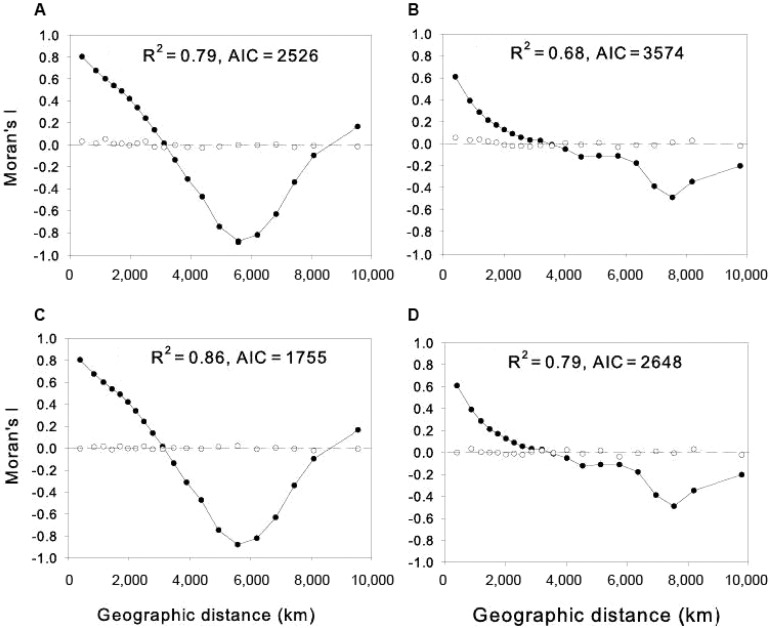
b : the modeling of the spatial patterns of autocorrelation of MDiv and SR - We modeled the spatial structure of MDiv and SR by the spatial eigenvector mapping (SEVM) routine in SAM v4 (Rangel et al. 2010). We conducted separate SVEM analyses for MDiv and SR. The SEVM uses the spatial coordinates of the grid cells to construct a spatial matrix from which to extract eigenvectors that allow the decomposition of the whole spatial structure in the data into spatial patterns at different spatial scales [see Borcard and Legendre (2002) for a formal description of method] (Diniz-Filho & Bini 2005, Rangel et al. 2010). In this way, the neighborhood relationships among the grid cells were used to reveal the spatial autocorrelation of our data set over the whole range of scales encompassed by the sampling design (Borcard & Legendre 2002, Borcard et al. 2004, Diniz-Filho & Bini 2005).

We detrended the data on SR from a significant linear longitudinal trend fitted by least squares and data on MDiv from two significant (linear and quadratic) latitudinal trends so that the method would be able to recover finer spatial structures (Borcard & Legendre 2002, Borcard et al. 2004). We adopted the criterion of minimisation of Moran’s I in model residuals available in SAM v.4 to select those eigenvectors that were the best spatial descriptors of the spatial patterns of autocorrelation for MDiv and SR (Rangel et al. 2010).

SAM v.4 selected 61 positive eigenvectors as spatial descriptors of the latitudinally detrended MDiv and 63 were selected to model the spatial variation in longitudinally detrended SR (eigenvectors not shown) that reduced the spatial structure in MDiv and SR at all spatial scales to almost zero (Fig. S3A, B). The spatial descriptors of SR and MDiv were poorly correlated with the environmental variables retained in models shown on Table I; for SR, the correlation coefficients (r) ranged from r = -0.32-0.31 and for MDiv, from -0.38-0.28. Hence, the spatial descriptors provided complementary information about the spatial structure of MDiv and SR not fully accounted by the environmental variables.

c: partial regression analysis to partition the variation in MDiv and SR - We combined the spatial descriptors obtained from SEVM with the environmental predictors shown in Table I (main text) in a partial regression analysis. Given that the environmental predictors and spatial descriptors were poorly correlated (see above), the combination of them in statistical models did not introduce a serious problem of multicollinearity (Hawkins 2012).

As explained in Borcard et al . (1992), we partitioned the variation in MDiv and SR into: (a) the fraction of MDiv and SR explained by environmental descriptors independently of any spatial structure; (b) the fraction of the variation in MDiv and SR explained by the shared variation between spatial descriptors and environmental variables; (c) the spatial variation in MDiv or SR not shared by the environmental variables analysed, which suggests the operation of some underlying biological process that has no apparent relation to the environmental variables that were included in our analysis and (d) the fraction of the MDiv and SR variation explained neither by the spatial coordinates nor by environmental data. All calculations were done for MDiv and SR separately and based on:

The R² of the regression model that combined the environmental descriptors in Table I (main text) that provided information of fractions (a) and (b) above (R² = a + b).

The R² of the regression model that combined the spatial descriptors obtained from SVEM and that provided information about fractions (c) and (b) above (R² = c + b). The spatial descriptors of MDiv were the linear and quadratic terms of latitude and 61 positive eigenvectors selected by the SVEM routine; for SR, the spatial descriptors were longitude and 63 positive eigenvectors.

The R² of the regression model that combined the whole set of environmental and spatial descriptors (full regression model) that provided information about fractions (a), (b) and (c) above (R² = a + b + c).

According to Borcard et al. (1992), each component of variation was computed from simple calculations:

Results are given in main text.

Fig. S2. spatial correlograms for (A) morphological diversity and (B) species richness (SR) (solid circles) and residuals (open circles) of morphological diversity (A) and SR (B) after fitting the environmental models shown on Table I (main text). AIC: Akaike’s information criterion.

Fig. S3. spatial correlograms for morphological diversity (MDiv) and species richness (SR) (solid circles) and residuals (open circles) after fitting the spatial models to MDiv (A) and SR (B) and full models that combined environmental predictors in Table I (main text) and spatial descriptors obtained from spatial eigenvector mapping to MDiv (C) and SR (D). AIC: Akaike’s information criterion.

Supplementary data 3

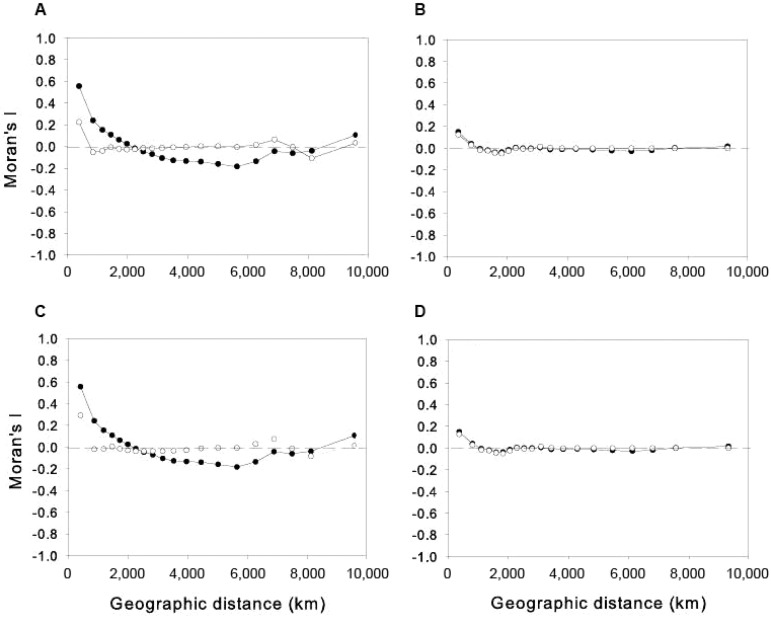
a: the spatial patterns of autocorrelation in the occurrence of local species assemblages that are significantly structured with respect to MDiv - The spatial correlogram for the occurrence of non-random assemblages of species more similar than expected by chance showed that the spatial autocorrelation increases up to 0.56 only at the shortest distant classes (395 km); lower levels of spatial autocorrelation occurred for the other distant classes (between -0.18-0.24) (solid circles on Fig. S4A).

The spatial correlogram for the occurrence of non-random assemblages of species more dissimilar than expected by chance showed low levels of spatial autocorrelation at all distance classes (-0.04-0.15) (solid circles on Fig. S4C).

b: evaluation of the effect of spatial autocorrelation on the performance of environmental models fitted to MDiv and SR - We used spatial generalised linear mixed model in R (GLMM) [Dormann et al. (2007) for review] to address the spatial autocorrelation in models with binomial distribution of errors (Table II, main text). We used glmmPQL of the MASS package in R [according to the script provided in Dormann et al. (2007)], with a Gaussian correlation structure in the residuals to estimate the coefficients of the environmental variables that were preserved in the final models shown on Table II (main text).

GLM and GLMM models resulted in rather similar results, although GLMM tends to reduce the magnitude of the regression coefficients (compare Table II, main text, and Table S2 below). The spatial autocorrelation that remained in the residuals after the fit of GLM and GLMM models was low (i.e. Moran’s I equal or less than 0.29 at the shortest distance classes) (Fig. S4B, D).

TABLE SII. Spatial generalised linear mixed model to account for the presence of structure in the organisation of local species assemblages with respect to morphological diversity (MDiv).

	MDiv lower than expected by chance			MDiv greater than expected by chance
Environmental variables	b	p		b	p
Constant	-3.217	0.000		-5.397	0.000
Potential evapotranspiration	-0.346	0.000		-	-
Mean annual temperature	0.175	0.345		4.839	0.001
Mean altitude	-	-		-	-
Mean precipitation	-3.336	0.000		-	-
Actual evapotranspiration	-	-		-	-
Colwell’s precipitation predictability index	-2.882	0.000		-	-
Mean standard deviation altitude	0.603	0.000		-	-
Coefficient of variation in temperature	-	-		-	-
Coefficient of variation in precipitation	-3.531	0.000		-	-
Number of ecoregions	-	-		-	-
Distance of each cell in the grid map to major rivers	-	-		-2.698	0.012

b : coefficients that indicates the magnitude of the association; p : the probability level.

Fig. S4. spatial correlograms for the binomial variable that represents the presence of random/non-random assemblages with respect to morphological diversity (MDiv) (solid circles). A, B: non-random assemblages are more similar than expected by chance; C, D: non-random assemblages are more dissimilar than expected by chance. Residuals after the fit of environmental models (open circles) are given for non-spatial GLM (A, C) and spatially explicit GLMM (B, D) models (see Materials and Methods).

Supplementary data 4

Fig. S5. political divisions of Brazil (states) and Argentina (provinces) overlapped onto the spatial pattern of variation in triatomine species richness. AC: Acre; AL: Alagoas; AM: Amazonas; AP: Amapá; BA: Bahia; CE: Ceará; ES: Espírito Santo; GO: Goiás; MA: Maranhão; MG: Minas Gerais; MS: Mato Grosso do Sul; MT: Mato Grosso; PA: Pará; PB: Paraíba; PE: Pernambuco; PI: Piauí; PR: Paraná; RJ: Rio de Janeiro; RN: Rio Grande do Norte; RO: Rondônia; RR: Roraima; RS: Rio Grande do Sul; SC: Santa Catarina; SE: Sergipe; SP: São Paulo; TO: Tocantins; BA: Buenos Aires; CC: Chaco; CD: Córdoba; CH: Chubut; CR: Corrientes; CT: Catamarca; ER: Entre Ríos; FO: Formosa; JY: Jujuy; LP: La Pampa; LR: La Rioja; MN: Misiones; MZ: Mendoza; NQ: Neuquén; RN: Río Negro; SA: Salta; SC: Santa Cruz; SE: Santiago del Estero; SF: Santa Fe; SJ: San Juan; SL: San Luis; TF: Tierra del Fuego; TU: Tucumán.

Fig. S6. political divisions of Brazil (states) and Argentina (provinces) overlapped onto the spatial pattern of variation in morphological diversity. AC: Acre; AL: Alagoas; AP: Amapá; AM: Amazonas; BA: Bahia; CE: Ceará; ES: Espírito Santo; GO: Goiás; MA: Maranhão; MT: Mato Grosso; MS: Mato Grosso do Sul; MG: Minas Gerais; PA: Pará; PB: Paraíba; PR: Paraná; PE: Pernambuco; PI: Piauí; RJ: Rio de Janeiro; RN: Rio Grande do Norte; RS: Rio Grande do Sul; RO: Rondônia; RR: Roraima; SC: Santa Catarina; SP: São Paulo; SE: Sergipe; TO: Tocantins; BA: Buenos Aires; CT: Catamarca; CC: Chaco; CH: Chubut; CD: Córdoba; CR: Corrientes; ER: Entre Ríos; FO: Formosa; JY: Jujuy; LP: La Pampa; LR: La Rioja; MZ: Mendoza; MN: Misiones; NQ: Neuquén; RN: Río Negro; SA: Salta; SJ: San Juan; SL: San Luis; SC: Santa Cruz; SF: Santa Fe; SE: Santiago del Estero; TF: Tierra del Fuego; TU: Tucumán.

Fig. S7. the geographical distribution of species that were included in continental initiatives to control the main vectors of Chagas disease [mentioned in Guhl (2009)] overlapped onto the spatial patterns of triatomine species richness (SR). The distributional range of each species is shown as a shaded area. x-y graphs show the proportion of cells in each richness class recorded on the continent that is encompassed by the geographical range of each species.

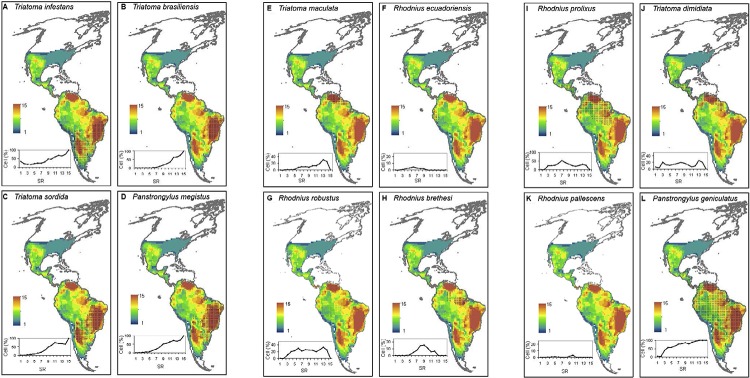
Fig. S8. the geographical distribution of species that were included in continental initiatives to control the main vectors of Chagas disease [mentioned in Guhl (2009)] overlapped onto the spatial patterns of morphological diversity (MDiv). The distributional range of each species is shown as a shaded area. x-y graphs show the proportion of cells in three (arbitrarily defined) morphological diversity classes recorded on the continent that is encompassed by the geographical range of each species.

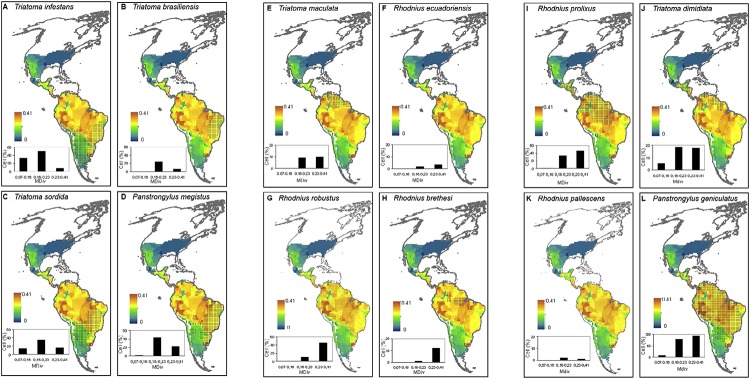
Fig. S9. the geographical distribution of species (in black) that were included in continental initiatives to control the main vectors of Chagas disease [mentioned in Guhl (2009)] compared with the location of assemblages with species more similar (in green) or more dissimilar (in pink) with respect to morphology than expected by chance (for details, see main text and Figs 2, 3).