Abstract
Messenger RNA (mRNA) secondary structure decreases the elongation rate, as ribosomes must unwind every structure they encounter during translation. Therefore, the strength of mRNA secondary structure is assumed to be reduced in highly translated mRNAs. However, previous studies in vitro reported a positive correlation between mRNA folding strength and protein abundance. The counterintuitive finding suggests that mRNA secondary structure affects translation efficiency in an undetermined manner. Here, we analyzed the folding behavior of mRNA during translation and its effect on translation efficiency. We simulated translation process based on a novel computational model, taking into account the interactions among ribosomes, codon usage and mRNA secondary structures. We showed that mRNA secondary structure shortens ribosomal distance through the dynamics of folding strength. Notably, when adjacent ribosomes are close, mRNA secondary structures between them disappear, and codon usage determines the elongation rate. More importantly, our results showed that the combined effect of mRNA secondary structure and codon usage in highly translated mRNAs causes a short ribosomal distance in structural regions, which in turn eliminates the structures during translation, leading to a high elongation rate. Together, these findings reveal how the dynamics of mRNA secondary structure coupling with codon usage affect translation efficiency.
INTRODUCTION
Current understanding of the ribosome and the mechanism of translation has been significantly strengthened and expanded by recent research efforts (1–4). Gene translation is a highly regulated process with intricate interactions among messenger RNAs (mRNAs), ribosomes and mRNA-binding factors, leading to changes in protein abundance, thus enabling the cell to respond rapidly to a wide range of environmental conditions (5–10). Although the underlying factors have been analyzed extensively, the determinants of translation efficiency are still under debate (11–17).
The central dogma of molecular biology deals with the flow of genetic information from DNA via mRNA to protein. It is well understood how an mRNA is sequentially translated into amino acid chains. However, the correlation between mRNA level and protein abundance varies across species [R2 = ∼0.1–0.7, reviewed in (11) and (12)], suggesting widespread regulations occurring at translational and post-translational levels. Translation consists of three stages, namely, initiation, elongation and termination. The initiation has been regarded as rate-limiting for translation in general (18,19). Yet this seems to be uncertain for some genes. For instance, genes with high initiation rate might be subject to non-optimal codon usage or bad codon order downstream, resulting in ribosomal traffic jam, thus significantly decreasing translation efficiency (15,20–23). Moreover, numerous studies have shown that mRNA tends to fold into local secondary structures (so-called mRNA secondary structures) (24–30). These structures are unevenly distributed within mRNA (30) and can act as roadblocks that might influence the rhythm of protein synthesis. During translation, ribosomes move along mRNA and pause at paired sites until the base pairings are broken (31,32). Although it is known that mRNA secondary structure decreases elongation rate (28,31,33,34), a surprising finding in vitro showed a strong positive correlation between the strength of mRNA secondary structure and protein abundance in yeast (17,35). The counterintuitive finding indicates an intricate interaction between translating ribosomes and mRNA secondary structures, affecting translation efficiency in an undetermined manner.
Local secondary structures are distributed densely within mRNA. The distance between adjacent structures in vitro (6.8 nt on average, Figure 1A) is significantly shorter than 28 nt [the length of the footprint that a ribosome protects its mRNA from nuclease digestion (36)]. This suggests that most of the translating ribosomes are located in structural regions and thereby undergo mRNA structural dynamics (folded and unfolded) (Figure 1B). On one hand, mRNA secondary structure blocks ribosomal migration (31,32,37). On the other hand, translating ribosomes constrain mRNA folding. As a ribosome moves along a structural region, mRNA secondary structures disappear, and they may appear after the ribosome passes through the region. The re-folded structures hold until the next ribosome arrives at this region and re-unwinds it. Previous studies (21,38–41) proposed a series of stochastic models to explore the determinant of translation efficiency. mRNA secondary structure was usually integrated into their models (15,21). However, these models used fixed mRNA secondary structures estimated in vitro and did not consider the dynamics of structure during translation. To date, the mechanism by which the dynamics of mRNA secondary structure affect translation efficiency at the genome-wide scale remains unclear.
Figure 1.
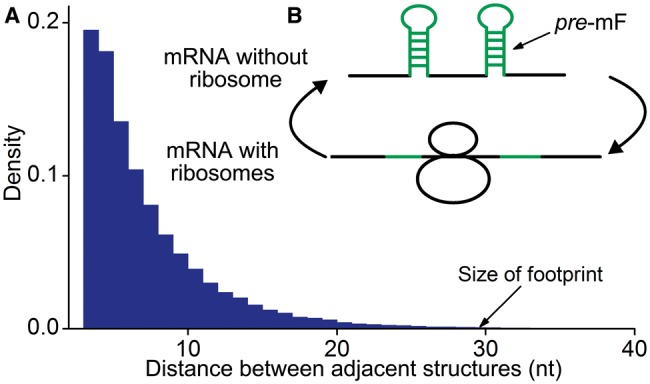
A schematic illustration of the interaction between mRNA secondary structure and translating ribosomes. (A) The distance between adjacent secondary structures within mRNA. mRNA secondary structures in yeast were obtained from the work of Kertesz et al. (27). (B) Structural dynamics when a ribosome moves along mRNA. pre-mF refers to the folding of mRNA without ribosome binding (see text).
With this background, we hypothesized that mRNA secondary structures exert their regulatory effect on translation efficiency through the interactions among translating ribosomes, codon usage and mRNA secondary structures. To test this hypothesis, in the current study, we performed a genome-wide analysis of the effect of mRNA secondary structure on translation efficiency based on a novel computational model, taking into account the dynamics of mRNA secondary structure during elongation. In our model, in contrast to mRNA folding strength (mF strength) during translation, the folding strength of mRNA without ribosome binding was termed previous mF strength (pre-mF strength). Using the model, we first analyzed the association between ribosomal distance and structural dynamics. Then, we revealed a general mechanism by which dynamics of mRNA secondary structure, coupling with other sequence features, likely regulate the organism’s translation efficiency.
MATERIALS AND METHODS
Data collection
Coding sequence
Coding sequences (CDSs) of Saccharomyces cerevisiae S288C were downloaded from the National Center for Biotechnology Information FTP server. Considering that prediction for secondary structures of long sequences is very resource-demanding, we excluded the CDSs longer than 2000 nt. In total, 5369 sequences were obtained.
Experimentally determined mRNA secondary structures
The data were downloaded from the study of Kertesz et al. (27), which provided parallel analysis of RNA structure (PARS) scores at all sites and PARS-assisted secondary structures of 3002 CDSs (2534 CDSs shorter than 2000 nt). PARS score measures the probability of a nucleotide to be in double-stranded conformation, which is significantly correlated with minimum folding free energy (Supplementary Figure S1).
Protein abundance
Protein abundance data were obtained from the PaxDb (42). In total, 2974 data on S. cerevisiae were used when analyzing the correlation between PARS score and protein abundance.
Transfer RNA gene copy numbers
Transfer RNA (tRNA) gene copy numbers of S. cerevisiae were downloaded from the Genomic tRNA Database (43).
Calculation of pre-mF strength and mF strength
pre-mF strength was defined as the mean predicted base pairing probability (PP) of CDS. PPs of CDS were predicted by RNAfold in Vienna RNA package (44) using default parameters. During translation, mF strength was defined as the mean PP of CDS with ribosomal constraints (see following text).
The relationship between ribosomal distance and mF strength
We investigated the variation pattern of mF strength against ribosomal distance. First, we randomly assigned ribosomes on CDS. The number of ribosomes on each CDS was obtained by dividing sequence length by the mean ribosomal distance [154 nt on average (45)]. Second, we used RNAfold with the parameter −C to predict the PPs of CDS under ribosomal constraints (46). Note that the bases near a ribosome cannot be paired with others due to the constraints of spatial structure of the ribosome. Therefore, in our analysis, the region constrained by a ribosome consists of three subregions: the region covered by the ribosome (28 nt) and two flanking regions (14 nt in all). The length of constrained region was set to 42 nt. Third, for each region between adjacent ribosomes, we calculated the mean PP difference (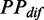
) by Equation (1).
 |
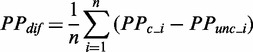(1) |
where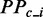 
refers to the predicted PP at site i of the region when ribosomal constraints on CDS exist. 
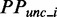refers to the predicted PP without constraint. 
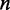is the length of the region.
To exclude the effect of ribosomal positions that we randomly assigned, the aforementioned processes were repeated five times, and the mean value of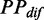 
given a ribosomal distance was obtained by averaging the values of 
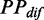with same distance. In addition, all mRNAs were divided into five groups based on their pre-mF strength from high to low (G1–G5), which was used to test whether the pattern we estimated is sequence-specific.
Calculation of tRNA adaptation index
The tRNA adaptation index (tAI) of CDS was calculated by Equation (2).
 |
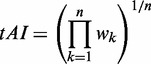(2) |
where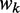 
is the relative adaptiveness value of codon k, the values for all 64 codons were calculated according to the work of dos Reis et al. (47), and 
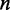is the length of CDS. In addition, we refer to the 
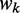of a single codon as the codon’s tAI.
Simulation of translation process by taking into account the interactions among translating ribosomes, codon usage and mRNA secondary structures
Model
Inspired by previous studies reporting a significant positive correlation between the mean PARS score of CDS and protein abundance (Supplementary Figure S2) (17,35), we decided to investigate how mRNA secondary structure exerts a positive effect on translation efficiency, as there are numerous lines of evidence in vitro revealing that mRNA secondary structure decreases elongation rate. To this end, we developed a novel computational model (Figure 2) to simulate the process of translation. Translation process is divided into three phases: initiation, elongation and termination. In our model, ribosomes arrive at the start site with initiation rate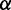 
. At the last codon, ribosomes detach and release proteins with termination rate 
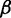. During elongation, translation cycle consists of two steps. The first step is that cognate tRNA arrives at ribosome A site (codon i) with rate 
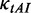, and that ribosome unwinds base pairings located at codon i + L/2 (L is set to 42 nt) with rate 
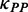simultaneously. The second step is translocation. Translocation rate is fast and codon-independent, thus a constant rate was used. Therefore, the rate 
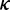that a ribosome moves from the current codon to the next codon is determined by 
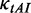and 
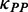(see the following subsection for details). Moreover, the ribosome cannot translocate if the next codon is occupied by the former ribosome. In addition, the ribosomes can capture a cognate tRNA when they are waiting for the next codon to become vacant.
Figure 2.
The model. In our model, ribosomes arrive at translation start site with rate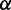 
, and release proteins with rate 
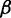. During elongation, translating ribosomes wait for their cognate tRNAs at position i and simultaneously unwind the base pairings located at position i + L/2 (L = 42 nt). (A) shows the structure that the first ribosome encounters (the first ribosome is blue). (B) shows the structure that the third ribosome encounters. mRNA secondary structure is weakened due to the constraints of ribosomes. In our model, we assume that different ribosomes might encounter the structure with different folding strength at the same site because the pattern of mRNA folding might be changed when ribosomes have bound to mRNA (see text for details).
Importantly, in contrast to other models using fixed mRNA secondary structures, our model considers dynamic structures during translation, which means that different ribosomes might be subject to different folding strength at the same codon (Figure 2). This assumption is based on our finding that the folding strength of the region between adjacent ribosomes is strongly dependent on ribosomal distance (Figure 3). Moreover, we focus on the folding behavior of mRNA secondary structure during elongation and its effect on ribosomal distance. Other factors affecting ribosomal distance were controlled. Therefore, a relative rate instead of an absolute rate was used in the model. We set an arbitrary value for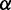 
. To obtain the relative rate of elongation, 
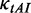and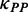 
were multiplied by the weights 
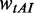and 
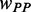, respectively (see following text for details). Unless otherwise indicated, we used the values listed in Table 1 for all simulations.
Figure 3.
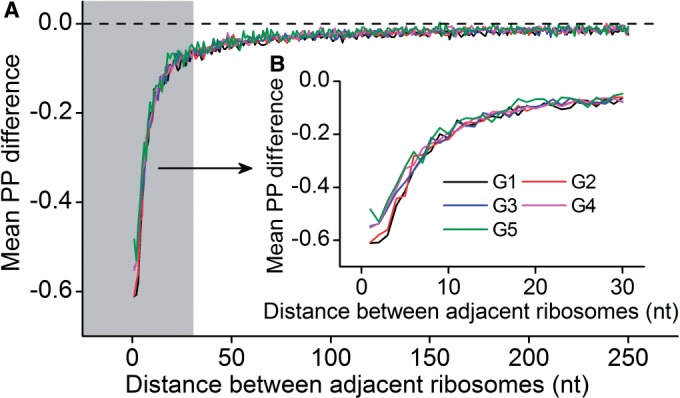
Variation of mF strength against ribosomal distance. All mRNAs were divided into five groups (G1–G5) based on their pre-mF strength from high to low. (A) There is no significant difference in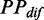 
(see ‘Materials and Methods’ section for the calculation of 
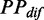) among the five groups when ribosomal distance is longer than 5 nt. (B) When the distance is shorter than 5 nt, there is no structure between adjacent ribosomes, 
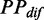is determined by pre-mF strength.
Table 1.
Parameters used in simulation
| Parameter | Value | Descriptions |
|---|---|---|
 |
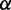8 | Initiation rate (s). |
 |
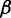0.1 | Termination rate (s). |
 |
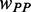0.5 | The weight for  . |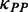
 |
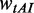1.0 | The weight for  . |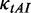
 |
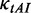0.12/Various | Dwell time at a codon caused by codon usage (s). When investigating the function of mRNA secondary structure without considering the effect of codon usage, an equal rate for all codons is used (0.12). When investigating the combined effect of mRNA secondary structure and codon usage, the value of 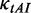 depends on codon’s tAI (various). |
 |
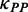Various | Dwell time at a codon caused by mRNA secondary structure (s). Various means that the value depends on the PP of the codon. |
 |
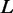42 | The length of the region constrained by a ribosome (nt). |
 |
Constant | Translocation time (s). Translocation time is equal to the running time that a ribosome moves from the current codon to the next. |
Parameters required for simulation
We used the multiple threads in Perl 5.12 (Supplementary files: Simulation.pl) to simulate translation process (Figure 2 and Supplementary Figure S3). The parameters required for simulation are:
-
1)
Initiation rate (
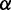): Although the initiation rate for individual mRNA has been estimated by previous studies based on ribosomal density or codon usage (39,48), we set an equal rate for all mRNAs to exclude the effect of initiation rate on ribosomal density. -
2)
Termination rate (
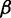): Termination process is assumed to be fast compared with other processes (e.g. elongation) (49). Therefore, the effect of termination was neglected. A constant rate (0.1 s) was used for all mRNAs. -
3)Elongation rate (
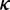): Elongation rate is determined by codon usage and mRNA secondary structure. The dwell time at a codon caused by codon usage (
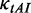) was calculated as follows. First, the relative adaptiveness values of 64 codons (
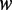, Supplementary Table S1) were calculated according to the work of dos Reis et al. (47). Then, 
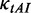of each codon was obtained by Equation (3).
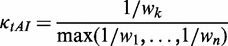
(3) where
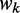is the adaptiveness value of codon k. In particular, 
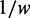of the codon CGA is very large (Supplementary Table S1) compared with others. Therefore, this codon was excluded when we calculated 
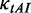of each codon. 
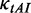of this codon was set to be equal to the maximum value of 
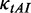(1.0, Supplementary Table S1). In addition, when investigating the functions of mRNA secondary structure without considering the effect of codon usage, the values of 
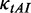for all codons are equal and set to 0.12 (Table 1).
It is not feasible to estimate the dwell time at a codon caused by mRNA secondary structure (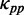
), we thus introduced a simplification in our analysis. Note that there are many identical mRNAs expressed at the same time in the same cell. PP at codon i (averaging PPs of the three sites of codon i) can be treated as the proportion of identical mRNAs whose sites at codon i are paired. Therefore, higher PP at codon i indicates that ribosomes unwind base pairings of this codon with a lower rate on average (averaging rates at codon i of all identical mRNAs). With this simplification, we assume that 
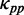of a codon is equal to the PP of the codon. Here, we did not calculate the PP of a codon directly during translation (because this requires massive computational effort), but set it to be equal to the mean PP of the codons present in the region between adjacent ribosomes, which was estimated based on the fitting of ribosomal distance and 
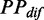(Figure 3). Moreover, we showed that the variation of mF strength against ribosomal distance is not position-specific (Supplementary Figure S4) and sequence-specific (Figure 3). Therefore, 
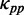at different codons in different mRNAs was estimated based on the same pattern shown in Figure 3 (also listed in Supplementary Table S2). In addition, if ribosomal distance is longer than 200 nt, we assume that the two ribosomes cannot hinder the folding of the region between them. In this case, 
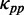at a codon is equal to the PP of the codon without ribosomal constraint. In summary, 
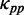was calculated by Equation (4).
 |
(4) |
where 
indicates that PP was calculated based on ribosomal distance.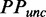 
refers to the predicted PP without ribosomal constraint.
Together, the elongation rate (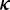
) at a codon is determined by Equation (5).
 |
(5) |
where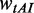 
and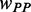 
are the weights for 
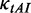and 
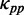, respectively. Note that unwinding base pairings and waiting for tRNA occur at two different codons (Figure 2). The distance of the two codons was set to 21 nt (L/2) in our analysis (32).
-
4)
Translocation rate (
): During simulation, translocation rate was set to be equal to the running time that a ribosome moves from the current codon to the next codon. The time is very short (Supplementary Figure S5) and thus treated as ‘constant’.
Estimation of parameters
For each mRNA, we simulated translation processes of 60 ribosomes. Generally, translation arrives at the steady state (the number of ribosomes on mRNA remains unchanged, Supplementary Figure S6) when the 10th ribosome detaches. We estimated parameters by averaging the values of 11 ribosomes (from the 30th to 40th ribosomes, Supplementary files: Para.pl and Pause.pl). The parameters are number of ribosomes per mRNA, distance between adjacent ribosomes, mean dwell time at each codon (averaging the values at the same position of mRNAs), the time that a ribosome completes a translation cycle (translation time), mean elapsed time after initiation (elongation time, averaging the values at the same position of mRNAs), pause sites and percentage of collision sites per mRNA and flag at each codon (averaging the values at the same position of mRNAs). Here, we used a flag to record whether mRNA secondary structure is used during elongation. If mRNA secondary structure determines the rate at a codon (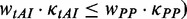
, the flag at this codon is set to 1, and if the determinant is codon usage (
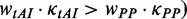, the flag is set to 2.
Calculation of the correlation
All correlations reported in this study are Spearman’s rank correlations.
RESULTS
Regulation on ribosomal distance through the variation of mF strength
There is a significant positive correlation between pre-mF strength and ribosomal density when controlling for sequence length [ρ(PP, ribosomal density | sequence length) = 0.10, P = 4.8 × 10−9, Supplementary Figure S7], indicating that mRNA secondary structure can shorten the distance of the ribosomes in structural regions. During translation, ∼30% of coding regions are covered by ribosomes (45,49). The pattern of mRNA folding during translation is significantly different from that without ribosome binding (50–52) (Supplementary Figure S8). To date, the way in which pre-mF strength affects ribosomal distance during translation remains elusive. To address this question, we simulated the translation processes of CDSs by setting an equal initiation rate. An equal rate was used to exclude the effect of initiation rate on ribosomal density (22), which notably influences ribosomal distance (high ribosomal density is sufficient but not necessary for short ribosomal distance). Moreover, to exclude the effect of codon usage, the rates for all 64 codons were set to be equal. The main parameters required for simulation are listed in Table 1. We calculated the number of ribosomes on mRNA and the distance between adjacent ribosomes when translation reaches the steady state. Consistent with previous studies based on the data of ribosomal profiling (15), when considering structural dynamics during translation, we also found a positive correlation between the number of ribosomes per mRNA and pre-mF strength (ρ = 0.41, P < 2.2 × 10−16, Figure 4A). More importantly, there is a strong negative correlation between pre-mF strength and ribosomal distance (ρ = −0.81, P < 2.2 × 10−16, Figure 4B). We validated the correlations by setting different weights for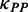 
. Similar results were obtained (Supplementary Figure S9A and B). Moreover, the results were not changed significantly when we used different initiation rates (Supplementary Figure S10A and B).
Figure 4.
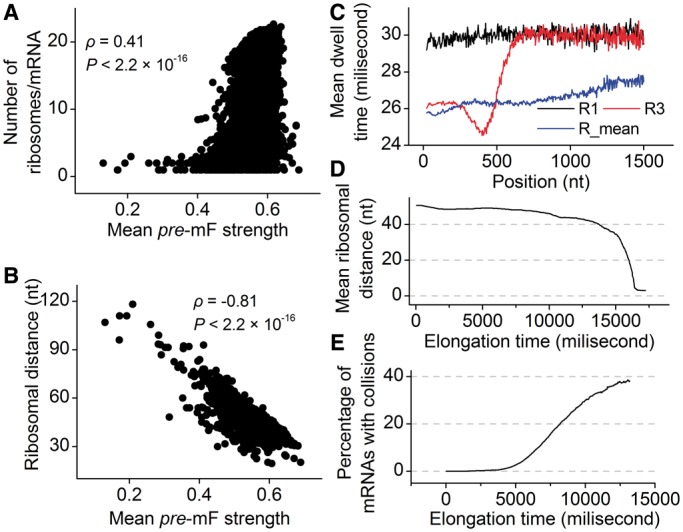
mRNA secondary structure shortens ribosomal distance. (A) Correlation between the number of ribosomes and pre-mF strength. (B) Correlation between ribosomal distance and pre-mF strength. (C) Mean dwell time at each codon. R1 and R3 indicate the mean dwell time (averaging the values of all mRNAs) of the first and third ribosomes at each codon, respectively. R3 shows translation pattern of the ribosomes when translation does not reach steady state. R_mean indicates the mean dwell time at each codon during steady state. (D) Ribosomal distance decreases over time. (E) The variation of the percentage of mRNAs with ribosomal collisions against elongation time during steady state.
For details, we analyzed the variations of dwell time and ribosomal distance along mRNA. We found that the first ribosome (R1 in Figure 4C) on mRNA has longer dwell time than following ribosomes (Figure 4C), suggesting that following ribosomes are subject to a lower mF strength when the first ribosome has bound to mRNA. A lower mean mF strength (i.e. a lower value for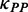 
) between adjacent ribosomes causes a higher movement rate of the latter ribosome compared with the rate that the former ribosome passes through this region, thereby leading to a decrease in ribosomal distance, which further reduces the mean mF strength of the region between the two ribosomes (Figure 3). The process continues until the following ribosome collides with its former one. When only considering the effect of mRNA secondary structure, we found that ribosomal distance decreases over time (Figure 4D). Notably, the percentage of mRNAs with ribosomal collisions increases over time (Figure 4E). Again, we considered different weights for 
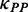and different initiation rates. We found that the increase in the weight for 
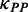(corresponding to increase mean mF strength) or in the initiation rate significantly decreases ribosomal distance (Supplementary Figures S9C and S10C) and increases the probability of ribosomal collisions (Supplementary Figures S9D and S10D). Taken together, our results revealed that mRNA secondary structure shortens ribosomal distance through the variation of mF strength during translation.
The effect of the location of mRNA secondary structure
Based on our model, the simulation of translation process revealed how pre-mF strength affects ribosomal distance. To investigate the effect of the location of mRNA secondary structure, we ran a simulation on an artificial sequence of 600 nt. Because the effect of codon usage was not considered, the codons of the sequence were generated randomly based on their genomic frequencies. A sliding window with a length of 100 nt and a step of 3 nt was used to specify the structural region (Figure 5A), where PPs at all sites were set to 0.5 (other PPs were also tested, Supplementary Figure S11). We applied our model to this sequence with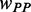 
= 1.0 (a higher weight for 
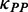was used to make the pattern more obvious). The other parameters are listed in Table 1. In addition, we ran a simulation with 
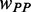= 0 to obtain the mean ribosomal distance when no structure exists within the sequence, which was used as control. We found that mean ribosomal distance varies significantly when changing the position of mRNA secondary structure. Longer ribosomal distance was observed when the structure is in 5′ regions. In particular, the distance is longer than the control if the structure is located at the head of the sequence, which supports the hypothesis that mRNA secondary structure at the beginning of CDS decreases the probability of ribosomal traffic jams (21). The mean ribosomal distance decreases notably when the structure moves toward the tail of the sequence (Figure 5B). Similar results were obtained when different PPs in structural region were used (Supplementary Figure S11). The results based on the artificial sequence raise the possibility that increased pre-mF strength tends to emerge at the end of sequence to meet the requirement for a high level of ribosomal density. When analyzing the association between the experimentally determined data of ribosomal density (36) and mean PARS score, we found a significant difference in pre-mF strength at the end of CDS (Wilcoxon test, P = 0.02) between the two groups with ribosomal densities at the top and bottom 30% (Figure 5C).
Figure 5.
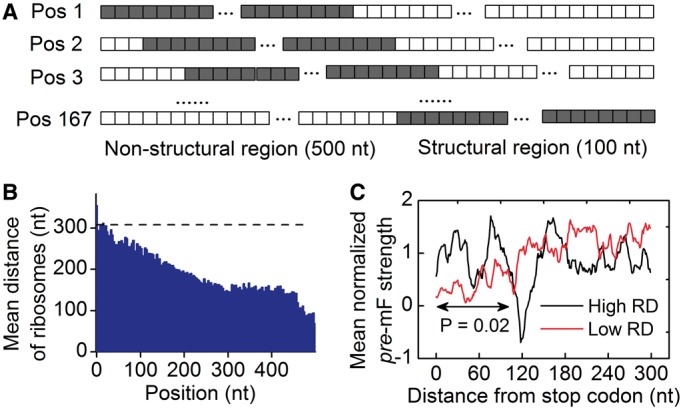
Effect of mRNA secondary structure at different positions. (A) The sliding structural region on an artificial sequence. The paired sites are indicated by gray lattices (each lattice represents a site). The PP of paired site was set to 0.5. (B) The variation of ribosomal distance during steady state when mRNA secondary structure is located in different regions. The distance without considering the effect of secondary structure is indicated by dashes. (C) Comparison of normalized PARS scores at the end of CDSs between the two groups with ribosomal densities at the top and bottom 30%. PARS score at each site was normalized by the mean score of CDS. RD, ribosomal density.
The effect of codon usage
When only considering the effect of mRNA secondary structure, as reported earlier, we found that mRNA secondary structure can cause a high frequency of ribosomal collisions if translation time is long enough (Figure 4). The collision should be avoided because ribosomal traffic jam might lead to premature termination of translation or prolonged elongation time, increasing the translational cost. When simulating translation process using the parameters in Table 1 (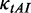
= 0.12), we found that the mean value of the flag (see ‘Materials and Methods’ section) increases obviously with the decrease in ribosomal distance (Figure 6A), suggesting that codon usage becomes the determinant of elongation rate when ribosomal distance is short (Figure 6A). This result raises the possibility that the effect of codon usage can prevent the collisions caused by mRNA secondary structures.
Figure 6.
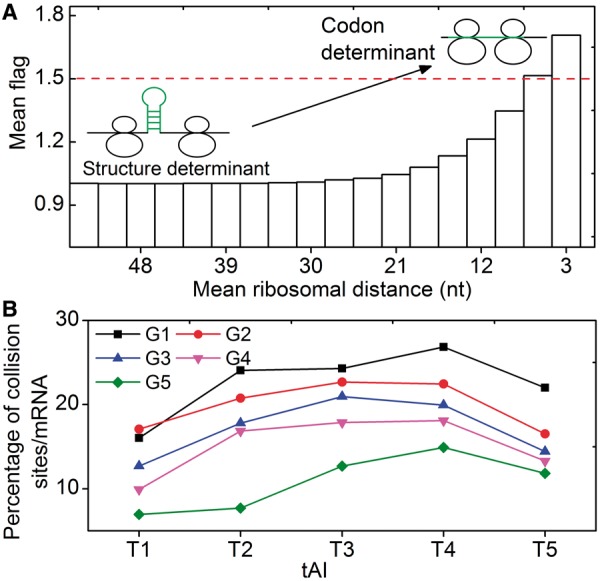
Effect of codon usage. (A) The variation of the mean value of flag against ribosomal distance. The mean value of flag increases sharply with the decrease in ribosomal distance when the distance is <30 nt. If the value is <1.5 (below the red dashes), mRNA secondary structure determines elongation rate. If the value is >1.5, indicating that most of mRNA secondary structures disappear, codon usage determines elongation rate. (B) All mRNAs were classified into five groups (G1–G5) based on their pre-mF strength from high to low. For each group, mRNAs were classified into five subgroups (T1–T5) based on their tAI from low to high (see text).
To test this possibility, we simulated translation process by considering the effect of codon usage (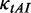
= various, Table 1). Moreover, we classified all mRNAs into five groups (G1–G5) according to their pre-mF strength from high to low. In this case, mRNAs in the same group have similar pre-mF strength. For each group, mRNAs were also divided into five subgroups (T1–T5) based on their tAI from low to high (∼320 mRNAs in each subgroup). We found that the percentage of collision sites per mRNA increases with the increase in tAI (from T1 to T4 and Figure 6B), suggesting that low tAI codons can decrease the probability of the ribosomal collisions caused by mRNA secondary structures. We reasoned that when two adjacent ribosomes are close enough, mRNA secondary structures between them disappear, and codon usage determines the elongation rate (Figure 6A). Unlike mRNA secondary structure, codon usage does not significantly decrease ribosomal distance (Supplementary Figure S12). Besides, the lower the tAI, the higher the probability that codon usage determines the rate [Equation (5)]. Therefore, the probability of the collisions caused by mRNA secondary structures is lower in those mRNAs with lower tAI.
Moreover, in all groups, we found that mRNAs in T5 have a lower probability of collisions compared with those in T4. A possible reason is as follows. If the tAI of an mRNA is high (T5 in Figure 6B), the dwell time caused by codon usage is low and ribosomes pass through non-structural regions rapidly on average (averaging the rates in all non-structural regions of mRNA). In this case, the effect of codon usage can partly counteract the negative effect (decreasing elongation rate) of mRNA secondary structure, thus mRNAs in T5 have a higher elongation rate compared with those in T4, leading to a lower ribosomal density and hence lower probability of ribosomal collisions (Figure 6B).
The way in which mRNA secondary structure affects translation efficiency
mRNA is a single-strand molecule with a strong potential to fold back on itself if no ribosome binds to it. Although mRNA secondary structure slows down translation elongation, a considerable number of mRNA secondary structures are kept in highly expressed mRNAs during evolution (24,27,29,30), suggesting an important role of mRNA secondary structure during translation. The results in previous subsections raise a hypothesis (Figure 7A) describing how mRNA secondary structure affects translation efficiency through structural dynamics. We propose that high pre-mF strength leads to a short ribosomal distance (Figure 4), which in turn significantly decreases the mF strength during translation. In particular, mRNA secondary structures disappear if translating ribosomes are close enough. In this case, codon usage becomes the determinant of elongation rate, and the negative effect of mRNA secondary structure (decreasing elongation rate) is negligible. In contrast, ribosomes on the mRNAs with lower pre-mF strength are more distant, and hence, a higher fraction of mRNA regions can fold into secondary structures during translation. The effect of mRNA secondary structure cannot be neglected. Therefore, higher translation efficiency is observed in the mRNAs with higher pre-mF strength compared with that in the mRNAs with lower pre-mF strength.
Figure 7.
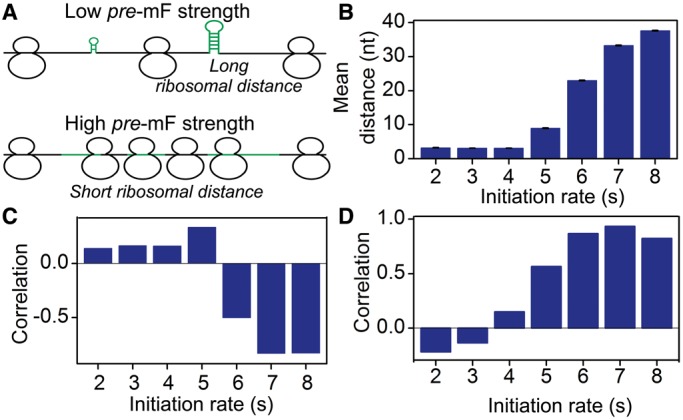
Correlation between pre-mF strength and translation time. (A) A schematic illustration of the effect of mRNA secondary structure on translation efficiency. We propose that high pre-mF strength leads to a short ribosomal distance, which in turn eliminates the effect of mRNA secondary structure during translation (see descriptions in the ‘Results’ and ‘Discussion’ sections). (B) Mean ribosomal distance at different initiation rates. (C) Correlation between pre-mF strength and the mean value of flag (averaging the value of flag at all sites of mRNA). A positive correlation is observed when ribosomes are close (corresponding initiation rate = 2, 3, 4 or 5 s), suggesting that high pre-mF strength leads to a less use of mRNA secondary structure during elongation. (D) Correlation between pre-mF strength and translation time/sequence length. A negative correlation indicates that high pre-mF strength leads to high translation efficiency.
We tested this hypothesis by running a series of simulations with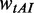 
= 2.0 (a higher weight for 
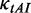was used to decrease the probability of the collisions caused by mRNA secondary structures) and different initiation rates. 
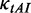was set to 0.12. We used a flag to estimate the usage of structures during elongation (see ‘Materials and Methods’ section for details). We found that there is a negative correlation between the value of flag and pre-mF strength when ribosomal distance is long (corresponding to a low initiation rate: 8, 7 or 6 s. ρ < −0.4, P < 10−15, Figure 7B and C). Surprisingly, the correlation becomes positive when ribosomes are close (corresponding to a high initiation rate: 2, 3, 4 or 5 s. ρ > 0.1, P < 10−15, Figure 7B and C), suggesting that high pre-mF strength leads to a less use of mRNA secondary structure during elongation when ribosomal distance is short. Moreover, we calculated the correlation between translation time and pre-mF strength. Consistent with our hypothesis, we found a positive correlation between translation time and pre-mF strength when initiation rate is low (Figure 7D), whereas the correlation becomes negative when initiation rate = 2 or 3 s. Overall, the results support our hypothesis that mRNAs with high pre-mF strength have high elongation rates because high pre-mF significantly shortens ribosomal distance, which in turn eliminates mRNA secondary structures during translation.
DISCUSSION
mRNA accommodates numerous regulatory signals delineated along the protein coding regions in an intricate overlapping manner (22,53). These signals, such as codon usage bias and mRNA secondary structure, are all known to modulate protein synthesis. Although the functions of the individual signal have been investigated extensively by previous studies (7,23,32,38,39,54–57), how these signals combine to affect translation efficiency remains elusive.
In the current study, we used a computational model to investigate the effect of mRNA secondary structure during translation. Our model takes into consideration the interactions among translating ribosomes, codon usage and mRNA secondary structures. In particular, for the first time, our model allows us to analyze the structural dynamics during translation. The simulation of translation based on our model revealed that mRNA secondary structure shortens ribosomal distance through the variation of mF strength. Moreover, we found that low tAI codons can decrease the probability of the ribosomal collisions caused by mRNA secondary structures when ribosomal distance is short. Based on these results, we explained how structural dynamics affect translation efficiency.
Why is high pre-mF strength favored? mRNA secondary structure blocks the migration of ribosomes, thereby decreasing elongation rate. For highly expressed mRNAs, mRNA secondary structures should be eliminated to meet the requirement for a high level of elongation rate. However, removing all non-functional structures by natural selection is difficult. First, because there is a tendency to increase the frequency of the codons with high translation efficiency (so-called optimal codons) in highly translated mRNAs. Increase in optimal codon usage leads to an increase in pre-mF strength (Supplementary Figure S13). Second, mRNA is a single-strand molecule with a strong tendency to fold back on itself, making it impossible to prevent the mRNA from folding into secondary structures. Because removing all non-functional structures is difficult, another strategy, increasing pre-mF strength, is used to eliminate mRNA secondary structures during translation. Together, these findings explain why highly expressed mRNAs have undergone stronger natural selection for high pre-mF strength than infrequently expressed mRNAs (35).
There are many factors affecting ribosomal distance. In particular, increase in the initiation rate or the frequency of non-optimal codons greatly increases ribosomal density, thus significantly decreasing ribosomal distance. Why is high pre-mF strength required for a short ribosomal distance? The possible reasons are as follows. On one hand, the availability of free ribosomes is limited, making it difficult to significantly increase initiation rate (41). On the other hand, high initiation rate is not sufficient for short ribosomal distance. A lower elongation rate is also required [reviewed in ref (22)]. In addition, although both non-optimal codon and mRNA secondary structure can decrease ribosomal distance, non-optimal codon will decrease translation accuracy and efficiency. Importantly, non-optimal codon affects all translating ribosomes, while mRNA secondary structure usually decreases the rate of the first several ribosomes. mRNA secondary structures disappear when ribosomes are close (Supplementary Figure S14).
Although our model enables us to investigate the effect of structural dynamics during elongation, there are many simplifying assumptions. For instance, to develop the translation model, we first investigated the relationship between ribosomal distance and mF strength by predicting mF strength under the constraints of ribosomes that were assigned on mRNAs randomly. Note that the predicted PPs during translation for single mRNA might be different from the PPs in vivo. To decrease the estimation error of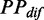 
given a specific ribosomal distance, we calculated the mean value of 
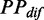(see ‘Materials and Methods’ section) by averaging the values with same ribosomal distance. In addition, the length of the region constrained by a ribosome during translation is unclear. In reality, the true length might be longer than 42 nt that we used in our analysis (58). Therefore, the ribosomal distance, which efficiently eliminates mRNA secondary structures during translation, might be reached more easily. Our model also did not distinguish between functional structures and other structures. Functional structures refer to those involved in co-translational regulations, such as co-translational folding of proteins and ribosomal frameshifts. Generally, functional structures are necessary for translation, thus they will not disappear during translation. In our model, it is difficult to retain the folded conformations for functional structures due to the constraints of ribosomes, especially for those in highly translated mRNAs. Therefore, it is worth investigating how these functional structures are maintained during elongation, probably involving the interaction between codon usage bias and mRNA secondary structures (e.g. a cluster of rare codon is assigned before a functional structure).
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
Funding for open access charge: National Natural Science Fund Program [31271917].
Conflict of interest statement. None declared.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank Elizabeth M. Anderson for English editing. They thank Li Qian, Wang Chen and Yu Haopeng for the comments on the simulation. They also thank the two anonymous reviewers for their excellent suggestions.
REFERENCES
- 1.Aitken CE, Lorsch JR. A mechanistic overview of translation initiation in eukaryotes. Nat. Struct. Mol. Biol. 2012;19:568–576. doi: 10.1038/nsmb.2303. [DOI] [PubMed] [Google Scholar]
- 2.Hinnebusch AG, Lorsch JR. The mechanism of eukaryotic translation initiation: new insights and challenges. Cold Spring Harb. Perspect. Biol. 2012;4:a01154. doi: 10.1101/cshperspect.a011544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dever TE, Green R. The elongation, termination, and recycling phases of translation in eukaryotes. Cold Spring Harb. Perspect. Biol. 2012;4:a013706. doi: 10.1101/cshperspect.a013706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ramakrishnan V. Ribosome structure and the mechanism of translation. Cell. 2002;108:557–572. doi: 10.1016/s0092-8674(02)00619-0. [DOI] [PubMed] [Google Scholar]
- 5.Sangthong P, Hughes J, McCarthy JE. Distributed control for recruitment, scanning and subunit joining steps of translation initiation. Nucleic Acids Res. 2007;35:3573–3580. doi: 10.1093/nar/gkm283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Firczuk H, Kannambath S, Pahle J, Claydon A, Beynon R, Duncan J, Westerhoff H, Mendes P, McCarthy JE. An in vivo control map for the eukaryotic mRNA translation machinery. Mol. Syst. Biol. 2013;9:635. doi: 10.1038/msb.2012.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Weill L, Belloc E, Bava F-A, Méndez R. Translational control by changes in poly (A) tail length: recycling mRNAs. Nat. Struct. Mol. Biol. 2012;19:577–585. doi: 10.1038/nsmb.2311. [DOI] [PubMed] [Google Scholar]
- 8.Shoemaker CJ, Green R. Translation drives mRNA quality control. Nat. Struct. Mol. Biol. 2012;19:594–601. doi: 10.1038/nsmb.2301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wu L, Candille SI, Choi Y, Xie D, Jiang L, Li-Pook-Than J, Tang H, Snyder M. Variation and genetic control of protein abundance in humans. Nature. 2013;499:79–82. doi: 10.1038/nature12223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wang T, Cui Y, Jin J, Guo J, Wang G, Yin X, He Q-Y, Zhang G. Translating mRNAs strongly correlate to proteins in a multivariate manner and their translation ratios are phenotype specific. Nucleic Acids Res. 2013;41:4743–4754. doi: 10.1093/nar/gkt178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Greenbaum D, Colangelo C, Williams K, Gerstein M. Comparing protein abundance and mRNA expression levels on a genomic scale. Genome Biol. 2003;4:117. doi: 10.1186/gb-2003-4-9-117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Maier T, Güell M, Serrano L. Correlation of mRNA and protein in complex biological samples. FEBS Lett. 2009;583:3966–3973. doi: 10.1016/j.febslet.2009.10.036. [DOI] [PubMed] [Google Scholar]
- 13.Gingold H, Pilpel Y. Determinants of translation efficiency and accuracy. Mol. Syst. Biol. 2011;7:481. doi: 10.1038/msb.2011.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kudla G, Murray AW, Tollervey D, Plotkin JB. Coding-sequence determinants of gene expression in Escherichia coli. Science. 2009;324:255–258. doi: 10.1126/science.1170160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tuller T, Waldman YY, Kupiec M, Ruppin E. Translation efficiency is determined by both codon bias and folding energy. Proc. Natl Acad. Sci. USA. 2010;107:3645–3650. doi: 10.1073/pnas.0909910107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Olivares-Hernandez R, Bordel S, Nielsen J. Codon usage variability determines the correlation between proteome and transcriptome fold changes. BMC Syst. Biol. 2011;5:33. doi: 10.1186/1752-0509-5-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zur H, Tuller T. Strong association between mRNA folding strength and protein abundance in S. cerevisiae. EMBO Rep. 2012;13:272–277. doi: 10.1038/embor.2011.262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gandin V, Miluzio A, Barbieri AM, Beugnet A, Kiyokawa H, Marchisio PC, Biffo S. Eukaryotic initiation factor 6 is rate-limiting in translation, growth and transformation. Nature. 2008;455:684–688. doi: 10.1038/nature07267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.McClure WR. Rate-limiting steps in RNA chain initiation. Proc. Natl Acad. Sci. USA. 1980;77:5634–5638. doi: 10.1073/pnas.77.10.5634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tuller T, Carmi A, Vestsigian K, Navon S, Dorfan Y, Zaborske J, Pan T, Dahan O, Furman I, Pilpel Y. An evolutionarily conserved mechanism for controlling the efficiency of protein translation. Cell. 2010;141:344–354. doi: 10.1016/j.cell.2010.03.031. [DOI] [PubMed] [Google Scholar]
- 21.Tuller T, Veksler-Lublinsky I, Gazit N, Kupiec M, Ruppin E, Ziv-Ukelson M. Composite effects of gene determinants on the translation speed and density of ribosomes. Genome Biol. 2011;12:R110. doi: 10.1186/gb-2011-12-11-r110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Plotkin JB, Kudla G. Synonymous but not the same: the causes and consequences of codon bias. Nat. Rev. Genet. 2011;12:32–42. doi: 10.1038/nrg2899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Agashe D, Martinez-Gomez NC, Drummond DA, Marx CJ. Good codons, bad transcript: large reductions in gene expression and fitness arising from synonymous mutations in a key enzyme. Mol. Biol. Evol. 2013;30:549–560. doi: 10.1093/molbev/mss273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Katz L, Burge CB. Widespread selection for local RNA secondary structure in coding regions of bacterial genes. Genome Res. 2003;13:2042–2051. doi: 10.1101/gr.1257503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Meyer IM, Miklós I. Statistical evidence for conserved, local secondary structure in the coding regions of eukaryotic mRNAs and pre-mRNAs. Nucleic Acids Res. 2005;33:6338–6348. doi: 10.1093/nar/gki923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pedersen JS, Bejerano G, Siepel A, Rosenbloom K, Lindblad-Toh K, Lander ES, Kent J, Miller W, Haussler D. Identification and classification of conserved RNA secondary structures in the human genome. PLoS Comput. Biol. 2006;2:e33. doi: 10.1371/journal.pcbi.0020033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kertesz M, Wan Y, Mazor E, Rinn JL, Nutter RC, Chang HY, Segal E. Genome-wide measurement of RNA secondary structure in yeast. Nature. 2010;467:103–107. doi: 10.1038/nature09322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zheng Q, Ryvkin P, Li F, Dragomir I, Valladares O, Yang J, Cao K, Wang L-S, Gregory BD. Genome-wide double-stranded RNA sequencing reveals the functional significance of base-paired RNAs in Arabidopsis. PLoS Genet. 2010;6:e1001141. doi: 10.1371/journal.pgen.1001141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li F, Zheng Q, Ryvkin P, Dragomir I, Desai Y, Aiyer S, Valladares O, Yang J, Bambina S, Sabin LR. Global analysis of RNA secondary structure in two metazoans. Cell Rep. 2012;1:69–82. doi: 10.1016/j.celrep.2011.10.002. [DOI] [PubMed] [Google Scholar]
- 30.Mao Y, Li Q, Wang W, Liang P, Tao S. Number variation of high stability regions is correlated with gene functions. Genome Biol. Evol. 2013;5:484–493. doi: 10.1093/gbe/evt020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wen J-D, Lancaster L, Hodges C, Zeri A-C, Yoshimura SH, Noller HF, Bustamante C, Tinoco I. Following translation by single ribosomes one codon at a time. Nature. 2008;452:598–603. doi: 10.1038/nature06716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chen C, Zhang H, Broitman SL, Reiche M, Farrell I, Cooperman BS, Goldman YE. Dynamics of translation by single ribosomes through mRNA secondary structures. Nat. Struct. Mol. Biol. 2013;20:582–588. doi: 10.1038/nsmb.2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wachter A. Riboswitch-mediated control of gene expression in eukaryotes. RNA Biol. 2010;7:67–76. doi: 10.4161/rna.7.1.10489. [DOI] [PubMed] [Google Scholar]
- 34.Locker N, Chamond N, Sargueil B. A conserved structure within the HIV gag open reading frame that controls translation initiation directly recruits the 40S subunit and eIF3. Nucleic Acids Res. 2011;39:2367–2377. doi: 10.1093/nar/gkq1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Park C, Chen X, Yang J-R, Zhang J. Differential requirements for mRNA folding partially explain why highly expressed proteins evolve slowly. Proc. Natl Acad. Sci. USA. 2013;110:E678–E686. doi: 10.1073/pnas.1218066110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ingolia NT, Ghaemmaghami S, Newman JRS, Weissman JS. Genome-wide analysis in vivo of translation with nucleotide resolution using ribosome profiling. Science. 2009;324:218–223. doi: 10.1126/science.1168978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tholstrup J, Oddershede LB, Sørensen MA. mRNA pseudoknot structures can act as ribosomal roadblocks. Nucleic Acids Res. 2012;40:303–313. doi: 10.1093/nar/gkr686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Reuveni S, Meilijson I, Kupiec M, Ruppin E, Tuller T. Genome-scale analysis of translation elongation with a ribosome flow model. PLoS Comput. Biol. 2011;7:e1002127. doi: 10.1371/journal.pcbi.1002127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ciandrini L, Stansfield I, Romano MC. Ribosome traffic on mRNAs maps to gene ontology: genome-wide quantification of translation initiation rates and polysome size regulation. PLoS Comput. Biol. 2013;9:e1002866. doi: 10.1371/journal.pcbi.1002866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cannarozzi G, Schraudolph NN, Faty M, von Rohr P, Friberg MT, Roth AC, Gonnet P, Gonnet G, Barral Y. A role for codon order in translation dynamics. Cell. 2010;141:355–367. doi: 10.1016/j.cell.2010.02.036. [DOI] [PubMed] [Google Scholar]
- 41.Shah P, Ding Y, Niemczyk M, Kudla G, Plotkin JB. Rate-limiting steps in yeast protein translation. Cell. 2013;153:1589–1601. doi: 10.1016/j.cell.2013.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wang M, Weiss M, Simonovic M, Haertinger G, Schrimpf SP, Hengartner MO, von Mering C. PaxDb, a database of protein abundance averages across all three domains of life. Mol. Cell. Proteomics. 2012;11:492–-500. doi: 10.1074/mcp.O111.014704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chan PP, Lowe TM. GtRNAdb: a database of transfer RNA genes detected in genomic sequence. Nucleic Acids Res. 2009;37:D93–D97. doi: 10.1093/nar/gkn787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gruber AR, Lorenz R, Bernhart SH, Neuböck R, Hofacker IL. The vienna RNA websuite. Nucleic Acids Res. 2008;36:W70–W74. doi: 10.1093/nar/gkn188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zenklusen D, Larson DR, Singer RH. Single-RNA counting reveals alternative modes of gene expression in yeast. Nat. Struct. Mol. Biol. 2008;15:1263–1271. doi: 10.1038/nsmb.1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Mathews DH, Disney MD, Childs JL, Schroeder SJ, Zuker M, Turner DH. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc. Natl Acad. Sci. USA. 2004;101:7287–7292. doi: 10.1073/pnas.0401799101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Reis M, Savva R, Wernisch L. Solving the riddle of codon usage preferences: a test for translational selection. Nucleic Acids Res. 2004;32:5036. doi: 10.1093/nar/gkh834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Miyasaka H. The positive relationship between codon usage bias and translation initiation AUG context in Saccharomyces cerevisiae. Yeast. 1999;15:633–637. doi: 10.1002/(SICI)1097-0061(19990615)15:8<633::AID-YEA407>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 49.Arava Y, Wang Y, Storey JD, Liu CL, Brown PO, Herschlag D. Genome-wide analysis of mRNA translation profiles in Saccharomyces cerevisiae. Proc. Natl Acad. Sci. USA. 2003;100:3889. doi: 10.1073/pnas.0635171100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ding Y, Tang Y, Kwok CK, Zhang Y, Bevilacqua PC, Assmann SM. In vivo genome-wide profiling of RNA secondary structure reveals novel regulatory features. Nature. 2013;505:696–700. doi: 10.1038/nature12756. [DOI] [PubMed] [Google Scholar]
- 51.Kwok CK, Ding Y, Tang Y, Assmann SM, Bevilacqua PC. Determination of in vivo RNA structure in low-abundance transcripts. Nat. Commun. 2013;4:2971. doi: 10.1038/ncomms3971. [DOI] [PubMed] [Google Scholar]
- 52.Rouskin S, Zubradt M, Washietl S, Kellis M, Weissman JS. Genome-wide probing of RNA structure reveals active unfolding of mRNA structures in vivo. Nature. 2013;505:701–705. doi: 10.1038/nature12894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Shabalina SA, Spiridonov NA, Kashina A. Sounds of silence: synonymous nucleotides as a key to biological regulation and complexity. Nucleic Acids Res. 2013;41:2073–2094. doi: 10.1093/nar/gks1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gingold H, Dahan O, Pilpel Y. Dynamic changes in translational efficiency are deduced from codon usage of the transcriptome. Nucleic Acids Res. 2012;40:10053–10063. doi: 10.1093/nar/gks772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Dvir S, Velten L, Sharon E, Zeevi D, Carey LB, Weinberger A, Segal E. Deciphering the rules by which 5′-UTR sequences affect protein expression in yeast. Proc. Natl Acad. Sci. USA. 2013;110:E2792–E2801. doi: 10.1073/pnas.1222534110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Mauger DM, Siegfried NA, Weeks KM. The genetic code as expressed through relationships between mRNA structure and protein function. FEBS Lett. 2013;587:1180–1188. doi: 10.1016/j.febslet.2013.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Zhang J, Ferré-D’Amaré AR. Co-crystal structure of a T-box riboswitch stem I domain in complex with its cognate tRNA. Nature. 2013;500:363–366. doi: 10.1038/nature12440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ben-Shem A, de Loubresse NG, Melnikov S, Jenner L, Yusupova G, Yusupov M. The structure of the eukaryotic ribosome at 3.0 Å resolution. Science. 2011;334:1524–1529. doi: 10.1126/science.1212642. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.