In silico prediction of brain exposure: drug free fraction, unbound brain to plasma concentration ratio and equilibrium half-life

Abstract

The focus of CNS drug pharmacokinetics programs has recently shifted from determining the total concentrations in brain and blood to considering also unbound fractions and concentrations. Unfortunately, assessing unbound brain exposure experimentally requires demanding in vivo and in vitro studies.

We propose a physical model, based on lipid binding and pH partitioning, to predict in silico the unbound volume of distribution in the brain. The model takes into account the partition of a drug into lipids, interstitial fluid and intracellular compartments of the brain. The results are in good agreement with the experimental data, suggesting that the contributions of lipid binding and pH partitioning are important in determining drug exposure in brain. The predicted values are used, together with predictions for plasma protein binding, as corrective terms in a second model to derive the unbound brain to plasma concentration ratio starting from experimental values of total concentration ratio. The calculated values of brain free fraction and passive permeability are also used to qualitatively determine the brain to plasma equilibration time in a model that shows promising results but is limited to a very small set of compounds.

The models we propose are a step forward in understanding and predicting pharmacologically relevant exposure in brain starting from compounds’ chemical structure and neuropharmacokinetics, by using experimental total brain to plasma ratios, in silico calculated properties and simple physics-based approaches. The models can be used in central nervous system drug discovery programs for a fast and cheap assessment of unbound brain exposure. For existing compounds, the unbound ratios can be derived from experimental values of total brain to plasma ratios. For both existing and hypothetical compounds, the unbound volume of distribution due to lipid binding and pH partitioning can be calculated starting only from the chemical structure.

Introduction

The assessment of brain penetration is of central importance in the discovery of drugs targeting the central nervous system. The classic approach to determine brain exposure is based on measuring total drug levels in rodents. Total brain levels however, expressed as brain/plasma ratio, are mainly driven by lipophilicity [1,2] and do not necessarily correlate with the in vivo efficacy of the compounds, even when good in vitro potency is observed [3]. A key concept that is not addressed properly in such an approach is that the total brain and plasma concentrations depend on plasma protein and brain tissue binding, and do not reflect the amount of drug that is available to reach the target. For this reason, a new concept has recently emerged that distinguishes rate from extent of brain penetration, and focuses on unbound rather than total drug levels [3] (free-drug hypothesis). The measurement of unbound brain and unbound plasma concentrations is directly related to the amount of drug that is available for target binding, and it has been shown to correlate with CNS activity in some cases [4,5,6,7,8,9,10].

While total levels are easily measured, typically by liquid chromatography and mass spectroscopy, on brain and plasma samples, the direct quantification of the free concentration in brain is possible only through in vivo intracerebral microdialysis [11], a complex and invasive technique that is not practicable in a high throughput manner. For this reason, new methods have been developed to complement the in vivo measure of total levels with in vitro measurement of the free fraction, a corrective term that allows to estimate free drug concentrations starting from total concentrations. The in vitro measure of brain free fraction can be achieved with the brain homogenate [12] or with the brain slice [13, 14] methods. The homogenate method is easier to setup and to perform, and it is the most common method used in the drug industry [15]. Since it uses homogenized tissue, however, it cannot distinguish between different intra- and extra-cellular compartments. On the other hand, the brain slice method is more demanding but keeps the structure of the brain tissue intact, maintaining the differences in concentrations between the interstitial fluid and intracellular compartments during the measurements. Brain homogenate and slice methods both measure drug distribution by two inversely related properties [14]: the fraction of unbound drug in the homogenized tissue (f_u,brain) and the unbound volume of distribution in brain (V_u,brain), respectively. In this work we propose (i) a physical model to calculate in silico the unbound volume of distribution, in order to better understand the processes involved in drug delivery to the brain. We then use the predicted values, together with in silico predicted plasma protein binding, as corrective terms to derive in a second model (ii) the unbound brain to plasma ratios starting from the total ratios. In addition, an attempt to predict the brain to plasma equilibrium half-life for a very small set of compounds is presented (iii), for which preliminary good results are obtained.

Currently, most of the computational tools used to predict brain penetration are quantitative structure-activity relationships (QSARs) methods aimed at predicting total brain to plasma concentration ratios [16, 17, 18]. Only a few have been developed to predict the unbound levels [15, 19, 20] or brain tissue binding [21], due to the complexity of the system and to our limited understanding of the processes involved. Active transport is usually taken into consideration specifically by tools predicting P-glycoprotein binding [22, 23, 24] or by pharmacokineticpharmacodynamic models where parameters are fitted by experimental measurements [25]. Our models are aimed at the prediction of unbound drug levels from chemical structure and attempt to derive key parameters involved in brain drug delivery from a physical point of view, when possible, in order to better understand the mechanisms involved and to provide predictive tools complementary to in vitro and in vivo techniques.

Materials and Methods

Dataset

Compounds with known structure and available experimental values of (i) free drug fractions in brain and in plasma, or (ii) unbound brain to plasma concentration ratios were collected from different sources [5, 12, 13, 15, 26, 27, 28, 29]. The experiments were performed after intravenous doses on mouse and rat, using tissue homogenate, brain slice and microdialysis methods. A total of 146 compounds with experimental values of brain unbound fraction (or unbound volume of distribution) and 133 with experimental values of unbound brain to plasma concentration ratio were collected. Compounds present in more than one dataset were retained as duplicates. Total brain to plasma concentration ratios (K_p) where calculated from AUC values measured in plasma and brain, when available. Unbound brain to plasma concentration ratios (K_p,uu,b) were calculated by correcting total values with free fractions in brain and plasma. For the Ooie dataset [28], the fraction of unbound drug in brain was calculated by dividing the compound concentration in the interstitial fluid (estimated from brain dyalisate) and the total concentration in brain. Seven compounds with experimental data from Liu et al. [30] were used to model the brain equilibrium half-life.

The compounds were downloaded from PubChem [31] when available or generated with Maestro [32], followed by preparation with LigPrep [33]. The logP and QPlogK_hsa descriptors were calculated with QikProp [34]. pKa values were calculated with Epik [35]. Permanent cations were discarded because the calculation of QikProp properties require the compounds to be neutralized.

Unbound volume of distribution (V_u,brain) model

Our V_u,brain model is based on the hypothesis that lipid binding and pH partitioning are the main mechanisms determining the amount of unbound drug in the brain intersititial fluid. Our aim is to test if, under these assumptions, it is possible to adequately predict V_u,brain for a given set of compounds. Other relevant mechanisms that are not included in the current model are active transport (from interstitial fluid to the cells in the brain parenchyma and vice versa) and metabolism, as well as shape and size of the compounds [36].

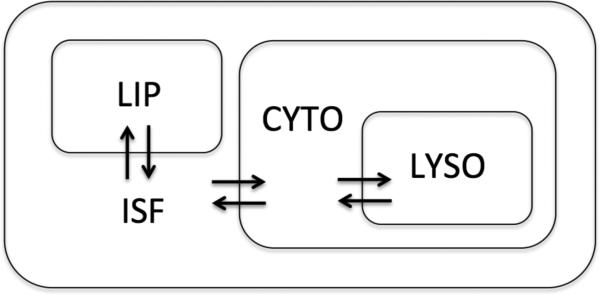
In our study three aqueous compartments are considered: brain interstitial fluid (isf), cytoplasm (cyto) and lysosomes as representative of the cellular acidic compartments (lyso). The pH partitioning component is based on Friden's partition model [15] proposed by the authors in order to reproduce V_u,brain values (measured with the brain slice method) starting from f_u,brain values (measured with the homogenate method):

$$V_{u,brain}=\frac{K_{p,uu,cell}}{f_{u,brain}}$$ (1)

and

$$\begin{array}{cc}\hfill K_{p,uu,cell}=& V_{isf}+K_{p,uu,cyto}\ast \left(V_{cyto}+V_{lyso}\ast K_{p,uu,lyso}\right)\hfill \\ \hfill =& V_{isf}+\frac{1+{10}^{pKa-pHcyto}}{1+{10}^{pKa-pHisf}}\ast \left(V_{cyto}+V_{lyso}\ast \frac{1+{10}^{pKa-pHlyso}}{1+{10}^{pKa-pHcyto}}\right)\hfill \end{array}$$ (2)

where V_u,brain is the unbound volume of distribution as measured by the brain slice method, K_p,uu,cell is the unbound drug partitioning coefficient of the cell, and f_u,brain is the free brain fraction obtained wit the homogenate method. The above equations describe the partitioning of the compounds due solely to different pH in the interstitial fluid and cellular compartments, but they do not include active transport mechanisms. Physiological values are used for pH and relative volumes [15] (pH_isf=7.3; pH_cyto=7.0; pH_lyso=5.0; V_isf=0.2; V_cyto=0.79; V_lyso=0.01). K_p,uu,cell acquires values around 1 for neutral compounds, lower then 1 for acids and higher than 1 for bases.

In addition to the aqueous compartments, a lipid compartment (lip) is included as follows and as shown in Figure 1. In the hypothesis that f_u,brain obtained from the homogenate method estimates primarily non-specific binding, and that non-specific binding is largely due to partitioning between lipid and aqueous environments, we attempt to use in silico predicted values of the octanol-water partition coefficient (logP), corrected by the volume of lipids in the brain, as a surrogate of the experimental f_u,brain. Under these assumptions, we can approximate f_u,brain with the following equation:

$$\frac{1}{f_{u,brain}}\cong \frac{C_{wat}\ast V_{wat}+C_{oct}\ast V_{lip}}{C_{wat}\ast V_{wat}}=1+\frac{C_{oct}}{C_{wat}}\ast \frac{V_{lip}}{V_{wat}}=1+({10}^{logP}\ast 0.12)$$ (3)

where C_wat and C_oct are the concentrations of the compounds in aqueous and lipidic environments at steady state, V_wat and V_lip are the volumes of the aqueous and lipid compartments in the brain tissue, logP is the octanol-water partition coefficient, and the V_lip/V_isf ratio is calculated assuming that lipids occupy 11% of the brain volume [37].

Figure 1.

Compartments considered in this study to compose the brain parenchyma. ISF: interstitial fluid; LIP: lipids; CYTO: intracellular compartment; LYSO: lysosomes.

By combining equations (1), (2) and (3) we obtain a physical model to estimate V_u,brain entirely in silico:

$$\begin{array}{cc}\hfill V_{u,brain}& =\left[V_{isf}+\frac{1+{10}^{kPa-pHcyto}}{1+{10}^{pKa-pHisf}}\ast \left(V_{cyto}+V_{lyso}\ast \frac{1+{10}^{pKa-pHlyso}}{1+{10}^{pKa-pHcyto}}\right)\right]\hfill \\ \hfill & \ast [1+({10}^{logP}\ast 0.12)]\hfill \end{array}$$ (4)

Values of logP and pKa are calculated with QikProp and Epik, respectively.

Unbound brain to plasma concentration ratio (K_p,uu,b) model

Unbound brain exposure is assessed by K_p,uu,b, which can be derived by total exposure with the following equation [3]

$$K_{p,uu.b}=K_p\ast \frac{f_{u,b}}{f_{u,p}}$$ (5)

where K_p,uu,b, is the unbound brain to unbound plasma concentration ratio, K_p is the total brain to plasma concentration ratio (measured as AUC_brain/AUC_plasma), f_u,b is the free fraction in brain, and f_u,p is the free fraction in plasma. We used each term of equation (5), in logarithmic form, to build a regression model where the coefficients are fitted to experimental values of K_p and calculated values of f_u,b and of f_u,p in order to reproduce observed K_p,uu,b values:

$$\log \left(K_{p,uu,b}\right)=a+b\log \left(K_{p,exp}\right)+c\log \left(f_{u,b}\right)-d\log \left(f_{u,p}\right)$$ (6)

where

$$f_{u,b}={\left[\frac{1}{V_{u,brain}}\right]}_{range[0,1]}and$$ (7)

Since the value of the free fraction in brain or plasma is a number between 0 and 1, we scale the calculated f_u,b and f_u,p values to be comprised in the range [0, 1]. When f_u,b or f_u,p is equal to 0, the value of log(f_u,b) or log(f_u,p) is set to the minimum finite value. Values of V_u,brain are calculated with (4) and values of QPlogK_hsa are human serum albumin predictions performed with QikProp. The coefficients a, b, c and d are parameters fitted with the least square method through the generalized linear models module of R2.13.0 [38]. All the plots are also produced with R. The goodness of fit is measured by the coefficient of determination (R²):

$$R^2=1-\frac{RSS}{TSS}=1-\frac{{\Sigma }_1^n{(y_i-\widehat{y})}^2}{{\Sigma }_1^n{(y_i-\stackrel{‒}{y})}^2}$$ (9)

where RSS is the residual sum of square, TSS the total sum of squares, y_i is the experimental value of the molecule i, ŷ is the value predicted by the model built on the training set and ȳ is the average experimental value of the training set.

Equilibrium half-life model

Liu et al. [30, 39] proposed to quantify the time required by a drug to achieve brain equilibrium by the intrinsic brain equilibrium half-life (t_1/2eq,in), which is inversely correlated with permeability and free fraction in brain:

$$t_{1∕2eq,in}\propto \frac{1}{PS\ast f_{u,b}}$$ (10)

where PS is the permeability-surface area product and f_u,b is the free fraction in brain. We attempt to qualitatively determine the intrinsic brain equilibrium half-life entirely in silico, by calculating f_u,b with equations (4) and (7), and PS with the physical model of passive membrane permeation from Leung et al. [40]. Since the permeability coefficient calculated by the model from Leung et al. is a general measure of passive membrane permeability that is not fitted to reproduce the permeability-surface area product, the values of calculated passive permeability have been scaled in the range of the PS values measured for the studied compounds [30] (max value=1024 ml*h^-1*kg^-1; min value=6.4 ml*h^-1*kg^-1).

Results and Discussion

Unbound volume of distribution (V_u,brain) model

V_u,brain is an apparent volume term that indicates how much of a compound is distributed in the interstitial fluid, compared to both the amounts entering into interstitial fluid and intracellular compartments [3]. Depending on whether the target of interest is present in the interstitial fluid or inside the brain cells (neurons, astrocytes, pericytes), it would be desirable to tune the value of V_u,brain accordingly. Small values of V_u,brain (0.2 ml/g brain) indicate that the compound is primarily present in the interstitial fluid; higher values (0.8 ml/g brain) indicate that the compound is distributing between interstitial fluid and intracellular compartments; very high values (>0.8 ml/g brain) indicate non-specific binding [3]. A predictive tool for V_u,brain would be beneficial in this context.

Since our model includes partitioning into cellular compartments, the performance of the model is better evaluated through comparison with measurements by the slice method rather then those by the homogenate method. For this reason, we applied equation (4) to Friden's library [15] to predict V_u,brain obtained with the slice method. The calculated values show a good correlation (R²=0.70) with the experimental values (see Table 1 and Figure 2), especially considering that no parameter has been fitted to the model. The equation is derived only from the physical principles that we hypothesize describe the major contributions affecting the free drug fraction in brain: lipid binding and pH partitioning. The correlation of logP alone with the experimental data (R²=0.52) indicates that logP provides a good, albeit crude, estimate of brain non-specific binding. By including pH partitioning, we can significantly improve the correlation for this set of data, suggesting that pH partitioning indeed plays an important role in brain distribution.

Table 1.

Correlations on the different data sets used between experimental and predicted V_u,brain values provided by our physical model.

# Compounds	Reference	Type of data	R2
52	Friden 2011	Slice	0.70
33	Maurer 2005	Homogenate	0.69
12	Becker 2006 + Ooie 1997	Slice, Microdialysis	0.79
34	Kalvass 2007	Homogenate	0.32
15	Summerfield 2006	Homogenate	0.13
146	All data sets	Slice, Homogenate	0.55

Figure 2.

Experimental and predicted log(V_u,brain) for the partition model on the Friden's dataset. The solid line indicates the trend between predicted and experimental values calculated on all data sets, the dotted lines are drawn at one logarithmic unit from the trend line. Predicted values are computed from chemical structure alone, with no adjustable parameters.

The slope of the fitted line is smaller then one (0.43), indicating that the calculated values span a broader range relative to the experimental data. This behaviour is due to the fact that the single factors contributing to the calculated V_u,brain have not been weighted to fit the experimental data. A possible improvement in prediction could be obtained by training our model with experimental data, with the potential disadvantage of lower transferability. Given the reasonable correlation obtained, we prefer to keep the model independent from any dataset and aim at a broader applicability. Another possibility for improving our model would be to include active transport, both uptake and efflux, which due to its complex nature is not accounted for by the present model.

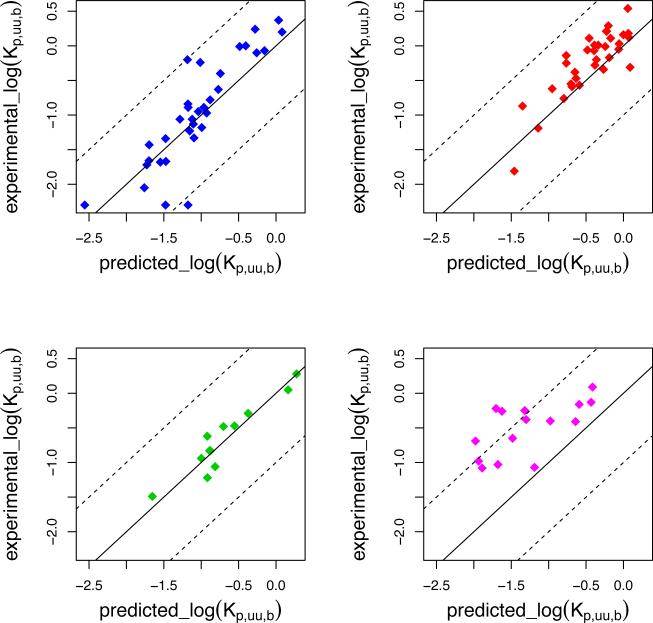
We then tested our model on several other data sets, including data obtained with the homogenate method. The correlations with experimental data, reported in Table 1 and Figure 3, indicate that the model has a good predictive power for most of the data sets. The Ooie dataset contains only 4 compounds and was therefore merged with the Becker dataset. The model has a lower correlation coefficient for the Kalvass and Summerfield data sets, implying that, for those sets, factors other than logP and pH partitioning might be required to explain the measurements. For the Kalvass dataset indeed, active transport can explain the under-predicted values for 5 compounds: digoxin, doxorubicin, ivermectin, nelfinavir and saquinavir, which have been shown to interact with P-glycoprotein [41]. The remaining compounds of the dataset are all within or slightly exceed (vinblastine) one logarithmic unit from the trend line. From the Summerfield dataset, only one compound (ciglitazone) is largely under-predicted but no information about active efflux was found.

Figure 3.

Experimental and predicted log(V_u,brain) for the partition model on several data sets: Kalvass, blue; Maurer, red; Becker+Ooie, green; Summerfield, magenta. The solid line indicates the trend between predicted and experimental values calculated on all data sets, the dotted lines are drawn at one logarithmic unit from the trend line. Predicted values are computed from chemical structure alone, with no adjustable parameters.

Unbound brain to plasma concentration ratio (K_p,uu,b) model

K_p,uu,b is a measure of the extent of the distribution of the unbound compound between brain and plasma [3]. Values close to one indicate passive diffusion across the blood brain barrier, values greater than one indicate uptake, and values less than one indicate efflux from the blood brain barrier. Given the abundance of K_p values in the literature, it would be of interest to infer K_p,uu,b values from K_p without performing additional experiments. Here we calculate unbound levels (K_p,uu,b) using equation (6), starting from experimental total levels (K_p) and free fractions in brain and plasma (f_u,b, f_u,p) calculated in silico. By using Friden's dataset as a training set to fit the parameters of our model, we obtain a good correlation between experimental and predicted values for these compounds (R²=0.79, Figure 4). To check the predictive ability of our model, we apply it to calculate K_p,uu,b values for all of the remaining data sets: the prediction rate is high for Kalvass (R²=0.74, 27 compounds), Maurer (R²=0.82, 33 compounds) and Becker and Ooie (R²=0.89, 12 compounds) data sets. Like in the case of the V_u,brain model, the correlation coefficient is low for the Summerfield dataset (R²=-2.2, 15 compounds). However, only for three compounds (flurbiprofen, ibuprofen and naproxen) the error in prediction is largely exceeding one logarithmic unit. An improved correlation (R²=0.57) can be obtained for this set by parametrizing the model separately. The performance of the model is particularly good considering that only 30% of the data (40 compounds from the Friden data set) were used to train the model and 70% of the data (93 compounds coming from different sources) were used to test the predictive power of the model. In all cases, we observe an improvement in correlation when using our model instead of using the K_p values alone (the correlation between K_p,uu,b and K_p is R²=0.62 on all the data sets combined). The predictions for all compounds are shown in Figure 4 and 5.

Figure 4.

Experimental and predicted K_p,uu,b values for the model on Friden dataset, used as a training set. The solid line indicates the agreement between experimental and predicted values and the dotted lines are drawn at one logarithmic unit difference.

Figure 5.

Experimental and predicted K_p,uu,b values for the model on several data sets, used as test sets: Kalvass, blue; Maurer, red; Becker+Ooie, green; Summerfield, magenta. The solid line indicates the agreement between experimental and predicted values and the dotted lines are drawn at one logarithmic unit difference.

Equilibrium half-life model

The time needed by a drug to reach equilibrium in the brain is inversely related to permeability and free brain fraction [30]. By calculating permeability and free brain fraction in silico, we built a model that is able to correctly distinguish slow from fast equilibrating molecules for 6 out of 7 compounds from the study of Liu et al. [30] (Figure 6). These compounds were administered subcutaneously, which allows a relatively constant blood level, well suited for steady-state measurements. The slower compounds, fluoxetine and CP-141938, which both need one hour to reach brain equilibrium after subcutaneous dose, are correctly classified as slower molecules by our model, while caffeine, propranolol, theobromine and theophylline, which equilibrate quickly in 0.1 hours, are also correctly identified as faster molecules. The compound NFPS (N[3-(4′-fluorophenyl)-3-(4′-phenylphenoxy)propyl]sarcosine) is the slowest compound to reach the equilibrium and it is not correctly classified by our model. Our predictions are only qualitative and, more importantly, seven compounds are too few to draw any solid conclusion. However, preliminary results are encouraging and an application to a bigger dataset is underway to validate our model.

Figure 6.

Observed experimental equilibrium half-life plotted against the product of in silico calculated permeability and free brain fraction. Red circles: rapidly equilibrating compounds (observed t_1/2eq=0.1 hours: caffeine, propranolol, theobromine, theophylline). Orange squares: medium equilibrating compounds (observed t_1/2eq=1 hour: Fluoxetine and methoxy-3-[(2-phenylpiperadinyl-3-amino)-methyl]-phenyl-N-methyl-methane-sulfonamide). White triangle: slowly equilibrating compound NFPS.

Conclusions

We presented a simple physical model to predict the unbound volume of distribution in brain (V_u,brain) from chemical structure, which was validated on several data sets. The model is based on predicted lipid binding and pH partitioning in interstitial fluid, intracellular and lysosomal compartments. It does not include fitted parameters and it is therefore independent of the dataset used. Even if the model does not include active transport processes, the good predictions observed for numerous data sets confirms that lipid binding and pH partitioning are important aspects of brain exposure. To our knowledge, the presented model is the first published in silico model for predicting the unbound volume of distribution in brain.

A second model, based on the calculated values of unbound volume of distribution and free fraction in plasma, was developed to derive unbound brain to plasma concentration ratios (K_p,uu,b) starting from experimental values of total ratios. The use of calculated brain and plasma free fractions is shown to improve the predictions over a model that uses K_p alone. Our model, trained on a dataset of 40 compounds, produced good agreement on several external sets, where the experimental values were determined in different laboratories and even using different methods, suggesting that the model is general and is minimally dependent on the specific training set.

Finally, a model that predicts brain equilibrium half-life by the use of calculated permeability coefficient and calculated brain free fraction is proposed. The preliminary results obtained for a small dataset of 7 compounds are encouraging.

Future developments are underway to improve the in silico tools for designing drugs targeting the central nervous system, with the aim of identifying and quantifying the most important processes involved in determining the rate and extent of brain exposure. For example, the effects of active transport across the blood brain barrier and metabolism require further investigation, and incorporating these aspects into the presented model is likely to be beneficial in improving the accuracy of predicting K_p,uu,b in silico.

Abbreviations

AUC

area under the curve

f_u,brain

fraction of unbound drug in brain

f_u,plasma

fraction of unbound drug in plasma

icf

intracellular fluid

isf

interstitial fluid

lip

lipidic compartment

K_p

total brain to plasma concentration ratio

K_p,uu,b

unbound brain to unbound plasma concentration ratio

K_p,uu,cell

unbound drug partitioning coefficient of the cell

logP

logarithm of the octanol water partition coefficient

PS

permeability-surface area product

QPlogK_hsa

prediction of binding of human serum albumin

t_1/2eq

equilibrium half-life

V_u,brain

unbound volume of distribution