Abstract
The aortic stiffness has been found to be a useful independent indicator of several cardiovascular diseases such as hypertension and aneurysms. Existing methods to estimate the aortic stiffness are either invasive, e.g. catheterization, or yield average global measurements which could be inaccurate, e.g., tonometry. Alternatively, the aortic pulse wave velocity (PWV) has been shown to be a reliable marker for estimating the wall stiffness based on the Moens–Korteweg (M–K) formulation. Pulse Wave Imaging (PWI) is a relatively new, ultrasound-based imaging method for noninvasive and regional estimation of PWV. The present study aims at showing the application of PWI in obtaining localized wall mechanical properties by making PWV measurements on several adjacent locations along the ascending thoracic to the suprarenal abdominal aortic trunk in its intact vessel form. The PWV estimates were used to calculate the regional wall modulus based on the M-K relationship and were compared against conventional mechanical testing. The findings indicated that for the anisotropic aortic wall, the PWI estimates of the modulus are smaller than the circumferential modulus by an average of −32.22% and larger than the longitudinal modulus by an average of 25.83%. Ongoing work is focused on the in vivo applications of PWI in normal and pathological aortas with future implications in the clinical applications of the technique.
1. Introduction
Changes in the vascular mechanical properties such as the increase in the aortic stiffness may prove to have a significant contribution to the onset and progression of cardiovascular diseases such as systolic blood pressure (Safar, 1989), coronary events and stroke in hypertensive patients (Laurent et al., 2003), calcification (Verbeke and et al., 2010) and aortic aneurysms (Fujikura et al., 2007; He and Roach, 1994). Collectively, there has been a consensus that assessing arterial stiffness should be part of the routine clinical procedures (Mancia and et al., 2007). Methods for measuring arterial stiffness typically fall into two broad categories. The first set of methods is based on radial pulsation such as diameter–pressure data. A major drawback in using these methods is a requirement of the central pressure either invasively by catheterization (Danpinid et al., 2010; Nichols and O’Rourke, 2005; Nichols and McDonald, 1972; Wells et al., 1998) or with low accuracy using empirical transfer functions (Khamdaeng et al., 2012; O'Rourke et al., 2002). The next set of methods are based on measuring the longitudinal aortic pulse wave velocity(PWV) which has been shown to be related to the underlying tissue stiffness through the Moens–Korteweg (M–K) equation (Korteweg, 1878; Moens, 1878) and has been used in a variety of applications (Fung, 1997; Kinsler et al., 2000; Olufsen, 1999). The quantitative stiffness measurements based on the M–K relationship could be inaccurate in applications where the underlying assumptions, e.g. infinitely long, straight and circular cylinder with elastic thin walls, etc., are not met (Fung, 1997; Nichols and O’Rourke, 2005). However, the qualitative relationship between the wall modulus and PWV remains valid and forms the basis of the wall stiffness estimation methods.
Among different methods proposed for the noninvasive estimation of PWV (O'Rourke and Franklin, 2006), the current clinical gold standard is to obtain the global PWV based on the temporal pulse pressures at two remote sites, e.g. carotid and femoral (Laurent et al., 2006). The time between the two ECG–synchronized waveforms (Chiu and Shroff, 1991) is divided by the over–the–skin measured distance between them to estimate the global PWV. Such methods are at the core of clinical studies involving the measurement of arterial stiffness (Lantelme et al., 2002; Millasseau et al., 2005). Similarly, studies have shown the applications of two pressure catheters placed at a known distance for measuring the pressure wave speed on open-chest dogs in situ (Greene and Gerson, 1985; Nichols and McDonald, 1972), and sheeps in vivo and in vitro (Wells et al., 1998). However, existing drawbacks of the carotid–femoral PWV method can largely impair its accuracy. For instance, lack of knowledge of the exact arterial geometry and the assumption of a single longitudinal flow direction may lead to underestimating/overestimating the true distance (Vappou et al., 2010a). More importantly, changes in wall stiffness and PWV under most pathological conditions have been shown to be localized (Choke et al., 2006; Nichols and O’Rourke, 2005; Vande Geest et al., 2008) and may not be detected via global PWV estimates (Shahmirzadi and Konofagou, 2012). Details of the fundamental limitations of such methods can be found elsewhere (Segers et al., 2009).
Different imaging modalities such as ultrasound (Benthin et al., 1991; Brands et al., 1998; Couade et al., 2011; Danpinid et al., 2010; Eriksson et al., 2002; Hartley et al., 1997; Hermeling et al., 2007; Hoctor et al., 2007; Khamdaeng et al., 2012; Meinders et al., 2001; Rabben et al., 2004; Williams et al., 2007) and MRI (Boese et al., 2000; Bolster et al., 1998; Macgowan et al., 2002; Shao et al., 2004; Yu et al., 2006) have been used for noninvasive imaging of the arterial wall at multiple time points to track the propagation of the transient vibrations along the arterial wall in 2D and to estimate the PWV; in some cases, along with simultaneous pressure measurements to determine parameters such as augmentation index and modulus. More recently, the ultrasound–based method of Pulse Wave Imaging(PWI) has been developed to fully analyze the wave propagation with high temporal and spatial resolutions and to measure the regional PWV. The reliability of the PWI has been assessed in normal and aneurysmal mouse (Fujikura et al., 2007; Luo et al., 2009) and human aortas in vivo (Luo et al., 2008; Vappou et al., 2010b; Wang et al., 2008), human carotid in vivo (Luo et al., 2012), aneurysmal and hypertensive patients (Li et al., 2011; Li et al., 2012a), canine aorta ex vivo (Shahmirzadi et al., 2012), experimental phantoms (Shahmirzadi et al., 2012; Vappou et al., 2010a), in fully–coupled fluid– structure interaction(FSI) aortic simulations (Shahmirzadi and Konofagou, 2012; Shahmirzadi et al., 2012; Vappou et al., 2008), and in comparison against applanation tonometry (Vappou et al., 2011a).
Measuring regional wall properties is a significant advantage of the PWI method, distinguishing it from other global PWV estimation alternatives. While variations among different species have been previously reported (Danpinid et al., 2010; Han and Fung, 1995a; Han and Fung, 1991; Liu and Fung, 1989), it has been shown that the mechanical and geometrical properties of the aortic wall vary along the longitudinal direction on the aorta from the proximal(to the heart) toward the distal regions. Han et al. used a normalized coordinate system describing each longitudinal location on different aortas by the distance from the thoracic end, x, divided by the total length of the aortic trunk, L (Han and Fung, 1995b), and have applied uniaxial mechanical testing of the thoracic segment, defined as x/L ≈ 0.2–0.8, in the longitudinal direction in situ (Han and Fung, 1995a). Similar to the observations on circumferential residual stress when cut radially (Chuong and Fung, 1986; Hesses, 1926; Shahmirzadi et al., 2008; Vaishnav and Vossoughi, 1983), a longitudinal cut of the aorta has also shown the existence of the longitudinal residual stretch in the canine and porcine aortas (Rachev and Greenwald, 2003; Vossoughi, 1992) with a maximum occurring at x/L ≈ 0.8 (Han and Fung, 1995a). For a constant stretch ratio, a 54% increase in stress was reported at the distal wall compared to the proximal wall of an elastin–purified porcine aorta which was translated into a 30–40% increase in the modulus (Lillie and Gosline, 2007), and was explained in part by the increase in the elastin content (Indik et al., 1987; Lillie and Gosline, 2007). It has also been shown that both the longitudinal strain and the cross section area decrease from proximal to distal locations in canine aorta ex vivo (Bergel, 1961), and in pressurized rabbit thoracic aortas in situ (Sugawara et al., 1997); the latter study has shown non-uniform variations in longitudinal strain. Given the biaxial state of physiological loading, wall modulus has been obtained in vivo by measuring the pressure–diameter relationship for canine (Gow and Taylor, 1968) and murine (Danpinid et al., 2010) aortas. Other studies have been shown to obtain wall modulus of rabbit carotid and abdominal arteries (Fonck et al., 2007; Fronek et al., 1976; Wolinsky and Glagov, 1964) and human thoracic descending aortas (Groenink et al., 1999) under a similar biaxial loading by applying internal pressure in situ. Lu et al. has used an independently controlled pressurizing-stretching machine to characterize the circumferential and longitudinal properties of porcine coronary arteries (Lu et al., 2003). Applications of multiple radially– and axially–mounted piezoelectric elements have been shown successful in measuring the longitudinal and circumferential properties of pressurized urethane tubes and porcine arteries in vitro (Bernal et al., 2011). In order to obtain the modulus of the wall under residual stress, Apter et al. performed uniaxial testing of closed ring segments from canine pulmonary arteries (Apter et al., 1966). Characterizing the mechanical behavior of vascular tissues under uniaxial loading has been widely used and found to properly describe the tissue mechanical properties (Haslach, 2005; Holzapfel, 2006; Shahmirzadi et al., 2013). In this study, we will assess the capability of PWI to capture the regional changes in the aortic wall stiffness by estimating the regional PWV on adjacent locations along the thoracic–abdominal trunk of canine descending aortas in its intact vessel form. The wall stiffness measurements from PWI will be validated against conventional mechanical testing results.
2. Materials and Methods
2.1. Sample Preparation
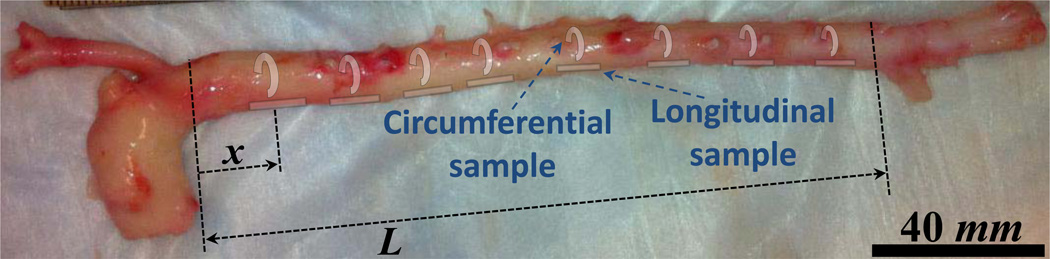
Descending aortas from male mongrel dogs between the thoracic (post–arch) and infrarenal abdominal locations were freshly excised immediately after animal euthanasia (weight 20–25 kg, total ex vivo length L = 177.50±23.45 mm; n=8) and were preserved in phosphate–buffered saline (PBS) at all times during the experiments. A normalized coordinate system was set on individual aortas describing each longitudinal location by the distance from the thoracic end, x, divided by L (Fig.1). Based on this normalized coordinate system, x/L = 0 and 1 indicate the thoracic (proximal) and abdominal (distal) ends, respectively.
Figure 1.
Example image of a canine aorta indicating the normalized coordinate system: x and L are the axial location of each point under study and the total length of the aortic trunk ex vivo, respectively. Also, the schematics of excised circumferential and longitudinal samples from multiple locations –to be used for consequent mechanical testing– are shown in the figure.
2.2. Pulse Wave Imaging
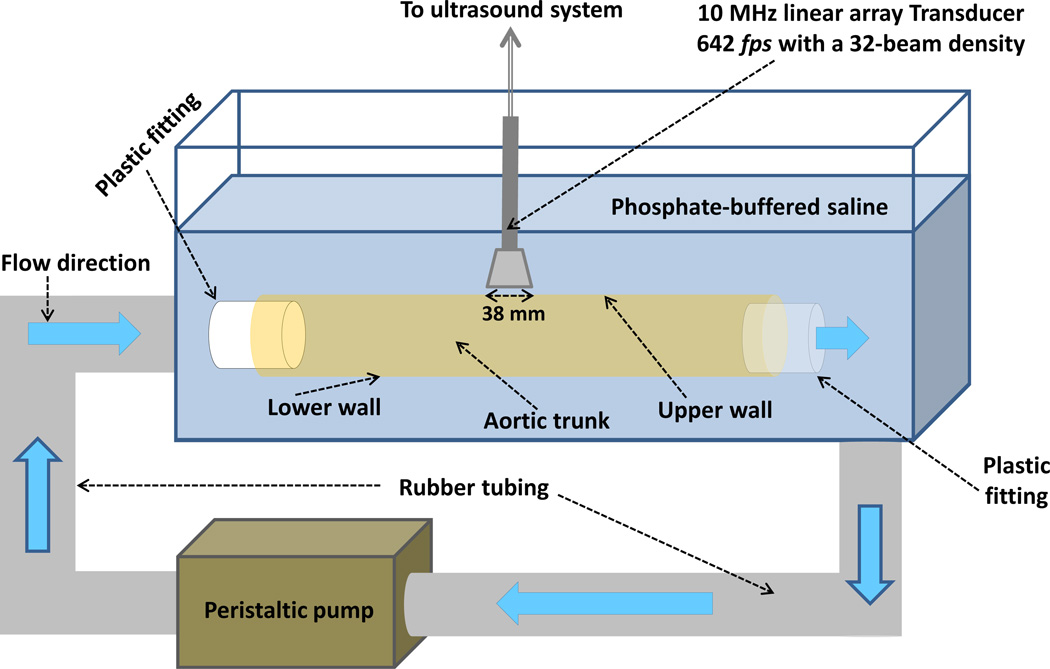
Figure 2 depicts the schematics of a customized experimental set up which was used to perform the PWI on the canine aortas in its intact vessel form ex vivo. The aortic trunk was kept inside a PBS bath and secured at its ends on two fittings. The inlet of the aorta was connected to a peristaltic pump (Manostat Varistaltic, Barrington, IL) providing a sinusoidal flow of V − V0 sin (2πft) − 4 sin (2π(1.5)t) cm/s through the lumen and causing a wall periodic motion. The wall displacement was imaged using an ultrasound system and the PWV was obtained based on the spatio-temporal map of the wall displacement as explained in Appendix A.1.
Figure 2.
Schematic of the PWI experimental set up for the canine aorta ex vivo. A peristaltic pump was used to induce pulsatile motion in the wall of the aortic trunk, and an ultrasound system was used to image the wave propagation along the upper wall.
2.3. Geometry and Density Measurements
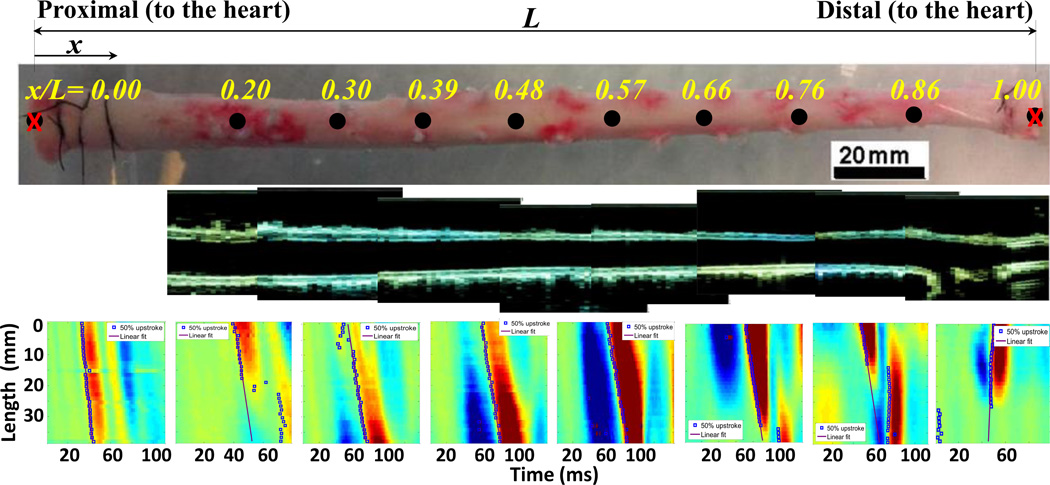
The same ultrasound B-mode images were used to measure the lumen diameter and wall thickness at each location used for PWV calculations, (Fig. 3). To minimize the measurement error due to geometry variations in the lumen, an average of three separate measurements of diameter and thickness was used from each image segment. Consequently, the aortic wall was excised at the same imaged locations in order to prepare circumferential samples (n=48) of w = 6.52±1.21 mm, l = 11.33±3.24 mm and h = 1.54±0.27 mm, and longitudinal samples (n=13) of w = 6.09±1.43 mm, l = 10.48±2.97 mm and h = 1.53±0.33 mm (Fig.1). The density of each sample was obtained by separate measurements of the volume using a graduated cylinder of 1 mL precision (Fisher Scientific, Pittsburgh, PA) and the mass using a digital scale of 0.1 g precision (Ohaus®, Pleasant Prairie, WI).
Figure 3.
(Row 1): An illustration of the aortic trunk between the proximal (x/L=0) and distal (x/L=1) locations and eight selected points along the aorta. (Row 2): The B-mode images at each of the same aorta trunk indicating the top and bottom walls. (Row 3): The wall displacement spatio-temporal plots at each of the above locations, obtained by the PWI.
2.4. Modulus Estimation
The geometry, density and PWV measurements were used with the thick–wall M–K equation to obtain the wall modulus estimates from PWI method (Appendix A.2). For comparison purposes, cyclic uniaxial tensile mechanical testing was performed on the previously extracted circumferential and longitudinal samples, separately, (Appendix A.4). The inter- and intravariations of regional modulus estimates were obtained as explained in Appendix A.5.
3. Results
Figure 3 provides a snapshot of the PWI results obtained from one of the aortas. The first row shows an example of aortic trunk (top view) marked at 8 equally separated sites from proximal to distal with normalized coordinates as follows: x/L = 0.20, 0.30, 0.39, 0.48, 0.57, 0.66, 0.76 and 0.86. As indicated, no PWI measurement was made at the very end points due to boundary effects by the fittings. The second row illustrates the B-mode images of the upper and lower walls (side view) at each of the above locations that were used for geometrical measurements. The third row shows the corresponding spatio-temporal maps of the upper wall displacement at each location, along with the propagation of the 50% upstroke points and the linear fit to them, slope of which is the PWV.
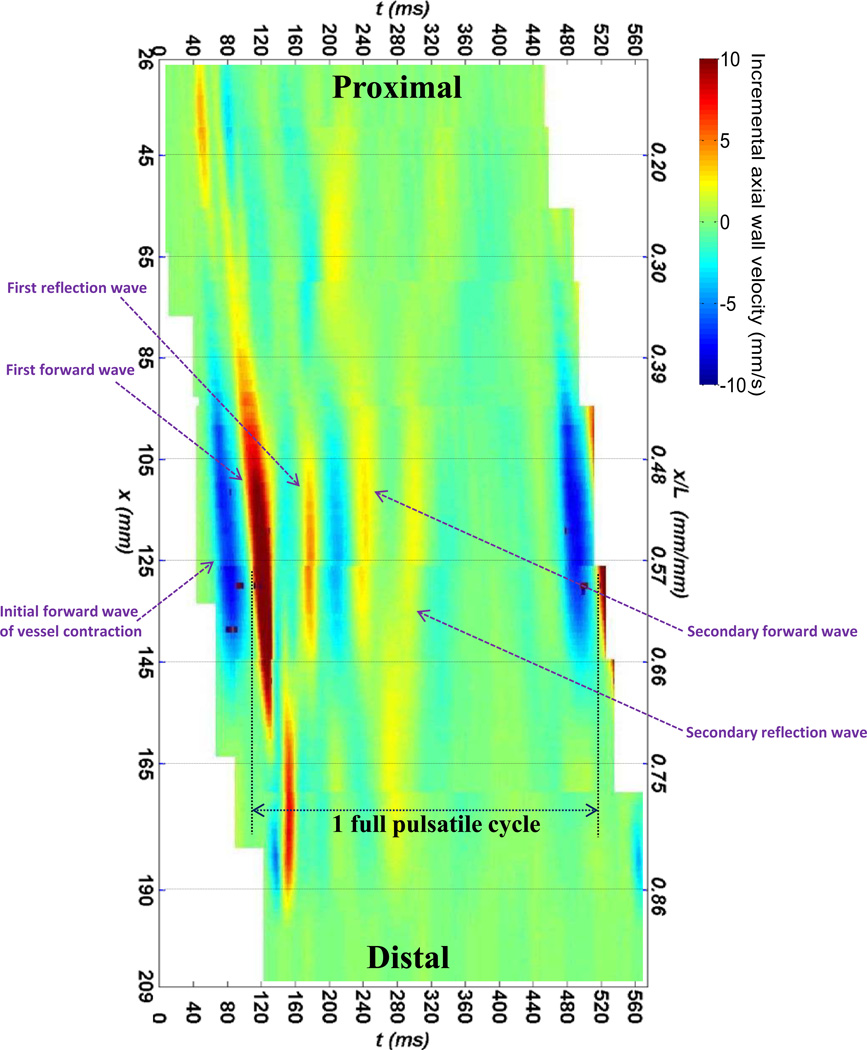
Figure 4 illustrates a full spatio–temporal map of the upper wall displacement from the entire aortic trunk, by merging the regional spatio-temporal plots from each of the eight different locations shown in Fig. 3. This spatio–temporal plot allows for tracking of the wall motion and understanding the patterns of pulse wave propagation, globally. It particularly shows a full cycle of forward and backward traveling of a pulse wave along the aortic trunk, followed by a similar full cycle traveling of a secondary wave with a lower wave magnitude due to wave energy attenuation.
Figure 4.
A spatio-temporal plot of the wall displacement extended over the entire aortic length, obtained by combining all the eight spatio-temporal plots from adjacent locations given in Fig. 3 (row 3).
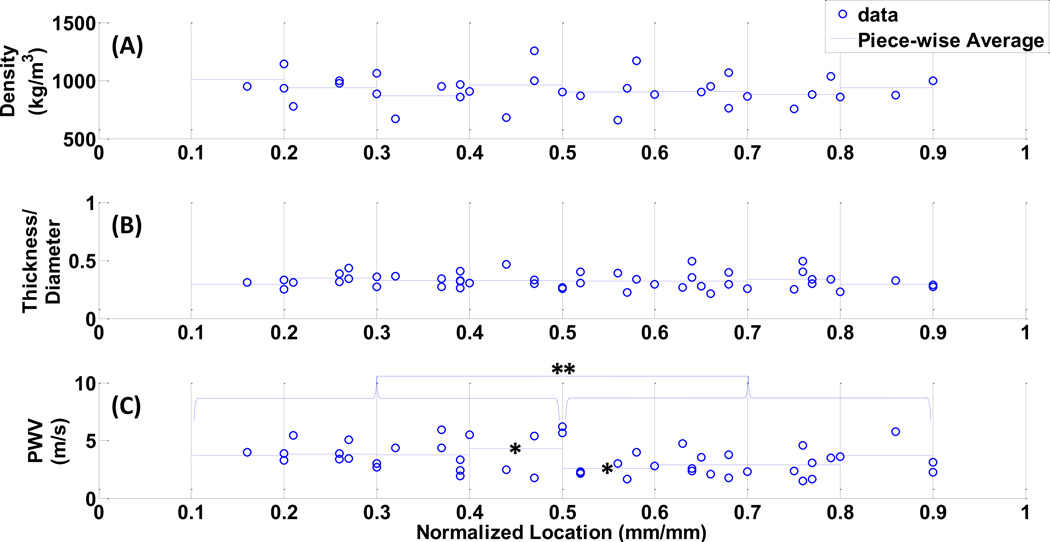
The entire set of density, h/di and PWV measurements are shown in Fig. 5. The results show only slight variations of density and h/di, measuring an average of 925.23 ± 45.06 kg/m3 and 0.32 ± 0.01, respectively, across the entire length with no statistical significance between regional measurements. For the PWV estimates, it should be noted that different patterns of variations were obtained on individual dog specimens. On the average, no statistical significance was obtained between individual regional measurements. However, the difference between the PWV estimates from upper–mid thoracic (i.e. x/L = 0.1–0.5) and suprarenal abdominal (i.e. x/L = 0.5–0.9) were found to be highly statistically significant (p=0.006), (Fig. 5.C).
Figure 5.
The spatial variations in the (A)wall density, (B)the h/di, and the (C)PWV, obtained on the canine aortas. The * and ** indicate the statistical significance of p=0.0064 and p=0.06, respectively.
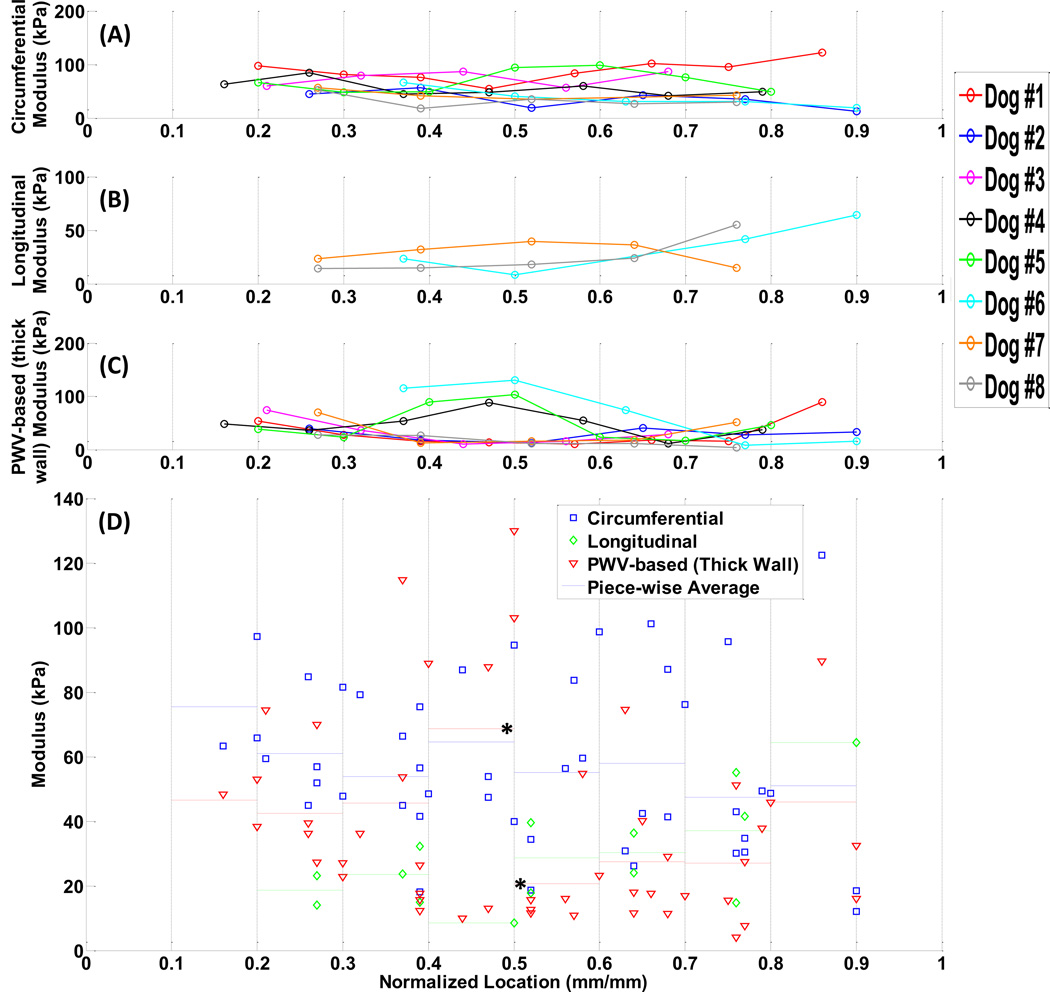
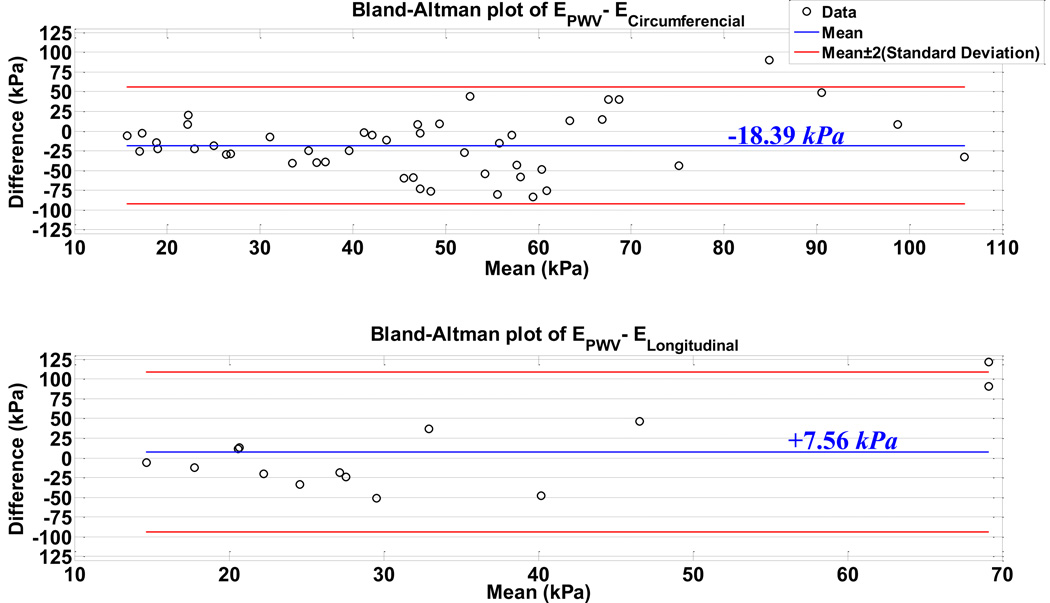
Based on the measurements in Fig. 5, the modulus estimates from individual specimens (n=8) are illustrated in Figs. 6.A–6.C: (A)mechanical testing on circumferential samples, (B)mechanical testing on longitudinal samples (only on last three dogs), (C)PWI examination. It is seen that the regional variations in the modulus are different across animals. The measurements by the PWI method were found to be more consistent and reproducible from most animals (Fig. 6.C). Figure 6.D shows the combined data of modulus measurements along with separate piece-wise average values. In order to compare the PWI results to those with mechanical testing, the Bland-Altman plots of the PWV-based modulus estimates versus circumferential and longitudinal modulus measurements are shown in Fig. 7.
Figure 6.
The spatial variations in the modulus measured on each single dog specimen (n=8). (A)circumferential samples, and (B)longitudinal samples, obtained by mechanical testing, (C)PWV-based obtained by PWI, (D)All methods, combined, along with piece-wise average values in each method. The * indicates statistically significant data (p<0.05).
Figure 7.
Bland-Altman plots of the PWV-based modulus estimation versus the mechanical testing measurements on (A)circumferential, and (B)longitudinal. The blue line indicates the difference mean, and the red lines indicate the twice standard deviation upper and lower bounds to the difference mean.
Additionally, Table 1 lists the results of PWV and geometrical measurements obtained from the aortas under longitudinal stretch ex vivo (Appendix A.3). The h/di is found to remain nearly constant, however, the PWV estimates change up to 2.15–fold for the maximum tested longitudinal strain of 41.10%.
Table 1.
Geometrical and PWV estimates on the canine aortas under longitudinal stretch ex vivo (n=4).
| Longitudinal Strain (%) |
0 | 6.66±0.16 | 13.48±0.18 | 20.30±0.35 | 34.08±0.16 | 40.14±1.26 |
|---|---|---|---|---|---|---|
| h/di (mm/mm) | 0.33±0.11 | 0.31±0.07 | 0.32±0.05 | 0.32±0.07 | 0.32±0.05 | 0.31±0.08 |
| PWV (m/s) | 2.44±0.36 | 2.82±0.89 | 3.54±1.44 | 4.09±1.15 | 4.78±0.68 | 5.25±2.25 |
4. Discussion
Disadvantage of global PWV measurements, such as femoral–carotid, is previously discussed considering that the majority of the vascular diseases induce localized changes (Choke et al., 2006; Palmieri and et al., 2011). This study reports the use of Pulse Wave Imaging (PWI) –a recently developed method by our group– to characterize the axial regional variations in PWV and wall stiffness of intact vessel–form canine aortas ex vivo. The primary aim in using the PWI is to noninvasively detect the wall heterogeneities in applications where invasive mechanical characterization can not be obtained such as pathological aortas in vivo. For that matter, qualitative assessment of the localized changes in the modulus carries as much significance as the quantitative results do.
The spatial changes in the wall modulus of aortic trunk when moved from upper–thoracic toward mid–thoracic and further down toward suprarenal abdominal regions obtained here prove the PWI capable of describing the localized change in wall stiffness. The effective application of PWI is relied on the correlation between the E and the PWV2, allowing detection of the localized changes in stiffness based on the PWV estimation. This assumption is largely valid given that it has both reported by others and verified in this study, (Fig. 5), that the variations in other tissue properties are negligible compared to that in E. Indeed, the geometrical variations –as measured by h/d– were shown to be extremely minimal both along the unstretched aortic trunk (Fig. 5.B) and during its stretching (Table 1). Based on both PWI and mechanical testing findings, both methods were found to indicate the regional variations in mechanical properties of canine descending aorta (Fig. 6). Quantitatively, the modulus estimates by PWI were found to lie between the circumferential and longitudinal moduli of the anisotropic aortic wall, as indicated by the average difference of –18.39 kPa (–32.22%) and +7.56 kPa (+25.84%) from circumferential and longitudinal modulus measurements, respectively (Fig.7). It is also seen that compared to those from mechanical testing, the PWI results are more consistent across different aortas demonstrating the reproducibility of the method (Figs. 6.A–6.C). Similar quantitative difference between the PWV–based and conventional methods has also been reported in previous studies (Shahmirzadi and Konofagou, 2012; Vappou et al., 2010a; Vappou et al., 2011b; Vappou et al., 2008) and can be explained largely based on a variety of factors associated with the different testing protocols in each method. For instance, PWI is performed on vessel–form aortas whereas the mechanical testing is performed on rectangular samples, (Fig.1). It has been shown that cutting circumferential aortic specimens releases the wall residual stress and changes the tissue mechanical state (Han and Fung, 1995b; Shahmirzadi et al., 2008; Vaishnav and Vossoughi, 1983). Our observations showed the existence of residual stress in circumferential specimens as indicated by non-zero force in initial straightened specimens, however, the longitudinal specimens were found to be residual stress-free. The PWI technique examines the tissue under a physiologically–relevant biaxial stress state by applying the internal pressure on the intact vessel–form aortas whereas the mechanical samples were tested only under uniaxial loading. It has been shown that the cardiovascular(anisotropic) tissue biomechanics can be different under uniaxial and biaxial loading states (Bernal et al., 2011; Fronek et al., 1976; Fung, 1993; Haskett et al., 2010). However, PWI findings reflect a more realistic state of tissue because it is tested on the intact vessel form and therefore the entire material and geometrical heterogeneities in the tissue are taken into account, whereas the mechanical testing samples were prepared from a homogeneous areas of the wall without any apparent heterogeneities such as intercostal branching and extreme wall thinning. It is expected that intercostal branching and regional heterogeneities affect the overall dynamic of the formation and propagation of the forward and reflected waves. However, in order to image the smooth propagation of the wave along the anterior (upper) wall without being exposed to wall irregularities and discontinuities, the aortic trunk was placed in such a way that the intercostal branching lines lay on the posterior (lower) wall (i.e. away from the imaging probe).
As a result of having different geometries, the boundary conditions on the test samples were also different and caused a separate set of issues, e.g. the varying circumferential pre– stretch and the slippage at the tissue/grip interface in mechanical testing, and the varying longitudinal pre–stretch and the wave reflections in PWI. In our PWI experiments, we have applied a consistent pre–stretch across different aortas tested (e.g. 3–5%) as the minimum needed to hold the aortas straight in–place. It has been shown that the aortic trunk shrinks longitudinally upon excision. A 38.88% strain has been reported for sheep aortas in vivo compared to the retracted ex vivo length (Wells et al., 1998). Our preliminary measurements have shown that compared to the ex vivo length, the in situ aorta is under 58.13±18.28 % (n=4) longitudinal strain. Given the nonlinear behavior of aortic tissues, it is expected that the degree of the longitudinal stretch applied on the aorta ex vivo affects the apparent modulus and the velocity of the traveling wave. Our preliminary studies have shown that for the maximum longitudinal strain of 41.10% tested, the PWV estimates increased by up to a 2.15–fold, (Table 1). Therefore, it is expected that the pulse wave velocity measurements in vivo (which expectedly has a length closely matching that of in situ) should also be higher than those obtained here ex vivo. In particular, it has been shown that the distribution of longitudinal strain could be non-uniform along the aortic trunk (Han and Fung, 1995b; Sugawara et al., 1997). Therefore, it is expected that locally-dependent adjustments to the axial variations of ex vivo PWV (Fig.5.C) and underlying modulus (Fig.6.C) might be needed in order to implicate the results to the in vivo state. Additionally, Gow et al. have shown that the mid-thoracic canine aorta can undergo larger strains up to around 10% (Gow and Taylor, 1968), and therefore larger modulus estimates could be anticipated from PWI measurements in vivo. Ongoing studies entail application of PWI on canine abdominal aortas in vivo in order to obtain the physiological pulse propagation.
It should also be noted that the modulus is the direct measurement in mechanical testing, however, the PWI is based on the direct measurement of PWV and its translation into the modulus using the M–K relationship with assumptions such as infinitely long and isolated cylinder with a thin, homogenous and linearly elastic wall (Korteweg, 1878; Moens, 1878). These assumptions are being violated in the present study on canine aortas and therefore can impair the modulus estimation (Fung, 1997; Nichols and O’Rourke, 2005). In particular, the M-K formula has originally been developed for thin-wall tubes but was later modified slightly to adjust for applications with thick wall tubes (Fung, 1997). Wells et al. used the pressure-diameter-based thick-wall formula to calculate the pressure wave speed in sheep and lamb aortas in vitro where h/d = 0.1–0.2 (Wells et al., 1998). The difference between the two equations equals h/d, (Eq.1), and the thin-wall equations can be reasonably used for h/d<0.05. Our preliminary studies on phantoms with identical diameter di=9 mm and increasing h/d = 0.2, 0.4, 0.8 have shown that the thick-wall M–K equation may reasonably be used for h/d = 0.2, 0.4. In our application, the average h/di = 0.32 ± 0.01, (Fig. 5.B), and therefore any minor effects from wall thickness were accounted for using the modified thick-wall formula.
As described in the methods, the PWV was calculated as the slope of the linear fit of the spatio-temporal PWI plot. It has been shown that the wave peak is the least robust feature to track the wave propagation (Li et al., 2011; Luo et al., 2009). Our previous parametric study on testing different measures of the foot has shown that the 50% upstroke is optimal –assessed by the highest Signal-to-Noise (SNR) ratio and linear correlation coefficient (r2)– to be used in PWI examinations on human aortas in vivo, aortic phantoms and canine aortas in vitro (Li et al., 2012b; Li et al., 2013).
Given that the geometrical measurements were on the B-mode images (Fig. 3, row 2), the precision of the measurement depends on the wavelength of the ultrasound beam, calculated here as λ = 0.15 mm. Therefore, the diameter and thickness measurements, which were in the range of 1.1–3.08 mm and 3.87–8.26 mm, respectively, were found to be precise. Additionally, the thickness measurements were also validated against those separately made by caliper during the mechanical testing.
The wave propagation along the entire vessel ex vivo was obtained –for the first time to the authors' knowledge– by combining the regional images together to cover the whole length, (Fig.4), resembling the PWI image acquisition using a wide ultrasound probe, e.g. 185 mm. The global spatio–temporal plot indicates the propagation of the first(strong) forward wave which reflects at the end of the vessel and forms a secondary(weaker) forward–reflecting wave, i.e. a total of 2 full cycles of wall pulsation for 1 full cycle of pulsatile flow. The discontinuities in the wave propagation could indicate geometrical irregularities such as intercostal branching on the aortic wall. Also, the main forward wave is preceded by an earlier forward wave caused by the lumen contraction (dark blue wave), which has been reported on similar phantom and simulation studies (Shahmirzadi and Konofagou, 2012; Shahmirzadi et al., 2012). Obtaining similar spatio– temporal plots of global wave propagation in vivo could significantly help obtaining a more in– depth understanding of the physiological mechanisms of pulse wave propagation along the entire vascular system. Implementation of PWI–based stiffness mapping on the canine aortas in vivo is currently under investigation.
5. Conclusion
Reliable implementation of the noninvasive PWI can be of paramount significance in estimating the localized changes in the arterial wall stiffness in vivo, thereby guiding cardiovascular diagnosis and treatment. In this study, PWI was successfully implemented to characterize the regional wall stiffness in canine aortas ex vivo. The quantitative PWI findings were compared against mechanical testing measurements of the wall modulus. The PWI was found to provide more consistent and reproducible results and estimated an average modulus value which is 32.22% smaller than circumferential and 25.84% larger than the longitudinal modulus measurements. The study demonstrated the efficiency of using PWI for obtaining regional variations in the wall modulus without compromising the mechanical and geometrical configurations of the vessel.
Acknowledgements
This project was funded in part by the NIH R01-HL098830. We thank the lab members E. Bunting for helping with the aorta excision and Dr. S. Nandlall for the helpful discussions throughout the study. We also thank our collaborators Prof. P.A. Boyd for supplying the animal specimens. We wish to extend our gratitude to Prof. V.C. Mow, director of the Functional Tissue Engineering Lab in the biomedical engineering department at Columbia University for mechanical testing systems.
Nomenclature
- da
Average diameter of the lumen
- di
Internal diameter of the lumen
- f
Linear frequency
- h
Thickness of the mechanical testing sample
- l
Length of the mechanical testing sample
- L
Total length of the aortic trunk
- t
Time
- V
Fluid velocity
- w
Width of the mechanical testing sample
- x
Axial location on the aortic trunk
- x/L
Normalized axial coordinate on the aortic trunk
- α
Proportionality coefficient
- ε
Strain
- λ
Wavelength
- ν
Poisson’s ratio
- ρ
Density
- ω
Radial frequency
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interests
There are no conflicts of interest in this study to disclose.
References
- Apter JT, Rabinowitz M, Cummings DH. Correlation of Visco-elastic Properties of Large Arteries with Microscopic Structure. Circ Res. 1966;19:104–121. [Google Scholar]
- Benthin M, Dahl P, Ruzicka R, Lindstrom K. Calculation of pulse-wave velocity using cross-correlation - Effects of reflexes in the arterial tree. Ultrasound Med Biol. 1991;17:461–469. doi: 10.1016/0301-5629(91)90182-v. [DOI] [PubMed] [Google Scholar]
- Bergel DH. The static elastic properties of the arterial wall. J. Physiol. 1961;156:445–457. doi: 10.1113/jphysiol.1961.sp006686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernal M, Urban MW, Rosario D, Aquino W, Greenleaf JF. Measurement of biaxial mechanical properties of soft tubes and arteries using piezoelectric elements and sonometry. Phys Med Biol. 2011;56:3371–3386. doi: 10.1088/0031-9155/56/11/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boese J, Bock M, Schoenberg S, Schad L. Estimation of aortic compliance using magnetic resonance pulse wave velocity measurement. Phys Med Biol. 2000;45:1703–1713. doi: 10.1088/0031-9155/45/6/320. [DOI] [PubMed] [Google Scholar]
- Bolster B, Atalar E, Hardy C, McVeigh E. Accuracy of arterial pulse-wave velocity measurement using MR. Magn. Reson. Imaging. 1998;8:878–888. doi: 10.1002/jmri.1880080418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brands P, Willigers J, Ledoux L, Reneman R, Hoeks A. A noninvasive method to estimate pulse wave velocity in arteries locally by means of ultrasound. Ultrasound in Med & Biol. 1998;24:1325–1335. doi: 10.1016/s0301-5629(98)00126-4. [DOI] [PubMed] [Google Scholar]
- Chiu Y, Shroff S. Determination of pulse velocities with computerised algorithms. Am Heart J. 1991;121:1460–1469. doi: 10.1016/0002-8703(91)90153-9. [DOI] [PubMed] [Google Scholar]
- Choke E, Cockerill G, Dawson J, Wilson RW, Jones A, Loftus IM, Thompson MM. Increased Angiogenesis at the Site of Abdominal Aortic Aneurysm Rupture. Ann. N.Y. Acad Sci. 2006;1085:315–319. doi: 10.1196/annals.1383.007. [DOI] [PubMed] [Google Scholar]
- Chuong CJ, Fung YC. On residual stress in arteries. J Biomech Eng. 1986;108:189–192. doi: 10.1115/1.3138600. [DOI] [PubMed] [Google Scholar]
- Couade M, Pernot M, Messas E, Emmerichc J, Hagege A, Fink M, Tanter M. Ultrafast imaging of the arterial pulse wave. IRBM. 2011;32:106–108. [Google Scholar]
- Danpinid A, Luo J, Vappou J, Terdtoon P, Konofagou E. In vivo characterization of the aortic wall stress-strain relationship. Ultrasonics. 2010;50:654–665. doi: 10.1016/j.ultras.2010.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson A, Greiff E, Loupas T, Persson M, Pesque P. Arterial pulse wave velocity with tissue Doppler imaging. Ultrasound Med Biol. 2002;28:571–580. doi: 10.1016/s0301-5629(02)00495-7. [DOI] [PubMed] [Google Scholar]
- Fonck E, Prodhom G, Roy S, Augsburger L, Rufenacht DA, Stergiopulos N. Effect of elastin degradation on carotid wall mechanics as assessed by a constituent-based biomechanical model. Am J Physiol Heart Circ Physiol. 2007;292:H2754–H2763. doi: 10.1152/ajpheart.01108.2006. [DOI] [PubMed] [Google Scholar]
- Fronek K, Schmid-Schoenbein G, Fung YC. A noncontact method for three-dimensional analysis of vascular elasticity in vivo and in vitro. Appl. Physiol. 1976;40:634–637. doi: 10.1152/jappl.1976.40.4.634. [DOI] [PubMed] [Google Scholar]
- Fujikura K, Luo J, Gamarnik V, Pernot M, Fukumoto R, Tilson M, Konofagou E. A novel noninvasive technique for pulse-wave imaging and characterization of clinically-significant vascular mechanical properties in vivo. Ultrason Imaging. 2007;29:137–154. doi: 10.1177/016173460702900301. [DOI] [PubMed] [Google Scholar]
- Fung Y. Biomechanics: Mechanical Properties of Living Tissues. 2nd Ed ed. New York: Springer-Verlag; 1993. [Google Scholar]
- Fung Y. Biomechanics: Circulation. 2nd Ed ed. New York, NY: Springer-Verlag; 1997. [Google Scholar]
- Gow BS, Taylor MG. Measurement of Viscoelastic Properties of Arteries in the Living Dog. Circ Res. 1968;23:111–122. doi: 10.1161/01.res.23.1.111. [DOI] [PubMed] [Google Scholar]
- Greene ES, Gerson JI. Arterial Pulse Wave Velocity: A Limited Index of Systemic Vascular Resistance during Normotensive Anesthesia in Dogs. Clin Monit. 1985;1:219–226. doi: 10.1007/BF02832814. [DOI] [PubMed] [Google Scholar]
- Groenink M, Langerak SE, Vanbavel E, van der Wall EE, Mulder BJM, van der Wai AC, Spaan JAE. The Influence of Aging and Aortic Stiffness on Permanent Dilation and Breaking Stress of the Thoracic Descending Aorta. Cardiovascular Research. 1999;43:471–480. doi: 10.1016/s0008-6363(99)00095-4. [DOI] [PubMed] [Google Scholar]
- Han H-C, Fung Y. LONGITUDINAL STRAIN OF CANINE AND PORCINE AORTAS. Biomechanics. 1995a;28:637–641. doi: 10.1016/0021-9290(94)00091-h. [DOI] [PubMed] [Google Scholar]
- Han H-C, Fung YC. Species dependence of the zero-stress state of aorta: pig versus rat. J. biomech. Eng. 1991;113:446–451. doi: 10.1115/1.2895425. [DOI] [PubMed] [Google Scholar]
- Han H-C, Fung YC. Longitudinal Strain of Canine and Porcine Aortas. Biomechanics. 1995b;28:637–641. doi: 10.1016/0021-9290(94)00091-h. [DOI] [PubMed] [Google Scholar]
- Hartley C, Taffet G, Michael L, Pham T, Entman M. Noninvasive determination of pulse-wave velocity in mice. Am J Physiol Heart Circ Physiol. 1997;42:H494–H500. doi: 10.1152/ajpheart.1997.273.1.H494. [DOI] [PubMed] [Google Scholar]
- Haskett D, Johnson G, Zhou A, Utzinger U, Vande Geest J. Microstructural and biomechanical alterations of the human aorta as a function of age and location. Biomech Model Mechanobiol. 2010;9:725–736. doi: 10.1007/s10237-010-0209-7. [DOI] [PubMed] [Google Scholar]
- Haslach HW. Nonlinear Viscoelastic, Thermodynamically Consistent, Models for Biological Soft Tissue. Biomech Model Mechanobiol. 2005;3:172–189. doi: 10.1007/s10237-004-0055-6. [DOI] [PubMed] [Google Scholar]
- He C, Roach MR. The composition and mechanical properties of abdominal aortic aneurysms. J Vase Surg. 1994;20:6–13. doi: 10.1016/0741-5214(94)90169-4. [DOI] [PubMed] [Google Scholar]
- Hermeling E, Reesink K, Reneman R, Hoeks A. Measurement of local pulse wave velocity: Effects of signal processing on precision. Ultrasound Med Biol. 2007;33:774–781. doi: 10.1016/j.ultrasmedbio.2006.11.018. [DOI] [PubMed] [Google Scholar]
- Hesses M. Uber die pathologischen Veranderungen der Arterien der oberen extremitat. Virchows Arch. Path. Anat. Physiol. 1926;261:225–252. [Google Scholar]
- Hoctor R, Dentinger A, Thomenius K. Array signal processing for local arterial pulse wave velocity measurement using ultrasound. IEEE Trans Ultrason Ferroelectr Freq Control. 2007;54:1018–1027. doi: 10.1109/tuffc.2007.347. [DOI] [PubMed] [Google Scholar]
- Holzapfel GA. Determination of Material Models for Arterial Walls from Uniaxial Extension Tests and Histological Structure. Theoretical Biol. 2006;238:290–302. doi: 10.1016/j.jtbi.2005.05.006. [DOI] [PubMed] [Google Scholar]
- Indik Z, Yeh H, Ornsteingoldstein N, Sheppard P, Anderson N, Rosenbloom, J.C, Peltonen L, Rosenbloom J. Alternative splicing of human elastin messenger-RNA indicated by sequenceanalysis of cloned genomic and complementary-DNA. Proceedings of the National Academy of Sciences of the United States of America. 1987:5680–5684. doi: 10.1073/pnas.84.16.5680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khamdaeng T, Luo J, Vappou J, Terdtoon P, Konofagou EE. Arterial stiffness identification of the human carotid artery using the stress-strain relationship in vivo. Ultrasonics. 2012;52:402–411. doi: 10.1016/j.ultras.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinsler L, Frey A, et al. Fundamentals of Acoustics. New York, NY: Wiley; 2000. [Google Scholar]
- Korteweg D. Uber die Fortpflanzungsgeschwindigkeit des Schalles in Elastiischen Rohren. Ann Phys Chem. 1878;5:52–537. [Google Scholar]
- Lantelme P, Mestre C, et al. Heart rate: an important cofounder of pulse wave velocity assessment. Hypertension. 2002;39:1083–1087. doi: 10.1161/01.hyp.0000019132.41066.95. [DOI] [PubMed] [Google Scholar]
- Laurent S, Cockcroft J, Van Bortel L, Boutouyrie P, Giannattasio C, Hayoz D, Pannier B, Vlachopoulos C, Wilkinson I, Struijker-Boudier H. Expert consensus document on arterial stiffness: methodological issues and clinical applications. Eur Heart J. 2006;27:2588–2605. doi: 10.1093/eurheartj/ehl254. [DOI] [PubMed] [Google Scholar]
- Laurent S, Katsahian S, Fassot C, Tropeano A, Gautier I, Laloux B, Boutouyrie P. Aortic stiffness is an independent predictor of fatal stroke in essential hypertension. Stroke. 2003;34:1203–1206. doi: 10.1161/01.STR.0000065428.03209.64. [DOI] [PubMed] [Google Scholar]
- Li R, Luo J, Balaram S, Chaudhry F, Lantis J, Shahmirzadi D, Konofagou E. In-vivo Application of Pulse Wave Imaging for Arterial Stiffness Measurement under Normal and Pathological Conditions. 33rd Annual International IEEE EMBS Conference; Boston, MA. 2011. pp. 567–570. [DOI] [PubMed] [Google Scholar]
- Li R, Luo J, Balaram S, Chaudhry F, Lantis J, Shahmirzadi D, Konofagou E. Pulse Wave Imaging (PWI) in Normal, Hypertensive and Aneurysmal Human Aortas In Vivo: A Feasibility Study. Phys Med Biol. 2012a doi: 10.1088/0031-9155/58/13/4549. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R, Qaqish W, Shahmirzadi D, Konofagou E. Performance Assessment and Optimization of Pulse Wave Imaging for Pulse Wave Analysis in Ex Vivo Canine Aortas and In Vivo Normal Human Aortas. International Tissue Elasticity Conference; Deauville, France. 2012b. [DOI] [PubMed] [Google Scholar]
- Li RX, Qaqish WW, Shahmirzadi D, Konofagou EE. Performance assessment and optimization of Pulse Wave Imaging (PWI) in canine aortas ex vivo and normal human arteries in vivo. IEEE Trans UFFC. 2013 doi: 10.1109/EMBC.2012.6346640. submitted. [DOI] [PubMed] [Google Scholar]
- Lillie MA, Gosline JM. Mechanical properties of elastin along the thoracic aorta in the pig. Biomechanics. 2007;40:2214–2221. doi: 10.1016/j.jbiomech.2006.10.025. [DOI] [PubMed] [Google Scholar]
- Liu SQ, Fung YC. Relation between residual strain, hypertension, and hypertrophy in arteries following aortic construction. J. biomech. Eng. 1989;111:325–335. doi: 10.1115/1.3168386. [DOI] [PubMed] [Google Scholar]
- Lu X, Yang J, Zhao JB, Gregersen H, Kassab GS. Shear Modulus of Porcine Coronary Artery: Contributions of Media and Adventitia. Am J Physiol. 2003;285:H1966–1975. doi: 10.1152/ajpheart.00357.2003. [DOI] [PubMed] [Google Scholar]
- Luo J, Fujikura K, Tyrie L, Tilson M, Konofagou E. Pulse Wave Imaging of Normal and Aneurysmal Abdominal Aortas In Vivo. IEEE TRANSACTIONS ON MEDICAL IMAGING. 2009;28:477–486. doi: 10.1109/TMI.2008.928179. [DOI] [PubMed] [Google Scholar]
- Luo J, Konofagou E. Effects of various parameters on lateral displacement estimation in ultrasound elastography. Ultrasound Med Biol. 2009;35:1352–1366. doi: 10.1016/j.ultrasmedbio.2009.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo J, Konofagou E. A Fast Normalized Cross-Correlation Calculation Method for Motion Estimation. IEEE Trans UFFC. 2010;57:1347–1357. doi: 10.1109/TUFFC.2010.1554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo J, Lee W-N, Wang S, Konofagou E. Pulse Wave Imaging of Human Abdominal Aortas In Vivo. Proc of IEEE Ultrasonics Symp. 2008;2008:859–862. [Google Scholar]
- Luo J, Li RX, Konofagou EE. Pulse wave imaging of the human carotid artery: an in vivo feasibility study. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 2012;59:174–181. doi: 10.1109/TUFFC.2012.2170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macgowan C, Henkelman R, Wood M. Pulse-wave velocity measured in one heartbeat using MR tagging. Magn Reson Med. 2002;48:115–121. doi: 10.1002/mrm.10177. [DOI] [PubMed] [Google Scholar]
- Mancia G, et al. ESH-ESC Practice Guidelines for the Management of Arterial Hypertension: ESH- ESCTask Force on the Management of Arterial Hypertension. J Hypertens. 2007:1751–1762. doi: 10.1097/HJH.0b013e3282f0580f. [DOI] [PubMed] [Google Scholar]
- Meinders J, Kornet L, Brands P, Hoeks A. Assessment of local pulse wave velocity in arteries using 2D distension waveforms. ultrasound imaging. 2001;23:199–215. doi: 10.1177/016173460102300401. [DOI] [PubMed] [Google Scholar]
- Millasseau S, Stewart A, et al. Evaluation of carotid-femoral pulse wave velocity: influence of timing algorithm and heart rate. Hypertension. 2005;45:222–226. doi: 10.1161/01.HYP.0000154229.97341.d2. [DOI] [PubMed] [Google Scholar]
- Moens A. Die Pulskurve [The Pulse Curve] Leiden, The Netherlands: E.J. Brill; 1878. [Google Scholar]
- Nichols W, O'Rourke M. McDonald's Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles. 5th Ed ed. London, UK: Hodder Arnold Publication; 2005. [Google Scholar]
- Nichols WW, McDonald DA. Wave-Velocity in the Proximal Aorta. Med & Biol Eng. 1972;10:327–335. doi: 10.1007/BF02474213. [DOI] [PubMed] [Google Scholar]
- O'Rourke M, Franklin S. Arterial stiffness: reflections on the arterial pulse. Eur Heart J. 2006;27:2497–2498. doi: 10.1093/eurheartj/ehl312. [DOI] [PubMed] [Google Scholar]
- O'Rourke M, Staessen J, Vlachopoulos C, Duprez D, Plante G. Clinical applications of arterial stiffness; definitions and reference values. Am J Hypertens. 2002;15:426–444. doi: 10.1016/s0895-7061(01)02319-6. [DOI] [PubMed] [Google Scholar]
- Olufsen M. Structured tree outflow condition for blood flow in larger systemic arteries. Am J Physiol. 1999;276:H257–H268. doi: 10.1152/ajpheart.1999.276.1.H257. [DOI] [PubMed] [Google Scholar]
- Palmieri D, et al. Resveratrol counteracts systemic and local inflammation involved in early abdominal aortic aneurysm development. Surg Res. 2011;171:237–246. doi: 10.1016/j.jss.2011.07.041. [DOI] [PubMed] [Google Scholar]
- Rabben S, Stergiopulos N, Hellevik L, Smiseth O, Slordahl S, Urheim S, Angelsen B. An ultrasound-based method for determining pulse wave velocity in superficial arteries. Biomechanics. 2004;37:1615–1622. doi: 10.1016/j.jbiomech.2003.12.031. [DOI] [PubMed] [Google Scholar]
- Rachev A, Greenwald SE. Residual Strains in Conduit Arteries. Biomechanics. 2003;36:661–670. doi: 10.1016/s0021-9290(02)00444-x. [DOI] [PubMed] [Google Scholar]
- Safar M. Pulse pressure in essential hypertension: clinical and therapeutical implications. Hypertens. 1989;7:769–776. doi: 10.1097/00004872-198910000-00001. [DOI] [PubMed] [Google Scholar]
- Segers P, Kips J, Trachet B, Swillens A, Vermeersch S, Mahieu D, Rietzschel E, De Buyzere M, Van Bortel L. Limitations and pitfalls of non-invasive measurement of arterial pressure wave reflections and pulse wave velocity. Artery Research. 2009;3:79–88. [Google Scholar]
- Shahmirzadi D, Bruck H, Hsieh A. Measurement of Mechanical Properties of Soft Tissues In Vitro under Controlled Tissue Hydration. Exp Mech. 2013;53(3) [Google Scholar]
- Shahmirzadi D, Hsieh A, Haslach H. Effects of Arterial Tissue Storage and Burst Failure on Residual Stress Relaxation. 34th Annual Northeast Bioengineering Conference; Providence, RI. 2008. [Google Scholar]
- Shahmirzadi D, Konofagou E. Detection of Aortic Wall Inclusions Using Regional Pulse Wave Propagation and Velocity In Silico . Artery Research. 2012;6:114–123. doi: 10.1016/j.artres.2012.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahmirzadi D, Li R, Konofagou E. Pulse-Wave Propagation in Straight-Geometry Vessels for Stiffness Estimation: Theory, Simulations, Phantoms and In Vitro Findings. Biomechanical Engineering. 2012;134:114502.114501–114502.114506. doi: 10.1115/1.4007747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao X, Fei D, Kraft K. Computer-assisted evaluation of aortic stiffness using data acquired via magnetic resonance. Comput. Med. Imaging Graph. 2004;28:353–361. doi: 10.1016/j.compmedimag.2004.04.006. [DOI] [PubMed] [Google Scholar]
- Sugawara S, Matsumoto T, Takasawa K, Sato M. A Technique for Measuring Arterial Deformation in Vivo. Proceedings of the 11th Autumn Conference of the Japan Society of Medical Electronics and Biological Engineering; Year. [Google Scholar]
- Vaishnav RN, Vossoughi J. Estimation of residual strain in aortic segments. Oxford, UK: Pergamon Press; 1983. [Google Scholar]
- Vande Geest JP, Schmidt DE, Sacks MS, Vorp DA. The Effects of Anisotropy on the Stress Analyses of Patient-Specific Abdominal Aortic Aneurysms. Annals of Biomedical Engineering. 2008;36:921–932. doi: 10.1007/s10439-008-9490-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vappou J, Luo J, Konofagou E. Pulse wave imaging for noninvasive and quantitative measurement of arterial stiffness in vivo. Am J Hypertens. 2010a;23:393–398. doi: 10.1038/ajh.2009.272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vappou J, Luo J, Konofagou E. Regional measurement of arterial stiffness using Pulse Wave Imaging: Phantom validation and preliminary clinical results. Proc of IEEE Ultrasonics Symp; San Diego, CA, USA. 2010b. pp. 1332–1335. [Google Scholar]
- Vappou J, Luo J, Okajima K, Tullio M, Konofagou E. Aortic pulse wave velocity measured by pulse wave imaging (PWI): A comparison with applanation tonometry. Artery Research. 2011a;5:65–71. doi: 10.1016/j.artres.2011.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vappou J, Luo J, Okajima K, Tullio MD, Konofagou EE. Non-invasive measurement of local pulse pressure by pulse wave-based ultrasound manometry (PWUM) Physiological Measurements. 2011b;32:1653–1662. doi: 10.1088/0967-3334/32/10/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vappou J, Zervantonakis I, Luo J, Konofagou EE. Finite Element Modeling of the Pulse Wave propagation in the aorta for simulation of the Pulse Wave Imaging (PWI) method. New York, NY: Computational Biomechanics for Medicine (MICCAI 2008 Workshop); 2008. pp. 118–127. [Google Scholar]
- Verbeke F, et al. Role of aortic calcification, stiffness and wave reflections in cardiovascular risk in dialysis patients: Baseline data from the CORD study. Artery Research. 2010;4:81–90. [Google Scholar]
- Vossoughi J. Longitudinal residual strain in arteries. 11th Southern Biomedical Engineering Conference; Memphis, TN. Year. [Google Scholar]
- Wang S, Lee W-N, Provost J, Luo J, Konofagou E. A composite high-frame-rate system for clinical cardiovascular imaging. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 2008;55:2221–2233. doi: 10.1109/TUFFC.921. [DOI] [PubMed] [Google Scholar]
- Wells SM, Langillr BL, Adamson SL. In vivo and in vitro mechanical properties of the sheep thoracic aorta in the perinatal period and adulthood. Am J Physiol. 1998;274:H1749–H1760. doi: 10.1152/ajpheart.1998.274.5.H1749. [DOI] [PubMed] [Google Scholar]
- Williams R, Needles A, Cherin E, Zhou Y, Henkelman R, Adamson S, Foster F. Noninvasive ultrasonic measurement of regional and local pulse-wave velocity in mice. Ultrasound Med Biol. 2007;33:1368–1375. doi: 10.1016/j.ultrasmedbio.2007.03.012. [DOI] [PubMed] [Google Scholar]
- Wolinsky H, Glagov S. Structural Basis for the Static Mechanical Properties of the Aortic Media. Circ Res. 1964;14:400–413. doi: 10.1161/01.res.14.5.400. [DOI] [PubMed] [Google Scholar]
- Yu H, Peng H, Wang J, Wen C, Tseng W. Quantification of the pulse wave velocity of the descending aorta using axial velocity profiles from phase-contrast magnetic resonance imaging. Magn Reson Med. 2006;56:876–883. doi: 10.1002/mrm.21034. [DOI] [PubMed] [Google Scholar]