Nanoporous micro-element arrays for particle interception in microfluidic cell separation

Abstract

The ability to control cell-surface interactions in order to achieve binding of specific cell types is a major challenge for microfluidic immunoaffinity cell capture systems. In the majority of existing systems, the functionalized capture surface is constructed of solid materials, where flow stagnation at the solid-liquid interface is detrimental to the convection of cells to the surface. We study the use of ultra-high porosity (99%) nanoporous micro-posts in microfluidic channels for enhancing interception efficiency of particles in flow. We show using both modelling and experiment that nanoporous posts improve particle interception compared to solid posts through two distinct mechanisms: the increase of direct interception, and the reduction of near-surface hydrodynamic resistance. We provide initial validation that the improvement of interception efficiency also results in an increase in capture efficiency when comparing nanoporous vertically aligned carbon nanotube (VACNT) post arrays with solid PDMS post arrays of the same geometry. Using both bacteria (~1 μm) and cancer cell lines (~15 μm) as model systems, we found capture efficiency increases by 6-fold and 4-fold respectively. The combined model and experimental platform presents a new generation of nanoporous microfluidic devices for cell isolation.

Introduction

The efficient isolation of specific cell types in lab-on-a-chip platforms is important for many applications in clinical diagnostics and biomedical research. Examples include CD4+ T-cells, neutrophils, dentritic cells, circulating tumor cells and antigen-specific T-cells from blood, fungus from blood or other bodily fluids, and bacteria from processed sputum. Most microfluidic systems designed for specific cell isolation operate on the principle of immunoaffinity capture.^1–3 The simplest devices consist of rectangular micro-channels where the walls are coated with chemical binding moieties.^4,5 This design comes up against the challenge that in the Poiseuille flow profile seen in microfluidic channels, the majority of the flow volume passes through the center of the channel, and diffusive transport for cell sized particles is too slow to be of assistance in bringing cells into contact with the channel walls. A popular method to enhance efficiency is by the addition of micro-post arrays perpendicular to the flow, spanning across the height of the channel.^6–9 This improves cell-surface interactions by increasing the overall surface area, as well as by bringing capture surfaces closer to cells passing through the center of the channel. The micro-post array design is used in some of the most efficient microfluidic devices for rare cell isolation.^6,7 However, this efficiency is achieved at the cost of using large arrays occupying many square centimetres of footprint area. This is because when the posts are constructed of solid materials such as silicon or a polymer, the isolation efficiency of each individual post in the array is extremely small. There are two main reasons for this: (i) a bulk flow effect where flow stagnation occurs at the solid-liquid interface due to the no-slip boundary condition at solid surfaces; (ii) a near-surface effect due to hydrodynamic resistance as a particle approaches a solid surface. If the isolation efficiency of each post in the array can be improved, we can reduce the array size and footprint area needed. This would in turn increase the surface (and volume) concentration of the isolated cells, and reduce microscopy time if that is the chosen readout.

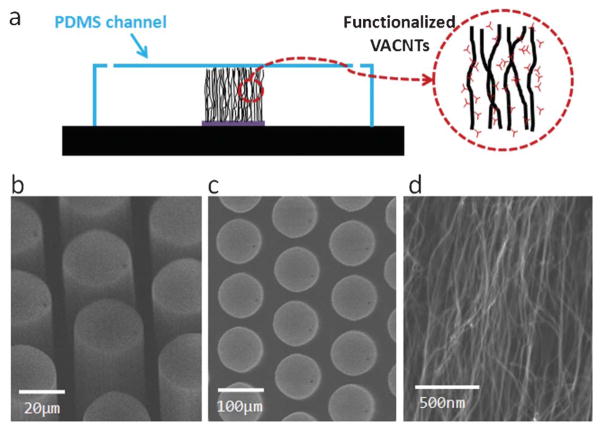
Isolation efficiency is a function of the interception efficiency (the fraction of particles in flow that is intercepted by the collector) and the binding efficiency (the probability that a particle will bind to the collector if it is intercepted). In this work we focus on the former. We examine the different factors that affect interception efficiency in the flow regime of a typical microfluidic system, and show that we can greatly improve the interception efficiency by using nanoporous posts instead of solid posts. To date, the use of porous materials in microfluidics have largely been limited to monolithic plugs that fill the channel,^10,11 or membranes sandwiched between two channels.^12,13 These platforms have very limited geometric patternability and have not been able to provide a viable alternative to solid materials as structural elements in microfluidics. Recently, we introduced the integration of micropatterned nanoporous carbon nanotube forests inside microfluidic channels.¹⁴ The forests consist of vertically aligned carbon nanotubes (VACNTs) with ultra-high (99%) porosity and high permeability (1 × 10⁻¹³ m²). We use photolithography to define forest geometries independent of the channel boundaries, and manipulation of the CNT growth conditions allows for the fabrication of high aspect ratio features, up to millimetres in height.¹⁵ Fig. 1 shows a schematic of a VACNT post element integrated inside a microfluidic channel, and scanning electron micrographs (SEMs) of the patterned VACNT micro- and nano-structures. The VACNT posts can be functionalized for cell capture, or treated to block biological binding. In this study, we compare nanoporous posts made using our VACNT technology with solid posts made from traditional soft lithography in their interception efficiencies for particles in flow.

Fig. 1.

Device images: (a) schematic of a microfluidic device with nanoporous features inside a PDMS channel; (b) SEM angled view of a patterned VACNT post array; (c) SEM top view of a patterned VACNT post array; (d) SEM of the nanostructure of a VACNT forest.

Particle interception by cylindrical posts

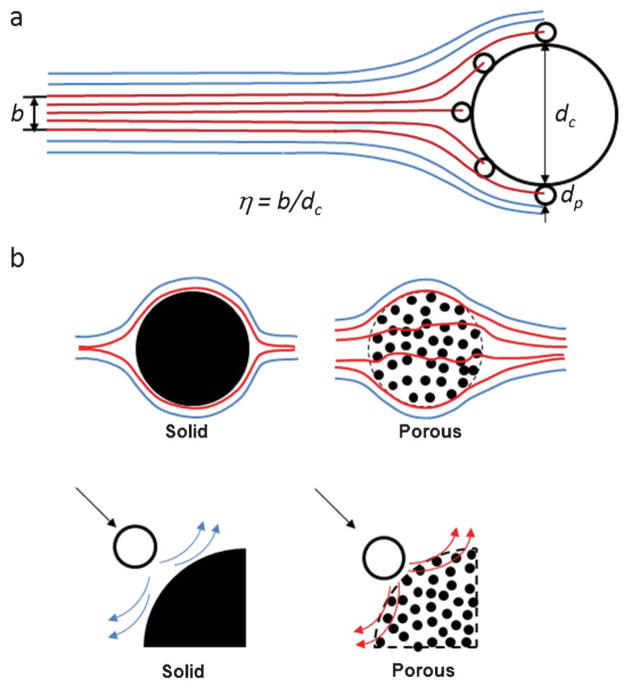
A number of theoretical and experimental studies exist on particle interception across scientific disciplines ranging from aerosol science^16,17 to marine ecology.^18,19 The widely used definition of interception efficiency is given by η = b/d_c, where b is the span of particles upstream that are ultimately intercepted by the collector, and d_c is the collector diameter (Fig. 2a).

Fig. 2.

Interception efficiencies for solid and nanoporous cylindrical posts: (a) definition of interception efficiency; (b) schematic illustrating modifications to bulk flow streamlines by fluid passage through a porous element; (c) schematic illustrating the reduction of near-surface hydrodynamic resistance for a porous post compared to a solid post.

There are four classical mechanisms for interception: direct interception, diffusion, inertial compaction, and gravitational sedimentation. Contribution from each mechanism is additive to the overall efficiency. Direct interception occurs when a particle of a finite size travels along a streamline that approaches a collector by a distance less than the particle radius. The particle is brought directly into contact with the collector by the fluid streamline. For creeping flows, the interception efficiency due to direct interception has been analytically solved as:²⁰

$$\eta =A_F{\left(\frac{d_p}{d_c}\right)}^2$$ (1)

where d_p denotes particle diameter and

$$A_F={\left[2-ln\left(\frac{2d_{c}U}{\nu }\right)\right]}^{-1}$$ (2)

where U denotes average flow velocity and v denotes the kinematic viscosity, for isolated cylinders, and

$$A_F={\left[-ln\mathrm{\alpha }-\frac{3}{2}+2\mathrm{\alpha }-\frac{{\mathrm{\alpha }}^2}{2}\right]}^{-1}$$ (3)

for cylinder arrays with volume fraction α.

Brownian diffusion of small particles in a fluid can cause them to randomly cross streamlines, increasing their probability of getting intercepted by the collector. This probability is greatly enhanced as their diffusive activity increases, due to increases in temperature, small particle size, or long residence time in proximity to the collector. The contribution of Brownian diffusion as a mechanism of interception is additive with the effect due to direct interception, and is derived for a cylindrical collector as:²¹

$${\eta }_{\mathit{diff}}=\frac{3.64A_F}{{Pe}^{2/3}}$$ (4)

where Pe is the Peclet number (convection/diffusion) given by LU/D, where L is the characteristic length, U is the average velocity, and D = kT/6πμa_p is the diffusion coefficient. As we will later show, diffusion is a significant contributor for the experiments where particle size is 2 μm or smaller.

Inertial compaction occurs when a particle’s inertia causes it to deviate from the fluid streamlines and intercept with the collector. This is the dominant mechanism for aerosols particles in air. The relative importance of inertial compaction is given by the Stoke’s number:

$$\mathit{Stk}=\frac{1}{9}Re{\left(\frac{d_p}{d_c}\right)}^2(s-1)$$ (5)

where s is the specific gravity and Re is the Reynolds number. Aerosol theory states that inertial impaction is negligible for Stk < 0.125.¹⁷ For our experimental conditions, Stk < 5 × 10⁻⁴, well below the critical value.

Gravitational sedimentation can give rise to particle interception when the cylindrical axis of the collector is oriented horizontally, such that particles traveling along streamlines above the collector can settle on top of it.²² To eliminate the effects of this mechanism, all or our posts are oriented with their cylindrical axis in a vertical direction. The effect of gravitational sedimentation can also be minimized by using particles that are neutrally buoyant with the fluid medium.

Of the four classical mechanisms of interception described, direct interception is the dominant effect in our system of concern, that is, low Reynolds number flows with particle sizes >1 μm. Diffusion also plays a role for the smallest particle sizes. However, the previous analysis of interception neglects some important physical effects that come into play when the particle is in the immediate proximity of a solid surface. These near-surface effects include hydrodynamic resistance between the particle and collector, and London forces of molecular attraction. Hydrodynamic resistance (sometimes referred to a ‘lubrication’ force) arises as a particle approaching a solid surface ‘squeezes out’ fluid from the gap in between them. According to the no-slip condition, this would result in infinitesimally slow fluid drainage as the gap size reduces, and the particle would never contact the surface. The particle is saved from this fate by the opposing attractive London (or van de Waals) force that dominates when the gap length approaches molecular dimensions.²⁰ Goren²³ and Spielman²⁴ analyzed the effects of these forces and summarized their combined effect on direct interception using the parameter N_Ad, known as the adhesion coefficient:

$$N_{Ad}=\frac{{Hd}_c^2}{9\pi \mu d_p^2{UA}_F}$$ (6)

where H is the Hamaker constant. The value of N_Ad is related to a proportional modifier that is applied to the value of interception efficiency η derived from the classical mechanisms. This modifier was calculated for a cylindrical collector for different values of N_Ad by Fitzpatrick,²⁵ and the results summarized into a plot in Fig. 13 of Spielman’s paper.²⁴ At large values of N_Ad, the London force dominates, resulting in a higher interception efficiency than that predicted by classical mechanisms; at small values of N_Ad, hydrodynamic resistance has the largest effect, resulting in a lower interception efficiency than that predicted by classical mechanisms. In general, for larger particle sizes (>1 μm), which is our operating regime, N_Ad is small, and hydrodynamic resistance dominates. Several experimental studies have validated predictions from Spielman’s near surface model for solid cylindrical collectors.^22,26 Chang’s experiments²⁶ also measured the effect on interception efficiency of using a nanoporous hollow fiber as a collector. He found that there is a far more dramatic increase in interception efficiency than can be explained by fluid displacement into the hollow fiber alone. He attributed this effect to the reduction in hydrodynamic resistance near the surface of the porous hollow fiber.

Based on our understanding of particle interception, we propose that there are two mechanisms in which a porous collector can improve interception efficiency compared to a solid collector. The first mechanism, shown in Fig. 2b, is the flow field modification that occurs as a result of fluid passage through the porous collector. This allows more fluid streamlines to come into contact with the collector, and increases the efficiency by direct interception. The second mechanism, shown in Fig. 2c, is the reduction of hydrodynamic resistance near the surface of the collector. We demonstrate these effects through a combination of numerical modeling and experimental validation.

Modeling parameters for solid and porous post flows

We used COMSOL Multiphysics v3.5a to create 2D streamline models for flows through our solid and nanoporous devices. Navier–Stokes equations are used in the free media flow region and Brinkman’s equations for the porous flow region.²⁷ This model for mixed porous and free media flow has been widely used in literature.^28–30 A porosity of 99% and permeability of 1 × 10⁻¹³ m² is used for the porous micropost, identical to the porosity and permeability of the nanoporous VACNT materials measured.³¹ Flow speed is set to 0.5 mm s⁻¹, the same as the flow speed used in experiments, while fluid viscosity is assumed to be that of water (0.001 Pa s). Device geometries are replicated for the isolated post devices, and symmetrical boundary conditions are used for post arrays. Previous models have shown that the degree of fluid accessibility inside a porous post is related to its Darcy number, defined as Da = κ/d_c², where κ is the permeability of the porous material, and d_c is the characteristic length, or the post diameter.^30,32,33 Since in our experimental system the material permeability is constant, we varied the Darcy number by changing the post dimensions, both experimentally and in the model. No other fitting parameters were used. Streamlines were plotted which pass exactly one particle radius away from the top and bottom edges of the post. Grid meshing was iteratively refined until the difference in the interception band width (defined by the distance between these two streamlines upstream of the post) between iterations was less than 0.2%. Interception efficiencies based on direct interception are calculated by measuring the interception band width and dividing by the post diameter.

For solid posts, we calculated N_Ad based on our flow conditions. A Hamaker constant of 0.6 × 10⁻²⁰ J is used, which is the value calculated by Visser³⁴ for a polystyrene particle-water-glass collector system. Spielman and Fitzpatrick’s result in Fig. 13 of their paper²⁴ was used to determine modifications to the interception efficiency according to the calculated N_Ad values.

For nanoporous posts, we hypothesize that the effect of near-surface hydrodynamic resistance is reduced to zero, and that interception efficiencies would follow trends predicted by the streamline model alone.

Materials and methods

Patterning and growth of VACNT forests

The nanoporous VACNT posts are patterned and grown using the method by Garcia et al.³⁵ Standard photolithography is used to pattern plain <100> 6 inch silicon wafers, followed by electron beam deposition of a 10 nm Al₂O₃ layer and a 1 nm Fe layer. Catalyst areas are then defined by photoresist lift-off, which is achieved by soaking the wafers in acetone for 8 min with mild sonication. CNT growth is performed in a 4 inch quartz tube chemical vapor deposition furnace at atmospheric pressure using reactant gases of C₂H₄, H₂, and He (400/400/1900 sccm). Annealing of the catalyst is carried out in a reducing He/H₂ environment at 680 °C. This leads to the formation of iron (Fe) catalyst nanoparticles ~10 nm in average diameter, corresponding approximately to the diameter of the grown CNTs. C₂H₄ is then introduced into the furnace to initiate CNT growth. The growth occurs at approximately 100 μm min⁻¹ until the flow of C₂H₄ is discontinued. For the experiments in this paper, the CNTs are grown for 1.2–1.6 min, corresponding to post heights of 80–100 μm. The technique results in forests of multiwalled VACNTs (three to four concentric walls), with an average tube diameter of 8 nm and an average intra-CNT spacing of ~80 nm, thus yielding a 1% volume fraction of CNTs in the forest (99% bulk porosity).³⁶

Microfluidic channel fabrication and integration with VACNT elements

Standard soft lithography is used to make microfluidic channels from polydimethylsiloxane (PDMS).³⁷ Photolithography is used to pattern SU-8 photoresist (Microchem, MA) onto a silicon wafer to form a negative mold. PDMS pre-polymer and curing agent (Sylgard 184, Dow Corning, MI) is mixed at a 10 : 1 ratio and poured onto the mold and baked at 75 °C until cured. The PDMS channels are then bonded to the silicon wafers containing the CNT structures after a 30 s oxygen plasma treatment. The PDMS channels are made several microns shorter than the height of the CNT structures so that the ceiling of the channel slightly compresses the top of the CNTs to create a seal. To make ‘solid’ devices for comparison, both the channel and the posts are fabricated from PDMS by the soft lithography method described above, and the channels are bonded to 1 × 3 inch glass microscope slides after oxygen plasma treatment.

Interception efficiency experiments

For the interception efficiency experiments, the devices are treated with 0.5% Tween-20 (Sigma Aldrich, MO) in deionized (DI) water. Tween-20 is an amphiphilic molecule that attaches well to CNTs and allows them to be hydrophilic. It also prevents non-specific binding.³⁸ For the isolated post experiments, the Darcy number is adjusted by changing the post diameter. Channel side walls are positioned a minimum of 5 post diameters away to approximate a truly isolated post. For the array experiments, channels are 2 mm wide and 80 mm tall. Polystyrene particles (Thermo Scientific, MA) of the appropriate sizes are used to create the desired particle to post diameter ratio. The particles are suspended in a neutral density solution of DI water, Optiprep density gradient medium (Sigma Aldrich, MO), and 0.1% Tween-20. Flow is introduced using a syringe pump (Harvard instruments, MA) at 0.5 mm s⁻¹ for all experiments. Videos of the flow around the posts are captured using an optical microscope (90i, Nikon, NY) and NIS Elements software. The videos are then analyzed using ImageJ particle tracking. A minimum of 20 intercepting particles are analyzed per device. Interception events are determined by eye as particles make contact with the posts. The maximum interception band width b (as defined in Fig. 2a) was measured, and interception efficiency by calculating η = b/d_c. Results from 4 devices are averaged per data point. Error bars show standard deviation of the average interception efficiencies measured.

Device functionalization

For the cell capture experiments, the CNT devices are functionalized according to the non-covalent method by using 1,1-carbonyldiimidazole (CDI)-activated Tween.³⁸ Tween-20 is reacted with CDI (Sigma Aldrich, MO) under dimethyl sulfoxide (DMSO, Sigma Aldrich, MO) for 2 h at 40 °C, and then dried using a Rotovap. CDI-activated Tween (1%) in DI water is injected into bonded VACNT-microfluidic devices and incubated for 30 min. They are then flushed with DI water, injected with 20 μg ml⁻¹ NeutrAvidin (Thermo Scientific, MA) in PBS and incubated at room temperature for 30 min. This is followed by incubation with 20 ug ml⁻¹ of biotinylated antibody in PBS for 30 min. Biotinylated anti-Escherichia coli (rabbit polyclonal, Abcam, MA) is used for the bacteria capture experiments, and biotinylated anti-EPCAM (Clone BAF960, R&D systems, MN) is used for the cell capture experiments.

The PDMS devices used for capture comparison are functionalized using previously described methods.¹ Directly after oxygen plasma bonding of PDMS channels to glass slides, devices are treated with a 4% (v/v) solution of 3-mercaptopro-pyltrimethoxysilane in ethanol for 30 min at room temperature. This is followed by incubation with 0.01 μmol mL⁻¹ N-γ-maleimidobutyryl-oxysuccinimide ester (GMBS, Sigma Aldrich, MO) in ethanol for 15 min at room temperature. NeutrAvidin and biotinylated antibodies are then injected as described above.

Cell capture experiments

Fluorescent heat killed Escherichia coli bacteria (Invitrogen, NY) at 5 × 10⁶ particles per mL and Calcein-stained PC3 cancer cells (ATCC, VA) at 2 × 10⁵ are suspended in PBS and injected into the devices using a syringe pump, at 0.5 mm s⁻¹, for 4 min. After the capture stage, the devices are rinsed in PBS at 0.5 mm s⁻¹ for 2 min. The devices are scanned under fluorescent microscopy and the capture in the first row of each device was counted manually. Capture efficiency of the first row was found by dividing the number of captured cells by the total number of cells injected into the device. To study the location of the captured cells, each post was divided into 8 sectors, and the number of captured cells on the surface of each sector was manually counted. The data were used to create polar histograms (rose plots) mapping the percentage of captured cells found on the surface of each sector.

Results and discussion

Interception efficiencies of isolated posts

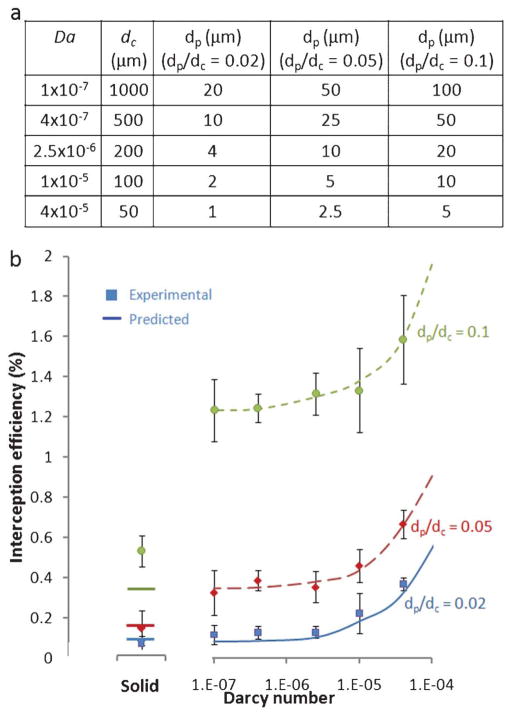
We first investigate the interception efficiencies of single isolated nanoporous posts of varying Darcy numbers and compare them with the efficiency solid posts. Fig. 3a shows the experimental conditions used to vary the Darcy number and particle-to-post diameter (d_p/d_c) ratios across different values. Fig. 3b compares the measured values of interception efficiencies for solid and nanoporous posts with our model predictions. Looking at the results for the nanoporous posts, we see that the experimental measurements match very closely with the theoretical predictions for all three d_p/d_c ratios.

Fig. 3.

Predicted and measured results for interception efficiencies of isolated posts: (a) Darcy number, post size and particle size of nanoporous posts tested; (b) experimental and predicted interception efficiencies for solid posts and nanoporous posts of varying Darcy number, at three different particle to post size ratios.

Recall that the predictions for the porous posts are based only on the direct interception mechanism and diffusion, the results seem to support our initial hypothesis that the effects of near-surface hydrodynamic resistance are greatly reduced by porous surfaces. The second observation we make is that as we increase the Darcy number, interception efficiency increases non-linearly.

The highest Darcy number tested in our experiments is 4 × 10⁻⁴, corresponding to a post size of 50 μm at our material permeability of 1 × 10⁻¹³ m². This was the smallest post size at which our method could reliably measure interception efficiencies. However, our theory predicts that if we can increase the Darcy number further, we can greatly improve the interception efficiency through the mechanism of direct interception. Since Da = κ/d_c², we can increase Da by either increasing the material permeability or decreasing the post dimensions. We have previously explored methods to vary material permeability by changing growth parameters for the CNTs.³¹ For post dimensions, we are able to reliably grow high aspect ratio (up to 100) nanoporous posts down to 10 μm in diameter. Smaller post sizes are possible at lower aspect ratios.

Turning to the results for isolated solid posts, we see again that experimental results match predictions relatively closely. The theoretical predictions for solid posts include the effects of near-surface hydrodynamic resistance as well as direct interception. If hydrodynamic resistance had not been accounted for, the predictions from streamlines alone would show little difference in interception between the solid posts and the lowest Darcy number porous posts. Instead, we see both from theory and experiments that hydrodynamic resistance greatly reduces interception efficiencies for solid posts compared to even the low Darcy number porous posts. In addition, the effect is more significant for larger d_p/d_c ratios. This is because at small d_p/d_c ratios, London forces begin to have an influence on the interception efficiency and cancel out some of the effects of hydrodynamic resistance. We also see that the prediction for d_p/d_c = 0.1 does not match the experimental result as well as the other data points. This may be because the near-surface model developed by Spielman and Goren makes the assumption that d_p ≪ d_c, which begins to break down at higher d_p/d_c ratios.

There are several possible sources that contribute to errors in our experimental results. First, the particles that we purchased from manufacturers have a non-uniform size distribution around the nominal particle diameter, typically around 5%. However, since interception efficiency varies according to the square of the d_p/d_c ratio, this 5% non-uniformity could correspond to a 10% error in interception efficiency measurement. Second, the determination of whether a particle is intercepted by the collector is made manually from the videos, and this could have errors due to both camera resolution (at least 1/20^th of the particle diameter) and operator subjectivity. Third, we sampled around 20 intercepting particles per device, and this will have an associated sampling error. Assuming that particle distribution is uniform in the interception band, the probability that the collection efficiency is underestimated by 10% or more is 12.2%, based on a binomial distribution with a sample of 20.

Interception efficiencies of post arrays with varying array density

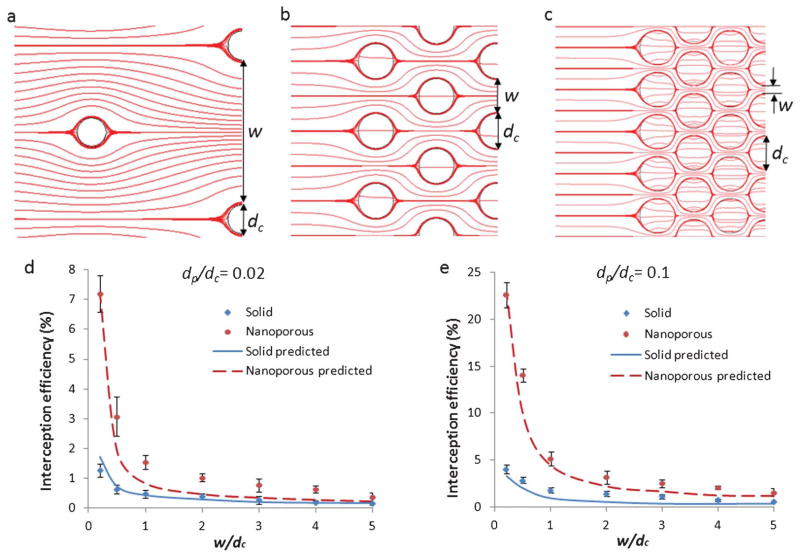
Fig. 4 investigates the effect of arraying on the interception efficiencies of individual posts. To isolate the effect of array density, all arrays are configured to a hexagonal packing geometry, and all post sizes are kept at 100 μm, corresponding to a Darcy number of 10⁻⁵. Array density is defined by the parameter w/d_c, where w is the distance between the edges of neighboring posts, and d_c is the post diameter. Modeling shows that as w/d_c decreases, the neighboring posts act to squeeze more streamlines inside the nanoporous posts (Figs. 4a, 4b and 4c), and this effect increases the interception efficiency of individual posts in the array. From the velocity profile along the channel cross section in the first row of the array, we could calculate from the model that when w/d_c = 5, only 0.003% of the flow passes inside of one of the nanoporous posts in this row, whilst at w/d_c = 0.2, 1.4% of the flow travels inside a nanoporous post. For solid posts, although streamlines are also squeezed tighter together, they cannot penetrate inside the posts. Figs. 4d and 4e show experimental compared with theoretical results for interception efficiency as w/d_c varies for both solid and nanoporous posts. We see that although closer array spacing improves interception for both solid and nanoporous posts, the efficiency increase for nanoporous posts is much more dramatic. For both d_p/d_c values, the ratio of interception efficiencies of nanoporous posts to solid posts increases from ~2-fold at w/d_c = 5, to ~6-fold at w/d_c = 0.2. We see that the experimental results match the model values relatively well, although there is a trend for under-prediction. This may be due to the limited assumptions of our model system. For example, we have modelled our particles essentially as point particles that follow streamlines except where near-surface effects come into play. We have accounted for the size of the particles only when making calculations on the direct interception efficiency. However, we have not included in our model the effect of fluid displacement by the volume of particles, which could affect the accuracy of the model, especially for closer array spacings.

Fig. 4.

Predicted and measured results for interception efficiencies of post arrays: (a) schematic model streamlines for w/d_c = 5; (b) model streamlines for w/d_c = 1; (c) model streamlines for w/d_c = 0.2; (d) predicted and measured interception efficiencies for different array spacings, with d_p/d_c = 0.02; (e) predicted and measured interception efficiencies for different array spacings, with d_p/d_c = 0.1.

Capture efficiency of nanoporous and solid post arrays

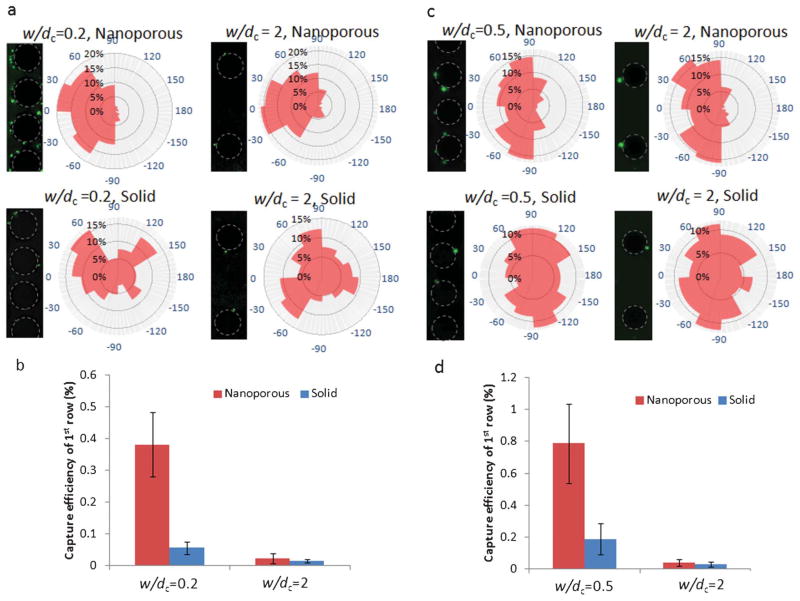
We are interested to see if the improvements in interception efficiency for nanoporous post arrays compared to solid post arrays translate to similar improvements in capture efficiency. We see from Fig. 5 that this is indeed the case. The same post configurations (100 μm diameter, hexagonal packing) are used as in the experiments for Fig. 4, and capture efficiency of the first row in the array is compared between nanoporous and solid post array devices. Only the first row was selected because the interception efficiencies measured in Fig. 4 also apply to those posts found in the first row, so this allows us to make an equivalent comparison between the interception experiments and the capture ones. The rose plots in Figs. 5a and 5c show that for nanoporous posts, almost all the capture occurs on the front surface of the posts, whilst for solid posts capture occurs on both front and back surfaces. This is because fluid flow enters porous posts on the front surface and exits through the back, such that particles at the back surface are likely to be pushed off. With solid posts, particles are able to roll along the post surface and be captured at any location.

Fig. 5.

Capture of E. coli and PC3 cancer cells on post arrays at different spacings; (a) fluorescent images and angular capture locations of E. coli cells on nanoporous and solid post arrays with 20 and 200 μm gap. Post outlines are traced in dotted lines. Flow direction from left to right. Angular capture locations are plotted as percentage of cells captured in 30° segments; (b) capture efficiency of the first row of each array of nanoporous and solid posts; (c) fluorescent images and angular capture locations of PC3 cancer cells on nanoporous and solid post arrays with 50 and 200 μm gap. Post outlines are traced in dotted lines. Flow direction from left to right. Angular capture locations are plotted as percentage of cells captured in 30° segments; (d) capture efficiency of the first row of each array of nanoporous and solid posts.

Figs. 5a and 5b show the capture of Escherichia coli particles in buffer, comparing capture values between solid and nanoporous post arrays at two different array spacings. Escherichia coli are rod shaped bacteria with a length of ~2 μm, corresponding to a d_p/d_c = 0.02. We see a ~6-fold capture improvement at w/d_c = 0.2 and a ~2-fold capture improvement at w/d_c = 2, very close to the observed improvement in interception for the same d_p/d_c ratio. Figs. 5c and 5d show the capture of a PC3 cancer cell line in buffer, again comparing between solid and nanoporous post arrays at two different array spacings. PC3 cells are between 10 and 20 μm in size, roughly corresponding to a d_p/d_c = 0.1 with our posts. We see a ~4-fold capture improvement at w/d_c = 0.5 (we did not use w/d_c = 0.2 because the largest cells could bridge the gap and be physically trapped) and a ~1.5-fold capture improvement at w/d_c = 2. These values are slightly lower than the 5- and 2-fold interception improvements seen at these spacings for d_p/d_c = 0.1.

As we already noted, capture efficiency is a function of both the interception efficiency and the binding efficiency between the particle and the functionalized surface. In previous work,¹⁴ we have qualitatively compared the level of receptor density on the surface of VACNT posts versus PDMS posts, based on our current functionalization methods for each, using fluorescent proteins, and showed that the PDMS surface had a higher level of receptors. This is not surprising as the surfaces of the VACNT posts are 99% porous. From our capture results, it appears that for bacteria cells, this difference in functionalization does not significantly affect capture results when comparing nanoporous with solid posts, and that the same order of improvement is seen in capture as in interception. However, for large mammalian cancer cells, the relative size of the capture improvement of nanoporous posts over solid posts is slightly reduced compared to the interception improvement. This is most likely because larger cancer cells experience a much greater shear stress at the post surface than smaller bacteria cells, such that the higher receptor density on the solid posts provide an advantage in the binding efficiency, which somewhat offsets its comparative disadvantage in interception efficiency. Despite this effect, there is still a dramatic improvement in capture observed for both cell types. It can also be noted from the rose plots that the locations of cancer cell capture are more clustered around the top and bottom surfaces of the posts (close to ±90°) compared to locations of bacteria cell capture, which are more concentrated at the very front edge of the post (between ±30°). This suggests that more rolling is needed for capture of the larger cancer cells.

These experiments show capture improvements in the first row of a simple hexagonal post array when comparing solid post arrays with nanoporous arrays of the same geometry. Since the main goal of the capture experiments was to verify the improvement in interception that we found also by looking at posts in the first row of the array, we have not optimized the geometry for subsequent rows of the array. The careful design of array geometry, for example by staggering each row of the array differently, will help to ensure that the interception bands of later rows cover flow streams missed by the interception bands of earlier rows. This would help to achieve good overall capture efficiency for the device. Future work on optimization of device design would also include exploring geometries other than circular cylinders as the individual array elements, and characterization of flow to ensure good binding efficiency.

Conclusions

In this work, we studied the interception efficiencies of particles in solution by cylindrical posts in microfluidic channels, through both theoretical analysis and experimental studies. Solid posts fabricated using standard soft lithography were compared with nanoporous posts fabricated using ultra-high porosity carbon nanotube forests. We showed that nanoporous posts significantly improve particle interception through two mechanisms: first, fluid streamlines passing through the porous post bring particles that traverse along them directly to the post surface; second, the highly porous post surface reduces the hydrodynamic resistance that prevents particles from contacting solid surfaces. The interception efficiency can be further enhanced by increasing the Darcy number of individual nanoporous posts or increasing the packing density of post arrays. We demonstrated using both bacteria and cancer cells that the increase in interception efficiency also results in improved capture efficiency under idealized conditions. Although we chose the simple geometry of circular microposts in these experiments, other micro-element geometries may be explored. Future work could include optimization of both interception efficiency and binding efficiency to produce a new class of high isolation efficiency, low footprint area devices for specific cell isolation using porous microfluidics, and validation of the idea under realistic conditions in bodily fluids such as peripheral blood.