Variation in Outcomes for Risk-Stratified Pediatric Cardiac Surgical Operations: An Analysis of the STS Congenital Heart Surgery Database

Abstract

Background.

We evaluated outcomes for groups of risk-stratified operations in The Society of Thoracic Surgeons Congenital Heart Surgery Database to provide contemporary benchmarks and examine variation between centers.

Methods.

Patients undergoing surgery from 2005 to 2009 were included. Centers with more than 10% missing data were excluded. Discharge mortality and postoperative length of stay (PLOS) among patients discharged alive were calculated for groups of risk-stratified operations using the five Society of Thoracic Surgeons-European Association for Cardio-Thoracic Surgery Congenital Heart Surgery mortality categories (STAT Mortality Categories). Power for analyzing between-center differences in outcome was determined for each STAT Mortality Category. Variation was evaluated using funnel plots and Bayesian hierarchical modeling.

Results.

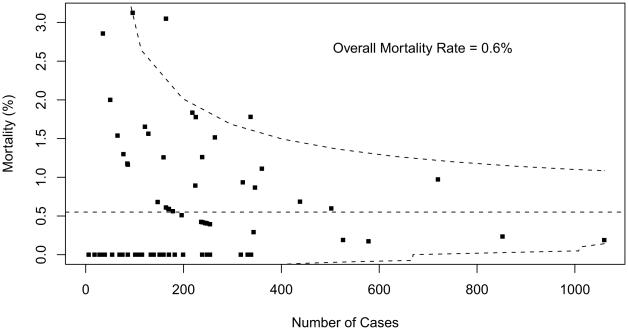
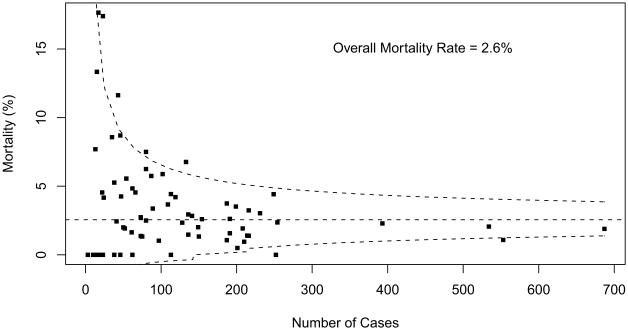
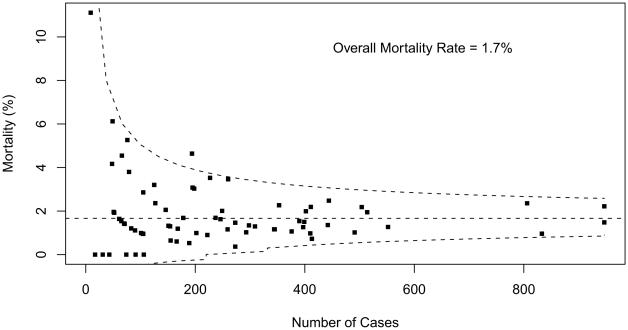
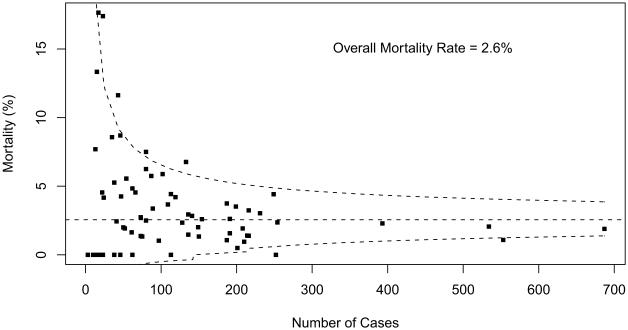
In this analysis of risk-stratified operations, 58,506 index operations at 73 centers were included. Overall discharge mortality (interquartile range among programs with more than 10 cases) was as follows: STAT Category 1 = 0.55% (0% to 1.0%), STAT Category 2 = 1.7% (1.0% to 2.2%), STAT Category 3 = 2.6% (1.1% to 4.4%), STAT Category 4 = 8.0% (6.3% to 11.1%), and STAT Category 5 = 18.4% (13.9% to 27.9%). Funnel plots with 95% prediction limits revealed the number of centers characterized as outliers by STAT Mortality Categories was as follows: Category 1 = 3 (4.1%), Category 2 = 1 (1.4%), Category 3 = 7 (9.7%), Category 4 = 13 (17.8%), and Category 5 = 13 (18.6%). Between-center variation in PLOS was analyzed for all STAT Categories and was greatest for STAT Category 5 operations.

Conclusions.

This analysis documents contemporary benchmarks for risk-stratified pediatric cardiac surgical operations grouped by STAT Mortality Categories and the range of outcomes among centers. Variation was greatest for the more complex operations. These data may aid in the design and planning of quality assessment and quality improvement initiatives.

The Society of Thoracic Surgeons Congenital Heart Surgery Database (STS-CHSDB) is the largest database in North America that tracks the outcomes of pediatric and congenital cardiac surgery [1-3]. As of January 1, 2011, participants in the STS-CHSDB include 96 of the estimated 122 congenital cardiac surgical programs in the United States [4]. One of the major goals of the STS-CHDB is to facilitate the improvement of quality in pediatric cardiac surgical programs in North America.

Our group previously published an analysis of variation in outcomes for eight common pediatric cardiac surgical benchmark operations, which demonstrated that even with the use of 5 years of data, it is not possible to perform statistically meaningful comparisons of mortality between centers for most individual operations because of the relatively small datasets for many operations at most centers [5]. Separately, we previously published an empirically derived method of grouping congenital and pediatric cardiac operations with similar estimated risk of in-hospital mortality to create larger pooled datasets for analyzing and comparing outcomes [6]. This proposed system of grouping operations, known as The Society of Thoracic Surgeons-European Association of Cardio-Thoracic Surgery Congenital Heart Surgery Mortality Categories (STAT Mortality Categories), has been incorporated into statistical models to adjust for case mix when analyzing outcomes of participants in the STS-CHSDB [6].

The purpose of this analysis is to document current outcomes for groups of risk-stratified operations in the STS-CHSDB, using the STAT Mortality Categories, in order to provide contemporary benchmarks and examine variation in outcomes between centers. In this manuscript, the terms “centers” and “participants” are used as synonyms to denote pediatric and congenital cardiac surgical programs that participate in the STS-CHSDB. The specific goal of the analysis was to describe discharge mortality and postoperative length of stay (PLOS) for risk-stratified operations grouped by STAT Mortality Category and to examine between-participant variation in these endpoints.

Material and Methods

Study Population

The study population consists of patients who underwent operations that met the inclusionary and exclusionary criteria listed in Table 1.

Table 1.

Inclusionary and Exclusionary Criteria

The study population includes patients who met the following   criteria:

Age less than 18 years

Surgical dates, January 1, 2005 to December 31, 2009,   inclusive

Operation type: CPB or No CPB Cardiovascular

Operation was index operation of admission (ie, first   operation of a given admission with operation type CPB   or No CPB Cardiovascular)

The record of the operation had nonmissing data for   discharge mortality status and PLOS

STS participant had at least 90% complete data for   discharge mortality, PLOS, preoperative risk factors, and   noncardiac abnormalities

Operation was classified into one of the five STAT   Categories

Patients weighing 2,500 g or less undergoing patent ductus   arteriosus ligation as the primary procedure were   excluded from analysis [7]

Patients who died before discharge from the hospital were   excluded from all analyses of PLOS

CPB = cardiopulmonary bypass; PLOS = postoperative length of stay; STAT = The Society of Thoracic Surgeons (STS)-European Association for Cardio-Thoracic Surgery (EACTS) Congenital Heart Surgery Mortality Categories.

STAT Mortality Categories

The methodology of the development of the STAT Mortality Score and the STAT Mortality Categories was previously described [6]. Briefly, mortality risk was estimated for 148 types of operative procedures using data from 77,294 operations entered into the EACTS Congenital Heart Surgery Database (33,360 operations) and the STS-CHSD (43,934 patients) between 2002 and 2007. Operations were sorted by increasing risk and grouped into five categories (the STAT Mortality Categories [2009]) that were chosen to be optimal with respect to minimizing within-category variation and maximizing between-category variation in mortality risk. STAT Categories 1, 2, 3, 4, and 5 contained 26, 52, 27, 37, and 6 procedures, respectively; patients undergoing an index operation in STAT Categories 1, 2, 3, 4, and 5 had an aggregate discharge mortality of 0.8%, 2.6%, 5.0%, 9.9%, and 23.1%, respectively [6].

Analytic Methods

OUTCOME VARIABLES

Outcome variables in this analysis are mortality before discharge from the hospital (“discharge mortality”) and PLOS among patients discharged alive. In this manuscript, the word “mortality” is used to represent “discharge mortality” [7, 8]. Previous publications from the STS-CHSDB have used PLOS as one measure of operative morbidity [7-9]. In these prior analyses, prolonged PLOS was regarded as a very general proxy measure of morbidity [9].

RAW DATA SUMMARY

For each STAT Category, the overall and participant-specific discharge mortality rates and the overall and participant-specific average PLOS were calculated. Participant-specific results were summarized by the median (50th percentile), range (minimum and maximum), and interquartile range (25th and 75th percentiles). Data are presented for all sites and for sites with 10 or more cases during the study period in the specified STAT Category.

FUNNEL PLOTS

For each STAT Category, participant-specific unadjusted mortality rates were plotted against the number of eligible cases (ie, the denominator). Lines depicting exact 95% binomial prediction limits were overlaid to make a “funnel plot” [10]. For each individual participant, the probability of observing a mortality rate that falls on or outside of the plotted prediction limits is less than 5%, if the participant's true mortality rate is equal to the overall aggregate mortality rate of all STS participants in the analysis.

SAMPLE SIZE CONSIDERATIONS

Before analyzing participant-specific outcomes, we performed a simple simulation to shed light on the potential statistical precision available across hospitals. First, for each STAT Category, we calculated the minimum sample size required to achieve 50% power to detect a twofold increase in the mortality rate [11] (versus the overall aggregate mortality rate of all participants) using a one-sided type I error rate of 0.05. For example, assuming an overall aggregate mortality rate of 7%, a sample size of 48 operations would be required to attain 50% power to detect a doubling of the mortality rate to 14%. We then counted the number of participants who met this minimum required sample size. Similarly, for PLOS, we counted the number of participants who met the sample size required to achieve 50% power to detect a doubling of the mean PLOS with a one-sided 0.05-level test. For simplicity, power for PLOS was calculated by assuming an exponential distribution for time to hospital discharge. (This assumption was only made for sample size calculations, not for the actual data analysis.)

BAYESIAN ESTIMATION OF BETWEEN-PARTICIPANT VARIATION

Bayesian hierarchical modeling was used to estimate the distribution of true unadjusted and adjusted participant-specific mortality rates and average PLOS. Methods of estimation were described in our previous publication examining between-center variation in outcomes for individual “benchmark” operations [5]. Covariates for risk-adjustment included age (linear and quadratic), weight-for-age-and-sex z score, sex (male versus female/other/ missing), any preoperative risk factor (yes/no), and any noncardiac abnormality (yes/no). The STS-CHSDB contains standard definitions adopted in 2007 for preoperative risk factors and noncardiac abnormalities [12]. Un-adjusted and risk-adjusted mortality rates and average PLOS were estimated by calculating their Bayesian point estimates (posterior means) along with 95% probability intervals (PIs). Inferences were based on Markov-Chain Monte Carlo (MCMC) simulations as implemented in Win-BUGS version 1.4 software. A participant's risk-adjusted mortality rate and risk-adjusted average PLOS were defined as the mortality rate and average PLOS that would be predicted for a participant if risk factor values for each of their patients were equal to the STS population average.

Two approaches were used for quantifying overall between-participant signal variation in mortality. First, we estimated the ratio of the average probability of mortality among hospitals above the 90th percentile of the mortality distribution (high mortality hospitals) compared with those below the 10th percentile (low mortality hospitals). Second, we estimated the Gini index of hospital-specific mortality probabilities. The Gini index ranges from 0 to 1. A larger number means more variation between hospitals.

All analyses were performed using SAS version 9.2 (SAS Institute, Cary, NC), R version 2.8, and WinBUGS version 1.4.

Institutional Review Board Approval

This study was approved by the Duke University Health System Institutional Review Board. Because the data used in analysis represent a limited data set (no direct patient identifiers) that was originally collected for non-research purposes, and the investigators do not know the identity of individual patients, the analysis of these data was declared by the Duke University Health System Institutional Review Board to be research not involving human subjects [13].

Results

From 2005 to 2009, inclusive, 85 centers (United States and Canada) submitted data to STS-CHSDB, and discharge mortality of index cardiac operations was 4.0% (3,418 of 86,297). For patients aged less than 18 years, from 2005 to 2009, inclusive, 85 centers submitted data to STS-CHSDB, and discharge mortality of index cardiac operations was 4.1% (3,309 of 81,062). Overall, 58,506 index operations at 73 centers were included in this analysis of risk-stratified operations.

Raw Data and Funnel Plots

Table 2 summarizes overall aggregate and participant-specific results for mortality and PLOS for each STAT Category. Mortality data are also displayed as funnel plots for these five STAT Categories (Figs 1 to 5). These funnel plots demonstrate that most programs fall within the 95% prediction limits and are not considered outliers within the STAT Category. Table 3 documents the number of outliers identified in the funnel plots stratified by STAT Category. Funnel plots revealed the number of centers characterized as outliers (based on two one-sided 0.025-level tests) by STAT Categories: Category 1 = 3 (4.1%), Category 2 = 1 (1.4%), Category 3 = 7 (9.7%), Category 4 = 13 (17.8%), and Category 5 = 13 (18.6%). By design, approximately 5% of participants would be expected to have mortality rates that fall outside of the 95% prediction interval even if true probability of mortality did not vary across centers. For Categories 1 and 2, the fact that fewer than 5% of participants were outside the 95% prediction limit may be attributed to the lack of statistical power for assessing mortality rates in groups of procedures with few deaths.

Table 2.

Raw Data Summary

Variable	STAT Category 1	STAT Category 2	STAT Category 3	STAT Category 4	STAT Category 5
All participants (centers)
Number of participants	73	73	72	73	70
Number of operations	15,441	17,994	8,989	13,375	2,707
Average, participant-specific sample size	211.5	246.5	124.8	183.2	38.7
Range, participant-specific sample sizes	6–1,060	9–947	3–687	3–872	1–212
Aggregate mortality rate	0.55%	1.7%	2.6%	8.0%	18.4%
Median participant-specific mortality rate	0.23%	1.41%	2.40%	8.33%	20.78%
Range, participant-specific mortality rates	0%–3.1%	0%–11.1%	0%–17.6%	0%–21.9%	0%–100%
IQR, participant-specific mortality rates	0.0%–0.9%	1.0%–2.2%	1.1%–4.4%	5.7%–10.9%	12.0%–28.6%
Aggregate average PLOS per patient, days	5.9	9.9	12.7	19.6	33.5
Median participant-specific average PLOS, days	5.8	9.9	12.7	19.6	34.1
Range, participant-specific average PLOS, days	3.5–9.7	4.9–22.9	6.0–23.4	8.3–46.4	12.0–109.0
IQR, participant-specific average PLOS	5.0–6.7	8.1–11.7	11.2–14.8	16.9–22.8	28.5–40.7
Sites with n ≥10
Number of participants	72	72	71	71	52
Number of operations	15,435	17,985	8,986	13,369	2,628
Average, participant-specific sample size	214.4	249.8	126.6	188.3	50.5
Range, participant-specific sample sizes	18–1060	17–947	10–687	20–872	10–212
Aggregate mortality rate	0.55%	1.7%	2.6%	8.0%	18.4%
Median participant-specific mortality rate	0.26%	1.4%	2.4%	8.6%	21.5%
Range, participant-specific mortality rates	0%–3.1%	0%–6.1%	0%–17.6%	0%–21.9%	4.8%–50%
IQR, participant-specific mortality rates	0%–1.0%	1.0%–2.2%	1.1%–4.4%	6.3%–11.1%	13.9%–27.9%
Aggregate average PLOS per patient (days)	5.9	9.9	12.7	19.6	33.5
Median participant-specific average PLOS, days	5.8	9.9	12.8	19.8	33.5
Range, participant-specific average PLOS, days	3.5–9.7	4.9–22.9	6.9–23.4	11.9–46.4	13.5–84.4
IQR, participant-specific average PLOS	5.0–6.6	8.2–11.7	11.2–15.0	16.9–22.9	28.9–42.7

IQR = interquartile range; PLOS = postoperative length of stay; STAT = The Society of Thoracic Surgeons (STS)-European Association for Cardio-Thoracic Surgery (EACTS) Congenital Heart Surgery Mortality Categories.

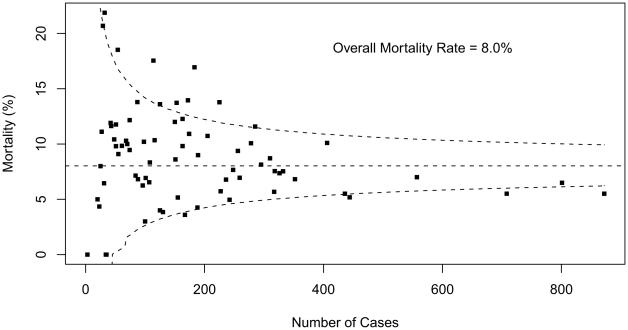
Fig 1.

Mortality data are displayed as a funnel plot for STAT Category 1 operations. The horizontal dashed line depicts aggregate STS mortality before discharge. Dashed lines depicting exact 95% binomial prediction limits were overlaid to make a funnel plot. Squares represent the number of cases and mortality before discharge for individual STS Congenital Heart Surgery Database participants (centers). (STAT = The Society of Thoracic Surgeons [STS]-European Association for Cardio-Thoracic Surgery [EACTS] Congenital Heart Surgery Mortality Categories.)

Fig 5.

Mortality data displayed as a funnel plot for STAT Category 5 operations. The horizontal dashed line depicts aggregate STS mortality before discharge. Dashed lines depicting exact 95% binomial prediction limits were overlaid to make a funnel plot. Squares represent the number of cases and mortality before discharge for individual STS Congenital Heart Surgery Database participants (centers). (STAT = The Society of Thoracic Surgeons [STS]-European Association for Cardio-Thoracic Surgery [EACTS] Congenital Heart Surgery Mortality Categories.)

Table 3.

Number of Outliers by Funnel Plots Stratified by STAT Category

All Participants	STAT Category 1	STAT Category 2	STAT Category 3	STAT Category 4	STAT Category 5
Number of participants	73	73	72	73	70
Number of operations	15,441	17,994	8,989	13,375	2,707
Number of outliers	3	1	7	13	13
Percentage of outliers	4.1%	1.4%	9.7%	17.8%	18.6%
Number of high-performing outliers	0	0	2	4	7
Percentage of high-performing outliers	0.0%	0.0%	2.8%	5.5%	10.0%
Number of low-performing outliers	3	1	5	9	6
Percentage of low-performing outliers	4.1%	1.4%	6.9%	12.3%	8.6%

STAT = The Society of Thoracic Surgeons (STS)-European Association for Cardio-Thoracic Surgery (EACTS) Congenital Heart Surgery Mortality Categories.

Feasibility of Analyzing Between-Center Variation

The number of cases required to detect a twofold increase in the mortality rate with at least 50% power ranged from 697 for STAT Category 1, to 18 for STAT Category 5 (Table 4). Only in STAT Categories 4 and 5 did more than half the centers meet the criterion for having enough cases to detect a twofold increase in the mortality rate with at least 50% power. Based on these results, Bayesian estimation of between-participant variation was only analyzed for STAT Categories 4 and 5.

Table 4.

Feasibility of Analyzing Between-Center Variation

Variable	STAT Category 1	STAT Category 2	STAT Category 3	STAT Category 4	STAT Category 5
Number of participants included in analysis	73	73	72	73	70
Aggregate mortality rate	0.55%	1.7%	2.6%	8.0%	18.4%
Sample size required for 50% power to detect 2× increase in  mortality	697	230	150	42	18
Number of participants meeting mortality requirement	3	31	21	62	44
Number of participants meeting PLOS requirement (≥5 cases)	73	73	71	71	60

PLOS = postoperative length of stay; STAT = The Society of Thoracic Surgeons (STS)-European Association for Cardio-Thoracic Surgery (EACTS) Congenital Heart Surgery Mortality Categories.

The required sample size to detect a doubling of the mean PLOS is five operations (Table 4). Based on these results, between-participant variation in PLOS was analyzed for all operations. All participants were included regardless of sample size.

Bayesian Estimation of Between-Participant Variation

Table 5 documents unadjusted and risk-adjusted Bayesian estimation of between-participant variation for mortality and PLOS. The estimated 25th and 75th percentiles for risk-adjusted mortality in STAT Category 5 are 12.9% and 21.8%, respectively. We estimate that 25% of participants have a true risk-adjusted mortality rate less than 12.9%, and that 75% of participants have a true mortality rate less than 21.8%. The estimated minimum and maximum true risk-adjusted mortality rates are 6.5% and 38.4%, respectively. We estimate that the highest mortality rate is approximately sixfold higher than the lowest. Variation in PLOS was also substantial, with a trend suggesting greater variation for highest risk operations.

Table 5.

Results of Bayesian Hierarchical Models: Estimated Percentiles of Distribution of Hospital-Specific Mortality Rates and Average Postoperative Length of Sta

		Estimate (95% Bayesian Probability Interval)
STAT Category	Minimum	25th Percentile	50th Percentile	75th Percentile	Maximum	Bottom 10%/ Top 10%	Estimated Gini Index, X100
Hospital-specific mortality rates, unadjusted
4	4.2 (2.8–5.3)	6.7 (6.0–7.4)	8.2 (7.6–9.0)	10.1 (9.2–11.1)	16.3 (13.1–21.1)	2.8 (2.1–3.7)	16.6 (12.4–21.0)
5	7.3 (4.0–10.4)	14.7 (12.4–16.9)	19.5 (17.4–21.9)	25.0 (21.9–28.4)	43.3 (33.6–56.7)	3.8 (2.6–5.6)	21.2 (15.8–26.7)
Hospital-specific mortality rates, risk adjusted
4	3.1 (2.1–4.2)	5.2 (4.6–5.9)	6.4 (5.7–7.0)	7.8 (6.9–8.7)	12.8 (9.8–16.9)	2.6 (1.9–3.4)	16.8 (11.8–21.3)
5	6.5 (3.5–9.4)	12.9 (10.8–15.0)	16.9 (14.9–19.2)	21.8 (18.9–25.0)	38.4 (28.7–52.3)	3.8 (2.6–5.7)	21.0 (15.3–27.3)
Hospital-specific average PLOS, unadjusted
1	4.7 (4.3–4.9)	5.7 (5.5–5.8)	6.2 (6.1–6.4)	6.9 (6.7–7.1)	8.8 (8.2–9.7)	1.6 (1.6–1.7)	8.4 (7.6–9.2)
2	7.0 (6.1–7.7)	9.0 (8.7–9.3)	9.9 (9.6–10.1)	10.9 (10.6–11.2)	14.0 (12.7–16.2)	1.6 (1.5–1.8)	8.0 (7.0–9.0)
3	9.2 (8.2–10.1)	11.7 (11.3–12.1)	12.7 (12.4–13.1)	13.7 (13.3–14.1)	18.5 (16.9–20.6)	1.6 (1.5–1.8)	7.4 (6.1–8.7)
4	13.2 (11.6–14.7)	17.4 (16.8–18.0)	19.4 (18.7–20.0)	21.5 (20.8–22.2)	29.0 (25.8–34.3)	1.7 (1.6–1.9)	8.8 (7.6–10.1)
5	18.5 (14.9–22.4)	30.1 (28.3–32.0)	35.1 (33.1–37.1)	40.8 (38.1–43.9)	62.3 (51.9–80.2)	2.3 (2.0–2.8)	13.4 (10.9–16.1)
Hospital-specific average PLOS, risk adjusted
1	4.6 (4.3–4.8)	5.5 (5.4–5.6)	6.0 (5.8–6.1)	6.7 (6.5–6.9)	8.2 (7.7–9.0)	1.5 (1.4–1.6)	7.7 (7.0–8.4)
2	7.0 (6.3–7.6)	8.8 (8.5–9.0)	9.7 (9.4–9.9)	10.5 (10.3–10.8)	13.8 (12.5–15.9)	1.5 (1.4–1.6)	7.8 (6.9–8.8)
3	9.2 (8.3–10.0)	11.4 (11.1–11.8)	12.4 (12.1–12.7)	13.4 (13.0–13.8)	17.2 (15.8–19.4)	1.5 (1.4–1.6)	6.9 (5.8–8.1)
4	13.1 (11.7–14.3)	16.8 (16.2–17.4)	18.8 (18.2–19.5)	20.8 (20.2–21.5)	27.8 (25.1–32.6)	1.6 (1.5–1.7)	9.0 (7.9–10.1)
5	18.1 (14.7–22.0)	30.1 (28.5–31.9)	34.7 (32.8–36.7)	40.2 (37.8–42.9)	61.3 (50.9–79.6)	2.2 (1.9–2.6)	12.8 (10.3–15.3)

PLOS = postoperative length of stay; STAT = The Society of Thoracic Surgeons (STS)-European Association for Cardio-Thoracic Surgery (EACTS) Congenital Heart Surgery Mortality Categories.

Comment

The STS-CHSDB is the largest congenital heart surgery database in North America. This analysis documents contemporary benchmarks for risk-stratified pediatric cardiac surgical operations of varying levels of risk, and the degree of variation in outcome between centers. Variation in outcome was most prominent for the more complex operations. These data can aid in quality assessment and quality improvement initiatives [14]. Variation in outcomes across centers demonstrates opportunities for multiinstitutional collaboration to improve quality [14].

Knowledge of the distribution of adverse event rates across hospitals can be used to establish benchmarks and facilitate quality improvement. However, estimation of outcomes for an individual hospital is not straightforward because the number of patients per hospital is often quite small. Grouping of operations into strata of similar average risk will increase the number of patients available for analysis. We [2] previously reported, “It is apparent that even with 5 years of data, many individual operations are not performed frequently enough at any given institution to detect a doubling of mortality.... Nevertheless, the strategy of analyzing mortality using funnel plots can help to identify programs that are outliers with respect to mortality for specific operations.” Funnel plots have been utilized by the United Kingdom Central Cardiac Audit Database since 2000 and form the basis of their public reporting initiative [2]. This current report presents the initial use of data from the STSCHSDB to generate funnel plots that report outcomes of operations grouped into strata of similar average risk of discharge mortality. These data create an opportunity for interinstitutional collaboration in optimizing structure and process, with a goal of improving overall quality of care and outcome. The identification of high-performing centers creates opportunities for learning from these high-performing centers. Similarly, the identification of low-performing centers creates opportunities for optimizing structure and process at these low-performing centers to improve outcome.

Risk stratification using the five STAT Mortality Categories [6] allows the grouping of operations into similar strata of risk and, therefore, permits analysis of higher volumes of cases than using individual operations. This grouping strategy allows center-specific mortality rates and other outcomes to be estimated with relatively greater statistical precision compared with a strategy of analyzing individual operations. Combining operations of roughly comparable complexity into the five STAT Mortality Categories allows for the identification of more outliers than is possible using individual operations [5]. For purposes of comparing outcomes across centers, identifying areas of variability, and determining objectives for quality improvement initiatives, it is very informative to combine operations into the five STAT Mortality Categories because this methodology provides more information and greater discrimination than similar analyses based on individual operations. This concept is especially important because many individual congenital cardiac operations are performed too rarely to support accurate estimation or comparison of center-specific results [5]. This analysis of variation in outcomes of mortality and PLOS stratified by the five STAT Mortality Categories represents the development of a tool to aid the rational implementation of interinstitutional sharing of structure and process to improve overall quality of care and outcome.

In conclusion, this analysis documents (1) contemporary benchmarks for risk-stratified pediatric cardiac surgical operations, and (2) the range of outcomes across centers. Variation in outcome was most prominent for more complex operations. Even with the use of 5 years of data, because of the relatively small datasets for many operations at most centers, it is not possible to perform statistically meaningful comparisons between centers based on mortality after individual benchmark operations. Grouping of operations into strata of similar risk facilitates interinstitutional comparisons. Funnel plots of risk-stratified operations can help to identify outliers. These data can aid in quality assessment and quality improvement initiatives. Variation in outcomes across centers demonstrates opportunities for multiinstitutional collaboration to improve quality.

DISCUSSION

DR RICHARD MAINWARING (Stanford, CA): Jeff, I want to congratulate you on a great presentation and for forwarding the manuscript. Basically, I am going to have one comment and one question.

The STS Congenital Heart Surgery Database analyzed a wide variety of outcome variables, as we saw in your presentation. Each institution receives in the report a summary of these, and you can sort of compare on your own how you compare to the national averages. I would think that it would now be possible to generate a comprehensive score based on outcomes and risk adjustment for each program and rank them 1 through 103. These data would most likely create a bellshaped curve. There would be a group to the left that would represent the 5% of excellent programs and a similar triangle to the right that would represent the underperforming programs.

It seems to me the one important way to improve quality would be to focus on those underperforming programs and see if we couldn't offer some help or aid to those programs. That would be where the biggest impact would be on quality. In your manuscript you allude to this in the discussion, and I quote, “the identification of low-performing centers creates opportunities for optimizing structure and process to improve outcome.” And this concept would seem to be similar to the initiative that was implemented in England after the Bristol affair. So my question is whether you think the STS database will be utilized to identify and provide help for underperforming programs, and if so, whether you could speculate on a time line for this?

I enjoyed the paper and would like to thank the Society for the privilege of discussing the paper.

DR JACOBS: Thank you, Rick. I think that the point that you are raising is really the most important point related to these data. I agree that variation in quality of care can likely be graphically depicted with a bell-shaped curve. One end of the bell-shaped curve would contain the five percent of programs that can be classified as lower performing programs. The other end of the bell curve would contain the five percent of programs that can be classified higher performing programs. The identification of high-performing centers creates opportunities for learning from these high-performing centers. Similarly, the identification of low-performing centers creates opportunities for optimizing structure and process at these low-performing centers to improve outcome.

Based on this bell-shaped curve, I would like to describe two different ways to approach quality improvement. One strategy involves eliminating the lower 5% of programs, an approach that truly does little to affect overall system quality. I feel strongly that this approach is not a strategy that we should implement. A second more favorable strategy involves eliminating unnecessary variation by standardizing structure and process in order to achieve and document continuous improvement in outcome. Therefore, instead of trying to just focus on eliminating the lower 5%, one should focus on ways that one could learn from the high-performing programs, transfer those lessons to the lower-performing programs, and at the same time narrow the width of the overall bell-shaped curve to minimize interinstitutional variability. This preferred strategy will narrow the width of the bell-shaped curve through reducing unnecessary variation, and simultaneously shift the mean of the bell-shaped curve towards higher quality. This approach represents the ideal strategy for overall quality improvement. So, the goal is not really to chop off one end of the bell curve but rather to narrow overall institutional variability and have a narrower bell-shaped curve, with the overall mean quality moved in the direction toward better quality.

This strategy is how we plan to use STS data. Under John Mayer's Presidency of STS, committees were established to operationalize some of these ideas. We are actively working toward developing methods to use STS data to try to learn from the better performing programs and improve quality overall. Thanks.

DR JEFFREY S. HEINLE (Houston, TX): Jeff, are these funnel curves part of the summary the centers get, or will they be, or are they now?

DR JACOBS: In the STS Congenital Heart Surgery Database Feedback Reports that are currently distributed by STS every 6 months, we provide graphs that are pretty similar to these funnel plots, but not identical to these funnel plots. In these graphs currently in the Feedback Reports, we sort de-identified programs from low volume to high volume as one moves from left to right on the x-axis; meanwhile, the y-axis is discharge mortality. The mortality of each program is displayed as a dot with a vertical bar that represents the 95% confidence interval. A horizontal line represents the aggregate STS mortality, allowing one to determine whether the mortality of a given program differs from the STS aggregate with 95% confidence. Thus, programs that are outliers in any STAT Category can be identified. These graphs are in the Feedback Report, and although they are not identical to the funnel plots shown in this presentation, they do convey similar information. In the future, we actually may transition to something even closer to these funnel plots, because they really allow one to identify where a given program is, and if the difference between the performance of a given program and the STS aggregate is actually statistically identical to the aggregate or statistically different.

DR JAMES S. TWEDDELL (Milwaukee, WI): I thought that was a great presentation. It was very interesting and thought-provoking information. I have one comment. The funnel plots and the 95% confidence interval always impress me as being fairly physician and program friendly.

DR JACOBS: Correct, yes. But, the funnel plots and the 95% confidence intervals do clearly allow for the identification of outliers.

DR TWEDDELL: If you showed any one of those funnel plots and did a best-fit line, it would look like there is an important volume effect.

DR JACOBS: Jim, I do agree. In fact, one could also say that more lower performing outliers exist in the low-volume centers than in the high-volume centers, and more high performing outliers exist in the high-volume centers than in the low-volume centers. But, the other critical fact is that one cannot really apply this rule to every program, because there are some low-volume programs that do great and there are some high-volume programs that do not do as well. So although that rule (or relationship) about program volume and outcome makes sense on the whole, it really cannot be applied to every individual program.

DR TWEDDELL: Thank you.

DR ANDREW J. LODGE (Durham, NC): Jeff, these data may be very useful for us to try and initiate quality improvement within the community of congenital heart surgeons and cardiologists, but how do you foresee being able to protect them so that they are not used inappropriately by people who don't understand them as well as we do?

DR JACOBS: That is a good question. Before I answer this question, I would like to emphasize that our strategy to use these data to improve quality will include the implementation of an optional web based Quality Module of the STS Congenital Heart Surgery Database that will be available in early 2012. The development and implementation of this Quality Module is funded by an NIH grant that we have, and our hope is that this Quality Module will help us transform the STS Congenital Heart Surgery Database from a tool for just doing outcomes analysis to a platform for doing more quality improvement initiatives. We are also exploring strategies to create collaboratives aimed at quality improvement, using the STS Congenital Heart Surgery Database as a foundation.

To address your question, these data are owned by STS, and the STS decides who gets these data. Efforts are underway to develop strategies to publicly report these data in a responsible professional manner, with a pilot project underway in the State of Pennsylvania. This initiative is similar to the public reporting initiative that is already operationalized based on the STS Adult Cardiac Surgery Database. As a professional society, it is our job to be certain that these data are used properly. We must strive to use these data to help us all improve our outcomes and not to close down programs. As a professional society, it is our professional responsibility to assure appropriate use of these data. Thank you.

Fig 2.

Mortality data displayed as a funnel plot for STAT Category 2 operations. The horizontal dashed line depicts aggregate STS mortality before discharge. Dashed lines depicting exact 95% binomial prediction limits were overlaid to make a funnel plot. Squares represent the number of cases and mortality before discharge for individual STS Congenital Heart Surgery Database participants (centers). (STAT = The Society of Thoracic Surgeons [STS]-European Association for Cardio-Thoracic Surgery [EACTS] Congenital Heart Surgery Mortality Categories.)

Fig 3.

Mortality data displayed as a funnel plot for STAT Category 3 operations. The horizontal dashed line depicts aggregate STS mortality before discharge. Dashed lines depicting exact 95% binomial prediction limits were overlaid to make a funnel plot. Squares represent the number of cases and mortality before discharge for individual STS Congenital Heart Surgery Database participants (centers). (STAT = The Society of Thoracic Surgeons [STS]-European Association for CardioThoracic Surgery [EACTS] Congenital Heart Surgery Mortality Categories.)

Fig 4.

Mortality data displayed as a funnel plot for STAT Category 4 operations. The horizontal dashed line depicts aggregate STS mortality before discharge. Dashed lines depicting exact 95% binomial prediction limits were overlaid to make a funnel plot. Squares represent the number of cases and mortality before discharge for individual STS Congenital Heart Surgery Database participants (centers). (STAT = The Society of Thoracic Surgeons [STS]-European Association for CardioThoracic Surgery [EACTS] Congenital Heart Surgery Mortality Categories.)