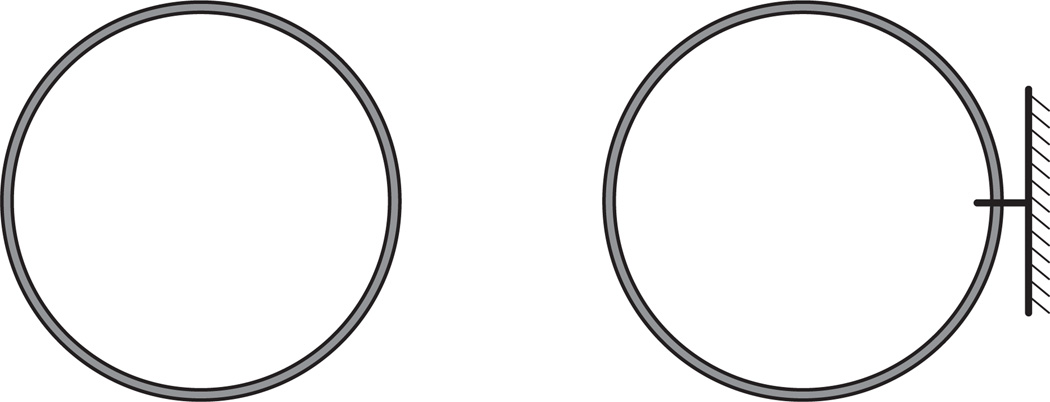Effect of the boundary conditions and influence of the rotational inertia on the vibrational modes of an elastic ring

Abstract

We present the small-amplitude vibrations of a circular elastic ring with periodic and clamped boundary conditions. We model the rod as an inextensible, isotropic, naturally straight Kirchhoff elastic rod and obtain the vibrational modes of the ring analytically for periodic boundary conditions and numerically for clamped boundary conditions. Of particular interest are the dependence of the vibrational modes on the torsional stress in the ring and the influence of the rotational inertia of the rod on the mode frequencies and amplitudes. In rescaling the Kirchhoff equations, we introduce a parameter inversely proportional to the aspect ratio of the rod. This parameter makes it possible to capture the influence of the rotational inertia of the rod. We find that the rotational inertia has a minor influence on the vibrational modes with the exception of a specific category of modes corresponding to high-frequency twisting deformations in the ring. Moreover, some of the vibrational modes over or undertwist the elastic rod depending on the imposed torsional stress in the ring.

1 Introduction

The determination of the natural frequencies and modes of vibration of elastic rings is a classical textbook problem. In his Treatise on the Mathematical Theory of Elasticity, Love [1] reported the vibrational frequencies for periodic boundary conditions, i.e. for a free ring, and several other authors have since complemented and enriched these results. The case of a ring clamped at one point, however, has received little, if any, attention (to the best of our knowledge there is only one reference, by Zakrzhevskii et al. [2], that addresses the subject). The lack of attention may stem in part from the fact that, for such boundary conditions, the relevant equations need to be solved numerically. The vibration of a ring clamped at one point is, nevertheless, a problem that arises in various contexts, such as the design of antennae [2], the study of fluctuations in circular biopolymers [3–6], and the dynamics of nano-structures [7,8].

We consider here the modes of vibration of elastic rods that at equilibrium are circular rings. Our study focuses on isotropic, inextensible, naturally straight rods. A ring is built by deforming a straight rod into a circle and sealing its two ends. In addition, we also account for the presence of a torsional stress in the rod, which can be achieved by twisting the ends of the rod before sealing them. We describe the dynamics of the ring by the Kirchhoff equations [9] and study small-amplitude oscillations around the undeformed ring. That is, we linearize the Kirchhoff equations around a static circular solution. We take advantage of an appropriate rescaling to study the influence of the rotational inertia of the rod on its vibrational modes and also to compare the vibrations of the ring with periodic boundary conditions to the vibrations of the clamped ring. Imposition of a normalization condition for the energy of the ring makes it possible to determine the amplitudes of the components of the vibrations. The vibrations can take place in the plane of the undeformed ring or normal to this plane or can also produce a twisting motion of the cross sections of the ring. In addition, the chirality and total twist of the vibrations are characterized through the calculation of the writhing number of each mode. Many of the results presented for periodic boundary conditions have already been described in the literature [10–15]. Our findings, however, provide new insights into the role played by the rotational inertia of the rod. For clamped boundary conditions, we believe that this is the first time these vibrational modes and their dependence on the imposed torsional stress have been reported. We also find for clamped boundary conditions that the rotational inertia causes a mixing between the twisting and flexural vibrations of the rod depending on the magnitude of the torsional stress in the ring. The dependence of the vibrations on the imposed torsional moment reveals other interesting behavior, such as nontrivial increases or decreases in the torsional stress in the ring caused by the vibrations.

We first introduce the Kirchhoff equations for a naturally straight rod (Section 2), and use these expressions to derive the equations for small-amplitude vibrations (Section 3). We then develop the apparatus required to describe the topology of the vibrating ring (Section 4) and briefly describe our approach to normal mode analysis (Section 5). Finally, we present our results (Section 6), and discuss the validity and the possible applications of our work (Section 7). The various appendices contain the details of the calculations, which have been omitted in the text for the sake of clarity.

2 Kirchhoff equations for an elastic rod

We present in this section the Kirchhoff equations [9] for elastic rods and rewrite them in a dimensionless form. The derivation of these equations is not presented here, and the interested reader can refer to other papers that address these details. For example, references [16–20] introduce the Kirchhoff equations with the use of a variational approach, while references [11, 21–23] present derivations based on momenta conservation laws.

We limit our work to the study of an isotropic, inextensible, and naturally straight elastic rod with a circular cross section of radius h. The elastic rod material is characterized by its Young modulus E and its shear modulus μ, which are related by the formula E = 2μ (1 + ν) where ν is the Poisson ratio (for most elastic materials $0\le \nu \le \frac{1}{2}$).

In the rest of this paper, we will denote the arc length of the rod as s and the time as t; derivatives with respect to s will be indicated by primes or upper-indices in parentheses, that is, for example, $\frac{{\partial }^{2}f(s,t)}{\partial s^2}=f″(s,t)=f^{(2)}(s,t)$. Derivatives with respect to time will be indicated by dots, that is, for example, $\frac{{\partial }^{2}f(s,t)}{\partial t^2}=\mathrm{f̈}(s,t)$.

2.1 Kirchhoff equations

The elastic rod is represented by its centerline and a material frame attached to the centerline. At any point along the centerline the orientation of the cross section is given by the axes, or directors, of the material frame. We first present the equations related to the kinematics of the rod, and then move on to the equations describing the mechanics of the rod.

2.1.1 Rod kinematics

The rod centerline is a three-dimensional curve and its path is denoted r(s,t) with s the arc length and t the time. The tangent of the centerline is defined as

$$\mathit{t}(s,t)=\mathit{r}\prime (s,t),$$ (1)

and the condition of inextensibility can be written as

$$\mathit{t}(s,t)·\mathit{t}(s,t)=1.$$ (2)

The material frame is a right-handed orthonormal triad denoted (d₁(s,t),d₂(s,t),d₃(s,t)), and defined in such a way that d₁(s,t) and d₂(s,t) span the plane of the cross section while d₃(s,t) is normal to it. This definition implicitly assumes that the cross sections remain planar and undeformed during the motion of the rod. In addition, we also assume that the cross sections remain normal to the centerline, that is,

$$\mathit{t}(s,t)={\mathit{d}}_3(s,t).$$ (3)

This assumption, known as the Navier-Bernoulli assumption, implies that we do not consider shear deformations in the rod. We henceforth use the notation d₃ to refer to the tangent.

It follows from these considerations that the motion of the material frame along the rod centerline at a fixed time and its time-dependence at a fixed arc length can be completely described by two vectors Ω(s,t) and ω(s,t) defined such that

$${\mathit{d}}_i^{\prime }(s,t)=\mathit{\Omega }(s,t)\times {\mathit{d}}_i(s,t)(i=1,2,3),$$ (4a)

$${\mathit{ḋ}}_i(s,t)=\mathit{\omega }(s,t)\times {\mathit{d}}_i(s,t)(i=1,2,3).$$ (4b)

The vector Ω(s,t) is referred to as the curvature vector and can be written as

$$\mathit{\Omega }(s,t)=\mathit{K}(s,t)+{\Omega }_3(s,t){\mathit{d}}_3(s,t),$$ (5)

where K(s,t) is the binormal curvature vector, that is,

$$\mathit{K}(s,t)={\mathit{d}}_3(s,t)\times {\mathit{d}}_3^{\prime }(s,t),$$ (6)

and Ω₃(s,t), the tangential component of Ω(s,t), is the twist density in the rod, i.e., the rate of rotation of the material frame around the tangent d₃(s,t). Similarly, the vector ω(s,t), referred to as the spin vector, corresponds to the angular velocities of the material frame around its axes and can be defined as

$$\mathit{\omega }(s,t)={\mathit{d}}_3(s,t)\times {\mathit{ḋ}}_3(s,t)+{\omega }_3(s,t){\mathit{d}}_3(s,t),$$ (7)

where ω₃(s,t), the tangential component of ω(s,t), is the axial spin velocity, i.e., the angular velocity of the material frame around d₃(s,t). The curvature and spin vectors both describe infinitesimal rotations of the material frame. The compatibility between these rotations implies that the cross derivatives of any of the material frame directors are equal. It then follows from Eq. (4a) and Eq. (4b) that

$$\mathit{\omega }\prime (s,t)=\mathit{\Omega ̇}(s,t)-\mathit{\omega }(s,t)\times \mathit{\Omega }(s,t).$$ (8)

2.1.2 Rod mechanics

The internal stress in the rod is described by the internal force n(s,t) and the internal moment m(s,t). These quantities are defined with respect to the centerline orientation given by s, that is, n(s,t) and m(s,t) are the stresses exerted by the part of the rod after s (∀s*, s* > s) onto the part of the rod before s (∀s*, s* < s). The internal force and internal moment are applied to the cross section center located at r(s,t) and correspond to the integrated stress transmitted across the cross sections.

The internal stress is related to the deformation of the rod, i.e., to the curvature K(s,t) = |K(s,t)| and the twist density Ω₃(s,t), through the constitutive relations. Within the linear elasticity approximation, the constitutive relations between the internal moment and the deformation are written as

$$\mathit{m}(s,t)=EI\mathit{K}(s,t)+\mu J{\Omega }_3(s,t){\mathit{d}}_3(s,t),$$ (9)

where I and J are, respectively, the moment of inertia and the axial moment of inertia of the rod cross sections. We recall that for a circular cross section I = πh⁴/4 and J = 2I = πh⁴/2. We implicitly assume here that in its undeformed state, i.e., free of any external loading, the rod is straight and untwisted. In other words, the reference configuration of the rod corresponds to a configuration with zero curvature and zero twist density. We point out that the undeformed state of the rod can be taken as twisted, in which case the tangential component of the moment is proportional to the excess twist density Ω₃(s,t) − τ⁰(s,t), where τ⁰(s,t) is the twist density in the undeformed state, taken to be zero in our case.

The Kirchhoff equations for an isotropic elastic rod are then obtained with the use of the momenta conservation laws (see, for example, the derivations in [22, 23]) and are written as

$$\mathit{n}\prime (s,t)=\rho \pi h^2\mathit{r̈}(s,t),$$ (10a)

$$\mathit{m}\prime (s,t)+{\mathit{d}}_3(s,t)\times \mathit{n}(s,t)=\rho I(\mathit{\omega ̇}(s,t)+\frac{\partial }{\partial t}({\omega }_3(s,t){\mathit{d}}_3(s,t))).$$ (10b)

Here we used the fact that J = 2I and ρ is the material density of the rod. The first equation corresponds to the balance of forces applied to the rod cross section, while the second corresponds to the balance of moments. We also note that the right-hand side of the last equation takes account of the rotational inertia of the rod. This will be discussed in further detail after we rescale the equations.

Conservation law for the twist density

The twisting moment U (s,t) in the rod (or torsional moment), defined as U (s,t) = m(s,t) · d₃(s,t) = μJΩ₃(s,t), can be related to the axial spin velocity of the material frame of the rod. The use of the tangential component of the second Kirchhoff equation (Eq. (10b)) yields the following conservation law for the twist density

$${\Omega }_3^{\prime }(s,t)=\frac{\rho }{\mu }{\mathrm{\omega ̇}}_3(s,t).$$ (11)

The interested reader is referred to [24] for a detailed study of the different conservation laws in the theory of elastic rods.

2.2 Rescaled Kirchhoff equations

We now rewrite the Kirchhoff equations in a dimensionless form. We note that the different assumptions underlying this elastic rod theory provide a natural rescaling of the equations. In particular, the Navier-Bernoulli assumption (Eq. (3)) and the linear elasticity approximation (Eq. (9)) require the rod to have a large aspect ratio 𝒜 = L/ h, that is, the length of the rod L is large compared to its radius (L ≫ h). Moreover, it is also necessary to assume that the magnitude of the bending and twisting deformations in the rod are small, that is, if we denote as R the length such that |Ω(s,t)| ~ 1/R, we must have R ≫ h. We use the length R as the characteristic length, which in our study of the vibration of an elastic ring will be naturally identified with the radius of the ring. We introduce the following rescaled quantities (our rescaling is similar to the one used in [25]), indicated by a hat symbol,

$$ŝ=s/R,\mathrm{t̂}=t/T,T=\left(\frac{2R}{h}\right)R\sqrt{\frac{\rho }{E}},$$ (12a)

$$\mathit{r̂}(ŝ,\mathrm{t̂})=\mathit{r}(s,t)/R,{\mathit{d̂}}_i(ŝ,\mathrm{t̂})={\mathit{d}}_i(s,t),$$ (12b)

$$\mathit{m̂}(ŝ,\mathrm{t̂})=\frac{R}{EI}\mathit{m}(s,t),\mathit{n̂}(ŝ,\mathrm{t̂})=\frac{R^2}{EI}\mathit{n}(s,t),$$ (12c)

$$\mathit{\Omega ̂}(ŝ,\mathrm{t̂})=R\mathit{\Omega }(s,t),\mathit{\omega ̂}(ŝ,\mathrm{t̂})=T\mathit{\omega }(s,t).$$ (12d)

The rescaled Kirchhoff equations then read as

$$\mathit{n̂}\prime (ŝ,\mathrm{t̂})=\ddot{\widehat{\mathit{r}}}(ŝ,\mathrm{t̂}),$$ (13a)

$$\mathit{m̂}\prime (ŝ,\mathrm{t̂})+{\mathit{d̂}}_3(ŝ,\mathrm{t̂})\times \mathit{n̂}(ŝ,\mathrm{t̂})={\eta }^2(\dot{\widehat{\mathit{\omega }}}(ŝ,\mathrm{t̂})+\frac{\partial }{\partial \mathrm{t̂}}({\mathrm{\omega ̂}}_3{\mathit{d̂}}_3(ŝ,\mathrm{t̂})\left)\right),$$ (13b)

where η = h/(2R) ≪ 1. The dimensionless constitutive relations (Eq. (9)) becomes

$$\mathit{m̂}(ŝ,\mathrm{t̂})={\mathit{d̂}}_3(ŝ,\mathrm{t̂})\times {\mathit{d̂}}_3^{\prime }(ŝ,\mathrm{t̂})+2\Gamma {\mathrm{\Omega ̂}}_3(ŝ,\mathrm{t̂}){\mathit{d̂}}_3(ŝ,\mathrm{t̂}),$$ (14)

where Γ = μ/E, and the conservation law for the twist density (Eq. (11)) is given by

$$\Gamma {\mathrm{\Omega ̂}}_3^{\prime }(ŝ,\mathrm{t̂})={\eta }^2{\dot{\widehat{\omega }}}_3(ŝ,\mathrm{t̂}).$$ (15)

We remark that our rescaling procedure naturally introduces the parameter η = h/ (2R) as a pre-factor of the rotational inertia term in the Kirchhoff equations. We note that η is inversely proportional to the aspect ratio of the rod 𝒜, through the relation η = π/𝒜. The assumptions underlying our model require that η ≪ 1, which simply means that the ring is expected to have a large aspect ratio (i.e., the ring radius is much larger than the rod radius). Typical values of η should be of the order of 10⁻² or less. We will later use some larger values of η for illustrative purposes but it has to be understood that, for these values, the shearing deformations in the rod and the three-dimensional elasticity effects may no longer be negligible.

The zero rotational inertia approximation

The limit η → 0 therefore corresponds to the approximation of zero rotational inertia and the Kirchhoff equations take the following simpler form,

$$\mathit{n̂}\prime (ŝ,\mathrm{t̂})=\ddot{\widehat{\mathit{r}}}(ŝ,\mathrm{t̂}),$$ (16a)

$$\mathit{m̂}\prime (ŝ,\mathrm{t̂})+{\mathit{d̂}}_3(ŝ,\mathrm{t̂})\times \mathit{n̂}(ŝ,\mathrm{t̂})=0.$$ (16b)

In addition, the conservation law for the twist density (Eq. (11)) becomes

$${\mathrm{\Omega ̂}}_3^{\prime }(ŝ,\mathrm{t̂})=0,$$ (17)

which means that the twist density is uniform in the rod. Indeed, from a general point of view, neglecting the rotational inertia of the rod implies that the twist waves propagate with an infinite velocity, which is exact in the case of an infinitely thin rod (h → 0). We shall see that this approximation appears to be acceptable when we describe the vibration of an elastic ring.

3 Linearization around a static circular configuration

We proceed in this section with the linearization of the Kirchhoff equations around a static circular solution, that is, an elastic ring. We first obtain the static circular solution and then perform a first-order perturbation to obtain the linearized equations. We also provide in Appendix B the results of a second-order perturbation, which will be useful to characterize the topology of the vibrating elastic ring.

3.1 Circular solution

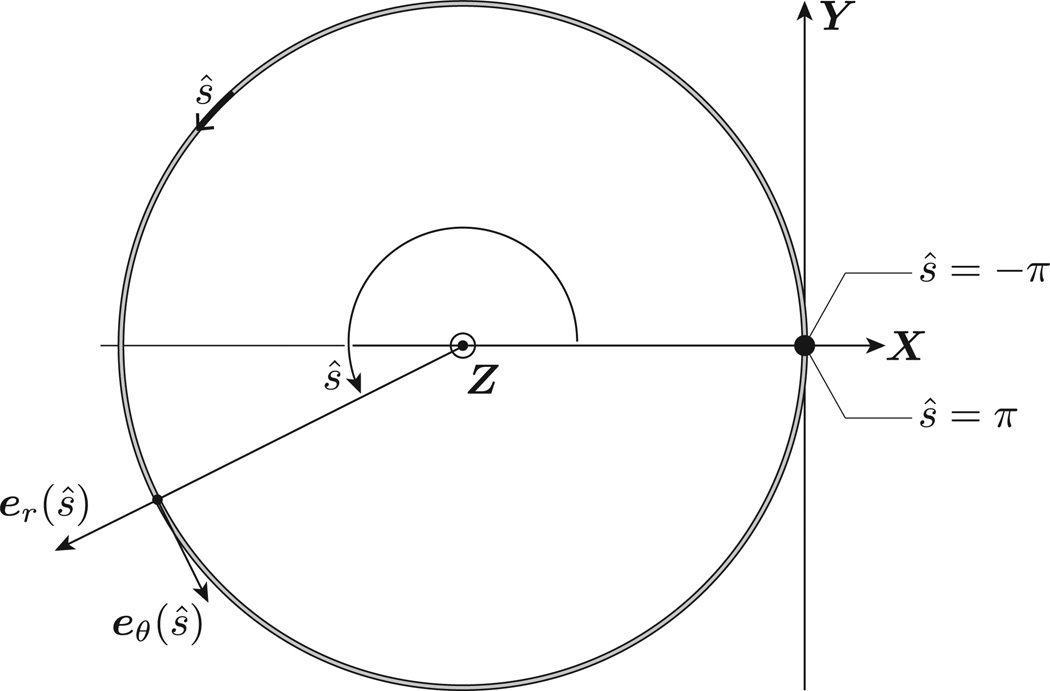
The static circular solution corresponds to a circle of radius R̂_c = 1 lying in the (X,Y) plane, where (X,Y,Z) is the reference inertial frame. The two ends of the rod, ŝ = ±π, are located at r̂(±π) = (1,0,0) with respect to the origin of the reference frame located at the center of the ring, as shown in Fig. 1. We assume that the ring never penetrates itself, which implies that η < 0.5.

Fig. 1.

Geometry of the static circular ring. The ends of the rod are located at r̂(±π) = (1, 0, 0) and the ring lies in the plane defined by the X and Y axes. The origin of the reference frame (X,Y,Z) is located at the center of the ring. In rescaled units, the arc length ŝ corresponds to the polar angle.

We introduce the cylindrical basis (Z, e_r(ŝ), e_θ (ŝ)) such that ${\mathit{e}}_r^{\prime }(ŝ)={\mathit{e}}_{\theta }(ŝ)$ and ${\mathit{e}}_{\theta }^{\prime }(ŝ)=-{\mathit{e}}_r(ŝ)$. We will denote vectors expressed in this basis by using square brackets.

The ring centerline and tangent are given by

$${\mathit{r̂}}^0(ŝ)={\mathit{e}}_r(ŝ)=-\text{cos}ŝ\mathit{X}-\text{sin}ŝ\mathit{Y},$$ (18a)

$${\mathit{d̂}}_3^0(ŝ)={\mathit{e}}_{\theta }(ŝ)=\text{sin}ŝ\mathit{X}-\text{cos}ŝ\mathit{Y}.$$ (18b)

It follows that the curvature vector (Eq. (5)) is given by

$${\mathit{\Omega ̂}}^0(ŝ)=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill {\mathrm{\Omega ̂}}_3^0\hfill \end{array}\right],$$ (19)

where ${\mathrm{\Omega ̂}}_3^0$ is the constant twist density in the elastic ring¹. The latter quantity corresponds to an imposed torsional moment ${Û}^0=2\Gamma {\mathrm{\Omega ̂}}_3^0$, and the internal moment is

$${\mathit{m̂}}^0(ŝ)=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \\ \hfill {Û}^0\hfill \end{array}\right].$$ (20)

The internal force, obtained directly from the Kirchhoff equations (Eq. (13)), is

$${\mathit{n̂}}^0(ŝ)=\left[\begin{array}{c}\hfill {Û}^0\hfill \\ \hfill 0\hfill \\ \hfill 0\hfill \end{array}\right].$$ (21)

We remark that the only parameter involved in the description of the static circular solution is the imposed torsional moment Û⁰. We shall see in the results of the normal mode analysis how the vibrational modes depend on Û⁰.

3.2 Perturbed solution

The linearization of the equations consists of the addition of a small arbitrary perturbation to the static circular ring solution. This perturbation is required to satisfy the equations of motion, i.e., the Kirchhoff equations. In other words, we write a solution as a first-order expansion in ε, with ε ≪ 1, where the zero-order term corresponds to the static circular solution (Eq. (18) to Eq. (21)). For example, an arbitrary quantity A(s,t) will be written as the following expansion A(ŝ,t̂) ≃ A⁰(ŝ) + εa(ŝ,t̂) + O(ε²), which we will write A(ŝ,t̂) = A⁰(ŝ) + εa(ŝ,t̂) for short. The term a(s,t) will be referred to as the first-order term and higher-order terms will be named according to the power of ε.

We start with the perturbation of the rod centerline and write

$$\mathit{r̂}(ŝ,\mathrm{t̂})={\mathit{r̂}}^0(ŝ)+\epsilon \left[\begin{array}{c}\hfill \alpha (ŝ,\mathrm{t̂})\hfill \\ \hfill \beta (ŝ,\mathrm{t̂})\hfill \\ \hfill \gamma (ŝ,\mathrm{t̂})\hfill \end{array}\right].$$ (22)

The expansion for the tangent is given by

$${\mathit{d̂}}_3(ŝ,\mathrm{t̂})={\mathit{d̂}}_3^0(ŝ)+\epsilon \left[\begin{array}{c}\hfill \alpha \prime (ŝ,\mathrm{t̂})\hfill \\ \hfill -(\gamma ″(ŝ,\mathrm{t̂})+\gamma (ŝ,\mathrm{t̂}))\hfill \\ \hfill 0\hfill \end{array}\right].$$ (23)

Here we used the condition of inextensibility (Eq. (2)) to obtain the relation β (ŝ,t̂) + γ′ (ŝ,t̂) = 0, which makes it possible to simplify the last component in the tangent expansion. It follows that the binormal curvature vector (Eq. (6)) is

$$\mathit{K̂}(ŝ,\mathrm{t̂})=\mathit{Z}+\epsilon \left[\begin{array}{c}\hfill {\gamma }^{(3)}+{\gamma }^{(1)}\hfill \\ \hfill {\alpha }^{(2)}\hfill \\ \hfill -{\alpha }^{(1)}\hfill \end{array}\right],$$ (24)

where we used the notation f⁽ⁿ⁾(ŝ) = f^′⋯′ (ŝ) and omitted the dependence on ŝ and t̂ for the sake of clarity. We introduce the following perturbation for the twist density

$${\mathrm{\Omega ̂}}_3(ŝ,\mathrm{t̂})={\mathrm{\Omega ̂}}_3^0+\epsilon \delta (ŝ,\mathrm{t̂}),$$ (25)

which implies that the torsional moment in the rod is given by Û (ŝ,t̂) = Û⁰ + ε2Γδ(ŝ,t̂).

The internal moment in the rod is derived from the expansions of the binormal curvature vector and the twist density given above, and is written as

$$\mathit{m̂}(ŝ,\mathrm{t̂})={\mathit{m̂}}^0(ŝ,\mathrm{t̂})+\epsilon \left[\begin{array}{c}\hfill {\gamma }^{(3)}+{\gamma }^{(1)}+{Û}^0{\alpha }^{(1)}\hfill \\ \hfill {\alpha }^{(2)}-{Û}^0({\gamma }^{(2)}+\gamma )\hfill \\ \hfill 2\Gamma \delta -{\alpha }^{(1)}\hfill \end{array}\right].$$ (26)

We introduce the following expansion for the axial spin velocity

$${\mathrm{\omega ̂}}_3(ŝ,\mathrm{t̂})=\epsilon \varphi (ŝ,\mathrm{t̂}),$$ (27)

and then obtain for the expansion of the spin vector

$$\mathit{\omega ̂}(ŝ,\mathrm{t̂})=\epsilon \left[\begin{array}{c}\hfill {\mathrm{\gamma ̇}}^{(2)}+\mathrm{\gamma ̇}\hfill \\ \hfill {\mathrm{\alpha ̇}}^{(1)}\hfill \\ \hfill \varphi \hfill \end{array}\right],$$ (28)

where we used the definition given by Eq. (7) and the expansion of the tangent (Eq. (23)). Finally, the linearized compatibility condition (Eq. (8)) reads as

$$\mathrm{\delta ̇}={\varphi }^{(1)}+{\mathrm{\alpha ̇}}^{(1)}.$$ (29)

3.3 Linearized Kirchhoff equations

We can now insert the perturbed solution into the Kirchhoff equations, Eqs. (13), to obtain the linearized equations. The first Kirchhoff equation (Eq. (13a)) can be used to express the internal force in the derivative of the second Kirchhoff equation (Eq. (13b)), yielding the following system of three differential equations,

$$\mathrm{\alpha ̈}-{\eta }^2{\mathrm{\alpha ̈}}^{(2)}+{\alpha }^{(4)}+{\alpha }^{(2)}-{Û}^0({\gamma }^{(2)}+{\gamma }^{(4)})-2\Gamma {\delta }^{(1)}=0,$$ (30a)

$$-\mathrm{\gamma ̈}+{\mathrm{\gamma ̈}}^{(2)}-{\eta }^2(\mathrm{\gamma ̈}+2{\mathrm{\gamma ̈}}^{(2)}+{\mathrm{\gamma ̈}}^{(4)})+{\gamma }^{(2)}+2{\gamma }^{(4)}+{\gamma }^{(6)}+{Û}^0({\alpha }^{(2)}+{\alpha }^{(4)})=0,$$ (30b)

$$-{\eta }^2\mathrm{\delta ̈}+{\eta }^2{\mathrm{\alpha ̈}}^{(1)}+\Gamma {\delta }^{(2)}=0,$$ (30c)

where we used Eq. (29) to write the last equation. Note that these linearized equations are written in terms of the variables α, γ and δ because this is a convenient choice to express the periodic and clamped boundary conditions that will be detailed below. Other comparable equations can be obtained by choosing a different set of variables.

Within the zero rotational inertia approximation (η → 0), the twist density is constant in the rod, i.e., δ′(ŝ,t̂) = 0, and hence, these equations reduce to the following two differential equations,

$$\mathrm{\alpha ̈}+{\alpha }^{(4)}+{\alpha }^{(2)}-{Û}^0({\gamma }^{(2)}+{\gamma }^{(4)})=0,$$ (31a)

$$-\mathrm{\gamma ̈}+{\mathrm{\gamma ̈}}^{(2)}+{\gamma }^{(2)}+2{\gamma }^{(4)}+{\gamma }^{(6)}+{Û}^0({\alpha }^{(2)}+{\alpha }^{(4)})=0.$$ (31b)

We note that if the elastic ring is not twisted, i.e., Û⁰ = 0, the in-plane motion (described by γ(s,t)) is independent of the out-of-plane and twisting motions (described, respectively, by α(s,t) and δ(s,t)). In addition, the out-of-plane and twisting motions are coupled through the parameter η, which is related to the rotational inertia of the rod. Indeed, Love himself described this relation between the out-of-plane displacement and the twisting of the rod [26] as a consequence of the conservation of angular momentum. We shall later use these properties of the equations to classify the different vibrational modes of the elastic ring. Finally, we emphasize the fact that, because these equations have been obtained by linearization around a static circular solution, they can be applied to open circular rings, for example, a semi-circular ring.

3.4 Boundary conditions

We present two choices of boundary conditions that we will use in the normal mode analysis: periodic and clamped boundary conditions as illustrated in Fig. 2.

Fig. 2.

Representation of the two choices of boundary conditions for the elastic ring. The periodic boundary conditions (left) correspond to a free elastic ring and the clamped boundary conditions (right) correspond to a ring held at a particular point in a such way that the position and the tangent are kept unchanged from the equilibrium solution. In the latter case, the ring is held by a static and infinitely massive support.

The periodic boundary conditions require that the different functions describing the kinematics and the mechanics of the ring are periodic functions in space. In other words, we can write these boundary conditions as

$${\alpha }^{(k)}(ŝ,\mathrm{t̂})={\alpha }^{(k)}(ŝ+2\pi ,\mathrm{t̂}),k=0,\dots ,3,$$ (32a)

$${\gamma }^{(k)}(ŝ,\mathrm{t̂})={\gamma }^{(k)}(ŝ+2\pi ,\mathrm{t̂}),k=0,\dots ,5,$$ (32b)

$${\delta }^{(k)}(ŝ,\mathrm{t̂})={\delta }^{(k)}(ŝ+2\pi ,\mathrm{t̂}),k=0,1.$$ (32c)

The clamped boundary conditions are defined with respect to the circular solution defined in Section 3.1: the positions and the orientations of the two cross sections at the ends of the rod (ŝ = ±π) remain unchanged. In other words, the geometry is imposed at both ends of the rod and we need to determine the loadings (force and moment) that are needed to hold the ends of the rod in such a configuration. These conditions also imply that the ends of the rod are fixed. Such boundary conditions are equivalent to having an immobile and infinitely heavy rigid body attached to the rod and holding the two ends of the rod together. These conditions translate into the following equations

$$\alpha (\pi ,\mathrm{t̂})=\alpha (-\pi ,\mathrm{t̂})=0,$$ (33a)

$$\gamma (\pi ,\mathrm{t̂})=\gamma (-\pi ,\mathrm{t̂})=0,$$ (33b)

$${\alpha }^{(1)}(\pi ,\mathrm{t̂})={\alpha }^{(1)}(-\pi ,\mathrm{t̂})=0,$$ (33c)

$${\gamma }^{(1)}(\pi ,\mathrm{t̂})={\gamma }^{(1)}(-\pi ,\mathrm{t̂})=0,$$ (33d)

$${\gamma }^{(2)}(\pi ,\mathrm{t̂})={\gamma }^{(2)}(-\pi ,\mathrm{t̂})=0,$$ (33e)

$${\delta }^{(1)}(\pi ,\mathrm{t̂})={\delta }^{(1)}(-\pi ,\mathrm{t̂})=0,$$ (33f)

where the last equation is obtained from the conservation of the twist density (see Eq. (15) with ϕ̇ (±π,t̂) = 0 since the cross sections at both ends are fixed). These equations are equivalent to the conditions: r̂(±π) = 0, d̂₃(±π) =Y and d̂₁(±π) = Z.

The differential system formed by the linearized equations is of dimension twelve, which is also the number of conditions introduced by each set of boundary conditions. In other words, we have a well-defined boundary-value problem.

4 Topology of the vibrating elastic ring

The topology of an elastic rod can be characterized by several quantities known as the linking number, writhing number, and total twist. These quantities are defined for three-dimensional closed curves and can be used for an elastic rod to quantify its global folding and twisting. We first give brief definitions of these quantities and then we describe how they can be applied to the vibrational modes of the twisted elastic ring.

4.1 Topology of closed curves

The linking number, an integer, is a global quantity describing the entanglement of two closed space curves. It can be defined as the algebraic sum of all signed intersections that one of the curves makes with a surface bounded by the other curve [27, 28]. It is often referred to as a topological invariant because for any changes in the geometry of the two curves, the linking number remains invariant as long as the curves are not allowed to cross each other or themselves. For two nonintersecting closed curves C₁ and C₂ described by r₁(s₁) and r₂(s₂), the linking number can be defined as a Gauss integral [29, 30],

$$\text{Lk}(C_2,C_1)=\frac{1}{4\pi }\oint \oint \frac{{\mathit{t}}_2(s_2)\times {\mathit{t}}_1(s_1)·({\mathit{r}}_2(s_2)-{\mathit{r}}_1(s_1))}{{|{\mathit{r}}_2(s_2)-{\mathit{r}}_1(s_1)|}^3}\mathrm{d}{s}_1\mathrm{d}{s}_2,$$ (34)

where t₁(s₁) and t₂(s₂) are the unit tangents to C₁ and C₂ respectively, and s₁ and s₂ are, respectively, the arc lengths of C₁ and C₂.

The writhing number Wr(C) of a closed curve C describes the global folding of the curve. It is a measure of the chiral distortion of that curve from planarity. Like the linking number, the writhing number can be expressed as a Gauss integral [31–33],

$$\text{Wr}(C)=\frac{1}{4\pi }\oint \oint \frac{\mathit{t}(s\prime )\times \mathit{t}(s)·(\mathit{r}(s\prime )-\mathit{r}(s))}{{|\mathit{r}(s\prime )-\mathit{r}(s)|}^3}\mathrm{d}s\prime \mathrm{d}s,$$ (35)

where t(s) is the unit tangent to C and s and s′ denote two positions on the curve.

The last quantity to be introduced is the total twist of one curve around another. The total twist is also a global quantity but unlike the writhing and linking numbers it can be calculated for open curves. Consider two curves C₁ and C₂ and the vector k(s), with s a common parametrization of both curves, joining every point on C₁ to a single point on C₂. We can then introduce the vector ν(s) = k(s) − (k(s) · t(s)) t(s) as the normal component of k(s) with respect to the tangent of C₁. The total twist then corresponds to the number of turns the vector ν(s) makes around C₁ [34], that is,

$$\text{Tw}(C_2,C_1)=\frac{1}{2\pi }\oint (\mathit{t}(s)\times \frac{\mathit{\nu }(s)}{|\mathit{\nu }(s)|})·\frac{\mathrm{d}}{\mathrm{d}s}\frac{\mathit{\nu }(s)}{|\mathit{\nu }(s)|}\mathrm{d}s.$$ (36)

Finally, it can be shown that for any pair of non-intersecting closed curves C₁ and C₂ the linking number is equal to the sum of the writhing number and the total twist [27],

$$\text{Lk}(C_2,C_1)=\text{Wr}(C_1)+\text{Tw}(C_2,C_1).$$ (37)

4.2 Application to the twisted elastic ring

These definitions can easily be used to describe the topology of an elastic rod as long as the curves involved in the calculation of the different quantities are clearly defined. A natural choice is to take the rod centerline as the first curve and the curve traced out by any of the material frame directors (d̂₁(ŝ,t̂) or (d̂₂(ŝ,t̂)) as the second curve, that is, we take C₁ ≡ r̂(ŝ,t̂) and C₂ ≡ r̂(ŝ,t̂) + ad̂₁(ŝ,t̂), where a is a fixed parameter chosen small enough such that the curves C₁ and C₂ are not intersecting or self-intersecting. We can now refer to the linking number of the rod as Lk = Lk (C₂,C₁) and to the total twist of the rod as Tw = Tw (C₂,C₁). The writhing number of the rod is simply the writhing number of the rod centerline, that is, Wr = Wr (C₁). It can be shown from the definition of the total twist given by Eq. (36) that choosing ν(s) / |ν(s)| = d̂₁(ŝ,t̂) (choosing d̂₂(ŝ,t̂) is strictly equivalent) leads to

$$\text{Tw}=\frac{1}{2\pi }\oint {\mathrm{\Omega ̂}}_3(ŝ,\mathrm{t̂})\mathrm{d}ŝ.$$ (38)

In other words, the total twist is simply the integral of the twist density.

For the static circular configuration the writhing number is zero since the configuration is planar. The linking number is then equal to the total twist of the twisted elastic ring,

$${\text{Lk}}^0={\text{Wr}}^0+{\text{Tw}}^0=\frac{1}{2\pi }\oint {\mathrm{\Omega ̂}}_3^0\mathrm{d}ŝ={\mathrm{\Omega ̂}}_3^0,$$ (39)

where we use upper zero indices to denote the static circular configuration. We notice that for arbitrary values of the imposed twist density ${\mathrm{\Omega ̂}}_3^0$ there is no guarantee that the linking number will be an integer. This issue arises from the fact that, in general the material frame directors do not coincide at ŝ = ±π, that is, the curve traced out by the vector d̂₁(ŝ,t̂) or d̂₂(ŝ,t̂) is not necessarily closed. The angle between d̂₁(π,t̂) and d̂₁(−π,t̂) is known as soon as a specific value of ${Û}^0=2\Gamma {\mathrm{\Omega ̂}}_3^0$ is chosen and for both types of boundary conditions this angle is constant and cannot be altered by the vibration of the ring (see Appendix A for the material frame director expressions). In other words, we can consider non-integral values of the linking number. In addition, the linking number does not vary through time, that is, Lk = Lk⁰. Finally, the linking number of the twisted elastic ring has a simple geometrical meaning corresponding to the total rotation that have been applied to the rod ends before they are joined and sealed to form the ring.

The writhing number of the vibrating elastic ring can be calculated with the help of Fuller’s formula [33], which relates the writhing numbers of two closed curves. If we choose as the first curve the centerline of the static circular configuration and as the second curve the centerline of the vibrating elastic ring (this choice satisfies the requirements of Fuller’s formula; in particular, the absence of antipodal points), Fuller’s formula reads as

$$\text{Wr}(\mathrm{t̂})-{\text{Wr}}^0=\text{Wr}(\mathrm{t̂})=\frac{1}{2\pi }{\int }_{-\pi }^{\pi }\frac{{\mathit{d̂}}_3^0\times {\mathit{d̂}}_3}{1+{\mathit{d̂}}_3^0·{\mathit{d̂}}_3}·({\mathit{d̂}}_3^{0\prime }+{\mathit{d̂}}_3^{\prime })\mathrm{d}ŝ.$$ (40)

For periodic and clamped boundary conditions, it can be shown that the first-order term of the writhing number is zero. The second-order term can be expressed as a sum of products of first-order terms (see the details of the calculation in Appendix B), and is written as

$$\text{Wr}(\mathrm{t̂})=\frac{{\epsilon }^2}{2\pi }{\int }_{-\pi }^{\pi }{\alpha }^{(2)}(\gamma +{\gamma }^{(2)})\mathrm{d}ŝ.$$ (41)

This quantity characterizes the chiral distortion of the vibrating elastic ring, that is, the writhing number of a normal mode is, at the same time, a measure of the non-planarity and the chirality of the mode.

We can now take advantage of the linking number conservation to express the total twist of the vibrating elastic ring. At the second order of the perturbation the total twist is given by

$$\text{Tw}(\mathrm{t̂})={\mathrm{\Omega ̂}}_3^0+\frac{{\epsilon }^2}{2\pi }{\int }_{-\pi }^{\pi }\Delta (ŝ,\mathrm{t̂})\mathrm{d}ŝ,$$ (42)

where Δ (ŝ,t̂) is the second order of the twist density (see Eq. (B.4) in Appendix B). The first-order term of the total twist is zero as explained in Appendix A. It then follows that

$${\int }_{-\pi }^{\pi }\Delta (ŝ,\mathrm{t̂})\mathrm{d}ŝ=-{\int }_{-\pi }^{\pi }{\alpha }^{(2)}(\gamma +{\gamma }^{(2)})\mathrm{d}ŝ.$$ (43)

This result allow us to express the second order of the twist density, Δ (ŝ,t̂), in terms of first-order quantities.

Finally, because of the conservation of the linking number we can expect different behavior for the vibrational modes. The modes that increase the writhing number of the twisted elastic ring will have a lower total twist. On the other hand, the modes that lower the writhing number of the ring will have a higher total twist.

5 Normal modes analysis

Normal mode analysis makes it possible to obtain the natural frequencies of vibration for the twisted elastic ring. Each normal mode corresponds to a vibration, i.e., oscillation, of the system. A normal mode is characterized by its wavenumber n, which is related to the number of nodes in the oscillation, and its frequency σ̂_n. The period of the oscillation for a mode is given by 2π / σ̂_n.

Normal mode analysis consists of the study of small-amplitude vibrations around the static circular solution, that is, the deviations α(ŝ,t̂), γ(ŝ,t̂), and δ(ŝ,t̂) from the equilibrium solution are written as

$${\alpha }_n(ŝ,\mathrm{t̂})={\mathrm{\alpha ̃}}_n(ŝ)e^{\mathrm{i}{\mathrm{\sigma ̂}}_{n}t},{\gamma }_n(ŝ,\mathrm{t̂})={\mathrm{\gamma ̃}}_n(ŝ)e^{\mathrm{i}{\mathrm{\sigma ̂}}_{n}t},{\delta }_n(ŝ,\mathrm{t̂})={\mathrm{\delta ̃}}_n(ŝ)e^{\mathrm{i}{\mathrm{\sigma ̂}}_{n}t}.$$ (44)

Here we focus on the real part of these expressions. The set of functions α̃, γ̃, and δ̃ is referred to as a spatial normal mode of vibration. The linearized Kirchhoff equations (Eq. (30)) will be rewritten in terms of these new functions. The equations are then solved for a choice of boundary conditions to obtain the frequency σ̂_n.

5.1 Classification of the normal modes

The classification of the normal modes, although arbitrary, makes it easier to describe and compare the modes. A common practice is to sort the modes based on the number of nodes in the oscillation, that is, the modes are indexed using the wavenumber n. Such a classification ensures that the first mode will be of lower frequency than the second. In addition, we know from the structure of the equations that for a given mode index n, the vibrations of the ring can be of different types. For the non-twisted elastic ring, that is, Û⁰ = 0, the in-plane motion is not coupled to the out-of-plane and twisting motions. Moreover, in the limit η → 0, the twisting motions do not exist, which makes it possible to discriminate between out-of-plane and twisting motions. We then describe a normal mode in terms of its mode index n and type of motion found when Û⁰ = 0 and η → 0. When Û⁰ ≠ 0 and η ≠ 0 the different types of motions are coupled but, nevertheless, we will still refer to the nature of the mode in terms of the results obtained for Û⁰ = 0 and η → 0. In other words, for a given n, a mode can be an in-plane, an out-of-plane or a twisting mode. We will refer to the in-plane and out-of-plane modes as flexural modes.

5.2 Normalization condition

The normal mode analysis does not yield the amplitudes of the different modes. We can, however, add a normalization condition which imposes the values of the mode amplitudes. We normalize the time average of the kinetic energy of each mode to 1/2. As shown in Appendix C, the energy of the elastic ring can be calculated up to its second order. It follows from these results, that the normalization condition is given by

$$\langle \frac{1}{2}{\int }_{-\pi }^{\pi }[{\mathrm{\alpha ̇}}^2+{\eta }^2{\mathrm{\alpha ̇}}^{{(1)}^2}+{\mathrm{\gamma ̇}}^2+{\mathrm{\gamma ̇}}^{{(1)}^2}+{\eta }^2{(\mathrm{\gamma ̇}+{\mathrm{\gamma ̇}}^{(2)})}^2+2{\eta }^2{\varphi }^2]\mathrm{d}ŝ\rangle =\frac{1}{2},$$ (45)

where 〈…〉 denotes the time average defined as

$$\langle f(ŝ,\mathrm{t̂})\rangle =\frac{\mathrm{\sigma ̂}}{2\pi }{\int }_{-\pi /\mathrm{\sigma ̂}}^{\pi /\mathrm{\sigma ̂}}f(ŝ,\mathrm{t̂})\mathrm{d}\mathrm{t̂}.$$ (46)

The details of the integration over time are given in Appendix C, where we show that the condition of normalization can be rewritten as

$$\frac{1}{4}{\int }_{-\pi }^{\pi }\left[{\mathrm{\sigma ̂}}_n^2\right({\mathrm{\alpha ̃}}_n^2+{\mathrm{\gamma ̃}}_n^2+{\mathrm{\gamma ̃}}_n^{{(1)}^2}+{\eta }^2{\mathrm{\alpha ̃}}_n^{{(1)}^2}+{\eta }^2{({\mathrm{\gamma ̃}}_n+{\mathrm{\gamma ̃}}_n^{(2)})}^2)+2\Gamma ({\mathrm{\delta ̃}}_n^2+{\mathrm{\alpha ̃}}_n{\mathrm{\delta ̃}}_n^{(1)}\left)\right]\mathrm{d}ŝ-\frac{1}{2}=0.$$ (47)

5.3 Periodic boundary conditions

For the elastic ring with periodic boundary conditions, we expect the normal modes to be periodic functions in space, that is, we write

$${\alpha }_n(ŝ,\mathrm{t̂})=[A_n^{\alpha }{e}^{\mathrm{i}nŝ}+{Ā}_n^{\alpha }{e}^{-\mathrm{i}nŝ}]e^{i{\mathrm{\sigma ̂}}_{n}t},$$ (48a)

$${\gamma }_n(ŝ,\mathrm{t̂})=[A_n^{\gamma }{e}^{\mathrm{i}nŝ}+{Ā}_n^{\gamma }{e}^{-\mathrm{i}nŝ}]e^{i{\mathrm{\sigma ̂}}_{n}t},$$ (48b)

$${\delta }_n(ŝ,\mathrm{t̂})=[A_n^{\delta }{e}^{\mathrm{i}nŝ}+{Ā}_n^{\delta }{e}^{-\mathrm{i}nŝ}]e^{i{\mathrm{\sigma ̂}}_{n}t},$$ (48c)

where Ā denotes the complex conjugate of A. These definitions show that in the periodic case there are always two possible solutions for the spatial mode: a cosine and a sine. In other words, there is a two-fold degeneracy for the periodic normal modes. Note that for a given normal mode, the superposition of the two types of solutions with arbitrary phases will give rise to traveling waves.

We can now substitute these expressions into the linearized Kirchhoff equations (Eq. (30)) to obtain a linear system of equations for the amplitudes $A_n^{\alpha },A_n^{\gamma }$ and $A_n^{\delta }$, that is, we obtain the following linear problem

$$\mathit{M̲}({\mathrm{\sigma ̂}}_n,n)\left(\begin{array}{c}\hfill A_n^{\alpha }\hfill \\ \hfill A_n^{\gamma }\hfill \\ \hfill A_n^{\delta }\hfill \end{array}\right)=0.$$ (49)

A similar system is obtained for the complex conjugate amplitudes with the conjugate matrix M̲̅(σ̂_n, n).

The non-trivial solutions of the linear system in Eq. (49) are given by the condition detM̲(σ̂_n, n) = 0, which yields the normal-mode frequencies as functions of n and of the other parameters of the problem. Then, for each value of the frequency the linear system can be solved, together with the normalization condition (Eq. (47)) to obtain the amplitudes of the normal modes. The details of the normal mode analysis for periodic boundary conditions are given in Appendix D.

5.4 Clamped boundary conditions

In contrast to the periodic case, we cannot find analytical forms of the spatial modes, i.e., the functions α̃, γ̃, and δ̃, for clamped boundary conditions. We are then left with a boundary-value problem that can be solved in two steps: i) we consider the uncoupled problem for Û⁰ = 0 and solve it by numerical integration to identify the normal mode frequencies; ii) we make use of a numerical continuation method to solve the problem for any value of Û⁰. The details of the numerical normal mode analysis are given in Appendix E.

6 Vibrational modes for periodic and clamped rings

We give in this section the results of our normal mode analysis for both types of boundary conditions. We start with some remarks about the normal modes related to the symmetry of the elastic ring and then move on to the description of the flexural modes and the twisting modes. This particular presentation is motivated by the fact that the twisting modes strongly depend on the rotational inertia of the rod, i.e., on the value of the parameter η, and exhibit specific features that need to be addressed separately.

We find that the rotational inertia has a minor influence on the frequencies and amplitudes of the flexural modes, especially for acceptable values of η (see Section 2.2 for a discussion on the effect of η on the validity of the model). We then present our results for the case η → 0 and η = 0.05. The latter case corresponds to a thick ring. For example, η = 0.05 is the value associated with a DNA minicircle of 185 base pairs (assuming that the DNA radius is 10 Å). Most of our results will be presented as functions of the imposed torsional moment in the ring Û⁰. It follows from Eq. (39) that Û⁰ is related to the number of turns Lk⁰ applied to the ends of the ring before sealing them,

$${\text{Lk}}^0=\frac{{Û}^0}{2\Gamma },$$ (50)

where Γ is the ratio of the shearing and Young moduli. In the case of an isotropic rod we have Γ = 2C/B where C and B are the respective twisting and bending stiffnesses. In the case of DNA, several recent experiments have shown that B = 50k_BT nm and C = 75k_BT nm are reasonable choices yielding Γ = 0.75 [35–37]. Unless mentioned otherwise we take Γ = 0.75. For comparison, a mild steel wire corresponds to Γ = 0.38 (shearing modulus μ = 80 GPa and Young modulus E = 210 GPa).

6.1 Preliminaries

We introduce here the quantities that will be used to describe the modes. The magnitude of each mode is characterized by the root-mean-square (RMS) amplitudes of the out-of-plane (α̃(ŝ)), in-plane (β̃ (ŝ)), and twisting (δ̃ (ŝ)) components of the ring motion. These RMS amplitudes are defined as

$${\mathrm{\alpha ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}=\sqrt{\frac{1}{2\pi }{\int }_{-\pi }^{\pi }\mathrm{\alpha ̃}{(ŝ)}^2\mathrm{d}ŝ},$$ (51a)

$${\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}=\sqrt{\frac{1}{2\pi }{\int }_{-\pi }^{\pi }\mathrm{\beta ̃}{(ŝ)}^2\mathrm{d}ŝ}=\sqrt{\frac{1}{2\pi }{\int }_{-\pi }^{\pi }\mathrm{\gamma ̃}\prime {(ŝ)}^2\mathrm{d}ŝ},$$ (51b)

$${\mathrm{\delta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}=\sqrt{\frac{1}{2\pi }{\int }_{-\pi }^{\pi }\mathrm{\delta ̃}{(ŝ)}^2\mathrm{d}ŝ}.$$ (51c)

The amplitudes ${\mathrm{\alpha ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}},{\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}},{\mathrm{\delta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$ will be referred to, respectively, as the out-of-plane, in-plane and twisting RMS amplitudes, and should not be mistaken for the type of the mode. In other words, the three RMS amplitudes are obtained for every type of mode and, for example, we will talk about the in-plane RMS amplitude ${\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$ of an out-of-plane mode.

In addition, the modes will also be characterized by their writhing numbers (Eq. (41)). The writhing number of a mode is a second-order quantity, which only depends on the time t̂. We therefore introduce the time average of the writhe as

$$\langle \text{Wr}\rangle =\frac{1}{{\epsilon }^2}\frac{\mathrm{\sigma ̂}}{2\pi }{\int }_{-\pi /\mathrm{\sigma ̂}}^{\pi /\mathrm{\sigma ̂}}\text{Wr}(\mathrm{t̂})\mathrm{d}\mathrm{t̂}.$$ (52)

6.2 Normal modes and symmetry

For both types of boundary conditions we found a few normal modes of zero frequency. Such modes correspond to rigid-body motions that are related to the symmetry of the system.

In the case of the periodic ring, all three frequencies are zero for n = 0. These modes include a rotation about the Z axis and a translation along the Z axis (see Fig. 1 for the definitions of axes), as well as a twisting mode corresponding to a uniform rotation of the cross sections about their normals (see [10] for a description of the latter mode). For n = 1, however, only the flexural modes have zero frequency. These two modes correspond to a rotation of the ring about one of its diameters and to an arbitrary in-plane translation of the ring. The non-zero frequency twisting mode for n = 1 will be commented upon later. In other words, it is only for n ≥ 2 that there are three modes with non-zero frequency for the periodic ring.

When the ring is clamped it is easy to understand from the above descriptions, that these periodic zero-frequency modes are not necessarily compatible with the clamped boundary conditions. Indeed, the only zero-frequency mode for clamped boundary conditions is an out-of-plane mode corresponding to a rotation about the Y axis. This is the only transformation that leaves the system invariant and satisfies the boundary conditions. We will see that the other zero-frequency periodic modes become modes with non-zero frequency for clamped boundary conditions.

The definition of the mode index n is different for the two types of boundary conditions: for the periodic case n is the number of nodes in the vibrating ring divided by two, whereas for clamped conditions it is the number of nodes (excluding the clamped point). As noted above, non-zero-frequency flexural modes for the periodic ring start with n = 2 (n = 1 for twisting modes) while the first non-zero-frequency modes for the clamped ring are obtained for n = 1. In spite of the different indices, the normal modes for the two types of boundary conditions will be compared based on their order of appearance, that is, the periodic mode of lowest frequency (n = 2) will be compared with the clamped mode of lowest frequency (n = 1) and so on. We will see that this pairing is consistent with the stability of the modes. In addition, the modes will also be compared based on their types of motions (in-plane, out-of-plane or twisting).

6.3 Flexural modes

We present here the results of our normal mode analysis for the flexural modes, starting with a discussion of the mode frequencies and shapes and then focusing on the mode amplitudes and writhing numbers.

6.3.1 Mode frequencies

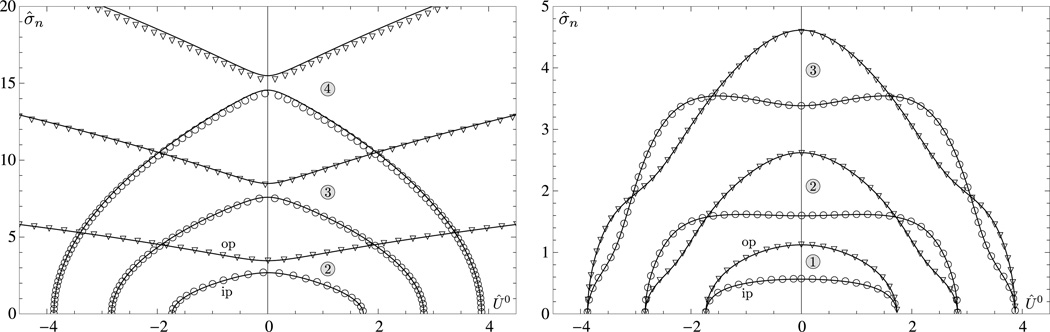
The central results of our normal mode analysis are the vibrational frequencies of the elastic ring. We show in Fig. 3 the dependence of the six lowest frequencies on the imposed torsional moment for both periodic and clamped boundary conditions. We shall comment later on the fact that the flexural-mode frequencies are always smaller than the twisting-mode frequencies (at least, for reasonable values of η). The first remark is that the frequencies for the clamped ring are noticeably smaller than those for the periodic ring. We notice that in the case of the periodic ring the only unstable modes are the in-plane modes: these instabilities are reached for specific values of the imposed torsional moment corresponding to the Michell-Zajac [38–40] instability $({Û}^0=\pm \sqrt{3},\pm \sqrt{8},\pm \sqrt{15},\dots ,\pm \sqrt{n^2-1})$. For the clamped ring all flexural modes are unstable when Û⁰ reaches its critical values. We will see later that the oscillatory pattern appearing in the plotted frequencies of the clamped modes gives rise to localized maxima and minima in the amplitudes and writhing numbers of these modes. Finally, the rotational inertia parameter η has a stronger influence on the frequencies of the periodic modes than those of the clamped ones (as depicted by the downward discrepancy between the symbols and the solid lines in the left plot of Fig. 3), although in both cases the effect is rather limited.

Fig. 3.

Frequencies of the first six flexural modes σ̂_n as functions of the imposed torsional moment Û⁰ for periodic (left) and clamped (right) boundary conditions. On both plots the solid black lines correspond to the frequencies in the limit η → 0 and the symbols represent the frequencies for η = 0.05 (the circle ○ and triangle ▽ represent, respectively, the in-plane and out-of-plane mode frequencies). The labels ”ip” and ”op” denote the in-plane and out-of-plane frequency branches for the first two modes (the other modes are ordered similarly). Finally, the numbers in the gray circles indicate the indices of the modes.

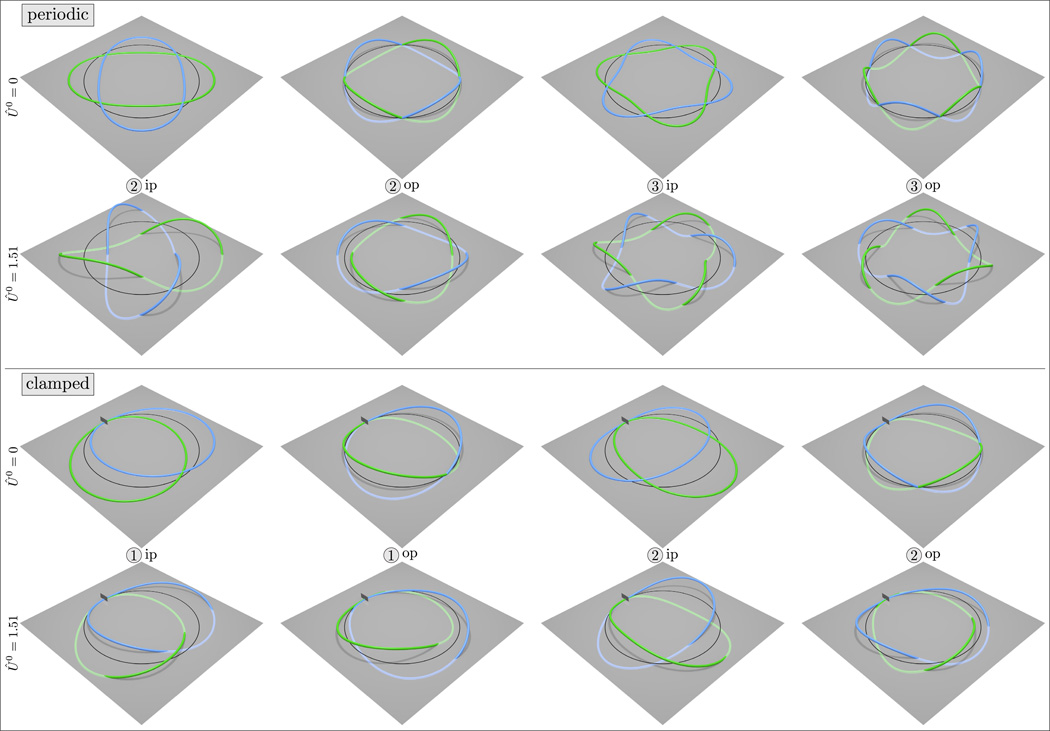
6.3.2 Mode shapes

We present in Fig. 4 three-dimensional representations of the first four flexural modes for periodic and clamped boundary conditions. As expected, from the structure of the equations, there is a clear distinction between in-plane (”ip”) and out-of-plane (”op”) modes for Û⁰ = 0. When Û⁰ ≠ 0 the in-plane and out-of-plane motions are coupled (Fig. 4). Moreover, the first two modes shown in Fig. 4 for clamped boundary conditions correspond to the zero-frequency modes described earlier for periodic conditions and the last two modes are the clamped equivalent of the first two periodic modes. In particular, the first clamped mode arises from the invariance of the periodic ring under a rotation about the Z axis, while the second clamped mode is related to the invariance of the ring under a rotation about one of its diameters.

Fig. 4.

Three-dimensional shapes of flexural modes for periodic (top) and clamped (bottom) boundary conditions with Û⁰ = 0 and Û⁰ = 1.51 (both cases with η = 0). For each type of boundary condition we represent extremum shapes (i.e., the maximum and minimum of the oscillation) of the first four modes in blue and green. The gray plane denotes the horizontal plane and the dark line on the plane denotes the geometry of the equilibrium solution. The mode indices and types are given by the numbers in the light gray circles and by the labels ”ip” and ”op”. For clamped boundary conditions the small dark gray rectangle represents the support. The light blue and green colors denote the parts of the rod below the horizontal plane. Finally, the radius of the rod and the amplitudes of the displacements have been chosen to allow a clear representation of each mode.

6.3.3 Mode amplitudes

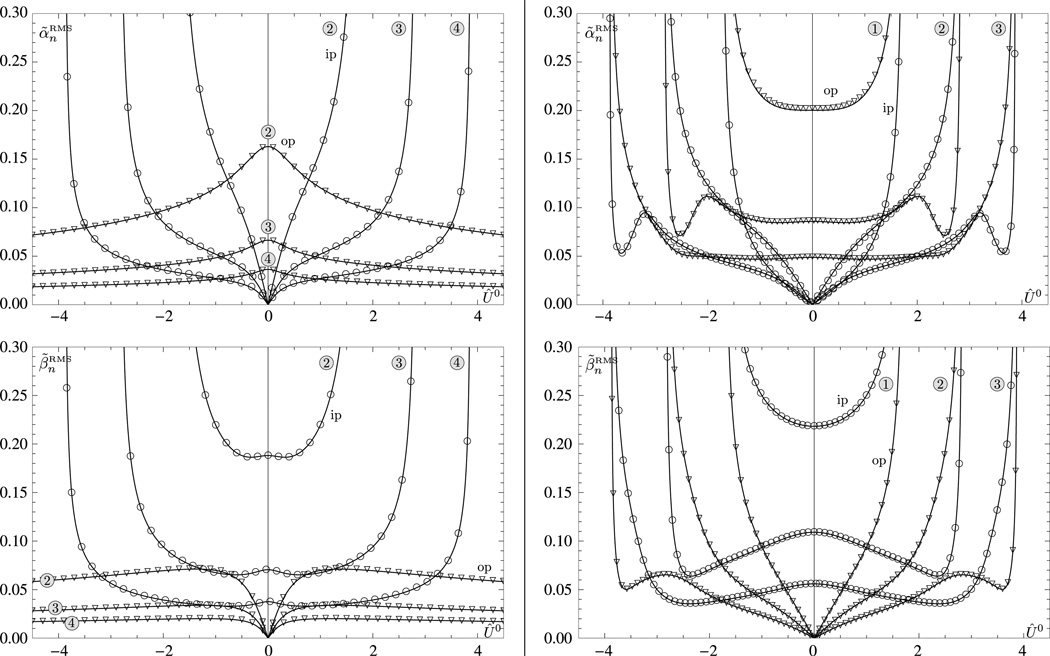
The dependence of the RMS amplitudes on the imposed torsional moment Û⁰ is plotted for the first six modes in Fig. 5. We first remark that the divergent amplitudes are, for both types of boundary conditions, always related to the unstable modes (i.e., in-plane modes for periodic boundary conditions and all modes for clamped conditions): when the frequency of a particular mode reaches zero, the normalization condition given by Eq. 47 forces the RMS amplitudes to diverge. Because the clamped frequencies are lower than the periodic ones, the in-plane and out-of-plane RMS amplitudes, ${\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$ and ${\mathrm{\alpha ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$, for out-of-plane modes (labelled ”op” in Fig. 5) are always larger for clamped boundary conditions than for periodic conditions. For in-plane modes the situation is more subtle. In general for these modes, the in-plane and out-of-plane RMS amplitudes are larger for clamped conditions than for the periodic ones. The oscillations noted above in the clamped frequencies, however, produce localized maxima and minima which sufficiently decrease the amplitudes of the clamped modes to make them smaller than their periodic counterparts at specific values of Û⁰. Overall, our results show that in the domain of stability of the equilibrium solution $(|{Û}^0|<\sqrt{3})$ the amplitudes of the clamped modes are larger than those of the periodic modes.

Fig. 5.

In-plane and out-of-plane RMS amplitudes of the first six flexural modes as functions of the imposed torsional moment Û⁰ for periodic (left) and clamped (right) boundary conditions. For each type of boundary conditions, the out-of-plane, ${\mathrm{\alpha ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$, and the in-plane, ${\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$, amplitudes are given respectively in the top and bottom plots. The styles and symbols on all plots are identical to those used in Fig. 3.

6.3.4 Mode writhing numbers

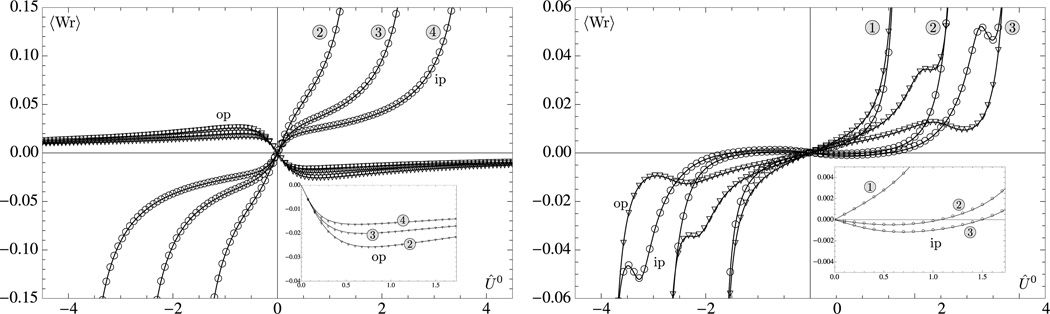
In addition to the amplitudes of the modes, we can also characterize the overall chirality and total twist of the vibrating ring by calculating the associated writhe as shown in Fig. 6. We recall that the writhing number of each mode is a second-order quantity, which means that overall the vibrations produce small chiral distortions. We first remark that the writhe of the periodic modes is significantly larger than that for the clamped modes, despite the latter having larger amplitudes. In the case of the periodic modes, there is also a clear difference between in-plane and out-of-plane modes: the former have a writhe of the same sign as Û⁰, while the latter have the opposite sign. In other words, the in-plane modes untwist the ring while the out-of-plane modes overtwist it. The results for the clamped modes reveal a different situation, since most of the modes untwist the ring. We note, however, that some of the in-plane modes exhibit an overtwisting behavior for small values of Û⁰ (see the inset in the right plot in Fig. 6), although the overtwisting is much smaller than in the periodic case. We found in our numerical results that only a finite number of in-plane modes possess this untwisting behavior and it appears that higher frequency in-plane modes lose this feature.

Fig. 6.

Time average of the writhing number 〈Wr〉 for the first six flexural modes as functions of the imposed torsional moment Û⁰ for periodic (left) and clamped (right) boundary conditions for the first six modes. The styles and symbols on all plots are identical to those used in Fig. 3. The insets make clear the dependence of the periodic out-of-planes modes (left) and the clamped in-plane modes (right) on small positive values of Û⁰.

Finally, we see from our results for the flexural modes that the rotational inertia has a rather small influence on the properties of these modes. The mode frequencies, amplitudes, and writhing numbers for η = 0.05 are almost identical to those in the limit η → 0. Of course, the effect of the rotational inertia of the rod will be more pronounced for high-frequency modes but these high-frequency modes are unlikely to contribute in a significant way to the dynamics of the elastic ring. The zero rotational inertia approximation neglects the variation in the twist density; however, we found that the twisting amplitudes are always much smaller than the flexural amplitudes (see the results given in Appendix F.1) and, hence, this approximation can be considered as accurate for rings with large aspect ratios.

6.4 Twisting modes

We now focus on the description of the twisting modes for the periodic and clamped rings. These modes are directly related to the rotational inertia of the rod, and do not exist in the limit η → 0.

For the periodic ring we can directly obtain the twisting-mode frequencies and amplitudes (see Appendix D for the details of the calculations) and, as we noted earlier, the first periodic twisting mode is obtained for n = 1. A general feature of these twisting modes is that their frequencies are higher than those of the flexural modes: for η = 0.05, which is a high value for the rotational inertia parameter, the first twisting mode frequency of the periodic ring exceeds the frequencies of the first six flexural modes. In addition, these frequencies are nearly independent of the imposed torsional moment Û⁰ and a good approximation for the first ten modes is given by ${\mathrm{\sigma ̂}}_n\simeq n\sqrt{\Gamma }(\eta +1/\eta )$. Some of these frequencies are shown in Appendix F.2 (see Fig F.2). The other characteristic of the periodic twisting modes is that the amplitude of the twisting motion is always much larger than the in-plane and out-of-plane amplitudes. Moreover, we find that the twisting RMS amplitude ${\mathrm{\delta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$ is nearly independent of the mode index and the imposed torsional moment. For periodic boundary conditions, we can solve the normalization condition assuming the in-plane and out-of-plane amplitudes are zero to find ${\mathrm{\delta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}\simeq 0.65147$, and we observe only very small deviations from this value when Û⁰ ≠ 0. The in-plane, ${\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$, and out-of-plane, ${\mathrm{\alpha ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$, RMS amplitudes for the first four twisting modes with η = 0.05 are given in Appendix F.2 (see Fig F.2). We found that these amplitudes remain small compared to the twisting amplitude. In other words, the periodic twisting modes correspond to high-frequency modes with very small in-plane and out-of-plane amplitudes but large twisting deformations. In particular, it is interesting to note that the mode described by Coleman et al. in [10], which corresponds to the first twisting mode, has a very small out-of-plane amplitude (the in-plane amplitude is zero as shown in Fig. F.2) and is equivalent to a planar ring with oscillating cross sections. Finally, the writhe associated with the periodic twisting modes is found to be almost zero and, hence, negligible.

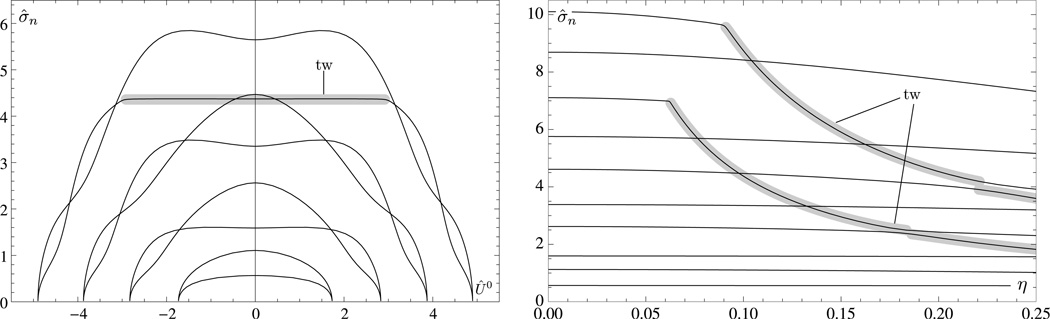
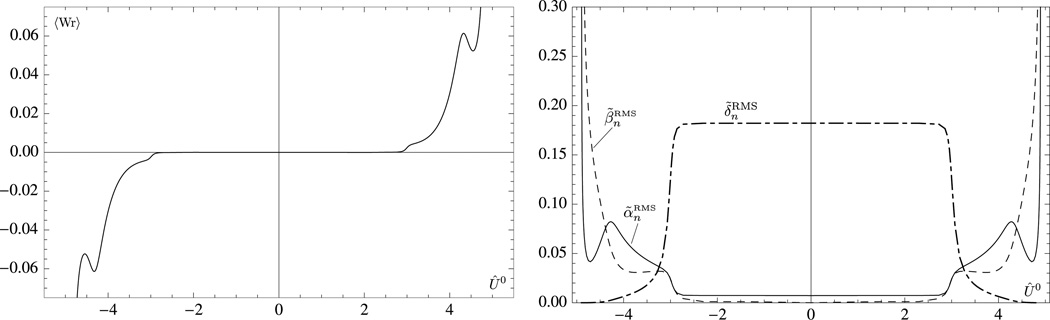
The twisting modes of the clamped ring are radically different from those of the periodic one. The clamped boundary conditions combine the flexural modes and the twisting modes depending on the values of η and the imposed torsional moment Û⁰. As shown in the left plot of Fig. 7, the twisting modes dominate the flexural modes over a certain range of Û⁰. Within this range, we find that the frequency is nearly independent of Û⁰, a characteristic of the twisting modes seen in the periodic case. In addition, we find that the value of η changes the type of normal mode as we see in the right plot of Fig. 7. The clamped twisting modes have the same characteristics as the periodic ones, that is, large twisting amplitudes and small in-plane and out-of-plane amplitudes, and, hence, negligible writhing numbers. These quantities are plotted in Fig. 8 for the first clamped twisting mode obtained with η = 0.1 (that is, the one highlighted in the left plot of Fig. 7) and we see that within the range of values of the imposed torsional moment Û⁰ for which the mode is a twisting mode the writhe is almost zero and the twisting RMS amplitude ${\mathrm{\delta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$ dominates the in-plane and out-of-plane RMS amplitudes (${\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$ and ${\mathrm{\alpha ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$). When the imposed torsional moment is such that the mode is no longer a twisting mode, we find that the mode behaves like a flexural mode. The clamped twisting modes are high-frequency modes and that is why we have to use a large value of η to illustrate them. For smaller values of η, the same effects will take place but at much higher frequency, that is, the clamped twisting modes are mixed with the high-frequency flexural modes.

Fig. 7.

Normal mode frequencies σ̂_n for the clamped modes as functions of the imposed torsional moment Û⁰ for η = 0.1 (left) and as functions of the rotational inertia parameter η (right) for clamped boundary conditions at Û⁰ = 0. On both plots, the solid black lines represent the frequencies and the thick gray lines highlight the parts of the frequency branches corresponding to twisting modes.

Fig. 8.

Time average of the writhing number 〈Wr〉 (left) and RMS amplitudes (right) of the first clamped twisting mode for η = 0.1 as functions of the imposed torsional moment Û⁰. In the RMS amplitudes plot, the solid black line represents the out-of-plane RMS amplitude $({\mathrm{\alpha ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}})$, the dashed black line the in-plane RMS amplitude $({\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}})$ and the mixed dashed black line the twisting RMS amplitude $({\mathrm{\delta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}})$.

7 Discussion

We have described in this paper the vibrational modes of an elastic ring with periodic and clamped boundary conditions. In addition, we have obtained the dependence of these modes on the imposed torsional stress in the ring and on the aspect ratio of the rod (through the parameter η = h/ (2R) = π/𝒜 with 𝒜 the aspect ratio of the rod). Our results show that in most cases, the rotational inertia of the rod can be neglected in the calculation of the mode frequencies, amplitudes, and writhing numbers. The rotational inertia plays a significant role for specific vibrational modes, the twisting modes. These modes are characterized by small bending deformations and large twisting deformations in the rod. These modes, however, are high-frequency modes and, except for thick rings, they are unlikely to contribute appreciably to the dynamics of the ring. Our work also addresses the effect of the boundary conditions on the vibrational modes. In the case of periodic boundary conditions, we found a clear distinction between the two types of flexural modes (in-plane and out-of-plane modes). In this case, the vibrations of the in-plane modes produce a decrease in the torsional stress of the ring, while the vibrations of the out-of-plane modes increase the torsional stress. Note that, as can be expected, the periodic twisting modes always produce an overtwisting of the ring. When the elastic ring is clamped, the mechanical response to the vibrations is different. For both types of flexural modes we found that the vibrations tend to reduce the torsional stress in the ring. Some of the in-plane modes, however, can increase the torsional stress in the ring when the imposed torsional moment is small. Another effect of clamped boundary conditions is the mixing between flexural and twisting modes depending upon the imposed torsional moment Û⁰ in the ring and the value of the parameter η, which is inversely proportional to the aspect ratio of the rod. In contrast to the periodic case, for which the values of Û⁰ and η have no effect on the type of mode (flexural or twisting), the modes for the clamped ring do change types when the imposed torsional stress is increased or decreased. Similarly, changes in the aspect ratio of the rod can affect the types of modes.

Our model neglects the extensibility of the rod and shearing deformations in the rod. The latter are expected to be negligible for rods with large aspect ratios (i.e., rods for which η is small), and when the magnitude of the bending and twisting deformations remain small. The extensibility of the rod might have some influence on the vibrational modes. Our results for the frequencies in the clamped case with no imposed torsional moment show, however, almost no difference from the findings reported in [2], which account for the extensibility of the rod. In addition, the results obtained in [12, 13], which use the same model as that described in this paper, show good agreement with experimental measurements of writhe fluctuations in short DNA minicircles. This suggests that extensibility and shearing play a minor role in the vibrations of elastic rings.

From a general point of view, our results can be applied to different problems related to the vibrations of an elastic ring. For example, the clamped boundary conditions can be seen as the limiting case of a very heavy protein bound to a DNA minicircle. According to our results, the binding of the protein will dampen the fluctuations in the writhing number, a key parameter in the description of DNA geometry and topology. In addition, our results can be used with an approach along the lines of that described in [12, 13] to perform the statistical physics of the vibrational modes and to study how the modes contribute to the fluctuations in the geometry and topology of circular biopolymers. Within this context, it will be interesting to see how the mixing between flexural and twisting modes caused by clamped boundary conditions could affect the fluctuations of a DNA minicircle. Our work can also be extended to study the vibrations of an elastic rod about an arbitrary equilibrium solution. For example, one could study the vibrations of a buckled elastic ring when the imposed torsional moment exceeds the critical values of the Zajac instability.

A Elastic ring material frame directors

We derive in this appendix explicit expressions for the material frame directors d̂₁(ŝ,t̂) and d̂₂(ŝ,t̂) of the elastic ring.

We choose, without any loss of generality, the initial condition ${\mathit{d̂}}_1^0(-\pi ,\mathrm{t̂})=\mathit{Z}$, and with the use of Eq. (4a) and the condition d̂₁ · d̂₃ = 0, we obtain

$${\mathit{d̂}}_1(ŝ,\mathrm{t̂})=\left[\begin{array}{c}\hfill \text{cos}({\mathrm{\Omega ̂}}_3^0(ŝ+\pi ))\hfill \\ \hfill \text{sin}({\mathrm{\Omega ̂}}_3^0(ŝ+\pi ))\hfill \\ \hfill 0\hfill \end{array}\right]+\epsilon \left[\begin{array}{c}\hfill g_1\hfill \\ \hfill g_2\hfill \\ \hfill {\alpha }^{(1)}\text{cos}({\mathrm{\Omega ̂}}_3^0(ŝ+\pi ))-({\gamma }^{(2)}+\gamma )\text{sin}({\mathrm{\Omega ̂}}_3^0(ŝ+\pi ))\hfill \end{array}\right],$$ (A.1)

where g₁(ŝ,t̂) and g₂(ŝ,t̂) are two unknown functions.

We now introduce the vector q̂(ŝ,t̂) such that ${\mathit{d̂}}_i(ŝ,\mathrm{t̂})-{\mathit{d̂}}_i^0(ŝ)=\mathit{q̂}(ŝ,\mathrm{t̂})\times {\mathit{d̂}}_i^0(ŝ)$ (the existence of such a vector is guaranteed since we assume that the material frame of the rod remains orthonormal). The identification with the tangent expansion (Eq. (23)) leads to

$$\mathit{q̂}(ŝ,\mathrm{t̂})=\epsilon \left[\begin{array}{c}\hfill {\gamma }^{(2)}+\gamma \hfill \\ \hfill {\alpha }^{(1)}\hfill \\ \hfill \xi \hfill \end{array}\right],$$ (A.2)

where ξ (ŝ,t̂) is an unknown function. We now compare the expansions for d̂₁(ŝ,t̂) and $\mathit{q̂}(ŝ,\mathrm{t̂})\times {\mathit{d̂}}_1^0(ŝ)$ and find

$$g_1(ŝ,\mathrm{t̂})=-\xi (ŝ,\mathrm{t̂})\text{sin}({\mathrm{\Omega ̂}}_3^0(ŝ+\pi )),$$ (A.3a)

$$g_2(ŝ,\mathrm{t̂})=\xi (ŝ,\mathrm{t̂})\text{cos}({\mathrm{\Omega ̂}}_3^0(ŝ+\pi )).$$ (A.3b)

In addition, we also have from the definition of the curvature vector (Eq. (4a)) the relation ${\mathrm{\Omega ̂}}_3(ŝ,\mathrm{t̂})={\mathit{d̂}}_1^{\prime }(ŝ,\mathrm{t̂})·({\mathit{d̂}}_3(ŝ,\mathrm{t̂})\times {\mathit{d̂}}_1(ŝ,\mathrm{t̂}))$, which at the first order is

$$\delta (ŝ,\mathrm{t̂})=\xi \prime (ŝ,\mathrm{t̂})+\alpha \prime (ŝ,\mathrm{t̂}).$$ (A.4)

In the static circular configuration we do not require ${\mathit{d̂}}_1^0(-\pi ,t)={\mathit{d̂}}_1^0(\pi ,t)$, that is, ${\mathrm{\Omega ̂}}_3^0$ is not necessarily an integer. In other words, when the static elastic ring is formed by bringing the two ends of the rod together, the material frame directors do not need to coincide. The difference between those vectors is imposed and constant such that ${\mathit{d̂}}_1(-\pi ,t)-{\mathit{d̂}}_1(\pi ,t)={\mathit{d̂}}_1^0(-\pi ,t)-{\mathit{d̂}}_1^0(\pi ,t)$. This implies that ξ (−π,t̂) = ξ (π,t̂) for both periodic and clamped boundary conditions; in the case of clamped boundary conditions this condition becomes ξ (−π,t̂) = ξ (π,t̂) = 0. In particular, it implies that

$${\int }_{-\pi }^{\pi }\delta (ŝ,\mathrm{t̂})\mathrm{d}ŝ=0,$$ (A.5)

for periodic and clamped boundary conditions (see Eq. (32) and Eq. (33)).

B Second-order perturbation

We give in this appendix the details of a second-order perturbation, that is, the expansions of the rod kinematical quantities up to O(ε³). These expansions are needed to assess the topology of the normal modes of vibration as well as to calculate the energies of the modes.

We first introduce the second-order perturbation of the rod centerline as

$$\mathit{r̂}(ŝ,\mathrm{t̂})=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right]+\epsilon \left[\begin{array}{c}\hfill \alpha \hfill \\ \hfill -{\gamma }^{(1)}\hfill \\ \hfill \gamma \hfill \end{array}\right]+{\epsilon }^2\left[\begin{array}{c}\hfill \Lambda \hfill \\ \hfill \Xi \hfill \\ \hfill \Upsilon \hfill \end{array}\right],$$ (B.1)

We obtain from the definition of the tangent (Eq. (1)) and the condition of inextensibility (Eq. (2)) the following expansion

$${\mathit{d̂}}_3(ŝ,\mathrm{t̂})=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill 1\hfill \end{array}\right]+\epsilon \left[\begin{array}{c}\hfill {\alpha }^{(1)}\hfill \\ \hfill -(\gamma +{\gamma }^{(2)})\hfill \\ \hfill 0\hfill \end{array}\right]+{\epsilon }^2\left[\begin{array}{c}\hfill {\Lambda }^{(1)}\hfill \\ \hfill -{\alpha }^{(2)}{\alpha }^{(1)}-({\gamma }^{(1)}+{\gamma }^{(3)})(\gamma +{\gamma }^{(2)})-{\Upsilon }^{(2)}-\Upsilon \hfill \\ \hfill -\frac{1}{2}({\alpha }^{{(1)}^2}+{(\gamma +{\gamma }^{(2)})}^2)\hfill \end{array}\right].$$ (B.2)

The square of the curvature vector is given by $\mathit{K̂}{(ŝ,\mathrm{t̂})}^2={\mathit{d̂}}_3^{\prime }(ŝ,\mathrm{t̂})·{\mathit{d̂}}_3^{\prime }(ŝ,\mathrm{t̂})$, that is,

$$\mathit{K̂}{(ŝ,\mathrm{t̂})}^2=1+2\epsilon ({\gamma }^{(1)}+{\gamma }^{(3)})+{\epsilon }^2(-{\alpha }^{{(1)}^2}+3{\alpha }^{{(2)}^2}+2{\alpha }^{(3)}{\alpha }^{(1)}+3{({\gamma }^{(1)}+{\gamma }^{(3)})}^2+2({\gamma }^{(2)}+{\gamma }^{(4)}\left)\right(\gamma +{\gamma }^{(2)})+2{\Upsilon }^{(1)}+2{\Upsilon }^{(3)}).$$ (B.3)

The twist density in the rod up to second order is defined as

$${\mathrm{\Omega ̂}}_3(ŝ,\mathrm{t̂})={\mathrm{\Omega ̂}}_3^0+\epsilon \delta (ŝ,\mathrm{t̂})+{\epsilon }^2\Delta (ŝ,\mathrm{t̂}),$$ (B.4)

and the axial spin velocity as

$${\mathrm{\omega ̂}}_3(ŝ,\mathrm{t̂})=\epsilon \varphi (ŝ,\mathrm{t̂})+{\epsilon }^2\Phi (ŝ,\mathrm{t̂}).$$ (B.5)

As for the first-order perturbation, we can use the compatibility condition (Eq. (8)) to relate the axial spin velocity and the twist density and we find

$$\mathrm{\Delta ̇}={\Phi }^{(1)}+{\mathrm{\Lambda ̇}}^{(1)}+{\gamma }^{(1)}{\mathrm{\alpha ̇}}^{(1)}+{\gamma }^{(3)}{\mathrm{\alpha ̇}}^{(1)}-{\alpha }^{(2)}\mathrm{\gamma ̇}-{\alpha }^{(2)}{\mathrm{\gamma ̇}}^{(2)}.$$ (B.6)

Finally, the periodic boundary conditions at the second order are similar to those at the first order (Eq. (32)) for the functions Λ (ŝ,t̂), ϒ (ŝ,t̂) and Δ (ŝ,t̂). The clamped conditions can easily be extended to second order. We have, in this case,

$$\Lambda (-\pi ,\mathrm{t̂})=\Lambda (\pi ,\mathrm{t̂})=0,$$ (B.7a)

$$\Upsilon (-\pi ,\mathrm{t̂})=\Upsilon (\pi ,\mathrm{t̂})=0,$$ (B.7b)

$$\Lambda \prime (-\pi ,\mathrm{t̂})=\Lambda \prime (\pi ,\mathrm{t̂})=0,$$ (B.7c)

$$\Upsilon \prime (-\pi ,\mathrm{t̂})=\Upsilon \prime (\pi ,\mathrm{t̂})=0,$$ (B.7d)

$$\Upsilon ″(-\pi ,\mathrm{t̂})=\Upsilon ″(\pi ,\mathrm{t̂})=0,$$ (B.7e)

$$\Delta \prime (-\pi ,\mathrm{t̂})=\Delta \prime (\pi ,\mathrm{t̂})=0.$$ (B.7f)

C Elastic ring energy

We derive in this appendix the expression of the energy of the elastic ring. The energy can be calculated up to second order of the perturbation, that is, it can be obtained as an O(ε³) expansion.

We recall that within the Kirchhoff elastic rod theory, the energy of the rod is defined as

$$ℰ={ℰ}_{\text{el}}+{ℰ}_{\text{kin}},$$ (C.1)

where ℰ_el is the potential energy of elastic deformation and ℰ_kin is the kinetic energy.

The elastic energy is defined as

$${ℰ}_{\text{el}}(\mathrm{t̂})=\frac{1}{2}{\int }_{-\pi }^{\pi }[\mathit{K̂}{(ŝ,\mathrm{t̂})}^2+2\Gamma {\mathrm{\Omega ̂}}_3{(ŝ,\mathrm{t̂})}^2]\mathrm{d}ŝ,$$ (C.2)

where K̂(ŝ,t̂) is the binormal curvature vector (see Eq. (6)) and Ω̂₃(ŝ,t̂) is the twist density in the rod (we recall that the undeformed state corresponds to a straight and untwisted rod, that is, a rod configuration with zero curvature and zero twist density).

The kinetic energy of the rod is given by

$${ℰ}_{\text{kin}}(\mathrm{t̂})=\frac{1}{2}{\int }_{-\pi }^{\pi }[\dot{\widehat{\mathit{r}}}{(ŝ,\mathrm{t̂})}^2+{\eta }^2(\mathit{\omega ̂}{(ŝ,\mathrm{t̂})}^2+{\mathrm{\omega ̂}}_3{(ŝ,\mathrm{t̂})}^2)]\mathrm{d}ŝ.$$ (C.3)

We express the energy of elastic deformation and the kinetic energy as

$${\mathrm{ℰ̂}}_{\text{el}}(\mathrm{t̂})={\mathrm{ℰ̂}}_{\text{el}}^{[0]}(\mathrm{t̂})+\epsilon {\mathrm{ℰ̂}}_{\text{el}}^{[1]}(\mathrm{t̂})+{\epsilon }^2{\mathrm{ℰ̂}}_{\text{el}}^{[2]}(\mathrm{t̂})+O({\epsilon }^3),$$ (C.4a)

$${\mathrm{ℰ̂}}_{\text{kin}}(\mathrm{t̂})={\mathrm{ℰ̂}}_{\text{kin}}^{[0]}(\mathrm{t̂})+\epsilon {\mathrm{ℰ̂}}_{\text{kin}}^{[1]}(\mathrm{t̂})+{\epsilon }^2{\mathrm{ℰ̂}}_{\text{kin}}^{[2]}(\mathrm{t̂})+O({\epsilon }^3).$$ (C.4b)

It follows from the expansion of the squared curvature (Eq. (B.3)), that the zero-order and first-order terms of the elastic energy for periodic and clamped boundary conditions are, respectively,

$${\mathrm{ℰ̂}}_{\text{el}}^{[0]}=\pi (1+\frac{{Û}^{0^2}}{2\Gamma }),$$ (C.5)

and

$${\mathrm{ℰ̂}}_{\text{el}}^{[1]}(\mathrm{t̂})={[\gamma +{\gamma }^{(2)}]}_{-\pi }^{\pi }+{Û}^0{\int }_0^{2\pi }\delta \mathrm{d}ŝ=0.$$ (C.6)

The second-order term of the energy of elastic deformation is given by

$${\mathrm{ℰ̂}}_{\text{el}}^{[2]}(\mathrm{t̂})={\left[\right(\Upsilon +{\Upsilon }^{(2)})+{\alpha }^{(1)}{\alpha }^{(2)}+(\gamma +{\gamma }^{(2)}\left)\right({\gamma }^{(1)}+{\gamma }^{(3)}\left)\right]}_{-\pi }^{\pi }+\frac{1}{2}{\int }_{-\pi }^{\pi }[{\alpha }^{{(2)}^2}-{\alpha }^{{(1)}^2}+{({\gamma }^{(1)}+{\gamma }^{(3)})}^2+2\Gamma {\delta }^2+2{Û}^0\Delta ]\mathrm{d}ŝ.$$ (C.7)

For the kinetic energy we directly have ${\mathrm{ℰ̂}}_{\text{kin}}^{[0]}=0$ and ${\mathrm{ℰ̂}}_{\text{kin}}^{[1]}=0$, since the equilibrium solution around which we linearize the Kirchhoff equations is static. For the second-order term we find

$${\mathrm{ℰ̂}}_{\text{kin}}^{[2]}(\mathrm{t̂})=\frac{1}{2}{\int }_{-\pi }^{\pi }[{\mathrm{\alpha ̇}}^2+{\eta }^2{\mathrm{\alpha ̇}}^{{(1)}^2}+{\mathrm{\gamma ̇}}^2+{\mathrm{\gamma ̇}}^{{(1)}^2}+{\eta }^2{(\mathrm{\gamma ̇}+{\mathrm{\gamma ̇}}^{(2)})}^2+2{\eta }^2{\varphi }^2]\mathrm{d}ŝ.$$ (C.8)

The periodic and clamped boundary conditions imply that the integrated terms (i.e., boundary terms) in the previous expansions are zero. It follows that the total energy of the elastic ring is

$$ℰ-{ℰ}^0=\frac{{\epsilon }^2}{2}{\int }_{-\pi }^{\pi }[{\alpha }^{{(2)}^2}-{\alpha }^{{(1)}^2}+{({\gamma }^{(1)}+{\gamma }^{(3)})}^2+2\Gamma {\delta }^2+2{Û}^0\Delta ]\mathrm{d}ŝ+\frac{{\epsilon }^2}{2}{\int }_{-\pi }^{\pi }[{\mathrm{\alpha ̇}}^2+{\eta }^2{\mathrm{\alpha ̇}}^{{(1)}^2}+{\mathrm{\gamma ̇}}^2+{\mathrm{\gamma ̇}}^{{(1)}^2}+{\eta }^2{(\mathrm{\gamma ̇}+{\mathrm{\gamma ̇}}^{(2)})}^2+2{\eta }^2{\varphi }^2]\mathrm{d}ŝ,$$ (C.9)

where ℰ⁰ is the energy of the static elastic ring.

C.1 Normal modes energy time average

We now calculate the time average (see Eq. (46)) of the elastic ring energy for a given normal mode. We omit the dependence of the modes on the mode index n for the sake of clarity. We start with the potential energy of elastic deformation

$$\langle {\mathrm{ℰ̂}}_{\text{el}}^{[2]}(\mathrm{t̂})\rangle =\frac{1}{4}{\int }_{-\pi }^{\pi }[{\mathrm{\alpha ̃}}^{{(2)}^2}-{\mathrm{\alpha ̃}}^{{(1)}^2}+{({\mathrm{\gamma ̃}}^{(1)}+{\mathrm{\gamma ̃}}^{(3)})}^2+2\Gamma {\mathrm{\delta ̃}}^2-2{Û}^0{\mathrm{\alpha ̃}}^{(2)}(\mathrm{\gamma ̃}+{\mathrm{\gamma ̃}}^{(2)}\left)\right]\mathrm{d}ŝ,$$ (C.10)

where we use Eq. (43) to express the second order of the twist density. For the kinetic energy we obtain

$$\langle {\mathrm{ℰ̂}}_{\text{kin}}^{[2]}(\mathrm{t̂})\rangle =\frac{1}{4}{\int }_{-\pi }^{\pi }{\mathrm{\sigma ̂}}^2[{\mathrm{\alpha ̃}}^2+{\mathrm{\gamma ̃}}^2+{\mathrm{\gamma ̃}}^{{(1)}^2}+{\eta }^2{\mathrm{\alpha ̃}}^{{(1)}^2}+{\eta }^2{(\mathrm{\gamma ̃}+{\mathrm{\gamma ̃}}^{(2)})}^2]\mathrm{d}ŝ+{\eta }^2{\int }_{-\pi }^{\pi }\langle {\varphi }^2\rangle \mathrm{d}ŝ.$$ (C.11)

With the use of the conservation law for the twist density (given by Eq. (15)) the last term in the previous expression can be written as

$${\int }_{-\pi }^{\pi }\langle {\varphi }^2\rangle \mathrm{d}ŝ=\frac{1}{2}{\int }_{-\pi }^{\pi }{\mathrm{\varphi ̃}}^2\mathrm{d}ŝ=\frac{1}{2}\frac{{\Gamma }^2}{{\eta }^4{\mathrm{\sigma ̂}}^2}{\int }_{-\pi }^{\pi }{\mathrm{\delta ̃}}^{{(1)}^2}\mathrm{d}ŝ=-\frac{1}{2}\frac{{\Gamma }^2}{{\eta }^4{\mathrm{\sigma ̂}}^2}{\int }_{-\pi }^{\pi }\mathrm{\delta ̃}{\mathrm{\delta ̃}}^{(2)}\mathrm{d}ŝ.$$ (C.12)

We can substitute in the last integral the third linearized Kirchhoff equation (see Eq. (30)) to obtain

$${\int }_{-\pi }^{\pi }\langle {\varphi }^2\rangle \mathrm{d}ŝ=\frac{\Gamma }{2{\eta }^2}{\int }_{-\pi }^{\pi }{\mathrm{\delta ̃}}^2+{\mathrm{\delta ̃}}^{(1)}\mathrm{\alpha ̃}\mathrm{d}ŝ.$$ (C.13)

It follows for the time average of the kinetic energy that

$$\langle {\mathrm{ℰ̂}}_{\text{kin}}^{[2]}(\mathrm{t̂})\rangle =\frac{1}{4}{\int }_{-\pi }^{\pi }{\mathrm{\sigma ̂}}^2[{\mathrm{\alpha ̃}}^2+{\mathrm{\gamma ̃}}^2+{\mathrm{\gamma ̃}}^{{(1)}^2}+{\eta }^2{\mathrm{\alpha ̃}}^{{(1)}^2}+{\eta }^2{(\mathrm{\gamma ̃}+{\mathrm{\gamma ̃}}^{(2)})}^2]\mathrm{d}ŝ+\frac{1}{4}{\int }_{-\pi }^{\pi }[2\Gamma {\mathrm{\delta ̃}}^2+2\Gamma \mathrm{\alpha ̃}{\mathrm{\delta ̃}}^{(1)}]\mathrm{d}ŝ.$$ (C.14)

The time averages of the potential and kinetic energies can be rewritten with the help of integrations by parts in such a way that the equality $\langle {\mathrm{ℰ̂}}_{\text{kin}}^{[2]}(\mathrm{t̂})\rangle =\langle {\mathrm{ℰ̂}}_{\text{el}}^{[2]}(\mathrm{t̂})\rangle$ directly follows from the linearized Kirchhoff equations (Eq. (30)). The details of such calculations are left to the reader.

D Normal mode analysis for periodic boundary conditions

This appendix presents detailed results for the normal mode analysis of an elastic ring subjected to periodic boundary conditions.

D.1 Normal mode frequencies

The normal-mode frequencies for the periodic case are the roots of the equation detM̲(σ̂_n,n) = 0, where M̲ is obtained by substituting the expressions given in Eq. (48) into the linearized Kirchhoff equations (Eq. (30)), yielding

$$\mathit{M̲}({\mathrm{\sigma ̂}}_n,n)=\left(\begin{array}{ccc}\hfill n^4-{\mathrm{\sigma ̂}}_n^2-n^2(1+{\eta }^2{\mathrm{\sigma ̂}}_n^2)\hfill & \hfill -n^2(n^2-1){Û}^0\hfill & \hfill -2\mathrm{i}n\Gamma \hfill \\ \hfill n^2(n^2-1){Û}^0\hfill & \hfill (n^2+{(n^2-1)}^2{\eta }^2+1){\mathrm{\sigma ̂}}_n^2-n^2{(n^2-1)}^2\hfill & \hfill 0\hfill \\ \hfill \mathrm{i}n{\eta }^2{\mathrm{\sigma ̂}}_n^2\hfill & \hfill 0\hfill & \hfill {\eta }^2{\mathrm{\sigma ̂}}_n^2-n^2\Gamma \hfill \end{array}\right).$$ (D.1)

The determinant of M̲ is given by a polynomial of degree six containing only even powers of σ̂_n,

$$\text{det}\mathit{M̲}({\mathrm{\sigma ̂}}_n,n)=C_3{\mathrm{\sigma ̂}}_n^6+C_2{\mathrm{\sigma ̂}}_n^4+C_1{\mathrm{\sigma ̂}}_n^2+C_0,$$ (D.2)

where the coefficients C_i are

$$C_0=\Gamma n^6{(n^2-1)}^2(n^2-1-{Û}^{0^2}),$$ (D.3a)

$$C_1=n^4(n^2-1)(-2n^2\Gamma -(n^2-1)(\Gamma -1+n^2(1+2\Gamma )){\eta }^2)+n^4{\eta }^2{(n^2-1)}^2{Û}^{0^2}$$ (D.3b)

$$C_2=n^2(1+n^2)\Gamma +n^2(n^2(\Gamma -2)+2n^4(1+\Gamma )+3\Gamma ){\eta }^2+{(n-n^3)}^2(-1+2\Gamma +n^2(2+\Gamma )){\eta }^4,$$ (D.3c)

$$C_3=-{\eta }^2(1+n^2{\eta }^2)(1+n^2+{\eta }^2{(n^2-1)}^2).$$ (D.3d)

Since the determinant is a cubic equation in ${\mathrm{\sigma ̂}}_n^2$ it can be solved with the help of Cardano’s formulae. We introduce the following auxiliary quantities

$$P=\frac{3C_3{C}_1-C_2^2}{9C_3^2},$$ (D.4a)

$$Q=\frac{9C_3{C}_2{C}_1-27C_3^2{C}_0-2C_2^3}{54C_3^3},$$ (D.4b)

$$\Theta =P^3+Q^2,$$ (D.4c)

$$D_1={(Q+\sqrt{\Theta })}^{1/3},$$ (D.4d)

$$D_2={(Q-\sqrt{\Theta })}^{1/3},$$ (D.4e)

where Θ is the discriminant, which depending on its sign, determines the quality (real or complex) and the degeneracy of the roots. The three roots are given by

$${\mathrm{\sigma ̂}}_{n,1}^2=D_1+D_2-\frac{C_2}{3C_3},$$ (D.5a)

$${\mathrm{\sigma ̂}}_{n,2}^2=-\frac{D_1+D_2}{2}-\frac{C_2}{3C_3}+\frac{\mathrm{i}\sqrt{3}}{2}(D_1-D_2),$$ (D.5b)

$${\mathrm{\sigma ̂}}_{n,3}^2=-\frac{D_1+D_2}{2}-\frac{C_2}{3C_3}-\frac{\mathrm{i}\sqrt{3}}{2}(D_1-D_2).$$ (D.5c)

The normal-mode frequencies are then obtained by taking the positive square root of each expression. If a frequency happens to have a non-zero imaginary part, the associated normal mode will grow exponentially, that is, the normal mode is unstable.

Frequencies for the zero rotational inertia approximation

For the zero rotational inertia approximation, the same method can be used to obtain the normal-mode frequencies. In this case, the linearized equations (Eq. (31)) are simpler and the linear system is reduced to a two-dimensional problem. Moreover, in the limit Û⁰ → 0 the two equations are uncoupled. One equation describes the in-plane motion of the ring and the other equation the out-of-plane motion. It follows that in this limit, the identification of the modes, in-plane or out-of-plane, is direct (see the discussion in Section 5.1). The frequencies for the in-plane and out-of-plane modes are given by the following expressions

$${\mathrm{\sigma ̂}}_{n,\text{ip}}^2=\frac{n^2(n^2-1)(n^2-\sqrt{1+(1+n^2){Û}^{0^2}})}{1+n^2},$$ (D.6a)

$${\mathrm{\sigma ̂}}_{n,\mathrm{o}\mathrm{p}}^2=\frac{n^2(n^2-1)(n^2+\sqrt{1+(1+n^2){Û}^{0^2}})}{1+n^2},$$ (D.6b)

where the superscript ”ip” and ”op” designate the in-plane and out-of-plane modes, respectively. Note that analytical expressions for the case Û⁰ = 0 and η ≠ 0 are given in [14, 15].

Classification of the modes

We take the limit η → 0 in Eq. (D.5) to identify the modes. We first find that ${\mathrm{\sigma ̂}}_n^1\to +\infty$, which shows that this frequency is related to the twisting mode. Then, we identify the limits of ${\mathrm{\sigma ̂}}_n^2$ and ${\mathrm{\sigma ̂}}_n^3$ with the expressions given in Eq. (D.6). Finally, we obtain the following classifications

$${\mathrm{\sigma ̂}}_{n,1}={\mathrm{\sigma ̂}}_{n,\text{tw}},$$ (D.7a)

$${\mathrm{\sigma ̂}}_{n,2}={\mathrm{\sigma ̂}}_{n,\text{ip}},$$ (D.7b)

$${\mathrm{\sigma ̂}}_{n,3}={\mathrm{\sigma ̂}}_{n,\mathrm{o}\mathrm{p}},$$ (D.7c)

where the superscript ”tw” designates the twisting mode.

D.2 Normal mode amplitudes

Once the normal-mode frequencies are known we obtain the amplitudes by solving the linear system given by Eq. (49), together with the normalization condition for the kinetic energy as written in Eq. (47). The outcome of these calculations is the set of amplitudes $(A_n^{\alpha },A_n^{\gamma },A_n^{\delta })$ as functions of the imposed twist density, i.e., the imposed linking number, Û⁰. The amplitude of the radial component β (ŝ,t̂) (Eq. (22)), denoted $A_n^{\beta }$, is obtained with the use of the relation β (ŝ,t̂) + γ′ (ŝ,t̂) = 0.

E Normal mode analysis for clamped boundary conditions

Here we present the details of our numerical method for the clamped boundary conditions.

E.1 Differential system

We start by rewriting of the linearized Kirchhoff equations (Eq. (30)) as a first-order differential system. It is convenient for the sake of clarity, to write this system in terms of the cylindrical components of the kinematical and mechanical variables. For example, we will use r̂_z, r̂_r and r̂_θ to denote the first-order components of the centerline path, that is, r̂_z = α̃, r̂_r = − γ̃′ and r̂_θ = γ̃. It follows that

$${\mathrm{r̂}}_z^{\prime }={\mathrm{d̂}}_{3z},{\mathrm{r̂}}_r^{\prime }={\mathrm{d̂}}_{3r}+{\mathrm{r̂}}_{\theta },{\mathrm{r̂}}_{\theta }^{\prime }=-{\mathrm{r̂}}_r,$$ (E.1a)

$${\mathrm{d̂}}_{3z}^{\prime }={\mathrm{m̂}}_r-{Û}^0{\mathrm{d̂}}_{3r},{\mathrm{d̂}}_{3r}^{\prime }=-{\mathrm{m̂}}_z+{Û}^0{\mathrm{d̂}}_{3z},$$ (E.1b)

$${\mathrm{m̂}}_z^{\prime }={\eta }^2{\mathrm{\sigma ̂}}^2{\mathrm{d̂}}_{3r}+{\mathrm{n̂}}_r,{\mathrm{m̂}}_r^{\prime }=-(1+{\eta }^2{\mathrm{\sigma ̂}}^2){\mathrm{d̂}}_{3z}+2\Gamma \mathrm{\delta ̂}-{\mathrm{n̂}}_z,$$ (E.1c)

$${\mathrm{n̂}}_z^{\prime }=-{\mathrm{\sigma ̂}}^2{\mathrm{r̂}}_z,{\mathrm{n̂}}_r^{\prime }=-{\mathrm{\sigma ̂}}^2{\mathrm{r̂}}_r+{\mathrm{n̂}}_{\theta },{\mathrm{n̂}}_{\theta }^{\prime }=-{\mathrm{\sigma ̂}}^2{\mathrm{r̂}}_{\theta }-{\mathrm{n̂}}_r,$$ (E.1d)

$$\delta \prime =\mathrm{\nu ̂},\Gamma \mathrm{\nu ̂}\prime =-{\eta }^2{\mathrm{\sigma ̂}}^2\delta +{\eta }^2{\mathrm{\sigma ̂}}^2{\mathrm{d̂}}_{3z},$$ (E.1e)

where we have again omitted labeling these functions and the frequency in terms of the wavenumber n. Note that this differential system is of dimension 12, which is also the dimension of the system given by Eq. (30). The twelve boundary conditions simply read as

$${\mathrm{r̂}}_z(-\pi )={\mathrm{r̂}}_z(\pi )=0$$ (E.2a)

$${\mathrm{r̂}}_r(-\pi )={\mathrm{r̂}}_r(\pi )=0$$ (E.2b)

$${\mathrm{r̂}}_{\theta }(-\pi )={\mathrm{r̂}}_{\theta }(\pi )=0$$ (E.2c)

$${\mathrm{d̂}}_{3z}(-\pi )={\mathrm{d̂}}_{3z}(\pi )=0$$ (E.2d)

$${\mathrm{d̂}}_{3r}(-\pi )={\mathrm{d̂}}_{3r}(\pi )=0$$ (E.2e)

$$\mathrm{\nu ̂}(-\pi )=\mathrm{\nu ̂}(\pi )=0.$$ (E.2f)

E.2 Numerical strategy

The first step is to identify the different solutions for Û⁰ = 0 and then each of these solutions can be continued for different values of Û⁰ (see [41] for an introduction to numerical continuation of ODE solutions). Each solution corresponds to a normal mode of vibration of the clamped ring. The integration and the continuation of the solutions of this differential system have been carried out using the AUTO-07p software (see [42–45]). The main difficulty of our problem is that the solutions are subjected to an integral constraint given by the normalization condition (see Eq. (47)). The AUTO-07p software ensures that this constraint is satisfied along the numerical path obtained for each solution (we found that the relative error along the different paths was of the order of 10⁻⁸–10⁻⁹).

The successive continuation steps are as follows:

• –we start with the trivial solution (every function is zero for every value of ŝ),
• –we perform a first continuation along the parameters σ̂_n and ℰ_kin: the bifurcations occurring along this path correspond to the normal-mode solutions,
• –for each bifurcation we then perform a new continuation for which the frequency is fixed and the kinetic energy parameter is increased until the normalization condition is satisfied,
• –the previous paths are continued with the frequency and η as free parameters until a fixed value of η is reached,
• –finally, the last solution of the previous continuation is used to start a new path on which the energy is held constant and only the frequency and the imposed torsional moment Û⁰ can change; this last path corresponds to the set of solutions for distinct values of Û⁰.

The input files used to generate the solutions are available upon request to the authors.

F Additional results

F.1 Twisting amplitudes for flexural modes

We give here the twisting amplitudes ${\mathrm{\delta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$ for the flexural modes obtained with periodic and clamped boundary conditions. These amplitudes can be compared to those given in Fig. 5. It is clear that the twisting amplitudes are much smaller than the flexural amplitudes. In addition, the twisting amplitudes scale as η², which means that for smaller values of η these amplitudes will also become much smaller. We note that in the clamped case, the twisting amplitudes always reach zero when the modes become unstable. Also of interest is the fact that the twisting amplitudes increase with the mode index, unlike the flexural amplitudes.

Fig. F.1 Twisting RMS amplitudes ${\mathrm{\delta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}}$ for the first six flexural modes as functions of the imposed torsional moment Û⁰ for periodic (left) and clamped (right) boundary conditions for η = 0.05. On both plots the solid black lines represent the amplitudes of the in-plane modes and the dashed lines correspond to the amplitudes of the out-of-plane modes. The numbers in the gray circles indicate the indices of the modes.

F.2 Twisting modes for periodic boundary conditions

The frequencies and flexural RMS amplitudes for the twisting modes of the periodic ring are given in Fig. F.2. We see that even for large values of η, the twisting mode frequencies are significantly higher than those of the flexural modes (compare with the frequencies in Fig. 3). In addition, the in-plane and out-of-plane RMS amplitudes are always much smaller than the twisting RMS amplitude, which for periodic boundary conditions is close to 0.65147.

Fig. F.2 Frequencies σ̂_n (left) and in-plane $({\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}})$ and out-of-plane $({\mathrm{\alpha ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}})$ RMS amplitudes (right) for the first four twisting modes with periodic boundary conditions. In the left plot, the solid black lines and the dashed black lines correspond, respectively, to the twisting mode frequencies for η = 0.005 and for η = 0.05. In the right plot, the solid black lines and the dashed black lines correspond, respectively, to the out-of-plane RMS amplitudes $({\mathrm{\alpha ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}})$ and to the in-plane RMS amplitudes times one hundred $({10}^2{\mathrm{\beta ̃}}_n^{\mathrm{R}\mathrm{M}\mathrm{S}})$ for η = 0.05. The in-plane RMS amplitude for n = 1 is zero. On both plots the numbers in the gray circles denote the mode indices.