Alternative radical pairs for cryptochrome-based magnetoreception

Abstract

There is growing evidence that the remarkable ability of animals, in particular birds, to sense the direction of the Earth's magnetic field relies on magnetically sensitive photochemical reactions of the protein cryptochrome. It is generally assumed that the magnetic field acts on the radical pair [FAD^•− TrpH^•+] formed by the transfer of an electron from a group of three tryptophan residues to the photo-excited flavin adenine dinucleotide cofactor within the protein. Here, we examine the suitability of an [FAD^•− Z^•] radical pair as a compass magnetoreceptor, where Z^• is a radical in which the electron spin has no hyperfine interactions with magnetic nuclei, such as hydrogen and nitrogen. Quantum spin dynamics simulations of the reactivity of [FAD^•− Z^•] show that it is two orders of magnitude more sensitive to the direction of the geomagnetic field than is [FAD^•− TrpH^•+] under the same conditions (50 µT magnetic field, 1 µs radical lifetime). The favourable magnetic properties of [FAD^•− Z^•] arise from the asymmetric distribution of hyperfine interactions among the two radicals and the near-optimal magnetic properties of the flavin radical. We close by discussing the identity of Z^• and possible routes for its formation as part of a spin-correlated radical pair with an FAD radical in cryptochrome.

1. Introduction

The mechanisms by which animals sense the direction of the Earth's magnetic field as an aid to navigation are still largely a mystery [1–4]. In 2000, Ritz and Schulten proposed the protein cryptochrome as the primary sensor in birds [5]. They suggested that a radical pair formed photochemically in cryptochrome molecules located in the retina could be sensitive to the direction of the Earth's magnetic field. Composed of radicals derived from the flavin adenine dinucleotide (FAD) cofactor and a tryptophan (Trp) residue in the protein, this short-lived radical pair would interconvert coherently between its electronic singlet and triplet states in such a way that the yields of its reaction products could be influenced by weak magnetic fields [5,6]. Over the last few years, evidence in support of a role for cryptochrome in magnetic sensing has been accumulating (reviewed in [7–12]) although it has not yet been established that this protein is actually the sensor or that the FAD–Trp radical pair is the crucial chemical entity.

Photo-excitation of cryptochromes containing FAD in its fully oxidized state leads to the formation of radicals via sequential electron transfers along a chain of three tryptophan residues, the ‘Trp-triad’ [13–16]. Electron abstraction from the Trp-triad by photo-excited FAD leads to the flavin radical anion, FAD^•− and the radical cation of the terminal residue of the Trp-triad, TrpH^•+, approximately 2 nm distant from the flavin. The [FAD^•− TrpH^•+] radical pair has recently been studied spectroscopically in cryptochrome-1 from the plant Arabidopsis thaliana and in the closely related DNA photolyase from Escherichia coli [17,18]. In both proteins, the lifetimes and yields of photo-induced radicals were observed to change when magnetic fields between 1 and 30 mT were applied. Although these findings suggest that [FAD^•− TrpH^•+] is fit for purpose as a magnetic sensor, they do not prove that it functions in the same way in vivo. Nor has it yet been demonstrated that any cryptochrome-based radical reaction responds to an Earth-strength magnetic field (approx. 50 µT) or that those effects are anisotropic, as required of a direction sensor.

Behavioural experiments, however, point towards a different cryptochrome-derived radical pair. The magnetic orientation of European robins appears to be disrupted by extraordinarily weak (down to 15 nT) magnetic fields oscillating at a frequency of approximately 1.3 MHz [19], a remarkable observation that has yet to be independently replicated. In order for there to be a resonant response at this frequency, one of the radicals should be devoid of internal (hyperfine) magnetic interactions [19]. As neither FAD^•− nor TrpH^•+ satisfies this condition, it was suggested that FAD^•− in cryptochrome might be paired with a radical much simpler than TrpH^•+, one with no magnetic nuclei in the vicinity of the electron spin [19]. We refer to this radical, which could be positively or negatively charged or neutral, as Z^•. It was also noted that an [FAD^•− Z^•] radical pair might offer a higher sensitivity to weak magnetic fields than would one with hyperfine interactions in both radicals [19–22]. This recipe for efficient sensing of the direction of an external magnetic field was subsequently developed into a ‘reference-probe’ model in which one radical (the reference) has large anisotropic hyperfine interactions and determines the anisotropy of the reaction yields while the other (the probe) has no hyperfine interactions and is responsible for efficiently coupling the radical pair to the magnetic field [11]. Although it has been assumed that FAD^•−, or its protonated form FADH^•, would be the reference radical, the identity of the probe radical, Z^•, remains enigmatic [23,24].

The performance of a radical pair compass sensor is expected to depend on a number of factors—chemical, structural, kinetic, dynamic and magnetic [8]. Chief among the magnetic properties of the radicals is their hyperfine interactions. Within each radical, the spin motion of the unpaired electron is determined principally by its hyperfine coupling to the nuclear spins of hydrogen and nitrogen atoms. In both FAD^•− and TrpH^•+, the semi-occupied molecular orbital is delocalized over the aromatic ring system such that the electron spin interacts with the ring nitrogens, the hydrogens attached to the ring carbons and a few other nearby hydrogens. In general, the hyperfine interaction of each of these nuclei has isotropic and anisotropic components, determined by the local electron spin density. These interactions are critical because they condition the response of the radical pair to an external magnetic field. In particular, the anisotropic components cause the yields of the reaction products to depend on the orientation of the radical pair with respect to the external magnetic field vector. It is generally assumed that this effect forms the basis of the directional properties of the compass sensor [25–27].

In this report, we use spin dynamics simulations to: (i) determine the extent to which [FAD^•− Z^•] is superior to [FAD^•− TrpH^•+] as a magnetic compass detector; (ii) assess the suitability of FAD radicals in cryptochrome as components of a radical pair compass; and (iii) determine the source of the favourable properties of FAD radicals in [FAD^•− Z^•]-type radical pairs. We discuss the identity of Z^• and the routes by which it could be formed as part of a magnetically sensitive cryptochrome-based radical pair.

2. Results

2.1. Flavin–tryptophan radical pair

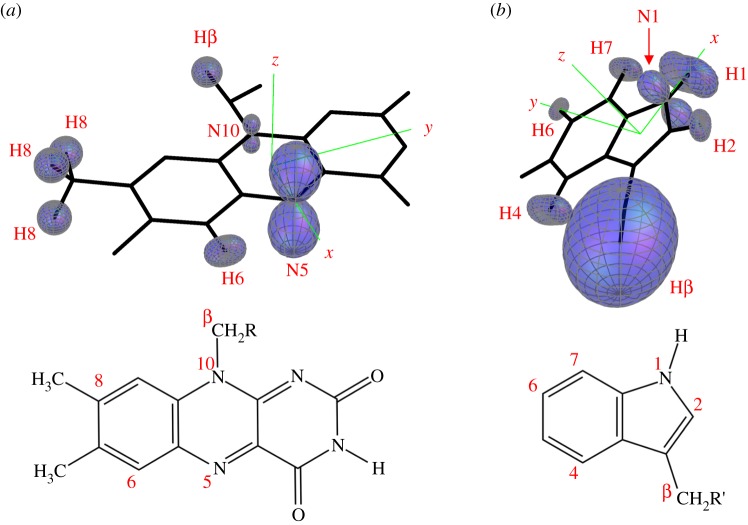
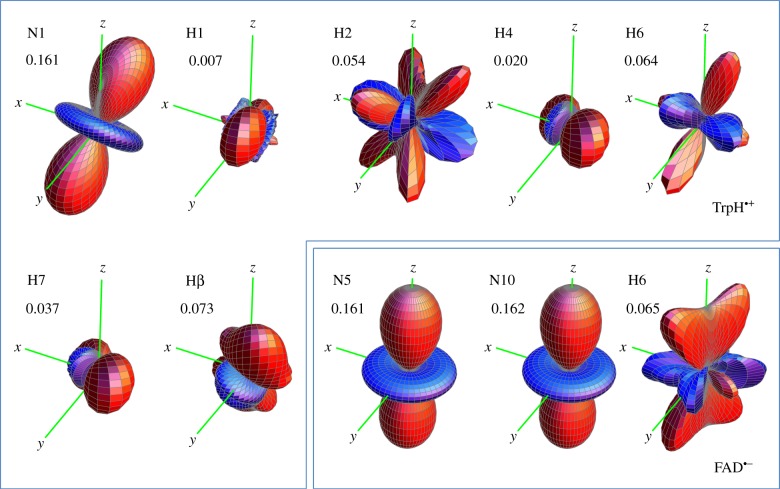
In figure 1, the seven largest hyperfine interactions in FAD^•− and in TrpH^•+are represented as three-dimensional surface plots each centred on the relevant hydrogen or nitrogen atom. The distance from the atom to the surface in any direction is proportional to the strength of the magnetic interaction of the electron spin and the nuclear spin; nuclei with almost isotropic hyperfine interactions have near-spherical surfaces. In TrpH^•+, six of the hyperfine interactions are significantly anisotropic; the seventh, one of the two β-methylene hydrogens, is strong and almost isotropic. In FAD^•−, by contrast, only the two ring nitrogens, N5 and N10, and to a lesser extent the H6 hydrogen, have marked anisotropy; all the other hydrogens have hyperfine interactions that are relatively small and nearly isotropic.

Figure 1.

Representations of the seven largest hyperfine tensors in (a) FAD^•− and (b) TrpH^•+ superimposed on the structures of the parent molecules. The orientation of TrpH relative to FAD is that of Trp-342 relative to the FAD cofactor in the cryptochrome from D. melanogaster [28,29]. The hyperfine tensors, which are listed in the electronic supplementary material, tables S1 and S2, were calculated in Gaussian-03 [30] at the UB3LYP/EPR-III level of theory. The adenine group of FAD is omitted and the ribityl side chain is truncated after the first carbon. Only the side chain and the β-CH₂ group of TrpH are shown.

To model the effect of the geomagnetic field on the [FAD^•− TrpH^•+] radical pair, we follow previous practice and assume for simplicity that its singlet and triplet states react spin-selectively at identical rates to form distinct products [5,31–34]. The external magnetic field modulates the coherent interconversion of the singlet and triplet states and so changes the proportions of radical pairs that proceed along the two competing pathways. The intensity of the Earth's field and the reaction rate constant were taken as 50 µT and 10⁶ s⁻¹, respectively. The latter gives a radical pair lifetime of 1 μs, which is probably close to the optimum for a 50 µT magnetic field [8]. Shorter lifetimes would not allow the geomagnetic field to have its full effect; longer lifetimes run the risk that spin relaxation would attenuate the magnetic sensitivity. The magnetic field effect was calculated as Φ_S, the fractional yield of the singlet reaction product once all radical pairs have reacted. Φ_S lies in the range [0,1] and is related to the triplet product yield by Φ_T = 1 − Φ_S. To quantify the effectiveness of a radical pair as a magnetic compass, we define the anisotropy of the reaction yield, ΔΦ_S, as the difference between the maximum and minimum values of Φ_S calculated as a function of the direction of the magnetic field vector. The only difference between the treatment of hydrogen and nitrogen nuclei in the modelling lies in their spin quantum numbers (I = 1/2 and I = 1, respectively). Details of the calculations can be found in the electronic supplementary material.

The singlet yield, Φ_S, for [FAD^•− TrpH^•+] was simulated using the 14 hyperfine interactions depicted in figure 1. The relative orientation of the two radicals was taken to be that of the FAD cofactor and Trp-342 (the terminal tryptophan of the Trp-triad) in the crystal structure of Drosophila melanogaster cryptochrome (DmCry, PDB entry 4GU5 [28,29]). The result is shown in figure 2a. As expected, the reaction yield has inversion symmetry, i.e. the effect of the magnetic field is independent of its polarity in accordance with the properties of the avian compass determined from behavioural experiments [35]. The magnitude of the anisotropy, ΔΦ_S, is small: Φ_S,max = 0.2776 and Φ_S,min = 0.2762, giving ΔΦ_S = 0.0014.

Figure 2.

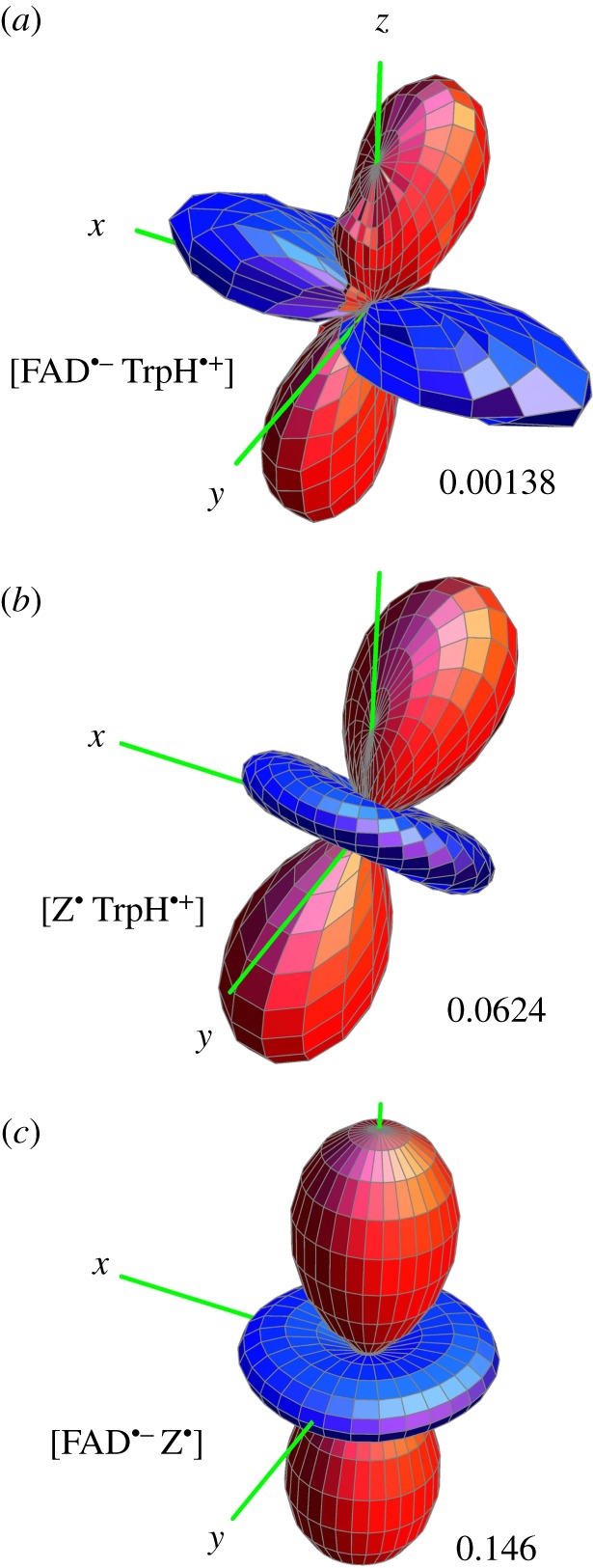
Singlet yield anisotropy plots for the radical pairs (a) [FAD^•− TrpH^•+], (b) [Z^• TrpH^•+] and (c) [FAD^•− Z^•], where Z^• is a radical with no hyperfine interactions. The spherical average of the reaction yield, i.e. the part of Φ_S that is independent of the magnetic field direction, has been subtracted to reveal the anisotropic component, which contains the directional information. The distance in any direction from the centre of the pattern to the surface is proportional to the value of 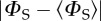when the magnetic field has that direction. Red/blue regions correspond to reaction yields larger/smaller than 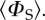FAD^•− and TrpH^•+ each have the seven hyperfine interactions shown in figure 1. The values of ΔΦ_S for the three radical pairs are as shown. The three anisotropy patterns are not drawn to scale. The coordinate system is that of FAD^•− (figure 1a). The orientation of TrpH^•+ relative to FAD^•− is as shown in figure 1. Details of the simulations are given in the electronic supplementary material.

Despite the complexity of the 16-spin system of [FAD^•− TrpH^•+] and the multiplicity of dissimilar hyperfine tensors in the two radicals, the information encoded in the reaction yield (figure 2a) has a relatively simple dependence on the orientation of the radical pair, albeit one of low amplitude. As we shall see next, the form of figure 2a can be understood qualitatively in terms of the magnetic properties of the individual radicals.

2.2. Truncated flavin–tryptophan radical pairs

Insight into the size and shape of the singlet yield anisotropy of [FAD^•− TrpH^•+] can be obtained by the artificial device of ‘switching off’ selected hyperfine interactions. This would clearly be impossible in an experiment but is trivial in a simulation—one simply omits the relevant nuclear spins. We have performed such calculations for various truncated versions of [FAD^•− TrpH^•+] with the aim of understanding the form of figure 2a and why ΔΦ_S for this radical pair is so small.

First, we turned off all seven hyperfine interactions in the FAD^•− radical, leaving TrpH^•+ untouched. We refer to this radical pair as [Z^• TrpH^•+], where Z^• is a radical whose spin system consists of an isolated electron spin, free from hyperfine interactions. The calculated singlet yield anisotropy of [Z^• TrpH^•+] (figure 2b) bears some resemblance to that of the intact radical pair (figure 2a) but is almost 50 times larger: ΔΦ_S = 0.062.

Next, we restored the hyperfine interactions in FAD^•− and eliminated those in TrpH^•+. The singlet yield anisotropy of this [FAD^•− Z^•] radical pair (ΔΦ_S = 0.146; figure 2c) is more than twice that of [Z^• TrpH^•+] (figure 2b), a hundred times larger than that of [FAD^•− TrpH^•+] (figure 2a).

The shapes of the anisotropic responses of [Z^• TrpH^•+] and [FAD^•− Z^•] (figure 2b,c) are essentially identical: both have approximate axial symmetry with an angular dependence of the approximate form (3 cos²ψ − 1), where ψ is the angle between the magnetic field and the symmetry axis of the pattern. In the case of [FAD^•− Z^•], the symmetry axis is the normal to the plane of the FAD ring system (the z-axis in figure 1a). In the case of [Z^• TrpH^•+], the symmetry axis is the normal to the plane of the indole (the z-axis in figure 1b). The angle between the planes of the FAD and Trp-342 rings in DmCry (approx. 40°) [28,29] is also the angle between the symmetry axes of the anisotropy patterns in figure 2b,c. Thus, the singlet yield anisotropy patterns of the two truncated radical pairs clearly reflect the relative orientations of the constituent radicals.

It appears from figure 2 that the singlet yield anisotropy of the intact radical pair, [FAD^•− TrpH^•+], is an approximate composite of the patterns for [FAD^•− Z^•] and [Z^• TrpH^•+]. The different directions of the symmetry axes for the two truncated pairs mean that the pattern for [FAD^•− TrpH^•+] (figure 2a) is not itself axially symmetric although the positions of its positive (red) and negative (blue) regions can be traced back to the corresponding regions in the [Z^• TrpH^•+] and [FAD^•− Z^•] patterns (figure 2b,c).

It may be inferred that the larger values of ΔΦ_S for [FAD^•− Z^•] and [Z^• TrpH^•+] compared to [FAD^•− TrpH^•+] arise from the presence of hyperfine interactions in both radicals in the latter. This is confirmed by the data in tables 1 and 2. Table 1 gives ΔΦ_S values for truncated versions of [FAD^•− Z^•] containing just N5, or N5 and N10, or N5 and N10 plus up to five of the hydrogens in FAD^•−. When N10 is added to N5, ΔΦ_S rises from 0.161 to 0.206 but when the hydrogens are added one by one, ΔΦ_S gradually falls to 0.146 when all seven nuclei are present. Thus, two nitrogens are better than one and the hydrogens do not reduce the anisotropy too much. The value of 0.206 for the N5 + N10 case is not far short of the optimum for a two-nitrogen radical pair under the same conditions (ΔΦ_S = 0.219, see below).

Table 1.

Singlet yield anisotropies calculated for truncated versions of [FAD^•− Z^•]. The nuclei in FAD^•− are introduced one at a time in the following order: N5, N10, H6, 3×H8, Hβ. The hyperfine tensors are given in electronic supplementary material, table S1.

no. FAD•− nuclei	1	2	3	4	5	6	7
ΔΦS	0.161	0.206	0.185	0.176	0.157	0.160	0.146

Table 2.

Singlet yield anisotropies calculated for truncated versions of [FAD^•−TrpH^•+]. The FAD^•− radical contains N5 and N10. The nuclei in TrpH^•+ are introduced one at a time in the following order: H1, H4, H7, Hβ, N1, H2, H6. The hyperfine tensors are given in electronic supplementary material, table S2.

no. TrpH•+ nuclei	0	1	2	3	4	5	6	7
ΔΦS	0.206	0.0054	0.026	0.0085	0.017	0.011	0.0092	0.0076

However, when truncated versions of [FAD^•− TrpH^•+] are simulated, a very different picture emerges (table 2). Starting with an FAD^•− radical containing N5 and N10, and introducing the nuclei in TrpH^•+ one at a time, one finds that ΔΦ_S drops abruptly from 0.206 to less than 0.01 when all seven TrpH^•+ nuclei are present. Thus, although the large anisotropy afforded by N5 and N10 in FAD^•− is not greatly degraded by the other nuclei in FAD^•− (table 1) it is disastrously attenuated by the nuclear spins in TrpH^•+ (table 2).

To summarize, the shape of the reaction yield anisotropy of [FAD^•− TrpH^•+] reflects the relative orientations of the two radicals and its small amplitude arises from the presence of hyperfine interactions in both radicals.

2.3. One-nucleus flavin–tryptophan radical pairs

The general shapes of the three anisotropy plots (figure 2) can be understood in more detail by simulations of radical pairs in which all but one of the 14 hyperfine interactions have been switched off. When the sole remaining hyperfine interaction is in the TrpH^•+ radical, we find reaction yield anisotropy patterns (figure 3) that vary greatly in size and appearance. However, one of the seven stands out. The plot for N1, the indole nitrogen, is not only the largest, but it also looks identical to that of [Z^• TrpH^•+] (figure 2b) in both shape and orientation.

Figure 3.

Singlet yield anisotropy plots for radical pairs containing a single hyperfine interaction selected from those in FAD^•− and TrpH^•+ (electronic supplementary material, tables S1 and S2). The values of ΔΦ_S for the 10 spin systems are as shown. The anisotropy patterns are not drawn to scale. The coordinate system is that of FAD^•− (figure 1a). The orientation of TrpH^•+ relative to FAD^•− is as shown in figure 1. Details of the simulations are given in the electronic supplementary material.

In FAD^•−, only three of the nuclei considered (N5, N10 and H6) have anisotropic hyperfine interactions. H6 gives rise to a relatively small reaction yield anisotropy with a complex shape (figure 3). The two nitrogens (N5 and N10) in the central ring of the flavin, however, both have similar, strong anisotropy plots which, to the eye, are identical in shape and orientation to that of [FAD^•− Z^•] (figure 2c).

All three of these one-nitrogen radical pairs have ΔΦ_S ≈ 0.16, which is close to the optimum value of 1/6 for this spin system (see below). Moreover, N1 in TrpH^•+ and N5 and N10 in FAD^•− are the only nuclei in [FAD^•− TrpH^•+] that have near-axial hyperfine interactions.

To summarize, the axial magnetic anisotropy patterns of [FAD^•− Z^•] and [Z^• TrpH^•+] appear to be dominated by the axial hyperfine tensors of the nitrogen nuclei: N5 and N10 in FAD^•− and N1 in TrpH^•+. For both of these radical pairs, the symmetry axis of the anisotropy pattern is determined by that of the nitrogen hyperfine tensors. And, as we saw above, the anisotropy pattern of the intact radical pair, [FAD^•− TrpH^•+], clearly reflects those for [FAD^•− Z^•] and [Z^• TrpH^•+].

2.4. Model radical pairs

The calculations described above suggest that FAD^•−, when paired with a radical containing no magnetic nuclei, could form the basis of a much more sensitive magnetic compass than [FAD^•− TrpH^•+] in which both radicals have hyperfine interactions. The reasons why [FAD^•− Z^•] seems to be particularly suitable for magnetic direction sensing will now be explored through simulations of simple model radical pairs. In these calculations, the hyperfine interaction of each nuclear spin is defined in terms of its three principal values, A_xx, A_yy and A_zz, which are related to the isotropic hyperfine coupling by a_iso = 1/3 (A_xx + A_yy + A_zz). Axial hyperfine interactions, i.e. A_xx = A_yy, will be of particular interest, especially those with A_xx = A_yy = 0 (so that A_zz = 3a_iso).

We start with a radical pair containing just one nitrogen. All the simulations here, like those in the other sections, were done for radical pairs with a lifetime of 1 µs, subjected to a 50 µT magnetic field. We focus on hyperfine interactions comparable in magnitude to the larger hyperfine interactions in [FAD^•− TrpH^•+]. There are cases where the simulations predict sizeable ΔΦ_S values for unrealistically small hyperfine couplings (approx. 1 µT) but we do not consider them here.

The maximum singlet yield anisotropy calculated numerically for a radical pair containing one nitrogen and no other magnetic nucleus is ΔΦ_S = 0.164. This comes about when (i) the hyperfine interaction is axial, (ii) the two perpendicular components are zero (A_xx = A_yy = 0), and (iii) the isotropic component a_iso is larger than approx. 100 µT (electronic supplementary material, figures S2 and S3). Qualitatively similar results have been found by Cai et al. [36] for a radical pair with a single hydrogen.

The maximum ΔΦ_S calculated for a radical pair with two nitrogens in the same radical is 0.219, about a third larger than that for the one-nitrogen case. Keeping 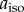for the first nitrogen fixed at 500 µT, this optimum is found when (a) both nuclei are coupled to the same electron spin, i.e. in the same radical; (b) both satisfy A_xx = A_yy = 0; (c) the symmetry axes of the two hyperfine interactions are parallel; and (d) the isotropic coupling of the second nitrogen is either in the range of (100–400 µT) or is larger than 600 µT. As can be seen in figure 4a, the value of ΔΦ_S drops if the two nuclei have isotropic couplings that are too similar. When the two nitrogens are in different radicals and both nuclei satisfy condition (b), ΔΦ_S is smaller and falls, as a_iso for the second nitrogen is increased beyond 20 µT (figure 4a). Figure 4b shows that rotating one hyperfine axis away from the other steadily reduces ΔΦ_S, the effect being similar whether the two nitrogens are in the same or different radicals.

Figure 4.

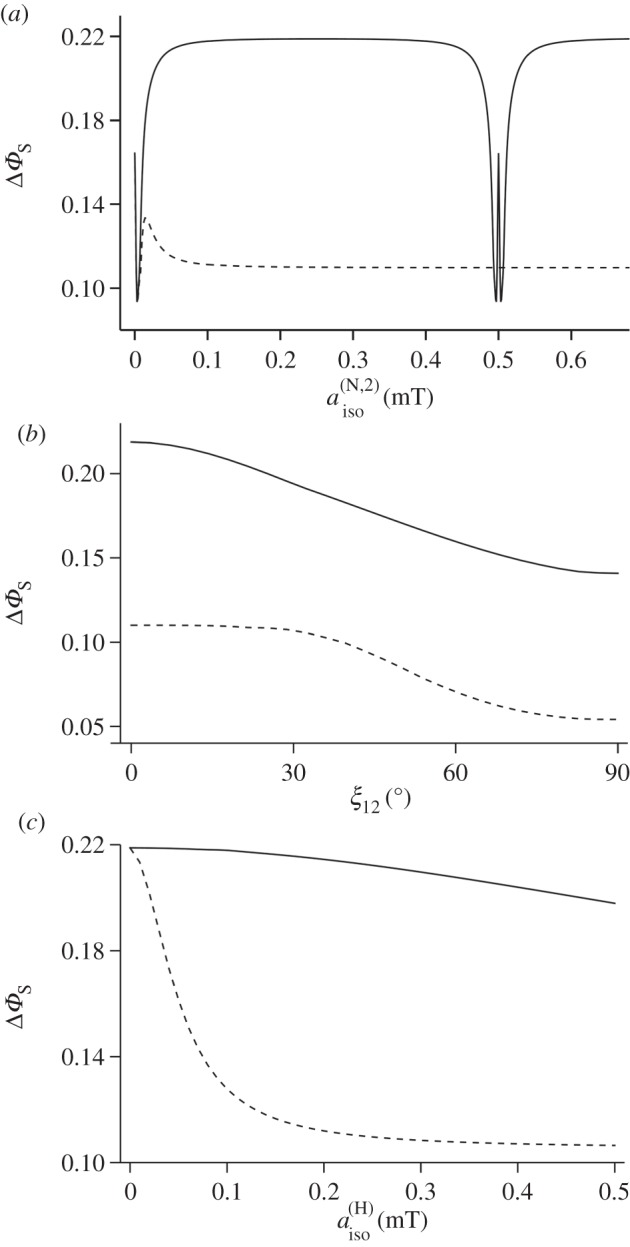
Calculations of the reaction yield anisotropy ΔΦ_S of simple model systems. (a) Two nitrogens in the same radical (solid line) and in different radicals (dashed line). A_xx = A_yy = 0 for both nuclei, parallel hyperfine z-axes, 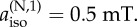The graphs show ΔΦ_S as a function of 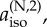the isotropic hyperfine coupling of the second nitrogen. (b) Two nitrogens in the same radical (solid line) and in different radicals (dashed line). A_xx = A_yy = 0 for both nuclei,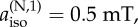 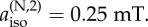The graphs show ΔΦ_S as a function of the angle ξ₁₂ between the z-axes of the two hyperfine tensors. (c) Two nitrogens and a hydrogen with an isotropic hyperfine interaction, The hydrogen is either in the same radical as the nitrogens (solid line) or in the other radical (dashed line). A_xx = A_yy = 0 for both nitrogens, 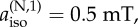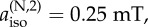parallel hyperfine axes. The graphs show ΔΦ_S as a function of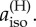

The effect on the two-nitrogen radical pair of adding a hydrogen with an isotropic hyperfine interaction is shown in figure 4c. Choosing the isotropic couplings of the two nitrogens to be 500 and 250 µT and maintaining A_xx = A_yy = 0 for both, the presence of the hydrogen reduces ΔΦ_S, an effect that is much less pronounced when all three nuclei are in the same radical.

To summarize, ΔΦ_S can be as large as 0.219 for a radical pair in which one radical has no hyperfine interactions and the other has two nitrogens whose hyperfine interactions satisfy a number of conditions (listed above). This favourable situation is degraded but not too seriously by the presence of a hydrogen with an isotropic hyperfine interaction provided it is in the radical that contains the nitrogens. Inspection of figure 1 and the hyperfine data in the electronic supplementary material (table S1) shows that these criteria are almost exactly satisfied by [FAD^•− Z^•]. The two nitrogens, N5 and N10, in the central ring of the flavin group in FAD^•− have large, near-axial hyperfine interactions. Their symmetry axes are parallel, the principal values of the two hyperfine tensors in the plane of the ring system are small and the two isotropic couplings (523 and 189 µT) are significantly different. Furthermore, the other nuclei in FAD^•− have hyperfine interactions that are either small or isotropic or both. Thus, the properties of [FAD^•− Z^•] fulfil all of the favourable design criteria identified from simulations of simple model systems.

2.5. Analytical solutions

For almost all of the radical pairs considered here, the spin dynamics can only be obtained by numerical solution of the appropriate quantum mechanical equations of motion. However, there are a few cases of interest in which analytical solutions can be found. One such is a radical pair containing a single nitrogen and no other magnetic nuclei. When the hyperfine interaction is axial and large compared with the external magnetic field, and two of the principal components are zero (A_xx = A_yy = 0), and the radical pair lifetime is long, the singlet yield is given by Φ_S = 5/9 + 1/18 (3 cos²ψ−1), where ψ is the angle between the hyperfine axis and the magnetic field vector (an outline of the derivation is given in the electronic supplementary material). For this radical pair: Φ_S,max = 2/3 (when ψ = 0), Φ_S,min = 1/2 (when ψ = 90°) and ΔΦ_S = 1/6. This is the maximum possible reaction yield anisotropy for a one-nitrogen radical pair with at least one hyperfine component larger than 50 µT, whether the hyperfine interactions are axial or not.

An analytical solution is also possible for a radical pair with two nitrogens when they are both in the same radical and their hyperfine interactions satisfy A_xx = A_yy = 0 and have parallel symmetry axes. When the two interactions are not too similar in magnitude and are both much larger than the applied magnetic field, the singlet yield for a long-lived radical pair is Φ_S = 11/27 + 2/27 (3 cos²ψ − 1), which gives an anisotropy, ΔΦ_S = 2/9. This is the optimum anisotropy for a two-nitrogen radical pair if, once again, one excludes unrealistically small (less than 50 µT) hyperfine interactions.

The numerical calculations (§2.4) give values of ΔΦ_S (0.164 for one nitrogen, 0.219 for two) that are slightly smaller than the optimum values (1/6 ≈ 0.167 and 2/9 ≈ 0.222, respectively) because the field strength (50 µT) and lifetime (1 µs) are not sufficiently small and large, respectively, to satisfy the conditions used to obtain the analytical solutions.

The same analytical method can be used for a three-nitrogen spin system in which all three nuclei are in the same radical and have (i) A_xx = A_yy = 0, (ii) parallel symmetry axes, and (iii) sufficiently different isotropic hyperfine couplings. The result is Φ_S = 29/81 + 13/162 (3 cos²ψ − 1) and ΔΦ_S = 13/54 ≈ 0.241, i.e. approximately 8% larger than the two-nitrogen case above. No doubt one could increase ΔΦ_S still further (e.g. by the addition of a fourth nitrogen) but it seems likely that the improvement would not be dramatic. Our feeling, based on simulating a large number of model spin systems, is that the nitrogen hyperfine interactions in FAD^•−, though not the best possible, are very close to optimal.

2.6. [FADH^• Z^•] radical pair

We have focused on FAD^•− and TrpH^•+ rather than their neutral protonated/deprotonated forms (FADH^• and Trp^•) because in vitro [FAD^•− TrpH^•+] is the magnetically sensitive radical pair in A. thaliana cryptochrome and E. coli photolyase [18]. However, as discussed below, an [FADH^• Z^•]-type radical pair could conceivably be formed in cryptochrome. We therefore repeated the above calculations (table 1) for truncated versions of [FAD^•− Z^•] with FAD^•− replaced by FADH^•. The results are given in table 3. Comparing the values of ΔΦ_S in tables 1 and 3, it is clear that the two radical pairs show similar behaviour. When N10 is added to N5 in the FADH^• radical, ΔΦ_S for [FADH^• Z^•] rises and then falls as the hydrogens are subsequently introduced, one at a time. Even though the additional hydrogen (H5) attached to N5 in FADH^• has a large anisotropic hyperfine interaction (electronic supplementary material, table S3), it does not have a drastic effect on ΔΦ_S. When the seven largest hyperfine interactions in FADH^• are included, the shape of the singlet yield anisotropy is identical by eye to figure 2c; the only notable difference between [FAD^•− Z^•] and [FADH^• Z^•] is the value of ΔΦ_S: 0.146 and 0.116, respectively. The greater sensitivity of the former is also evident when only N5 and N10 are included in the flavin radical: 0.206 and 0.168, respectively (tables 1 and 3). It appears that the small differences in the nitrogen hyperfine tensors (electronic supplementary material, tables S1 and S3) in the two FAD radicals are responsible.

Table 3.

Singlet yield anisotropies calculated for truncated versions of [FADH^•Z^•]. The nuclei in FADH^• are introduced one at a time in the following order: N5, N10, H5, 3×H8, Hβ. The hyperfine tensors are given in electronic supplementary material, table S3.

no. FADH• nuclei	1	2	3	4	5	6	7
ΔΦS	0.160	0.168	0.136	0.127	0.129	0.122	0.116

2.7. Reference-probe model

Finally, we examine how well [FAD^•− Z^•] corresponds to the optimum design of a radical pair compass as envisaged in the reference-probe model [11]. FAD^•− plays the role of the ‘reference radical’ that controls the anisotropy and Z^• the ‘probe radical’ that couples the system to the magnetic field. The simulation reported above for [FAD^•− Z^•] (figure 2c, ΔΦ_S = 0.146) was repeated, switching off the interaction of the FAD^•− electron spin with the external magnetic field. This simple device implements the reference-probe assumption that the spin motion of the reference radical is dominated by its hyperfine interactions. The result is a reaction yield anisotropy pattern that looks identical to figure 2c and has almost the same ΔΦ_S (0.143). Similar results were found for [Z^• TrpH^•+]: ΔΦ_S = 0.062 for the exact calculation, ΔΦ_S = 0.064 for the reference-probe approach and an anisotropy pattern indistinguishable by eye from figure 2b. Thus, the reference-probe approximation seems to be reasonably accurate for these two radical pairs under the conditions of our simulations (seven nuclei in each radical, 50 µT field, 1 µs lifetime). To the best of our knowledge, this is the first quantitative test of the model.

A distinct advantage of the reference-probe approximation is that it greatly accelerates the calculation of anisotropic magnetic field effects. As in the case of the exact simulations reported above, the spin dynamics of the two radicals can be computed separately; this is permissible because they are assumed not to interact [37]. The isolated electron spin of the probe radical has a very simple time dependence, which can be obtained analytically; its evaluation is therefore extremely fast even though it must be done for multiple directions of the external magnetic field. The calculation for the much larger spin system of the reference radical must be performed numerically and is much more time-consuming but it only has to be done once in the absence of the magnetic field.

3. Discussion

3.1. Simulation methods

Before discussing the above results, we comment briefly on the methods by which we have obtained them.

The reaction yield anisotropy ΔΦ_S has been adopted here and elsewhere [33,34,36] as a figure of merit by which to judge the fitness of a radical pair magnetoreceptor. However, it is not the only metric that could be used. Although a strongly anisotropic response is presumably an advantage in any compass sensor, there may be other properties that are at least as important. For example, a narrower, more elongated shape than those in figure 2 could provide a more precise compass bearing. Alternatively, a more structured three-dimensional pattern, e.g. with a larger number of positive (red) and negative (blue) regions than those in figure 2, might convey more nuanced directional information than merely the magnetic north–south axis [38]. Nevertheless, given the relatively simple angular dependence of the singlet yield patterns in figure 2, ΔΦ_S would appear to be an acceptable measure of their suitability as direction sensors under the conditions of our simulations.

The approximations and assumptions underlying the simulations also need some comment. Both electron spin-relaxation and inter-radical (exchange and dipolar) interactions have been neglected. Neither assumption is strictly valid and both could affect [FAD^•− TrpH^•+] and [FAD^•− Z^•] differently. For example, the centre-to-centre separation of FAD and TrpH in cryptochrome (approx. 1.9 nm) corresponds to a dipolar interaction (approx. 400 µT) that could attenuate the response of the radical pair to a 50 μT magnetic field [20]. If the radicals in [FAD^•− Z^•] were further than 1.9 nm apart, the dipolar interaction would be smaller and might therefore interfere less with the desired spin dynamics. Similarly, spin relaxation might be slower in [FAD^•− Z^•] than in [FAD^•− TrpH^•+] owing to the absence of hyperfine interactions in Z^• and so could tip the balance even further in favour of [FAD^•− Z^•]. Despite such uncertainties, it seems unlikely that these approximations would overturn the conclusion that [FAD^•− Z^•] appears to be much better suited than [FAD^•− TrpH^•+] as a compass sensor.

A further assumption made here, and in most other comparable treatments [5,31–34], is that singlet and triplet radical pairs react spin-selectively along separate, parallel pathways to give chemically distinct (singlet and triplet) products. Furthermore, in common with others, we have assumed for simplicity that the rates of the singlet and triplet decay channels are identical. The latter is clearly an approximation but not one that would seriously affect the conclusions reached here unless, in reality, the spin-selective rate constants differed by more than about an order of magnitude. The use of spin-selective reaction channels for both singlet and triplet radical pairs is also questionable. The triplet state of [FAD^•− TrpH^•+] cannot undergo reverse electron transfer because the triplet states of both FAD and tryptophan have energies well above that of the radical pair. An experimental study of magnetic field effects on [FAD^•− TrpH^•+] in cryptochrome and photolyase has shown that only one of the two competing radical pair reactions is spin-selective [18]. Singlet radical pairs undergo reverse electron transfer to regenerate the ground state of the protein, while both singlet and triplet states react at the same rate to produce a longer lived radical pair in which either FAD^•− is protonated or TrpH^•+ deprotonated. However, such details, although important for quantitative interpretation of experimental data [18], are not critical here. The fundamental conclusions still hold: the spin dynamics of [FAD^•− Z^•] are much more strongly anisotropic than those of [FAD^•− TrpH^•+].

3.2. [FAD^•− TrpH^•+] versus [FAD^•− Z^•]

The FAD^•− radical in cryptochrome appears to have magnetic properties, identified above, which make it a particularly favourable choice as a constituent of a compass sensor. However, those properties manifest fully only when its partner in the radical pair—the radical we refer to as Z^•—has no significant hyperfine interactions. When FAD^•− is paired instead with TrpH^•+, the sensitivity of the compass drops by two orders of magnitude under the conditions of the simulations. We now summarize the evidence and arguments for and against the two radical pairs, [FAD^•− TrpH^•+] and [FAD^•− Z^•], and review various possible identities for Z^•.

As mentioned in §1, [FAD^•− TrpH^•+] was first proposed by Ritz et al. [5] and has been widely assumed to be the magnetic sensor in any cryptochrome-dependent magnetoreception system. Biophysical studies have confirmed the magnetic sensitivity of this species in vitro [17,18]. A [FAD^•− Z^•] or [FADH^• Z^•] radical pair derived from cryptochrome has been proposed to explain what appears to be a resonant effect of radiofrequency fields on the magnetic compass orientation of European robins [19]. Simulations show that any hyperfine interaction in Z^• larger than approximately 20 µT would banish the apparent resonance [23]. Even if one accepts the existence of an [FAD^•− Z^•] sensor, there remain serious problems in understanding how a radiofrequency field as weak as 15 nT could disrupt the directional response to a static field (50 µT) some 3000 times stronger [39]. Hyperfine interactions in Z^• somewhat larger than 20 µT can be tolerated if the radiofrequency results are set aside. As indicated by figure 4c, the compass sensitivity, ΔΦ_S, is only halved by introducing a single isotropic hyperfine interaction in Z^• even when it is much larger than 50 µT. Such a radical pair would still be much more sensitive than [FAD^•− TrpH^•+].

3.3. Possible identity of Z^•

If an [FAD^•− Z^•] or [FADH^• Z^•] species is involved, what might Z^• be and how could it be formed as part of a spin-correlated radical pair with FAD^•− or FADH^•? So as not to compromise the favourable magnetic properties of the FAD radical, Z^• should (a) have few and small hyperfine interactions; (b) not undergo fast (less than 1 µs) electron spin relaxation; and in addition (c) be chemically and biologically plausible.

The only specific candidates suggested so far are superoxide, 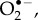and dioxygen, O₂ [23,24]. Although the ground state of the latter is a triplet (two unpaired electrons), it could in principle play the role of Z^• [23]. Both 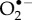and O₂ ostensibly satisfy condition (a) (¹⁶O, the only abundant isotope of oxygen, has no nuclear spin) and probably (c): both are potent oxidants of singly (FAD^•− and FADH^•) and doubly (FADH⁻) reduced flavins. Moreover, O₂ is biologically ubiquitous and an FAD-superoxide radical pair could arise during the dark oxidation of fully reduced FAD: FADH⁻ + O₂ → [FADH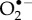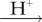^• ] FAD + H₂O₂ [40]. However, the strong spin–orbit coupling in 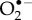[41], and the zero-field splitting in O₂ [42], almost certainly lead to extremely fast (less than 1 ns) electron spin relaxation [23,43,44] which would preclude any significant response to a 50 µT magnetic field. The only way in which 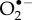might relax sufficiently slowly would be if it were strongly and asymmetrically bound to cryptochrome so that its orbital angular momentum was quenched [23]. However, there is no known or obvious O₂-binding site in cryptochrome and such interactions would probably introduce hyperfine interactions with nuclei in the protein [23]. Similar arguments apply to the hydroperoxy radical, 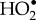(the protonated form of superoxide), which has a large (approx. 1 mT) anisotropic hyperfine interaction [45] and probably relaxes very rapidly.

Another conceivable identity for Z^• would be a metal ion that had appropriate redox chemistry, slow electron spin relaxation, a reasonably abundant non- or weakly magnetic isotope and small hyperfine couplings to ligand nuclei. No obvious candidates suggest themselves.

Alternatively, one could envisage cases in which the effects of hyperfine interactions partially cancel. For example, a radical containing two magnetically equivalent hydrogens has a 25% statistical chance of being in a nuclear singlet state, which would have no hyperfine interaction. However, this requires the two hydrogens to have identical hyperfine tensors, which would exclude, for example, a 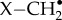radical in which the two methylene hydrogens necessarily have non-parallel hyperfine axes. We have been unable to propose a plausible radical that meets this condition.

Finally, there is the possibility that Z^• might be free from hyperfine interactions as a result of electron hopping between molecules, as can be observed for radicals in solution [46]. However, it is difficult to imagine how this could happen in cryptochrome. For example, fast electron hopping among the tryptophans of the Trp-triad would reduce the isotropic hyperfine couplings in TrpH^•+ by at most a factor of three (in the case when the electron spin spent one-third of the time on each Trp [47]).

3.4. Origin of [FAD^•− Z^•]

The other problematic aspect of a cryptochrome-based [FAD^•− Z^•] magnetoreceptor is to envisage how the unknown Z^• radical might be formed as part of a spin-correlated radical pair with FAD^•− or FADH^•. One possibility, mentioned above, is electron transfer from FADH⁻ to dioxygen. The fully reduced form of the cofactor required for this reaction could arise via a two-stage photoreduction process: FAD 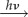FAD^•− or FADH^• FADH⁻ involving electron transfer along the Trp-triad [40,48,49]. But the electron acceptor that oxidizes FADH^• does not have to be O₂: as suggested by the DNA-repair reaction of photolyase [50], an oxidant molecule bound to cryptochrome in what would be the DNA-binding site in a photolyase could undergo a reaction of the type, FADH⁻ + A → [FADH^• A^•−].

Alternatively, a Z^•-type radical pair could be formed directly from the fully oxidized form of the FAD. Reduction of photo-excited FAD by an electron donor situated in the equivalent of the DNA-binding site might be fast enough to compete with reduction via the Trp-triad and so produce an alternative magnetically sensitive radical pair: FAD + D → [FAD^•− D^•+].

Finally, an [FAD^•− Z^•] radical pair could be formed by electron transfer to the TrpH^•+ radical in [FAD^•− TrpH^•+]. This appears to happen in A. thaliana cryptochrome in which a tyrosine residue in the protein acts as the reducing agent [14]. But tyrosyl radicals have hyperfine interactions just as strong as TrpH^•+ [51], so this would not generate a Z^•-type radical. However, it is conceivable that in vivo there is an external electron donor. An advantage of such an arrangement is that the radical–radical separation in [FAD^•− Z^•] could be larger than that for [FAD^•− TrpH^•+], meaning less attenuation of the magnetic field effect by the dipolar interaction [20]. A disadvantage is that spin-selective recombination of the radicals would probably be slower allowing more time for spin relaxation to dilute the magnetic response.

3.5. A suggestion

We end with a very tentative and speculative suggestion for the identity of the putative Z^• radical. Ascorbic acid (figure 5), a common biological reductant, can reduce photo-excited flavins [53] and Trp radicals [54] by hydrogen atom or electron transfer to form a radical in which there is one small (approx. 200 µT) and several very small (10−20 µT) hyperfine interactions [52,55]. The ascorbyl radical paired with FAD^•− or FADH^• would not be compatible with the radiofrequency disorientation data [19] and has an expected compass sensitivity about half that of [FAD^•− Z^•] (figure 4c), but it would still be approximately 50 times more sensitive than [FAD^•− TrpH^•+] under the same conditions. If the radiofrequency experiments cannot be independently replicated, [FAD^•−ascorbyl^•−] or [FADH^• ascorbyl^•−] could come to be seen as a good compromise between compass sensitivity and biological feasibility. Although one could speculate further on the involvement of ascorbic acid, we just make two observations here. First, for the operation of the compass it is only essential that one of the two radicals is immobilized [8]. If the cryptochrome molecules, and therefore the FAD radicals produced photochemically within them, are prevented from rotating, then there is no reason why the other radical could not be mobile. It would therefore not be necessary for ascorbate to bind to cryptochrome. Second, an FAD/ascorbyl radical pair would not be compatible with the recent proposal that the magnetically sensitive species in cryptochrome is a radical pair formed by oxidation of the fully reduced form of FAD [40].

Figure 5.

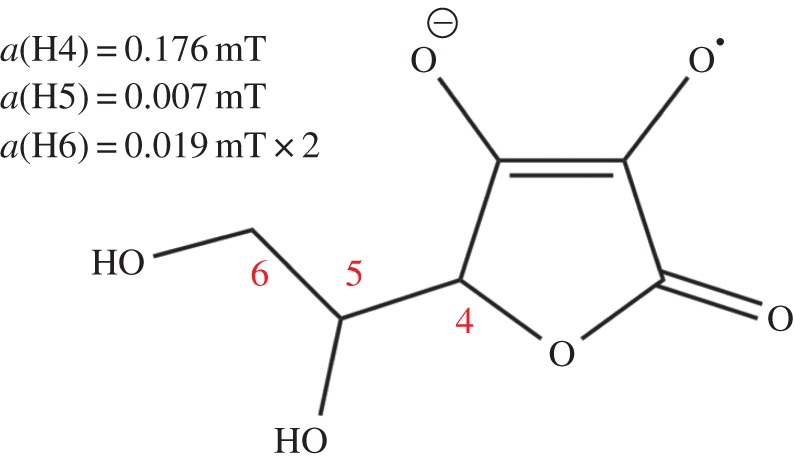
Ascorbyl radical. The isotropic ¹H hyperfine interactions are as indicated [52]. (Online version in colour.)

4. Conclusion

We have shown that, other things being equal, a radical pair in which a cryptochrome-bound FAD radical is partnered by a radical (Z^•) with no or a few, weak hyperfine interactions can be two orders of magnitude more sensitive to the direction of the geomagnetic field than the FAD–tryptophan radical pair that is generally assumed to be the magnetically sensitive entity in cryptochrome. The favourable magnetic properties of [FAD^•− Z^•] arise from the highly asymmetric distribution of hyperfine interactions among the two radicals and the near-optimum character of the two nitrogens in the central ring of the flavin radical. The spin motion of [FAD^•− Z^•] is accurately described by the ‘reference-probe’ concept previously suggested as an optimal magnetoreceptor design. The identity and origin of Z^• are obscure; we have tentatively suggested ascorbic acid as the source of a radical that, when paired with an FAD radical in cryptochrome, could be almost as sensitive a compass sensor as [FAD^•− Z^•].

Funding statement

We thank EPSRC, DARPA (QuBE: N66001-10-1-4061), ERC and the EMF Biological Research Trust for financial support, and the Nuffield Foundation for an Undergraduate Research Bursary (for A.L.). T.B. thanks the Deutsche Forschungsgemeinschaft (DFG) for financial support (grant nos. BI 1249/1-1 and BI 1249/1-2).