Systems level approach reveals the correlation of endoderm differentiation of mouse embryonic stem cells with specific microstructural cues of fibrin gels

Abstract

Stem cells receive numerous cues from their associated substrate that help to govern their behaviour. However, identification of influential substrate characteristics poses difficulties because of their complex nature. In this study, we developed an integrated experimental and systems level modelling approach to investigate and identify specific substrate features influencing differentiation of mouse embryonic stem cells (mESCs) on a model fibrous substrate, fibrin. We synthesized a range of fibrin gels by varying fibrinogen and thrombin concentrations, which led to a range of substrate stiffness and microstructure. mESCs were cultured on each of these gels, and characterization of the differentiated cells revealed a strong influence of substrate modulation on gene expression patterning. To identify specific substrate features influencing differentiation, the substrate microstructure was quantified by image analysis and correlated with stem cell gene expression patterns using a statistical model. Significant correlations were observed between differentiation and microstructure features, specifically fibre alignment. Furthermore, this relationship occurred in a lineage-specific manner towards endoderm. This systems level approach allows for identification of specific substrate features from a complex material which are influential to cellular behaviour. Such analysis may be effective in guiding the design of scaffolds with specific properties for tissue engineering applications.

1. Introduction

Embryonic stem cells (ESCs) have the potential to be used in many therapeutic applications owing to their unlimited self-renewal capacity and ability to differentiate into cells of any of the three germ layers (endoderm, mesoderm and ectoderm) [1,2]. These germ layers can subsequently give rise to cells of every tissue type in the body, including pancreatic, hepatic and lung from endoderm, bone, blood and muscle from mesoderm as well as neural and epidermal from ectoderm (reviewed in [3]). Both self-renewal and differentiation of stem cells can be modulated by careful manipulation of the cellular microenvironment. ESCs are extremely sensitive to their surrounding microenvironment and are influenced by the perturbations caused by changes in the chemical composition of the immediate solution environment as well as the physico-chemical changes brought about by the substrate in direct contact with the ESCs.

While soluble cues are predominantly used to modulate stem cell fate, more recently cues from the underlying substrate have also been shown to have a significant role in stem cell fate commitment. Numerous aspects of the stem cell niche can influence the cues from the substrate, including extracellular matrix (ECM) and substrate topology (reviewed in [4,5]). Crucial cues from the underlying substrate which are increasingly gaining importance, particularly in the area of stem cells, are the physical properties of the substrate, in particular, substrate mechanical properties [6]. Numerous materials have been used as stem cell substrates to investigate how modulation of mechanical properties affects cellular response [7–9]. In our earlier studies, using the natural polymer fibrin, we have observed that the fibrin fabrication condition affects ESC differentiation during germ layer commitment [10]. In addition, we have studied the effect of alginate substrates on differentiation. In this system, our results indicated that while mesoderm and ectoderm germ layers responded weakly to substrate stiffness in the chosen range (300–1500 Pa), endoderm markers were strongly responsive, with softer substrates upregulating the endoderm-specific markers [11].

Substrate microstructural features have been shown to be influential in guiding cellular behaviour [12–14]. Synthetic substrates have been extensively used as platforms to study this behaviour, with studies also being performed on the control of their microstructure [15–18]. While synthetic substrates allow for precise and controlled microstructure manipulation, parallel studies in natural substrates, such as fibrin, become difficult owing to their heterogeneous and complex nature [19,20]. In addition, such studies become challenging using a purely experimental approach for several reasons. Primarily, it is difficult to determine a cause–effect relationship by systematically perturbing a single physical parameter of the substrate microenvironment while keeping the other parameters invariant. Hence, a rigorous systems analysis is needed to draw meaningful conclusions regarding the effect of a complex microstructure on cellular response.

In this paper, we have developed a systems level methodology to identify and isolate contributing substrate features from a complex microenvironment affecting the first stage of cellular differentiation, that to the germ layers. This is achieved by integrating substrate image processing and microstructure quantification with gene expression analysis in a statistical modelling platform to identify (i) specific substrate features contributing towards differentiation and (ii) preferential lineage commitment arising from the substrate interaction. The developed methodology allows the segregation of the effect of macroscopic and microscopic properties of the complex fibrous network in inducing stem cell differentiation. More importantly, the quantitative approach has the potential to provide an understanding of the relative importance of the contributing substrate attributes towards a specific cellular behaviour.

In this paper, we have applied our methodology to fibrin substrates to investigate the influence of their microstructure as an insoluble cue inducing stem cell differentiation. Fibrin serves as an ideal substrate platform because its microstructural features can be easily modified by appropriate modification of the fabrication conditions [21]. Such modification also affects the substrate macroscopic property of stiffness, thereby providing a means to investigate the relative importance of macroscopic stiffness and microscopic architecture as cues to which the cells respond. Twelve different fibrin gels were synthesized by varying fibrinogen and thrombin concentration. Mouse embryonic stem cells (mESCs) were cultured on each of these gels and analysed for the extent of differentiation by quantifying pluripotency and germ layer markers with quantitative polymerase chain reaction (qRT-PCR). The network topology of the fibrin gels was then characterized by analysing the electron micrographs of the gels with an image processing algorithm [22]. The complete network topology, which included nine different microstructural attributes, was quantified, and a subset of these features which were most important in describing the conditions and their variability was identified via principal component analysis (PCA). The mechanical response of the gels was also measured by both rheology and atomic force microscopy (AFM). The relationship between these explanatory variables (stiffness and microstructural features) and differentiation was then modelled via a second-order polynomial. Inclusion of all explanatory variables into the model would require an immense dataset, which is often impractical to obtain in the stem cell system. We therefore used a combinatorial approach to analyse two-dimensional subsets of the feature space at a time, with the important relationships being determined through significance tests. Overall, it was shown that for the presented class of fibrous substrates, the contribution of substrate microstructure to mESC differentiation was stronger than that of macroscopic stiffness. Furthermore, it was found that fibrous microstructural features had a strong influence on ESC differentiation to endoderm lineage, with fibre alignment being the most influential.

2. Material and methods

2.1. Fibrin gel fabrication, mouse embryonic stem cell differentiation and gene expression quantification

Culture of mESCs on fibrin gels with subsequent gene expression quantification was reported previously [10]. In brief, 12 different fibrin gels were fabricated by adjusting the fibrinogen concentration (1, 2, 4 and 8 mg ml⁻¹ fibrinogen) and fibrinogen to thrombin ratios (1.25, 2.5 and 10 mg fibrinogen U⁻¹ thrombin). Each of these gels was used as a substrate for mESC differentiation for both two- and three-dimensional culture. For the former, cells were seeded onto the preformed fibrin gel, whereas for the latter, cells were embedded in the gel by suspending them in the fibrinogen before polymerization ensued. For both two- and three-dimensional cultures, the cells were cultured for a total of 4 days in Dulbecco's modified Eagle medium (Cellgro) supplemented with 10% fetal bovine serum (Cellgro). At the end of 4 days of differentiation, cells were harvested, and gene expression was analysed for 16 specific germ layer and pluripotency markers with qRT-PCR on a Stratagene MX3005P (Agilent). Primer sequences used for the analysis, and the genes’ associated germ layer, are shown in table 1. Gene expression data were reported as fold change values calculated herein as 2^−ΔΔct, where ct values are first normalized to the house-keeping gene β-actin, and then to the control (undifferentiated cells).

Table 1.

Primer sequences used during PCR analysis of differentiation.

	gene	left sequence	right sequence
house-keeping	β-actin	cagcagttggttggagca	tgggagggtgagggactt
endoderm	sox17	atccaaccagcccactga	acaccacggaggaaatgg
	afp	ctctggcgatgggtgttt	aactggaagggtgggaca
	hnf4	catcgtcaagcctccctct	ccctcagcacacggtttt
	foxa2	gttaaagtatgctgggagccg	cgcccacataggatgacatg
	cxcr4	cgggatgaaaacgtccattt	atgaccaggatcaccaatcca
	gata4	ggcccctcattaagcctcag	caggacctgctggcgtctta
	ttr	ttcacagccaacgactctgg	ggcaagatcctggtcctcct
mesoderm	brachyury T	aagaacggcaggaggatg	gcgagtctgggtggatgta
	fgf8	acggcaaaggcaaggact	tgaagggcgggtagttga
	gsc	gcaccgcaccatcttca	tcgcttctgtcgtctcca
ectoderm	nestin	ggaggatgtggtggaggat	ttcccgtctgctctggtt
	fgf5	ttcaagcagtccgagcaa	taggcacagcagagggatg
	bmp4	atctggtctccgtccctga	cgctccgaatggcacta
pluripotency	rex1	aaggtcatccacggcaca	tgggagtcatcgcttggt
	oct4	ggagaagtgggtggaggaa	gctgattggcgatgtgag
	sox2	ctggactgcgaactggaga	ttggatgggattggtggt

2.2. Gel stiffness measurements

To assess the mechanical response of the different fibrin gels, stiffness measurements were taken via two different methods: AFM and rheology. AFM nanoindentation measurements were performed using an MFP-3D atomic force microscope (Asylum Research). For all measurements, a glass borosilicate sphere (diameter 15.9 μm; Thermo Scientific) was attached to the tip of a commercially available silicon nitride cantilever with a spring constant (k) of approximately 0.1 N m⁻¹ (Bruker). A thermal fluctuation method was used for calibrating the cantilever stiffness [23]. The stiffness of each fibrin gel was then investigated by nanoindentation with indentations made at randomly chosen locations considering approximately n = 16 force indentation curves at three locations on the fibrin gel [24–26]. The stiffness modulus was determined by applying the Sneddon model to nanoindentation curves from corresponding gels [24,25,27,28]. Curve fitting of the sample indentation depth with the force applied was conducted for a spherical tip model using the following equation relating the force (f) and the sample indentation size (d):

2.1

where E is Young's modulus, R is the radius of the spherical indenter and ν is Poisson's ratio. The sample indentation (d) is calculated as follows:

2.2

where z₀ is the initial indentation contact point, z is the position of the piezoelectric cantilever and d is the cantilever deflection. Poisson's ratio was approximated to be 0.5 for all experiments. Curves were fitted to small indentation in comparison with the thickness of the samples. The apparent Young's modulus was obtained by fitting the force–indentation curves to equations (2.1) and (2.2) with the initial deflection point and Young's modulus (E) as the fitting parameters [29].

Rheological measurements are discussed in detail in Jaramillo et al. [10]. In brief, fibrin was allowed to gel on glass slides and submersed in differentiation medium. The slides were then secured to the Peltier cell of a stress-controlled rheometer (TA Instruments AR2000), and the gels subjected to an oscillatory strain, with the stress required to achieve the strain being determined. The storage modulus was then determined from these data.

2.3. Fibre network imaging and microstructural characterization

To determine the microscopic structural characteristics of the fibrin, the gels were analysed by scanning electron microscopy (SEM). First, excess water was removed from the fabricated fibrin gels through serial ethanol dilutions. The ethanol was removed while preserving the fibrin structure through critical point drying with CO₂. Samples were then sputter coated with palladium on a 108 auto sputter coater (Cressington) with subsequent imaging on a Philips XL30 field emission gun SEM (FEI Company). Three different images were taken for each fabrication condition, selected at random points on the gel.

To characterize the SEM images, an image-based structural analysis algorithm, which has been previously implemented and described [22], was used. In brief, a cascade of image processing steps, including local thresholding segmentation, morphological processing and Delaunay triangulation, was adopted to identify and associate an artificial struts and nodes network to the real material fibre network. This approach has been qualitatively and quantitatively demonstrated [22] and adopted on a variety of engineered constructs [15,30,31]. Nine different fibrin gel topological attributes were quantified: pore size, fibre node density (node being determined by the intersection of two or more fibres; density being nodes per unit area), connectivity (number of fibres per node), pore orientation, fibre orientation, pore aspect ratio, fibre length (length between nodes), fibre diameter and bulk porosity. The pore and fibre orientation are reported as an index. The orientation index (OI) provides a measure of how an angular distribution is concentrated around a specific direction. The fibre index is calculated as

2.3

where n represents the number of fibre segments and θ represents the angle between the segment and assumed alignment direction [22]. This formulation offers a dimensionless number ranging from 0.5 for purely isotropic structures characterized by a random angular distribution to 1 for a set of objects oriented parallel to a specific direction. Therefore, this fibre OI gives a measure of fibre alignment in the system. For pore orientation, an ellipse was associated with each pore, and the major axis was considered to calculate a single pore angle with respect to the horizontal direction. For those features which were not scalars (e.g. fibre diameter output being a histogram of the diameters of all fibres in a given image), the mean value was taken. All results reported herein are from analyses using the mean data. This image analysis was performed on the three separate images taken.

Once the fibre network topology was quantified with the image processing algorithm, a PCA was performed on the data. This analysis created a new set of orthogonal variables each being a linear combination of the microstructural features, and allowing the elucidation of how system variance was distributed. PCA was performed in Matlab (Mathworks).

2.4. Predictive model, regression and statistical analysis

To describe the relationship between stiffness and the response variable (gene expression), two different approaches were used. First, the strength of the linear relationship was quantified via calculating the Pearson product–moment correlation coefficient. In the second approach, a second-order polynomial was used, modelled as

2.4

which was able to capture linear as well as nonlinear effects. Equation (2.4) was used to model stiffness (x) versus gene expression levels (y), and was therefore one-dimensional in the feature space (k = 1, where k is feature space dimensionality).

The various microstructural features were expected to exhibit cooperative influence towards cell behaviour. Incorporating these into one regression model to analyse the cooperative influence of all parameters would introduce a large number of variables which would not be feasible to estimate with the limited availability of data points. We addressed this restriction via a combinatorial approach in which two microstructural features were analysed per regression. This model was therefore a two-dimensional (k = 2) second-order polynomial, shown in equation (2.5). In equation (2.5), y is the gene expression and x_i is the ith feature. This regression model was analysed for each combination of features; as there were nine features that were quantified, a total of 36 combinations were analysed:

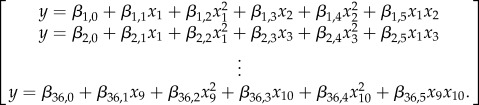2.5

Using the above model, regression was performed to estimate the unknown coefficients (β) by fitting the model to the experimental data (y) (Matlab, Mathworks). The experimental inputs (stiffness or microstructural feature values) were standardized by centring (by the mean) and scaling (by the s.d.). Once the regression was performed, statistical tests were carried out to check significance of the overall correlation (p ≤ 0.05, based on the F-distribution). This analysis was done for each gene (16) and for each condition (two- and three-dimensional), giving a total of 64 regressions using equation (2.4) (16 genes × 2 conditions × 2 stiffness datasets; AFM and rheometry) and 1152 regressions using equation (2.5) (16 genes × 2 conditions × 36 feature space combinations). The flow diagram of this screening method is shown in figure 1.

Figure 1.

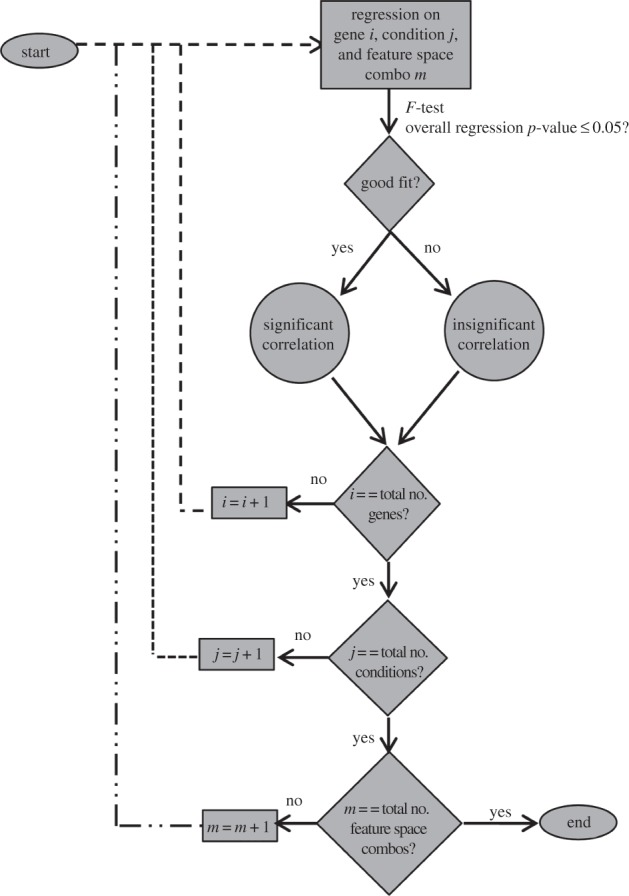
Flow diagram of regression and screening methodology to determine significance.

3. Results

3.1. Fibrin gel stiffness and mouse embryonic stem cell differentiation

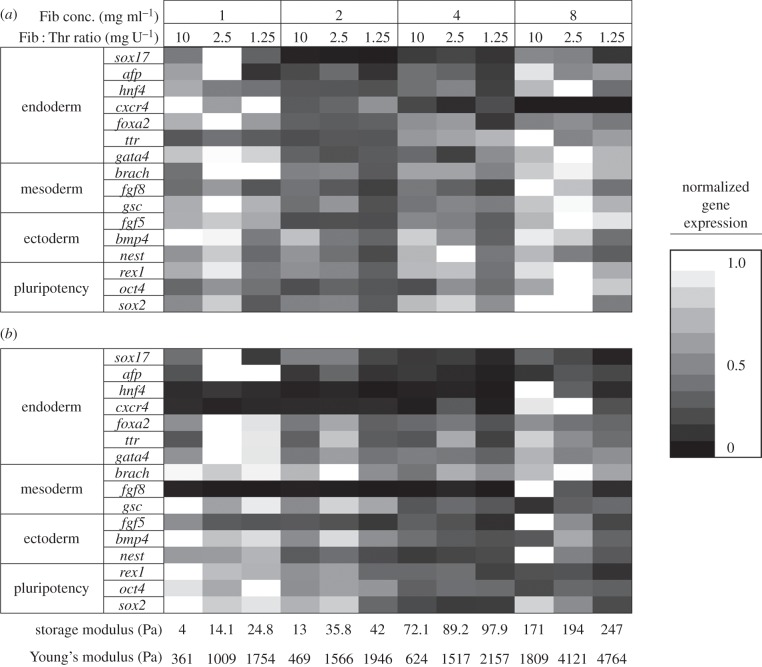
Fibrin was fabricated under 12 different conditions by varying the amounts of fibrinogen and thrombin. The stiffness of the fibrin gels at each of the 12 fabrication conditions as determined by AFM and rheometry is shown in figure 2. The overall trend observed was that the stiffness increased with increased fibrinogen and thrombin. mESCs were cultured in the synthesized gels both on the gels (two-dimensional condition) or embedded in the gels (three-dimensional condition). After 4 days of culture, the cells were analysed for pluripotent and germ layer gene expression. Day 4 was chosen as an appropriate time point to harvest the cells, because the first stage of differentiation normally involves a 4–6 day protocol [32,33]. At this point, the cells are committed to a specific germ layer, and further differentiation to subsequent developmental stages can commence. In our previous study, we thoroughly characterized the behaviour of the mESC on these substrates [10]. In this study, we are investigating specific features of the substrate which are influencing differentiation. This requires a thorough, quantitative and sensitive characterization of the differentiated cells, which we perform by qPCR. Figure 3 presents a heat map to compare the expression levels of representative pluripotency and germ layer (endoderm, mesoderm and ectoderm) markers at different fibrin gel fabrication conditions, for both two- and three-dimensional cultures. For each row (gene), the expression values are normalized by the gene's maximum level. The greater the dependency of gene expression on fabrication condition, the greater the colour variation. While it is observed that most genes are affected to some extent by varying fibrin gel conditions, it seems as if the endoderm gene expression levels change more strongly. In the two-dimensional condition (figure 3a), the general trend seems to be higher expression for ectoderm and pluripotency genes with conditions fabricated with more fibrinogen. Interestingly, this trend seems to be reversed in the three-dimensional condition (figure 3b). From this figure, it is difficult to discern clear trends for the endoderm and mesoderm genes. A more analytical approach was therefore taken to determine possible relationships between fabrication conditions and gene expression. In order to quantitatively analyse the effect of stiffness on differentiation patterning, the strength of the linear relationship between AFM/rheometry measurements and gene expression was determined via the Pearson product–moment correlation coefficient. Table 2 reports the significance values of the correlation coefficients which represent how significant this linear correlation was. Most genes did not show a statistically significant linear correlation between substrate stiffness (either AFM or rheometry measurements) and expression levels. Of the few significant relationships, the majority are for pluripotency genes: OCT4 and REX. Very few of the germ layer markers showed a strong linear correlation with substrate stiffness. In order to examine the presence of nonlinear correlations, second-order polynomial regression (equation (2.4)) was implemented, and the significance values of the overall regression were determined (table 2). Still, only a few genes showed significance with the quadratic model (those genes which showed significance in the linear model); this alludes to the possibility that other features of the fibrin substrates, other than stiffness, might have a stronger influence on differentiation.

Figure 2.

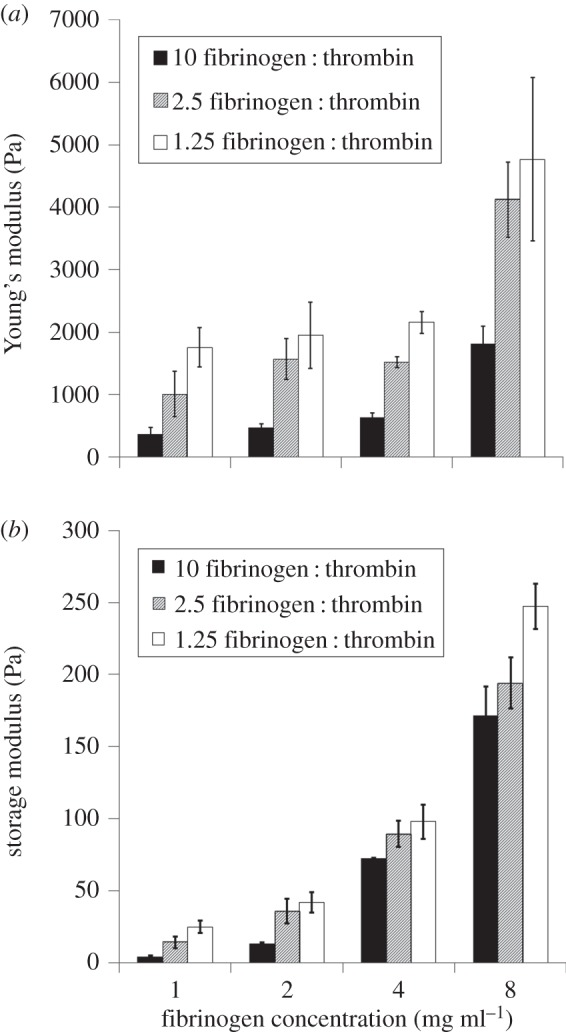
Fibrin gel elasticity measurements across various fabrication conditions. (a) Young's modulus measured by AFM. (b) Storage modulus measured by rheometry. Legend: mg fibrinogen U⁻¹ thrombin.

Figure 3.

Heat map displaying relative gene expression data of various genes (vertical axis), representing markers for pluripotent cells and each of the three germ layers, across different fibrin gel cultures, shown as fabrication condition (top horizontal axis) and gel stiffness measured by rheometry (first line, bottom horizontal axis) and AFM (second line, bottom horizontal axis). Top horizontal axis represents fibrin fabrication condition by its fibrinogen concentration and fibrinogen to thrombin ratio. Data measured by PCR represent cells harvested at day 4 of culture in either two-dimensional (a) or three-dimensional (b) fibrin conditions. For each gene, expression levels were normalized to the gene's maximum level across all gel conditions. Expression values calculated by 2^−ΔΔct method, where ct values are first normalized to the house-keeping gene β-actin, and then to the control (undifferentiated cells).

Table 2.

p-Values for correlation coefficients and second-order polynomial regressions for the relationship of fibrin gel elasticity and gene expression. Values calculated for both two- (2D) and three-dimensional (3D) conditions, with significance (p ≤ 0.05) denoted by an asterisk. Elasticity measured by both AFM and rheology.

	AFM				rheology
	correlation coefficient		second-order regression		correlation coefficient		second-order regression
gene	2D	3D	2D	3D	2D	3D	2D	3D
rex1	0.5764	0.0154*	0.5416	0.0441*	0.1789	0.0014*	0.4237	0.0009*
oct4	0.0025*	0.1859	0.013*	0.4369	0.0024*	0.0069*	0.0104*	0.004*
sox2	0.7729	0.2198	0.9585	0.4786	0.1792	0.1476	0.1633	0.1344
brach	0.3321	0.8619	0.6304	0.9858	0.3488	0.6504	0.6336	0.4936
fgf8	0.6048	0.5994	0.8363	0.6928	0.1277	0.0993	0.3332	0.196
gsc	0.3124	0.2509	0.5681	0.5108	0.3411	0.0123*	0.3902	0.0031*
sox17	0.8181	0.1321	0.9675	0.3229	0.9162	0.1	0.8771	0.1656
afp	0.8672	0.7262	0.6726	0.9156	0.3994	0.2465	0.4794	0.2559
hnf4	0.3911	0.6683	0.5988	0.7135	0.1876	0.1441	0.4382	0.2854
fgf5	0.084	0.859	0.1139	0.9826	0.0582	0.3938	0.0732	0.6853
bmp4	0.1864	0.3583	0.1239	0.5809	0.6757	0.0488*	0.8429	0.0241*
cxcr4	0.1007	0.0932	0.2799	0.241	0.0046*	0.0152*	0.0054*	0.0443*
foxa2	0.4988	0.3423	0.5617	0.6138	0.5383	0.1514	0.5406	0.221
nest	0.1452	0.8587	0.3616	0.8613	0.7292	0.9013	0.517	0.8961
ttr	0.343	0.9349	0.4852	0.5058	0.0157*	0.7881	0.0055*	0.9612
gata4	0.2656	0.6815	0.471	0.9	0.3861	0.4862	0.3054	0.4164

3.2. Microstructural features of fibrin gels

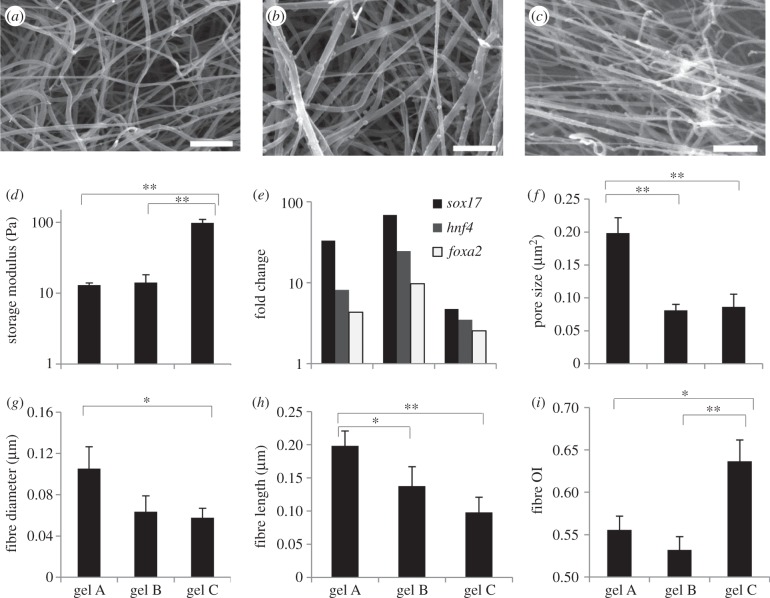
Fibrin substrates are highly fibrous in nature, and because the cells are directly interacting with the substrate microstructure, we hypothesized the fibrin microstructural features to be influential in directing cell fate. In order to analyse this further, we first examined the network topology of the synthesized substrates from SEM images. Representative SEM images of gels fabricated at three different conditions are shown in figure 4a–c. These conditions represent a wide range of stiffness and resulting differentiation behaviour (figure 4d,e). Even a qualitative comparison revealed differences in the substrate microstructure. In order to accurately determine the differences in the microstructural topology between the fabrication conditions, the fibrous gel characteristics needed to be quantified. The above-described image processing algorithm [22] was applied to the SEM images of all fibrin conditions (three images per gel condition) with the output being quantification of the fibrin topology. Figure 4f–i shows the algorithm output of six fibrous attributes for the gel conditions shown in figure 4a–c. There are clearly significant differences in the fibrous features between the three conditions. An interesting observation was that the microstructural features and macroscopic properties are not necessarily linearly related. For example, the gels fabricated under the first two conditions in figure 4 gave similar stiffness (d). However, microscopic comparison of these two gels shows differences in pore size and fibre length (figure 4a,b,f,h). Gene expression resulting from culture on these two gels is also different, supporting the hypothesis that factors other than stiffness might be more influential in guiding differentiation. Examination of gels at a higher stiffness (figure 4c) also showed microstructural differences from the softer gels, but these differences vary depending on the type of feature and fabrication condition, further demonstrating the complexity of the system.

Figure 4.

Variable characteristics and behaviour associated with fibrin gels fabricated under different conditions. (a–c) SEM images of fibrin gels fabricated with 2 mg ml⁻¹ fibrinogen and a fibrinogen to thrombin ratio of 10 mg U⁻¹ (a), with 1 mg ml⁻¹ fibrinogen and a ratio of 2.5 mg U⁻¹ (b) and with 4 mg ml⁻¹ fibrinogen and a ratio of 1.25 mg U⁻¹ (c). Scale bar, 1 μm. (d) Stiffness of these gels as measured by rheometry. (e) Differentiation patterning of cells cultured for 4 days in the aforementioned fibrin gels, three-dimensional condition. Fold change calculated by the ΔΔ Ct method as described in the Material and methods section. (f–i) Various fibrin fibrous attributes for the three gels quantified by the image processing algorithm. In (d–i), x-axis labels represent fibrin gels fabricated under different conditions: ‘gel A’ with 2 mg ml⁻¹ fibrinogen and 10 mg U⁻¹ fibrinogen : thrombin ratio; ‘gel B’ with 1 mg ml⁻¹ and 2.5 mg U⁻¹ and ‘gel C’ with 4 mg ml⁻¹ and 1.25 mg U⁻¹. The average values of the features are presented. In all graphs, significance performed via a Student's t-test. *p < 0.05, **p < 0.01.

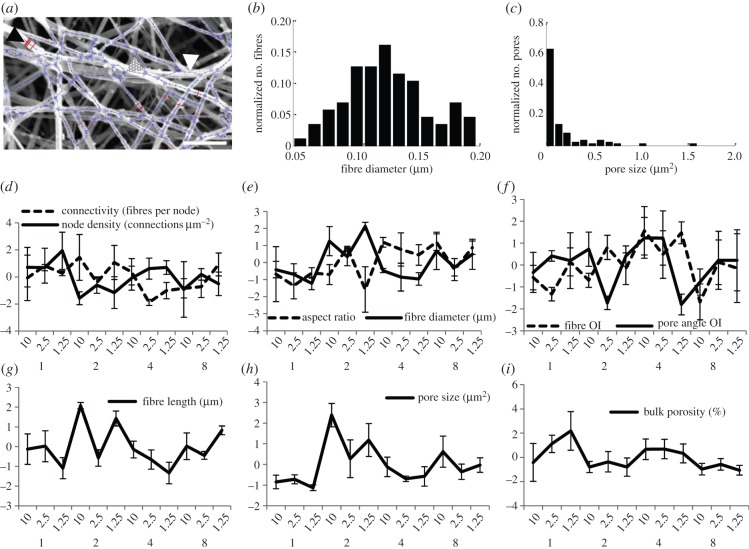
To quantify the entire microstructural topology, the image processing algorithm was applied to the SEM images of all 12 gel conditions. Figure 5a displays the fibrous network, identified by the algorithm, for a representative image. The algorithm does an excellent job identifying the individual fibres and their connections. Two representative topological attribute histograms generated from this identification are shown in figure 5b,c for fibre diameter and pore area, respectively. This image and quantification reveal differences in the distribution of these two fibre network features: fibre diameter was approximately normally distributed; pore distribution, while dominant in a narrow range of small pores, still contained numerous outliers of large area. Nine different attributes were likewise quantified for three different images of all the 12 gel conditions to characterize the network, as outlined in the Material and methods section. How these attributes change with varying fibrin fabrication conditions is represented in figure 5d–i, where the data represent averages over three representative images.

Figure 5.

Results of the image processing algorithm applied to the SEM images of the different fibrin gels. (a) SEM image and identified fibre network. Lines traversing fibre width (black arrow head) indicate detected diameters, with several of the lines in bold for clarity; lines running along the fibre length (white arrow head) denote identified fibres; large circles (dotted arrow head) indicate nodes. Scale bar, 1 μm; (b,c) output histograms of fibre diameter and pore size, respectively (a–c are representative outputs for fibrin gels fabricated with 2 mg ml⁻¹ fibrinogen and 1.25 mg fibrinogen U⁻¹ thrombin); (d–i) compiled output (standardized, by centring by the mean and scaling by the s.d.) for all nine features (error bars represent 1 s.d., n = 3 images). Categories on horizontal axes represent fibrin fabrication condition: top row, mg fibrinogen U⁻¹ thrombin; bottom row, mg fibrinogen ml⁻¹. Fibre length represents distance between two nodes. OI denotes orientation index. (Online version in colour.)

These attributes were further analysed by PCA in order to quantitatively determine the microstructural features more sensitive to the gel fabrication conditions. This data reduction technique, performed via singular value decomposition of the data, leads to generation of orthogonal variables and subsequent identification of those which maximize data variance (first principal components). The resulting biplot (figure 6) shows the contributions of each of these features towards the first and second principal components. By projecting the feature vector values onto the x-axis, one can determine the importance of the features to the first component, which is responsible for most of the system variability. The most influential features are the ones which show the largest projection magnitude. Considering 0.1 as a lower threshold, features which contribute the least to feature space variability were identified to be pore angle OI and pore aspect ratio, which were excluded from subsequent analyses. The more influential features which were retained for subsequent analysis were fibre length, fibre diameter, pore size, node density, porosity, connectivity and fibre OI (fibre alignment).

Figure 6.

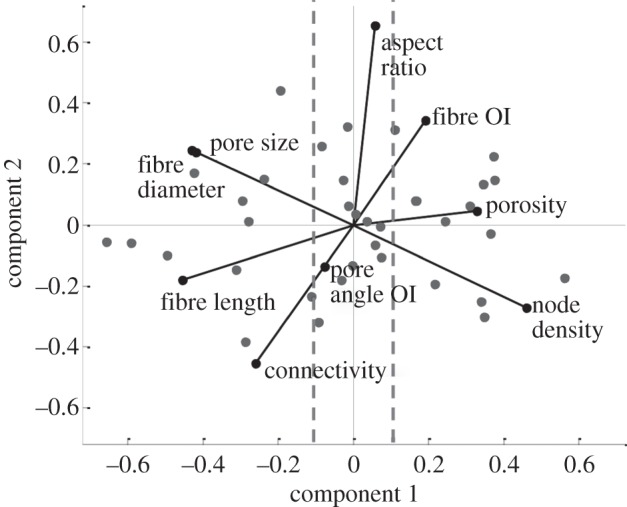
Identified influential microstructural features. Biplot of the principal component analysis (PCA) of the feature space. Filled circles represent observations in the principal component space, whereas vectors indicate the contributions of each feature to the first (x-axis) and second (y-axis) principal component. OI denotes orientation index. Vertical dashed lines represent the 0.1 magnitude threshold value of the first principal component coefficients used to screen important features.

3.3. Correlating microstructural features and differentiation

Having identified the dominant microstructural features sensitive to the gel fabrication conditions, the next task was to analyse the gene expression data with respect to the gel microstructure, and to determine whether specific genes were strongly correlated with this feature space. Incorporating all dominant microstructural features into the correlation would require an immense dataset. To use a limited dataset, this correlation was determined by performing a regression analysis for each of the 16 genes against a two-dimensional second-order polynomial (equation (2.5)), considering combinations of two dominant features at a time (independent variables, x₁ and x₂). The analysis was repeated for both the two- and three-dimensional culture conditions (see figure 1 for algorithm). The output of each regression was a set of best-fit polynomial coefficients and the corresponding regression surface. Shown in figure 7 is an example of two significant correlations relating FOXA2 (figure 7a) and SOX17 (figure 7b) gene expression to fibre length and diameter. The feature space is in its centred and scaled form, transformed as such for the regression analysis. As shown in both surfaces, a minimum seems to occur. Highest expression is achieved when fibre length is high and diameter low, or vice versa. The power of this analysis lies in the possibility of using the microstructural information to aid in the design of materials which guide stem cells towards desired phenotype fates. By isolating important features of the fibrin substrate and determining how they affect cellular behaviour during mechanical differentiation induction, one can try to mimic these features and recapitulate this substrate topology on prospective future synthetic induction substrates, rather than relying on a ‘guess-and-check’ method.

Figure 7.

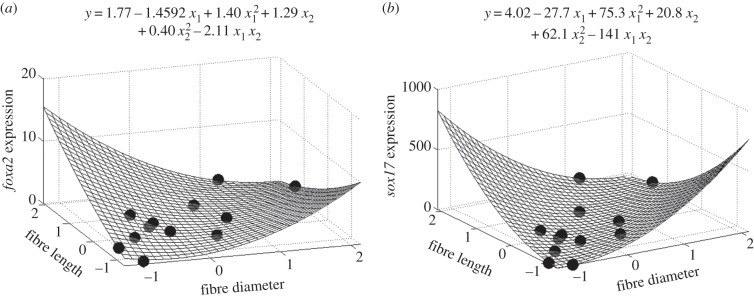
Regression surface and associated best-fit regression polynomial showing the regressed relationship between the influential features of fibre diameter/length and FOXA2 expression, two-dimensional condition (a) and SOX17 expression, three-dimensional condition (b). In the equations, x₁ denotes fibre diameter and x₂ fibre length. Expression values are in relative fold change, and features have been centred and scaled (previously described). Circles denote experimental data.

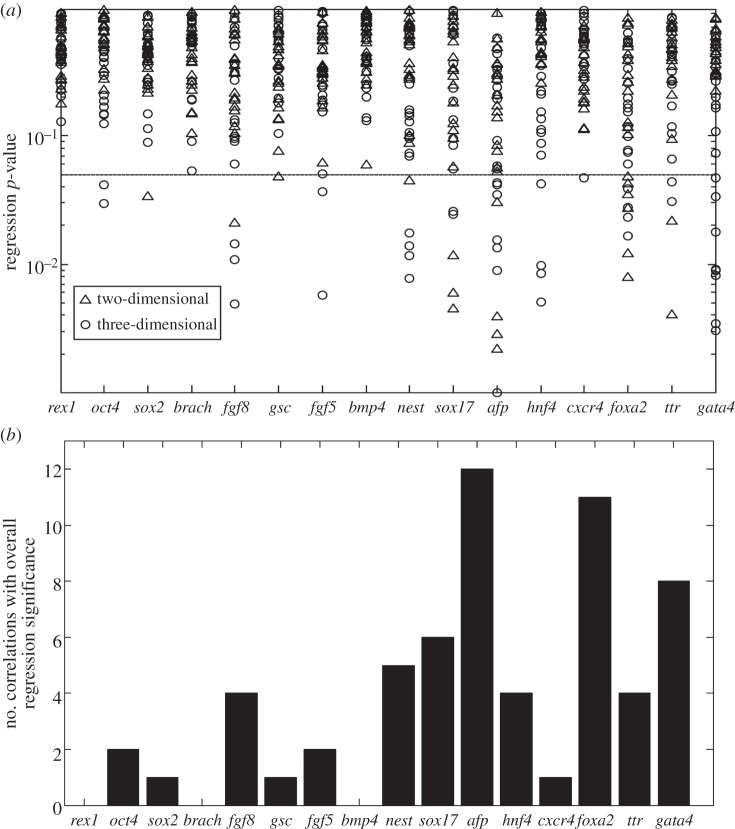
A screening procedure was next implemented to isolate the most significant correlations and parameters. As stated in §2, 1152 regressions resulted from the nine different feature space, two gel condition and 16 gene combinations. However, in order to isolate the effect of important microstructural features, only combinations of the seven influential features identified by PCA were considered for the feature space. Therefore, for each gene, 21 regressions per condition (two- and three-dimensional) were analysed. Out of these regressions, significance was analysed by determining the p-value of the overall regression. The resulting p-value for 42 regressions (21 × 2 conditions) for each gene is shown in figure 8a. In the figure, each point represents each individual regression and the resulting significance levels (y-axis). Those correlations which have an overall p-value ≤ 0.05 were considered significant. These significant regressions are recorded in table 3 (and the electronic supplementary material, table S1), which records the microstructural feature combinations which showed strong relationships to specific genes. Figure 8b displays the number of correlations per gene with p-value ≤ 0.05. As shown, gene expression levels of REX1, BRACHYURY and BMP4 do not show any strong relationships with microstructural features. The genes of AFP, FOXA2 and GATA4 show the strongest relationship with microstructural features, having the highest number of significant correlations with the features space (12, 11 and 8 significant correlations, respectively).

Figure 8.

Significance levels for each regression. (a) The expression level data for each gene were regressed onto each two-dimensional feature space combination (using the seven most prominent microstructural features previously identified), and the overall regression significance level is recorded. Each data point represents a single regression (for each gene, 21 regressions per condition (two-/three-dimensional) were performed). Those correlations which had an overall p-value ≤ 0.05 (horizontal line) were considered significant. (b) For each gene, the total number of correlations (both two- and three-dimensional) having an overall regression p-value ≤ 0.05 were compiled per gene.

Table 3.

p-values for the significant (p ≤ 0.05) second-order polynomial regressions relating two microstructural features to gene expression, two-dimensional gel condition.

gene	feature 1	feature 2	regression p-value
sox2	porosity	connectivity	0.0339
fgf8	porosity	connectivity	0.0208
gsc	fibre diameter	fibre OI	0.0478
nestin	porosity	fibre OI	0.0449
sox17	pore size	fibre OI	0.0117
sox17	node density	fibre OI	0.0044
sox17	fibre diameter	fibre OI	0.0059
afp	pore size	fibre OI	0.0303
afp	node density	fibre OI	0.0028
afp	fibre diameter	fibre OI	0.0039
afp	fibre length	fibre OI	0.0022
foxa2	pore size	fibre length	0.012
foxa2	pore size	fibre OI	0.0425
foxa2	node density	fibre length	0.0476
foxa2	node density	fibre OI	0.0272
foxa2	fibre diameter	fibre length	0.0078
foxa2	fibre diameter	fibre OI	0.0348
foxa2	porosity	fibre length	0.0346
ttr	pore size	fibre OI	0.0041
ttr	node density	fibre OI	0.0216

3.4. Germ layer specificity in response to microstructural features

Next, we systematically investigated whether any specific germ layers showed a stronger response to the microstructural feature space. From the screened significant correlations (table 3 and electronic supplementary material, table S1), the gene markers were segregated, and the results compiled, based on germ layer (table 1). Figure 9a shows the compiled results of the combined two- and three-dimensional conditions; overwhelmingly, genes from the endoderm lineage showed more significant correlations with microstructural features than those of mesoderm, ectoderm and pluripotency. Figure 9 shows that the average number of significant regressions per gene for endoderm is at least 2.8-fold higher than the other markers. These data suggest that while the examined microstructural features govern differentiation to some extent for several phenotypes, this effect is much stronger for endodermal genes.

Figure 9.

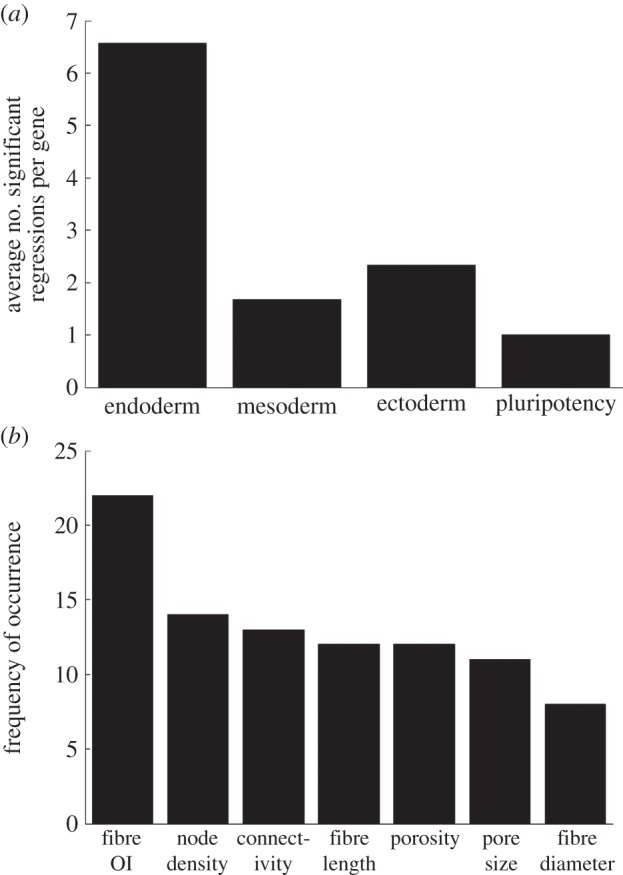
Comparison of the effect of microstructural features on gene expression between germ layer/pluripotency markers. (a) The average number of significant correlations per gene is organized for each phenotype. (b) Frequency of occurrence of influential microstructural features in significant endoderm correlations. Results out of a total of 46 significant regressions. OI denotes orientation index (representing fibre alignment).

Endoderm, being identified as the lineage which was most significantly affected by fibrin gel microstructure, was further analysed to determine if any specific microstructural feature(s) were most prominent in guiding differentiation behaviour. The regressions against endodermal gene expression which were found to be significant were first tallied. Of these significant correlations, the microstructural features present in the regressed equations were analysed for frequency of occurrence. This can be done by analysing table 3 (and the electronic supplementary material, table S1) for only endoderm genes, and determining the frequency of occurrence of each microstructural feature. These results are compiled in figure 9b. All of the features identified by PCA occurred to some extent in guiding endoderm differentiation, as they were all present to some degree in the significant correlations. However, figure 9b shows that fibre alignment (represented by the fibre OI) was the most important, as it appeared most frequently, greater than 50% more often than any of the other features.

4. Discussion

The most common method to drive ESC differentiation is through chemical cues [34–36]. Recently, however, substrate properties have been reported to modulate cellular behaviour, including elasticity and fibrous characteristics [6,37]. However, identification of specific physical cues in a complex substrate which are most influential in guiding cellular behaviour still remains a challenge. In this report, we have developed a systems level approach to guide this identification and applied it to analyse the effect of fibrin substrate microstructure on ESC differentiation without the use of any chemical cues. The highly fibrous nature of fibrin and the ease with which its fibrous topology can be adjusted make it amenable to investigation of cell–substrate behaviour [21,38]. The fibrous microstructure of fibrin consists of various attributes with which cells are likely to interact, including fibre diameter and orientation [37,39]. Analysis of such complex interactions and identification of dominant attributes governing cellular behaviour require an integrated experimental and mathematical approach. This was accomplished with a systems level approach incorporating experimental, statistical, and image processing techniques in the analysis. Differentiation was quantified by PCR, and the relationship between differentiation and stiffness/microstructural features determined through a combinatorial statistical modelling approach. This combinatorial approach enabled the utilization of the complete microstructural feature space in the correlation analysis even with limited experimental data. Through this screening method, we were able to elucidate the relative strength of the correlations.

Fibrin is becoming increasingly popular as cellular scaffolds, and is known to support cell survival, growth and differentiation [40,41], with its biodegradable nature making it appealing for possible transplantation applications [21,42]. Fibrin has been studied as a scaffold for mESC-derived progenitor cells [43,44], and shows promise for future regenerative therapies, as has been shown by fibrin/mESC in vivo studies using rats [45] and engineered therapeutic protein delivery vehicles [46]. With more techniques being reported on the modification and control of fibrin substrate properties [47,48], it may be possible to tailor fibrin substrates to guide cellular behaviour, thereby improving its therapeutic uses. This potential could be realized to a larger extent if more information was available on how the substrate affects cellular behaviour. Through the current approach, we offer a platform to advance this understanding.

In this study, we have shown that during mESC differentiation on fibrin substrates, the microstructural characteristics of the substrate show stronger correlations with differentiation patterning of mESC than stiffness alone. We first tested the relationship of the latter by changing fibrinogen and thrombin amounts to create fibrin gels of varying stiffness, each of which being used to induce differentiation. Increasing fibrinogen and thrombin increased the stiffness of the fibrin substrate, an effect which corresponds to previous reports [38]. Although a trend was qualitatively observed between fibrin stiffness and differentiation (figure 3), a statistically significant correlation was not present between these two variables (p > 0.05) for the majority of the genes. In addition to stiffness, microstructural features also differed between substrate fabrication conditions (representative images shown in figure 4); we therefore attempted to quantify the fibrin network topology and investigate whether certain microstructural attributes are important in phenotype commitment. While limited research has focused on analysing the relationship between network topology and cellular behaviour, it is particularly important when considering the scale of the interactions: the fibre microstructural features identified herein are on the micrometre scale. These features are on the same scale as cellular components, and therefore can facilitate scaffold–cell interactions. Prior studies have examined substrate microstructure and how microcharacteristics affect behaviour of cells [37,39,49]; however, these studies have typically focused on a few isolated microcharacteristics. We chose to perform a more exhaustive analysis by screening for nine different topological features, and further expand on the research area by interrogating the effect of these features on stem cell phenotype commitment. It should be noted that the current method is applicable to fibrous network topology, and would not be amenable to more amorphous substrates, although other characterization approaches [50,51] might be useful when identifying fibre orientation and angle distribution in amorphous materials.

Screening for significant correlations between microstructural features and gene expression was performed via a second-order polynomial regression. Developing correlations and mathematical models between these variables, although more complex, was advantageous over simple comparison for numerous reasons. While comparison can give statistical differences between conditions, mathematical correlations can give a better understanding of how the observed variable changes with the features space. Furthermore, optimization can be performed on the model to yield possible optimal responses. Ideally, this polynomial would include all features, with reduction of terms and subsequent selection of influential features being performed by such techniques as ridge regression, lasso or backward stepwise selection [52]. However, because of the limited amount of data, combinations of two features were selected at a time. It is important to note that a proper design of experiments (e.g. central composite design) can enable more information to be extracted from the system via response surface methodology [53] (for an example of the use of this technique for investigating cell–substrate interactions, see [54]). This would entail performing experiments at precise points in the microstructure feature space. Because of the nature of our system, the microstructural features could not be precisely controlled, and therefore a design of experiments analysis was not feasible. Furthermore, exact information on the individual parameters is difficult to extract because of possible collinearity of the features (figure 6). However, these restrictions do not prevent the significance level of the overall correlation (using the second-order polynomial model) from being obtained and from being used to determine whether the microstructural features are strongly correlated to gene expression.

The response between substrate characteristics and differentiation was taken to be a second-order polynomial. If a different form, for instance sigmoidal, existed between the variables, it is possible that the current model would not identify the correlation as significant, even if a strong relationship was present. However, specific functional forms of a response are usually only considered when theory dictates that specific behaviour. When little theoretical information is known, as is the case with the current system, polynomial models are most often used, and are very appropriate to capture first-order, second-order and interaction behaviour. It should also be noted that for those microstructural features giving a range of values per image as opposed to a single value (e.g. fibre diameter versus bulk porosity), the mean of this range was used in the polynomial model. If the whole of the data were to be used (using the whole histogram as explanatory variable values in the correlation), more sophisticated methods would have to be used, which is not in the scope of this work.

In the presented system of mESCs on fibrin gels, microstructural features exhibited a strong correlation with differentiation, while that with stiffness was relatively weak. This is in contrast to studies which have shown that substrate stiffness influences differentiation [6,7,9,54–58]. Most of these studies, however, use synthetic polymer substrates that do not exhibit a discernable microstructure. Indeed, in a previous study, we have also shown that in the system of mESCs on alginate gel, differentiation does seem to be a function of the alginate stiffness [11]. However, this polymer is much more amorphous in nature, and does not have a fibrous microstructure. Furthermore, alginate is inert, and does not directly interact with the cells. In contrast to these studies, this study has used a fibrous fibrin substrate with which the cells directly interact, and hence are likely to be more sensitive to the microstructure.

The relationship between gene expression patterning and microstructural features was determined to be lineage-specific. The endoderm germ layer most strongly correlated with fibrin microstructural topology, with the pluripotency, mesoderm and ectoderm germ layer phenotypes being less responsive to substrate modulation. More specifically, the endoderm genes of AFP and FOXA2 exhibited the most responsiveness to the fibrin microstructure, showing significant responses to the features in both two- and three-dimensional culture conditions. It is interesting to observe that while the downstream endoderm genes of GATA4 and HNF4 showed significant correlation with the fibrin topology, this is only present in the three-dimensional case and not the two-dimensional case. Further comparison of the different conditions shows that more significant correlations are present in the three-dimensional condition than two-dimensional. The fibrin gel was expected to have less interaction with the cells under two-dimensional conditions when compared with three-dimensional where the cells are completely embedded in the substrate. Therefore, the topological features of the fibrin could influence cell behaviour to a lesser extent on the two-dimensional gels, explaining the fewer significant correlations. While the current analysis shows that these specific genes were most strongly affected by network topology, a more rigorous analysis is needed to show co-regulation. This, for example, could be achieved through biclustering, which we have previously used to determine co-regulation across fibrin conditions [59], but could potentially be applied to microstructural features.

This work focused on comparing the effect of different fibrin substrate cues on mESC differentiation. Because fibrin is biodegradable, temporal changes in the substrate, in addition to degradation products, could influence differentiation. However, this study was performed for a relatively short time period of 4 days, and while some fibrin gel degradation was observed, it was not significant and only becomes somewhat visible towards the very end of the differentiation protocol. Furthermore, this degradation was similar in all of the synthesis conditions, and would therefore not affect the correlation results significantly. In addition to substrate characteristics, the cellular niche is comprised of other factors, including ECM [60] and varying amounts of fibrin-bound thrombin [61,62]. While these other factors might influence cellular behaviour to some extent, because of the strong correlation found between microstructural features and differentiation, we feel that, in the current system, this relationship is the most influential. There are also media-related factors, including diffusion of ligands and growth factors to the cells, which would affect differentiation. However, because the medium is the same between conditions, differences in these factors would be a function of microstructure. For instance, the diffusion of soluble factors to the cells would be a function of fibrin porosity. Therefore, the microstructural features are the independent variables in this system, although their effect on the cells could be considered through modulation of associated factors. The described screening approach and utilization of the image processing algorithm did not require selection of these microstructural features to analyse, but allowed the testing of correlations involving the complete fibrous network topology. Specific features identified to be influencing differentiation are fibre alignment, node density, fibre length, pore size, fibre diameter, porosity and connectivity, of which fibre alignment was by far the most influential. Interestingly, other investigators have also shown that certain of these features affect cellular behaviour, albeit in different systems and in different ways. Fibre alignment has been shown to be important for Schwann cell migration and neurite outgrowth [63]. The proliferation and morphology of osteoprogenitor cells seem to be affected by fibre diameter, whereas differentiation is not [39]. Fibre diameter and orientation have been shown to affect fibroblast morphology, but not proliferation [37]. Herbert et al. [49] studied the system of dorsal root ganglia on fibrin gels, and postulated that neurite behaviour was governed more by the fibrin density rather than the number of fibrin bundles or bundle diameter. While these studies showed that fibrous microcharacteristics are important in guiding cellular behaviour, the present report is the first systematic study to analyse the effect of fibrin fibre network topology on mESC differentiation.

The proposed systems level analysis offers a rigorous platform to identify and quantify cause–effect relationships. However, it does not provide any mechanistic information of the relationship. Such mechanistic studies have been reported in other systems. Mukhatyar et al. [63] investigated the effect of fibre alignment on Schwann cell migration and neurite outgrowth, and determined that more aligned fibres promote fibronectin adsorption which, in turn, influences these two cellular behaviours. Dalby et al. [64] demonstrated the importance of nano-topology on mesenchymal stem cell differentiation: substrate nanoscale disorder promoted bone mineral production, with this behaviour postulated to be governed by adhesion formation. Trappmann et al. showed that, in a collagen–polymer substrate system, polydimethylsiloxane substrate stiffness did not affect epidermal or mesenchymal stem cell fate, whereas the stiffness of polyacrylamide did. It was revealed that in polyacrylamide changes in porosity with stiffness led to changes in collagen anchoring points, which, in turn, affected differentiation [65]. In addition, specific integrins have been identified which interact with substrate microstructure to affect cellular behaviour, including the α2β1 integrin during osteoblastic differentiation on titanium substrates [66]. More studies such as these, focusing on the mESC–fibrin system, will be needed to extract how the aforementioned microstructural features affect differentiation patterning.

5. Conclusion

In this study, we have developed a systems level modelling approach to investigate the contributions of various microstructural cues towards the differentiation patterning of mESCs. A fibrin substrate amenable to fibre and elasticity manipulation was used together with an integrated experimental and mathematical analysis. The combinatorial treatment and statistical analysis of the complex feature space allowed for investigation of the relative influence of individual fibrous features on ESC differentiation without the need for one-at-a-time variable perturbations or large datasets. Interestingly, it was found that in this system of spontaneous mESC differentiation on fibrin gel substrates, the correlation between fibrin stiffness and gene expression was relatively weak. On the other hand, the correlation between gene expression patterning and microstructural features was strong, with fibre alignment being the most influential feature. These features preferably induced differentiation of mESCs to endodermal lineage, with the majority of significant correlations involving the endoderm genes FOXA2 and AFP. This information could aid in the design of materials with a preferred microstructure to more effectively guide lineage-specific stem cell differentiation. Furthermore, the generic procedure outlined herein should be applicable to any stem cell system which is cultured on a fibrous substrate.