Blind prediction of solvation free energies from the SAMPL4 challenge

Abstract

Here, we give an overview of the small molecule hydration portion of the SAMPL4 challenge, which focused on predicting hydration free energies for a series of 47 small molecules. These gas-to-water transfer free energies have in the past proven a valuable test of a variety of computational methods and force fields. Here, in contrast to some previous SAMPL challenges, we find a relatively wide range of methods perform quite well on this test set, with RMS errors in the 1.2 kcal/mol range for several of the best performing methods. Top-performers included a quantum mechanical approach with continuum solvent models and functional group corrections, alchemical molecular dynamics simulations with a classical all-atom force field, and a single-confor-mation Poisson-Boltzmann approach. While 1.2 kcal/mol is still a significant error, experimental hydration free energies covered a range of nearly 20 kcal/mol, so methods typically showed substantial predictive power. Here, a substantial new focus was on evaluation of error estimates, as predicting when a computational prediction is reliable vs. unreliable has considerable practical value. We found, however, that in many cases errors are substantially underestimated, and that typically little effort has been invested in estimating likely error. We believe this is an important area for further research.

1 Introduction

Small molecule transfer free energies, and in particular hydration free energies, have been an important topic of research in the last few years, and have formed a portion of every Statistical Assessment of Modeling of Proteins and Ligands (SAMPL) challenge to date[24, 19, 16, 22, 6, 7]. These are interesting in part because they are thought to provide a proxy for the level of accuracy which could be expected for free energy calculations in drug discovery applications, and because they often can be calculated quite precisely, providing a quantitative test of computational methods. Additionally, in many cases computational methods have not been empirically adjusted to reproduce hydration free energies, meaning that hydration free energies provide a fair test of methods. This is especially true when new experimental data is available, as a new set of experimental data can be used either to assess a current method, or to improve the method to better fit known data. The blind challenge format we use here is designed to ensure a fair comparison of the stated methods on new data.

Unfortunately, hydration free energies are measured only rarely experimentally, if at all, so it is difficult to stage a true hydration free energy prediction challenge. Typically, instead, SAMPL challenges have been based on careful extraction of experimental data from obscure older literature, where considerable expertise goes into identifying relevant data, converting it to the appropriate format, and curating it. This can include data on Henry's law constants, vapor pressures, solubilities, and a variety of other sources. This SAMPL challenge is no exception, and we are grateful to J. Peter Guthrie for his continued dedication to providing cu-rated experimental data for the challenge. His work for this challenge is detailed elsewhere in this issue[8]. As in previous SAMPL challenges, the hydration free energy component here is not truly “blind”, in the sense that experimental values for the compounds can actually be extracted from the literature, but the compounds examined here are typically not found in standard hydration free energy test sets, and values are typically difficult to extract from the primary literature. Additionally, participants were asked, when submitting predictions, to disclose any literature values consulted.

Here, our challenge involved 47 compounds selected from a hydration free energy dataset being prepared by J. Peter Guthrie. This set was actually divided into two portions, which we called “blind” and “supplementary”. While none of the compounds were truly blind (i.e. all experimental data used was previously published in one form or another) the supplementary compounds were relatively less obscure and values were easier to obtain from the primary literature. In this work, we have analyzed performance on both subsets separately, but most of our analysis will focus on the combined set, as overall conclusions are qualitatively similar. Statistics for the separate subsets are found in the Supporting Material.

In this work, we detail preparation for the SAMPL4 hydration free energy challenge, including challenge logistics, and describe the analysis methods and metrics used for evaluation of submissions. We also give an overview of results from the challenge, and highlight some of the range of methods applied. Full details of the methods applied will be provided in reports from the individual participants elsewhere in this issue.

2 SAMPL challenge preparation and logistics

The SAMPL4 challenge began with a set of 52 small molecules represented by chemical names and SMILES strings as provided by Guthrie [8]. From these, we generated 3D structures and isomeric SMILES strings using the OpenEye unified Python toolkits [1]. In cases where stereochemistry was not fully specified by the initial names we were provided, stereochemistry was specified by consultation with Guthrie who resolved the issue with reference to the original literature. In some cases, stereochemistry was unimportant. Particularly, for hydration free energy calculations, since water is an achiral solvent, hydration free energies of enantiomers with a single stereocenter are identical since handedness is unimportant for the hydration free energy.¹ In such cases, one enantiomer was selected at random for the challenge.

All SAMPL participants were provided with SMILES strings and 3D structures for all 52 compounds, and each compound was assigned a unique identifier from SAMPL4 001 through SAMPL4 052. Compound names were not provided to participants prior to data submission. Compounds with IDs through SAMPL4 021 were the “blind” subset, and later IDs were the “supplementary” subset.

The SAMPL4 challenge was advertised via the SAMPL website (http://sampl.eyesopen.com) and e-mails to past participants, others in the field, and the computational chemistry list (CCL), beginning in January, 2013. The hydration portion of the challenge was made available via the SAMPL website February 19, 2013. Submissions for all challenge components were due Friday, Aug. 16, and experimental values were provided to the participants shortly thereafter. Statistics comparing all submissions to experiment and to one another followed shortly thereafter. The challenge wound up with the SAMPL4 workshop on Sept. 20 at Stanford University. Submissions were allowed to be anonymous, though we received very few anonymous submissions. Because of this, however, we typically refer to submissions by their submission ID (a three digit number) rather than by the authors’ names. Method descriptions and submitter identities (from those who were willing to share this information) are provided in the Supporting Material.

SAMPL4 submissions involved a predicted hydration free energy (1M to 1M) in kcal/mol for each compound, a predicted statistical uncertainty, and a predicted model uncertainty. (Due to a late submission format change, a handful of participants provided a qualitative confidence estimate, ranging from 1 (not confident) to 5 (very confident) for each compound rather than the model uncertainty). Here, we chose to distinguish between statistical uncertainty and model uncertainty because a specific method can often yield free energy estimates which are very precise given the particular parameters, yet their expected discrepancy from experiment may be substantially larger than this level of precision. Our intent was that the statistical uncertainty would represent the level of uncertainty in the estimate given the particular model, while the model uncertainty would represent the level of uncertainty expected due to the details of the model. For example, a set of alchemical molecular dynamics simulations based on AM1-BCC and GAFF might yield hydration free energies to a precision of 0.2 kcal/mol (so that other participants using the same approach and simulation parameters, but different starting conditions or simulation packages, might see a typical variance of 0.2 kcal/mol) but the expected error relative to experiment could be substantially higher, perhaps 1.4 kcal/mol[20]. Similarly, for single-conformation methods, the statistical uncertainty might reflect variations in the selected solute conformation and other factors, while the model uncertainty would reflect expected error relative to experiment. Ideally a given approach would accurately quantify both of these uncertainties – the level of reproducibility given the overall approach, and the level of expected error relative to experiment.

After the challenge was launched, problems with experimental values, SMILES strings, or structures for a number of compounds were uncovered, resulting in removal of some five compounds from the challenge. Most of these removals occurred prior to the SAMPL meeting, and were reflected in the analysis provided to participants prior to the meeting. Specifically, SAMPL4 040, 018, and 031 were removed because they were not the intended compounds. However, investigation around and after the SAMPL meeting of several problematic members of the guaiacol series resulted in removal of 4,5-dichloroguaiacol (SAMPL4 007) and and 5-chloroguaiacol (SAMPL4 008) as late on Oct. 24. Additional, values of SAMPL4 006 (4-propyl-guaiacol), 024 (ami-triptyline), 013 (carveol), 012 (dihydrocarvone), 016 (menthol), 017 (menthone), and 015 (piperitone) were revised slightly at that time based on a re-analysis of the experimental data, though the only compound for which the value changed more than the experimental uncertainty was 4-propylguaiacol. These changes brought essentially every method into better agreement with experiment, but did not appear to substantially affect the overall rank-ordering of the performance of different submissions. The value of SAMPL4-021, 1-benzylimidazole, was also corrected post-SAMPL (Sept. 10) after a mistake was identified in a table reporting the original experimental data, and the authors provided a correction[8].

In some past SAMPLs, specific functional groups or of molecules have proven particularly challenging. In an anticipation that this might also be true here, we conceptually divided the set into five groups. Group 1 consists of linear or branched alkanes or alkenes with various polar functional groups. Group 2 consists of methoxyphenol and guaiacol, chlorinated derivatives, and other rather similar compounds. Group 3 consists of cyclohexane derivatives, often also with an attached oxygen or hydroxyl. Group 4 consists of anthracene derivatives, many of which have attached polar functional groups. And group 5 is polyfunctional or other compounds, and contains the largest and most flexible compounds in the set.

Several of the submissions discussed here came from the Mobley lab. Specifically, submission IDs 004, 005, 014, and 015 were run internally in the Mobley lab. 004 and 005 were run by KLW, an undergraduate student in the lab, who had no involvement in other portions of the hydration challenge setup or analysis. These predictions were done prior to the SAMPL submission deadline, and their blind nature means they were done on equal footing with any of the SAMPL submissions, despite the fact that they were conducted in the lab coordinating this aspect of the challenge. In contrast, 014 and 015 are null or comparison models run after the SAMPL challenge by DLM and KLW, and were done knowing (but not utilizing) the results of the challenge.

Submissions IDs 014 and 015 were included out of a desire to include a simplistic knowledge-based model for comparison with the more physical approaches employed by most participants. Both approaches compared each SAMPL challenge compound to a database of 640 small molecules studied previously by the Mobley lab including those from all previous SAMPLs[21, 20, 24, 19, 16, 22]. For each compound in this SAMPL, the submission assigned a “predicted” value equal to the experimental value of the most similar compound (submission 014) or the average of the three most similar compounds (submission 015). Chemical similarities were assigned based on OpenEye's Shape + color score. Thus, this provided a crude knowledge-based approach simply based on chemical similarity.

3 SAMPL analysis methods

3.1 Analysis metrics

SAMPL analysis was conducted via Python script, using NumPy and SciPy for numerics and Matplotlib for plots. All submissions were analyzed by a variety of standard metrics, including average error, average unsigned error, RMS error, Pearson correlation coefficient (R), and Kendall tau, as well as the slope of a best linear fit of calculated to predicted values, the “error slope”, explained below. We also looked at the largest error each method makes, by compound, to get a better sense of overall reliability. Furthermore, we computed the Kendall W, discussed below. Additionally, we compared the median Kullback-Leibler (KL) divergence for all methods, adjusted to avoid penalizing for predicted uncertainties that are smaller than the experimental error when the calculated value is close to the experimental value, as we explain further below. Because KL divergences are difficult to average when performance is poor, we also looked at the expected loss, L, given by

$$L=\langle 1-e^{-KL}\rangle$$ (1)

where KL is the KL divergence for an individual prediction, and the average runs over all predictions within a submission.

3.1.1 KL divergence

Our interest in KL divergence here was motivated partly by the realization that even an unreliable computational method could, in the right hands, be extremely useful as long as one can predict when it will be unreliable. Or, to put it another way, an ideal metric for evaluating methods would:

1. Maximally reward only predictions which are high confidence, high accuracy

2. Provide only a small reward to predictions which are low confidence, high accuracy

3. Provide only a small penalty to predictions which are low confidence, low accuracy

4. Maximally penalize only predictions which are high confidence, low accuracy

5. Recognize experimental measurements have error, and incorporate experimental uncertainties

6. Neither penalize nor reward predictions for being more precise than the experimental point of comparison, if they are consistent with it

On item 6, we can imagine a hypothetical computational method which could produce extremely accurate and precise predictions, with even greater precision than experiment. While we could not fully validate such predictions, there should be no penalty for methods which are more precise than experiment (but neither should there be any reward).

KL divergence is given by:

$$KL=\int p\ln \frac{p}{q}du$$ (2)

where p and q are the two distributions being compared (here, p represents the distribution of experimental values and q the distribution of calculated values). It is zero only if the two distributions are identical, and infinite when they have no overlap. If both the experimental and calculated distributions are modeled as Gaussians, as here, the expression simplifies further[7].

The KL divergence method was employed in a previous SAMPL because it has a number of the right properties[7]. Specifically, it essentially covers points 1-5. Both experimental and calculated values are modeled by distributions, and are rewarded for overlap, with overlap increasing both by increasingly accurate predictions, and (at least for predictions disagreeing with experimental values) improving uncertainty estimates.

Unfortunately, without further modification, KL divergence fails at handling item 6. Specifically, predicted values with uncertainty estimates smaller than the experimental uncertainty are penalized – effectively, the ideal method, within this framework, would be as precise as the experimental measurements but no more precise. This is problematic, so a first-order fix is to use the experimental error as the predicted error in all cases[7]. While this prevents unfairly penalizing precise computational methods, it also removes the penalty warranted by item 4 – high precision, low accuracy predictions are no longer penalized more than low precision, low accuracy predictions. Wood et al. alternatively addressed this problem by replacing the predicted error with the experimental error whenever the predicted error is smaller than the experimental error. Unfortunately, this too reduces the penalty for methods which are more precise than the experiment but substantially wrong 1.

We believe, if the KL divergence is to be employed as a metric, the correct approach is to smoothly transition between two limits. In one limit, when the experimental value and the prediction fundamentally agree, predictions should not be penalized for being more precise than experiment, and so if the predicted uncertainty is smaller than the experimental uncertainty, it should be made to match, for optimal overlap (minimal divergence). In the other limit, where the predicted and experimental values completely disagree, the original predicted uncertainty estimate should be retained. Thus, if two substantially incorrect predictions which are the same are compared to experiment, the one with the larger uncertainty estimate will always result in a better KL divergence. We would like to transition smoothly between these two limits.

Thus, here our approach for computing the KL divergence is to model the experimental value and the prediction as Gaussian distributions. The experimental distribution always has a variance σ_e, the experimental uncertainty. And the predicted distribution has a variance of max(σ_p, ${\sigma }_p^{\prime }$), where σ_p is the original uncertainty estimate for the prediction, ${\sigma }_p^{\prime }=f\times {\sigma }_e+(1-f)\times {\sigma }_p$, and f is a mixing factor given by either:

$$f=exp(-\mid \Delta \mu \mid ∕{\sigma }_c)$$ (3)

$$f=exp(-{(\Delta \mu ∕{\sigma }_c)}^2)$$ (4)

where ${\sigma }_c={\sigma }_e^2+{\sigma }_p^2$ is the mutual uncertainty, and Δμ = μ_e – μ_c is the difference between the predicted and experimental values (or the means of the predicted and experimental distributions). We call these the exponential and Gaussian mixing schemes, respectively. In either case, f = 0 when the calculated and experimental values are far separated, so that ${\sigma }_p^{\prime }={\sigma }_p$, and f = 1 when the predicted and experimental mean are identical, so that ${\sigma }_p^{\prime }={\sigma }_e$. This results in substantial changes in the KL divergence relative to alternative approaches, as we highlight in Figure 1. Here, while we see significant differences between KL divergences obtained via Eqn. 3 and 4 in a few cases, we are not aware of a strong reason to prefer one approach over the other so we use the simpler scheme, Eqn. 3 (Figure 1).

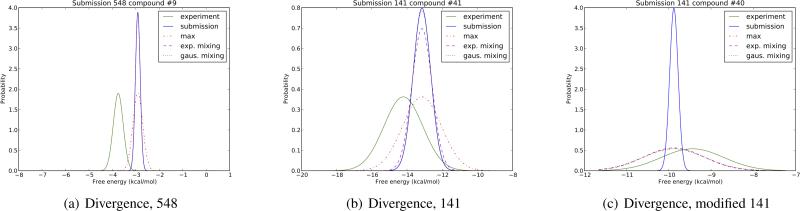
Fig. 1.

Experimental and predicted distributions used for KL divergence calculations for sample predictions. Experimental and predicted values are modeled with Gaussians, where the experimental distribution (solid green) has a variance σ_e and the predicted distribution has a variance ${\sigma }_p^{\prime }$ which either matches the uncertainty in the prediction, σ_p (solid blue), or is modified to be the maximum of σ_p and σ_e (“maximum” case, red dots and dashes), or to vary smoothly between σ_p and σ_e as the predicted mean approaches the experimental mean whenever σ_p < σ_e as per the mixing function in Eqn. 3 (“exponential”) or Eqn. 4 (“gaussian”). (a) shows submission 548, compound 9; (b) shows submission 141, compound 41, and (c) shows a sample modification of submission 141, compound 40, where the predicted uncertainty is taken to be very small to illustrate the significance of this issue. In (a), the “maximum” scheme clearly introduces spurious overlap between the experimental distribution and the prediction, while both the “exponential” and “gaussian” schemes retain essentially the original amount of overlap. In (b), because the predicted value is now approaching the experimental value, the exponential mixing scheme begins to modulate ${\sigma }_p^{\prime }$ to match σ_e as desired, increasing overlap (but not as far as the “maximum” scheme). A similar thing happens in (c). While in (a) and (b) the difference in divergence is not particularly significant, in (c) the approaches yield substantially different divergences, as discussed in the text.

There is one additional nuance here, in that submissions actually provided two uncertainty estimates – the statistical uncertainty and the model uncertainty. Ideally, we would have made it very clear to participants in advance how we intended to use these, but as our plans came together after we began analyzing submissions, we were unable to do so. Ideally, we would have made it clear that “model uncertainty” estimates would be used to assess how well participants did at estimating how well their methods would agree with experiment, on each compound. But since this was not sufficiently clear, for KL divergence, we used the larger of the two uncertainty estimates submitted, which in general resulted in more favorable KL divergences than alternative approaches.

In the examples shown in Figure 1, the change in KL divergence across the different schemes is not large, in part because σ_p values were not dramatically underestimated. So for ID 548 compound 9, the standard approach yields a divergence of 8.24, while the scheme of Wood et al. yields a divergence of 7.90, and the exponential and Gaussian schemes maintain essentially the same divergence as the standard approach. For ID 141 compound 41, the standard approach yields a divergence of 0.86, while the scheme of Wood et al. yields a divergence of 0.46, while the exponential and Gaussian mixing schemes yield 0.58 and 0.56, respectively. But that does not mean the distinction between these approaches is unimportant in general. To illustrate, we reanalyzed KL divergences using only the estimated statistical uncertainty as the predicted error estimate, and Figure 1(c) shows a representative example. In this case, the standard approach gives a divergence of 1.69, while the Wood et al. scheme gives a divergence of only 0.18. The exponential and Gaussian cases also give low divergences (0.35 and 0.25, respectively) because the predicted value is so close to the experimental value, so ${\sigma }_p^{\prime }$ is almost completely determined by σ_e. We believe this is a reasonable elimination of the penalty for predictions which are more precise than experiment, yet accurate.

3.1.2 Error slope

We also examined one additional metric, what we call the error slope, which evaluates how well submissions predicted uncertainties. This begins by looking at the fraction of experimental values (resampled with noise drawn from the experimental distribution) falling within a given multiple of a submissions assigned statistical uncertainty, and compares it to the fraction expected graphically. This initial plot is effectively a Q-Q plot, comparing the expected number of values within a particular quantile with the actual number within a particular quantile. A similar approach was used previously by Chodera and Noé to validate computed uncertainty estimates[3]. Here, however, we seek a numerical metric for the quality of uncertainty estimates, so we perform a linear least-squares fit to our Q-Q plot, with the intercept constrained to be zero. This gives us the slope of the best fit line which best relates the observed fraction of experimental values within a given number of quantiles of the calculated value to the expected fraction within the same range, as shown in 2. A slope of 1 corresponds to uncertainty estimates which are accurate on average, while a slope larger or smaller than 1 corresponds to uncertainty estimates which are on average too high or too low respectively, so the target value here is 1. We call this value the “error slope” for brevity.

Again, because we had not made our plans for handling of statistical uncertainty and model uncertainty sufficiently clear to participants, we had to be careful how to handle the two uncertainty estimates as they pertained to error slope. Our final solution was to compute the error slope both for the statistical uncertainty, and the model uncertainty, and report the slope value which was closer to 1. Effectively, we gave participants credit for whichever error estimate was the more reasonable of the two they submitted.

3.1.3 Kendall W

Here, we also applied the Kendall W statistic to assess the level of agreement about which submission or method performed best overall. Kendall W ranges from 0 to 1, and assesses the degree of consistency between evaluations, with 0 representing complete disagreement and 1 representing complete agreement. For example, a group of judges might rank a series of wines, and a W value of 1 would correspond to complete agreement between judges about which wine was best, while a W value of zero would correspond to complete disagreement. Here, each compound effectively serves as a judge, and we evaluate submissions based on their ranked performance on different compounds. A Kendall W value of 1 would mean that a single method was the top performer across all compounds, while a value not significantly different from 0 would mean no method was a clear leader across all compounds.

3.2 Error analysis

In addition to calculating various metrics comparing performance, we computed uncertainties in these values using a bootstrapping procedure accounting for experimental noise. Specifically, for every set of predicted values, we conducted 1000 bootstrap trials, and our uncertainty estimate was taken as the variance in each metric computed across those trials. Each bootstrap trial consisted of constructing a new set of calculated and experimental values (of the same length) by selecting compounds from the original set, with replacement. In each bootstrap trial, noise was added independently to each experimental value with a value drawn from a Gaussian distribution with a mean of zero and a variance equal to the experimental uncertainty. Thus bootstrapped error estimates effectively include both variation due to the composition of the set, and due to the experimental uncertainties themselves.

3.3 Significance testing

In some cases we sought to compare whether methods with marginally different performance are actually significantly different, or in other words we seek to determine whether our data (the comparison of predicted with experimental values for two different methods) is enough to reject the null hypothesis that two methods being compared are in fact no different. To do this, we here applied Student's paired t-test[26] to the difference between the calculated and experimental values for the sets being compared. This allowed us to test whether methods yielded predictions which were substantially different – predictions drawn from significantly different distributions. This test does not indicate whether one method is superior to another, but simply whether their predictions are different in a significant way. This allows us, among other things, to compare whether two top-performing methods are different in a statistically significant way, or whether a given method yields predictions which are different in a significant way from a control model such as a similarity-based model (submission 014 or 015).

4 Results and discussion

4.1 Performance statistics

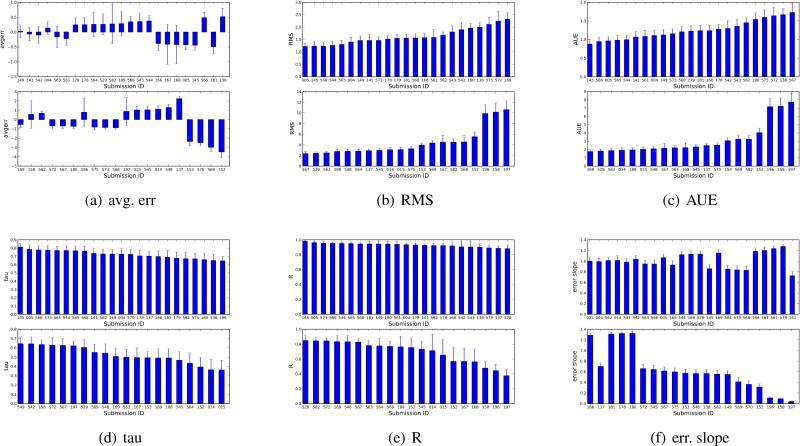
The SAMPL4 hydration challenge involved 49 submissions from 19 groups. As in past SAMPLs, many groups submitted multiple sets of predictions to test and cross-compare diverse methods. Overall, we ran the full range of statistics on all submissions, and results on the full set are shown in Table 1. To allow graphical comparison of methods, we also ranked all submissions by each metric we examined and provide the same statistics in bar graph form in Figure 3. It is worth highlighting that uncertainties are substantial, and in many cases larger than the difference between submissions, so while submissions can be ranked by these metrics, the precise order of the ranking would be subject to statistical fluctuations if the set were modified. Qualitatively, this can be seen graphically from the figures by looking at the level of overlap between error bars.

Table 1.

Statistics for SAMPL4 hydration prediction.

ID	avg. err.	RMS	AUE	tau	R	err. slope	max. err.
004	0.13 ± 0.13	1.40 ± 0.12	1.10 ± 0.10	0.73 ± 0.06	0.93 ± 0.02	0.99 ± 0.07	4.98 ± 0.47
005	–0.42 ± 0.18	1.22 ± 0.15	0.96 ± 0.12	0.78 ± 0.06	0.96 ± 0.01	1.06 ± 0.05	1.81 ± 0.67
014	1.11 ± 0.57	3.07 ± 0.72	1.90 ± 0.51	0.36 ± 0.15	0.71 ± 0.26	1.01 ± 0.10	10.69 ± 0.70
015	1.02 ± 0.49	3.09 ± 0.46	2.02 ± 0.34	0.36 ± 0.09	0.65 ± 0.20	1.00 ± 0.07	10.37 ± 0.42
137	2.24 ± 0.23	2.89 ± 0.30	2.48 ± 0.20	0.70 ± 0.06	0.89 ± 0.03	0.70 ± 0.08	8.38 ± 0.50
138	0.51 ± 0.29	2.00 ± 0.23	1.66 ± 0.20	0.65 ± 0.06	0.90 ± 0.05	0.57 ± 0.08	5.25 ± 0.23
141	–0.07 ± 0.28	1.46 ± 0.18	1.07 ± 0.11	0.74 ± 0.07	0.93 ± 0.02	0.72 ± 0.08	6.02 ± 0.46
145	–0.44 ± 0.16	1.23 ± 0.16	0.87 ± 0.09	0.81 ± 0.03	0.98 ± 0.01	0.86 ± 0.08	1.24 ± 0.89
149	0.03 ± 0.24	1.46 ± 0.14	1.12 ± 0.12	0.73 ± 0.05	0.94 ± 0.02	0.55 ± 0.04	2.74 ± 0.89
152	–3.48 ± 0.98	5.52 ± 1.25	4.05 ± 0.85	0.39 ± 0.08	0.57 ± 0.17	0.31 ± 0.06	3.93 ± 3.84
153	–2.35 ± 0.52	3.95 ± 0.40	3.07 ± 0.41	0.49 ± 0.04	0.75 ± 0.10	0.57 ± 0.06	2.95 ± 0.77
158	0.55 ± 1.76	10.14 ± 1.91	7.23 ± 1.09	0.63 ± 0.05	0.48 ± 0.08	0.09 ± 0.02	9.29 ± 6.10
166	–0.38 ± 0.22	1.58 ± 0.09	1.24 ± 0.08	0.70 ± 0.05	0.92 ± 0.05	1.28 ± 0.03	3.55 ± 0.33
167	–0.41 ± 0.52	4.48 ± 1.20	2.15 ± 0.61	0.49 ± 0.12	0.57 ± 0.14	1.20 ± 0.08	4.94 ± 3.18
168	–0.42 ± 0.89	4.53 ± 1.49	2.22 ± 0.72	0.49 ± 0.11	0.56 ± 0.17	1.18 ± 0.08	4.91 ± 5.36
169	–0.53 ± 0.29	2.32 ± 0.32	1.75 ± 0.24	0.51 ± 0.10	0.83 ± 0.07	1.15 ± 0.06	4.26 ± 1.42
178	0.25 ± 0.17	1.52 ± 0.11	1.28 ± 0.11	0.71 ± 0.05	0.93 ± 0.02	1.32 ± 0.03	3.42 ± 0.16
179	0.24 ± 0.29	1.55 ± 0.20	1.23 ± 0.16	0.68 ± 0.07	0.92 ± 0.02	1.27 ± 0.04	4.42 ± 0.39
180	–0.73 ± 0.18	1.96 ± 0.24	1.54 ± 0.17	0.66 ± 0.07	0.94 ± 0.03	1.32 ± 0.04	2.36 ± 0.86
181	–0.49 ± 0.23	1.55 ± 0.13	1.24 ± 0.12	0.69 ± 0.08	0.94 ± 0.04	1.31 ± 0.04	3.19 ± 0.74
189	0.28 ± 0.39	2.74 ± 0.43	1.95 ± 0.28	0.49 ± 0.11	0.76 ± 0.14	1.13 ± 0.06	8.72 ± 1.33
196	0.78 ± 1.36	9.88 ± 1.89	7.17 ± 1.19	0.64 ± 0.03	0.44 ± 0.08	0.11 ± 0.01	9.29 ± 8.23
197	0.87 ± 0.97	10.60 ± 1.15	7.74 ± 0.68	0.62 ± 0.05	0.38 ± 0.07	0.04 ± 0.01	10.29 ± 2.07
529	0.26 ± 0.30	2.39 ± 0.34	1.82 ± 0.25	0.60 ± 0.07	0.85 ± 0.05	1.13 ± 0.05	6.83 ± 0.69
542	–0.10 ± 0.29	1.89 ± 0.26	1.30 ± 0.18	0.64 ± 0.07	0.90 ± 0.07	1.04 ± 0.04	5.24 ± 0.26
543	0.35 ± 0.18	1.80 ± 0.22	1.35 ± 0.15	0.64 ± 0.05	0.90 ± 0.06	0.98 ± 0.04	5.44 ± 0.92
544	0.37 ± 0.18	1.26 ± 0.15	1.00 ± 0.09	0.77 ± 0.03	0.95 ± 0.01	1.12 ± 0.04	4.22 ± 0.20
545	1.04 ± 0.25	2.96 ± 0.28	2.32 ± 0.21	0.47 ± 0.11	0.73 ± 0.13	0.64 ± 0.07	8.02 ± 1.73
548	1.29 ± 0.31	2.80 ± 0.49	2.08 ± 0.31	0.54 ± 0.11	0.83 ± 0.13	0.57 ± 0.07	9.22 ± 0.91
561	–0.22 ± 0.26	1.58 ± 0.34	1.08 ± 0.19	0.77 ± 0.03	0.94 ± 0.02	1.23 ± 0.04	2.60 ± 1.47
562	0.67 ± 0.21	1.68 ± 0.13	1.45 ± 0.13	0.73 ± 0.06	0.92 ± 0.02	1.01 ± 0.06	3.66 ± 0.60
563	–0.16 ± 0.26	2.49 ± 0.28	1.87 ± 0.23	0.50 ± 0.09	0.78 ± 0.03	0.95 ± 0.09	7.30 ± 0.40
564	0.26 ± 0.29	2.82 ± 0.34	2.21 ± 0.25	0.43 ± 0.11	0.77 ± 0.08	0.85 ± 0.04	8.66 ± 1.14
565	0.48 ± 0.17	1.30 ± 0.20	0.98 ± 0.15	0.77 ± 0.04	0.95 ± 0.02	0.93 ± 0.05	4.34 ± 0.47
566	0.34 ± 0.14	1.23 ± 0.16	0.94 ± 0.11	0.78 ± 0.04	0.95 ± 0.01	0.95 ± 0.07	4.22 ± 0.25
567	–0.69 ± 0.21	2.34 ± 0.32	1.72 ± 0.19	0.63 ± 0.05	0.83 ± 0.04	0.62 ± 0.09	9.72 ± 0.61
568	–0.87 ± 0.18	1.56 ± 0.11	1.21 ± 0.11	0.76 ± 0.05	0.94 ± 0.02	0.83 ± 0.05	2.72 ± 0.15
569	–2.97 ± 0.59	4.34 ± 0.60	3.25 ± 0.50	0.55 ± 0.05	0.77 ± 0.05	0.41 ± 0.06	4.12 ± 2.05
570	–2.48 ± 0.33	3.27 ± 0.41	2.53 ± 0.31	0.72 ± 0.05	0.88 ± 0.04	0.36 ± 0.05	0.55 ± 0.57
572	–0.68 ± 0.18	2.24 ± 0.32	1.64 ± 0.22	0.63 ± 0.09	0.84 ± 0.03	0.66 ± 0.07	9.12 ± 0.24
573	–0.85 ± 0.16	1.46 ± 0.13	1.15 ± 0.12	0.78 ± 0.06	0.95 ± 0.03	0.83 ± 0.07	1.92 ± 0.54
575	–0.81 ± 0.25	2.11 ± 0.35	1.59 ± 0.19	0.67 ± 0.09	0.89 ± 0.05	0.60 ± 0.07	3.16 ± 1.33
582	0.27 ± 1.01	4.50 ± 0.79	3.25 ± 0.59	0.67 ± 0.11	0.84 ± 0.05	0.55 ± 0.09	8.50 ± 2.49

Shown are statistics for each submission, by submission ID. We report average error, RMS error, average unsigned error, Kendall tau, Pearson R, the slope of a best fit line comparing predicted error with actual error (with an ideal value of 1, as described in the text), and the maximum error on any individual compound. Units, when applicable, are kcal/mol. Submission 575 was apparently affected with a propagation bug when running the molecular dynamics simulations, introducing errors.[31]

Fig. 3.

Performance by submission ID, as ranked by different metrics. Shown (in kcal/mol) are the average error, the RMS error, and the the average unsigned error (AUE) (a-c). Additionally, we show the Kendall tau value and Pearson R, which measure correlation or ranking ability, and the error slope, which is a measure of whether submissions on average underestimated (slope < 1) or overestimated (slope > 1) their error relative to experiment, as discussed in the text. Because of the number of submissions, plots are divided into two panels. Note that the scale on the vertical axis differs, with the bottom panel of each graph showing lower performing submissions.

One participant (five submissions) focused exclusively on the blind component of the challenge, and thus statistics for these submissions could not be computed for the full set. Separate tables showing performance on the blind and supplementary portions of the challenge are provided in the Supporting Information. Submissions 530-534, which included only the blind set, fall roughly in the middle of the pack. In general, trends in performance were similar across the blind and supplementary sets, though the exact ranking of methods by each metric differs.

Each compound and experimental value essentially provides an opportunity to rank methods, and if a single method provided the best prediction for every compound considered, such a method would be a clear winner. The Kendall W statistic provides a way to measure agreement across tests (compounds predicted) about which method is best. It ranges from 0 to 1, where a value of 0 corresponds to no agreement about which method is best, while a value of 1 corresponds to complete agreement. Here, we obtain W = 0.28 ± 0.02, which is significantly different from 0, but not close to 1, indicating a small but significant level of agreement about which submissions performed best.

As noted in the analysis section above, we also computed the Kullback-Leibler (KL) divergence and the expected loss as measures which combine both method accuracy and accuracy of error estimation, so that methods which can predict when they are likely to fail and succeed are rewarded relative to those which cannot. For KL divergence, each predicted and calculated value is modeled as a separate Gaussian distribution and the KL divergence is based on overlap, with a value of infinity corresponding to no overlap between the predicted and experimental distributions, and a value of 0 corresponding to complete overlap (agreement). The expected loss modifies this by averaging the negative exponential of the KL divergence, yielding a value which ranges from 0 (perfect predictions) to 1 (a high KL divergence on average). The loss is more suitable for averaging than the KL divergence since it is bounded, but also has the deficiency that it doesn't substantially reward predictions which make marginal improvements.

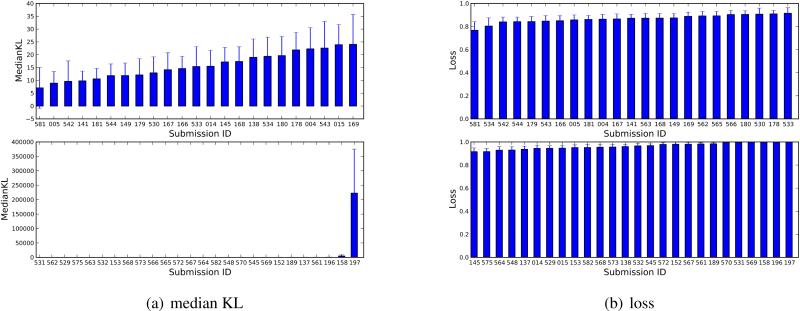
Results for KL divergence and loss are shown in Figure 4. We find that the average loss is quite high, and only a few methods have a loss substantially different from 1. This is in part because, we believe, relatively little effort has gone into predicting when predicted values are likely to be wrong, so even the best performing methods have several compounds for which the experimental and calculated values differ by substantially more than their uncertainties. These discrepancies have serious adverse consequences for the KL divergence and the loss. It is also interesting to note that the ranking of methods as judged by KL divergence is substantially different than the typical rank order by other metrics, with submission IDs 141 and 149 performing much better by this metric than by other metrics. This is in part because KL divergence assess success in a fundamentally different way.

Fig. 4.

Median KL divergence and average loss for different submissions in the SAMPL4 challenge. These are sorted in ranked order. Because of the number of submissions, plots are divided into two panels. Note that the scale on the vertical axis differs, with the bottom panel of each graph showing lower performing submissions.

We briefly examined whether methods overall performed better on any of our five classes of molecules relative to the others, but we did not observe any obvious trends. We were also interested to see whether typical predictions suggested any problems with the experimental data, so we averaged all submitted hydration free energies for each compound, and looked for cases where experimental values differed from these average predictions by more than twice the standard deviation across predictions. However, there were no such cases, in part because the variation across submissions was typically substantial. ²

4.2 A quick look at some top-performing submissions

Here, we want to highlight some of the range of participating methods by looking at a few of the top performers by different metrics in Figure 3. We find that some methods achieved low average errors simply by virtue of having an equal balance of large positive and negative errors, so we instead focus our attention on the methods which performed best as judged by RMS error and AUE, as well as Kendall tau and Pearson R. Of the top six performers by AUE and RMS, five occur in both lists (145, 005, 566, 544, and 565) while two occur in only one of the two lists (141 and 004), with small differences in the exact ranking. Similarly, Pearson R and Kendall tau mostly agree, with the top six submissions including five in common (145, 005, 566, 573, and 544) and two in only one list (561 and 565). Thus, submissions 145, 005, 566, and 544 are among the top six by all four metrics. For illustration, we show predictions from the first three of these methods in Figure 5, along with predictions from two other representative submissions, submission 529, which is near the middle by most metrics, and submission 197, which is near the bottom.

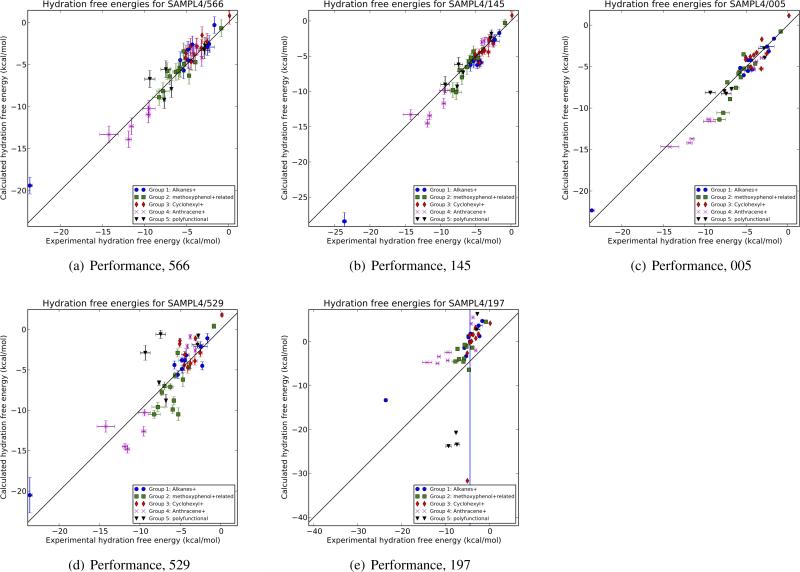
Fig. 5.

Comparison of several submissions. Shown are calculated versus experimental hydration free energies for several representative SAMPL submissions, including three of the top performers by most metrics (submissions 566, 145, and 005), a middle performer (ID 529), and one of the worst submissions (197). For ID 197, one compound could not be processed by the method in question and it was assigned a value of 0 kcal/mol with a large uncertainty estimate.

It is worth looking briefly at the differences between these top-performing methods. Submission ID 145, from the Sandberg group at the University of Dundee[28] used a quantum mechanical (QM) approach with implicit solvent and functional group corrections. Following a conformational search with Schrödinger tools, they conducted QM geometry optimization in continuum solvent, then separately computed polarization, electrostatic, dispersion, repulsion, and cavity formation components of solvation. Empirical functional group corrections were also incorporated. In contrast, submission 566[4] employed a single-conformation Poisson-Boltzmann (PB) approach from OpenEye using low energy gas-phase conformations, with AM1-BCC partial charges and ZAP9 radii, as in a previous SAMPL[25]. And submission 005 was a test from the Mobley lab using alchemical explicit solvent molecular dynamics simulations with essentially our standard approach[16] (AM1-BCC partial charges[14] with the GAFF small molecule force field[30]) but with new hydroxyl parameters updated to better fit pure solvent properties for simple alcohols, as described in more detail elsewhere[5]. This new parameter set outperforms our standard approach as represented by submission 004. Submission 544 applies standard AM1-BCC GAFF alchemical free energy calculations in GROMACS, and is nearly identical to submission 004 (but done independently in a different lab)[23]. It is worth briefly highlighting key metrics for these methods as well (Table 1). For 145, 566, 005, and 544, respectively, the RMS errors are 1.23 ± 0.20 kcal/mol, 1.23 ± 0.16 kcal/mol, 1.22 ± 0.14 kcal/mol, and 1.26 ± 0.15, while the AUEs are 0.87 ± 0.13 kcal/mol, 0.94 ± 0.12 kcal/mol, 1.00 ± 0.12 kcal/mol, and 1.00 ± 0.09 kcal/mol. Kendall tau values are 0.81 ± 0.05, 0.78 ± 0.05, 0.78 ± 0.06, and 0.77 ± 0.03, and Pearson R values are 0.98 ± 0.02, 0.95 ± 0.02, 0.96 ± 0.02, and 0.95 ± 0.01. Thus, performance differences between these approaches are clearly below the level of statistical significance. In contrast, the mid-level method highlighted in Figure 5, submission 529, has significantly but not dramatically worse performance by most metrics, while submission 197 is clearly worse by all metrics. Submission 529 used MD alchemical free energy calculations in explicit solvent with the GROMOS simulation package, using parameters from Automated Topology Builder[18, 2]. In contrast, submission 197 used the AMSOL solvation model[9] from the ZINC processing pipeline[13] for hydration free energy predictions, with conformations predicted by Open-Eye's Omega[11, 10, 1].

4.2.1 Evaluation of difficult compounds

In order to assess whether some compounds were more difficult than others, we calculated the average unsigned error (AUE) across all submissions for each compound in the set. A low value means that all submissions provided fairly accurate predictions, while a high value means that many methods agreed poorly with experiment. Average errors range fro 1.1 to 4.4 kcal/mol as in Table 2, where compounds are sorted from largest error to smallest.

Table 2.

Mean unsigned error by compound in the SAMPL4 challenge, sorted from largest to smallest.

Compound	SMILES	Name	MW	AUE
SAMPL4_022	Cc1c(cccc1Nc2ccccc2C(=O)O)C	mefenamic acid	241.29	4.36
SAMPL4_023	c1ccccc1C(c2ccccc2)OCCN(C)C	diphenhydramine	255.36	4.28
SAMPL4_027	O(N(=O)=O)C(CCON(=O)=O)C	1,3-bis-(nitrooxy)propane	166.09	4.26
SAMPL4_028	O(N(=O)=O)C(CCON(=O)=O)C	1,3-bis-(nitrooxy)butane	180.12	4.19
SAMPL4_009	Clc1c(C=O)c(Cl)c(OC)c(O)c1OC	2,6-dichlorosyringaldehyde	251.06	3.95
SAMPL4_001	C(C(C(C(C(CO)O)O)O)O)O	mannitol	182.18	3.94
SAMPL4_024	CN(C)CCC=C1c2ccccc2CCc3c1cccc3	amitriptyline	277.41	3.83
SAMPL4_041	N1CCCCC1	piperidine	85.15	3.54
SAMPL4_045	O=C1c2c(ccc(N)c2)C(=O)c2c1cccc2	2-amino-9,10-anthraquinone	223.23	2.99
SAMPL4_048	O=C1c2c(C(=O)c3c1cccc3)c(N)ccc2N	1,4-diamino-9,10-anthraquinone	238.25	2.85
SAMPL4_047	O=C1c2c(cccc2NCCO)C(=O)c2c1cccc2	1-(2-hydroxyethylamino)-9,10-anthraquinone	267.28	2.68
SAMPL4_011	Clc1c(OC)c(O)c(OC)cc1C=O	2-chlorosyringaldehyde	216.62	2.61
SAMPL4_010	Clc1cc(Cl)c(OC)c(O)c1OC	3,5-dichlorosyringol	223.05	2.54
SAMPL4_046	Nc1c2c(ccc1)C(=O)c3c(cccc3)C2=O	1-amino-9,10-anthraquinone	223.23	2.45
SAMPL4_051	Nc1c2c(c(cc1)O)C(=O)c3c(cccc3)C2=O	1-amino-4-hydroxy-9,10-anthraquinone	239.23	2.45
SAMPL4_029	O([N+](=O)[O−])CCCCCC	hexyl nitrate	147.17	2.4
SAMPL4_021	c1(ccccc1)Cn2cncc2	1-benzylimidazole	159.214	2.19
SAMPL4_032	Clc1cc(O)ccc1Cl	3,4-dichlorophenol	163	1.97
SAMPL4_035	Oc1ccccc1C=O	2-hydroxybenzaldehyde	122.12	1.89
SAMPL4_025	O(CC(O)C)CCCC	1-butoxy-2-propanol	132.2	1.87
SAMPL4_050	c12c(cc3c(c1)cccc3)cccc2	anthracene	178.23	1.84
SAMPL4_005	O(C)c1ccccc1OC	1,2-dimethoxybenzene	138.17	1.79
SAMPL4_020	C=C(c1ccccc1)c2ccccc2	1,1-diphenylethene	180.245	1.79
SAMPL4_019	C1c2c(Cc3c1cccc3)cccc2	9,10-dihydroanthracene	180.25	1.76
SAMPL4_002	CC(=CCCC(C)(C=C)OC(=O)C)C	linalyl acetate	196.29	1.73
SAMPL4_030	O(C(=O)C)CCCCCC	hexyl acetate	144.21	1.71
SAMPL4_003	CC(=CCCC(=CCO)C)C	nerol	154.25	1.7
SAMPL4_052	O(c1ccccc1)c1ccccc1	diphenyl ether	170.21	1.58
SAMPL4_004	OC\C=C(\CCC=C(C)C)/C	geraniol	154.25	1.53
SAMPL4_016	OC1CC(CCC1C(C)C)C	menthol	156.27	1.53
SAMPL4_026	C(C)OCCOC(=O)C	2-ethoxyethyl acetate	132.16	1.49
SAMPL4_042	O1CCCCC1	tetrahydropyran	86.13	1.48
SAMPL4_006	Oc1ccc(cc1OC)CCC	4-propylguaiacol	166.217	1.47
SAMPL4_013	OC1CC(CC=C1C)C(C)=C	carveol	152.24	1.43
SAMPL4_044	O1CCOCC1	1,4-dioxane	88.11	1.41
SAMPL4_014	O=C\C1=C\CC(\C(=C)C)CC1	l-perillaldehyde	150.22	1.38
SAMPL4_012	CC1C(=O)CC(CC1)C(=C)C	dihydrocarvone	152.238	1.32
SAMPL4_036	Oc1ccccc1CC	2-ethylphenol	122.17	1.32
SAMPL4_017	CC1CCC(C(=O)C1)C(C)C	menthone	154.25	1.29
SAMPL4_034	Cc1cc(c(cc1)O)OC	4-methyl-2-methoxyphenol	138.17	1.28
SAMPL4_033	O(C)c1cccc(OC)c1O	2,6-dimethoxyphenol	154.16	1.26
SAMPL4_015	CC1=CC(=O)C(CC1)C(C)C	piperitone	152.238	1.23
SAMPL4_038	O=Cc1ccccc1C	2-methylbenzaldehyde	120.15	1.22
SAMPL4_037	COc1c(cccc1)O	2-methoxyphenol	124.14	1.19
SAMPL4_049	O1c2c(Oc3c1cccc3)cccc2	dibenzo-p-dioxin	184.19	1.15
SAMPL4_043	C1CCC=CC1	cyclohexene	82.15	1.12
SAMPL4_039	c1cccc(C)c1CC	1-ethyl-2-methylbenzene	120.2	1.07

Energy units are kcal/mol.

The ten compounds which were most poorly predicted (with the largest average error) came from all five groups: three from group 1, one from group 2, one from group 3, two from group 4, and three from group 5. So the initial grouping was not effective at isolating problem compounds.

Instead, we found that the compounds which tended to be well-predicted were typically fairly simple, without strongly interacting functional groups, while compounds which presented more challenges were mostly polyfunctional with several interacting groups. There also seems to be a tendency for errors to be higher with greater molecular weight, but molecular weight alone is not a good predictor. And, since higher molecular weight compounds tend to have more functional groups, this may simply be due to increasing complexity.

Still, several compounds stand out as giving particularly high errors even given their molecular weights. If we fit a quadratic (passing through zero) to the error versus molecular weight, four compounds in particular stand out as having higher-than-expected errors. Three of these are unsurprising – 1,3-bis-(nitrooxy)propane, 1,3-bis-(nitrooxy)butane, and mannitol, all of which are polyfunctional with several interacting groups. The fourth is surprising: piperidine, which seems quite simple, yet has an AUE of 3.54 kcal/mol which is nearly as high as that of mannitol (3.94). Thus, even simple amines may pose a problem for a variety of methods. It is also worth noting that piperidine was a “supplementary” compound, meaning the experimental value is relatively readily available. If we instead do a linear fit to the error versus molecular weight, several additional compounds have higher-than-expected errors. These include mefenamic acid, 2,6-dichlorosyringaldehyde, and diphenhydramine. These, too, are unsurprising given their polyfunctional nature.

The overall tendency we see for error to rise with molecular weight seems somewhat disconcerting, given that drug-like molecules can have substantially higher molecular weights than any of the compounds in this set. Thus further work may be needed on polyfunctional compounds to improve accuracies for larger, drug-like molecules.

Of the 47 compounds in the challenge, only 17 had mean absolute errors less than 1.5 kcal/mol. A further 17 had mean absolute errors greater than 2.0 kcal/mol, suggesting further improvement is needed. Thus, we believe there remains a further need for solvation challenges to help drive further improvements in solvation modeling.

4.3 SAMPL methodologies

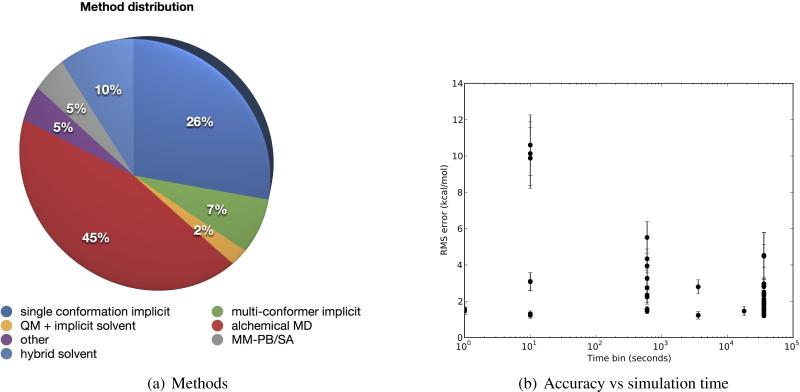
SAMPL4 submissions represented a broad range of methodologies (Figure 6). Interestingly, unlike previous SAMPL challenges, this challenge saw a surge of interest in explicit solvent alchemical free energy calculations based on molecular dynamics simulations, with more submissions in that category than any other. But single conformation implicit solvent calculations, such as with Poisson-Boltzmann calculations or semi-empirical models such as AMSOL, continued to play a major role. As noted above, an ab initio quantum calculation combined in implicit solvent also looked interesting in this challenge. Multiple conformation implicit solvent methods (COSMO, FiSH)[15, 29, 12, 27] also continued to play a role, as did a hybrid solvent model based on data from molecular dynamics simulations. We also saw several simulations based on an MM-PB/SA approach. Several newer methods, including a solvent density functional theory approach, filled out the challenge.

Fig. 6.

SAMPL methodologies and computational costs. SAMPL submissions included a broad range of methodologies, as shown in (a). Many calculations used single-conformation implicit solvent methods, but this SAMPL there was a sudden surge of interest in alchemical molecular dynamics (MD) simulations in explicit solvent. Several well-established implicit solvent methods also use multiple conformations and comprised a significant number of submissions, as well, as did an approach with a hybrid solvent model based on data from explicit solvent simulations[17]. (b) shows a scatter plot of RMS error as a function of simulation time. Participants self-reported simulation times in one of various categories as shown on the horizontal axis.

It is difficult to declare any particular class of methods the “victor”. As noted above, the top three submissions by most metrics involved a wide range of methods. As a function of simulation time, the methods with the lowest computational cost actually appear best (Figure 6(b)), but this is primarily because there were only two methods in this bracket (149 and 561), both of this did quite well. At the opposite end in terms of speed are alchemical molecular dynamics simulations, but using these simulations alone was no sure predictor of success. Simulation details, including force field and protocol, seem to have mattered a great deal.

As noted above, we also ran two simple knowledge-based models for comparison purposes, IDs 014 and 015, which “predict” hydration free energies based assigning the value of the most similar compound in a database of knowns (ID 014) or an average of the three most similar compounds (ID 015). These were in the bottom half of submissions by every metric of typical error, and performed worst by Kendall tau. We found this encouraging, as it suggests that even the more empirical methods tested here are building in substantially more transferability than a naive approach to knowledge-based modeling. Still, RMS errors in the vicinity of 3 kcal/mol were possible with this crude approach.

4.4 Significance testing

As noted above, we used Student's paired t-test on the error of different submissions to examine whether differences between methods were statistically significant. We find that, given the relatively small size of the set and the nearly comparable accuracy of many submissions, that many differences are in fact not statistically significant. Consider, for example, the best submission by ranked AUE, submission 145, with an AUE of 0.87 ± 0.13 kcal/mol. Comparing this to other submissions via the t-test with a significance threshold of p = 0.01, we find that only submissions 138, 015, 566, 544, 545, 014, 565, 153, 562, 548, 152, 569, 570, and 137 (ordered by significance, from least to most) yield significantly different predictions. This represents just 14 submissions out of the 44 full submissions examined here, and attests partially to the fact that the vast majority of submissions did quite well and yielded predictions tightly clustered around the true values. If we adjusted the threshold to p = 0.05, another four submissions would be considered significantly different, but still more than half of the total submissions are not significantly different than 145 by this analysis.

We also used the t-test to examine how many methods yielded predictions substantially different from our similarity-based control models, 014 and 015. Here, we found that some 16 submissions were significantly distinct from 014 (submissions 561, 169, 166, 567, 181, 005, 572, 145, 180, 575, 568, 573, 153, 152, 569, and 570) at p = 0.01, and 16 from submission 015 (169, 166, 005, 181, 567, 145, 572, 180, 575, 568, 573, 153, 152, 569, and 570). Thus, while these control models were certainly not top performers, they were also not particularly easy to beat in a statistically significant way, partly because their typical errors are not that large. This probably stems from the substantial size of the database they draw from.

On the whole, we believe these results are encouraging and indicate that a range of methods are converging on fairly high accuracy hydration free energy calculations, and are able to outperform a simple knowledge-based model in a statistically significant way.

4.5 Outlook for method evaluation and error estimation

Overall, we find that relatively little work seems to have gone into error estimation, but we believe this is extremely important, since a method which can predict when it will succeed and fail will be of much more practical value than one which cannot. Thus error estimation is, we believe, an important goal for computational methods. In this SAMPL, most participants estimated a constant error across all compounds for a given method/submission. So, while some participants were better than others at giving reasonable error estimates, error estimates had very little predictive power. As noted in the analysis section, for example, submissions which have superficially similar accuracies may actually have quite different performance when judged by metrics which reflect their ability to estimate likely errors.

We believe more work is needed in this area on both our metrics and from the standpoint of prediction methods. We still need error metrics which can penalize predictions which are precise but wrong more than those which are imprecise and wrong, and reward those which are precise and correct more than those which are imprecise and correct. While KL divergence has some of the right properties, it is unbounded in the case of profound disagreement with experiment. This is undesirable both from the standpoint of computing averages, and also because a more realistic metric would reflect the experimental reality that once a computational prediction is sufficiently bad, it becomes effectively useless and, in a discovery setting, would need to be tested experimentally to be of any value. We are not yet aware of a metric which has all the necessary properties in this regard.

At the same time, submitters and methods need to do a better job estimating error or model uncertainty. To a first approximation, one could simply compare compounds being predicted to a library of past predictions, and base error/uncertainty estimates on performance on similar compounds in the past. Compounds containing new chemical functionality not studied previously could be assigned substantially less confidence. As far as we are aware, such an experience-based approach has not yet been applied in SAMPL to help estimate uncertainty.

5 Conclusions

For the SAMPL4 hydration challenge, a remarkably broad range of methods were employed, and several very disparate methods performed remarkably well. Indeed, a substantial number of submissions typically performed within error of the top methods, making it difficult to declare clear winners and losers. One overall sense at the SAMPL4 meeting was that this was actually a plus – many methods are apparently converging on robust, predictive protocols with RMS errors under 1.5 kcal/mol. This is encouraging, and hopefully with further work we can begin to see similar levels of accuracy in more challenging problems which comprise the other components of SAMPL – in this case, host-guest binding and protein-ligand binding.

At the same time, we believe much work still needs to be done on how best to evaluate methods, and in particular we would like to see more emphasis from predictors on providing realistic error estimates. And better metrics to simultaneously evaluate prediction accuracy and confidence are needed.

Fig. 2.

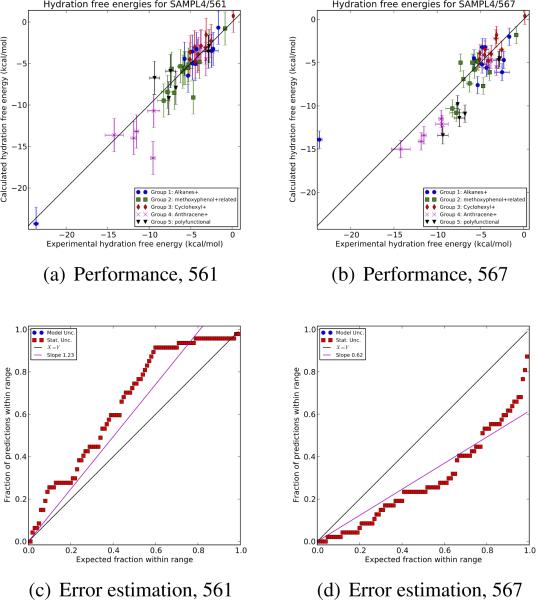
Overall performance and error estimation performance for submissions ID 561 and 567. The top plots show the overall performance at prediction hydration free energies for two representative submissions. Superficially, performance looks similar. However, in the top right panel, one compound has an extremely large error, and far more compounds are not within the predicted uncertainty of the experimental value. In other words, submission ID 567 underestimated uncertainties. This is supported by examining Q-Q plots (bottom) looking at the fraction of experimental values falling within a given range of the predicted value versus the expected fraction. The black line shows x = y, expected if uncertainty estimates are on average correct, and purple is the best-fit line with intercept 0; we call the slope of this line the error slope. Overall, submission 561 appears to overestimate uncertainties (slope 1.23 > 1) while submission 567 substantially underestimates uncertainties (slope 0.62 < 1).