The SAMPL4 hydration challenge: Evaluation of partial charge sets with explicit-water molecular dynamics simulations

Abstract

We used blind predictions of the 47 hydration free energies in the SAMPL4 challenge to test multiple partial charges models in the context of explicit solvent free energy simulations with the GAFF force field. One of the partial charge models, IPolQ-Mod, is a fast continuum solvent-based implementation of the IPolQ approach. The AM1-BCC, RESP and IpolQ-Mod approaches all perform reasonably well (R² > 0.8), while Vcharge, though faster, gives less accurate results (R² of 0.5). The AM1-BCC results are more accurate than those of RESP for tertiary amines and nitrates, but the overall difference in accuracy between these methods is not statistically significant. Interestingly, the IPolQ-Mod method is found to yield partial charges in very close agreement with RESP. This observation suggests that the success of RESP may be attributed to its fortuitously approximating the arguably more rigorous IPolQ approach.

Introduction

Water plays a ubiquitous role in biomolecular processes, including intermolecular recognition, protein folding, and enzymatic reaction kinetics, through its influence on intramolecular and intermolecular interactions [1]. Its influences include the hydrophobic effect [2, 3], electrostatic screening [4], and the formation of bridging hydrogen bonds [5]. It is therefore essential that computational models of protein-ligand binding and protein conformational dynamics accurately represent the effects of the aqueous environment [6]. However, any computer model of liquid water necessarily makes simplifying approximations, so that the calculations can be tractable. One widely used approach focuses on the electrostatic aspects of hydration, treating water as a dielectric continuum (e.g. Poisson-Boltzmann [7–9] and Generalized Born [10–14]) or a collection of polarizable dipoles (Langevin Dipoles [15]); such models usually include one or more additional terms to account for non-electrostatic aspects of hydration, notably the hydrophobic effect. These methods are efficient and capture much of the physics of hydration, but, because they treat water as a continuum, they may lose accuracy in regions where water is highly structured, such as in protein binding sites [6]. The more demanding 3D-RISM method [16, 17] uses approximate closures to allow solution of the Ornstein-Zernike integral equation for atomistic water models (e.g., TIP3P [18]) in the presence of a solute treated by an empirical force field. This approach is computationally more demanding than the continuum electrostatic models, and provides a detailed representation of water structure. However, because of the approximations made, its results do not correspond to those of a rigorous Boltzmann distribution for the force field and water model that are used. For this, more time-consuming sampling methods, like Monte Carlo or molecular dynamics (MD), are required.

Even when such rigorous sampling methods are used, however, explicit treatments of water can still exhibit significant deviations from experiment [19], due to inaccuracies in the force field used to compute the interaction energies of the solute and water molecules. Some of these inaccuracies represent incomplete optimization of numerical parameters, such as partial atomic charges and van der Waals parameters [20]. Others, however, are inherent in the functional forms of the interaction potentials themselves. Indeed, multiple functional forms have been put forward for van der Waals forces [21] and for the explicit treatment of electronic polarizability [22, 23], but it is not yet clear which will prove best. Thus, there is still a need to test the accuracy of force fields through comparison with experiment.

Measured hydration free energies are widely used as a basis for testing and improving force fields [24], because they are relatively easy to compute with detailed atomistic simulations, and because they report directly on the accuracy of the force field. Accordingly, they have been part of the Statistical Assessment of the Modeling of Proteins and Ligands (SAMPL) blind prediction challenge from its inception [25–30]. Hydration free energies are also of interest in their own right, in relation to the aqueous solubility of drug-like molecules and broader applications like atmospheric and environmental chemistry [31–33].

Here, we use the SAMPL4 hydration challenge [29] as a basis for testing five force field parameter sets, all within the paradigm of a standard, non-polarizable force field. We focus primarily on the choice of atomic partial charges. First we examine the accuracy of the general AMBER force field (GAFF) [34] with partial charges generated by the restrained electrostatic potential (RESP) [35], AM1-BCC [36, 37], and VCharge [38] methods. These calculations provide a rather standard baseline for the accuracy of explicit-water MD simulations for calculating the hydration free energies of small drug-like molecules [19]. We then examine a possible force field improvement, based on physical reasoning which suggests that the optimal partial charges for a non-polarizable force field may be the average of partial charges optimized to replicate accurate gas phase and aqueous phase electrostatic potentials [39, 40]. This concept is the basis of the IPolQ method for assigning partial charges. Here we propose and test a simpler, modified version of the IPolQ approach, which is termed IPolQ-Mod. We also put the present results into the context of recent progress in the development of enhanced hydroxyl parameters for the GAFF force field [41]. Overall, the present study appears to provide clear signals regarding the accuracy of the various approaches tested.

Methods

Decoupling free energy calculations

Hydration free energies were computed through stepwise decoupling of the solute from the solvent [42]. The decoupling was carried out in two main stages: first, the electrostatic interactions between solute and water were decoupled in 10 steps with coupling parameter values of λ = [0.00, 0.10, 0.20, 0.30, 0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 1.00]. Then the van der Waals interactions between the solute and water were decoupled in 14 steps with coupling parameter values λ = [0.00, 0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.50, 0.60, 0.70, 0.80, 0.90, 1.00]. Note that, during the decoupling of the solute from the solvent, the interactions of solute with itself remained fully coupled and unaltered. Although we used simple linear interpolation for decoupling electrostatic interactions, we used soft-core interactions for decoupling the van der Waals interactions [43]; these are given by

$$L{J}_{sc}(r,\lambda )={\lambda }^{n}4\epsilon (\frac{1}{{[\alpha {(1-\lambda )}^m+{\left(\frac{r}{\sigma }\right)}^6]}^2}-\frac{1}{[\alpha {(1-\lambda )}^m+{(\frac{r}{\sigma })}^6]})$$

where r is the interatomic distance; ε and σ are the standard well-depth and van der Waals diameter, respectively; α, m, and n, are soft-core parameters, which were set to 0.5, 1, and 1 respectively. The soft-core Lennard-Jones model removes the singularity in the potential and forces at r = 0 as soon as the decoupling process begins (λ > 0), and thus avoids excessive interatomic solute-solvent forces which could otherwise lead to poor convergence as the solute is partly decoupled from the solvent [43]. The free-energy difference between successive decoupling steps was calculated using the Bennett Acceptance Ratio (BAR) method [44]. The error in the free energy of each λ window was determined by splitting the data into 5 blocks, and computing the standard deviation in free energy differences between blocks. The error in the integrated free energy change of decoupling the solute from water was calculated through propagation of errors, assuming that the errors in free energies of different λ windows are uncorrelated. The resulting hydration free energies were converged to within 0.1 kcal/mol in all cases.

Molecular dynamics protocol

The MD simulations and free energy calculations were performed using the GROMACS simulation package (v. 4.5.5) [45], using the following procedures. Each of the solute structures was first solvated with TIP3P [18] water in a 30Å cubic box. The system was energy minimized using the steepest-descent algorithm and equilibrated for 500 ps under constant number, pressure, and temperature (NPT) conditions. Temperature was maintained at 300K with the velocity rescaling method, with a time constant of 0.1 ps. An isotropic pressure of 1 bar was maintained using Berendsen's weak coupling method [46], with a time constant of 1.0 ps. Production runs were carried under NPT conditions for a simulation time of 5 ns for each λ window, and the first 500 ps was considered as equilibration for each window and excluded from free-energy analysis. A 2 fs integration time step with the leapfrog integration algorithm was used in all simulations. Periodic boundary conditions were applied in all three coordinate dimensions. The Particle-Mesh-Ewald (PME) method [47] was used for electrostatic interactions, with a direct space cutoff of 10 Å, and cubic interpolation (PME order = 4) for the calculation of long-range interactions in the reciprocal space, with a Fourier transform grid of 1.2 Å maximum. Lennard-Jones (LJ) interactions were cut off at 10 Å. The bond-lengths of water molecules were constrained to their equilibrium lengths using the SHAKE algorithm [48], allowing for the 2 fs time step.

Structures and force field parameters

The SAMPL4 hydration challenge initially comprised 52 compounds [29], but five were later excluded, due to errors in chemical names/structures or ambiguity in experimental data. Starting with the solute structures provided by the SAMPL4 organizers, we optimized the geometries using Hartree-Fock (HF) quantum mechanical (QM) method with the 6-31G* basis set, using the program Gaussian G09 (revision A.1). Force-field parameters were then generated using the geometry-optimized structures. Bond, angle, torsion and van der Waals parameters were assigned according to the General AMBER Force Field (GAFF) [34], using the Antechamber program [49] in AmberTools13 software, with partial charges assigned using different methods, as described below. The topology and coordinate files generated in AMBER format (.inpcrd and .prmtop) were converted to GROMACS format using the amb2gmx.pl Perl script, downloadable from http://folding.cnsm.csulb.edu/ffamber-tools.php.

Assignment of partial atomic charges

Four different methods were used to calculate the atomic partial charges: 1) Restrained electrostatic potential (RESP) charges calculated using the Merz-Kollman scheme [35], as implemented in the program Antechamber [49] of AmberTools13, with electrostatic potentials calculated at the HF/6-31G* level of QM theory, using Gaussian G09. 2) AM1-BCC semiempirical QM charges with bond charge corrections, as implemented in Antechamber [36, 37]. 3) VCharge (VeraChem, Inc.) [38], which assigns charges based on the electronegativity equalization principle, with parameters adjusted to reproduce electrostatic potentials at the HF/6-31G* level. 4) IPolQ-Mod, a method inspired by the IPolQ approach [39], in which we determined solute partial charges as the average of gas-phase and solution-phase RESP charges calculated at the MP2/aug-cc-pVDZ level of QM theory. The solution-phase RESP charges were determined using the Polarizable Continuum Model (PCM) [50] for solvent, with a dielectric constant of 80.0 (i.e. water), and UFF cavity radii scaled by 1.1 for building the van der Waals molecular surface. The QM calculations were performed with Gaussian G09.

Results and Discussion

Comparison of partial charge models

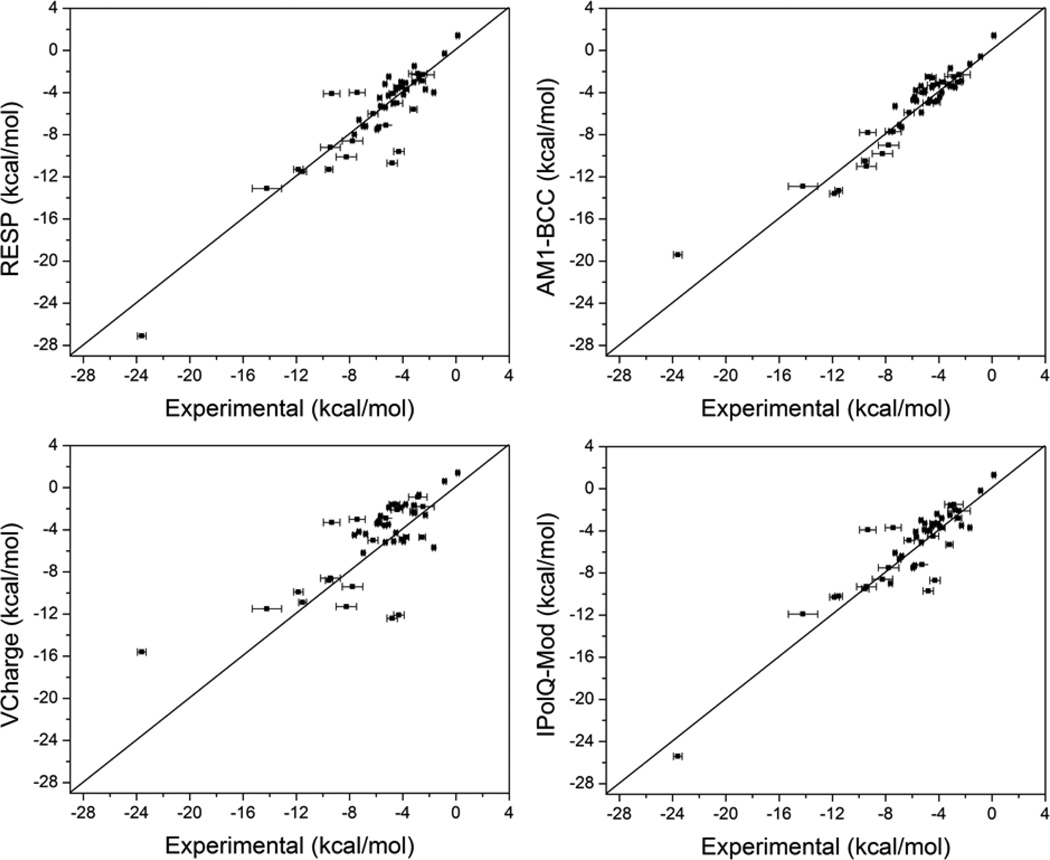
Figure 1 compares computed hydration free energies to experimental free energies for the 47 compounds in the SAMPL4 challenge set. The calculated hydration free energies of the individual molecules and the respective error statistics are summarized in Table 1. Hydration free energies computed using RESP, AM1-BCC, and IPolQ-Mod partial charges had near chemical accuracy (1 kcal/mol), with mean errors in the 1.0 – 1.4 kcal/mol range and root-mean squared (RMS) errors in the 1.3 - 1.9 kcal/mol range, which is similar to that previously observed in a retrospective study comparing different partial charge models [24, 51]. The correlation coefficients (R²) for these methods are greater than 0.8, which is also comparable to that reported in previous studies [24, 51, 52, 19]. Furthermore, these methods performed well at rank-ordering the compounds, with Kendall's tau between 0.6 and 0.8. Interestingly, despite the theoretical basis for the IPolQ-Mod method, the hydration free energies calculated using this method did not result in significant improvement over the standard RESP method. These results are discussed in more detail below. Even though AM1-BCC may seem to have performed slightly better than RESP and IPolQ-Mod, based on the error statistics reported in Table 1, the differences in the errors are statistically insignificant (p-value > 0.05) based on a paired Student's t-test. Thus, RESP, AM1-BCC, and IPolQ-Mod performed similarly in predicting hydration free energies. It is worth noting that the AM1-BCC partial charge calculation is computationally much less expensive than RESP or IPolQ-Mod. The VCharge partial charge method, which is based on the electronegativity equalization principle, resulted in hydration free energies with a mean error of 2.3 kcal/mol and an RMS error of 3.0 kcal/mol, greater than the other partial charge methods. Furthermore, the lower correlation coefficient of 0.5 and a Kendall's tau of 0.5, indicates that the errors are random rather than systematic. The difference in errors between VCharge and other partial charge methods was found to be statistically significant (p-value < 0.05) based on paired Student's t-test.

Figure 1.

Experimental vs. computed hydration free energies using different partial charge methods: RESP, AM1-BCC, VCharge, and IPolQ-Mod.

Table 1.

Experimental and computed hydration free energies (kcal/mol) of compounds in SAMPL4 hydration challenge set, for different partial charge sets coupled with GAFF.

ID	Exp.	RESP	IPolQ- Mod	AM1-BCC	Vcharge	AM1-BCC*
01	−23.6 ± 0.3	−27.1	−25.4	−19.4	−15.6	−18.6	(−22.3)
02	−2.5 ± 0.9	−2.3	−2.1	−2.3	−1.8	−2.6
03	−4.8 ± 0.3	−4.1	−4	−2.5	−1.6	−2.6	(−4.2)
04	−4.5 ± 0.2	−3.5	−3.3	−2.6	−1.6	−2.5	(−4.2)
05	−5.3 ± 0.1	−3.2	−3	−3.4	−3.6	−3.5
06	−5.3 ± 0.2	−7.1	−7.2	−4	−2.9	−4.1	(−5.2)
09	−8.2 ± 0.8	−10.1	−8.6	−9.8	−11.3	−9.9	(−11.4)
10	−6.2 ± 0.4	−6	−4.9	−5.9	−5.0	−6.1	(−7.6)
11	−7.8 ± 0.8	−8.6	−7.5	−9	−9.4	−9.2	(−10.6)
12	−3.8 ± 0.2	−3.7	−3.7	−3	−4.7	−3.3
13	−4.4 ± 0.4	−5	−4.5	−3.3	−2.1	−3.4	(−5.1)
14	−4.1 ± 0.2	−3.5	−3.3	−3.2	−4.9	−3.6
15	−4.5 ± 0.1	−3.7	−3.6	−3.5	−4.3	−3.8
16	−3.2 ± 0.3	−5.6	−5.3	−3.2	−2.3	−3.4	(−5.3)
17	−2.5 ± 0.3	−2.9	−2.8	−3	−4.7	−3.4
19	−3.8 ± 0.1	−3.1	−2.8	−4	−1.6	−4.4
20	−2.8 ± 0.1	−2.6	−2	−3.5	−0.7	−3.9
21	−7.6 ± 0.1	−8	−9	−7.7	−4.5	−7.9
22	−6.8 ± 0.1	−7.2	−6.4	−7.3	−4.4	−7.7
23	−9.3 ± 0.6	−4.1	−3.9	−7.8	−3.3	−8.2
24	−7.4 ± 0.6	−4	−3.7	−7.7	−3.0	−8.3
25	−5.7 ± 0.2	−4.5	−4.1	−3.8	−3.4	−3.8	(−5.2)
26	−5.3 ± 0.1	−5.4	−5.1	−5.9	−5.2	−6.0
27	−4.8 ± 0.4	−10.7	−9.7	−5	−12.4	−5.5
28	−4.3 ± 0.4	−9.6	−8.7	−4.9	−12.1	−5.4
29	−1.7 ± 0.1	−4	−3.7	−1.3	−5.7	−1.6
30	−2.3 ± 0.1	−3.7	−3.5	−2.9	−2.6	−3.2
32	−7.3 ± 0.1	−6.6	−6.1	−5.3	−4.2	−5.3	(−6.9)
33	−7.0 ± 0.1	−7.2	−6.7	−7.1	−6.2	−7.1	(−8.9)
34	−5.8 ± 0.1	−7.3	−7.3	−4.4	−3.2	−4.5	(−5.6)
35	−4.7 ± 0.1	−5	−4	−4.7	−5.1	−4.9	(−5.0)
36	−5.7 ± 0.1	−5.3	−4.6	−4.8	−2.7	−4.7	(−6.3)
37	−5.9 ± 0.1	−7.5	−7.5	−4.7	−3.4	−4.6	(−5.8)
38	−3.9 ± 0.1	−4.2	−3.6	−4.4	−5.1	−4.6
39	−0.9 ± 0.1	−0.3	−0.2	−0.6	0.6	−0.8
41	−5.1 ± 0.1	−2.5	−3.3	−3.8	−1.9	−3.9
42	−3.1 ± 0.1	−1.5	−1.6	−1.7	−1.7	−1.7
43	0.1 ± 0.1	1.4	1.3	1.4	1.4	1.1
44	−5.1 ± 0.1	−4.3	−3.9	−4	−3.5	−4.2
45	−11.5 ± 0.3	−11.5	−10.2	−13.3	−10.9	−13.7
46	−9.4 ± 0.7	−9.2	−9.3	−11	−8.6	−11.6
47	−14.2 ± 1.1	−13.1	−11.9	−12.9	−11.5	−13.3	(−14.7)
48	−11.9 ± 0.4	−11.3	−10.3	−13.6	−9.9	−14.2
49	−3.2 ± 0.1	−3	−2.5	−3.4	−2.4	−4.0
50	−4.1 ± 0.1	−3	−2.4	−4.8	−1.9	−5.3
51	−9.5 ± 0.3	−11.3	−9.5	−10.5	−8.8	−11.2	(−11.3)
52	−2.9 ± 0.7	−2.2	−1.5	−2.5	−0.9	−2.8
MAE		−0.1	0.4	0.4	1.0	0.1
MUE		1.3	1.4	1.0	2.3	1.1
RMSE		1.9	1.8	1.3	3.0	1.4
R2		0.82	0.82	0.90	0.53	0.87
Kendall's τ		0.64	0.64	0.77	0.47	0.73

^*Two sets of predictions from another SAMPL4 participant: one using the standard GAFF with AM1-BCC charges, and the other (shown in parenthesis) with modified GAFF AM1-BCC parameters for the hydroxyl group [41]. The statistical uncertainty of the computed hydration free energies is less than 0.1 kcal/mol, in all cases.

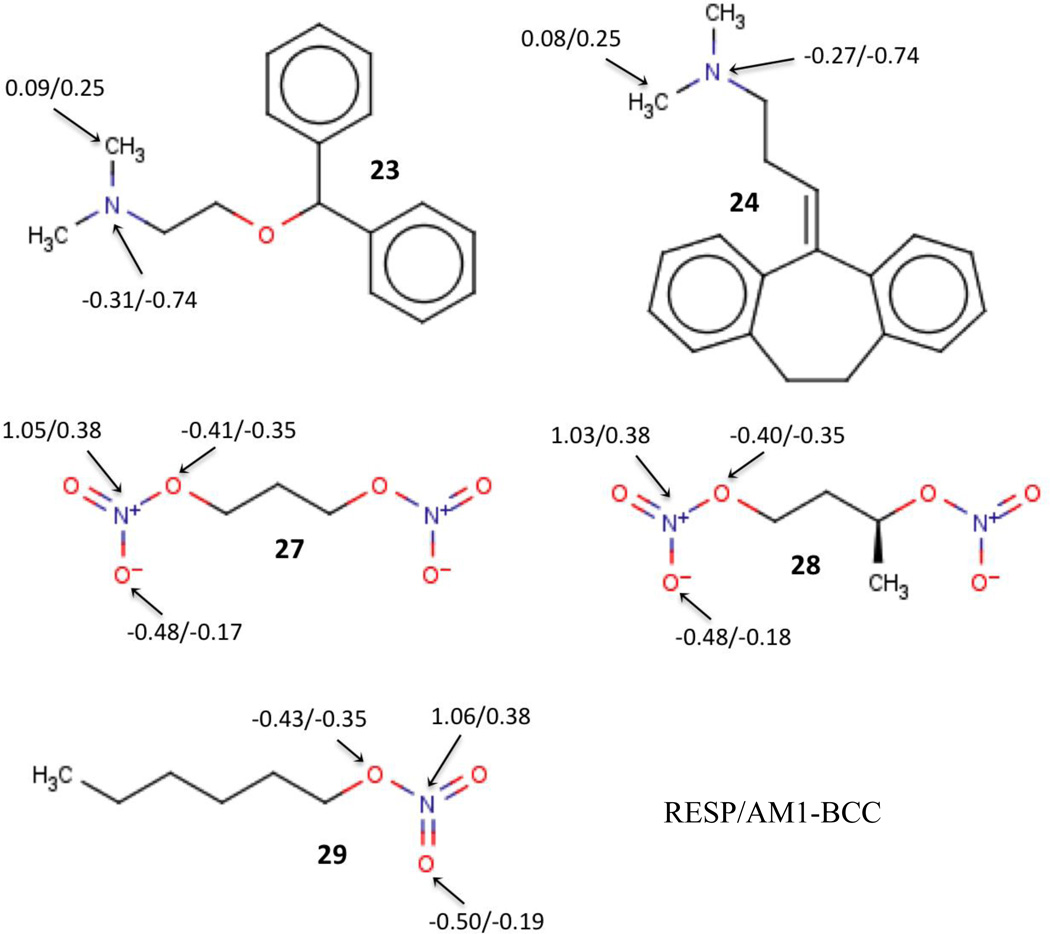
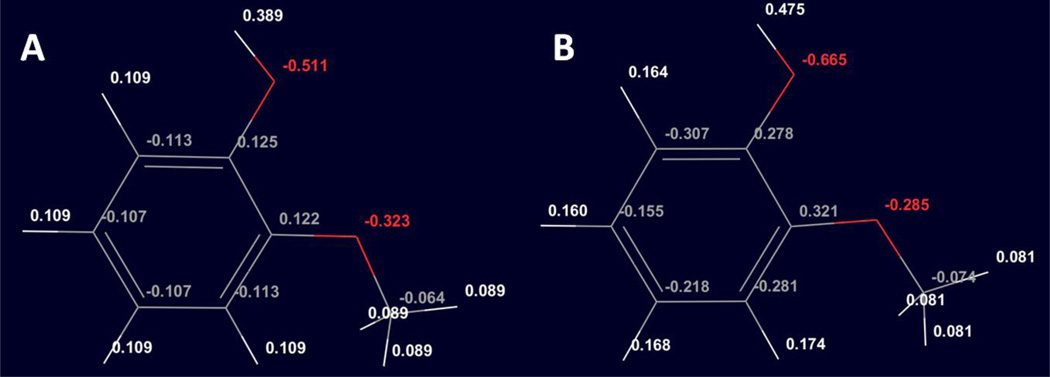
The RESP calculations yielded relatively large errors, > 3.2 kcal/mol, for compounds 23, 24, 27, 28, and 29 (Figure 2). These include either a tertiary amine or a nitrate group. Interestingly, the AM1-BCC partial charge model performed better for these compounds (Table 1), and the partial charges that AM1-BCC assigns to these compounds are indeed significantly different from the RESP charges (Figure 2). Even though the AM1-BCC method is in general parameterized to reproduce RESP-like charges, certain empirical adjustments were made to the BCC rules in AM1-BCC method based on experimental solvation free energies [37]. Specifically, the BCC rules were adjusted to reproduce solvation free energies of a series of amines and compounds with nitro-containing functional groups, and this presumably explains the overall slightly better performance of AM1-BCC over other partial charge methods for the SAMPL4 challenge set. Here, for both the tertiary amines and the nitrates, AM1-BCC assigns a more negative (or less positive) charge to the nitrogen atom. It is not clear, at least to the present authors, why AM1-BCC charges, which presumably do a poorer job of reproducing the QM electrostatic potential than RESP charges, should do a better job of reproducing hydration free energies for some compounds.

Figure 2.

SAMPL4 compounds (23, 24, 27, 28, and 29) that showed significant difference in hydration free energies between RESP and AM1-BCC partial charge sets. The partial charges of selected atoms are shown in the figure as RESP/AM1-BCC.

It is also worth noting that, although partial charges are strong determinants of the computed hydration free energy, van der Waals parameters are also important, partly because of their intrinsic energy contributions, and partly because they influence electrostatic interactions, by controlling the approach of water molecules to partially charged solute atoms. For flexible molecules, bonded interactions (i.e. bond, angle, and torsion) can also play an important role, by determining the solute's conformational distribution. As a consequence, the performance of a particular partial charge set in combination with GAFF Lennard-Jones and bonded parameters may not represent evidence for its general validity. In particular, the accuracy of the partial charge sets described here should be considered only within the context of the GAFF force field. In general, different generalized force fields use different strategies for assigning partial charges, and their non-electrostatic parameters, such as for van der Waals and bonded terms, are developed to be compatible with their selected partial charge model. For example, the GAFF force field is developed using RESP method for assigning partial charges [34]. Furthermore, AM1-BCC with GAFF is parameterized to reproduce RESP charges, and contains adjustments based on experimental hydration free energies [36, 37]. Therefore, the partial charge sets tested here may not show the same relative accuracy when used in conjunction with other force fields such as OPLS-AA [53] and CHARMM [54, 55].

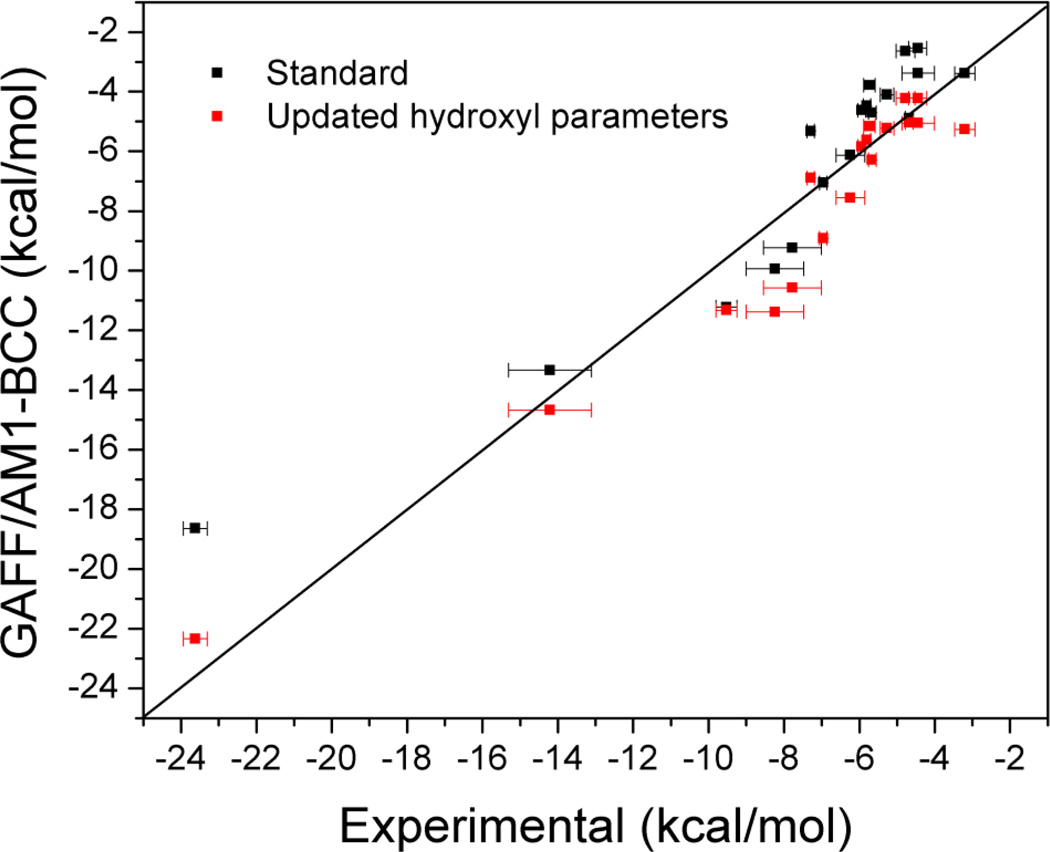
It is also of interest to put the present results into the context of another SAMPL4 participant's (David Mobley; personal communication) predictions for the same set of molecules, which also relied on the GAFF force field with AM1-BCC partial charges [41], but used a modified set of force field parameters for hydroxyl group atoms. In particular, the Lennard-Jones parameters, σ and ε, of the hydroxyl oxygen atom were modified from 3.07 Å and 0.21 kcal/mol, to 3.22 Å and 0.20 kcal/mol respectively; the partial charges of the hydroxyl oxygen and hydrogen atoms, as well as the carbon atom bonded to the hydroxyl oxygen, were scaled by a factor of 1.21; and the charge neutrality of the molecule was restored by adjusting the partial charge of the atoms bonded to the carbon atom. As shown in Figure 3 and Table 1, the updated hydroxyl parameters lead to an overall improvement in RMS error from 1.4 kcal/mol for standard GAFF/AM1-BCC to 1.2 kcal/mol. This improvement is statistically significant (p-value < 0.05) based on a paired Student's t-test. It is encouraging that the new hydroxyl parameters, which were derived based on neat liquid properties, are transferable to hydration free energies. Because Mobley's group used a somewhat different simulation protocol and included calculations for all SAMPL4 compounds with standard GAFF/AM1-BCC parameters, we also have an opportunity to validate the numerical reliability of our free energy simulations by comparing with the their calculations. Reassuringly, as shown in Table 1, the two sets of calculations agree well, with an RMSE of 0.3 kcal/mol.

Figure 3.

Comparison of experimental hydration free energies to those calculated using GAFF AM1-BCC force field with standard and updated hydroxyl group parameters, for hydroxyl-containing compounds in SAMPL4.

Comparison of AM1-BCC and VCharge with RESP

Whereas the RESP method adjusts partial charges directly to fit ab initio QM electrostatic potentials, the AM1-BCC and VCharge methods are faster because they do not require carrying out any ab initio quantum calculations. Instead, they use parameters which have been adjusted so that the partial charges they generate approach the results of direct fits to ab initio quantum calculations. Thus, AM1-BCC applies fitted bond-charge correction (BCC) rules to the population charges obtained from AM1 semiempirical QM calculation; and VCharge is an electronegativity equalization method with parameters adjusted to optimize agreement with QM electrostatic potentials. (Note, however, that some BCC rules were further adjusted to better replicate experimental hydration free energies.) It is thus of interest to compare the two faster approximations directly with the RESP method they emulate.

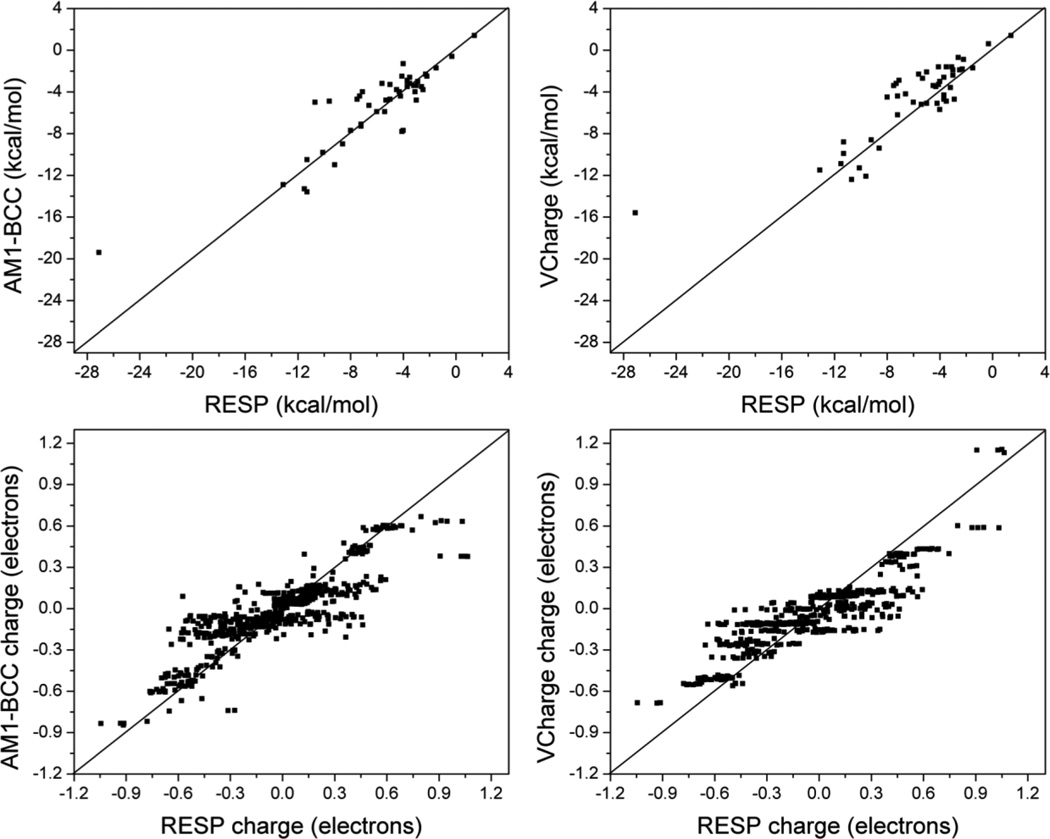
We therefore compared the hydration free energies computed for the SAMPL4 molecules with the AM1-BCC and VCharge models to those calculated with RESP charges (Figure 4); all other parameters are from GAFF. Hydration free energies calculated using AM1-BCC and VCharge charges correlate strongly, R² = 0.80 and 0.76 respectively, with those calculated using RESP charges, with a mean deviation of 1.4 and 1.8 kcal/mol, respectively. Upon detailed examination, we found that the deviation between AM1-BCC and RESP hydration free energies was particularly high for those compounds containing either a tertiary amine or a nitrate group, due to the empirically adjusted BCC rules for these classes of compounds, as noted above (Figure 2). On the other hand, the deviation between VCharge and RESP hydration free energies was largely due to compounds containing ortho-substituted phenol groups. RESP and VCharge charges for a representative molecule are shown Figure 5. It is not clear to us from the charge distributions, why this particular class of compounds with VCharge charges shows large errors against experimental hydration free energy. Direct comparison of AM1-BCC and VCharge partial charges with those from RESP indicates that both methods perform rather similarly in reproducing the partial charges (Figure 4), with a mean unsigned error of 0.1 electrons for both methods, and a correlation coefficient of 0.75 and 0.78 for AM1-BCC and VCharge methods, respectively. Overall, these results show that both AM1-BCC and VCharge methods exhibit a high degree of general validity, but fail to reproduce RESP-like charges for certain classes of compounds. VCharge is considerably faster than AM1-BCC and yields charges that agree at least as well with RESP, but, as noted above, yields less accurate hydration free energies.

Figure 4.

(Top) Comparison of hydration free energies calculated using AM1-BCC and VCharge partial charges to those computed using RESP partial charges. (Bottom) Comparison of AM1-BCC and VCharge partial charges to RESP partial charges.

Figure 5.

Comparison of VCharge (A) and RESP (B) charges for compound 37 in SAMPL4 challenge set.

Comparison of IPolQ-Mod and RESP

Hydration free energies based on IPolQ-Mod method performed as well as the RESP charges, in comparison to experiment (Table 1). This is non-trivial, since the IPolQ-Mod is not based on emulation of RESP charges, and it was not parameterized to replicate experimental hydration free energies. Note that GAFF is parameterized using RESP charges [34], and so in principle, RESP should give nearly optimal results when combined with GAFF. Since both agree well with experiment it is perhaps unsurprising that hydration free energies based on IPolQ-Mod and RESP charges agree well with each other, with a correlation coefficient (R²) of 0.82 and RMSE of 1.8 kcal/mol. More interesting is that IPolQ-Mod charges agree much more closely with RESP charges than do AM1-BCC or VCharge; compare Figure 6 (top) with Figure 4 (bottom panels): the mean signed deviation is only 0.02 electrons and the correlation coefficient of 0.99. It was by no means clear a priori that IPolQ-Mod charges, which are calculated as an average of the gas-phase and solution-phase charges at the higher MP2 level of QM theory, would virtually equal RESP charges based purely on gas-phase electrostatic potentials calculated at the lower HF level of QM theory.

Figure 6.

(top) Comparison of IPolQ-Mod to RESP partial charges. (bottom) Comparison of dipole moments of 504 small molecules calculated using HF/6-31G* RESP, MP2/6-31G* (gas), MP2/6-31G* (PCM), and MP2/6-31G* (IPolQ-Mod)

This agreement appears to bear on the success of RESP charges in condensed phase simulations. It has been suggested that the success of ESP and RESP-type partial charges based on relatively low-level gas-phase HF calculations may stem from the fact that such calculations overestimate gas-phase calculations to a degree that, fortuitously, is suitable for condensed phase calculations [35]. However, the physical basis for this convenient result has not been fully elucidated, and the IPolQ approach may offer some insight. IPolQ is motivated by a derivation suggesting that accurate solution-phase energies can be obtained by using partial charges halfway between partial charges that optimize agreement with ESPs from high level gas-phase and solute-phase quantum calculations [39, 40]. The logic is that condensed phase calculations with partial charges that underestimate the actual polarization in the condensed phase will implicitly account for the energy cost of polarizing the solute on transfer from vacuum to water [40, 39]. The success of our IPolQ-Mod partial charges, which are based on this concept, lends support to this analysis.

In addition, the agreement between RESP and IPolQ-Mod charges for the SAMPL4 hydration cases suggests that RESP charges fortuitously provide a level of polarization midway between that appropriate to the gas phase and aqueous phases. We examined the generality of this result by applying IPolQ-Mod to a larger set of small molecules (504) covering a range of chemical groups [19], and compared these gas/aqueous averaged dipole moments with those obtained from standard gas-phase RESP calculations at the HF/6-31G* level. As shown in Figure 6, the RESP dipole moments are, in fact, midway between gas-phase and aqueous-phase dipole moments obtained at the MP2 level, and linear regression of RESP versus IPolQ-Mod dipole moments yields a slope of 0.99. This suggests that the long-recognized success of the standard RESP procedure results from the fact that it provides a level of polarization midway between gas and aqueous phase, as called for by the IPolQ concept.

Conclusion

We used explicit-water free energy simulations to predict the hydration free energies of 47 compounds presented as part of the SAMPL4 challenge. We used the GAFF force-field, and evaluated the sensitivity of the results to atomic partial charges by testing three commonly used partial charge sets: RESP, AM1-BCC, and VCharge. The baseline RESP method performed well, yielding mean errors approaching chemical accuracy (commonly considered to be 1 kcal/mol). The AM1-BCC and VCharge methods, which are designed to emulate RESP charges at a significantly less computational cost, provided hydration free energies in reasonably good agreement with those calculated using RESP charge, with AM1-BCC provided higher accuracy than RESP for certain nitrogenous compounds, and Vcharge providing lower accuracy overall. We also tested a modified version of the IPolQ partial charge method that implicitly accounts for solute polarization upon solvation, and this provided a level of accuracy comparable to that of RESP. The fact that the IPolQ method is based on a defined physical rationale, and that its charges agree closely with those from RESP, may provide a theoretical basis for the success of the widely used RESP method.