Skip to main content
PMC home page
Acta Pharmacologica Sinica logoLink to Acta Pharmacologica Sinica
. 2013 Sep 23;34(11):1475–1483. doi: 10.1038/aps.2013.85

Energetic factors determining the binding of type I inhibitors to c-Met kinase: experimental studies and quantum mechanical calculations

Zhe Yu 1,2,#, Yu-chi Ma 1,#, Jing Ai 1, Dan-qi Chen 1, Dong-mei Zhao 2,*, Xin Wang 1, Yue-lei Chen 1, Mei-yu Geng 1, Bing Xiong 1,*, Mao-sheng Cheng 2, Jing-kang Shen 1,*
PMCID: PMC4006466  PMID: 24056705

Abstract

Aim:

To decipher the molecular interactions between c-Met and its type I inhibitors and to facilitate the design of novel c-Met inhibitors.

Methods:

Based on the prototype model inhibitor 1, four ligands with subtle differences in the fused aromatic rings were synthesized. Quantum chemistry was employed to calculate the binding free energy for each ligand. Symmetry-adapted perturbation theory (SAPT) was used to decompose the binding energy into several fundamental forces to elucidate the determinant factors.

Results:

Binding free energies calculated from quantum chemistry were correlated well with experimental data. SAPT calculations showed that the predominant driving force for binding was derived from a sandwich π–π interaction with Tyr-1230. Arg-1208 was the differentiating factor, interacting with the 6-position of the fused aromatic ring system through the backbone carbonyl with a force pattern similar to hydrogen bonding. Therefore, a hydrogen atom must be attached at the 6-position, and changing the carbon atom to nitrogen caused unfavorable electrostatic interactions.

Conclusion:

The theoretical studies have elucidated the determinant factors involved in the binding of type I inhibitors to c-Met.

Keywords: receptor tyrosine kinase, type I c-Met inhibitor, cancer, quantum chemistry, protein-ligand interaction, symmetry-adapted perturbation theory (SAPT)

Introduction

The receptor tyrosine kinase c-Met, discovered in 1984 by Vande Woude et al, is normally expressed in the epithelial cells of many organs during embryogenesis and in adulthood1. Through binding to its physiological ligand hepatocyte growth factor (HGF), c-Met induces several complex signaling pathways involved in cell proliferation, motility, migration, and survival2,3. Inappropriate c-Met activation, transcriptional overexpression, gene amplification, and activating mutations have been observed in virtually all types of solid tumors4,5. Overexpression or mutation of c-Met is also an important biomarker correlated with advanced disease state and poor prognosis6,7. These facts collectively justify emphasis on c-Met as an attractive target in human cancer therapeutics.

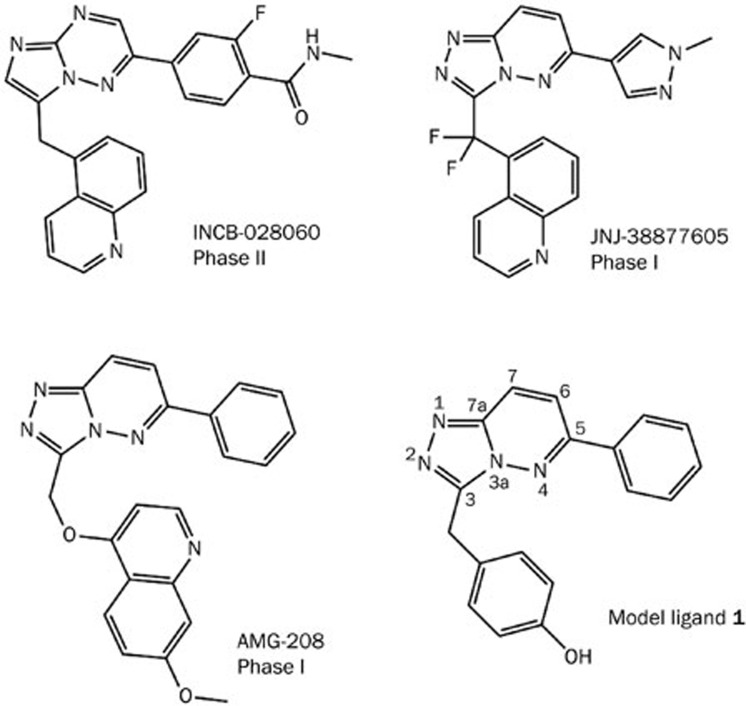
Several antibodies targeting HGF and numerous small molecules targeting the c-Met kinase catalytic domain have been identified and are currently in clinical trials1,5,8,9,10,11,12. Type I c-Met inhibitors, as shown in Figure 1, usually adopt “U-shaped” binding conformations and exhibit high selectivity toward c-Met. For example, INCB-028060 inhibits c-Met kinase activity with an average IC50 value of 0.13 nmol/L. In a selectivity profile against a panel of 57 human kinases, representing a structurally diverse cross-section of all known human kinases, this compound exhibited no more than 30% inhibition at 2 μmol/L13. Given that more than five hundred kinases are encoded in the human genome and that the majority of kinase inhibitors are ATP competitive, the identification of these c-Met type I inhibitors is a significant achievement. It is also thought that high specificity is crucial to the development of kinase inhibitors to minimize off-target effects. High target selectivity is thus expected to mitigate toxicity in subsequent medical applications.

Figure 1.

Figure 1

Open in a new tab

Representative type I inhibitors of c-Met kinase. The fused aromatic ring of model ligand 1 is numbered for reference.

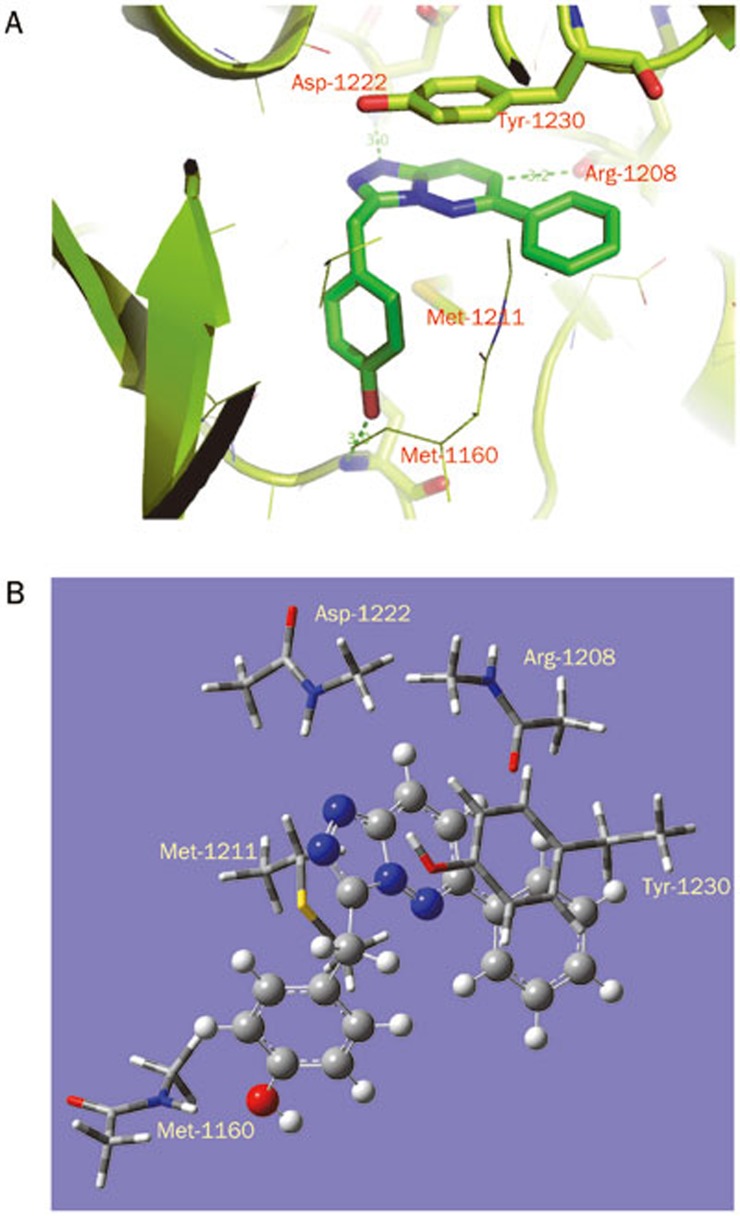
Analysis of three dimensional structures suggests that type I inhibitors adopt bent conformations and bind to the activated c-Met kinase. The co-crystal structure14 (Figure 2) shows the compound bound in the c-Met ATP binding site, which occurs at a deep groove formed by the N- and C-lobes of the kinase catalytic domain. The phenol moiety of the inhibitor interacts with the hinge of c-Met kinase, forming a hydrogen bond with the backbone carbonyl of Met-1160. The triazolopyridazine scaffold forms a typical π–π stacking interaction with Tyr-1230. Finally, one of the nitrogen atoms in triazole accepts a hydrogen bond from the backbone nitrogen of Asp-1222. These essential interactions between type I inhibitors and c-Met are considered prerequisites for binding and guide medicinal chemists in the design of novel c-Met inhibitors. Detailed investigations into the contributions of residues in c-Met ATP binding site will not only help to decipher the intermolecular forces behind kinase-inhibitor interactions but may also enable the design of novel compounds that bind to c-Met.

Figure 2.

Figure 2

Open in a new tab

(A) Illustration of the binding interactions of c-Met kinase with 1. Ligand 1 is shown in stick form together with key residues Arg-1208, Tyr-1230, Met-1211, and Asp-1222 in the binding site. The protein is shown in ribbon form. (B) The primary model used in quantum chemistry calculations. All analogs and derived models were built on the basis of this primary model.

In our current study, we sought to decompose the driving forces behind the interactions of type I inhibitors with c-Met. Based on the available crystal structure and straightforward synthesis, we selected ligand 1 as the reference compound. Three other analogs were also synthesized and assessed for c-Met inhibitory activity in an enzyme assay. We studied the binding free energy of these compounds with c-Met by adopting quantum chemistry calculations. The results showed that the calculated free energies correlated well with the experimental binding affinities of these compounds. Interestingly, although the dominant contribution comes from an aromatic stacking interaction with Tyr-1230, differential effects arise largely from the positioning of Arg-1208 at the edge of the ligand pyridazine ring. This finding may give medicinal chemists enhanced insight into the structure-activity relationships of type I c-Met inhibitors. Furthermore, we investigated the nature of several fundamental intermolecular interactions such as π–π, sulfur-π, and hydrogen bonding interactions15,16,17,18.

This study highlights the utility of quantum chemistry in calculating the free energy of a protein-ligand system and in elucidating the nature of typical protein-ligand interactions. These results may also facilitate the design of novel scaffolds as type I c-Met inhibitors.

Materials and methods

Preparation of model system

The initial coordinates were extracted from the high resolution crystal structure (PDB accession code 3CCN)14. As reported by Albrecht et al, ligand 1 is located in the ATP binding site of the c-Met kinase domain and makes direct contacts with Met-1160, Arg-1208, Met-1211, Asp-1222, and Tyr-1230 (all within 4 Å). Due to the large number of operations needed in the quantum chemistry calculation, we constructed a basic binding interaction model system (Model 1) by including only important residues close to the heterobicylic core of 1 (Arg-1208, Met-1211, Asp-1222, and Tyr-1230) and Met-1160 to constrain 1. As shown in Figure 2B, only the side chain atoms were retained for Met-1211 and Tyr-1230. For Met-1160, Arg-1208, and Asp-1222, only the interacting amide groups and bonded α carbon atoms were retained. To decompose the contribution of each residue, four derivative models were built by deleting one residue each from the group of Arg-1208, Tyr-1230, Met-1211, and Asp-1222; this process gave Model 1–1, Model 1–2, Model 1–3, and Model 1–4, respectively.

For the three analogs of 1, we modified Model 1 by mutating the atoms at certain positions (chemical structures are shown in Table 1) and adding or deleting hydrogen atoms accordingly to produce Model 2, Model 3 and Model 4. These models were further altered to generate variable binding models by deleting the interacting residues in the order described for Model 1. The resulting 20 protein-ligand models were subjected to QM calculations.

Table 1. The result of the c-Met enzymatic inhibition assay.

Compound Chemical structure Enzymatic activity (IC50 μmol/L)
Ligand 1 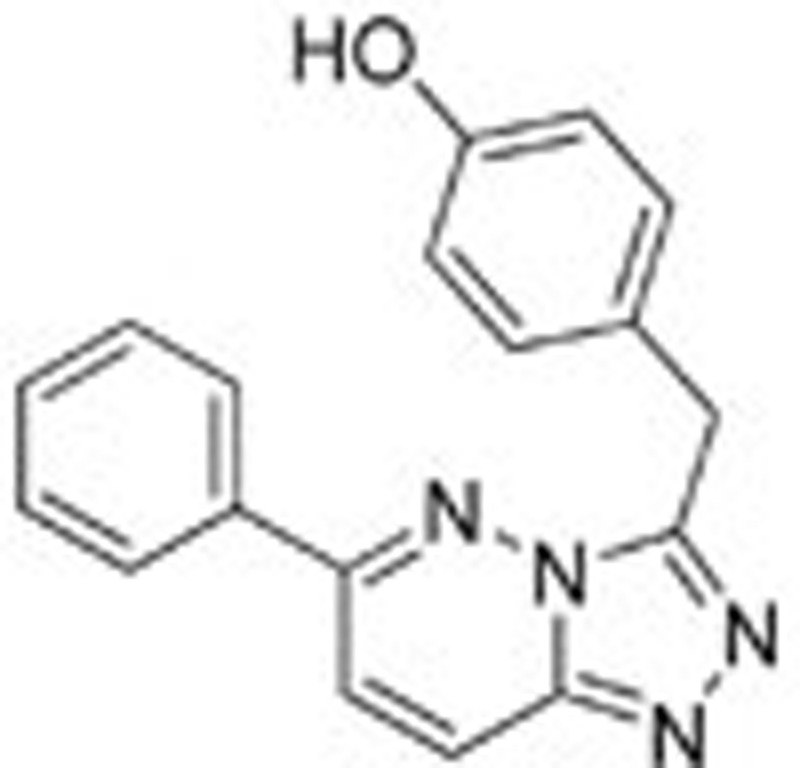graphic file with name aps201385i1.jpg 0.048±0.0005
Ligand 2 graphic file with name aps201385i1.jpg >100 000
Ligand 3 graphic file with name aps201385i1.jpg 0.57±0.14
Ligand 4 graphic file with name aps201385i1.jpg 1.52±0.56
Open in a new tab

Free energy calculations by QM method

Calculating the free energy of binding is a significant challenge in computational chemistry, even when utilizing the most accurate QM methods. To better reflect the energetic factors involved in the interactions of type I inhibitors with c-Met, we adapted the thermodynamic cycle method to calculate the difference in binding free energy between two ligands (as in Eq 1). The ΔΔG between two binding interactions could be calculated with Eq 2. To calculate ΔGRL_S, the free energy difference between two complexes, we can use the thermodynamic cycle shown in Eq 3. Because the protein-ligand interactions occur in the interior of the protein and these ligands are very similar in shape, we can assume that ΔΔGs_RL, the difference in solvation free energy between the two complexes, is equal to zero. Thus, there is almost no difference in solvent structure between the solvent molecules around these two complexes. We can also assume that the configurational entropy difference ΔSRL_g is equal to zero because each ligand has three rotatable bonds and all of the ligands have similar shapes. Therefore, ΔGRL_S can be calculated with Eq 4. Similarly, the free energy difference between two solvated ligands can be calculated using the thermodynamic cycle shown in Eq 5. We can assume that the ligand configurational entropies are identical, as was assumed in calculating the free energy difference between two solvated complexes. The solvation free energies of the two ligands can no longer be considered equal, as the ligands are now in solvent, and electrostatic properties can influence solvent organization around a ligand. The term ΔΔGs_L was therefore calculated explicitly.

graphic file with name aps201385e1.jpg
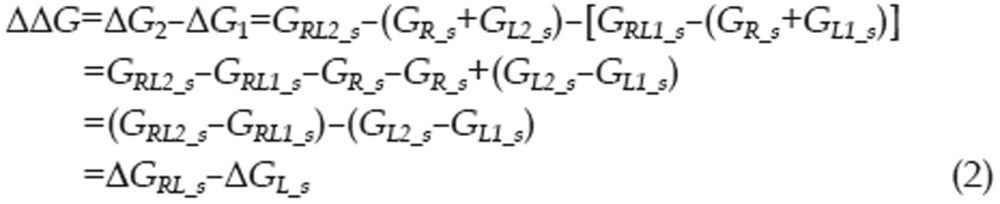graphic file with name aps201385e2.jpg
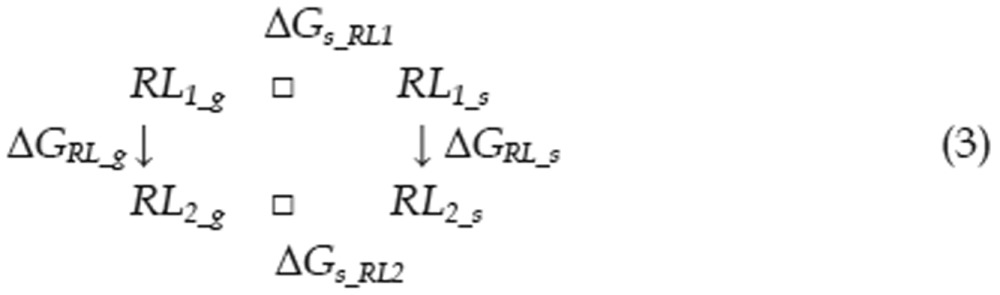graphic file with name aps201385e3.jpg
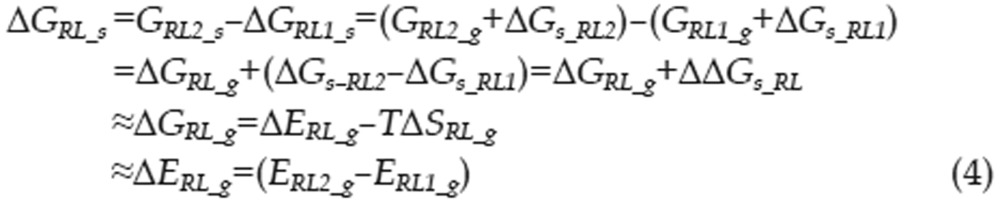graphic file with name aps201385e4.jpg
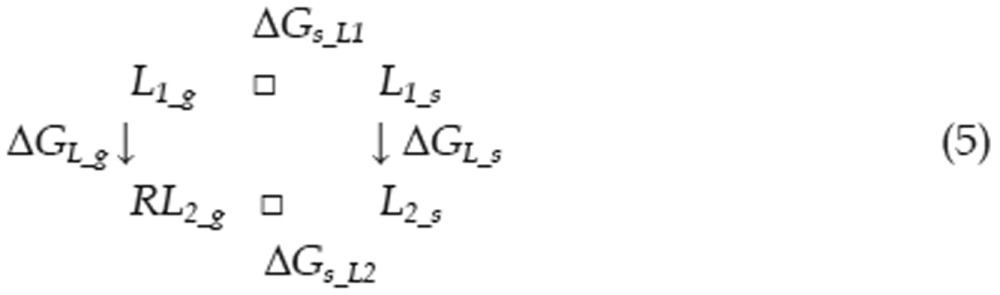graphic file with name aps201385e5.jpg
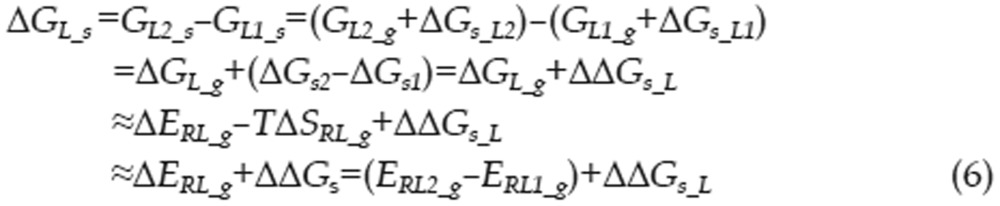graphic file with name aps201385e6.jpg

The ligands and complex models were first subjected to geometry optimization. We optimized ligand geometry in the gas phase by adapting a Gaussian program with the hybrid density functional M06-2X at the basis set 6–31+G(d) level. As devised by Zhao and Truhlar, this DFT-D method incorporates the empirical dispersion interaction model and was shown to be suitable for noncovalent interaction studies when combined with this basis set19,20,21. For complex models, quantum chemistry calculation would create demands on computational power beyond our capabilities. We thus utilized PM7, one of the most accurate semi-empirical methods implemented in the MOPAC2012 program22, to optimize complex geometries in the models by fixing the position of each heavy atom in the protein residues. The Gaussian program was then used to calculate the single point gas phase energy for the optimized complex, employing the hybrid density functional M06-2X at the basis set 6–31+G(d) level. It was necessary to account for the solvation free energies of ligands in aqueous media to determine the free energy differences between ligand pairs. Previous studies from Truhlar et al suggested that SMD, a continuum mean-field solvent model, could be used to treat the solute's electronic structure and its self-consistent field polarization by the solvent23. Combining this method with M06-2X at basis set 6–31+G(d), the predicted solvation free energy was found to have a mean unsigned error of only 1.9 kcal/mol. The SMD solvent model was then applied to calculate solvation free energies for the optimized ligands. Finally, differences in the free energy of binding were calculated for ligand pairs using Eq 3.

The symmetry-adapted perturbation theory (SAPT), implemented in the PSI4 program, was adopted for further analysis of the electrostatic, exchange, induction and dispersion forces involved in binding interactions24,25,26,27,28,29. After comparing the performance of many basis sets, the truncated aug-cc-PVDZ basis set was found to be accurate enough to give meaningful energy decompositions. The mean unsigned error of this basis set was approximately 0.47 kcal/mol relative to the high level CCSD(T) CBS Limit interaction energies. The interactions of four ligands with Arg-1208, Tyr-1230, Met-1211, and Asp-1222 were analyzed using this method to obtain detailed information about the energetic contributions of these residues to type I inhibitor binding.

Results and discussion

Probing the noncovalent interactions that determine the specificity of type I inhibitors of c-Met kinase is of primary importance for understanding the structure-activity relationships of such drugs. Scrutinizing the binding site of c-Met kinase in the presence of 1 has revealed several fundamental interactions that are involved in ligand binding. The backbone amide group of Asp-1222 donates a hydrogen bond to the ligand nitrogen. An aromatic residue, Tyr-1230, sits parallel to ligand aromatic rings and is typically thought to form face-to-face π–π interactions. The sulfur atom of Met-1211 lies only approximately 3.5 Å below the aromatic ring of 1. This type of interaction is commonly referred to as a sulfur-π interaction. There is also a close interaction between the backbone carbonyl of Arg-1208 and the aromatic C–H of 1. Among these interactions, only hydrogen bonding and π–π interactions are recognized by medicinal chemists as dominant factors for the development of c-Met inhibitors. However, it can be argued that all neighboring protein residues play important roles in ligand binding interactions.

To study these binding interactions, we synthesized three other ligands by varying the nitrogen atoms in the original triazolopyridazine scaffold (chemical syntheses of the model compounds and the method for the enzymatic assay are provided in the supporting material). Biological assays revealed that these compounds have very different levels of activity against c-Met. Ligand 1 is the most active compound among these model inhibitors, with an IC50 value of approximately 48.1 nmol/L. Surprisingly, if a nitrogen atom is moved from the 4 position to the 6 position (numbering as indicated in Figure 1), activity against c-Met is completely abrogated. Ligand 3 shows moderate potency, with an IC50 value of approximately 570.5 nmol/L. Changing one of the nitrogen atoms to carbon (4) leads to an approximately threefold reduction in potency. Although biological assays show the importance of the aromatic ring scaffold, it is difficult to discern which interactions make significant contributions to binding. Alterations to the aromatic ring scaffold will affect the overall electron density of the π system and charge distributions at specific positions, compounding the differential interactions with key residues lining the c-Met binding site.

Ligand conformations

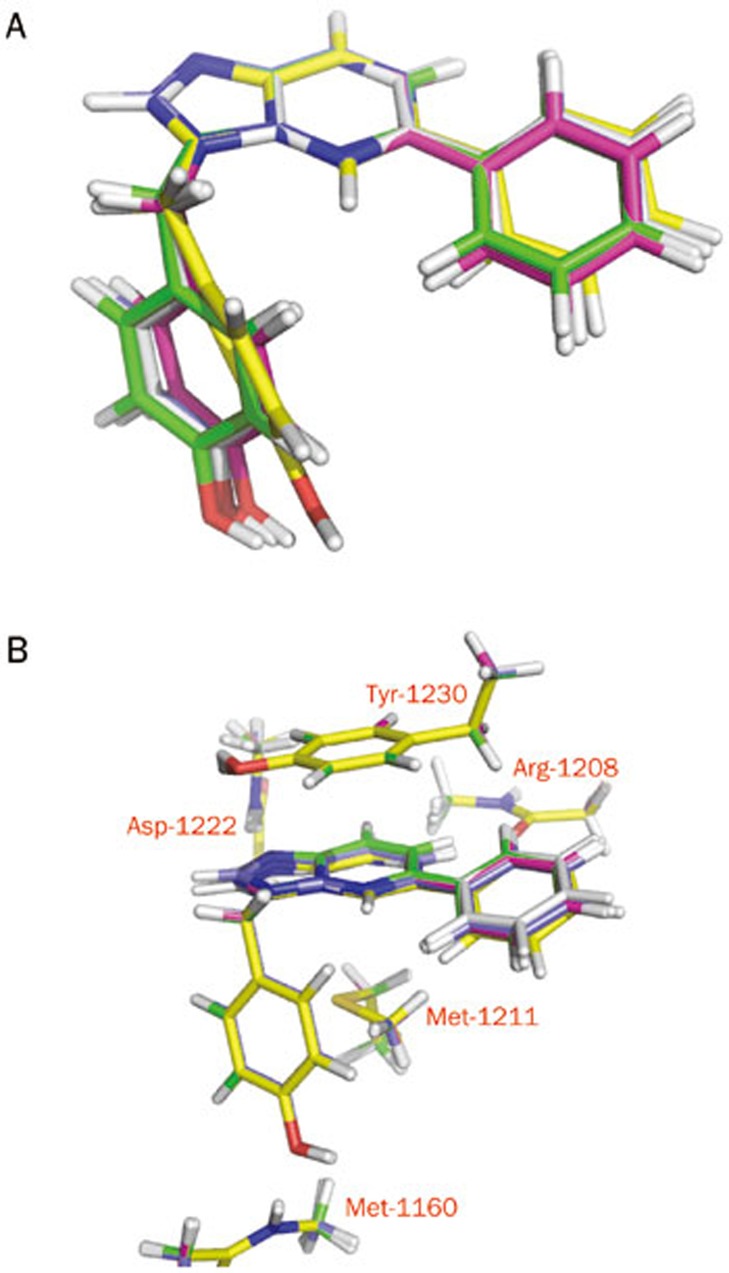
To investigate the detailed mechanism of binding, we constructed four ligands based on the co-crystal structure of ligand 1 with c-Met (PDB accession code 3CCN) and subjected them to quantum chemistry calculations. To calculate the energies of these four designed ligands, we initially mutated 1 to generate three new ligands. The four ligands were minimized using the M06-2X/6–31+G(d) method. As shown in Figure 3A, the minimized conformation of 1 is very similar to its conformation in the crystal structure, and the root mean squared deviation (RMSD) is only approximately 0.28 Å. Ligand 2 is structurally very similar to 1, as it features only a single atom change. The minimized conformation of 2 is quite different from the conformation of 1 in the crystal structure, with an RMSD value of approximately 1.2 Å. The other two ligands (3 and 4) show conformations very similar to that observed for 1, with RMSD values less than 0.8 Å. Close inspection of the conformations revealed the most visible difference to be rotation of the phenol and benzene groups attached to the scaffold. The crystal structure 3CCN shows that the N–N bonds in the fused 5-membered and 6-membered rings are both 1.2 Å. After quantum chemistry minimization, however, these bonds become slightly longer. The C–N bond lengths in the fused 6-membered rings are generally approximately 1.3 Å, while the C–C bond lengths are approximately 1.4 Å, with some variations observed in 1 and 2. These subtle differences in bond lengths cannot be expected from force field calculations and may affect charge distributions over the fused rings.

Figure 3.

Figure 3

Open in a new tab

(A) Superposition of optimized ligand structures. (B) Superposition of optimized complex structures.

Due to the intensity of computational resources required for ab initio quantum chemistry calculations, we implemented the semi-quantum chemistry method PM7 in MOPAC2012 to optimize the complex structures and to obtain ligand conformations in the c-Met binding site. As stated in the Materials and methods section, we assume that the protein binding site is rigid and that only the hydrogen atoms of the protein and ligand are allowed to relax. If no constraints are added in the optimizations, binding site residues may shift away, which may cause collisions with protein atoms excluded from the model. As shown in Figure 3B, the ligands superimpose well in the c-Met binding site, with RMSD values less than 0.5 Å. Visible differences arise from the connection of the phenyl group to the fused rings, which rotates the torsion angle slightly relative to the conformation seen in the crystal structure 3CCN.

Calculated free energy of models

The thermodynamic cycle method is an elegant means to calculate the difference in binding free energy between two ligands. Equations 1–6 (listed in the Materials and methods section) can be adapted to cancel out several important factors, such as the configurational entropy and solvation free energies of protein-ligand complexes. We did not include entropy in the current calculation due to the fact that the four ligands in the current study have only subtle differences between the fused rings, show good shape similarity, and contain the same three rotatable torsion angles. It was anticipated that this simplification would not sacrifice accuracy in the calculations. Most configurational entropy calculations are also based on the harmonic approximation, which is far from perfect in accounting for the entire anharmonic nature associated with entropy calculations.

No structural water is visible in the vicinity of the ligand binding site of c-Met in the co-crystal structure, indicating that the binding site is relatively deep in the interior of the protein. Based on the expectation that all ligands bind in positions very similar to those observed in the crystal structure, we assumed that the solvation free energies of the corresponding complexes are identical. Therefore, the free energy difference of two complex models in solution can be substituted with the difference of their gas phase energies. The calculated ΔΔG of two binding events can be determined from the free energy differences of ligand and complex pairs, as shown in Eq 2. This calculation also eliminates the consideration of basis set superposition error that commonly occurs in calculating the association energy of two molecules because we subtracted the energies of molecules of very similar size.

To investigate the binding free energy of these model systems, we calculated the gas phase energies of the optimized ligands and complexes (all energy values are listed in Table S1 of the supporting material). The newly developed SMD method was used to obtain the solvation free energies of the ligands (all energy values are listed in Table S1 of the supporting material). The values of ΔΔG between analogs and 1 were calculated and are listed in Table 2. Ligand 4 has the highest solvation free energy in this series, which correlated with the fact that it has one less nitrogen atom than the others and is thus more hydrophobic. Interestingly, 3 has the lowest solvation free energy, which may be due to the presence of a more solvent-exposed nitrogen at the 7 position of the fused ring. From Table 2, it was found that the calculated ΔΔG values qualitatively match with affinities from the binding assay. Ligand 2 has the largest difference in binding free energy (6.58 kcal/mol) compared with 1, followed by 4 (4.12 kcal/mol) and 3 (3.73 kcal/mol).

Table 2. Differences of calculated free energy between modelsa (energy unit: kcal/mol).

  Ligand 1 Ligand 2 Ligand 3 Ligand 4
ΔGL_solvation −18.31 −18.40 −20.23 −16.36
Full Model ΔΔG 0.0 6.58 3.73 4.12
No Arg-1208 ΔΔG 0.0 0.18 4.14 2.17
No Tyr-1230 ΔΔG 0.0 7.67 3.28 3.77
No Met-1211 ΔΔG 0.0 7.48 4.05 3.85
No Asp-1222 ΔΔG 0.0 5.70 2.54 3.50
Open in a new tab

a The value of free energy difference is obtained by using the models containing ligand 1 as reference.

To better account for the contribution of each residue, we constructed four derived models for each ligand by deleting each contacted residue in turn from the full model, as described in the Materials and methods section. In the four complex models of ligands bound to the binding site lacking Arg-1208, we used 1 as the reference and calculated the ΔΔG values of the other three analogs. The free energy gap between 2 and 1 was reduced dramatically. Ligand 2 has nearly the same free energy of binding as 1 in this model (ΔΔG=0.18 kcal/mol). This finding suggests that Arg-1208 makes much weaker interactions with 2 than with 1, resulting in a large difference of free energy in the full binding sites models. Ligand 4 showed similarly unfavorable interactions with Arg-1208, and the value of ΔΔG was decreased by approximately 2 kcal/mol. The free energy gap for 3 was slightly larger than that in the full model (from 3.73 kcal/mol to 4.14 kcal/mol), indicating favorable interactions between Arg-1208 and 3. For tall models lacking Tyr-1230, the free energy gap between 1 and 2 was found to be larger than in the full model. This finding suggests that 2 exhibits more favorable interactions with Tyr-1230. This finding runs counter to the common view that moving the nitrogen atom from the 4 position to the 6 position attenuates π–π interactions with Tyr-1230 and reduces binding affinity. The models lacking Met-1211 similarly suggest that 2 exhibits favorable interactions with Met-1211, with an increased energy difference of approximately 0.9 kcal/mol found in these models. The ΔΔG calculations on the four models lacking Asp-1222 showed no significant changes in the free energy gap with respect to the full model, and the most noticeable change was found for 3 (an increase of 1.2 kcal/mol).

Taken together, these calculations indicate that the loss of c-Met activity shown by 2 is not due to decreased π–π interaction with Tyr-1230 or π-S interaction with Met-1211. More likely, the reduced potency can be traced to a weaker interaction with Arg-1208 as compared with that seen for 1. It should be noted that the decreased free energy gap for a specific ligand in a particular missing residue model does not definitively imply unfavorable interactions between the ligand and the missing residue. It only indicates that the deleted residue shows weaker interactions with the analog ligand relative to 1. The energies of the complexes of 3 with the binding sites lacking Tyr-1230 and Asp-1222 indicated that this ligand has weak π–π interactions with Tyr-1230 and weak hydrogen bonding interactions with Asp-1222. It is clear that Arg-1208 is the major contributor to unfavorable interactions with 4, although each of the other three residues also contributes unfavorable interactions.

Energy decomposition

Many factors contribute to noncovalent interactions in nature. A common classification scheme divides the energies between electrostatic, exchange, induction and dispersion interactions. Electrostatic effects represent the classic coulombic electrostatic energy; the exchange term is derived from the principle of antisymmetry of wave functions; and the induction and dispersion forces are rooted in the multipolar interactions between two molecules and whether they are permanent or instantaneous, respectively. To further study the mechanism by which inhibitors bind to c-Met, the interaction energy components were decomposed using the SAPT method implemented in PSI4 software. Of the four key binding site residues, Tyr-1230 has the lowest interaction energy (-10.61 kcal/mol, Table 3) with 1, indicating that interaction with Tyr-1230 is a predominant factor for binding. Interaction with Asp-1222 is the second-most significant contributor to binding (-9.49 kcal/mol). The other two residues also interact favorably with 1 but play less important roles in binding.

Table 3. The results of SAPT calculations (energy unit: kcal/mol).

  Ligand 1 Ligand 2 Ligand 3 Ligand 4
Arg-1208 −6.73 0.64 −7.08 −4.41
Electrostatics −8.09 0.43 −8.20 −6.39
Exchange 9.12 6.02 8.52 9.55
Induction −3.12 −1.80 −2.93 −2.84
Dispersion −4.64 −4.02 −4.47 −4.74
Tyr-1230 −10.61 −11.22 −9.64 −9.56
Electrostatics −4.90 −5.08 −3.80 −3.57
Exchange 7.87 6.35 7.60 8.11
Induction −0.94 −0.91 −0.96 −0.95
Dispersion −12.65 −11.59 −12.47 −13.15
Met-1211 −6.65 −7.06 −7.16 −6.29
Electrostatics −4.94 −6.38 −6.88 −4.98
Exchange 11.93 13.68 14.28 12.43
Induction −1.34 −1.40 −1.58 −1.42
Dispersion −12.19 −12.97 −12.99 −12.32
Asp-1222 −9.49 −8.44 −8.54 −8.85
Electrostatics −11.84 −10.23 −10.79 −11.36
Exchange 10.37 8.71 10.17 10.28
Induction −3.65 −3.05 −3.69 −3.50
Dispersion −4.37 −3.88 −4.24 −4.26
Total SAPT energy −33.48 −26.08 −32.42 −29.11
Open in a new tab

Interactions between 2 and Arg-1208 are clearly unfavorable, with a positive interaction energy of approximately 0.64 kcal/mol. The interactions of 2 with Tyr-1230 and Met-1211 are slightly more favorable than the corresponding interactions of 1. The interaction between 2 and Asp-1222 is weaker than the interaction between 1 and Asp-1222. These effects are also reflected in the free energy calculations described in the previous section. These results collectively demonstrate that the reduced potency of 2 is mainly due to unfavorable interactions with Arg-1208. As shown in Table 3, the energy decomposition calculations show that this behavior is due mainly to a repulsive electrostatic interaction between Arg-1208 and 2. Ligand 1 features a C–H moiety at the 6 position that bears positive electrostatic potential, whereas the carbon atom has been changed to nitrogen in 2. This change carries with it a negative charge density, which in turn perturbs the interaction with the backbone carbonyl of Arg-1208. This finding is very important for the design of future c-Met inhibitors. We surveyed the literature for c-Met inhibitors containing nitrogen atoms at this position and noted that several compounds bearing a nitrogen atom at that position were reported by Ye et al. These compounds did indeed display much lower activity than compounds containing CH at that position30.

Ligand 3 shows moderate potency against c-Met kinase. It is apparent from the SAPT calculations that, in terms of binding interaction energies, 3 is the most similar of the three analogs to 1. The interaction between Tyr-1230 and 3 is weaker than the corresponding interaction with 1 by approximately 1 kcal/mol. A similar situation is observed for the interactions with Asp-1222. Ligand 1 is approximately ten fold more potent than 3 in enzymatic assays, which is a difference of 1.36 kcal/mol when expressed in terms of binding free energy. This result is consistent with the SAPT calculations that revealed a similar energy gap. Ligand 4 shows inferior interactions with all four residues in the c-Met binding site relative to 1. This result also reflects the experimental data trend for inhibitor binding affinities. As was seen for 2, the interaction between Arg-1208 and 4 shows a difference of more than 2 kcal/mol relative to 1, indicating that weaker electrostatic interactions account for most of the difference in binding free energy.

The SAPT calculation shows that the total interaction energy of 1 with the four residues in the c-Met binding site is -33.48 kcal/mol. Among the analogs, 2 shows the largest energy gap (7.4 kcal/mol) with respect to 1. Ligand 3 binds with an affinity only 1.06 kcal/mol less favorable than that of 1, followed by 4, with a difference of 4.37 kcal/mol. Although the energy difference does not correlate linearly with the free energy calculated from the M06-2X method, this method does rank the ligands in proper order with respect to their experimental binding affinities. Although these two quantum chemistry studies are very different, the similar results obtained from two theoretical methods reinforce the rationality of our hypothesis on the mechanism by which type I inhibitors interact with c-Met. These results clearly show that Tyr-1230 and Asp-1222 are the most important active site residues for binding to all three active inhibitors. The presence of Met-1211 below the fused aromatic rings not only constrains the inhibitor but also contributes favorably to binding interactions. For some type I c-Met inhibitors, exemplified by the ligand 2, Arg-1208 is the residue that determines binding. This factor deserves additional consideration from medicinal chemists.

π–π Interaction, sulfur-π interaction, and hydrogen bonding interaction

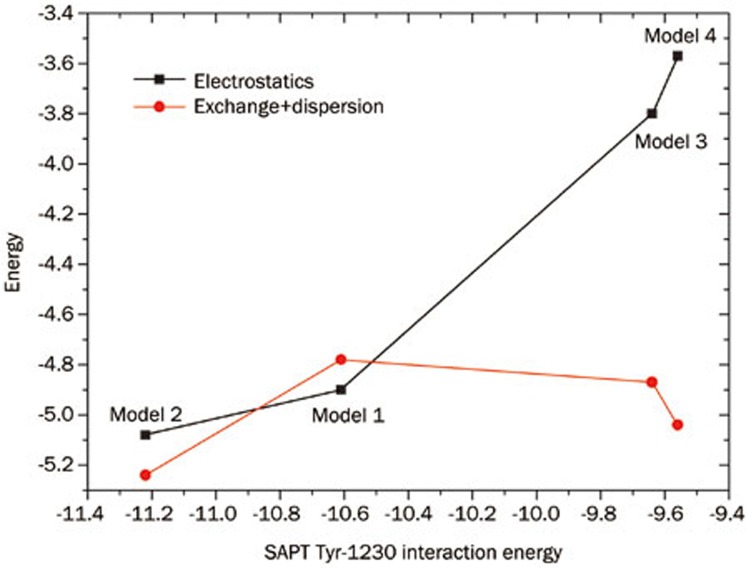
The binding of a type I inhibitor to c-Met kinase provides a model system for several important noncovalent interactions that occur commonly in drug design. These include π–π interactions, hydrogen bonding interactions, and sulfur-π interactions. The face-to-face π interaction has been studied by many researchers, and currently, three mechanisms exist to explain the nature of this type of interaction. In 1990, Hunter and Sanders proposed a simple electrostatic model to account for π–π stacking interactions31, which stated that although dispersion interactions contribute significantly to π–π interactions, electrostatic energy predicts substituent effects. As a consequence of the Hunter-Sander model, an electron-deficit π system would show favorable interactions with an electron-rich or benzene π system. This model was disputed by Sherrill and co-workers, as they found that both electron-donating substituents and electron-withdrawing substituents stabilize the benzene sandwich dimer32,33,34,35. The studies conducted by Sherrill et al led them to conclude that differential dispersion effects can dominate substituent effects in π–π stacking as well. The model combining dispersion and electrostatics may better reflect the nature of π–π interactions. Recently, several groups have identified substituent effects that can be correlated to the Hammett σm parameters15,32,36. This ultimately led to the proposal of a local direct interaction model for π–π stacking37,38. Based on this model, substituent effects can be explained solely by interactions between the local dipole associated with the substituent and the nearby local dipoles of the other ring. In the present study, we have synthesized inhibitors containing four different fused rings. It was found from SAPT calculations that these rings exhibit similar energies for their π–π interactions with Tyr-1230. Although the energy decomposition calculation demonstrates that dispersion energy is the dominant factor in the π–π interaction, it is interesting that the electrostatic energy correlates well to the overall SAPT interaction energy of Tyr-1230 (Figure 4). The sum of the exchange energies and dispersion energies are nearly equal in all four models. As most previous studies have focused on substituent effects, the calculation shown here indicates that the heterocycle π–π interactions are also predictable using the electrostatic model. Because the fused aromatic rings in the present study are difficult to decompose into local electrostatic contributions, it remains to be determined whether the local direct model is suitable for such systems.

Figure 4.

Figure 4

Open in a new tab

The plot of energy decomposition from SAPT calculations of Tyr-1230 with four ligands (energy units: kcal/mol).

The sulfur-π interaction occurs less commonly in protein-ligand systems than does the well-known π–π interaction39,40,41. Met-1211 interacts with the inhibitors described in this study, which may provide some clues about the nature of this type of interaction. As shown by the energy decomposition calculation, sulfur-π interactions are very similar to π–π interactions and are dominated by the dispersion energy. The distinct difference between these two types of interactions is found in the exchange energy. The exchange energy in sulfur-π interactions is larger than in π–π interactions, which may stem from the high polarizability of the sulfur atom. The electrostatic repulsion between a sulfur atom and a π system is therefore large.

The SAPT calculations clearly indicated that the main factor determining hydrogen bonding is rooted in electrostatic interaction. The dispersion energy associated with hydrogen bonding is considerably weaker than that in a π–π interaction, and its contribution is only approximately half that of electrostatic energy. Interestingly, the pattern of interactions between Arg-1208 and the ligands is very similar to the hydrogen bonding interaction. This similarity reinforces the importance of a hydrogen atom at the 6-position of the fused ring.

Conclusion

To decipher the interaction mechanism by which type I inhibitors bind to c-Met kinase, we synthesized four ligands that differ only in the nature of the fused ring. We ranked the relative activities of these inhibitors experimentally using an enzymatic inhibition assay. By adapting quantum chemistry calculations and the SAPT energy decomposition method, we found that the theoretical binding energies correlated well with the experimental binding affinities. The qualitative consistencies of these studies enable us to speculate on the mechanism of the binding interaction.

It was found that the predominant driving force for binding is derived from a sandwich π–π interaction with Tyr-1230. However, Arg-1208 is the differentiating factor, interacting with the 6-position of the fused aromatic ring system through the backbone carbonyl with a force pattern similar to hydrogen bonding. Therefore, a hydrogen atom must be attached at the 6-position, and changing the carbon atom to nitrogen will cause unfavorable electrostatic interactions. In summary, the present study not only can help medicinal chemists explain and explore the structure-activity relationships of type I c-Met kinase inhibitors but also may enable a deeper understanding of the fundamental intermolecular forces associated with typical protein-ligand interactions.

Author contribution

Bing XIONG, Dong-mei ZHAO and Jing-kang SHEN designed the research; Zhe YU, Yu-chi MA, Jing AI, Da-qi CHEN, Xin WANG, and Bing XIONG performed the research; Yue-lei CHEN, Mei-yu GENG, Mao-sheng CHENG, Bing XIONG, and Jing-kang SHEN analyzed the data; Bing XIONG and Jing-kang SHEN wrote the paper.

graphic file with name aps201385i2.jpg

Open in a new tab

graphic file with name aps201385i3.jpg

Open in a new tab

graphic file with name aps201385i4.jpg

Open in a new tab

Acknowledgments

The authors wish to thank Prof Ming-yue ZHENG for his critical reading of the manuscript. We are grateful for financial support from the Program of Excellent Young Scientists of the Chinese Academy of Sciences to Bing XIONG (Grant No KSCX2-EW-Q-3-01), from the National Natural Science Foundation of China to Bing XIONG (Grant No 81072580), and from the “Interdisciplinary Cooperation Team” Program for Science and Technology Innovation of the Chinese Academy of Sciences.

Footnotes

Supplementary Table is available at the Acta Pharmacologica Sinica website.

Supplementary Information

Supplementary Table S1

Energy of various models in gas phase with M06-2X/6-31G+(d) methods (energy unit is AU except for salvation free energy, 1AU=627.51 kcal/mol)

Click here for additional data file. (474.8KB, pdf)

References

  1. Gherardi E, Birchmeier W, Birchmeier C, Vande Woude G. Targeting MET in cancer: rationale and progress. Nat Rev Cancer. 2012;12:89–103. doi: 10.1038/nrc3205. [DOI] [PubMed] [Google Scholar]
  2. Trusolino L, Bertotti A, Comoglio PM. MET signalling: principles and functions in development, organ regeneration and cancer. Nat Rev Mol Cell Biol. 2010;11:834–48. doi: 10.1038/nrm3012. [DOI] [PubMed] [Google Scholar]
  3. Birchmeier C, Birchmeier W, Gherardi E, Vande Woude GF. Met, metastasis, motility and more. Nat Rev Mol Cell Biol. 2003;4:915–25. doi: 10.1038/nrm1261. [DOI] [PubMed] [Google Scholar]
  4. Peters S, Adjei AA. MET: a promising anticancer therapeutic target. Nat Rev Clin Oncol. 2012;9:314–26. doi: 10.1038/nrclinonc.2012.71. [DOI] [PubMed] [Google Scholar]
  5. Comoglio PM, Giordano S, Trusolino L. Drug development of MET inhibitors: targeting oncogene addiction and expedience. Nat Rev Drug Discov. 2008;7:504–16. doi: 10.1038/nrd2530. [DOI] [PubMed] [Google Scholar]
  6. Giordano S, di Renzo MF, Olivero M, Mondino A, Zhen Z, Medico E, et al. The c-met/HGF receptor in human tumours. Eur J Cancer Prev. 1992;1 Suppl 3:45–9. doi: 10.1097/00008469-199210003-00007. [DOI] [PubMed] [Google Scholar]
  7. Drebber U, Baldus SE, Nolden B, Grass G, Bollschweiler E, Dienes HP, et al. The overexpression of c-met as a prognostic indicator for gastric carcinoma compared to p53 and p21 nuclear accumulation. Oncol Rep. 2008;19:1477–83. [PubMed] [Google Scholar]
  8. Jung KH, Park BH, Hong SS. Progress in cancer therapy targeting c-Met signaling pathway. Arch Pharm Res. 2012;35:595–604. doi: 10.1007/s12272-012-0402-6. [DOI] [PubMed] [Google Scholar]
  9. Eder JP, Shapiro GI, Appleman LJ, Zhu AX, Miles D, Keer H, et al. A phase I study of foretinib, a multi-targeted inhibitor of c-Met and vascular endothelial growth factor receptor 2. Clin Cancer Res. 2010;16:3507–16. doi: 10.1158/1078-0432.CCR-10-0574. [DOI] [PubMed] [Google Scholar]
  10. Liu X, Newton RC, Scherle PA. Development of c-MET pathway inhibitors. Expert Opin Investig Drugs. 2011;20:1225–41. doi: 10.1517/13543784.2011.600687. [DOI] [PubMed] [Google Scholar]
  11. Liu X, Yao W, Newton RC, Scherle PA. Targeting the c-MET signaling pathway for cancer therapy. Expert Opin Investig Drugs. 2008;17:997–1011. doi: 10.1517/13543784.17.7.997. [DOI] [PubMed] [Google Scholar]
  12. Porter J. Small molecule c-Met kinase inhibitors: a review of recent patents. Expert Opin Ther Pat. 2010;20:159–77. doi: 10.1517/13543770903514137. [DOI] [PubMed] [Google Scholar]
  13. Liu X, Wang Q, Yang G, Marando C, Koblish HK, Hall LM, et al. A novel kinase inhibitor, INCB28060, blocks c-MET-dependent signaling, neoplastic activities, and cross-talk with EGFR and HER-3. Clin Cancer Res. 2011;17:7127–38. doi: 10.1158/1078-0432.CCR-11-1157. [DOI] [PubMed] [Google Scholar]
  14. Albrecht BK, Harmange JC, Bauer D, Berry L, Bode C, Boezio AA, et al. Discovery and optimization of triazolopyridazines as potent and selective inhibitors of the c-Met kinase. J Med Chem. 2008;51:2879–82. doi: 10.1021/jm800043g. [DOI] [PubMed] [Google Scholar]
  15. Wheeler SE. Understanding substituent effects in noncovalent interactions involving aromatic rings. Acc Chem Res. 2013;46:1029–38. doi: 10.1021/ar300109n. [DOI] [PubMed] [Google Scholar]
  16. Chakrabarti P, Bhattacharyya R. Geometry of nonbonded interactions involving planar groups in proteins. Prog Biophys Mol Biol. 2007;95:83–137. doi: 10.1016/j.pbiomolbio.2007.03.016. [DOI] [PubMed] [Google Scholar]
  17. Rozas I. On the nature of hydrogen bonds: an overview on computational studies and a word about patterns. Phys Chem Chem Phys. 2007;9:2782–90. doi: 10.1039/b618225a. [DOI] [PubMed] [Google Scholar]
  18. Zacharias N, Dougherty DA. Cation-pi interactions in ligand recognition and catalysis. Trends Pharmacol Sci. 2002;23:281–7. doi: 10.1016/s0165-6147(02)02027-8. [DOI] [PubMed] [Google Scholar]
  19. Valero R, Gomes JR, Truhlar DG, Illas F. Good performance of the M06 family of hybrid meta generalized gradient approximation density functionals on a difficult case: CO adsorption on MgO(001) J Chem Phys. 2008;129:124710. doi: 10.1063/1.2982923. [DOI] [PubMed] [Google Scholar]
  20. Valero R, Costa R, de PRMI, Truhlar DG, Illas F. Performance of the M06 family of exchange-correlation functionals for predicting magnetic coupling in organic and inorganic molecules. J Chem Phys. 2008;128:114103. doi: 10.1063/1.2838987. [DOI] [PubMed] [Google Scholar]
  21. Zhao Y, Truhlar DG. Density functionals with broad applicability in chemistry. Acc Chem Res. 2008;41:157–67. doi: 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
  22. MOPAC 6.0 for Windows 95. Nachr Chem Tech Lab. 1997;45:406. [Google Scholar]
  23. Marenich AV, Cramer CJ, Truhlar DG. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J Phys Chem B. 2009;113:6378–96. doi: 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
  24. Jeziorski B, Moszynski R, Szalewicz K. Perturbation-theory approach to intermolecular potential-energy surfaces of Van-Der-Waals complexes. Chem Rev. 1994;94:1887–930. [Google Scholar]
  25. Szalewicz K. Symmetry-adapted perturbation theory of intermolecular forces. Wires Comput Mol Sci. 2012;2:254–72. [Google Scholar]
  26. Turney JM, Simmonett AC, Parrish RM, Hohenstein EG, Evangelista FA, Fermann JT, et al. PSI4: an open–source ab initio electronic structure program. Wires Comput Mol Sci. 2012;2:556–65. [Google Scholar]
  27. Hohenstein EG, Parrish RM, Sherrill CD, Turney JM, Schaefer HF. Large-scale symmetry-adapted perturbation theory computations via density fitting and Laplace transformation techniques: Investigating the fundamental forces of DNA-intercalator interactions. J Chem Phys. 2011;135:174107–19. doi: 10.1063/1.3656681. [DOI] [PubMed] [Google Scholar]
  28. Hohenstein EG, Sherrill CD. Efficient evaluation of triple excitations in symmetry-adapted perturbation theory via second-order Moller-Plesset perturbation theory natural orbitals. J Chem Phys. 2010;133:104107–14. doi: 10.1063/1.3479400. [DOI] [PubMed] [Google Scholar]
  29. Hohenstein EG, Sherrill CD. Density fitting of intramonomer correlation effects in symmetry-adapted perturbation theory. J Chem Phys. 2010;133:014101–12. doi: 10.1063/1.3451077. [DOI] [PubMed] [Google Scholar]
  30. Ye LB, Tian YX, Li ZH, Jin H, Zhu ZG, Wan SH, et al. Design, synthesis and molecular docking studies of some novel spiro[indoline-3,4′-piperidine]-2-ones as potential c-Met inhibitors. Eur J Med Chem. 2012;50:370–5. doi: 10.1016/j.ejmech.2012.02.016. [DOI] [PubMed] [Google Scholar]
  31. Hunter CA, Sanders JKM. The nature of Pi–Pi interactions. J Am Chem Soc. 1990;112:5525–34. [Google Scholar]
  32. Ringer AL, Sherrill CD. Substituent effects in Sandwich configurations of multiply substituted benzene dimers are not solely governed By electrostatic control. J Am Chem Soc. 2009;131:4574–5. doi: 10.1021/ja809720r. [DOI] [PubMed] [Google Scholar]
  33. Arnstein SA, Sherrill CD. Substituent effects in parallel-displaced pi–pi interactions. Phys Chem Chem Physics. 2008;10:2646–55. doi: 10.1039/b718742d. [DOI] [PubMed] [Google Scholar]
  34. Ringer AL, Sinnokrot MO, Lively RP, Sherrill CD. The effect of multiple substituents on sandwich and T-shaped pi-pi interactions. Chemistry. 2006;12:3821–8. doi: 10.1002/chem.200501316. [DOI] [PubMed] [Google Scholar]
  35. Sherrill CD. Substituent effects in Pi–Pi interactions: electrostatics vs dispersion. Abstr Pap Am Chem S. 2004;228:U62. [Google Scholar]
  36. Watt M, Hardebeck LKE, Kirkpatrick CC, Lewis M. Face-to-Face Arene-Arene binding energies: dominated by dispersion but predicted by electrostatic and dispersion/polarizability substituent constants. J Am Chem Society. 2011;133:3854–62. doi: 10.1021/ja105975a. [DOI] [PubMed] [Google Scholar]
  37. Wheeler SE, Houk KN. Substituent effects in cation/pi interactions and electrostatic potentials above the centers of substituted benzenes are due primarily to through-space effects of the substituents. J Am Chem Soc. 2009;131:3126–7. doi: 10.1021/ja809097r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Wheeler SE, Houk KN. Substituent effects in the benzene dimer are due to direct interactions of the substituents with the unsubstituted benzene. J Am Chem Soc. 2008;130:10854–5. doi: 10.1021/ja802849j. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Daeffler KNM, Lester HA, Dougherty DA. Functionally important aromatic-aromatic and sulfur-pi interactions in the D2 dopamine receptor. J Am Chem Soc. 2012;134:14890–6. doi: 10.1021/ja304560x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Morgado CA, McNamara JP, Hillier IH, Burton NA. Density functional and semiempirical molecular orbital methods including dispersion corrections for the accurate description of noncovalent interactions involving sulfur-containing molecules. J Chem Theory Comput. 2007;3:1656–64. doi: 10.1021/ct700072a. [DOI] [PubMed] [Google Scholar]
  41. Tauer TP, Derrick ME, Sherrill CD. Estimates of the ab initio limit for sulfur-pi interactions: The H2S-benzene dimer. J Phys Chem A. 2005;109:191–6. doi: 10.1021/jp046778e. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Table S1

Energy of various models in gas phase with M06-2X/6-31G+(d) methods (energy unit is AU except for salvation free energy, 1AU=627.51 kcal/mol)

Click here for additional data file. (474.8KB, pdf)

Articles from Acta Pharmacologica Sinica are provided here courtesy of Nature Publishing Group

RESOURCES