Lineshape-based polarimetry of dynamically-polarized ¹⁵N₂O in solid-state mixtures

Abstract

Dynamic nuclear polarization (DNP) of ¹⁵N₂O, known for its long-lived singlet-state order at low magnetic field, is demonstrated in organic solvent/trityl mixtures at ~1.5 K and 5 T. Both ¹⁵N polarization and intermolecular dipolar broadening are strongly affected by the sample's thermal history, indicating spontaneous formation of N₂O clusters. In situ ¹⁵N NMR reveals four distinct powder-pattern spectra, attributed to the chemical-shift anisotropy (CSA) tensors of the two ¹⁵N nuclei, further split by the intramolecular dipolar coupling between their magnetic moments. ¹⁵N polarization is estimated by fitting the free-induction decay (FID) signals to the analytical model of four single-quantum transitions. This analysis implies (10:2 ± 2:2)% polarization after 37 h of DNP, and provides a direct, instantaneous probe of the absolute ¹⁵N polarization, without a need for time-consuming referencing to a thermal-equilibrium NMR signal.

1. Introduction

The field of metabolic magnetic resonance imaging [1] has enjoyed a remarkable expansion following the success of low-temperature dynamic nuclear polarization (DNP) of ¹³C-labelled biomolecules, where high ¹³C polarization (20–75%) [2–4] is retained at room temperature after a rapid dissolution [5,6]. However, very short T₁ relaxation times (~30 s) of these compounds have severely limited the applicability of ¹³C-DNP imaging, except for the fastest of metabolic pathways [7].

One possible way to address this problem is to utilize long-lived singlet order in homonuclear systems of spin-1/2 pairs [8–11]. A particularly attractive target system is doubly labelled ¹⁵N₂O, a non-toxic anesthetic gas, which has exhibited a nuclear singlet lifetime above 25 min in a deuterated solvent [12,13] and ~7 min in human blood [14].

Here we report the first observations of DNP in the solid-state ¹⁵N₂O matrix. The lineshape and the maximum achievable polarization are found to depend substantially on the thermal history of the sample, which we qualitatively explain in terms of pure-N₂O clustering effects similar to those we have reported earlier in ¹²⁹Xe DNP [15]. Surprisingly, cluster formation in ¹⁵N₂O mixtures leads to enhanced ¹⁵N polarization, showing no signs of spin-diffusion bottle neck observed in the xenon system. Using the rich spectral structure of ¹⁵N₂O NMR, we derive the detailed NMR line shape of the observed ¹⁵N₂O spectra, from which one can directly and instantaneously determine the absolute ¹⁵N polarization. Our line-shape analysis provides a valuable tool for assessing and modeling DNP conditions in situ, and eliminates the need for customary referencing to thermal-equilibrium NMR signals, which can take many days of acquisition due to extremely long T₁ relaxation times of ¹⁵N at these low temperatures. While the earlier studies [16] have demonstrated the effects of nuclear polarization on the overall spectral parameters such as line-shape moments, this is the first ab initio analysis of the detailed NMR spectrum observed in an isotropically oriented two-spin-1/2 solid-state molecular system, with the fit sensitivity sufficient for precise determination of the nuclear spin polarization.

2. Materials and methods

A hermetically-sealed retractable electric stirrer was used to mix Finland-acid radical [17] solution with distilled liquid ¹⁵N¹⁵NO (Cambridge Isotopes, >98% pure, >98% ¹⁵N) in an ethanol/solid CO bath (1.75 atm ¹⁵N₂O pressure at 195 K) for ~1 min. Sample I contained 9.4 mg (9.4 μmol) radical, 84 mg (1.4 mmol) 1-propanol, 31 mg (0.36 mmol) CD₂Cl₂, 0.9 mmol ¹⁵N₂O. Sample II contained 2.9 mg radical, 107 mg 1-propanol, 1.3 mmol ¹⁵N₂O. After a rapid switch to the liquid nitrogen (LN₂, 77 K) bath, the excess solid ¹⁵N₂O at the top of the sample was sub-limated with a soldering iron. The open sample tube was transferred to the DNP probe at 120 K, which was then cooled down to 1.4 K. A home-built spectrometer recorded ¹⁵N NMR at 21.56 MHz in our 140-GHz DNP system [15]. Switching on the microwaves increased the probe temperature by 5–200 mK. Prior to the microwave sweep, the magnet's field B₀ was determined by ¹H₂O NMR at room temperature and by solid-state ¹⁵N NMR at ~1.5 K. Free-induction decays (FID) were acquired using 1–4 μs small flip-angle pulses (7 ± 1 μs dead time). After applying a baseline correction, Gaussian broadening (50–170 Hz for plotting only), Fourier transform, and zero-order phase correction, the spectra were plotted using Igor Pro 6 (Wavemetrics).

3. Results

Fig. 1A shows the evolution of ¹⁵N NMR spectra during DNP in sample I. Four observed powder-pattern lineshape components are attributed to the chemical-shift anisotropy (CSA) tensors of the two ¹⁵N nuclei [18], further split by intramolecular dipolar coupling between them [19]. Fig. 1B shows the nuclear system's response to the DNP microwave frequency ν in sample II, plotted against ν/B₀ (to factor out small B₀ drift). The splitting between ν⁺ and ν^–, defined as the optimal frequencies for overpopulating the ground and the excited states of the nuclear Zeeman system, was found to be 57.3 MHz, on the order of the electron-resonance linewidth or twice the ¹⁵N nuclear Larmor frequency.

Fig. 1.

(A) Evolution of ¹⁵N₂O NMR spectra at T = 1:6 K and B = 4:9976 T in sample I during the first 18 h of DNP irradiation at ν⁺ = 140:0625 GHz, acquired using short rf pulses with a 3.7° flip angle. (B) The initial rate of increase of the area under the ¹⁵N NMR line due to DNP (dA/dt), measured in sample II (open circles) as a function of the microwave frequency-to-field ratio ν/B₀ at B₀ = 4:99618 T and T = 1.42 K. At each ν; ¹⁵N magnetization was destroyed by a pulse train, followed by 873 s of microwave irradiation and an ¹⁵N NMR acquisition. The dashed line is to guide the eye.

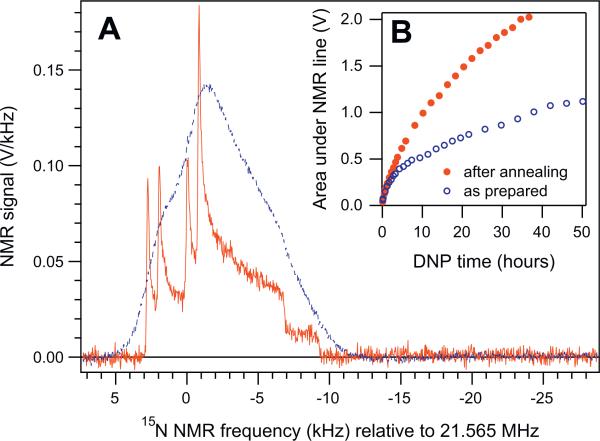
The ¹⁵N spectra shown in Fig. 1A are broadened by intermolecular interactions with the solvent atoms. This broadening strongly depends on the molecular environment of ¹⁵N₂O. Fig. 2A shows two ¹⁵N NMR spectra, taken 49 min apart on the same sample I after 50 h of DNP. The N₂O/solvent/trityl mixture was initially very homogeneous, as evidenced by the strong broadening of the first DNP spectrum (blue dashed line). Over several tens of seconds, this hyperpolarized sample was carefully transferred through room-temperature air and the ambient field of ~20 G to a 1.1 T holding field at 77 K. After about 3 min at 1.1 T, the sample was returned to the 5 T field of the DNP system. As can be seen from Fig. 2A, about half of the original hyperpolarization was preserved during this process. Remarkably, the strong uniform broadening of the spectrum was largely removed by this transient annealing of the sample, revealing a detailed quadruplet of powder-spectrum patterns characteristic of pure polycrystalline ¹⁵N₂O. This irreversible removal of NMR line broadening persisted throughout the next DNP experiment at T = 1:6 K (red solid circles, Fig. 2B). In subsequent controlled experiments with sample II, uniformly-mixed N₂O/1-propanol/trityl samples had to be annealed for tens of minutes at 160–180 K to reproduce this dramatic line narrowing and the increased DNP efficiency. At these temperatures the mixture undergoes a glass transition, whereby atomic diffusion leads to spontaneous partial segregation of the pure N₂O from the mixture, leading to cluster formation. This results in a pronounced change in the ¹⁵N spin–lattice relaxation time T₁ from 8 to 33 h at 1.41–1.44 K. We have also observed similar phenomena in ¹²⁹Xe/1-propanol/trityl mixtures [15]. However, in contrast to ¹²⁹Xe, DNP of the partially-segregated N₂O/solvent/trityl mixture resulted in substantially higher average ¹⁵N polarization compared to the homogeneous mixture at the same conditions, as can be seen in Fig. 2B.

Fig. 2.

(A) Solid-state ¹⁵N NMR spectra of DNP-polarized ¹⁵N₂O/solvent/trityl mixture immediately before and after (blue dashed and red solid lines, averaged over 5 and 1 scans) the annealing of sample I described in the text. (B) Evolution of the area A under the ¹⁵N NMR line during DNP at ν⁺ and T = 1.6 K before and after (open blue and solid red circles) the same annealing event. To avoid preamplifier saturation, the spectra with A ≥ 1.8 V were acquired with a 1.85° flip angle instead of the nominal 3.7°, and scaled up by 2.03. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Analytical model and discussion

The NMR spectra of the polarized ¹⁵N₂O solid may be analyzed by assuming that the ¹⁵N₂O molecules are randomly oriented and equally polarized, and that all intermolecular spin interactions only produce a uniform line broadening. The linear symmetry of N₂O ensures a uniaxial dependence of both the dipole–dipole and CSA tensors on the molecular angle θ (with respect to B₀) via the 2nd-rank Legendre polynomial $P_2\left(\cos \theta \right)=\frac{1}{2}(3{\cos }^2\theta -1)$. The spin Hamiltonian in the rotating frame of the resonant radio-frequency (rf) field is:

$$H\left(\theta \right)=\sum _{j=1,2}{\omega }_0\left({\delta }_j^{\mathrm{iso}}+{\delta }_j^{\mathrm{ani}}{P}_2\left(\cos \theta \right)\right)I_{jz}+{\omega }_j{\mathbf{I}}_1\cdot {\mathbf{I}}_2+b_{12}{P}_2\left(\cos \theta \right)(3I_{1z}{I}_{2z}-{\mathbf{I}}_1\cdot {\mathbf{I}}_2),$$ (1)

where ω₀ = –γB₀ is the nuclear Larmor frequency, γ = –2π × 4.316 MHz/T is the ¹⁵N magnetogyric ratio, ${\delta }_j^{\mathrm{iso}}$ and ${\delta }_j^{\mathrm{ani}}$ are the isotropic and anisotropic chemical shifts for the terminal (j = 1) and central (j = 2) ¹⁵N sites, ω_J = 2πJ₁₂ is the J-coupling, and $b_{12}=-({\mu }_0∕4\pi ){\gamma }^2\hslash r_{12}^{-3}$ is the nuclear dipole–dipole coupling constant for the internuclear ¹⁵N—¹⁵N distance r₁₂. In a liquid solution, the isotropic chemical shift difference is ${\delta }_2^{\mathrm{iso}}-{\delta }_1^{\mathrm{iso}}\simeq 82.3$ ppm [12]. The highest- and lowest-energy eigenstates of the Hamiltonian (Eq. (1)) are the Zeeman product states $\mid \alpha \alpha \rangle$ and $\mid \beta \beta \rangle$ respectively [11], while the two intermediate-energy states $\mid {\psi }^{+}\rangle =-\mid \alpha \beta \rangle \sin \frac{\xi }{2}+\mid \beta \alpha \rangle \cos \frac{\xi }{2}$ and $\mid {\psi }^{-}\rangle =\mid \alpha \beta \rangle \cos \frac{\xi }{2}+\mid \beta \alpha \rangle \sin \frac{\xi }{2}$ are coupled as shown in Fig. 3A–C. The coupling parameter is $\xi =\arg ({\omega }_{\Delta }^{\mathrm{iso}}+{\omega }_{\Delta }^{\mathrm{ani}}{P}_2+i[b_{12}{P}_2-{\omega }_J])$, using compact notation: ${\omega }_j={\omega }_0{\delta }_j,\stackrel{‒}{\omega }=\frac{1}{2}({\omega }_1+{\omega }_2)$ and ω_Δ = ω₂ – ω₁ for both “iso” or “ani” cases. The four single-quantum transitions (vertical arrows in Fig. 3A and C) can be parameterized by a pair of indices (Fig. 3B): m = ±1 selects the transitions connecting to either $\mid \alpha \alpha \rangle$ or $\mid \beta \beta \rangle$ states, whereas n = ±1 chooses a connection to one of the intermediate states $\mid {\psi }^{\pm }\rangle$. For a given molecular orientation P₂(cos θ), NMR transitions of Fig. 3A–C are located relative to the rotating-frame frequency ω₀ at:

$${\Omega }_{mn}\left(P_2\right)=\frac{m}{2}{\omega }_j+({\stackrel{‒}{\omega }}^{\mathrm{ani}}+m{b}_{12})P_2+{\stackrel{‒}{\omega }}^{\mathrm{iso}}\frac{mn}{2}\times \sqrt{{(P_2{\omega }_{\Delta }^{\mathrm{ani}}+{\omega }_{\Delta }^{\mathrm{iso}})}^2+{(b_{12}{P}_2-{\omega }_j)}^2}.$$ (2)

The spin-density operator of the uniformly-polarized sample consisting of two-spin molecules is:

$$\rho \left(p\right)=\left(\frac{1}{2}1-p{I}_{1z}\right)\left(\frac{1}{2}1-p{I}_{2z}\right),$$ (3)

where 1 is the unit operator, and |p| ≤ 1 is the polarization level. In most NMR experiments at thermal polarization, |p| is very small, and the quadratic terms in Eq. (3) may be ignored. This is not the case in DNP experiments at |p| ~ 1. For each single-quantum coherence $\mid r\rangle \langle s\mid$, a hard pulse with a flip angle ζ will generate an NMR signal amplitude $i\langle r\mid R_x\left(\zeta \right)\rho \left(p\right)R_x{\left(\zeta \right)}^{†}\mid s\rangle \langle r\mid I_x\mid s\rangle$, where $R_x\left(\zeta \right)=\exp (-i\zeta I_x)$ is a rotation operator. The NMR amplitudes of the four transitions of Fig. 3A–C are thus:

$$a_{mn}(\zeta ,p,P_2)=\frac{m}{8}(m-p\cos \zeta )p\sin \zeta [1-n\sin \xi \left(P_2\right)],$$ (4)

$$\text{for}-\frac{1}{2}\le P_2\left(\cos \theta \right)\le 1,$$ (5)

whereas a_mn(ζ, p, P₂) = 0 outside of the range of Eq. (5).

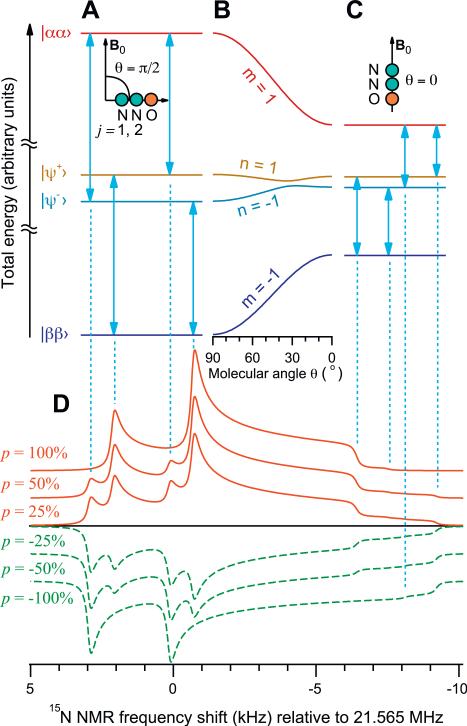
Fig. 3.

Total energy levels of the eigenstates of the Hamiltonian (Eq. (1)) for the molecules perpendicular (A: θ = π/2) and parallel (C: θ = 0) to the magnetic field B₀. The detailed dependence of the energy levels on the molecular orientation θ is shown in (B). Spectral line shapes (D) for different polarization values, calculated using Eqs. (4)–(8), using the parameters of Table 1. Note the spectral features in (D) corresponding to the transitions in (A and C). The dependence of the spectral line shape on the polarization is the basis of the polarimetry technique proposed here.

For a given molecule, each transition's NMR frequency ω = Ω_mn(P₂) can be used to express P₂(cos θ) by inverting Eq. (2) in the domain of interest:

$$P_2(\omega ,m,n)=\frac{\Lambda +4K{\omega }^{\prime }-mn\sqrt{4{({\omega }^{\prime }+\frac{K\Lambda }{\Gamma })}^2\Gamma +({\rm Y}-\frac{{\Lambda }^2}{\Gamma })}\varphi }{\varphi },$$ (6)

where ${\omega }^{\prime }=\omega -{\stackrel{‒}{\omega }}^{\mathrm{iso}}-\frac{m}{2}{\omega }_j$, $\Lambda ={\omega }_{\Delta }^{\mathrm{iso}}{\omega }_{\Delta }^{\mathrm{ani}}-b_{12}{\omega }_J$, $K={\stackrel{‒}{\omega }}^{\mathrm{ani}}+m{b}_{12}$, $\Gamma =b_{12}^2+{\left({\omega }_{\Delta }^{\mathrm{ani}}\right)}^2$, ${\rm Y}={\omega }_j^2+{\left({\omega }_{\Delta }^{\mathrm{iso}}\right)}^2$, and ϕ = 4K² – Γ. In an orientationally-disordered 3D sample, cos θ is uniformly distributed on [–1, 1]. To account for unequal number of molecules at each ω, NMR amplitudes of Eq. (4) must be divided by the statistical weights

$$\frac{d{\Omega }_{mn}\left(P_2\right)}{d\cos \theta }=\sqrt{3+6P_2}\times \left({\stackrel{‒}{\omega }}^{\mathrm{ani}}+m{b}_{12}-\frac{mn}{2}\frac{b_{12}(b_{12}{P}_2-{\omega }_J)+{\omega }_{\Delta }^{\mathrm{ani}}({\omega }_{\Delta }^{\mathrm{iso}}+{\omega }_{\Delta }^{\mathrm{ani}}{P}_2)}{\sqrt{{(b_{12}{P}_2-{\omega }_J)}^2+{({\omega }_{\Delta }^{\mathrm{iso}}+{\omega }_{\Delta }^{\mathrm{ani}}{P}_2)}^2}}\right)$$ (7)

to yield the sum of four Pake-like powder patterns [20]:

$$S(\omega ,p,\zeta )=\sum _{m=\pm 1,n=\pm 1}\frac{a_{mn}(\zeta ,p,P_2(\omega ,m,n))}{\mid \frac{d{\Omega }_{mn}\left(P_2(\omega ,m,n)\right)}{d\cos \theta }\mid },$$ (8)

where each element of the sum extends over its own ω range according to Eqs. (5) and (6). Although Eq. (6) is valid for ¹⁵N₂O, different analytical solutions or numerical simulations are required for some other parameter ranges.

To represent homogeneous line broadening, Eq. (8) is numerically convolved with a Lorentzian of full-width-at-half-height λ. Fig. 3D shows model line shapes for different spin polarizations p, assuming a flip angle of 1.85°. Note the dependence of the spectral line shape on both the magnitude and the sign of the polarization. Computed line shapes are found to have both strongly and weakly coupled eigenstates for certain molecular orientations, making it essential not to simplify the Hamiltonian of Eq. (1) any further. Additional nonsecular dipolar terms have perturbative contributions 4 orders of magnitude below those of Eq. (1) and are therefore omitted.

Eq. (4) predicts that the relative amplitudes of the four spectral components depend on the sign and magnitude of the polarization p as well as on the molecular orientation θ (Fig. 3D): when the polarization is large and positive, the lowest energy state $\mid \beta \beta \rangle$ is overpopulated. A small flip-angle pulse (cos ζ ~ 1) excites the corresponding m = –1 single-quantum transitions, and leads to a strong positive amplitude for the two single-quantum coherences terminating at state $\mid \beta \beta \rangle$. On the other hand, if the polarization is large and negative, the highest energy state $\mid \alpha \alpha \rangle$ is overpopulated, so that a small flip-angle pulse generates a large negative amplitude for the other two single-quantum transitions (m = 1). Since all four transitions have different frequencies, the shape of the spectrum, as well as its overall amplitude, thus depends on the sign and magnitude of p. The NMR spectrum of a multilevel spin system therefore provides a form of absolute polarimetry, which does not rely exclusively on the comparison of spectral amplitudes to those obtained at thermal equilibrium. This phenomenon has also been noted at millikelvin temperatures [21].

Our analytical lineshape model was fitted to the measured NMR data using a Bayesian statistical method [22–24]. 95% confidence-level intervals were computed in a Markov-chain Monte Carlo procedure [25,23,26] by minimizing the sum of square-deviations ${\sum }_i{w}_i{(s_i^{\mathrm{mod}}-s_i^{\exp })}^2$ between the model (s_i^mod) and experimental $\left(s_i^{\exp }\right)$ FID points. The fitting weights $w_i\propto {\left(s_i^{\mathrm{rms}}\right)}^{-2}$, representing the noise $s_i^{\mathrm{rms}}$ due to random rf-pulse ring-down at time-points t_i, were independently determined from the low-polarization spectra to fit w_i = (1 + α exp(–t_i/τ_noise))^–1, with α = 200 and τ_noise = 2 μs. Including the weights w_i into the fit deemphasizes the initial noisy data without discarding useful information at the rf ring-down's tail.

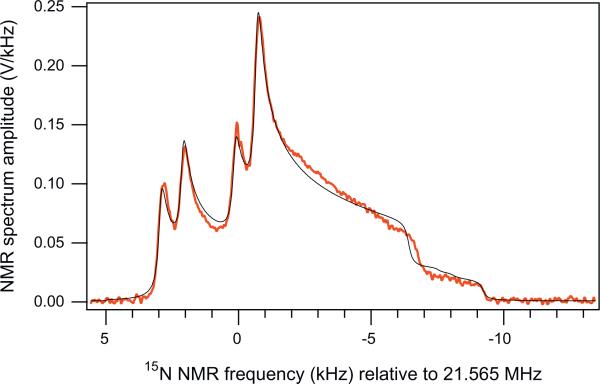
Fig. 4 shows the NMR spectrum along with the model line shape based on the best-fit parameters listed in Table 1. The J-coupling was set to the literature value –8.7 Hz [14,18]. Our isotropic chemical shift difference $({\delta }_2^{\mathrm{iso}}-{\delta }_1^{\mathrm{iso}})$ is in reasonable agreement with room-temperature data: 75 ppm in nematic-phase ¹⁵N₂O [18] and 82.3 ppm in isotropic solution [12]. Our chemical shift anisotropies are also consistent with the nematic-phase data [18]: ${\delta }_1^{\mathrm{ani}}=-246\pm 10\mathrm{ppm}$ and ${\delta }_2^{\mathrm{ani}}=-341\pm 6.7\mathrm{ppm}$ (using ${\delta }_j^{\mathrm{ani}}=\frac{2}{3}({\delta }_{\parallel }-{\delta }_{\perp })$). The best-fit dipolar coupling b₁₂/(2π) = –840 Hz corresponds to a N–N bond length r₁₂ = 113.7 pm, in reasonable agreement with 112.6 pm (¹⁴N₂O) and 118.6 pm (¹⁵N¹⁴NO) [27].

Fig. 4.

Comparison of the experimental spectrum (thick red curve), corresponding to the maxim-polarization data point of Fig. 2B, and the best-fit line-shape model based on Eqs. (4)–(8) and a Bayesian fitting method described in the text (thin black line). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 1.

Best-fit values and 95% confidence intervals of the essential free-fit parameters for the spectrum shown in Fig. 4.

Parameter	Unit	Value	Parameter	Unit	Value
$({\delta }_2^{\mathrm{iso}}-{\delta }_1^{\mathrm{iso}})$	ppm	74 ± 3.5	p	%	10.2 ± 2
${\delta }_1^{\mathrm{ani}}$	ppm	–223 ± 4	b12/(2π)	Hz	–840 ± 10
${\delta }_2^{\mathrm{ani}}$	ppm	–331 ± 4	λ	Hz	234 ± 10

5. Conclusion

In summary, we have achieved ¹⁵N₂O hyperpolarization by DNP in frozen mixtures with a trityl radical and an organic solvent. Annealing produces an order-of-magnitude narrowing of the NMR spectrum, suggesting the formation of pure ¹⁵N₂O clusters. We have also developed analytical tools for measuring the magnitude and sign of the polarization directly from the ¹⁵N NMR spectrum. The highest observed polarization was (10.2 ± 2:2)%, still growing after 37 h of DNP. Faster polarization build-up rates may be achievable by combining DNP with ¹H—¹⁵N cross-polarization [4,6]. We are now investigating how to convert the hyperpolarized solid ¹⁵N₂O into a room-temperature solution, while retaining the ¹⁵N polarization.